Abstract
Showing whether the longest-edge (LE) bisection of tetrahedra meshes degenerates the stability condition or not is still an open problem. Some reasons, in part, are due to the cost for achieving the computation of similarity classes of millions of tetrahedra. We prove the existence of tetrahedra where the LE bisection introduces, at most, 37 similarity classes. This family of new tetrahedra was roughly pointed out by Adler in 1983. However, as far as we know, there has been no evidence confirming its existence. We also introduce a new data structure and algorithm for computing the number of similarity tetrahedral classes based on integer arithmetic, storing only the square of edges. The algorithm lets us perform compact and efficient high-level similarity class computations with a cost that is only dependent on the number of similarity classes.
1. Introduction
The simplest method to subdivide tetrahedral meshes is probably the bisection method. In many areas of mathematics and engineering, this partitioning method is very useful for constructing discretized volumes of domain spaces, for example, in the finite element method. Refinement algorithms based on the longest edge (LE bisection) have been pursued by Rivara, Plaza, Carey, and Korotov and coworkers [1,2,3]. The stability condition means that the tetrahedra generated during the refinement process must not degenerate, i.e., the interior angles of all elements must be bounded uniformly away from zero.
In 2D, a consequence of the stability of the LE bisection algorithm is the self-improvement of quality. This scheme refinement improves interior angles [4], and this improvement has been studied in depth in [5]. In practice, the self-improvement confirms that the meshes obtained tend to be improved in the following sense: the minimum interior angle of triangles appearing in the refinement of meshes is bound from below. Unfortunately, in higher dimensions, it is still an open problem, in particular for the three-dimensional case [4,6,7,8,9,10]. Some works have addressed the so-called numerical regularity [1,2,3,10], although mathematical proofs have not been given yet.
It should be noted that for numerical studies trying to prove the behavior of minimum angles, in general, it is considered special targeted initial tetrahedral shapes. In previous works [1,2,3,10], the starting idea focuses on some prescribed initial meshes, usually a single well-defined initial tetrahedron. Experimental studies have provided restricted conclusions on LE bisection due to the high cost of achieving a large number of elements (less than a million) and the numerical error in relation to minimum angles or quality shapes.
As a methodology to study the stability of refinement methods, many authors concentrate on the number of similarity tetrahedral classes generated in subsequent refinement steps. Two tetrahedra are in the same equivalence class if one can be transformed into the other by translation, uniform scaling, etc. Thus, any pair of tetrahedra in the same equivalence class is similar to each other after any affine transformation. A finite number of similarity classes is necessary for stability. Moreover, for practical reasons, it is often desirable that the number of similarity classes is not only finite but also as small as possible.
In 1983, A. Adler in [11] set the following statement: “We have a proof of the finite family conjecture for certain classes of tetrahedral meshes”. Adler mentioned that if a tetrahedron is nearly equilateral and the second-largest edge is opposite to the longest edge, then new elements generated by the LE bisection will fall into ≤37 similarity classes. However, he did not give any rigorous definition of “nearly equilateral”, although he remarked on the difficulty of overcoming the definition. However, Adler offered the following significant idea: a nearly equilateral tetrahedron is satisfied if all its edge lengths are within 5% of each other. As far as we know, no other study has addressed the Adler conjecture.
The main contribution of this paper is to confirm that a special family of tetrahedra exists where the LE bisection introduces, at most, 37 similarity classes. We continue the work of Adler [11] and prove the existence of a family of tetrahedra where their similarity classes fall into ≤37. We confirm that there is such a family of tetrahedra and give some examples together with an algorithm as proof.
We also contribute with a data structure for representing tetrahedra based on square-of-edge lengths that let us perform compact and efficient high-level computations that reach up to 40 levels (up to 2^40 tetrahedra) of refinements in a reasonable time. In addition to the Adler study, experiments are provided for studying five other types of well-known shape tetrahedra, and we find new evidence for the stability of the LE bisection.
2. Computing Exact Number of Similarity Classes in the Longest Edge Bisection of Tetrahedra
Let T be an arbitrary (non-degenerate) tetrahedron, as depicted in Figure 1, where its six edge lengths are a, b, c, d, e, and f. A common representation of T is given by a sextuple of positive real numbers, each one representing the edge lengths, as seen, for example, in [12]. In this way, only the edge lengths of the tetrahedron are considered, no matter its position or orientation.
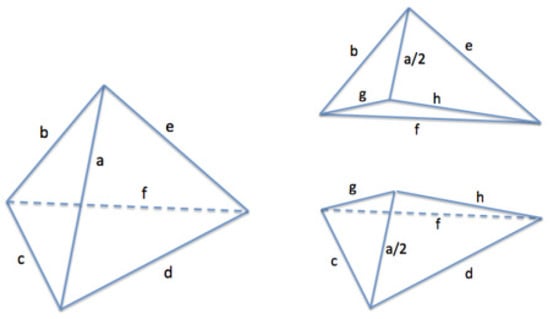
Figure 1.
(Left) Tetrahedron with edges a, b, c, d, e, and f. (Right) Two new tetrahedra that result from the bisection through edge a.
The order of edges in the array is important as different combinations may represent different tetrahedra. Then, to be consistent, we set the following order in the array representation:
- The first position in the array can be any one of the six edges; let us fix, for instance, edge a.
- Second edge b is any edge connected to a.
- Third edge c is the edge closing the triangle abc.
- Fourth edge d is the one connecting a and c.
- Fifth edge e is the edge closing triangle ade.
- Sixth edge f is the last edge opposite the initial edge a.
Then, performing the bisection of a tetrahedron, T = { a, b, c, d, e, f }, through edge a leads to two new tetrahedra, as in Figure 1 (right), where the new edges g and h are:
Thus, each new tetrahedron can be represented as { a/2, b, g, h, e, f } and { a/2, g, c, d, h, f }.
In order to remove the roots in the expressions of g and h, it is more appropriate to store not the edge lengths but the square of lengths. In this manner, the initial tetrahedron T becomes { a2, b2, c2, d2, e2, f2 } = { A, B, C, D, E, F }, and the new tetrahedra become { A/4, B, G, H, E, F } and { A/4, G, C, D, H, F }, where G = g2 and H = h2.
We can also remove all the fractions from these values, adding a seventh value in the array, n acting as a scaling factor, and considering that the six square lengths are divided by 2n. Therefore, the final proposed representation for tetrahedron T is {A, B, C, D, E, F, n }, where the edge lengths are
a2 = A/2n
b2 = B/2n
c2 = C/2n
d2 = D/2n
e2 = E/2n
f2 = F/2n
Thus, each new tetrahedron can be represented as
It is easy to see that
Proposition 1.
The longest-edge bisection of a given tetrahedron, T = [A, B, C, D, E, F, n], yields two new tetrahedra, T1 and T2, represented as:
T11 = [ A, 4B, 2B + 2C − A, 2E + 2D − A, 4E, 4F, n + 2]
T12 = [ A, 2B + 2C − A, 4C, 4D, 2E + 2D − A, 4F, n + 2]
Efficiency of Integer Arithmetic
Proposition 2.
The longest-edge bisection applied to a given tetrahedron, T = [A, B, C, D, E, F, n], where its seven values are integer values, yields two new tetrahedra, as depicted in Proposition 1, which are formed from integer values too.
Let us note that the last proposition guarantees that only integer arithmetic is needed for the whole process of LE subdivision. Using integer arithmetic provides three main benefits:
- Basic arithmetic operations are much faster than floating-point operations.
- Integer comparisons are exact, unlike floating-point comparisons that can produce inexact results due to accumulated errors. This fact is crucial for the computing of similarity classes, where we must match tetrahedra exactly if two tetrahedrons generated in different levels of the bisection are to be in the same class.
- There are no accumulated errors produced in the iterative process because only basic arithmetic operations are involved in every iteration. For instance, in each iteration, the square of the main edge of the tetrahedron is divided by 4, so after 100 recursive subdivision iterations, the initial value will have been divided by 2200. There is absolutely no error after all these iterations.
If we want to represent tetrahedra with coordinate values with a large number of decimal digits or even irrational coordinates, we will obviously have small precision errors due to the chosen numeric type in the computer. However, these errors are more similar to our representation than those obtained using double precision floating data types. A traditional double-precision floating point of 64 bits has an accuracy of 16 significant decimal digits approximately. This is very similar when using our representation with long integers of 64 bits, depending on the value we choose for our scale factor, n. For instance, let us consider an edge where its square length is a2 = 1/√2 ≈ 0.707106781186547. In this case, we can use n = 50 and A = round(a22n) = 796,131,459,065,722 and still keep a similar accuracy, representing the square length of the edge by A/2n.
3. Longest-Edge Bisection of a Single Tetrahedron
Given a tetrahedron, T, we have up to 24 different combinations for the array, depending on which edge we take as first and second positions. We must choose only one of the 24 possibilities and then use it as the pattern in the normalized form. It should be noted that comparing the shape of two tetrahedra to determine if they fall in the same similarity class will be straightforward as we are comparing integer length values and not coordinating the positions of the elements. This means that to compare the shape of two tetrahedra, we need to first obtain the normalized representation for both and then compare the array values to each other. Algorithm 1 shows the steps to convert a tetrahedron [A, B, C, D, E, F, n] into its normalized form.
| Algorithm 1 Normalize Tetrahedron (T) |
| Input: Tetrahedron T = [A, B, C, D, E, F, n] Output: A new tetrahedron in normalized form
|
Note that in the previous algorithm, we have as input an arbitrary tetrahedron represented by its edge-based data structure. Additionally, at the end, we get a new representation of it, where the normalization imposes a unique form for its representation. From now on, the edge data structure for representing tetrahedra will include the array described before and the normalization process depicted in this algorithm. Figure 2 shows in detail the trace of this algorithm for a sample tetrahedron.
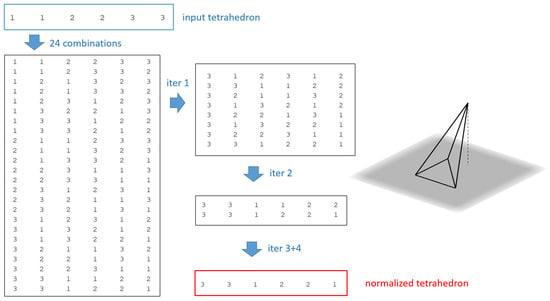
Figure 2.
Algorithm trace for the normalization of the tetrahedron T = [1, 1, 2, 2, 3, 3, 0].
It should be noted that the previous method of obtaining the normalized form of a tetrahedron ensures that the first value in the array is always the maximum edge value and, therefore, represents the longest edge in the tetrahedron. This is the reference edge used for subdivision.
Note also that, in some cases, a tetrahedron can yield more than two new subtetrahedra, depending on whether there is only one longest edge or if more than one longest edge exists. Therefore, the bisection algorithm must find these cases to apply bisections on all the edges that share the maximum value. It should be noted that it is quite important to cover all possible new shape elements arising from the LE bisection. New branches of tetrahedra refinement should be triggered through each one of the longest-edge paths. Algorithm 2 shows the steps to perform the LE bisection on a single tetrahedron using the edge-based data structure.
| Algorithm 2 Subdivide_Tetrahedron (T) |
| Input: Tetrahedron T = [A, B, C, D, E, F, n] Output: List L of new tetrahedra produced in the bisection
|
The iterative LE bisection applied to tetrahedron T is, therefore, a recursive algorithm: bisect T by its longest edges, giving a list of new tetrahedra, T1,i. Next, bisect each T1,i in the list by their longest edges, forming another list of new tetrahedra, T2,i. Continue thus, generating new lists for each level of subdivision. Thus, we may expect that the cost of computing bisections will be faster using integer operations.
4. Similarity Class Computations
We shall denote by sn the number of non-similar tetrahedra that have been generated during the first n steps of the LE bisection algorithm. The sequence {sn} for n = 0 to infinity, where s0 = 1, is non-decreasing. In many cases, we get sn < sn+1 for all n, but sometimes the sequence remains constant after several steps.
A low number of similarity classes is quite important in numerical computation, as, for example, in the Finite Element Method. One main consequence is that the construction of the stiffness matrix can be performed much faster. The element matrix can be computed only once for each similarity class of tetrahedra.
Comparing the shape of two tetrahedra, no matter their scale, is crucial for obtaining the similarity classes appearing in the LE bisection. Following the edge-based data structure introduced in Section 2, only the first six values of the tetrahedron are considered. In this way, let us define the similarity class of a tetrahedron as the array {A, B, C, D, E, F} that represents the six first values of the normalized representation.
Computing the Similarity Classes in LE Bisection
In order to examine similarity classes, many authors [3,6,7,9] use matrix mapping based on tetrahedra coordinates. This consists of, given two tetrahedra, confirming that one is the image of the other under congruency mapping. Following this idea, it is necessary to perform reflections, rotations, and uniform scaling. The problem can be viewed as checking whether two tetrahedra have the same shape. This numerical mapping may have difficulties in the computation, as the matrix computation leads to errors caused by floating-point arithmetic in the shape comparison.
It is important to compute tetrahedra classes with a reasonable fast response for high values of n. Especially when inspecting the iterative LE bisection of arbitrary shapes of tetrahedra, it is important to determine the behavior of the sequence {sn}, this is, whether we have a non-decreasing sequence or constant. For example, the sequence of the Adler tetrahedra studied in this paper is known to obtain 37 classes. At the same time, it is necessary to avoid representation errors due to computer operations, such as truncation errors.
In the present work, we provide an exact method to efficiently compute the similarity classes based on the edge-based data structure. Detecting if a new tetrahedron belongs to a similarity class already obtained is straightforward using an integer-based data structure. This consists of an integer array comparison as the six integers representing tetrahedral edges are compared to each other. Note that this single operation involves only integer values; then, the operations are faster and more accurate (no truncation errors) than using floating-point arithmetic.
The subdivision algorithm to compute similarity classes proposed here is an iterative process. In every subdivision step, we have as input a set of normalized tetrahedra (generated in the previous step), and all of them will be subdivided following the longest edge. After that, all new tetrahedra are normalized and compared with the rest of the similarity classes already obtained in previous subdivision levels. Algorithm 3 shows the steps to find all the similarity classes of a tetrahedron.
| Algorithm 3 Similarity_Classes (T) |
| Input: Tetrahedron T = [A, B, C, D, E, F, n] Output: List of similarity classes for T
|
5. Exact Number of Similarity Classes in the Adler Tetrahedra
We recall here the idea pointed out by Adler in [11], affirming the existence of nearly equilateral tetrahedra that produce, at most, 37 similarity classes in the iterated LE bisection. This allows us to theorize the existence of a family of tetrahedra where all its elements will show the same behavior as the Adler element; that is, they will generate up to 37 similarity classes in the LE bisection subdivision.
We use the edge data structure introduced in Section 2, which allows the use of integer arithmetic at a reasonable computational cost. An experimental study is conducted as follows:
- Start with an initial tetrahedron shape, given by its four vertices
- Convert to an array of a square-edge-based data structure of the form {A, B, C, D, E, F, n}
- Launch Similarity_Classes algorithm, iterating through a number of levels of refinement, and compute in each level the number of similarity classes.
In addition, we are also interested in inspecting:
- (i)
- Quality measures for each tetrahedron, [9] , to obtain min().
- (ii)
- The time consumed.
- (iii)
- Maximum edge lengths in each refinement level.
Here, we recall Adler’s conjecture by considering tetrahedra with all edge lengths within 5% of each other. We set up six nearly equilateral tetrahedra, T1, T2, T3, T4, T5, and T6, where all their edge lengths are within 5% of each other. Table 1 shows the four (x,y,z) coordinates of these tetrahedra and the seven edge-based values of our proposed representation.

Table 1.
Definition of the tetrahedra in TEST 1, T = [A, B, C, D, E, F, n].
Figure 3 shows the results for 40 iterations of the bisection process. Note that 37 similarity classes are obtained at the end of the 7th iteration for each tetrahedron considered, T1, T2, T3, T4, T5, and T6 (see Figure 3 (upper right)). After Level 7, no new classes are found, and then the 37 classes remain constant, as seen in Table 2. This is in concordance with the conjecture mentioned by Adler in [11], and, therefore, we confirm the existence of a family of prescribed tetrahedra with 37 similarity classes when applying the LE bisection. Several other examples for different tetrahedra with edge lengths within 5% (nearly-equilateral), not shown here, were tested and revealed the same results.
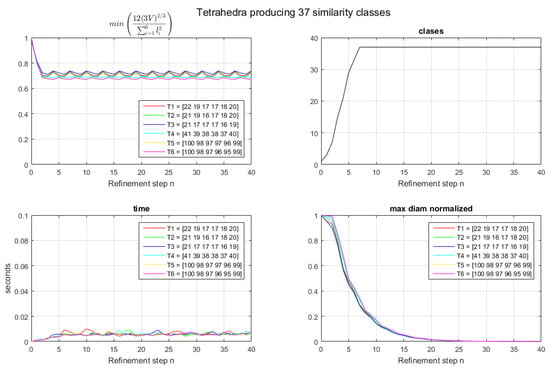
Figure 3.
TEST 1 results for (top left) min(); (top right) number of similarity classes; (bottom left); time consumed; and (bottom right) maximum edge length.

Table 2.
Number of total similarity classes obtained during several iterations of LE bisection to the tetrahedra in Table 1.
The quality measure min() in Figure 3 (upper left) shows that after the refinement of Level 3, we also get certain stabilization, where the worst value is never below 0.6706, as seen in Table 3. The consumed time, in seconds, is provided in Figure 3 (lower left). In view of this, we infer that the cost of the algorithm to obtain the similarity classes does not depend on the number of elements. As clearly seen in the figure, the cost is always below a fixed time of 0.02 s.

Table 3.
Quality measure values, min(), obtained during the first 20 iterations of LE bisection to the tetrahedra in Table 1.
Note that finally, as expected, the max diameter (maximum length of the tetrahedron) in each level decreases when approaching the horizontal axis x (see Figure 3, lower right).
In order to test the algorithms and data structure on different shapes, we study, in the following section, other non-Adler tetrahedra.
LE Bisection of Other Tetrahedra
Usually, in the literature, we find the following tetrahedral shapes—Regular, Cap, Wedge, Needle, and Sliver—as testing elements for different benchmarking or method comparisons. For these tetrahedra, numerical evidence has been shown for non-degeneracy [1,2,3,10]. Here, we corroborate, in Test 2, the same results after a high number (40 levels) of refinements, guaranteeing exact arithmetic in the computation. Moreover, we provide the exact similarity classes appearing in the LE bisection for those test cases. Table 4 shows the coordinates of these tetrahedra and the seven edge-based values of our proposed representation.

Table 4.
Definition of the tetrahedra in TEST 2, T = [A, B, C, D, E, F, n].
Figure 4 shows the results of 40 iterations of the LE bisection process. Note that the number of similarity classes increases for all the studied tetrahedra in every iteration (Figure 4, upper right), especially for the Needle tetrahedron, which produced more than one million similarity classes after 39 iterations in the experiment and an important curve increase in the number of classes from the 15th refinement step (Figure 4, upper right). Table 5 shows the number of classes for every tetrahedron and, for brevity, only shows refinement levels 1–20. Quality measures are shown in Figure 4 (upper left). Needle and Wedge tetrahedra show the worst quality, below 0.2, during all iterations. On the other hand, Cap, Sliver, and Regular tetrahedra keep quality levels higher than 0.32. The detailed results of min(ϑ) are presented in Table 6. Note that the time consumed of Needle is notably higher compared to the others, which is in concordance with the high number of similarity classes appearing during the LE bisection (Figure 4, lower left). Finally, as expected, the maximum length (diameter) per level decreases when approaching the horizontal axis x, as seen in Figure 4 (lower right).
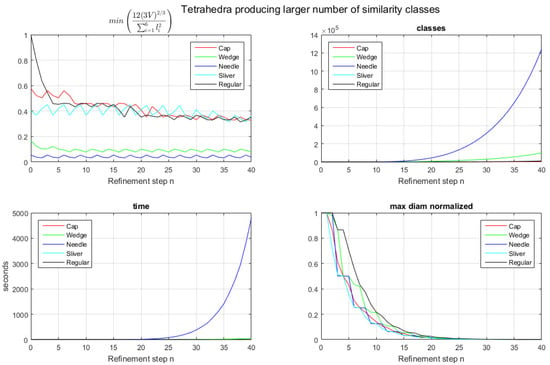
Figure 4.
TEST 2 results for (top left) min , (top right) number of similarity classes, (bottom left) time consumed, and (bottom right) max diameter.

Table 5.
Number of similarity classes obtained during 20 iterations of LE bisection from the tetrahedra in Table 4.

Table 6.
Quality measure values, min(), obtained during 20 iterations of LE bisection to the tetrahedra in Table 4.
6. Conclusions
We have introduced a data structure that lets us efficiently compute the similarity classes of tetrahedra shapes when applying LE bisection subdivision. This data structure facilitates the computation in integer arithmetic, for example, in order to compare the shape of two tetrahedra, no matter their scale. To put this in practice and validate both the new edge-based data structure and the algorithm, we recalled an open question formulated by Adler in [11], who argued for the existence of a family of tetrahedra, only mentioned but not studied in his paper, that may have a number of similarity classes ≤37. We prove that Adler’s assumption of nearly equilateral tetrahedra was right by providing a set of six different tetrahedra with exactly 37 similarity classes when applying LE bisections iteratively. We have also provided more numerical tests, giving evidence of the stability condition for the family of tetrahedra considered.
For practical reasons, getting a low number of similarity classes is quite desirable, as in the finite element method, where the construction of the stiffness matrix can be performed much faster, and the element matrix can be computed only once for each similarity class.
As future research, we may argue that new families of tetrahedra with a finite low number of similarity classes exist. Together with Adler’s nearly equilateral tetrahedra, other possible new families can be found, perhaps by extending the original definition of “nearly equilateral”. It would also be interesting to see if there is some connection with the Liu–Joe family of tetrahedra that produce no more than 92 classes, already proven in [8].
Author Contributions
Conceptualization, J.P.S., A.T., T.M.; methodology, J.P.S., A.T., T.M.; software A.T.; validation, J.P.S., A.T., T.M.; formal analysis, J.P.S., A.T.; investigation, J.P.S., A.T.; resources, J.P.S., A.T., T.M.; data curation, J.P.S., A.T.; writing—original draft preparation, J.P.S., A.T., T.M.; writing—review and editing, J.P.S., A.T., T.M.; visualization, J.P.S., A.T., T.M.; supervision, J.P.S., A.T., T.M.; project administration, J.P.S., A.T., T.M.; funding acquisition, J.P.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rivara, M.C.; Levin, C. A 3D refinement algorithm suitable for adaptive and multigrid techniques. Commun. Appl. Numer. Methods 1992, 8, 281–290. [Google Scholar] [CrossRef]
- Plaza, Á.; Padrón, M.A.; Suárez, J.P.; Falcón, S. The 8-tetrahedra longest-edge partition of right-type tetrahedra. Finite Elem. Anal. Des. 2004, 41, 253–265. [Google Scholar] [CrossRef][Green Version]
- Hannukainen, A.; Korotov, S.; Křížek, M. On numerical regularity of the face-to-face longest-edge bisection algorithm for tetrahedral partitions. Sci. Comput. Program. 2014, 90, 34–41. [Google Scholar] [CrossRef]
- Bern, M.; Eppstein, D. Mesh generation and optimal triangulation. In Computing in Euclidean Geometry; Du, D.-Z., Hwang, F.K., Eds.; Lecture Notes Series on Computing; World Scientific: Singapore, 1992; Volume 1, pp. 23–90. [Google Scholar]
- Plaza, Á.; Suárez, J.P.; Padrón, M.A.; Falcón, S.; Amieiro, D. Mesh quality improvement and other properties in the four-triangles longest-edge partition. Comput. Aided Geom. Des. 2004, 21, 353–369. [Google Scholar] [CrossRef]
- Bey, J. Simplicial grid refinement: On Freudenthal’s algorithm and the optimal number of congruence classes. Numer. Math. 2000, 85, 1–29. [Google Scholar] [CrossRef]
- Maubach, J.M. Local bisection refinement for N-simplicial grids generated by reflection. SIAM J. Sci. Comput. 1995, 16, 210–227. [Google Scholar] [CrossRef]
- Liu, A.; Joe, B. On the shape of tetrahedra from bisection. Math. Comput. 1994, 63, 141–154. [Google Scholar] [CrossRef]
- Aparicio, G.; Casado, L.G.; Hendrix, E.M.T.; Boglarka, G.-T.; García, I. On the minimum number of simplex shapes in longest edge bisection refinement of a regular n-simplex. Informatica 2015, 26, 17–32. [Google Scholar] [CrossRef]
- Padrón, M.A.; Suárez, J.P.; Plaza, Á.L. A comparative study between some bisection based partitions in 3D. Appl. Numer. Math. 2005, 55, 357–367. [Google Scholar] [CrossRef]
- Adler, A. On the bisection method for triangles. Math. Comp. 1983, 40, 571–574. [Google Scholar] [CrossRef]
- Wirth, K.; Dreiding, A.S. Edge lengths determining tetrahedrons. Elem. Math. 2009, 64, 160–170. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).