Global and Local Behavior of the System of Piecewise Linear Difference Equations x_n+1 = |x_n| − y_n − b and y_n+1 = x_n − |y_n| + 1 Where b ≥ 4

Abstract

The aim of this article is to study the system of piecewise linear difference equations $x_{n+1}=\left|x_n\right|-y_n-b$ and $y_{n+1}=x_n-\left|y_n\right|+1$ where $n\ge 0$. A global behavior for $b=4$ shows that all solutions become the equilibrium point. For a large value of $|x_0|$ and $|y_0|$, we can prove that (i) if $b=5$, then the solution becomes the equilibrium point and (ii) if $b\ge 6$, then the solution becomes the periodic solution of prime period 5.

1. Introduction

The first order system of the piecewise difference equation of the form

$$x_{n+1}=|x_n|-a{y}_n-b\mathrm{and}{y}_{n+1}=x_n-c\left|y_n\right|+d$$

(1)

for $n\ge 0$ with a given initial condition $(x_0,y_0)$ has been considered by several researchers. System (1) is actually motivated by the Lozi map [1,2] which is the system given by $x_{n+1}=-a\left|x_n\right|+y_n+1$ and $y_{n+1}=b{x}_n$, where $a,b\in \mathbb{R}$ and a system $x_{n+1}=\left|x_n\right|-y_n+1$ and $y_{n+1}=x_n$ given in [3,4] or, equivalently, the Devaney’s Gingerbread man map $x_{n+1}=\left|x_n\right|-x_{n-1}+1$ studied in [5]. It is known that if the sequences ${\left(x_n\right)}_{n=0}^{\infty }$ and ${\left(y_n\right)}_{n=0}^{\infty }$ satisfy (1) and the given initial conditions for all $n\ge 0$, then ${(x_n,y_n)}_{n=0}^{\infty }$ is called a solution of (1). Let ${(x_n,y_n)}_{n=0}^{\infty }$ be the solutions of (1) with a given initial condition $(x_0,y_0)$. If there exist real numbers $\overline{x}$ and $\overline{y}$ and an integer N such that $(x_n,y_n)=(\overline{x},\overline{y})$ for all $n\ge N$, then we say that the solution ${(x_n,y_n)}_{n=0}^{\infty }$ eventually becomes the equilibrium point $(\overline{x},\overline{y})$ of (1). On the other hand, if p is the smallest positive integer such that $(x_{n+p},y_{n+p})=(x_n,y_n)$ for all $n\ge N$, then we say that the solution ${(x_n,y_n)}_{n=0}^{\infty }$ eventually becomes the solution of prime period p of (1). For more details about the system of difference equations and their solutions, one may see [6,7]. Actually, to establish the stability of the system of difference equations involves derivatives of a function. However, the system (1) contains absolute value which is not differentiable. Thus, to study the behavior of the solution of (1), one needs to consider several regions of initial conditions and gather the information to obtain the results.

In 2010, Tikjha et al. [8] considered (1) when $a=b=c=1$ and $d=0$. They proved that, for a given initial condition $(x_0,y_0)\in {\mathbb{R}}^2$, the solution of (1) either eventually becomes the solution of prime period 5 or the equilibrium point of (1). For $a=b=1$, $c=-1$ and $d=0$, Grove et al. [9] showed that for a given initial condition $(x_0,y_0)\in {\mathbb{R}}^2$, the solution of (1) is either (from the beginning) the equilibrium point or eventually becomes the solution of prime period 3 of (1). In the doctoral dissertation written by Lapierre [10], he studied some properties of solutions for 81 possible forms of (1) where $a,b,c,d\in \{-1,0,1\}$. Kongtan and Tikjha [11] let $a=c=d=1$ and $b=2$, $x_0=0$ and $y_0\in \left(\frac{1}{2},\infty \right)$ and proved that the solution of (1) eventually becomes the solution of prime period 4 of (1). With $a=1$, $c=-1$, $d=0$ and $b\in (0,\infty )$, Tikjha et al. [12] showed that the solution of (1) either eventually becomes the solution of prime period 3 or the equilibrium point of (1) for all initial conditions $(x_0,y_0)\in {\mathbb{R}}^2$. In 2017, Tikjha et al. [13] considered the case that $a=c=1$, b and d in $(-\infty ,0)$ and proved that the solution of (1) eventually becomes the equilibrium point of (1) for all initial conditions $(x_0,y_0)\in {\mathbb{R}}^2$ within 6 iterations. In the same year, Tikjha [14] wrote a manuscript in Thai where, if $a=c=d=1$, $b=2$, $x_0=0$ and $y_0\in \left(0,\frac{1}{2}\right)$, then the solution of (1) eventually becomes the solution of prime period 4 of (1). Recently, Tikjha and Piasu [15] considered $a=c=d=1$ and $b=3$ with initial condition $(x_0,y_0)$ being in a specific region in the first quadrant and showed that the solution of (1) either eventually becomes the equilibrium point or the solution of prime period 4. Tikjha and Lapaierre [16] also studied (1) with $a=b=1$ and $c=d=-1$ and the initial condition $(x_0,y_0)$ is an element in the closed second or fourth quadrant. They proved that the solution of (1) either eventually becomes the solution of prime period 3 or 4. In addition, Tikjha et al. [17] proved that, if $a=c=d=1$, $b\in \{2,3\}$ and $y_0=0$, then under some conditions on $x_0$ the solution of (1) eventually becomes the solution of prime period 4.

In this paper, we let $a=c=d=1$ and $b\ge 4$. That is, we consider the system

$$x_{n+1}=|x_n|-y_n-b\mathrm{and}{y}_{n+1}=x_n-\left|y_n\right|+1.$$

(2)

Let us first establish the lemma about the equilibrium of (2).

Lemma 1.

Let $b\ge 3$.

(i)

The equilibrium point of (2) is $(-1,-b+2)$.

(ii)

Let ${(x_n,y_n)}_{n=0}^{\infty }$ be the solution of (2). Assume that there exists a positive integer N such that $y_N=-x_N-b+1\le 0$ and $x_N\le 0$. Then, $(x_n,y_n)=(-1,-b+2)$ for all $n>N$.

Proof. 

(i) By considering four cases of $\left|x\right|$ and $\left|y\right|$, we can solve the system of equations $x=\left|x\right|-y-b$ and $y=x-\left|y\right|+1$ and the only case that gives the solution is when x and y are negative, which is $(x,y)=(-1,-b+2)$.

(ii) Assume that there exists a positive integer N such that $y_N=-x_N-b+1\le 0$ and $x_N\le 0$. Then,

$$\begin{array}{cc}\hfill x_{N+1}& =|x_N|-y_N-b=-x_N-(-x_N-b+1)-b=-1\hfill \\ \hfill y_{N+1}& =x_N-\left|y_N\right|+1=x_N+(-x_N-b+1)+1=-b+2.\hfill \end{array}$$

Since $b\ge 4$, $-b+2<0$. Thus,

$$\begin{array}{cc}\hfill x_{N+2}& =|x_{N+1}|-y_{N+1}-b=1-(-b+2)-b=-1\hfill \\ \hfill y_{N+2}& =x_{N+1}-\left|y_{N+1}\right|+1=-1+(-b+2)+1=-b+2.\hfill \end{array}$$

Therefore, by mathematical induction, we have $(x_n,y_n)=(-1,-b+2)$ for all $n>N$. □

In Section 2 of this article, a global behavior for the case $b=4$ is proved. We can conclude that all solutions eventually become the equilibrium point $(-1,-2)$. Local behavior for $b\ge 5$ with large values of $|x_0|$ and $|y_0|$ is studied in Section 3. It is revealed that, locally, all solutions of Equation (2) for $b=5$ eventually become the equilibrium point. It can be seen that for $b\ge 6$, some solutions have a chance to becomes periodic. Finally, a conclusion and discussion about our work and our conjecture are provided in the last section.

2. Global Behavior for $\mathit{b}=\mathbf{4}$

In this section, we investigate the global behavior where $b=4$. The first four lemmas deal with the case when $x_0=0$ or $y_0=0$.

Lemma 2.

If $x_0\ge 0$ and $y_0=0$, then the solution ${(x_n,y_n)}_{n=0}^{\infty }$ of (2) eventually becomes the equilibrium point $(-1,-2)$ of (2).

Proof. 

Let $x_0\ge 0$ and $y_0=0$.

Case 1 $x_0\in \left[0,\frac{1}{8}\right)$. We have

$$\begin{array}{cccc}\hfill x_1& =|x_0|-y_0-4=x_0-4<0,\hfill & \hfill y_1& =x_0-\left|y_0\right|+1=x_0+1\ge 0\hfill \\ \hfill x_2& =|x_1|-y_1-4=-2x_0-1<0,\hfill & \hfill y_2& =x_1-\left|y_1\right|+1=-4\hfill \\ \hfill x_3& =|x_2|-y_2-4=2x_0+1>0,\hfill & \hfill y_3& =x_2-\left|y_2\right|+1=-2x_0-4<0\hfill \\ \hfill x_4& =|x_3|-y_3-4=4x_0+1>0,\hfill & \hfill y_4& =x_3-\left|y_3\right|+1=-2\hfill \\ \hfill x_5& =|x_4|-y_4-4=4x_0-1<0,\hfill & \hfill y_5& =x_4-\left|y_4\right|+1=4x_0\ge 0\hfill \\ \hfill x_6& =|x_5|-y_5-4=-8x_0-3<0,\hfill & \hfill y_6& =x_5-\left|y_5\right|+1=0\hfill \\ \hfill x_7& =|x_6|-y_6-4=8x_0-1<0,\hfill & \hfill y_7& =x_6-\left|y_6\right|+1=-8x_0-2=-x_7-4+1<0.\hfill \end{array}$$

By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 8$.

Case 2 $x_0\in \left[\frac{1}{8},\frac{3}{16}\right)$. We have the same $(x_1,y_1)-(x_7,y_7)$ as in Case 1, while, $x_7\ge 0$ and

$$\begin{array}{cccc}\hfill x_8& =|x_7|-y_7-4=16x_0-3<0,\hfill & \hfill y_8& =x_7-\left|y_7\right|+1=-2\hfill \\ \hfill x_9& =|x_8|-y_8-4=-16x_0+1<0,\hfill & \hfill y_9& =x_8-\left|y_8\right|+1=-16x_0-4=-x_9-4+1<0.\hfill \end{array}$$

By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 10$.

Case 3 $x_0\in \left[\frac{3}{16},\frac{1}{4}\right)$. We have the same $(x_1,y_1)-(x_8,y_8)$ as in Case 2, while

$$\begin{array}{cccc}\hfill x_9& =|x_8|-y_8-4=16x_0-5<0,\hfill & \hfill y_9& =x_8-\left|y_8\right|+1=16x_0-4<0\hfill \\ \hfill x_{10}& =|x_9|-y_9-4=-32x_0+5<0,\hfill & \hfill y_{10}& =x_9-\left|y_9\right|+1=32x_0-8=-x_{10}-4+1<0.\hfill \end{array}$$

By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 11$.

Case 4 $x_0\in \left[\frac{1}{4},1\right]$. Then, $x_5\ge 0$. We have the same $(x_1,y_1)-(x_5,y_5)$ as in Case 1, while

$$\begin{array}{cccc}\hfill x_6& =|x_5|-y_5-4=-5,\hfill & \hfill y_6& =x_5-\left|y_5\right|+1=0.\hfill \end{array}$$

Direct computation gives $x_{10}=\left|x_9\right|-y_9-4=-3<0$ and $y_{10}=x_9-\left|y_9\right|+1=-x_{10}-4+1=0$. By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 11$.

Case 5 $x_0\in (1,4)$. We have

$$\begin{array}{cccc}\hfill x_1& =|x_0|-y_0-4=x_0-4<0,\hfill & \hfill y_1& =x_0-\left|y_0\right|+1=x_0+1>0\hfill \\ \hfill x_2& =|x_1|-y_1-4=-2x_0-1<0,\hfill & \hfill y_2& =x_1-\left|y_1\right|+1=-4\hfill \\ \hfill x_3& =|x_2|-y_2-4=2x_0+1>0,\hfill & \hfill y_3& =x_2-\left|y_2\right|+1=-2x_0-4<0\hfill \\ \hfill x_4& =|x_3|-y_3-4=4x_0+1>0,\hfill & \hfill y_4& =x_3-\left|y_3\right|+1=-2\hfill \\ \hfill x_5& =|x_4|-y_4-4=4x_0-1>0,\hfill & \hfill y_5& =x_4-\left|y_4\right|+1=4x_0>0\hfill \\ \hfill x_6& =|x_5|-y_5-4=-5,\hfill & \hfill y_6& =x_5-\left|y_5\right|+1=0.\hfill \end{array}$$

Similar to Case 4, we can conclude that $(x_n,y_n)=(-1,-2)$ for all $n\ge 11$.

Case 6 $x_0\in [4,\infty )$. Then, $x_1\ge 0$. We have the same $(x_1,y_1)$ as in Case 5, while $x_2=\left|x_1\right|-y_1-4=-9$ and $y_2=x_1-\left|y_1\right|+1=-4$. By direct computation, we can conclude that $(x_n,y_n)=(-1,-2)$ for all $n\ge 11$. □

Lemma 3.

If $x_0=0$ and $y_0\ge 0$, then the solution ${(x_n,y_n)}_{n=0}^{\infty }$ of (2) eventually becomes the equilibrium point $(-1,-2)$ of (2).

Proof. 

By separate cases as in Lemma 2, we can conclude the behavior of the solution in

Table 1. Cases for $x_0=0$ and $y_0\ge 0$.

If ${\mathit{y}}_0\in \mathit{A}$,	Then $({\mathit{x}}_{\mathit{n}},{\mathit{y}}_{\mathit{n}})=(-1,-2)$ for All $\mathit{n}\ge \mathit{N}$
$A=\left(\frac{1}{4},\frac{1}{2}\right)$; $\left[\frac{1}{2},1\right]$	$N=6$
$A=\left[0,\frac{1}{4}\right]$; $\left(1,\frac{9}{8}\right)$	$N=7$
$A=\left[\frac{9}{8},\frac{19}{16}\right)$	$N=9$
$A=\left[\frac{19}{16},\frac{5}{4}\right)$; $\left[\frac{5}{4},\infty \right)$	$N=10$

.

□

Lemma 4.

If $x_0=0$ and $y_0<0$, then the solution ${(x_n,y_n)}_{n=0}^{\infty }$ of (2) eventually becomes the equilibrium point $(-1,-2)$ of (2).

Proof. 

By separate cases as in Lemma 2, we can conclude the behavior of the solution in

Table 2. Cases for $x_0=0$ and $y_0<0$.

If ${\mathit{y}}_0\in \mathit{A}$,	Then $({\mathit{x}}_{\mathit{n}},{\mathit{y}}_{\mathit{n}})=(-1,-2)$ for All $\mathit{n}\ge \mathit{N}$
$A=\{-3\}$	$N=1$
$A=[-4,-1)\backslash \{-3\}$	$N=2$
$A=\left(-\frac{9}{2},-4\right)$; $\left[-1,-\frac{1}{2}\right)$	$N=4$
$A=\left(-5,-\frac{9}{2}\right]$	$N=5$
$A=\left(-\frac{21}{4},-5\right]$; $\left[-\frac{1}{2},-\frac{1}{4}\right)$	$N=6$
$A=\left[-\frac{1}{4},0\right)$	$N=7$
$A=\left(-\frac{43}{8},-\frac{21}{4}\right]$	$N=8$
$A=\left(-\infty ,-\frac{11}{2}\right]$; $\left(-\frac{11}{2},-\frac{43}{8}\right]$	$N=9$

.

□

Lemma 5.

If $x_0<0$ and $y_0=0$, then the solution ${(x_n,y_n)}_{n=0}^{\infty }$ of (2) eventually becomes the equilibrium point $(-1,-2)$ of (2).

Proof. 

By separate cases as in Lemma 2, we can conclude the behavior of the solution in

Table 3. Cases for $x_0<0$ and $y_0=0$.

If ${\mathit{x}}_0\in \mathit{A}$,	Then $({\mathit{x}}_{\mathit{n}},{\mathit{y}}_{\mathit{n}})=(-1,-2)$ for All $\mathit{n}\ge \mathit{N}$
$A=\{-3\}$	$N=1$
$A=(-4,-1)\backslash \{-3\}$	$N=2$
$A=\left(-\frac{9}{2},-4\right]$; $\left[-1,-\frac{1}{2}\right)$	$N=4$
$A=\left(-5,-\frac{9}{2}\right]$	$N=5$
$A=\left(-\frac{21}{4},-5\right]$; $\left[-\frac{1}{2},-\frac{1}{4}\right)$	$N=6$
$A=\left[-\frac{1}{4},0\right)$	$N=7$
$A=\left(-\frac{43}{8},-\frac{21}{4}\right]$	$N=8$
$A=\left(-\infty ,-\frac{11}{2}\right]$; $\left(-\frac{11}{2},-\frac{43}{8}\right]$	$N=9$

.

□

The next four lemmas consider $(x_0,y_0)$ in each quadrant. The only complicated cases are the second and the forth quadrants. For the first and the third quadrants we just show the regions considered without the detail of the proof.

Lemma 6.

If $b=4$, $x_0>0$ and $y_0>0$, then the solution ${(x_n,y_n)}_{n=0}^{\infty }$ of (2) eventually becomes the equilibrium point $(-1,-2)$ of (2).

Proof. 

If $(x,y)\in A\subset {\mathbb{R}}^{+}\times {\mathbb{R}}^{+}$, then $(x_n,y_n)=(-1,-2)$ for all $n\ge N$, where:

• $A=\left\{\right(x,y\left)\right|x-y+1>0\mathrm{and}-2x+2y-1\ge 0\}$; $\left\{\right(x,y\left)\right|-2x+2y-1<0\mathrm{and}4x-4y+1<0\}$ and $N=6$.
• $A=\{(x,y)\in {\mathbb{R}}^{+}\times {\mathbb{R}}^{+}|4x-4y+1\ge 0\mathrm{and}4x-4y<0\}$; $\left\{\right(x,y\left)\right|-8x+8y-9<0\mathrm{and}x-y+1<0\}$ and $N=7$.
• $A=\left\{\right(x,y\left)\right|4x-4y\ge 0\mathrm{and}8x-8y-1<0\}$ and $N=8$.
• $A=\left\{\right(x,y\left)\right|-16x+16y-19<0\mathrm{and}-8x+8y-9\ge 0\}$ and $N=9$.
• $A=\left\{\right(x,y\left)\right|8x-8y-1\ge 0\mathrm{and}16x-16y-3<0\}$; $\left\{\right(x,y\left)\right|-4x+4y-5<0\mathrm{and}-16x+16y-19\ge 0\}$; $\left\{\right(x,y\left)\right|-4x+4y-5\ge 0\}$ and $N=10$.
• $A=\left\{\right(x,y\left)\right|x-y-4\ge 0\}$; $\left\{\right(x,y\left)\right|16x-16y-3\ge 0\mathrm{and}4x-4y-1<0\}$; $\left\{\right(x,y\left)\right|4x-4y-1\ge 0\mathrm{and}x-y-4<0\}$ and $N=11$.

□

Lemma 7.

If $b=4$, $x_0<0$ and $y_0<0$, then the solution ${(x_n,y_n)}_{n=0}^{\infty }$ of (2) eventually becomes the equilibrium point $(-1,-2)$ of (2).

Proof. 

If $(x,y)\in A\subset {\mathbb{R}}^{-}\times {\mathbb{R}}^{-}$, then $(x_n,y_n)=(-1,-2)$ for all $n\ge N$, where:

• $A=\left\{\right(-1,-2\left)\right\}$ and $N=0$.
• $A=\left\{\right(x,y\left)\right|-x-y-4<0\mathrm{and}x+y+1<0\}\backslash \{(-1,-2)\}$ and $N=2$.
• $A=\left\{\right(x,y\left)\right|-2x-2y-9<0\mathrm{and}-x-y-4\ge 0\}$; $\left\{\right(x,y\left)\right|x+y+1\ge 0\mathrm{and}2x+2y+1<0\}$ and $N=4$.
• $A=\left\{\right(x,y\left)\right|-2x-2y-10<0\mathrm{and}-2x-2y-9\ge 0\}$ and $N=5$.
• $A=\left\{\right(x,y\left)\right|-4x-4y-21<0\mathrm{and}-2x-2y-10\ge 0\}$; $\left\{\right(x,y\left)\right|2x+2y+1\ge 0\mathrm{and}4x+4y+1<0\}$ and $N=6$.
• $A=\left\{\right(x,y\left)\right|4x+4y+1\ge 0\}$ and $N=7$.
• $A=\left\{\right(x,y\left)\right|-8x-8y-43<0\mathrm{and}-4x-4y-21\ge 0\}$ and $N=8$.
• $A=\left\{\right(x,y\left)\right|-2x-2y-11\ge 0\}$; $\left\{\right(x,y\left)\right|-2x-2y-11<0\mathrm{and}-8x-8y-43\ge 0\}$ and $N=9$.

□

Lemma 8.

If $b=4$, $x_0<0$ and $y_0>0$, then the solution ${(x_n,y_n)}_{n=0}^{\infty }$ of (2) eventually becomes the equilibrium point $(-1,-2)$ of (2).

Proof. 

Let $x_0<0$ and $y_0>0$. Then,

$$\begin{array}{cccc}\hfill x_1& =|x_0|-y_0-4=-x_0-y_0-4,\hfill & \hfill y_1& =x_0-\left|y_0\right|+1=x_0-y_0+1.\hfill \end{array}$$

Case 1 $(x_0,y_0)\in \left\{(x,y)|x-y+1\ge 0\mathrm{and}y<\frac{1}{2}\right\}$. We have $x_1<-x_0+y_0-1\le 0$ and $y_1\ge 0$ and

$$\begin{array}{cc}\hfill x_2& =|x_1|-y_1-4=2y_0-1<0,y_2=x_1-\left|y_1\right|+1=-2x_0-4<-2(x_0-y_0+1)\le 0.\hfill \end{array}$$

By using the result of Lemma 7, we obtain that

• if $(x_0,y_0)\in \left\{(x,y)|4x-4y+1\ge 0\right\}$, then

  $$\begin{array}{cc}\hfill x_6& =|x_5|-y_5-4=-8x_0+8y_0-3<-2(4x_0-4y_0+1)\le 0,\hfill \\ \hfill y_6& =x_5-\left|y_5\right|+1=8x_0-8y_0<-8y_0<0\mathrm{and}{y}_6=-x_6-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 7$;
• if $(x_0,y_0)\in \left\{(x,y)|2x-2y+1\ge 0\mathrm{and}4x-4y+1<0\right\}$, then

  $$\begin{array}{cc}\hfill x_5& =|x_4|-y_4-4=-4x_0+4y_0-3<-2(2x_0-2y_0+1)\le 0,\hfill \\ \hfill y_5& =x_4-\left|y_4\right|+1=4x_0-4y_0<0\mathrm{and}{y}_5=-x_5-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 6$;
• if $(x_0,y_0)\in \left\{(x,y)|x-y+1\ge 0,2x-2y+1<0\mathrm{and}y<\frac{1}{2}\right\}$, then

  $$\begin{array}{cc}\hfill x_3& =|x_2|-y_2-4=2x_0-2y_0+1<0,\hfill \\ \hfill y_3& =x_2-\left|y_2\right|+1=-2x_0+2y_0-4<-2(x_0-y_0+1)\le 0\mathrm{and}{y}_3=-x_3-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 4$.

Case 2 $(x_0,y_0)\in \left\{(x,y)|x-y+1\ge 0,2x+2y-1<0\mathrm{and}y\ge \frac{1}{2}\right\}$. We have the same $(x_2,y_2)$ as in Case 1, while

$$\begin{array}{cc}\hfill x_3& =|x_2|-y_2-4=2x_0+2y_0-1<0,\hfill \\ \hfill y_3& =x_2-\left|y_2\right|+1=-2x_0+2y_0-4<-2(x_0-y_0+1)\le 0.\hfill \end{array}$$

By using the result of Lemma 7, we obtain that

$$\begin{array}{cc}\hfill x_4& =|x_3|-y_3-4=-4y_0+1<-2y_0+1\le 0,\hfill \\ \hfill y_4& =x_3-\left|y_3\right|+1=4y_0-4<-4(x_0-y_0+1)\le 0\mathrm{and}{y}_4=-x_4-4+1.\hfill \end{array}$$

By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 5$.

Case 3 $(x_0,y_0)\in \left\{(x,y)\right|x-y+1\ge 0\mathrm{and}2x+2y-1\ge 0\}$. We have the same $(x_2,y_2)$ and $(x_3,y_3)$ as in Case 2, while $x_3\ge 0$ and

$$\begin{array}{cc}\hfill & x_4=|x_3|-y_3-4=4x_0-1<0,y_4=x_3-\left|y_3\right|+1=4y_0-4\le 0.\hfill \end{array}$$

By using the result of Lemma 7, we obtain that

$$\begin{array}{cc}\hfill & x_5=\left|x_4\right|-y_4-4=-4x_0-4y_0+1<-2(2x_0+2y_0-1)\le 0\hfill \\ \hfill & y_5=x_4-\left|y_4\right|+1=4x_0+4y_0-4<-4x_0+4y_0-4\le 0\mathrm{and}{y}_5=-x_5-4+1.\hfill \end{array}$$

By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 6$.

Case 4 $(x_0,y_0)\in \left\{(x,y)|-x-y-4<0\mathrm{and}x-y+1<0\right\}$. We have $x_1<0$ and $y_1<0$. By using the result of Lemma 7, we obtain that

• if $y_0<\frac{1}{2}$, then $x_2=\left|x_1\right|-y_1-4=2y_0-1<0$, $y_2=x_1-\left|y_1\right|+1=-2y_0-2<0$ and $y_2=-x_2-4+1$. By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 3$;
• if $\frac{1}{2}\le y_0<\frac{3}{4}$, then

  $$\begin{array}{cc}\hfill x_4& =|x_3|-y_3-4=-4y_0+1<-2(2y_0-1)\le 0,\hfill \\ \hfill y_4& =x_3-\left|y_3\right|+1=4y_0-4<4y_0-3<0\mathrm{and}{y}_4=-x_4-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 5$;
• if $\frac{3}{4}\le y_0<1$, then

  $$\begin{array}{cc}\hfill x_5& =|x_4|-y_4-4=-8y_0+5<-2(4y_0-3)\le 0,\hfill \\ \hfill y_5& =x_4-\left|y_4\right|+1=8y_0-8<0\mathrm{and}{y}_5=-x_5-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 6$;
• If $1\le y_0<\frac{9}{8}$, then

  $$\begin{array}{cc}\hfill x_6& =|x_5|-y_5-4=8y_0-9<0,\hfill \\ \hfill y_6& =x_5-\left|y_5\right|+1=-8y_0+6<-8(y_0-1)\le 0\mathrm{and}{y}_6=-x_6-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 7$;
• If $\frac{9}{8}\le y_0<\frac{19}{16}$, then

  $$\begin{array}{cc}\hfill x_8& =|x_7|-y_7-4=-16y_0+17<-2(8y_0-9)\le 0,\hfill \\ \hfill y_8& =x_7-\left|y_7\right|+1=16y_0-20<16y_0-19<0\mathrm{and}{y}_8=-x_8-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 9$;
• If $\frac{19}{16}\le y_0<\frac{5}{4}$, then

  $$\begin{array}{cc}\hfill x_9& =|x_8|-y_8-4=-32y_0+37<-2(16y_0-19)\le 0,\hfill \\ \hfill y_9& =x_8-\left|y_8\right|+1=32y_0-40<0\mathrm{and}{y}_9=-x_9-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 10$;
• If $y_0\ge \frac{5}{4}$, then

  $$\begin{array}{cccc}\hfill x_5& =|x_4|-y_4-4=-5,\hfill & \hfill y_5& =x_4-\left|y_4\right|+1=0.\hfill \end{array}$$
  Similar to the proof of Case 4 of Lemma 2, we can conclude that $(x_n,y_n)=(-1,-2)$ for all $n\ge 10$.

Case 5 $(x_0,y_0)\in \left\{(x,y)|-x-y-4\ge 0\mathrm{and}x>-\frac{9}{2}\right\}$. We have $x_1>0$ and $y_1<-(-x_0-y_0-4)\le 0$. Then,

$$\begin{array}{cc}\hfill x_2& =|x_1|-y_1-4=-2x_0-9<0,y_2=x_1-\left|y_1\right|+1=-2y_0-2<0.\hfill \end{array}$$

By using the result of Lemma 7, we obtain that

$$\begin{array}{cc}\hfill x_3& =|x_2|-y_2-4=2x_0+2y_0+7<2x_0+2y_0+8\le 0,\hfill \\ \hfill y_3& =x_2-\left|y_2\right|+1=-2x_0-2y_0-10<-2x_0-9<0\mathrm{and}{y}_3=-x_3-4+1.\hfill \end{array}$$

By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 4$.

Case 6 $(x_0,y_0)\in \left\{(x,y)|-x-y-4\ge 0,-2x+2y-11<0,-2x-2y-10<0\mathrm{and}-5<x\le -\frac{9}{2}\right\}$. We have the same $(x_2,y_2)$ as in Case 5, while $x_2\ge 0$ and

$$\begin{array}{cccc}\hfill x_3& =|x_2|-y_2-4=-2x_0+2y_0-11<0,\hfill & \hfill y_3& =x_2-\left|y_2\right|+1=-2x_0-2y_0-10<0.\hfill \end{array}$$

By using the result of Lemma 7, we obtain that

• if $-5<x_0\le -\frac{9}{2}$, then

  $$\begin{array}{cc}\hfill x_4& =|x_3|-y_3-4=4x_0+17<4x_0+18=2(2x_0+9)\le 0,\hfill \\ \hfill y_4& =x_3-\left|y_3\right|+1=-4x_0-20<0\mathrm{and}{y}_4=-x_4-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 5$;
• if $-\frac{41}{8}<x_0\le -5$, then

  $$\begin{array}{cc}\hfill x_6& =|x_5|-y_5-4=-8x_0-41<0,\hfill \\ \hfill y_6& =x_5-\left|y_5\right|+1=8x_0+38<8x_0+40\le 0\mathrm{and}{y}_6=-x_6-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 7$;
• if $-\frac{83}{16}<x_0\le -\frac{41}{8}$, then

  $$\begin{array}{cc}\hfill x_8& =|x_7|-y_7-4=16x_0+81<16x_0+82=2(8x_0+41)\le 0,\hfill \\ \hfill y_8& =x_7-\left|y_7\right|+1=-16x_0-84<-16x_0-83<0\mathrm{and}{y}_8=-x_8-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 9$;
• if $x_0\le -\frac{83}{16}$, then

  $$\begin{array}{cc}\hfill & x_9=\left|x_8\right|-y_8-4=32x_0+165<32x_0+166=2(16x_0+83)\le 0,\hfill \\ \hfill & y_9=x_8-\left|y_8\right|+1=-32x_0-168=8(-2x_0+2y_0-11)+8(-2x_0-2y_0-10)<0\hfill \\ \hfill & \mathrm{and}{y}_9=-x_9-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 10$.

Case 7 $(x_0,y_0)\in \left\{(x,y)\right|-2x+2y-11<0,\mathrm{and}-2x-2y-10\ge 0\}$. We have the same $(x_2,y_2)$ and $(x_3,y_3)$ as in Case 6, while $y_3\ge 0$ and

$$\begin{array}{cc}\hfill x_4& =|x_3|-y_3-4=4x_0+17<4x_0+4y_0+20\le 0,y_4=x_3-\left|y_3\right|+1=4y_0>0\hfill \\ \hfill x_5& =|x_4|-y_4-4=-4x_0-4y_0-21<0,\hfill \\ \hfill y_5& =x_4-\left|y_4\right|+1=4x_0-4y_0+18<4x_0+4y_0+18\hfill \\ & =-2(-2x_0-2y_0-9)<-2(-2x_0-2y_0-10)\le 0.\hfill \end{array}$$

By using the result of Lemma 7, we obtain that

• if $y_0<\frac{1}{8}$, then

  $$\begin{array}{cc}\hfill x_6& =|x_5|-y_5-4=8y_0-1<0,\hfill \\ \hfill y_6& =x_5-\left|y_5\right|+1=-8y_0-2<0\mathrm{and}{y}_6=-x_6-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 7$;
• if $\frac{1}{8}\le y_0<\frac{3}{16}$, then

  $$\begin{array}{cc}\hfill x_8& =|x_7|-y_7-4=-16y_0+1<-16y_0+2=-2(8y_0-1)\le 0,\hfill \\ \hfill y_8& =x_7-\left|y_7\right|+1=16y_0-4<16y_0-3<0\mathrm{and}{y}_8=-x_8-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 9$;
• if $y_0\ge \frac{3}{16}$, then

  $$\begin{array}{cc}\hfill x_9& =|x_7|-y_7-4=-32y_0+5<-32y_0+6\le 0,\hfill \\ \hfill y_9& =x_7-\left|y_7\right|+1=32y_0-8=2y_8<0\mathrm{and}{y}_9=-x_9-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 10$.

Case 8 $(x_0,y_0)\in \left\{(x,y)\right|-2x+2y-11\ge 0,\mathrm{and}-2x-2y-10\ge 0\}$. We have the same $(x_2,y_2)$ and $(x_3,y_3)$ as in Case 6, while $x_3\ge 0$ and $y_3\ge 0$. By using the results of Lemmas 2, 3 and 7, we obtain that

• if $y_0\le \frac{1}{8}$, then

  $$\begin{array}{cc}\hfill x_8& =|x_7|-y_7-4=16y_0-3<16y_0-2\le 0,\hfill \\ \hfill y_8& =x_7-\left|y_7\right|+1=-16y_0<0\mathrm{and}{y}_8=-x_8-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 9$;
• if $\frac{1}{8}<y_0<\frac{3}{16}$, then

  $$\begin{array}{cc}\hfill x_8& =|x_7|-y_7-4=-16y_0+1<-16y_0+2<0,\hfill \\ \hfill y_8& =x_7-\left|y_7\right|+1=16y_0-4<16y_0-3<0\mathrm{and}{y}_8=-x_8-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 9$.
• if $\frac{3}{16}\le y_0<\frac{4}{16}$, then

  $$\begin{array}{cc}\hfill x_9& =|x_8|-y_8-4=-32y_0+5<-32y_0+6\le 0,\hfill \\ \hfill y_9& =x_8-\left|y_8\right|+1=32y_0-8<0\mathrm{and}{y}_9=-x_9-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 10$;
• if $\frac{4}{16}\le y_0<\frac{9}{32}$, then

  $$\begin{array}{cc}\hfill x_{10}& =|x_9|-y_9-4=32y_0-9<0,\hfill \\ \hfill y_{10}& =x_9-\left|y_9\right|+1=-32y_0+6<-2(16y_0-4)\le 0\mathrm{and}{y}_{10}=-x_{10}-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 11$;
• if $\frac{9}{32}\le y_0<\frac{19}{64}$, then

  $$\begin{array}{cc}\hfill x_{12}& =|x_{11}|-y_{11}-4=-64y_0+17<-2(32y_0-9)\le 0,\hfill \\ \hfill y_{12}& =x_{11}-\left|y_{11}\right|+1=64y_0-20<64y_0-19<0\mathrm{and}{y}_{12}=-x_{12}-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 13$;
• if $\frac{19}{64}\le y_0<\frac{5}{16}$, then

  $$\begin{array}{cc}\hfill x_{13}& =|x_{12}|-y_{12}-4=-128y_0+37<-2(64y_0-19)\le 0,\hfill \\ \hfill y_{13}& =x_{12}-\left|y_{12}\right|+1=128y_0-40<0\mathrm{and}{y}_{13}=-x_{13}-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 14$.
• if $\frac{5}{16}\le y_0<\frac{5}{4}$, then

  $$\begin{array}{cccc}\hfill x_9& =|x_8|-y_8-4=-5,\hfill & \hfill y_9& =x_8-\left|y_8\right|+1=0.\hfill \end{array}$$
  Similar to the proof of Case 4 of Lemma 2, we can conclude that $(x_n,y_n)=(-1,-2)$ for all $n\ge 14$;
• if $y_0\ge \frac{5}{4}$, then

  $$\begin{array}{cccc}\hfill x_5& =|x_4|-y_4-4=-9,\hfill & \hfill y_5& =x_4-\left|y_4\right|+1=-4.\hfill \end{array}$$
  Similar to the proof of Case 6 of Lemma 2, we can conclude that $(x_n,y_n)=(-1,-2)$ for all $n\ge 14$.

Case 9 $(x_0,y_0)\in \left\{(x,y)\right|-x-y-4\ge 0,-2x+2y-11\ge 0\mathrm{and}x>-5\}$. $1-y_0=5-y_0-4>-x_0-y_0-4\ge 0$. Then, $y_0<1<\frac{5}{4}$. We have the same $(x_2,y_2)$ and $(x_3,y_3)$ as in Case 6, while $x_3\ge 0$, $y_3<0$ and

$$\begin{array}{cc}\hfill x_4& =|x_3|-y_3-4=4y_0-5<0,y_4=x_3-\left|y_3\right|+1=-4x_0-20<0.\hfill \end{array}$$

By using the result of Lemma 7, we obtain that

$$\begin{array}{cc}\hfill x_5& =|x_4|-y_4-4=4x_0-4y_0+21<4x_0-4y_0+22\le 0,\hfill \\ \hfill y_5& =x_4-\left|y_4\right|+1=-4x_0+4y_0-24<4y_0-24<4-24<0\mathrm{and}{y}_5=-x_5-4+1.\hfill \end{array}$$

By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 6$.

Case 10 $(x_0,y_0)\in \left\{(x,y)|-x-y-4\ge 0,-2x+2y-11\ge 0,-2x-2y-10<0,x\le -5\mathrm{and}y\le \frac{5}{4}\right\}$. We have the same $(x_2,y_2)$-$(x_4,y_4)$ as in Case 9, while $y_4\ge 0$ and

$$\begin{array}{cc}\hfill x_5& =|x_4|-y_4-4=4x_0-4y_0+21<4x_0-4y_0+22\le 0,\hfill \\ \hfill y_5& =x_4-\left|y_4\right|+1=4x_0+4y_0+16=-4(-x_0-y_0-4)\le 0.\hfill \end{array}$$

By using the result of Lemma 7, we obtain that

• if $-\frac{41}{8}<x_0\le -5$, then

  $$\begin{array}{cc}\hfill x_6& =|x_5|-y_5-4=-8x_0-41<0,\hfill \\ \hfill y_6& =x_5-\left|y_5\right|+1=8x_0+38<8x_0+40\le 0\mathrm{and}{y}_6=-x_6-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 7$;
• if $-\frac{83}{16}<x_0\le -\frac{41}{8}$, then

  $$\begin{array}{cc}\hfill x_8& =|x_7|-y_7-4=16x_0+81<16x_0+82=2(8x_0+41)\le 0,\hfill \\ \hfill y_8& =x_7-\left|y_7\right|+1=-16x_0-84<-16x_0-83<0\mathrm{and}{y}_8=-x_8-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 9$;
• if $-\frac{84}{16}<x\le -\frac{83}{16}$, then

  $$\begin{array}{cc}\hfill x_9& =|x_8|-y_8-4=32x_0+165<32x_0+166\le 0,\hfill \\ \hfill y_9& =x_8-\left|y_8\right|+1=-32x_0-168=-2(16x_0+84)<0\mathrm{and}{y}_9=-x_9-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 10$;
• if $-\frac{85}{16}\le x_0<-\frac{339}{64}$, then

  $$\begin{array}{cc}\hfill x_{13}& =|x_{12}|-y_{12}-4=128x_0+667<2(64x_0+339)<0,\hfill \\ \hfill y_{13}& =x_{12}-\left|y_{12}\right|+1=-128x_0-680\le 0\mathrm{and}{y}_{13}=-x_{13}-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 14$;
• if $-\frac{339}{64}\le x_0<-\frac{169}{32}$, then

  $$\begin{array}{cc}\hfill x_{12}& =|x_{11}|-y_{11}-4=64x_0+337<2(32x_0+169)\le 0,\hfill \\ \hfill y_{12}& =x_{11}-\left|y_{11}\right|+1=-64x_0-340<0\mathrm{and}{y}_{12}=-x_{12}-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 13$;
• if $-\frac{169}{32}\le x_0\le -\frac{84}{16}$, then

  $$\begin{array}{cc}\hfill x_{10}& =|x_9|-y_9-4=-32x_0-169\le 0,\hfill \\ \hfill y_{10}& =x_9-\left|y_9\right|+1=32x_0+166<2(16x_0+84)\le 0\mathrm{and}{y}_{10}=-x_{10}-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 11$;
• if $x_0\le -\frac{85}{16}$, then

  $$\begin{array}{cccc}\hfill x_9& =|x_8|-y_8-4=-5,\hfill & \hfill y_9& =x_8-\left|y_8\right|+1=0.\hfill \end{array}$$
  Similar to the proof of Case 4 of Lemma 2, we can conclude that $(x_n,y_n)=(-1,-2)$ for all $n\ge 14$.

Case 11 $(x_0,y_0)\in \left\{(x,y)|-x-y-4\ge 0,-2x-2y-10<0\mathrm{and}y\ge \frac{5}{4}\right\}$. We have the same $(x_2,y_2)$-$(x_4,y_4)$ as in Case 9. Since $y_0\ge \frac{5}{4}$, $x_4\ge 0$ and $-x_0-\frac{5}{4}-4\ge -x_0-y_0-4\ge 0$. Then, $x_0\le -\frac{21}{4}<-5$ and $y_4=-4(x_0+5)>0$. By using the result of Lemma 6, we obtain that

• if $(x_0,y_0)\in \left\{(x,y)|-2x-2y-10<0,-16x-16y-65\ge 0\mathrm{and}y\ge \frac{5}{4}\right\}$, then

  $$\begin{array}{cc}\hfill x_9& =|x_8|-y_8-4=-5,y_9=x_8-\left|y_8\right|+1=0.\hfill \end{array}$$
  Similar to the proof of Case 4 of Lemma 2, we can conclude that $(x_n,y_n)=(-1,-2)$ for all $n\ge 14$;
• if $(x_0,y_0)\in \left\{(x,y)|-x-y-4\ge 0,-16x-16y-65<0\mathrm{and}y\ge \frac{5}{4}\right\}$, then

  $$\begin{array}{cc}\hfill & x_9=|x_8|-y_8-4=32x_0+32y_0+124<32x_0+32y_0+128\le 0,y_9=x_8-\left|y_8\right|+1=0.\hfill \end{array}$$
  By using the result of Lemma 5, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 11$.

Figure 1 shows region of each case presented in the proof of this lemma.

□

Lemma 9.

If $b=4$, $x_0>0$ and $y_0<0$, then the solution ${(x_n,y_n)}_{n=0}^{\infty }$ of (2) eventually becomes the equilibrium point $(-1,-2)$ of (2).

Proof. 

Let $x_0>0$ and $y_0<0$. Then,

$$\begin{array}{cccc}\hfill x_1& =|x_0|-y_0-4=x_0-y_0-4,\hfill & \hfill y_1& =x_0-\left|y_0\right|+1=x_0+y_0+1.\hfill \end{array}$$

Case 1 $(x_0,y_0)\in \left\{(x,y)\right|x-y-4<0\mathrm{and}x+y+1\ge 0\}$. We have $x_1<0$ and $y_1\ge 0$. By using the results of Lemmas 5 and 8, we have that

• if $(x_0,y_0)\in \left\{(x,y)\right|x+y+1\ge 0,2x+2y+1<0\mathrm{and}y>-2\}$, then

  $$\begin{array}{cc}\hfill x_3& =|x_2|-y_2-4=2x_0+2y_0+1<0,\hfill \\ \hfill y_3& =x_2-\left|y_2\right|+1=-2x_0-2y_0-4<-2(x_0+y_0+1)\le 0\mathrm{and}{y}_3=-x_3-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 4$;
• if $(x_0,y_0)\in \left\{(x,y)\right|2x+2y+1\ge 0,4x+4y+1<0\mathrm{and}y\ge -2\}$, then

  $$\begin{array}{cc}\hfill x_5& =|x_4|-y_4-4=-4x_0-4y_0-3<-2(2x_0+2y_0+1)\le 0,\hfill \\ \hfill y_5& =x_4-\left|y_4\right|+1=4x_0+4y_0<4x_0+4y_0+1<0\mathrm{and}{y}_5=-x_5-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 6$;
• if $(x_0,y_0)\in \left\{(x,y)\right|4x+4y+1\ge 0,4x+4y<0\mathrm{and}y\ge -2\}$, then

  $$\begin{array}{cc}\hfill x_6& =|x_5|-y_5-4=-8x_0-8y_0-3<-2(4x_0+4y_0+1)\le 0,\hfill \\ \hfill y_6& =x_5-\left|y_5\right|+1=8x_0+8y_0<0\mathrm{and}{y}_6=-x_6-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 7$;
• if $(x_0,y_0)\in \left\{(x,y)\right|4x+4y\ge 0\mathrm{and}8x+8y-1<0\}$, then

  $$\begin{array}{cc}\hfill x_7& =|x_6|-y_6-4=8x_0+8y_0-1<0,\hfill \\ \hfill y_7& =x_6-\left|y_6\right|+1=-8x_0-8y_0-2<-2(4x_0+4y_0)\le 0\mathrm{and}{y}_7=-x_7-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 8$;
• if $(x_0,y_0)\in \left\{(x,y)\right|8x+8y-1\ge 0\mathrm{and}16x+16y-3<0\}$, then

  $$\begin{array}{cc}\hfill x_9& =|x_8|-y_8-4=-16x_0-16y_0+1<-2(8x_0+8y_0-1)\le 0,\hfill \\ \hfill y_9& =x_8-\left|y_8\right|+1=16x_0+16y_0-4<16x_0+16y_0-3<0\mathrm{and}{y}_9=-x_9-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 10$;
• if $(x_0,y_0)\in \left\{(x,y)\right|16x+16y-3\ge 0\mathrm{and}4x+4y-1<0\}$, then

  $$\begin{array}{cc}\hfill x_{10}& =|x_9|-y_9-4=-32x_0-32y_0+5<-2(16x_0+16y_0-3)\le 0,\hfill \\ \hfill y_{10}& =x_9-\left|y_9\right|+1=32x_0+32y_0-8<0\mathrm{and}{y}_{10}=-x_{10}-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 11$;
• if $(x_0,y_0)\in \left\{(x,y)\right|4x+4y-1\ge 0\mathrm{and}x-y-4<0\}$, then

  $$\begin{array}{cccc}\hfill x_6& =|x_5|-y_5-4=-5,\hfill & \hfill y_6& =x_5-\left|y_5\right|+1=0.\hfill \end{array}$$
  Similar to the proof of Case 4 of Lemma 2, we can conclude that $(x_n,y_n)=(-1,-2)$ for all $n\ge 11$;
• if $(x_0,y_0)\in \left\{(x,y)|x-y-4<0,x+y+1\ge 0\mathrm{and}y\le -\frac{19}{8}\right\}$, then

  $$\begin{array}{cc}\hfill & x_7=\left|x_6\right|-y_6-4=16y_0+37<0,\hfill \\ \hfill & y_7=x_6-\left|y_6\right|+1=-16y_0-40=-8(x_0+y_0+1)+8(x_0-y_0-4)<0\hfill \\ & \mathrm{and}{y}_7=-x_7-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 8$;
• if $(x_0,y_0)\in \left\{(x,y)|x-y-4<0,x+y+1\ge 0\mathrm{and}-\frac{19}{8}<y\le -\frac{9}{4}\right\}$, then

  $$\begin{array}{cc}\hfill & x_6=\left|x_5\right|-y_5-4=8y_0+17<2(4y_0+9)\le 0,\hfill \\ \hfill & y_6=x_5-\left|y_5\right|+1=-8y_0-20=-4(x_0+y_0+1)+4(x_0-y_0-4)<0\hfill \\ \hfill & \mathrm{and}{y}_6=-x_6-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 7$;
• if $(x_0,y_0)\in \left\{(x,y)|x+y+1\ge 0,2x+2y+1<0\mathrm{and}-\frac{9}{4}<y\le -2\right\}$, then

  $$\begin{array}{cc}\hfill & x_4=\left|x_3\right|-y_3-4=-4y_0-9<0,\hfill \\ \hfill & y_4=x_3-\left|y_3\right|+1=4y_0+6<4(y_0+2)\le 0\mathrm{and}{y}_4=-x_4-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 5$;
• if $(x_0,y_0)\in \left\{(x,y)|2x+2y+1\ge 0,x-y-4<0,x<\frac{7}{4}\mathrm{and}y\le -2\right\}$, then

  $$\begin{array}{cc}\hfill x_5& =|x_4|-y_4-4=-4x_0-4y_0-3<-2(2x_0+2y_0+1)\le 0,\hfill \\ \hfill y_5& =x_4-\left|y_4\right|+1=4x_0+4y_0\le -1<0\mathrm{and}{y}_5=-x_5-4+1.\hfill \end{array}$$
  Since $x_0<\frac{7}{4}$ and $y_0\le -2$, $y_5=4x_0+4y_0<7-8<0$. By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 6$;
• if $(x_0,y_0)\in \left\{(x,y)|2x+2y+1\ge 0,x-y-4<0,x\ge \frac{7}{4}\mathrm{and}y\le -2\right\}$, then

  $$\begin{array}{cc}\hfill x_6& =|x_5|-y_5-4=-8x_0+13<-8x_0+14=-2(4x_0-7)\le 0,\hfill \\ \hfill y_6& =x_5-\left|y_5\right|+1=8x_0-16\mathrm{and}{y}_6=-x_6-4+1.\hfill \end{array}$$
  Since $x_0-y_0-4<0$ and $y_0\le -2$, $x_0<y_0+4\le 2$. Then, $y_6=8(x_0-2)<0$. By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 7$.

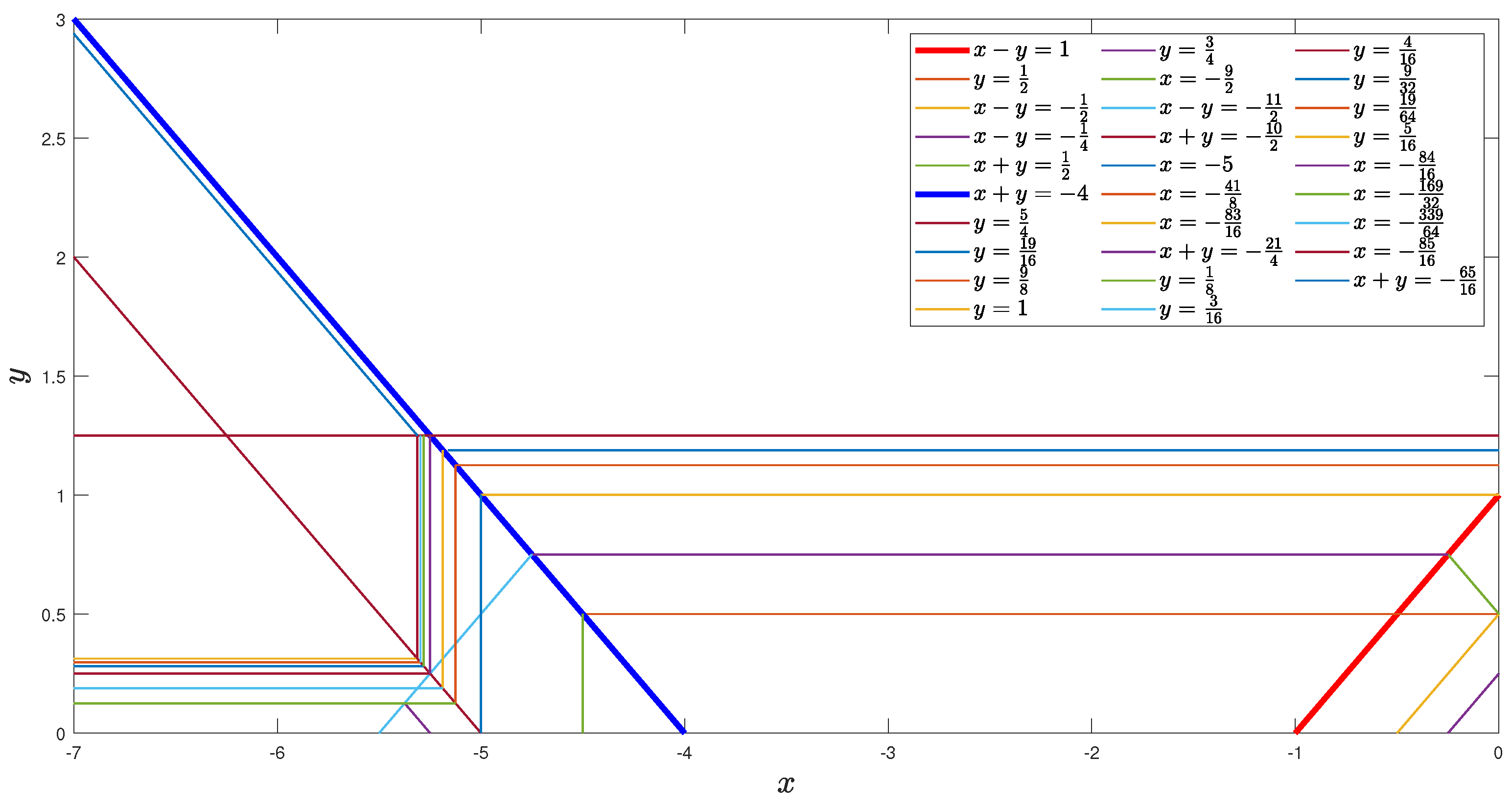
Figure 2 shows regions considered in the proof of Case 1 of this lemma.

Case 2 $(x_0,y_0)\in \left\{(x,y)\right|x-y-4<0\mathrm{and}x+y+1<0\}$. We have $x_1<0$ and $y_1<0$. By using the result of Lemma 7, we have that

• if $x_0<1$, then

  $$\begin{array}{cc}\hfill & x_2=|x_1|-y_1-4=-2x_0-1<0,y_2=x_1-\left|y_1\right|+1=2x_0-2<0\hfill \\ \hfill & \mathrm{and}{y}_2=-x_2-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 3$;
• if $1\le x_0<\frac{5}{4}$, then

  $$\begin{array}{cc}\hfill & x_4=|x_3|-y_3-4=4x_0-5<0,y_4=x_3-\left|y_3\right|+1=-4x_0+2\le 0\hfill \\ \hfill & \mathrm{and}{y}_4=-x_4-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 5$;
• if $\frac{5}{4}\le x_0<\frac{11}{8}$, then

  $$\begin{array}{cc}\hfill x_6& =|x_5|-y_5-4=-8x_0+9<-8x_0+10=-2(4x_0-5)\le 0,\hfill \\ \hfill y_6& =x_5-\left|y_5\right|+1=8x_0-12<8x_0-11<0\mathrm{and}{y}_6=-x_6-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 7$;
• if $x_0\ge \frac{11}{8}$, then

  $$\begin{array}{cc}\hfill x_7& =|x_6|-y_6-4=-16x_0+21<-2\left(8x_0-11\right)\le 0,\hfill \\ \hfill y_7& =x_6-\left|y_6\right|+1=16x_0-24=2y_6<0\mathrm{and}{y}_7=-x_7-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 8$.

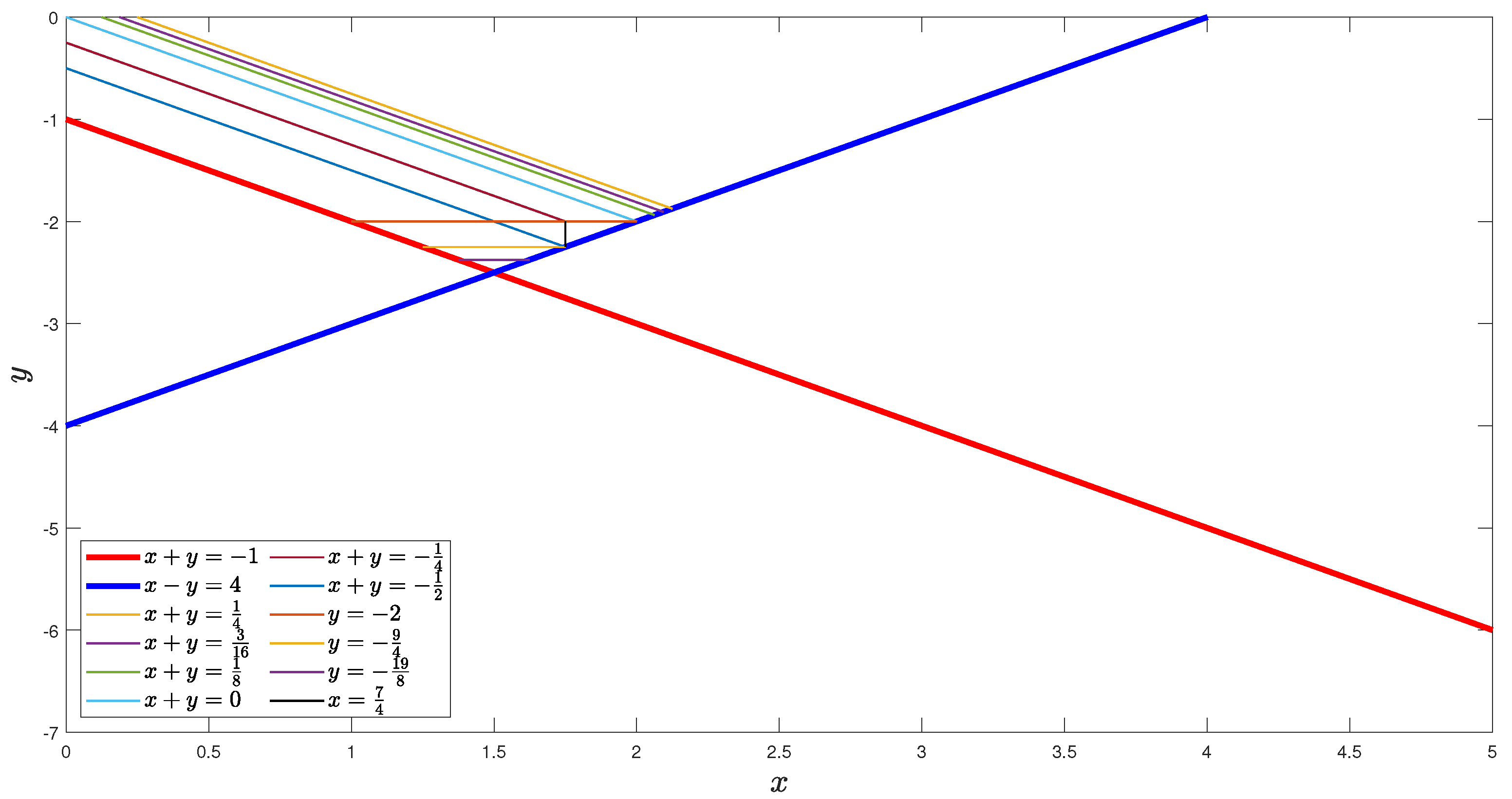
Figure 3 shows regions considered in the proof of Case 2 of this lemma.

Case 3 $(x_0,y_0)\in \left\{(x,y)\right|x-y-4\ge 0\mathrm{and}x+y+1<0\}$. We have $x_1\ge 0$ and $y_1<0$.

Case 3.1 $(x_0,y_0)\in \left\{(x,y)|x-y-4\ge 0,x<1\mathrm{and}y>-\frac{9}{2}\right\}$. Then,

$$\begin{array}{cccc}\hfill x_2& =|x_1|-y_2-4=-2y_0-9<0,\hfill & \hfill y_2& =x_1-\left|y_1\right|+1=2x_0-2<0.\hfill \end{array}$$

By using the result of Lemma 7, we have that

• if $(x_0,y_0)\in \left\{(x,y)|x-y-4\ge 0,2x-2y-10<0,x<1\mathrm{and}y>-\frac{9}{2}\right\}$, then

  $$\begin{array}{cc}\hfill x_3& =|x_2|-y_2-4=-2x_0+2y_0+7<-2(x_0-y_0-4)\le 0,\hfill \\ \hfill y_3& =x_2-\left|y_2\right|+1=2x_0-2y_0-10<0\mathrm{and}{y}_3=-x_3-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 4$;
• if $(x_0,y_0)\in \left\{(x,y)|2x-2y-10\ge 0,4x-4y-21<0,x<1\mathrm{and}y>-\frac{9}{2}\right\}$, then

  $$\begin{array}{cc}\hfill x_5& =|x_4|-y_4-4=4x_0-4y_0-21<0,\hfill \\ \hfill y_5& =x_4-\left|y_4\right|+1=-4x_0+4y_0+18\le 0\mathrm{and}{y}_5=-x_5-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 6$;
• if $(x_0,y_0)\in \left\{(x,y)|4x-4y-21\ge 0,8x-8y-43<0,x<1\mathrm{and}y>-\frac{9}{2}\right\}$, then

  $$\begin{array}{cc}\hfill x_7& =|x_6|-y_6-4=-8x_0+8y_0+41<-2(4x_0-4y_0-21)\le 0,\hfill \\ \hfill y_7& =x_6-\left|y_6\right|+1=8x_0-8y_0-44<8x_0-8y_0-43<0\mathrm{and}{y}_7=-x_7-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 8$;
• if $(x_0,y_0)\in \left\{(x,y)|8x-8y-43\ge 0,x<1\mathrm{and}y>-\frac{9}{2}\right\}$, then

  $$\begin{array}{cc}\hfill x_8& =|x_7|-y_7-4=-16x_0+16y_0+85<-2(8x_0-8y_0-43)\le 0,\hfill \\ \hfill y_8& =x_7-\left|y_7\right|+1=16x_0-16y_0-88<16+72-88=0\mathrm{and}{y}_8=-x_8-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 9$.

Case 3.2 $(x_0,y_0)\in \left\{(x,y)|x-y-4\ge 0,x+y+1<0,x\ge 1\mathrm{and}y>-\frac{9}{2}\right\}$. We have the same $(x_2,y_2)$ as in Case 3.1, while $x_2<0$ and $y_2\ge 0$. By using the results of Lemmas 5 and 8, we have that

• if $(x_0,y_0)\in \left\{(x,y)|-8x-8y-27\ge 0,1\le x<\frac{5}{4}\mathrm{and}y>-\frac{9}{2}\right\}$, then

  $$\begin{array}{cc}\hfill x_8& =|x_7|-y_7-4=16x_0+16y_0+53<-2(-8x_0-8y_0-27)\le 0,\hfill \\ \hfill y_8& =x_7-\left|y_7\right|+1=-16x_0-16y_0-56<-16+72-56=0\mathrm{and}{y}_8=-x_8-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 9$;
• if $(x_0,y_0)\in \left\{(x,y)\right|-8x-8y-27<0,-4x-4y-13\ge 0,1\le x<\frac{5}{4}\mathrm{and}y>-\frac{9}{2}\}$, then

  $$\begin{array}{cc}\hfill x_7& =|x_6|-y_6-4=8x_0+8y_0+25<-2(-4x_0-4y_0-13)\le 0,\hfill \\ \hfill y_7& =x_6-\left|y_6\right|+1=-8x_0-8y_0-28<-8x_0-8y_0-27<0\mathrm{and}{y}_7=-x_7-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 8$;
• if $(x_0,y_0)\in \left\{(x,y)\right|-4x-4y-13<0,-2x-2y-6\ge 0,1\le x<\frac{5}{4}\mathrm{and}y>-\frac{9}{2}\}$, then

  $$\begin{array}{cc}\hfill x_5& =|x_4|-y_4-4=-4x_0-4y_0-13<0,\hfill \\ \hfill y_5& =x_4-\left|y_4\right|+1=4x_0+4y_0+10<-2(-2x_0-2y_0-6)\le 0\mathrm{and}{y}_5=-x_5-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 6$;
• if $(x_0,y_0)\in \left\{(x,y)|4x-4y-23\ge 0,-2x-2y-6\ge 0,\mathrm{and}y>-\frac{9}{2}\right\}$, then

  $$\begin{array}{cc}\hfill & x_7=\left|x_6\right|-y_6-4=-8x_0+8y_0+45<-2(4x_0-4y_0-23)\le 0,\hfill \\ \hfill & y_7=x_6-\left|y_6\right|+1=8x_0-8y_0-48<-2(-4x_0+4y_0-23)\le 0\mathrm{and}{y}_7=-x_7-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 8$;
• if $(x_0,y_0)\in \left\{(x,y)|4x-4y-23<0,-2x-2y-6\ge 0,\mathrm{and}x>\frac{5}{4}\right\}$, then

  $$\begin{array}{cc}\hfill & x_6=\left|x_5\right|-y_5-4=-8x_0+9<-2(4x_0-5)<0,\hfill \\ \hfill & y_6=x_5-\left|y_5\right|+1=8x_0-12<8x_0-11=(4x_0-4y_0-23)-2(-2x_0-2y_0-6)<0\hfill \\ & \mathrm{and}{y}_6=-x_6-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 7$;
• if $(x_0,y_0)\in \left\{(x,y)|x-y-4\ge 0,x+y+1<0,-2x-2y-6<0\mathrm{and}1\le x<\frac{5}{4}\right\}$, then

  $$\begin{array}{cc}\hfill x_4& =|x_3|-y_3-4=4x_0-5<0,\hfill \\ \hfill y_4& =x_3-\left|y_3\right|+1=-4x_0+2<-4(x_0-1)\le 0\mathrm{and}{y}_4=-x_4-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 5$;
• if $(x_0,y_0)\in \left\{(x,y)|x-y-4\ge 0,-2x-2y-6<0\mathrm{and}\frac{5}{4}\le x<\frac{11}{8}\right\}$, then

  $$\begin{array}{cc}\hfill x_6& =|x_5|-y_5-4=-8x_0+9<-2(4x_0-5)\le 0,\hfill \\ \hfill y_6& =x_5-\left|y_5\right|+1=8x_0-12<8x_0-11<0\mathrm{and}{y}_6=-x_6-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 7$;
• if $(x_0,y_0)\in \left\{(x,y)|x-y-4\ge 0,-2x-2y-6<0\mathrm{and}\frac{11}{8}\le x<\frac{3}{2}\right\}$, then

  $$\begin{array}{cc}\hfill x_7& =|x_6|-y_6-4=-16x_0+21<-2(8x_0-11)\le 0,\hfill \\ \hfill y_7& =x_6-\left|y_6\right|+1=16x_0-24=8(2x_0-3)<0\mathrm{and}{y}_7=-x_7-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 8$;
• if $(x_0,y_0)\in \left\{(x,y)|x+y+1<0,\frac{3}{2}\le x<\frac{25}{16}\mathrm{and}y>-\frac{9}{2}\right\}$, then

  $$\begin{array}{cc}\hfill x_8& =|x_7|-y_7-4=16x_0-25<0,\hfill \\ \hfill y_8& =x_7-\left|y_7\right|+1=-16x_0+22<-8(2x_0-3)\le 0\mathrm{and}{y}_8=-x_8-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 9$;
• if $(x_0,y_0)\in \left\{(x,y)|x+y+1<0,\frac{25}{16}\le x<\frac{51}{32}\mathrm{and}y>-\frac{9}{2}\right\}$, then

  $$\begin{array}{cc}\hfill x_{10}& =|x_9|-y_9-4=-32x_0+49<-2(16x_0-25)\le 0,\hfill \\ \hfill y_{10}& =x_9-\left|y_9\right|+1=32x_0-52<32x_0-51<0\mathrm{and}{y}_{10}=-x_{10}-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 11$;
• if $(x_0,y_0)\in \left\{(x,y)|x+y+1<0,\frac{51}{32}\le x<\frac{13}{8}\mathrm{and}y>-\frac{9}{2}\right\}$, then

  $$\begin{array}{cc}\hfill x_{11}& =|x_{10}|-y_{10}-4=-64x_0+101<-2(32x_0-51)\le 0,\hfill \\ \hfill y_{11}& =x_{10}-\left|y_{10}\right|+1=64x_0-104<0\mathrm{and}{y}_{11}=-x_{11}-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 12$;
• if $(x_0,y_0)\in \left\{(x,y)|x+y+1<0,x\ge \frac{13}{8}\mathrm{and}y>-\frac{9}{2}\right\}$, then

  $$\begin{array}{cccc}\hfill x_7& =|x_6|-y_6-4=-5,\hfill & \hfill y_7& =x_6-\left|y_6\right|+1=0.\hfill \end{array}$$
  Similar to the proof of Case 4 of Lemma 2, we can conclude that $(x_n,y_n)=(-1,-2)$ for all $n\ge 12$.

Case 3.3 $(x_0,y_0)\in \left\{(x,y)|x+y+1<0,x<1\mathrm{and}y\le -\frac{9}{2}\right\}$. We have the same $(x_2,y_2)$ as in Case 3.2, while $x_2\ge 0$, $y_2<0$ and

$$\begin{array}{cc}\hfill & x_3=\left|x_2\right|-y_2-4=-2x_0-2y_0-11<2x_0-2y_0-10<0,\hfill \\ \hfill & y_3=x_2-\left|y_2\right|+1=2x_0-2y_0-10<0.\hfill \end{array}$$

By using the result of Lemma 7, we have that

• if $(x_0,y_0)\in \left\{(x,y)|2x-2y-10<0,x<1\mathrm{and}y\le -\frac{9}{2}\right\}$, then

  $$\begin{array}{cc}\hfill & x_4=\left|x_3\right|-y_3-4=4y_0+17<2(2y_0+9)\le 0,\hfill \\ \hfill & y_4=x_3-\left|y_3\right|+1=-4y_0-20<2(2x_0-2y_0-10)<0\mathrm{and}{y}_4=-x_4-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 5$;
• if $(x_0,y_0)\in \left\{(x,y)|2x-2y-10\ge 0,4x-4y-21<0\mathrm{and}y\le -\frac{9}{2}\right\}$, then

  $$\begin{array}{cc}\hfill x_5& =|x_4|-y_4-4=4x_0-4y_0-21<0,\hfill \\ \hfill y_5& =x_4-\left|y_4\right|+1=-4x_0+4y_0+18<-2(2x_0-2y_0-10)\le 0\mathrm{and}{y}_5=-x_5-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 6$;
• if $(x_0,y_0)\in \left\{(x,y)|4x-4y-21\ge 0,8x-8y-43<0\mathrm{and}y\le -\frac{9}{2}\right\}$, then

  $$\begin{array}{cc}\hfill x_7& =|x_6|-y_6-4=-8x_0+8y_0+41<-2(4x_0-4y_0-21)\le 0,\hfill \\ \hfill y_7& =x_6-\left|y_6\right|+1=8x_0-8y_0-44<8x_0-8y_0-43<0\mathrm{and}{y}_7=-x_7-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 8$;
• if $(x_0,y_0)\in \left\{(x,y)|8x-8y-43\ge 0,8x-8y-44<0\mathrm{and}y\le -\frac{9}{2}\right\}$, then

  $$\begin{array}{cc}\hfill x_8& =|x_7|-y_7-4=-16x_0+16y_0+85<-2(8x_0-8y_0-43)\le 0,\hfill \\ \hfill y_8& =x_7-\left|y_7\right|+1=16x_0-16y_0-88<0\mathrm{and}{y}_8=-x_8-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 9$;
• if $(x_0,y_0)\in \left\{(x,y)\right|8x-8y-44\ge 0,-2x-2y-11<0,16x-16y-89<0$ and $x<1\}$, then

  $$\begin{array}{cc}\hfill & x_9=\left|x_8\right|-y_8-4=16x_0-16y_0-89<0,\hfill \\ \hfill & y_9=x_8-\left|y_8\right|+1=-16x_0+16y_0+86<-2(8x_0-8y_0-44)\le 0\hfill \\ \hfill & \mathrm{and}{y}_9=-x_9-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 10$;
• if $(x_0,y_0)\in \left\{(x,y)\right|16x-16y-89\ge 0,-2x-2y-11<0,32x-32y-179<0\mathrm{and}x<1\}$, then

  $$\begin{array}{cc}\hfill & x_{11}=\left|x_{10}\right|-y_{10}-4=-32x_0+32y_0+177<-2(16x_0-16y_0-89)\le 0,\hfill \\ \hfill & y_{11}=x_{10}-\left|y_{10}\right|+1=32x_0-32y_0-180<32x_0-32y_0-179<0\hfill \\ \hfill & \mathrm{and}{y}_{11}=-x_{11}-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 12$;
• if $(x_0,y_0)\in \left\{(x,y)\right|32x-32y-179\ge 0,-2x-2y-11<0,8x-8y-45<0\mathrm{and}x<1\}$, then

  $$\begin{array}{cc}\hfill & x_{12}=\left|x_{11}\right|-y_{11}-4=-64x_0+64y_0+357<-2(32x_0-32y_0-179)\le 0,\hfill \\ \hfill & y_{12}=x_{11}-\left|y_{11}\right|+1=64x_0-64y_0-360<0\mathrm{and}{y}_{12}=-x_{12}-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 13$;
• if $(x_0,y_0)\in \left\{(x,y)|8x-8y-45\ge 0,-2x-2y-11<0\mathrm{and}x<1\right\}$, then

  $$\begin{array}{cccc}\hfill x_8& =|x_7|-y_7-4=-5,\hfill & \hfill y_8& =x_7-\left|y_7\right|+1=0.\hfill \end{array}$$
  Similar to the proof of Case 4 of Lemma 2, we can conclude that $(x_n,y_n)=(-1,-2)$ for all $n\ge 13$;
• if $(x_0,y_0)\in \left\{(x,y)|-2x-2y-11\ge 0\mathrm{and}x<\frac{1}{32}\right\}$, then

  $$\begin{array}{cc}\hfill & x_9=\left|x_8\right|-y_8-4=32x_0-1<0,\hfill \\ \hfill & y_9=x_8-\left|y_8\right|+1=-32x_0-2<0\mathrm{and}{y}_9=-x_9-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 10$;
• if $(x_0,y_0)\in \left\{(x,y)|-2x-2y-11\ge 0\mathrm{and}\frac{1}{32}\le x<\frac{3}{64}\right\}$, then

  $$\begin{array}{cc}\hfill & x_{11}=\left|x_{10}\right|-y_{10}-4=-64x_0+1<-2(32x_0-1)\le 0,\hfill \\ \hfill & y_{11}=x_{10}-\left|y_{10}\right|+1=64x_0-4<64x_0-3<0\mathrm{and}{y}_{11}=-x_{11}-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 12$;
• if $(x_0,y_0)\in \left\{(x,y)|-2x-2y-11\ge 0\mathrm{and}\frac{3}{64}\le x<\frac{1}{16}\right\}$, then

  $$\begin{array}{cc}\hfill & x_{12}=\left|x_{11}\right|-y_{11}-4=-128x_0+5<-2(64x_0-3)\le 0,\hfill \\ \hfill & y_{12}=x_{11}-\left|y_{11}\right|+1=128x_0-8<0\mathrm{and}{y}_{12}=-x_{12}-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 13$;
• if $(x_0,y_0)\in \left\{(x,y)|-2x-2y-11\ge 0\mathrm{and}\frac{1}{16}\le x<1\right\}$, then

  $$\begin{array}{cccc}\hfill x_8& =|x_7|-y_7-4=-5,\hfill & \hfill y_8& =x_7-\left|y_7\right|+1=0.\hfill \end{array}$$
  Similar to the proof of Case 4 of Lemma 2, we can conclude that $(x_n,y_n)=(-1,-2)$ for all $n\ge 13$.

Case 3.4 $(x_0,y_0)\in \left\{(x,y)|x+y+1<0,x\ge 1\mathrm{and}y\le -\frac{9}{2}\right\}$. We have the same $(x_2,y_2)$ as in Case 3.2, while $x_2\ge 0$ and $y_2\ge 0$. By using the results of Lemmas 2, 3 and 6, we have that

• if $(x_0,y_0)\in \left\{(x,y)|-2x-2y-6\ge 0,4x+4y+13\ge 0,x\ge 1\mathrm{and}y\le -\frac{9}{2}\right\}$, then

  $$\begin{array}{cc}\hfill x_7& =|x_6|-y_6-4=-8x_0-8y_0-27<-2(4x_0+4y_0+13)\le 0,\hfill \\ \hfill y_7& =x_6-\left|y_6\right|+1=8x_0+8y_0+24\le 0\mathrm{and}{y}_7=-x_7-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 8$;
• if $(x_0,y_0)\in \left\{(x,y)|4x+4y+13<0,-8x-8y-27<0,x\ge 1\mathrm{and}y\le -\frac{9}{2}\right\}$, then

  $$\begin{array}{cc}\hfill x_7& =|x_6|-y_6-4=8x_0+8y_0+25<2(4x_0+4y_0+13)<0,\hfill \\ \hfill y_7& =x_6-\left|y_6\right|+1=-8x_0-8y_0-28<-8x_0-8y_0-27<0\mathrm{and}{y}_7=-x_7-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 8$;
• if $(x_0,y_0)\in \left\{(x,y)\right|-8x-8y-27\ge 0,-8x-8y-28<0,x\ge 1\mathrm{and}y\le -\frac{9}{2}\}$, then

  $$\begin{array}{cc}\hfill x_8& =|x_7|-y_7-4=16x_0+16y_0+53<-2(-8x_0-8y_0-27)\le 0,\hfill \\ \hfill y_8& =x_7-\left|y_7\right|+1=-16x_0-16y_0-56<0\mathrm{and}{y}_8=-x_8-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 9$;
• if $(x_0,y_0)\in \left\{(x,y)\right|-8x-8y-28\ge 0,-16x-16y-57<0\mathrm{and}x\ge 1\}$, then

  $$\begin{array}{cc}\hfill x_9& =|x_8|-y_8-4=-16x_0-16y_0-57<0,\hfill \\ \hfill y_9& =x_8-\left|y_8\right|+1=16x_0+16y_0+54<-2(-8x_0-8y_0-28)\le 0\mathrm{and}{y}_9=-x_9-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 10$;
• if $(x_0,y_0)\in \left\{(x,y)\right|-16x-16y-57\ge 0,-32x-32y-115<0\mathrm{and}x\ge 1\}$, then

  $$\begin{array}{cc}\hfill & x_{11}=\left|x_{10}\right|-y_{10}-4=32x_0+32y_0+113<-2(-16x_0-16y_0-57)\le 0,\hfill \\ \hfill & y_{11}=x_{10}-\left|y_{10}\right|+1=-32x_0-32y_0-116<-32x_0-32y_0-115<0\hfill \\ \hfill & \mathrm{and}{y}_{11}=-x_{11}-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 12$;
• if $(x_0,y_0)\in \left\{(x,y)\right|-32x-32y-115\ge 0,-8x-8y-29<0\mathrm{and}x\ge 1\}$, then

  $$\begin{array}{cc}\hfill & x_{12}=\left|x_{11}\right|-y_{11}-4=64x_0+64y_0+229<-2(-32x_0-32y_0-115)\le 0,\hfill \\ \hfill & y_{12}=x_{11}-\left|y_{11}\right|+1=-64x_0-64y_0-232<0\mathrm{and}{y}_{12}=-x_{12}-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 13$;
• if $(x_0,y_0)\in \left\{(x,y)\right|-8x-8y-29\ge 0,-2x-2y-11<0\mathrm{and}x\ge 1\}$, then

  $$\begin{array}{cccc}\hfill x_8& =|x_7|-y_7-4=-5,\hfill & \hfill y_8& =x_7-\left|y_7\right|+1=0.\hfill \end{array}$$
  Similar to the proof of Case 4 of Lemma 2, we can conclude that $(x_n,y_n)=(-1,-2)$ for all $n\ge 13$;
• if $(x_0,y_0)\in \left\{(x,y)\right|-2x-2y-11\ge 0\mathrm{and}x\ge 1\}$, then

  $$\begin{array}{cccc}\hfill x_4& =|x_3|-y_3-4=-9,\hfill & \hfill y_4& =x_3-\left|y_3\right|+1=-4.\hfill \end{array}$$
  Similar to the proof of Case 6 of Lemma 2, we can conclude that $(x_n,y_n)=(-1,-2)$ for all $n\ge 13$;
• if $(x_0,y_0)\in \left\{(x,y)|-2x-2y-6<0,16x+16y+47<0\mathrm{and}y\le -\frac{9}{2}\right\}$, then

  $$\begin{array}{cc}\hfill & x_8=\left|x_7\right|-y_7-4=16x_0+16y_0+47<0,\hfill \\ \hfill & y_8=x_7-\left|y_7\right|+1=-16x_0-16y_0-50<8(-2x_0-2y_0-6)<0\hfill \\ \hfill & \mathrm{and}{y}_8=-x_8-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 9$;
• if $(x_0,y_0)\in \left\{(x,y)\right|16x+16y+47\ge 0,32x+32y+93<0,\mathrm{and}y\le -\frac{9}{2}\}$, then

  $$\begin{array}{cc}\hfill & x_{10}=\left|x_9\right|-y_9-4=-32x_0-32y_0-95<-2(16x_0+16y_0+47)\le 0,\hfill \\ \hfill & y_{10}=x_9-\left|y_9\right|+1=32x_0+32y_0+92<32x_0+32y_0+93<0\hfill \\ \hfill & \mathrm{and}{y}_{10}=-x_{10}-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 11$;
• if $(x_0,y_0)\in \left\{(x,y)\right|32x+32y+93\ge 0,8x+8y+23<0\mathrm{and}y\le -\frac{9}{2}\}$, then

  $$\begin{array}{cc}\hfill & x_{11}=\left|x_{10}\right|-y_{10}-4=-64x_0-64y_0-187<-2(32x_0+32y_0+93)\le 0,\hfill \\ \hfill & y_{11}=x_{10}-\left|y_{10}\right|+1=64x_0+64y_0+184<0\mathrm{and}{y}_{11}=-x_{11}-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 12$;
• if $(x_0,y_0)\in \left\{(x,y)|8x+8y+23\ge 0,x+y+1<0\mathrm{and}y\le -\frac{9}{2}\right\}$, then

  $$\begin{array}{cccc}\hfill x_7& =|x_6|-y_6-4=-5,\hfill & \hfill y_7& =x_6-\left|y_6\right|+1=0.\hfill \end{array}$$
  Similar to the proof of Case 4 of Lemma 2, we can conclude that $(x_n,y_n)=(-1,-2)$ for all $n\ge 12$.

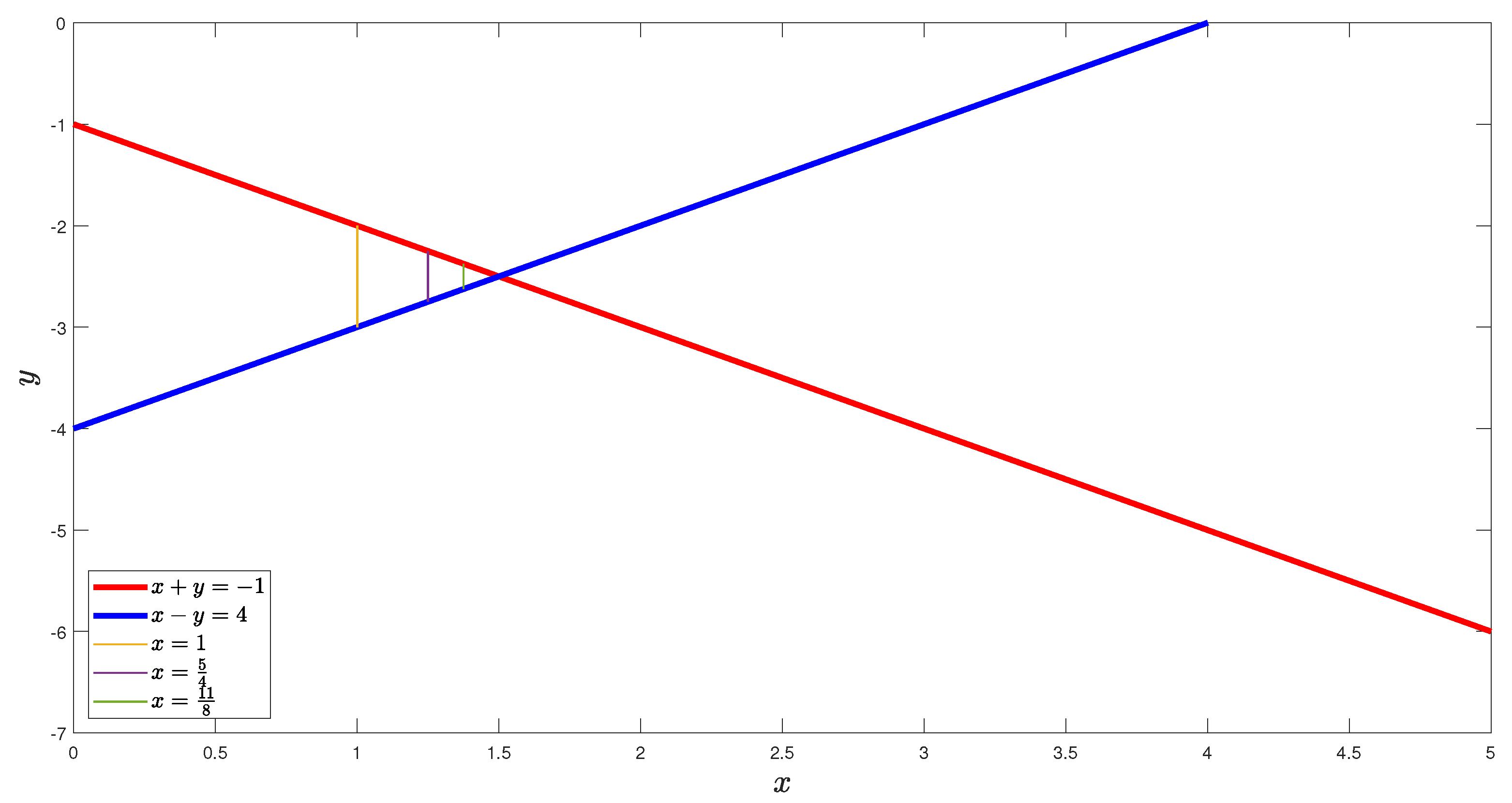
Figure 4 shows regions considered in the proof of Case 3 of this lemma.

Case 4 $(x_0,y_0)\in \left\{(x,y)\right|x-y-4\ge 0\mathrm{and}x+y+1\ge 0\}$. We have $x_1\ge 0$ and $y_1\ge 0$. By using the results of Lemmas 2, 3 and 6, we have that

• if $y_0\ge -\frac{15}{8}$, then

  $$\begin{array}{cc}\hfill x_6& =|x_5|-y_5-4=-5,y_6=x_5-\left|y_5\right|+1=0.\hfill \end{array}$$
  Similar to the proof of Case 4 of Lemma 2, we can conclude that $(x_n,y_n)=(-1,-2)$ for all $n\ge 11$;
• if $-\frac{61}{32}\le y_0<-\frac{15}{8}$, then

  $$\begin{array}{cc}\hfill x_{10}& =|x_9|-y_9-4=-64y_0-123<-2(32y_0+61)\le 0,\hfill \\ \hfill y_{10}& =x_9-\left|y_9\right|+1=64y_0+120<0\mathrm{and}{y}_{10}=-x_{10}-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 11$;
• if $-\frac{31}{16}\le y_0<-\frac{61}{32}$, then

  $$\begin{array}{cc}\hfill x_9& =|x_8|-y_8-4=-32y_0-63<-2(16y_0+31)\le 0,\hfill \\ \hfill y_9& =x_8-\left|y_8\right|+1=32y_0+60<32y_0+61<0\mathrm{and}{y}_9=-x_9-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 10$;
• if $-2\le y_0<-\frac{31}{16}$, then

  $$\begin{array}{cc}\hfill x_7& =|x_6|-y_6-4=16y_0+31<0,\hfill \\ \hfill y_7& =x_6-\left|y_6\right|+1=-16y_0-34<-16(y_0+2)\le 0\mathrm{and}{y}_7=-x_7-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 8$;
• if $-\frac{9}{4}<y_0<-2$, then

  $$\begin{array}{cc}\hfill x_6& =|x_5|-y_5-4=-8y_0-19<-2(4y_0+9)<0,\hfill \\ \hfill y_6& =x_5-\left|y_5\right|+1=8y_0+16<0\mathrm{and}{y}_6=-x_6-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 7$;
• if $-\frac{19}{8}<y_0\le -\frac{9}{4}$, then

  $$\begin{array}{cc}\hfill x_6& =|x_5|-y_5-4=8y_0+17<2(4y_0+9)\le 0,\hfill \\ \hfill y_6& =x_5-\left|y_5\right|+1=-8y_0-20<-8y_0-19<0\mathrm{and}{y}_6=-x_6-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 7$;
• if $-\frac{20}{8}<y_0\le -\frac{19}{8}$, then

  $$\begin{array}{cc}\hfill x_7& =|x_6|-y_6-4=16y_0+37<2(8y_0+19)\le 0,\hfill \\ \hfill y_7& =x_6-\left|y_6\right|+1=-16y_0-40<0\mathrm{and}{y}_7=-x_7-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 8$;
• if $-\frac{41}{16}<y_0\le -\frac{20}{8}$, then

  $$\begin{array}{cc}\hfill x_8& =|x_7|-y_7-4=-16y_0-41<0,\hfill \\ \hfill y_8& =x_7-\left|y_7\right|+1=16y_0+38<2(8y_0+20)\le 0\mathrm{and}{y}_8=-x_8-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 9$;
• if $-\frac{83}{32}<y_0\le -\frac{41}{16}$, then

  $$\begin{array}{cc}\hfill x_{10}& =|x_9|-y_9-4=32y_0+81<2(16y_0+41)\le 0,\hfill \\ \hfill y_{10}& =x_9-\left|y_9\right|+1=-32y_0-84<-32y_0-83<0\mathrm{and}{y}_{10}=-x_{10}-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 11$;
• if $-\frac{21}{8}<y_0\le -\frac{83}{32}$, then

  $$\begin{array}{cc}\hfill x_{11}& =|x_{10}|-y_{10}-4=64y_0+165<2(32y_0+83)\le 0,\hfill \\ \hfill y_{11}& =x_{10}-\left|y_{10}\right|+1=-64y_0-168<0\mathrm{and}{y}_{11}=-x_{11}-4+1.\hfill \end{array}$$
  By Lemma 1, we have $(x_n,y_n)=(-1,-2)$ for all $n\ge 12$;
• if $-\frac{9}{2}<y_0\le -\frac{21}{8}$, then

  $$\begin{array}{cccc}\hfill x_7& =|x_6|-y_6-4=-5,\hfill & \hfill y_7& =x_6-\left|y_6\right|+1=0.\hfill \end{array}$$
  Similar to the proof of Case 4 of Lemma 2, we can conclude that $(x_n,y_n)=(-1,-2)$ for all $n\ge 12$;
• if $y_0\le -\frac{9}{2}$, then

  $$\begin{array}{cccc}\hfill x_3& =|x_2|-y_2-4=-9,\hfill & \hfill y_3& =x_2-\left|y_2\right|+1=-4.\hfill \end{array}$$
  Similar to the proof of Case 6 of Lemma 2, we can conclude that $(x_n,y_n)=(-1,-2)$ for all $n\ge 13$.

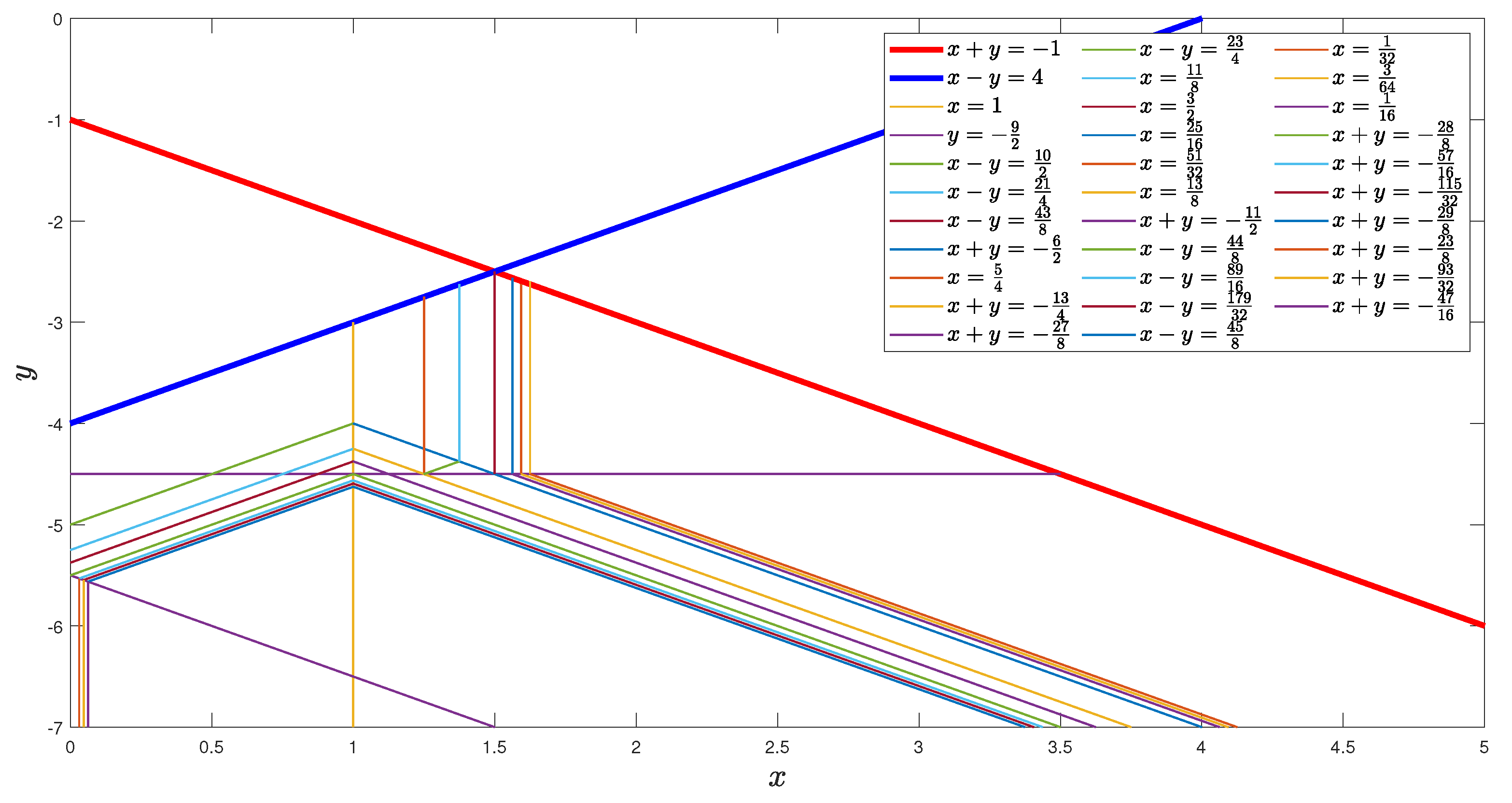
Figure 5 shows regions considered in the proof of Case 4 of this lemma.

□

Therefore, as we combine Lemmas 2–9, we can have the following theorem. It can be seen that the solutions do not show any periodic behavior. This is not the same as the other values of b considered in [11,14,15,17].

Theorem 1.

If $b=4$, $(x_0,y_0)\in {\mathbb{R}}^2$, then the solution ${(x_n,y_n)}_{n=0}^{\infty }$ of (2) eventually becomes the equilibrium point $(-1,-2)$ of (2) within 14 iterations.

3. Local Behavior for b ≥ 5

In this section, we investigate local behavior for several values of $b\ge 5$.

3.1. b = 5

First, let us start with $b=5$ where $x_0=0$ or $y_0=0$.

Lemma 10.

If $x_0\ge 0$ and $y_0=0$, then the solution ${(x_n,y_n)}_{n=0}^{\infty }$ of (2) eventually becomes the equilibrium point $(-1,-3)$ of (2).

Proof. 

By separate cases as in Lemma 2, we can conclude the behavior of the solution in

Table 4. Cases for $x_0\ge 0$ and $y_0=0$.

If ${\mathit{x}}_0\in \mathit{A}$,	Then $({\mathit{x}}_{\mathit{n}},{\mathit{y}}_{\mathit{n}})=(-1,-3)$ for All $\mathit{n}\ge \mathit{N}$
$A=\left[0,\frac{1}{8}\right)$	$N=7$
$A=\left[\frac{1}{8},\frac{3}{16}\right)$	$N=9$
$A=\left[\frac{3}{16},\frac{7}{32}\right]$	$N=11$
$A=\left[\frac{7}{32},\frac{1}{4}\right)$; $\left[\frac{1}{4},1\right]$; $(1,5)$; $[5,\infty )$	$N=12$

.

□

Lemma 11.

If $x_0=0$ and $y_0\ge 0$, then the solution ${(x_n,y_n)}_{n=0}^{\infty }$ of (2) eventually becomes the equilibrium point $(-1,-3)$ of (2).

Proof. 

By separate cases as in Lemma 2, we can conclude the behavior of the solution in

Table 5. Cases for $x_0=0$ and $y_0\ge 0$.

If ${\mathit{y}}_0\in \mathit{A}$,	Then $({\mathit{x}}_{\mathit{n}},{\mathit{y}}_{\mathit{n}})=(-1,-3)$ for All $\mathit{n}\ge \mathit{N}$
$A=\left(\frac{1}{4},\frac{1}{2}\right)$; $\left[\frac{1}{2},1\right]$; $\left(1,\frac{9}{8}\right]$	$N=6$
$A=\left[0,\frac{1}{4}\right]$	$N=7$
$A=\left(\frac{9}{8},\frac{19}{16}\right]$	$N=8$
$A=\left(\frac{19}{16},\frac{39}{32}\right]$	$N=10$
$A=\left(\frac{39}{32},\frac{5}{4}\right);\left[\frac{5}{4},\infty \right)$	$N=11$

.

□

Lemma 12.

If $x_0=0$ and $y_0<0$, then the solution ${(x_n,y_n)}_{n=0}^{\infty }$ of (2) eventually becomes the equilibrium point $(-1,-3)$ of (2).

Proof. 

By separate cases as in Lemma 2, we can conclude the behavior of the solution in

Table 6. Cases for $x_0=0$ and $y_0<0$.

If ${\mathit{y}}_0\in \mathit{A}$,	Then $({\mathit{x}}_{\mathit{n}},{\mathit{y}}_{\mathit{n}})=(-1,-3)$ for All $\mathit{n}\ge \mathit{N}$
$A=\{-4\}$	$N=1$
$A=(-5,-1)\backslash \{-4\}$	$N=2$
$A=\left(-\frac{11}{2},-5\right]$; $\left[-1,-\frac{1}{2}\right)$	$N=4$
$A=\left(-\frac{25}{4},-\frac{11}{2}\right]$	$N=5$
$A=\left[-\frac{1}{2},-\frac{1}{4}\right)$	$N=6$
$A=\left(-\frac{51}{8},-\frac{25}{4}\right]$; $\left[-\frac{1}{4},0\right)$	$N=7$
$A=\left(-\frac{103}{16},-\frac{51}{8}\right]$	$N=9$
$A=\left(-\infty ,-\frac{13}{2}\right]$; $\left(-\frac{13}{2},-\frac{103}{16}\right]$	$N=10$

.

□

Lemma 13.

If $x_0<0$ and $y_0=0$, then the solution ${(x_n,y_n)}_{n=0}^{\infty }$ of (2) eventually becomes the equilibrium point $(-1,-3)$ of (2).

Proof. 

By separate cases as in Lemma 2, we can conclude the behavior of the solution in

Table 7. Cases for $x_0<0$ and $y_0=0$.

If ${\mathit{x}}_0\in \mathit{A}$,	Then $({\mathit{x}}_{\mathit{n}},{\mathit{y}}_{\mathit{n}})=(-1,-3)$ for All $\mathit{n}\ge \mathit{N}$
$A=\{-4\}$	$N=1$
$A=(-5,-1)\backslash \{-4\}$	$N=2$
$A=\left(-\frac{11}{2},-5\right]$; $\left[-1,-\frac{1}{2}\right)$	$N=4$
$A=\left(-\frac{25}{4},-\frac{11}{2}\right]$	$N=5$
$A=\left[-\frac{1}{2},-\frac{1}{4}\right)$	$N=6$
$A=\left(-\frac{51}{8},-\frac{25}{4}\right]$; $\left[-\frac{1}{4},0\right)$	$N=7$
$A=\left(-\frac{103}{16},-\frac{51}{8}\right]$	$N=9$
$A=\left(-\infty ,-\frac{13}{2}\right]$; $\left(-\frac{13}{2},-\frac{103}{16}\right]$	$N=10$

.

□

3.2. $b\ge 5$ with Large Value of $|x_0|$ and $|y_0|$

It can be seen from Lemmas 2–5 and 10–13 that if ($x_0$ and $|y_0|$ is large enough) or ($y_0$ and $|x_0|$ is large enough), then we can easily determine the behavior of the solutions without considering several cases. However, for these initial conditions, it possesses the periodic behavior.

Lemma 14.

If $b\ge 6$, $x_0\ge b$ and $y_0=0$, then the solution ${(x_n,y_n)}_{n=0}^{\infty }$ of (2) eventually becomes the periodic solution of prime period 5 of (2).

Proof. 

Let $b\ge 6$, $x_0\ge b$ and $y_0=0$. Then,

$$\begin{array}{cccc}\hfill x_1& =|x_0|-y_0-b=x_0-b\ge 0,\hfill & \hfill y_1& =x_0-\left|y_0\right|+1=x_0+1\ge 0\hfill \\ \hfill x_2& =|x_1|-y_1-b=-2b-1<0,\hfill & \hfill y_2& =x_1-\left|y_1\right|+1=-b<0\hfill \\ \hfill x_3& =|x_2|-y_2-b=2b+1>0,\hfill & \hfill y_3& =x_2-\left|y_2\right|+1=-3b<0\hfill \\ \hfill x_4& =|x_3|-y_3-b=4b+1>0,\hfill & \hfill y_4& =x_3-\left|y_3\right|+1=-b+2\le -4<0\hfill \\ \hfill x_5& =|x_4|-y_4-b=4b-1\ge 23>0,\hfill & \hfill y_5& =x_4-\left|y_4\right|+1=3b+4>0\hfill \\ \hfill x_6& =|x_5|-y_5-b=-5,\hfill & \hfill y_6& =x_5-\left|y_5\right|+1=b-4\ge 2>0\hfill \\ \hfill x_7& =|x_6|-y_6-b=-2b+9\le -3<0,\hfill & \hfill y_7& =x_6-\left|y_6\right|+1=-b<0\hfill \\ \hfill x_8& =|x_7|-y_7-b=2b-9\ge 3>0,\hfill & \hfill y_8& =x_7-\left|y_7\right|+1=-3b+10\le -8<0\hfill \\ \hfill x_9& =|x_8|-y_8-b=4b-19\ge 5>0,\hfill & \hfill y_9& =x_8-\left|y_8\right|+1=-b+2\le -4<0\hfill \\ \hfill x_{10}& =|x_9|-y_9-b=4b-21\ge 3>0,\hfill & \hfill y_{10}& =x_9-\left|y_9\right|+1=3b-16\ge 2>0\hfill \\ \hfill x_{11}& =|x_{10}|-y_{10}-b=-5=x_6,\hfill & \hfill y_{11}& =x_{10}-\left|y_{10}\right|+1=b-4=y_6.\hfill \end{array}$$

By mathematical induction, we have $x_{n+5}=x_n$ and $y_{n+5}=y_n$ for all $n\ge 6$. □

Lemma 15.

If $b\ge 6$, $x_0=0$ and $y_0\ge \frac{b}{4}$, then the solution ${(x_n,y_n)}_{n=0}^{\infty }$ of (2) eventually becomes the periodic solution of prime period 5 of (2).

Proof. 

Let $b\ge 6$, $x_0=0$ and $y_0\ge \frac{b}{4}$. Then,

$$\begin{array}{cc}\hfill x_1& =|x_0|-y_0-b=-y_0-b<0,\hfill \\ \hfill y_1& =x_0-\left|y_0\right|+1=-y_0+1\le -\frac{-b+4}{4}\le -\frac{1}{2}<0\hfill \\ \hfill x_2& =|x_1|-y_1-b=2y_0-1\ge \frac{b-2}{2}\ge 2>0,\hfill \\ \hfill y_2& =x_1-\left|y_1\right|+1=-2y_0-b+2\le \frac{-3b+4}{2}\le -7<0\hfill \\ \hfill x_3& =|x_2|-y_2-b=4y_0-3\ge b-3\ge 3>0,y_3=x_2-\left|y_2\right|+1=-b+2\le -4<0\hfill \\ \hfill x_4& =|x_3|-y_3-b=4y_0-5\ge b-5\ge 1>0,y_4=x_3-\left|y_3\right|+1=4y_0-b\ge 0\hfill \\ \hfill x_5& =|x_4|-y_4-b=-5,y_5=x_4-\left|y_4\right|+1=b-4\ge 2>0.\hfill \end{array}$$

Similar to Lemma 14, we can conclude by mathematical induction that $x_{n+5}=x_n$ and $y_{n+5}=y_n$ for all $n\ge 5$. □

Lemma 16.

If $b\ge 6$, $x_0\le -\frac{3}{2}b+1$ and $y_0=0$, then the solution ${(x_n,y_n)}_{n=0}^{\infty }$ of (2) eventually becomes the periodic solution of prime period 5 of (2).

Proof. 

Let $b\ge 6$, $x_0\le -\frac{3}{2}b+1$ and $y_0=0$. Then,

$$\begin{array}{cc}\hfill x_1& =|x_0|-y_0-b=-x_0-b\ge \frac{3}{2}b-1-b\ge 2>0,\hfill \\ \hfill y_1& =x_0-\left|y_0\right|+1=x_0+1\le -\frac{3}{2}b+2\le -7<0\hfill \\ \hfill x_2& =|x_1|-y_1-b=-2x_0-2b-1\ge 3b-2-2b-1\ge 3>0,\hfill \\ \hfill y_2& =x_1-\left|y_1\right|+1=-b+2\le -4<0\hfill \\ \hfill x_3& =|x_2|-y_2-b=-2x_0-2b-3\ge 3b-2-2b-3\ge 1>0,\hfill \\ \hfill y_3& =x_2-\left|y_2\right|+1=-2x_0-3b+2\ge 3b-2-3b+2=0\hfill \\ \hfill x_4& =|x_3|-y_3-b=-5,y_4=x_3-\left|y_3\right|+1=b-4\ge 2>0.\hfill \end{array}$$

Similar to Lemma 14, we can conclude by mathematical induction that $x_{n+5}=x_n$ and $y_{n+5}=y_n$ for all $n\ge 4$. □

Lemma 17.

If $b\ge 6$, $x_0=0$ and $y_0\le -\frac{3}{2}b+1$, then the solution ${(x_n,y_n)}_{n=0}^{\infty }$ of (2) eventually becomes the periodic solution of prime period 5 of (2).

Proof. 

Let $b\ge 6$, $x_0=0$ and $y_0\le -\frac{3}{2}b+1$. Then,

$$\begin{array}{cc}\hfill x_1& =|x_0|-y_0-b=-y_0-b\ge \frac{3}{2}b-1-b\ge 2>0,\hfill \\ \hfill y_1& =x_0-\left|y_0\right|+1=y_0+1\le -\frac{3}{2}b+2\le -7<0\hfill \\ \hfill x_2& =|x_1|-y_1-b=-2y_0-2b-1\ge 3b-3-2b-1\ge 2>0,\hfill \\ \hfill y_2& =x_1-\left|y_1\right|+1=-b+2\le -4<0\hfill \\ \hfill x_3& =|x_2|-y_2-b=-2y_0-2b-3\ge 3b-2-2b-3\ge 1>0,\hfill \\ \hfill y_3& =x_2-\left|y_2\right|+1=-2y_0-3b+2\ge 3b-2-3b+2=0\hfill \\ \hfill x_4& =|x_3|-y_3-b=-5,y_4=x_3-\left|y_3\right|+1=b-4\ge 2>0.\hfill \end{array}$$

Similar to Lemma 14, we can conclude by mathematical induction that $x_{n+5}=x_n$ and $y_{n+5}=y_n$ for all $n\ge 4$. □

Next, if $x_0{y}_0>0$ and $|x_0|$ and $|y_0|$ are large enough, we can conclude the following theorem about the solution of (2) when $b\ge 5$.

Lemma 18.

If $b\ge 5$ and $(x_0,y_0)\in \{(x,y)\in {\mathbb{R}}^{+}\times {\mathbb{R}}^{+}|x-y-b\ge 0\}$, then the solution ${(x_n,y_n)}_{n=0}^{\infty }$ of (2) eventually becomes (i) the equilibrium point $(-1,-3)$ of (2) for $b=5$ and (ii) the periodic solution of prime period 5 of (2).

Proof. 

(i). Let $b=5$ and $(x_0,y_0)\in \{(x,y)\in {\mathbb{R}}^{+}\times {\mathbb{R}}^{+}|x-y-5\ge 0\}$. Then,

$$\begin{array}{cccc}\hfill x_1& =|x_0|-y_0-5=x_0-y_0-5,\hfill & \hfill y_1& =x_0-\left|y_0\right|+1=x_0-y_0+1>x_0-y_0-5\ge 0\hfill \\ \hfill x_2& =|x_1|-y_1-5=-11,\hfill & \hfill y_2& =x_1-\left|y_1\right|+1=-5\hfill \\ \hfill x_3& =|x_2|-y_2-5=11,\hfill & \hfill y_3& =x_2-\left|y_2\right|+1=15\hfill \\ \hfill x_4& =|x_3|-y_3-5=21,\hfill & \hfill y_4& =x_3-\left|y_3\right|+1=-3\hfill \\ \hfill x_5& =|x_4|-y_4-5=19,\hfill & \hfill y_5& =x_4-\left|y_4\right|+1=19\hfill \\ \hfill x_6& =|x_5|-y_5-5=-5,\hfill & \hfill y_6& =x_5-\left|y_5\right|+1=1.\hfill \end{array}$$

By direct computation, we can conclude that $(x_n,y_n)=(-1,-3)$ for all $n\ge 12$.

(ii) Let $b\ge 6$ and $(x_0,y_0)\in \{(x,y)\in {\mathbb{R}}^{+}\times {\mathbb{R}}^{+}|x-y-b\ge 0\}$. Then,

$$\begin{array}{cccc}\hfill x_1& =|x_0|-y_0-b=x_0-y_0-b,\hfill & \hfill y_1& =x_0-\left|y_0\right|+1=x_0-y_0+1>x_0-y_0-b\ge 0\hfill \\ \hfill x_2& =|x_1|-y_1-b=-2b-1<0,\hfill & \hfill y_2& =x_1-\left|y_1\right|+1=-b<0.\hfill \end{array}$$

Similar to Lemma 14, we can conclude by mathematical induction that $x_{n+5}=x_n$ and $y_{n+5}=y_n$ for all $n\ge 6$. □

Lemma 19.

If $b\ge 5$ and $(x_0,y_0)\in \left\{(x,y)\in {\mathbb{R}}^{-}\times {\mathbb{R}}^{-}|-x-y-\frac{3}{2}b+1\ge 0\right\}$, then the solution ${(x_n,y_n)}_{n=0}^{\infty }$ of (2) eventually becomes (i) the equilibrium point $(-1,-3)$ of (2) for $b=5$ and (ii) the periodic solution of prime period 5 of (2).

Proof. 

(i). Let $b=5$ and $(x_0,y_0)\in \left\{(x,y)\in {\mathbb{R}}^{-}\times {\mathbb{R}}^{-}|-x-y-\frac{17}{2}\ge 0\right\}$. Then,

$$\begin{array}{cc}\hfill x_1& =|x_0|-y_0-5=-x_0-y_0-5>-x_0-y_0-\frac{17}{2}\ge 0,\hfill \\ \hfill y_1& =x_0-\left|y_0\right|+1=x_0+y_0+1<x_0+y_0+\frac{17}{2}\le 0\hfill \\ \hfill x_2& =|x_1|-y_1-5=-2x_0-2y_0-11>2\left(-x_0-y_0-\frac{17}{2}\right)\ge 0,y_2=x_1-\left|y_1\right|+1=-3\hfill \\ \hfill x_3& =|x_2|-y_2-5=-2x_0-2y_0-13>2\left(-x_0-y_0-\frac{17}{2}\right)\ge 0,\hfill \\ \hfill y_3& =x_2-\left|y_2\right|+1=-2x_0-2y_0-13=x_3\ge 0\hfill \\ \hfill x_4& =|x_3|-y_3-5=-5,y_4=x_3-\left|y_3\right|+1=1.\hfill \end{array}$$

Similar to the proof of Lemma 18(i), we can conclude that $(x_n,y_n)=(-1,-3)$ for all $n\ge 10$.

Case (ii) Let $b\ge 6$ and $(x_0,y_0)\in \left\{(x,y)\in {\mathbb{R}}^{-}\times {\mathbb{R}}^{-}|-x-y-\frac{3}{2}b+1\ge 0\right\}$. Since $b\ge 6$, $-b+\frac{3}{2}b=\frac{1}{2}b\ge 3>1$, $2+1=3<b=-2b+3b$ and $3+1=4<b=-2b+3b$. Thus, $-b>-\frac{3}{2}b+1$, $-2b-1>-3b+2$ and $-2b-3>-3b+1$, respectively. Then,

$$\begin{array}{cc}\hfill x_1& =|x_0|-y_0-b=-x_0-y_0-b>-x_0-y_0-\frac{3}{2}b+1\ge 0,\hfill \\ \hfill y_1& =x_0-\left|y_0\right|+1=x_0+y_0+1<-\frac{3}{2}b+1+1\le -7<0\hfill \\ \hfill x_2& =|x_1|-y_1-b=-2x_0-2y_0-2b-1>-2x_0-2y_0-3b+2\ge 0,\hfill \\ \hfill y_2& =x_1-\left|y_1\right|+1=-b+2\le -4<0\hfill \\ \hfill x_3& =|x_2|-y_2-b=-2x_0-2y_0-2b-3>-2x_0-2y_0-3b+2\ge 0,\hfill \\ \hfill y_3& =x_2-\left|y_2\right|+1=-2x_0-2y_0-3b+2\ge 0\hfill \\ \hfill x_4& =|x_3|-y_3-b=-5,y_4=x_3-\left|y_3\right|+1=b-4\ge 2>0.\hfill \end{array}$$

Similar to Lemma 14, we can conclude by mathematical induction that $x_{n+5}=x_n$ and $y_{n+5}=y_n$ for all $n\ge 4$. □

4. Conclusions and Discussion

It is shown completely that for $b=4$, all solutions of (2) eventually becomes the equilibrium point $(-1,-2)$. It is also suspected from Lemmas 10–13 and Lemmas 18 (i)–19 (i) that for $b=5$, all solutions of (2) eventually becomes the equilibrium point $(-1,-3)$, while for $b\ge 6$, concerning the solutions of (2) with a chance to possess the periodic behavior of prime period 5 and for some small values of $|x_0|$ and $|y_0|$, it may also becomes the equilibrium point.

As we mentioned before that since the absolute value function is not differentiable, one needs to find an alternative method to analyze the behavior of (2). Thus, we choose to use a fundamental method to complete our full analysis. However, this give some insight to those who want to do further investigation concerning this type of problem. For example, (i) one can roughly see how many cases need to be considered for each value of b; (ii) one can see, for a big region, that the behavior of the solutions remains the same; (iii) one can estimate the maximum iteration until the behavior of the solutions become either equilibrium or periodic.

Finally, these complete results for $b=4$ and partial results for $b=5$, where all solutions asymptotically become equilibrium, are in contrast with the existing results concerning Equation (1) which usually involving periodic behavior. Thus, one may try to consider these cases of b and prove our conjecture that only for $b=4$ and 5 do all solutions eventually become the equilibrium point, while for $b\ge 6$ all solutions eventually become either equilibrium or periodic of prime period 5.