An Operator-Based Scheme for the Numerical Integration of FDEs
Abstract
1. Introduction
2. Preliminaries and Motivation
2.1. The Generalized Differential Operator Scheme for ODEs
2.1.1. The Construction of Analytic Solutions to ODEs in the Series Form
2.1.2. The Construction of Closed-Form Solutions to ODEs
2.1.3. Truncated Series and Shifted Centers of the Expansion
2.2. The Ordinary Riccati Equation and Its Solution
2.3. The Fractional Power Series and Caputo Differentiation
2.4. Motivation: The Fractional Riccati Equation
2.5. Transformation of the FDE into the Characteristic ODE
3. The Development of the Numerical FDE Integration Scheme
3.1. Adaptive Step-Size Selection Strategy for the FDE Integration Scheme
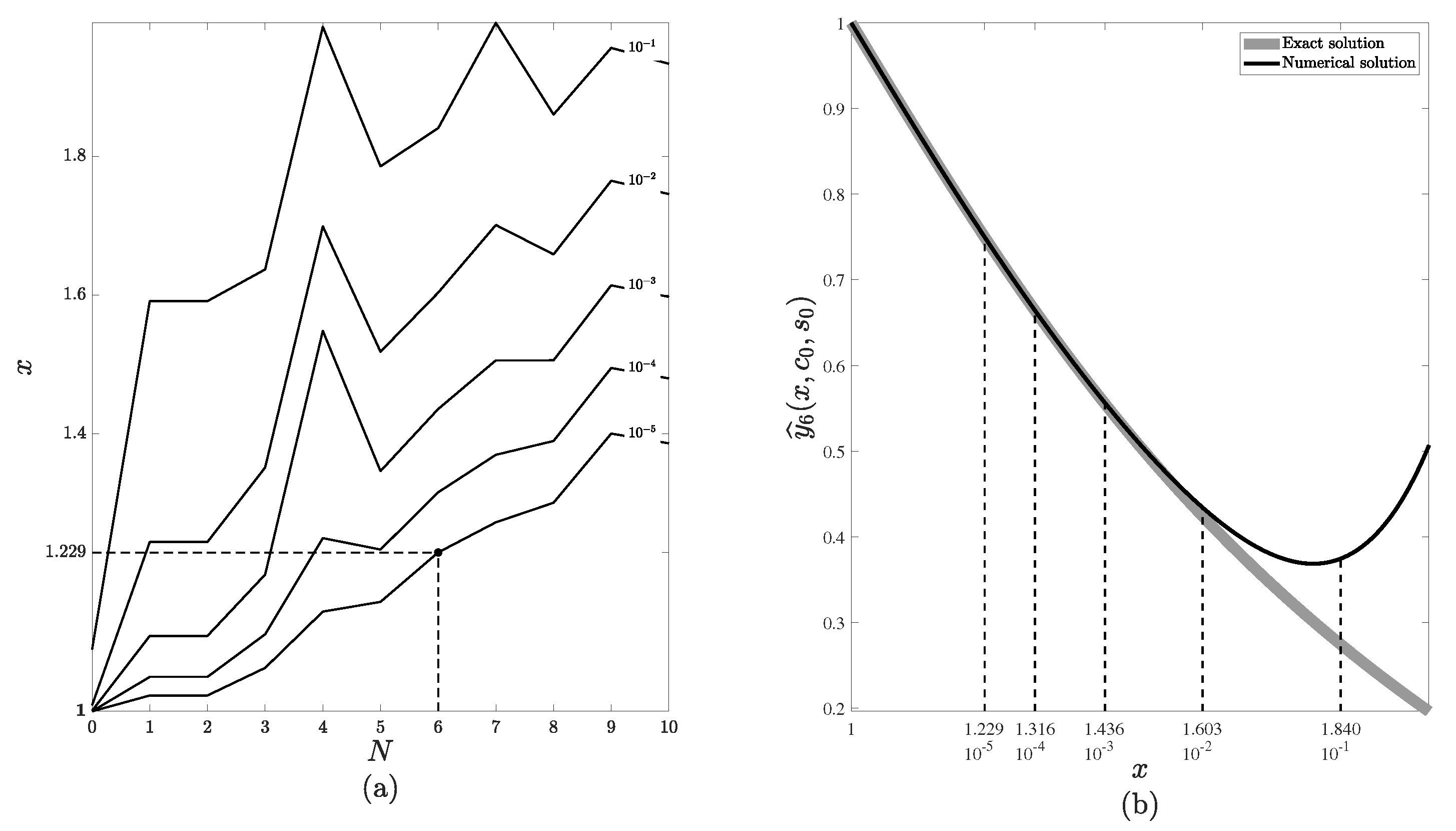
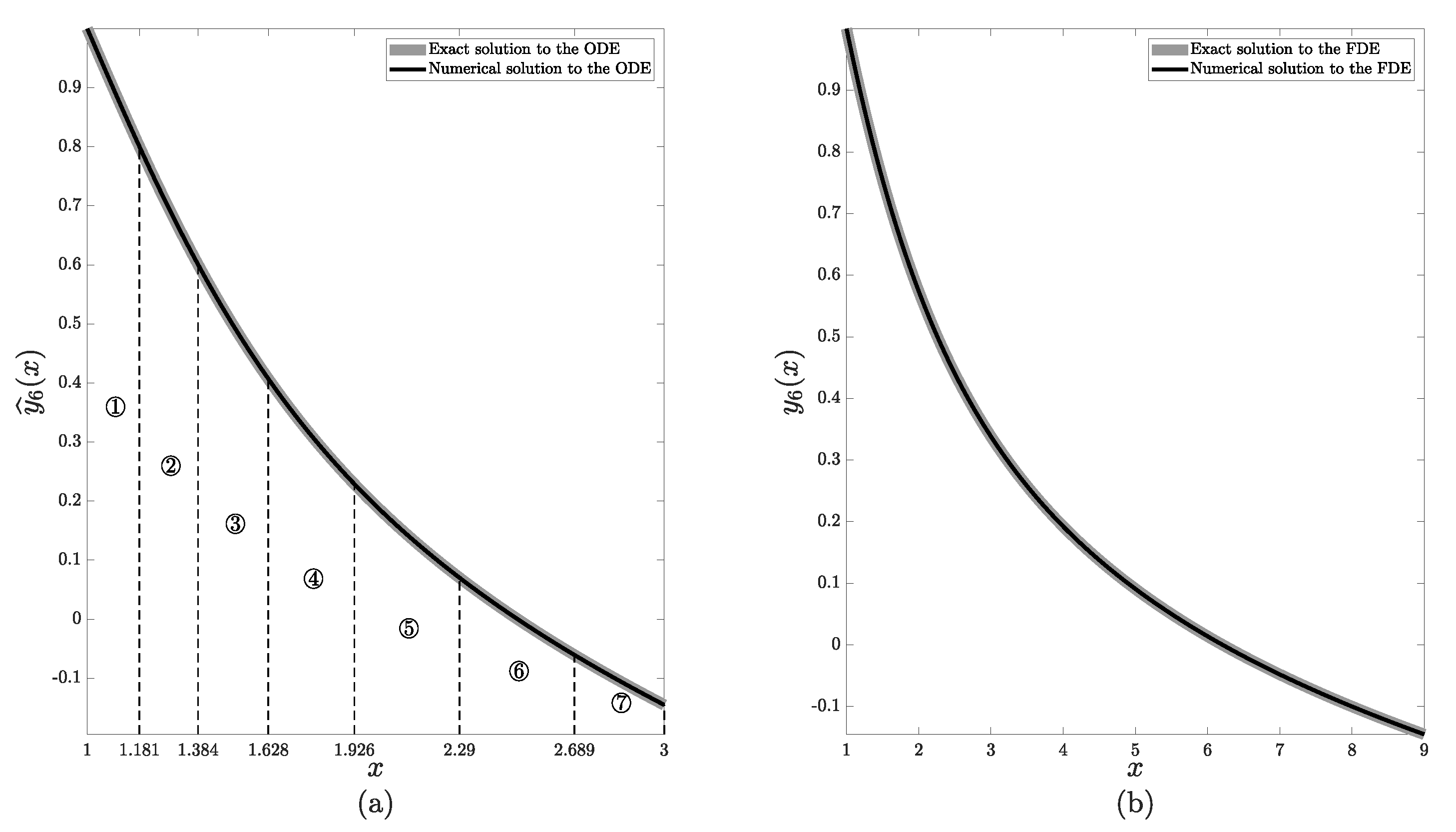
- Step 1. Let . The absolute differences are computed for and , where L is the upper bound of x. The contour plot depicting various levels of is presented in Figure 1a. It can be observed that for a fixed value of N the value of increases as x increases. New initial values , for the next approximation are computed as follows:where is the maximal allowed error of the numerical solution. Naturally, higher values of N result in larger values of at a cost of greater computation time. Let . Then, the resulting values of for different levels of are displayed in Figure 1b (denoted as black dashed lines, while the thick gray line denotes the analytical solution and the black solid line denotes the numerical solution). Figure 1 part (a) contains a contour plot with various levels of (absolute differences between the exact and numerical solutions to (32)–(33)). Parameter is set to for the remainder of this computational experiment, as shown by the point in Figure 1a.
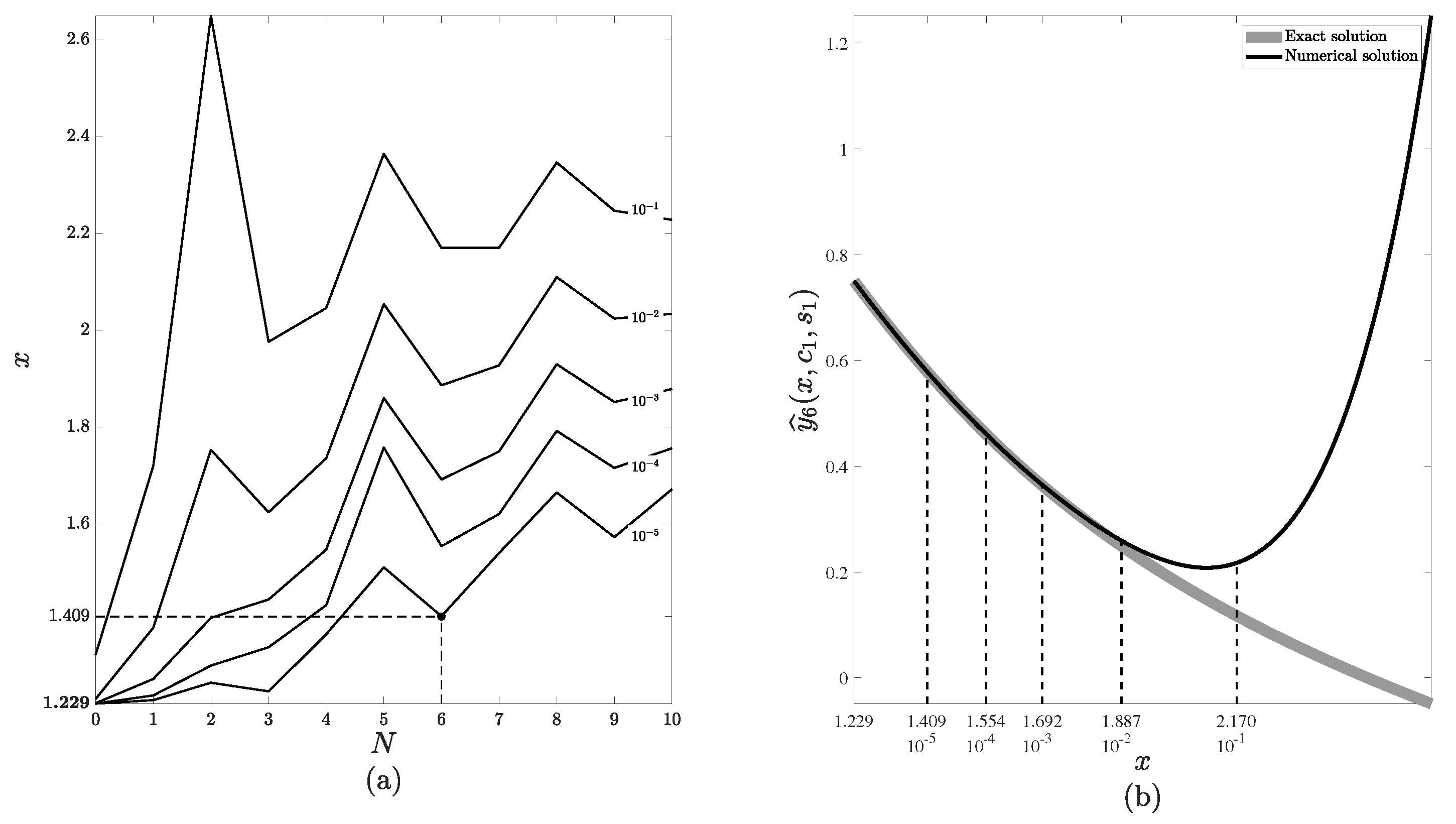
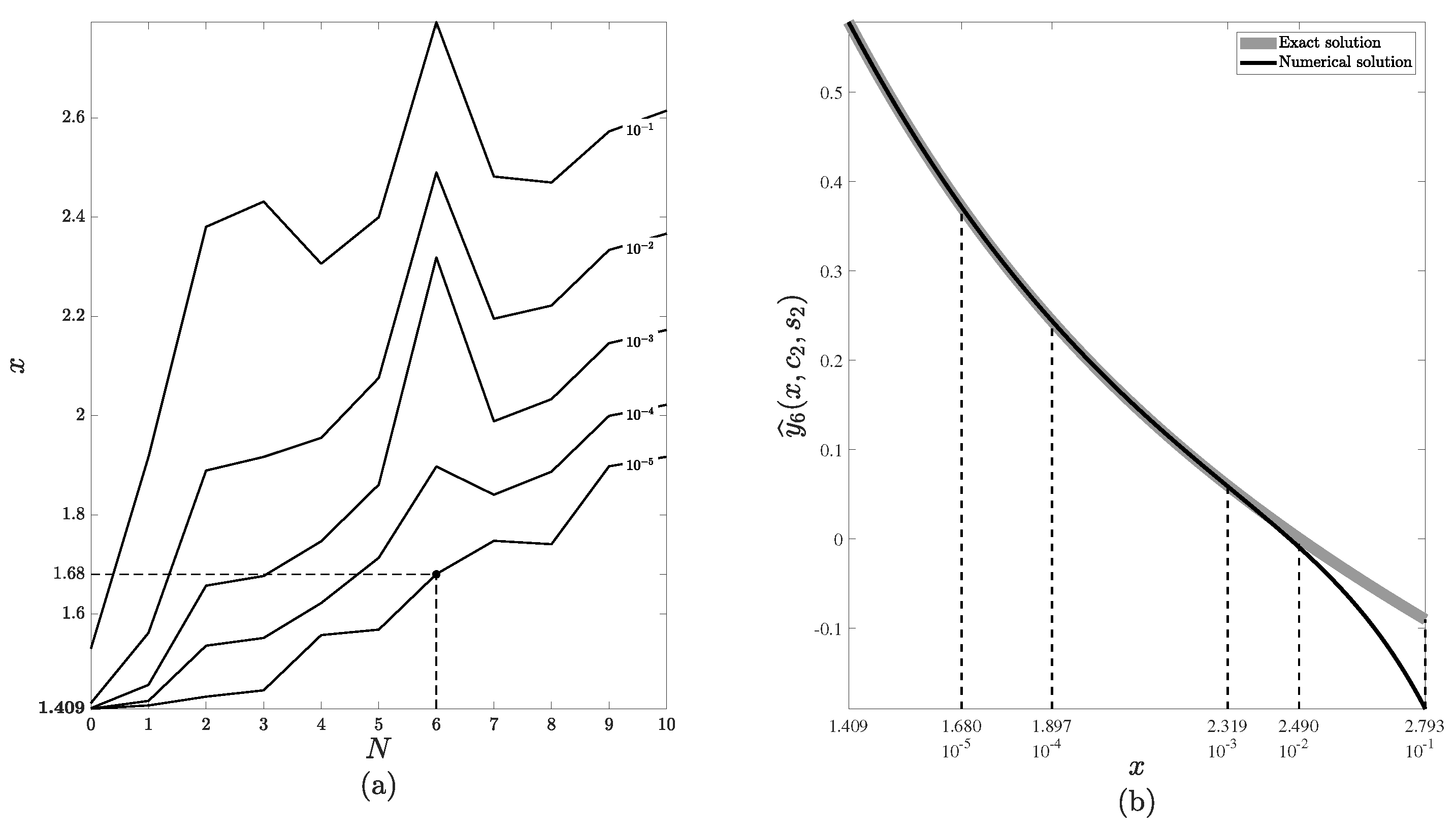
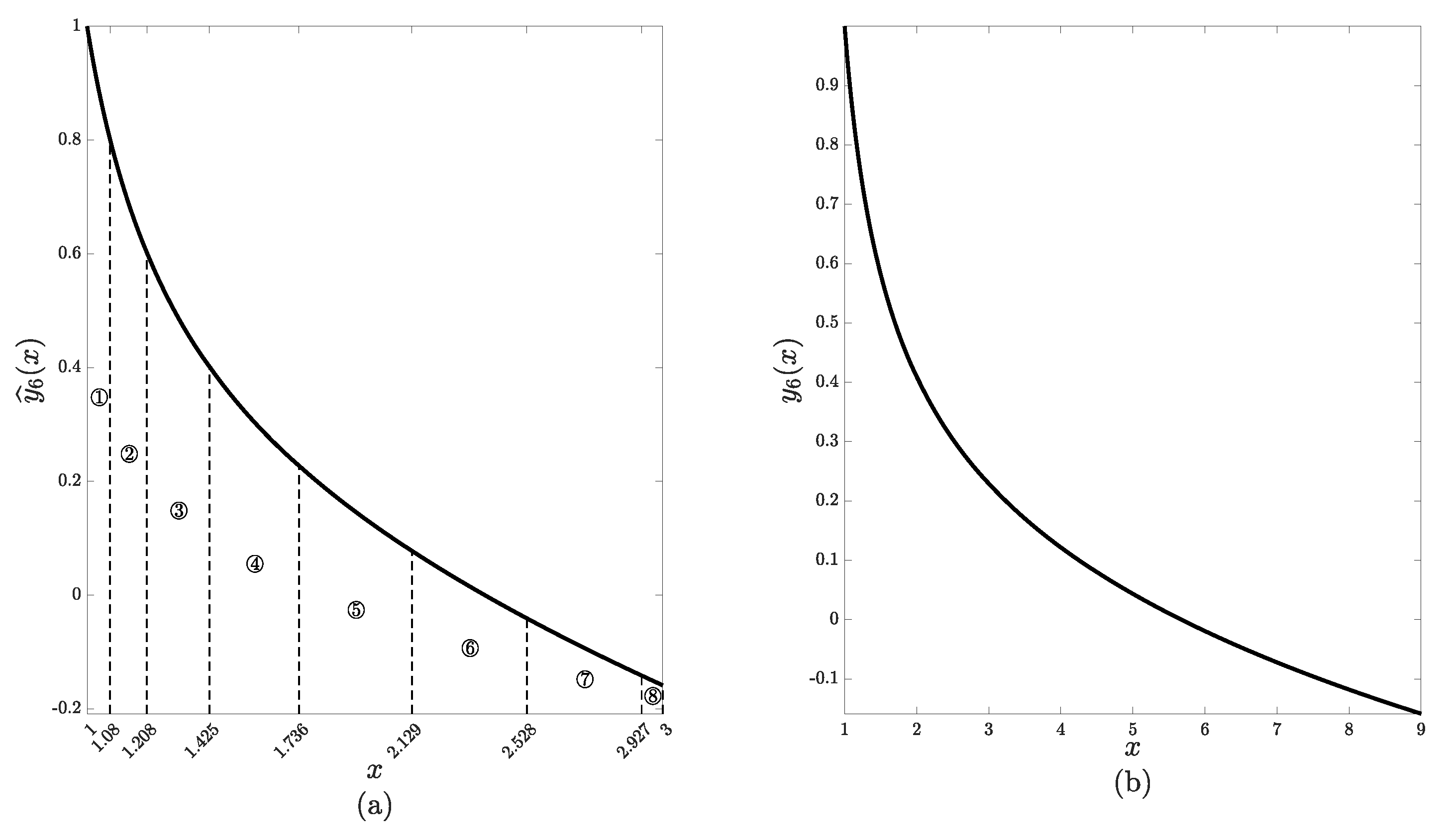
- Step . Analogous computations are performed for steps . Firstly, differences are evaluated for and and then new initial values , are computed:
3.2. The Implementation of the Numerical FDE Integration Scheme
- Transform the FDE (40)–(41) into the characteristic ODE using the procedure described in Section 2.5:
- Obtain analytic expressions of coefficients in the series solution (35) to the ODE (42)–(43) (see Section 2.1.1).
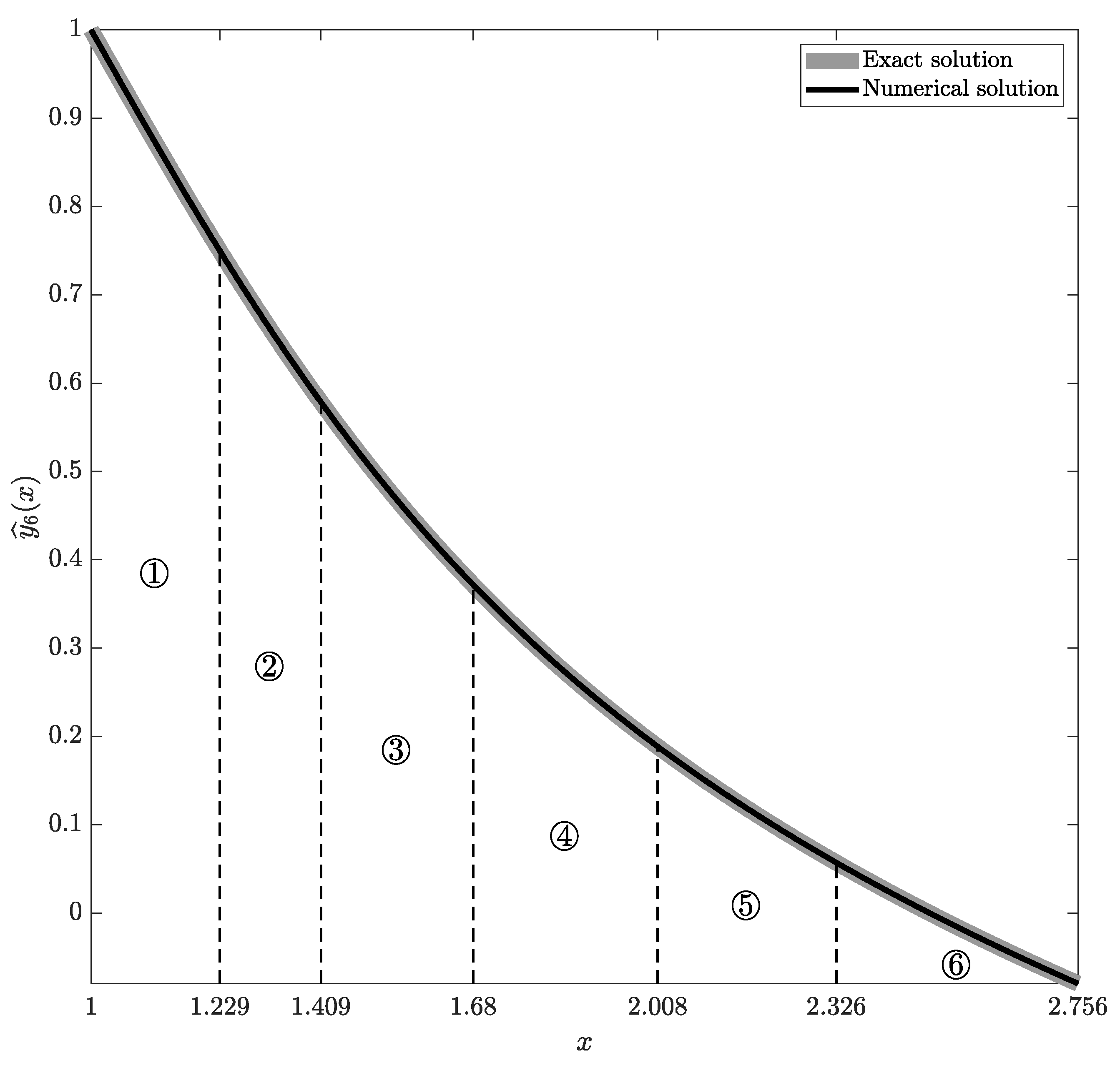
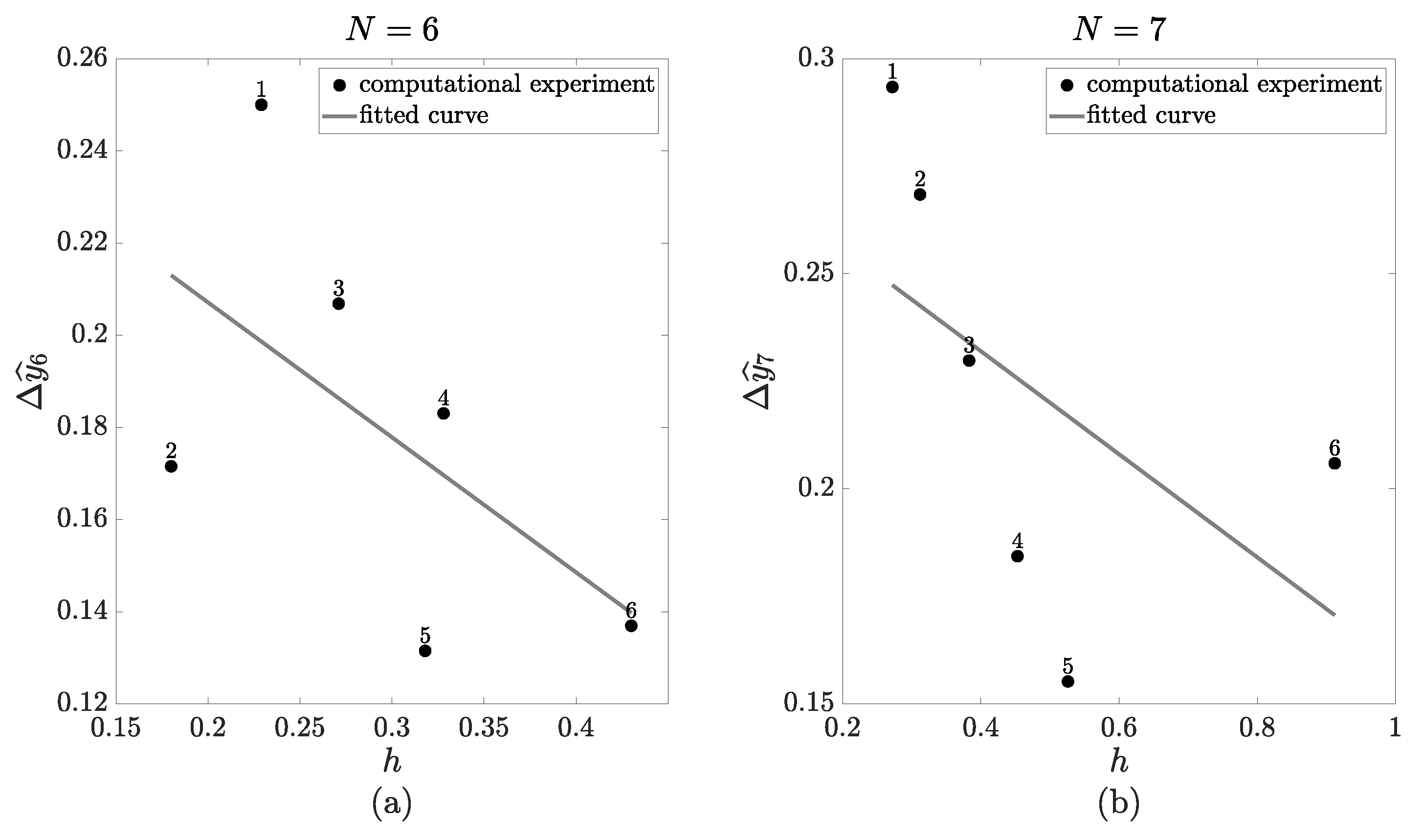
- Fix the values of the following parameters: the order of the approximation N, the upper bound of the independent variable L, the upper bound for the step-size , the upper bound for the change in the numerical solution . Note that the recommended values for the parameters and are derived from the study presented in the previous section (Figure 5). The value corresponds to the highest value of h on the regression line, while the value corresponds to the highest value of on the regression line.
- Repeat the following steps until the upper bound L is reached ():
- Evaluate coefficients .
- Find the lowest value of x at which at least one of the following conditions is violated:where , are regression coefficients determined in Section 3.1. The maximum and minimum values in (45) are necessary to ensure that the change in the numerical solution is computed correctly for non-monotonous and periodic functions.
- Assign new initial values:where is an arbitrary small number.
4. The Application of the Proposed Numerical FDE Integration Scheme
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A. Analytical Expressions of the Coefficients pj (c,s) for the ODE (30)–(31)
Appendix B. Transformation of FDE (49) into the Characteristic ODE (51)
Appendix C. Analytical Expressions of the Coefficients pj(c,s) for the ODE (51)–(52)
References
- Heymans, N. Fractional calculus description of non-linear viscoelastic behaviour of polymers. Nonlinear Dyn. 2004, 38, 221–231. [Google Scholar] [CrossRef]
- Li, X.; Tian, X. Fractional order thermo-viscoelastic theory of biological tissue with dual phase lag heat conduction model. Appl. Math. Model. 2021, 95, 612–622. [Google Scholar] [CrossRef]
- Dubey, V.P.; Dubey, S.; Kumar, D.; Singh, J. A computational study of fractional model of atmospheric dynamics of carbon dioxide gas. Chaos Solitons Fractals 2021, 142, 110375. [Google Scholar] [CrossRef]
- Acay, B.; Inc, M. Fractional modeling of temperature dynamics of a building with singular kernels. Chaos Solitons Fractals 2021, 142, 110482. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, F.; Yu, Q.; Li, T. Review of fractional epidemic models. Appl. Math. Model. 2021, 97, 281–307. [Google Scholar] [CrossRef]
- Biala, T.A.; Khaliq, A. A fractional-order compartmental model for the spread of the COVID-19 pandemic. Commun. Nonlinear Sci. Numer. Simul. 2021, 98, 105764. [Google Scholar] [CrossRef] [PubMed]
- Rezaei, M.; Yazdanian, A.; Ashrafi, A.; Mahmoudi, S. Numerical pricing based on fractional Black–Scholes equation with time-dependent parameters under the CEV model: Double barrier options. Comput. Math. Appl. 2021, 90, 104–111. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional econophysics: Market price dynamics with memory effects. Phys. A Stat. Mech. Appl. 2020, 557, 124865. [Google Scholar] [CrossRef]
- Betancur-Herrera, D.E.; Muñoz-Galeano, N. A numerical method for solving Caputo’s and Riemann-Liouville’s fractional differential equations which includes multi-order fractional derivatives and variable coefficients. Commun. Nonlinear Sci. Numer. Simul. 2020, 84, 105180. [Google Scholar] [CrossRef]
- Alchikh, R.; Khuri, S. Numerical solution of a fractional differential equation arising in optics. Optik 2020, 208, 163911. [Google Scholar] [CrossRef]
- Mendes, E.M.; Salgado, G.H.; Aguirre, L.A. Numerical solution of Caputo fractional differential equations with infinity memory effect at initial condition. Commun. Nonlinear Sci. Numer. Simul. 2019, 69, 237–247. [Google Scholar] [CrossRef]
- Firoozjaee, M.; Jafari, H.; Lia, A.; Baleanu, D. Numerical approach of Fokker–Planck equation with Caputo–Fabrizio fractional derivative using Ritz approximation. J. Comput. Appl. Math. 2018, 339, 367–373. [Google Scholar] [CrossRef]
- Kheybari, S. Numerical algorithm to Caputo type time–space fractional partial differential equations with variable coefficients. Math. Comput. Simul. 2021, 182, 66–85. [Google Scholar] [CrossRef]
- Esmaeili, S.; Shamsi, M.; Luchko, Y. Numerical solution of fractional differential equations with a collocation method based on Müntz polynomials. Comput. Math. Appl. 2011, 62, 918–929. [Google Scholar] [CrossRef]
- Han, W.; Chen, Y.M.; Liu, D.Y.; Li, X.L.; Boutat, D. Numerical solution for a class of multi-order fractional differential equations with error correction and convergence analysis. Adv. Differ. Equ. 2018, 2018, 1–22. [Google Scholar] [CrossRef]
- Hinze, M.; Schmidt, A.; Leine, R.I. Numerical solution of fractional-order ordinary differential equations using the reformulated infinite state representation. Fract. Calc. Appl. Anal. 2019, 22, 1321–1350. [Google Scholar] [CrossRef]
- Maleknejad, K.; Rashidinia, J.; Eftekhari, T. Numerical solutions of distributed order fractional differential equations in the time domain using the Müntz–Legendre wavelets approach. Numer. Methods Partial Differ. Equ. 2021, 37, 707–731. [Google Scholar] [CrossRef]
- Babaaghaie, A.; Maleknejad, K. Numerical solutions of nonlinear two-dimensional partial Volterra integro-differential equations by Haar wavelet. J. Comput. Appl. Math. 2017, 317, 643–651. [Google Scholar] [CrossRef]
- Garrappa, R. Numerical solution of fractional differential equations: A survey and a software tutorial. Mathematics 2018, 6, 16. [Google Scholar] [CrossRef]
- Jafari, H.; Tajadodi, H. He’s variational iteration method for solving fractional Riccati differential equation. Int. J. Differ. Equ. 2010, 2010, 764738. [Google Scholar] [CrossRef]
- Khan, N.A.; Ara, A.; Jamil, M. An efficient approach for solving the Riccati equation with fractional orders. Comput. Math. Appl. 2011, 61, 2683–2689. [Google Scholar] [CrossRef]
- Gohar, M. Approximate Solution to Fractional Riccati Differential Equations. Fractals 2019, 27, 1950128. [Google Scholar] [CrossRef]
- Timofejeva, I.; Navickas, Z.; Telksnys, T.; Marcinkevičius, R.; Yang, X.J.; Ragulskis, M.K. The extension of analytic solutions to FDEs to the negative half-line. AIMS Math. 2021, 6, 3257–3271. [Google Scholar] [CrossRef]
- Navickas, Z.; Bikulciene, L.; Ragulskis, M. Generalization of Exp-function and other standard function methods. Appl. Math. Comput. 2010, 216, 2380–2393. [Google Scholar] [CrossRef]
- Navickas, Z.; Marcinkevicius, R.; Telksnys, T.; Ragulskis, M. Existence of second order solitary solutions to Riccati differential equations coupled with a multiplicative term. IMA J. Appl. Math. 2016, 81, 1163–1190. [Google Scholar] [CrossRef]
- Kurakin, V.; Kuzmin, A.; Mikhalev, A.; Nechaev, A. Linear recurring sequences over rings and modules. J. Math. Sci. 1995, 76, 2793–2915. [Google Scholar] [CrossRef]
- Zaitsev, V.F.; Polyanin, A.D. Handbook of Exact Solutions for Ordinary Differential Equations; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Navickas, Z.; Ragulskis, M. How far one can go with the Exp-function method? Appl. Math. Comput. 2009, 211, 522–530. [Google Scholar] [CrossRef]
- Andrews, G.E.; Askey, R.; Roy, R. Special Functions; Number 71; Cambridge University Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Navickas, Z.; Telksnys, T.; Timofejeva, I.; Marcinkevičius, R.; Ragulskis, M. An operator-based approach for the construction of closed-form solutions to fractional differential equations. Math. Model. Anal. 2018, 23, 665–685. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, J.; Zhang, L. Basic Theory of Fractional Differential Equations; World Scientific: Singapore, 2016. [Google Scholar]
- Navickas, Z.; Telksnys, T.; Marcinkevicius, R.; Ragulskis, M. Operator-based approach for the construction of analytical soliton solutions to nonlinear fractional-order differential equations. Chaos Solitons Fractals 2017, 104, 625–634. [Google Scholar] [CrossRef]
- Scott, A. Encyclopedia of Nonlinear Science; Routledge: Abingdon-on-Thames, UK, 2006. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Timofejeva, I.; Navickas, Z.; Telksnys, T.; Marcinkevicius, R.; Ragulskis, M. An Operator-Based Scheme for the Numerical Integration of FDEs. Mathematics 2021, 9, 1372. https://doi.org/10.3390/math9121372
Timofejeva I, Navickas Z, Telksnys T, Marcinkevicius R, Ragulskis M. An Operator-Based Scheme for the Numerical Integration of FDEs. Mathematics. 2021; 9(12):1372. https://doi.org/10.3390/math9121372
Chicago/Turabian StyleTimofejeva, Inga, Zenonas Navickas, Tadas Telksnys, Romas Marcinkevicius, and Minvydas Ragulskis. 2021. "An Operator-Based Scheme for the Numerical Integration of FDEs" Mathematics 9, no. 12: 1372. https://doi.org/10.3390/math9121372
APA StyleTimofejeva, I., Navickas, Z., Telksnys, T., Marcinkevicius, R., & Ragulskis, M. (2021). An Operator-Based Scheme for the Numerical Integration of FDEs. Mathematics, 9(12), 1372. https://doi.org/10.3390/math9121372







