Abstract
Three-term conjugate gradient methods have attracted much attention for large-scale unconstrained problems in recent years, since they have attractive practical factors such as simple computation, low memory requirement, better descent property and strong global convergence property. In this paper, a hybrid three-term conjugate gradient algorithm is proposed and it owns a sufficient descent property, independent of any line search technique. Under some mild conditions, the proposed method is globally convergent for uniformly convex objective functions. Meanwhile, by using the modified secant equation, the proposed method is also global convergence without convexity assumption on the objective function. Numerical results also indicate that the proposed algorithm is more efficient and reliable than the other methods for the testing problems.
1. Introduction
In this paper, we consider the following unconstrained problem:
where function is continuously differentiable and bounded below. There are many methods for solving (1). such as the Levenberg–Marquardt methods [1], Newton methods [2] and quasi-Newton methods [3,4]. However, these methods are efficient for small and medium-sized problems and are not suitable for large scale problems in terms of the storage of a matrix for second order information or its approximation. Conjugate gradient (CG) methods [4,5,6,7,8,9,10,11,12] are much more effective for unconstrained problems, especially for large-scale cases by low memory requirements and strong convergence properties [6,8,9,10,11], etc. Meanwhile, CG methods have been applied to image restoration problems, optimal control problems and optimal problems in machine learning [13,14,15], etc. In this paper, we design a CG method for (1).
The nonlinear CG method was first proposed by Hestenes and Stiefel [16] for linear equations . In 1964, Fletcher and Reeves [17] extended the CG method in [16] to unconstrained optimization problems. After that, many researchers proposed various CG methods [6,7,8,9,10,12,18]. In CG methods, a sequence of iterative point is generated by an initial point and:
where is the step size which is determined by some line search technique and is the search direction. In a traditional CG method, the direction is usually defined by
Different conjugate parameter generates a different CG method which may be significantly different in theoretical properties and numerical performance. The Hestenes–Stiefel (HS) method [16] and Polak–Ribière–Polyak (PRP) method [19,20] have nice numerical performance and their conjugate parameters are:
where , and . Note that the HS method automatically satisfies the conjugate condition , independently of any line search technique. Dai and Liao [18] extended the above conjugate condition to:
where and . The new condition (4) gives a more accurate approximation for the Hessian matrix of the original objective function. Based on the condition (4), Dai and Liao [18] presented a new conjugate parameter:
In order to have global convergence, they selected the non-negative conjugate parameter, meaning that:
Under some mild conditions, the global convergence was established. However, the selection of the parameter t strongly affects the numerical performance, thus many scholars have focused on the choices for the parameter t, as can be seen in [21,22,23,24,25,26] etc.
Compared with the traditional two-term CG method, three-term CG methods [27,28,29,30,31] always have good numerical performance and nice theoretical properties, such as the sufficient descent property, independently of the accuracy of line search, i.e., it is always holds that:
where . Specifically, Zhang et al. [29] proposed a descent three-term PRP CG method in which the direction has the form:
and Zhang et al. [28] presented a descent three-term HS CG method in which the direction is:
and Babaie-Kafaki and Ghanbari [31] gave a modified three-term HS/DL method in which the direction owns the form:
For the above three directions, the sufficient descent property is always satisfied, i.e., . Note that the sufficient descent property is stronger that the descent property and may greatly improve the numerical performance of the corresponding methods.
Motivated by the above discussions, in this paper, we propose a new descent hybrid three-term CG algorithm. Under some mild conditions, the direction in this descent hybrid three-term CG algorithm may reduce the directions in [28,29,31], respectively, and another new three-term direction which also satisfies the sufficient descent property with (which is why we call our method as the hybrid three-term CG method). The new method owns the sufficient descent property independent of the accuracy of the line search technique. Under some mild conditions, the global convergence is established for uniformly convex objective functions. For general functions without convexity assumption, the global convergence is also established by using the modified secant condition in [32]. Numerical results indicate that the proposed algorithm is effective and reliable.
The paper is organized as follows. In Section 2, we firstly present the motivation for the hybrid three-term CG method and then propose the new hybrid three-term direction and prove some properties of the new direction and give the global convergence for uniformly convex objective functions at last. In Section 3, the global convergence for the general nonlinear functions is established with the help of the modified secant condition. Numerical tests are given in Section 4 to show the efficient and reliable nature of the proposed algorithm. Finally, the conclusions are presented in Section 5.
2. Motivation and Algorithm
In this section, we firstly present the motivation and give the form of the new direction.
It should be noted that if the exact line search technique is adopted, which implies , then it holds that:
If the inexact line search technique is adopted, these three methods may be different in theoretical property and numerical performance and the HS method and DL method may be not well defined (the denominator may be 0). Zhang [33] present a hybrid conjugate parameter for the traditional two-term Dai–Liao CG method:
The numerical results for general nonlinear equations show that the hybrid two-term conjugate residual method is effective and reliable.
Motivated by the above discussions and the nice properties of three-term CG methods, in the following, we propose a new hybrid descent three-term direction which has the following form: and:
where:
Note that the direction is well defined. In fact, if holds, the condition indicates that the method stops and the optimal solution () is obtained.
In the following, we give some remarks for the above direction. Note that if and hold, the direction reduces the direction in [28], and and hold, the direction reduces to the direction in [29]. Note also that if holds, then the parameter reduces to the conjugate parameter and the direction reduces to a modified vision of the direction in [31]. If holds, the direction reduces to a new three-term direction which also satisfies the sufficient descent property with . Overall, we regard the direction as the hybrid direction of the HS direction, the Dai–Liao direction and the PRP direction.
2.1. Algorithm for Uniformly Convex Functions
Now, based on the above analyses, we state the steps of our algorithm as follows:
| Algorithm 1: New hybrid three-term conjugate gradient method (HTTCG). |
|
Remark 1.
Note that in Algorithm 1, the line search technique is not explicitly given. In fact, any line search technique is accepted.
In the following, we show that Algorithm 1 owns the sufficient descent property independent of any line search technique.
Lemma 1.
For any line search technique, the sequence is generated by Algorithm 1, and it always holds that:
Proof.
If , we have , then it holds . For , by the definition of , we have the following inequality:
where the last inequality holds by . Then, (10) holds. This completes the proof. □
Lemma 1 means that the new direction satisfies the sufficient descent property independent of the line search technique. A conjugate condition also plays an important role in numerical performance. In the HS method, it automatically satisfies the condition ; in Dai–Liao method, the modified condition is always satisfied. In our part, by the design of the direction , we have:
2.2. Convergence for Uniformly Convex Functions
In the following, we present the global convergence analysis of the HTTCG method under the following assumptions.
Assumption 1.
The level set is bounded where is the starting point, namely, there exists a constant such that:
Assumption 2.
In some neighborhood of , the gradient of function , , is Lipschitz continuous, which means there exists a constant such that:
Note that based on Assumptions 1 and 2, there exists a positive constant G such that:
In the following, we show that the sequence generated by Algorithm 1 is bounded.
Lemma 2.
Assume and Assumptions 1 and 2 hold. For any line search technique, the sequence is generated by Algorithm 1. If the objective function f is uniformly convex on the set , then is bounded.
Proof.
Since function f is uniformly convex on the set , then for any , we have
where is the uniformly convex parameter. Especially, if we take and , then it holds that:
In the following, we prove the boundedness of parameters and . In fact, by their definitions, we have:
By the definition of , we have:
where the last inequality holds by (15). This completes the proof. □
The standard Wolfe line search technique is often referred to in CG methods (see [6,7,11] etc.). It has the following form:
where .
The following lemma plays an essential role for the global convergence theorem of our method. It can be seen in Lemma 3.1 in [34]. Hence, we only state it here and omit its proof.
Lemma 3.
Now, we establish the global convergence of Algorithm 1 for the uniformly convex objective functions.
Theorem 1.
Suppose that Assumptions 1 and 2 hold. Consider Algorithm 1 in which step size is computed by the line search technique (20). If the objective function f is uniformly convex on set , then Algorithm 1 globally converges in the sense that:
Proof.
From Lemma 1, we have that the direction satisfies the sufficient descent property with . By the first inequality in the line search technique (20), we have the sequence is non-increasing and . By the boundedness of in Lemma 2, we have that (21) holds. Then, (22) holds. Since f is uniformly convex, then we have (23). This completes the proof. □
3. Convergence for General Nonlinear Functions
In order to achieve the global convergence without convexity assumption for the general function, we adopt the modified secant condition in [32] (similar modified secant conditions can also be founded in [35,36] etc.). Concretely, the modified secant condition is:
where and and:
Based on the modified secant condition, we present the direction: and:
where:
Now, based on the above discussions, we state our algorithm as follows:
| Algorithm 2: Hybrid three-term CG method using modified secant condition (HTTCGSC). |
|
Note also that in Algorithm 2, the line search technique is not explicitly given. Similar to Lemma 1, we also have the following lemma. Here, we omit its proof.
Lemma 4.
For any line search technique, the sequence is generated by Algorithm 2, then it always holds that:
Lemma 5.
The sequences and are generated by Algorithm 2, then for any line search technique, we have:
and:
Proof.
In fact, for any line search technique, we consider two cases:
Case (i) holds. In this case, we have and . Then, we have:
Case (ii) holds. In this case, it holds that and . Then, we have:
Based on the above discussions, we have that for any line search technique, (27) always holds.
By the definition of , we have:
where the last inequality holds by . Then, (28) holds. This completes the proof. □
In the following, we assume that the limit (22) does not hold, otherwise Algorithm 2 converges. This means that there exists a positive constant such that:
Now, we give the global convergence of Algorithm 2 for general nonlinear problems without convex assumption.
Theorem 2.
4. Numerical Results
In this section, we firstly present the numerical performance of Algorithm 2 and compare it with other methods in [28,31]. Then, an accelerated technique is applied in our method.
4.1. Numerical Performance of Algorithm 2
In this subsection, we focus on the numerical performance of Algorithm 2 and compare it with the MTTDLCG method in [31] and the MTTHSCG method in [28]. For the MTTDLCG method and the MTTHSCG method, we take their settings for parameters. For the value of parameter t, authors in [37] point out that is a good choice for the Dai–Liao method and the authors in [18] suggest is a good choice. In this paper, we take .
We execute the tests on a personal computer with the Windows 10 operating system, AMD CPU with GHz, 16.00 GB of RAM. Meanwhile, the corresponding codes are written in MATLAB R2016b. The parameters referred are that: , , , if , otherwise. In the following, we present the stopping rules:
Stopping rules (Himmeblau rule): During the testing, if , set or let . Testing stops if or Tem holds. The values of these parameters are and . Meanwhile, the testing also stops if the total iteration number is larger than 10,000.
For the step size, will be chosen when the search number of the WWP line search is more than 6. Testing problems with initial points considered here are from [38], which are listed in Table 1. Meanwhile, for each problem, ten large-scale dimensions with 1500, 3000, 6000, 7500, 9000, 15,000, 30,000, 60,000, 75,000 and 90,000 variables are considered.

Table 1.
The testing problems.
To approximately assess the corresponding numerical performances, the performance profile introduced by Dolan and Moré in [39] is adopted. That is, for each method, we plot the fraction P of the testing problems for which the method is within a factor of the best time. The left side of the figure presents the percentage of the test problems for which a method is the fastest; the right side gives the percentage of the test problems that are successfully solved by each of the methods. Figure 1 presents the performance profile of the three methods in iterations.
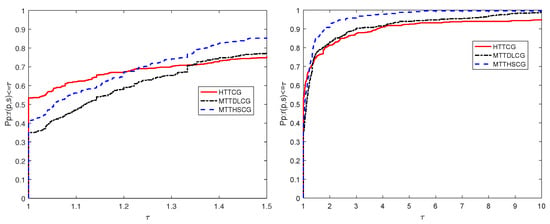
Figure 1.
Performance profiles of the numerical results for these methods in number of iterations case.
From Figure 1, we have that Algorithm 2 (the HTTCG method) in , the MTTDLCG method in and the MTTHSCG method in solve the test problems with the least iteration number. This indicates that Algorithm 2 performs best. Figure 2 presents the performance profile of the three methods in the function-gradient number case:
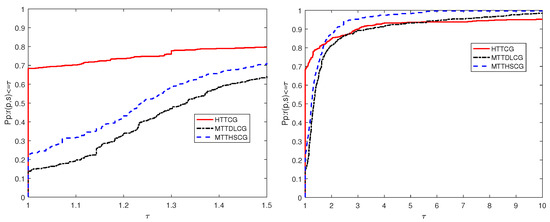
Figure 2.
Performance profiles of the numerical results for these methods in a number of function and gradient evaluations.
From Figure 2, we have that Algorithm 2 at , the MTTDLCG method at and the MTTHSCG method at solve the test problems with the least number of computing functions and gradients. This also indicates that Algorithm 2 performs best. Figure 3 presents the performance profile of the three methods in CPU time consumed.
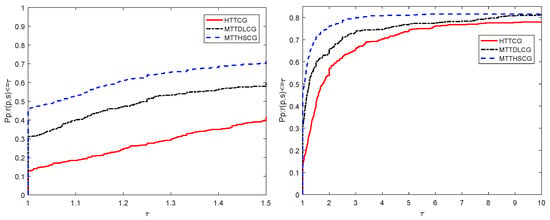
Figure 3.
Performance profiles of the numerical results for these methods in CPU time consumed case.
From Figure 3, we have that Algorithm 2 at , the MTTDLCG method at and the MTTHSCG method at solve the test problems with the least CPU time consumed. This indicates that the MTTHSCG method performs best in terms of CPU time consumed. From Figure 1, Figure 2 and Figure 3, we have that Algorithm 2 is effective and comparable with the MTTDLCG method and the MTTHSCG method for the test problems in Table 1.
4.2. Accelerated Strategy for Algorithm 2
In order to improve the numerical performances of Algorithm 2, in this subsection, we utilize the acceleration strategy in [40], which modifies the step in a multiplicative manner along iterations. Concretely, the iterative form (2) reduces to:
where and and if , , otherwise, .
We also test the problems in Table 1 and compare Algorithm 2 with the acceleration strategy with Algorithm 2. The corresponding parameters remain unchanged. The performance profiles can be founded in Figure 4, Figure 5 and Figure 6.
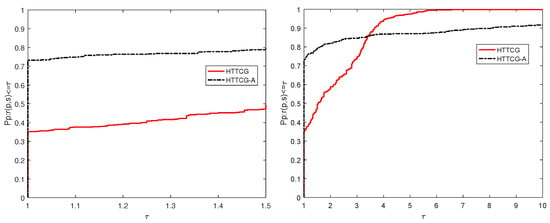
Figure 4.
Performance profiles of Algorithm 2 and the acceleration form in NI case.
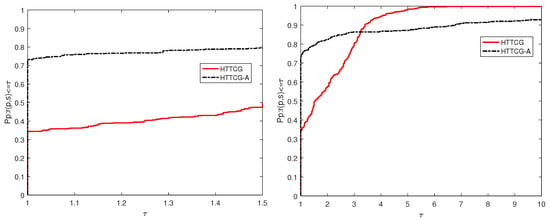
Figure 5.
Performance profiles of Algorithm 2 and the acceleration form in NFG case.
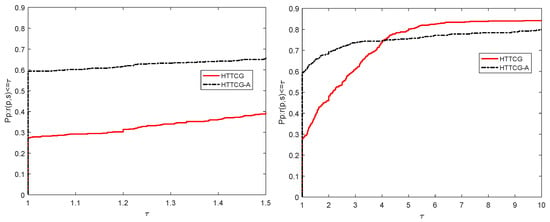
Figure 6.
Performance profiles of Algorithm 2 and the acceleration form in CPU Time case.
From Figure 4, we find that the Algorithm 2 with the acceleration strategy (HTTCG-A method) in and HTTCG method in solve the testing problems with the least iteration number. From Figure 5, we see that the HTTCG-A method in and HTTCG method in solve the testing problems with the least number of computing functions and gradient. From Figure 6, we see that the HTTCG-A method in and HTTCG method in solve the testing problems with the least CPU time consumed. These all indicate that the acceleration strategy works and can reduce the number of iterations, the number of computing functions and gradients and the time consumed.
5. Conclusions
Unconstrained smooth optimization problems can be found in many problems such as optimal control problems and machine learning problems, etc. In this paper, a hybrid three-term descent conjugate gradient algorithm is proposed. This hybrid three-term conjugate gradient algorithm owns the sufficient descent property independent of any line search technique. Meanwhile, it also satisfies the extent Dai–Liao conjugate condition. Under some mild conditions, this algorithm is globally convergent for the uniformly convex functions. For general nonlinear function, the hybrid method is also globally convergent by using some modified secant conditions. Numerical results indicate that the hybrid method is effective and reliable. Meanwhile, an acceleration strategy is adopted to improve the numerical performances. In the future, we will apply our conjugate gradient methods to some non-smooth problems by smoothing strategy and Moreau–Yosida regularization technique and to image restoration problems.
Author Contributions
Conceptualization, Q.T., X.W., L.P. and M.Z.; methodology, Q.T. and X.W.; software, X.W.; validation, X.W., L.P., M.Z. and F.M.; formal analysis, X.W., Q.T. and F.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by the Natural Science Foundation of Shandong Province with No. ZR2019BA014.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data can be found in the manuscript.
Acknowledgments
The authors would like to thank Gonglin Yuan of School of Mathematics and Information Science at Guangxi University for their assistance in the numerical experiment. The authors are grateful to the referees and the editor for their constructive comments and helpful suggestions which much improve the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fan, J.; Zeng, J. A Levenberg–Marquardt algorithm with correction for singular system of nonlinear equations. Appl. Math. Comput. 2013, 219, 9438–9446. [Google Scholar] [CrossRef]
- Yerina, M.; Izmailov, A. The Gauss–Newton method for finding singular solutions to systems of nonlinear equations. Comp. Math. Math. Phys. 2007, 47, 748–759. [Google Scholar] [CrossRef]
- Yuan, G.; Wei, Z.; Wang, Z. Gradient trust region algorithm with limited memory BFGS update for nonsmooth convex minimization. Comput. Optim. Appl. 2013, 54, 45–64. [Google Scholar] [CrossRef]
- Yuan, G.; Wei, Z.; Lu, X. Global convergence of BFGS and PRP methods under a modified weak Wolfe–Powell line search. Appl. Math. Model. 2017, 47, 811–825. [Google Scholar] [CrossRef]
- Yuan, G.; Lu, J.; Wang, Z. The PRP conjugate gradient algorithm with a modified WWP line search and its application in the image restoration problems. Appl. Numer. Math. 2020, 152, 1–11. [Google Scholar] [CrossRef]
- Dai, Y.; Han, J.; Liu, G.; Sun, D.; Yin, H.; Yuan, Y. Convergence properties of nonlinear conjugate gradient methods. SIAM J. Optim. 2000, 10, 345–358. [Google Scholar] [CrossRef]
- Yuan, G.; Wang, X.; Sheng, Z. Family weak conjugate gradient algorithms and their convergence analysis for nonconvex functions. Numer. Algorithms 2020, 84, 935–956. [Google Scholar] [CrossRef]
- Hager, W.; Zhang, H. A survey of nonlinear conjugate gradient methods. Pac. J. Optim. 2006, 2, 35–58. [Google Scholar]
- Andrei, N. Numerical comparison of conjugate gradient algorithms for unconstrained optimization. Stud. Inform. Control. 2007, 16, 333–352. [Google Scholar]
- Li, X.; Wang, X.; Sheng, Z.; Duan, X. A modified conjugate gradient algorithm with backtracking line search technique for large-scale nonlinear equations. Int. J. Comput. Math. 2018, 95, 382–395. [Google Scholar] [CrossRef]
- Wang, X.; Hu, W.; Yuan, G. A Modified Wei-Yao-Liu Conjugate Gradient Algorithm for Two Type Minimization Optimization Models; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Yuan, G.; Meng, Z.; Li, Y. A modified Hestenes and Stiefel conjugate gradient algorithm for large-scale nonsmooth minimizations and nonlinear equations. J. Optim. Theory Appl. 2016, 168, 129–152. [Google Scholar] [CrossRef]
- Cao, J.; Wu, J. A conjugate gradient algorithm and its applications in image restoration. Appl. Numer. Math. 2020, 152, 243–252. [Google Scholar] [CrossRef]
- Møller, F. A scaled conjugate gradient algorithm for fast supervised learning. Neural Netw. 1993, 6, 525–533. [Google Scholar]
- Zhou, Y.; Wu, Y.; Li, X. A New Hybrid PRPFR Conjugate Gradient Method for Solving Nonlinear Monotone Equations and Image Restoration Problems. Math. Probl. Eng. 2020, 2020, 1–13. [Google Scholar] [CrossRef]
- Hestenes, R.; Stiefel, L. Methods of conjugate gradients for solving linear systems. J. Res. Natl. Bur. Stand. 1952, 49, 409–436. [Google Scholar] [CrossRef]
- Fletcher, R.; Reeves, C.M. Function minimization by conjugate gradients. Comput. J. 1964, 2, 149–154. [Google Scholar] [CrossRef]
- Dai, Y.; Liao, L. New conjugacy conditions and related nonlinear conjugate gradient methods. Appl. Math. Opt. 2001, 43, 87–101. [Google Scholar] [CrossRef]
- Polak, E. The conjugate gradient method in extreme problems. USSR Comput. Math. Math. Phys. 1969, 9, 94–112. [Google Scholar] [CrossRef]
- Polak, E.; Ribière, G. Note sur la convergence de directions conjugees. Rev. Fr. Informat Rech. Opertionelle 1969, 16, 35–43. [Google Scholar]
- Zhang, K.; Liu, H.; Liu, Z. A new Dai-Liao conjugate gradient method with optimal parameter choice. Numer. Funct. Anal. Optim. 2019, 40, 194–215. [Google Scholar] [CrossRef]
- Andrei, N. A Dai-Liao conjugate gradient algorithm with clustering of eigenvalues. Numer. Algorithms 2018, 77, 1273–1282. [Google Scholar] [CrossRef]
- Babaie-kafaki, S.; Ghanbari, R. The Dai-Liao nonlinear conjugate gradient method with optimal parameter choices. Eur. J. Oper. Res. 2014, 234, 625–630. [Google Scholar] [CrossRef]
- Zheng, Y.; Zheng, B. Two new Dai-Liao-type conjugate gradient methods for unconstrained optimization problems. J. Optim. Theory Appl. 2017, 175, 502–509. [Google Scholar] [CrossRef]
- Peyghami, M.; Ahmadzadeh, H.; Fazli, A. A new class of efficient and globally convergent conjugate gradient methods in the Dai-Liao family. Optim. Method. Softw. 2015, 30, 843–863. [Google Scholar] [CrossRef]
- Yuan, G.; Wang, X.; Sheng, Z. The projection technique for two open problems of unconstrained optimization problems. J. Optim. Theory Appl. 2020, 186, 590–619. [Google Scholar] [CrossRef]
- Narushima, Y.; Yabe, H.; Ford, J. A three-term conjugate gradient method with sufficient descent property for unconstrained optimization. SIAM J. Optim. 2011, 21, 212–230. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, W.; Li, D. Some descent three-term conjugate gradient methods and their global convergence. Optim. Method. Softw. 2007, 22, 697–711. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, W.; Li, D. A descent modified Polak-Ribière-Polyak conjugate gradient method and its global convergence. IMA J. Numer. Anal. 2006, 26, 629–640. [Google Scholar] [CrossRef]
- Andrei, N. A simple three-term conjugate gradient algorithm for unconstrained optimization. J. Comput. Appl. Math. 2013, 241, 19–29. [Google Scholar] [CrossRef]
- Babaie-Kafaki, S.; Ghanbari, R. Two modified three-term conjugate gradient methods with sufficient descent property. Optim. Lett. 2014, 8, 2285–2297. [Google Scholar] [CrossRef]
- Li, D.; Fukushima, M. A modified BFGS method and its global convergence in nonconvex minimization. J. Comput. Appl. Math. 2001, 129, 15–35. [Google Scholar] [CrossRef]
- Zhang, L. A derivative-free conjugate residual method using secant condition for general large-scale nonlinear equations. Numer. Algorithms 2020, 83, 1277–1293. [Google Scholar] [CrossRef]
- Sugiki, K.; Narushima, Y.; Yabe, H. Globally convergent three-term conjugate gradient methods that use secant conditions and generate descent search directions for unconstrained optimization. J. Optim. Theory Appl. 2012, 153, 733–757. [Google Scholar] [CrossRef]
- Wei, Z.; Li, G.; Qi, L. New quasi-Newton methods for unconstrained optimization problems. Appl. Math. Comput. 2006, 175, 1156–1188. [Google Scholar] [CrossRef]
- Yuan, G.; Wei, Z. Convergence analysis of a modified BFGS method on convex minimizations. Comput. Optim. Appl. 2010, 47, 237–255. [Google Scholar] [CrossRef]
- Dai, Y.; Kou, C. A nonlinear conjugate gradient algorithm with an optimal property and an improved wolfe line search. SIAM J. Optim. 2013, 23, 296–320. [Google Scholar] [CrossRef]
- Andrei, N. An unconstrained optimization test functions collection. Adv. Model Optim. 2008, 10, 147–161. [Google Scholar]
- Dolan, E.; Moré, J. Benchmarking optimization software with performance profiles. Math. Program 2002, 91, 201–213. [Google Scholar] [CrossRef]
- Andrei, N. An acceleration of gradient descent algorithm with backtracking for unconstrained optimization. Numer. Algorithms 2006, 42, 63–73. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).