Abstract
If is a graph of order n, we call an isolating set if the graph induced by contains no edges. The minimum cardinality of an isolating set of G is called the isolation number of G, and it is denoted by It is known that and the bound is sharp. A subset is called dominating in G if . The minimum cardinality of a dominating set of G is the domination number, and it is denoted by In this paper, we analyze a family of trees T where , and we prove that implies Moreover, we give different equivalent characterizations of such graphs and we propose simple algorithms to build these trees from the connections of stars.
1. Introduction
We start by introducing the basic notation. Let be a simple, undirected, finite graph of order The open neighbourhood of a vertex denoted is the set of neighbours of thus, The closed neighborhood of v is the set The degree of a vertex denoted by is the number of neighbours of so A leaf in a graph G is a vertex of degree 1 in G and a support vertex is a vertex adjacent to a leaf. A strong support vertex is adjacent to at least two leaves.
The set of leaves of G is denoted by and the set of all support vertices of G is denoted by . The subgraph of G induced by is denoted by and the subgraph obtained from G by deleting all vertices in S, and all edges incident with vertices in S are denoted by . We say that a set is a two-packing one if for any two vertices .
A subset is called dominating in G if The minimum cardinality of a dominating set of G is the domination number, and is denoted by A dominating set of cardinality is called a minimum dominating set or -set. There is extensive literature on dominating sets in graphs. In particular, we refer to the books by Haynes et al. [1] and Yero [2] for a revision of theoretical, algorithmic and application aspects of domination in graphs.
In [3,4], the authors introduce the definition of an isolation number of a graph and consider bounds on it in terms of order and degree. For a family of graphs they call a set of vertices an -isolating set if the graph induced by the set contains no member of as a subgraph. In particular, -isolating sets coincide with the usual dominating sets.
The vertices not dominated by a -isolating set form an independent set. In the sequel, we use an isolating set instead of a -isolating set. The minimum cardinality of an isolating set of a graph G is denoted and is called the isolation number of An isolating set of cardinality is called a minimum isolating set or -set. In [4], the authors proved that and the bound is sharp. In a recent paper [5], this bound has been improved for outerplanar graphs by considering the number of vertices of degree 2.
Our work focuses on the characterization of trees considering the concept of an isolating set. We first study the relationship between isolation and domination numbers for such graphs, and then we investigate the trees for which the bound is reached. An important contribution of this work is the characterization of trees for which (see Theorem 5). We also provide different equivalent conditions of the fact that (see Theorem 8) and we show that, in particular, trees such that verify that .
Using the theoretical description of the trees, we obtain algorithms to build trees with the condition and . We show several examples of the utilization of these algorithms to obtain ad hoc networks.
This work is organized as follows. Section 2 presents theoretical results to characterize trees for which the domination number is equal to the isolation number. In Section 3, we deal with the study of a family of trees T such that These kinds of trees are a particular case of trees with Section 4 presents an algorithm to build this family of trees to determine the most important parameters studied in this paper. Finally, Section 5 is devoted to the conclusion.
2. Study of Trees with Domination Number Equal to Isolation Number
We begin by giving an exact value of the isolation number for paths.
Theorem 1.
If is a path with vertices, then
Proof.
The set is an isolating set of cardinality of for , and is an isolating set of cardinality of for so we obtain that
Now, let D be an isolating set of Since D is isolating, there are no four consecutive vertices in and the distance for Thus, we have □
We can characterize trees T for which Let be the family of trees T that can be obtained from a sequence of trees such that is a star and and if can be obtained from by adding a star and an edge where x is a vertex at a distance two from a leaf of and y is an end vertex of a star
The following observation gives the immediate properties of trees belonging to the family , and Figure 1 shows an example.
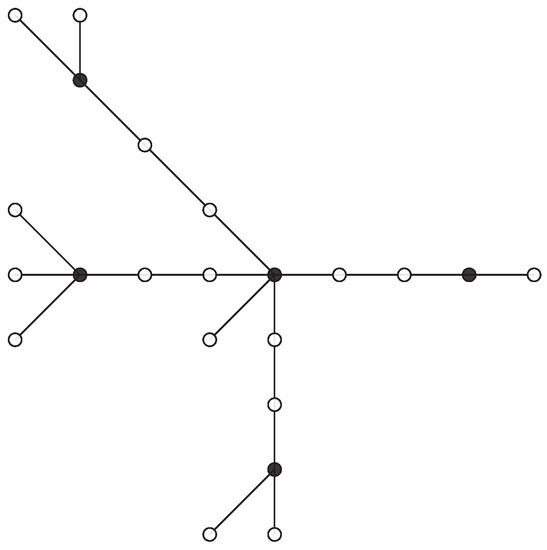
Figure 1.
Example of a tree from the family . The black dots correspond to vertices in set .
Observation 1.
If , then forms a maximum 2-packing, and it is the unique -set not containing leaves.
Observation 2.
Let T be a tree of order such that is a dominating set of T and forms a maximum 2-packing. If is a longest path in we have and . Since is a dominating set of T, we also get at a distance 2 from a leaf. Thus, is a tree, and we can obtain T from by attaching the star and the edge Therefore, implies
As consequence of the above observations, we have the following characterization of trees belonging to the family
Theorem 2.
Let T be a tree of order and forms a maximum 2-packing if, and only if .
Proof.
We prove by induction on If then Assume the result holds for every tree of order Now, we take T of order We are going to see that if is a longest path in then In fact, using the hypothesis, we have that is a maximum 2-packing in and Hence, by induction, By Observation 2, we infer that We finish the proof using Observation 1. □
We have the following consequence of Theorem 2.
Theorem 3.
Let T be a tree of order if, and only if for every vertex .
Proof.
Assume first that By Observation 1, for every If there exists a vertex x such that then there are two vertices with which contradicts that is a 2-packing. Now, if for every is then and is a 2-packing, so the result holds from Theorem 2. □
The following result is a characterization of trees T with
Theorem 4.
Let T be a tree of order if, and only if for every vertex
Proof.
Assume Let D be a minimum dominating set of First, we verify by contradiction that
If and there exists a vertex , then is an isolating set of If and there are two different support vertices such that , then is an isolating set of In both cases we have a contradiction with
Now, we prove by induction on l that
If then T is a star, and the result holds. Assume that Equation (3) is true for trees with Let T be a tree with , and let D be a minimum dominating set not containing leaves of Let be a longest path of From Equation (1), we have , and then We verify that by contradiction as follows. If , then Hence, is an isolating set of and we have a contradiction. Then we can consider the tree and By induction, is a dominating set of Using that , we conclude that , and the Equation (3) holds.
Now, we assume that every is By Theorem 3 we have
We prove by induction on that is a minimum isolating set of T and If then T is a star and Assume the result holds for trees with support vertices. Let T be a tree with support vertices. Take a longest path in T and Then, is a tree with and for every vertex By induction, is a minimum isolating set of and By Observation 1, is a set. Now, let W be a minimum isolating set of Therefore, the set is an isolating set of From the fact that , we have that is not an isolating set of Then,
and we conclude that □
The next theorem, which characterizes trees T with equality , is a final consequence of the results above.
Theorem 5.
Let T be a tree of order The following are equivalent:
- 1.
- 2.
- is a -set which forms a 2-packing of
- 3.
- for every vertex
- 4.
3. Extremal Trees
In this section, we will find the extremal trees, such as . We first introduce the following theorem proved in [4].
Theorem 6.
Let G be a connected graph on vertices, and different from the cycle Then, , and this bound is sharp.
We will characterize all trees for which the equality holds. We also show that these trees are special cases of graphs from the family for which From Theorem 1, we have that some paths are extremal trees.
Observation 3.
Let be a path with . Then if, and only if either or
Let be the family of trees T that can be obtained from a sequence of trees such that is a path and and, if can be obtained from by adding a path and an edge where x is a vertex at a distance two from a leaf of and y is a leaf of a joined path From the construction, we have the following result.
Observation 4.
For a tree T with at least three vertices, if, and only if and for every
Figure 2 shows an example of a tree from the family . The support vertices are in black.
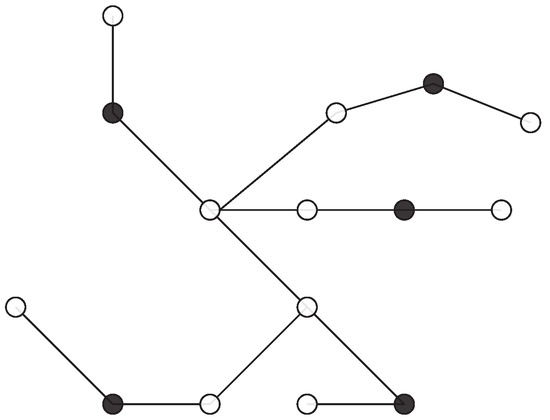
Figure 2.
Example of a tree from the family . The support vertices are in black.
The following results show that trees for which the equality holds are exactly the trees belonging to the family .
Lemma 1.
Let T be a tree of order If then
Proof.
From Theorem 6 we know that for any tree T. Let thus, T contains k copies of for some Let D be an -set of From the construction of at least one vertex of every must belong to so Thus, □
Theorem 7.
Let T be a tree of order We have that if, and only if
Proof.
The necessary condition follows from Lemma 1. To prove the sufficiency, we use induction on We show that if then If then so let Then or , and the result is true. Assume the result holds for every with less than n vertices.
Let be a longest path in a tree T with vertices, chosen in a way that is as big as possible, and let D be an -set of Assume first that , and let Observe that implies because If , then by induction and using the fact that and finally we obtain
Let now and assume first If then let Notice that and If then by induction and using the fact that and finally we obtain If then, from Lemma 1, , and we also obtain the final inequality. If then is a support vertex of T; thus, considering also , we conclude that , and similarly as for the case we obtain the desired inequality.
Let now and consider If then by induction , and since and we obtain the final inequality.
Consider the case when Then by Observation 4, Lemma 1 and Theorem 5, we have that is a -set and . Since is a dominating set of is a dominating set of T, and then is a minimum dominating set of T. We get . Since (by our assumption) by Observation 4 we know that either , or there is a support vertex with This last condition does not hold since and for any thus, . By Theorem 5, we have , and finally, we get □
The results above can be summarized as follows.
Theorem 8.
Let T be a tree of order The following are equivalent:
- 1.
- 2.
- 3.
- 4.
- is a 2-packing -set with vertices.
4. Algorithms
The pseudocode in Algorithm 1 shows the implementation of the procedure described in Section 2 to build trees of the family . The function receives a tree T of the family , a star K that is to be appended to the tree, and a set C made up of all the nodes in T that are a distance 2 from any leaf. These nodes are all the possible points of connection for the star. The function returns an updated tree that results from connecting a leaf to a node v chosen from C, and an updated set C.
| Algorithm 1 Build tree |
|
The procedure to update C is the following: if K had more than three vertices (i.e., more than two leaves), all its leaves are added to C. If it had three vertices (two leaves), only l is added to C. Additionally, if the chosen vertex v was a leaf, and its support had exactly two leaves (v and another vertex w), w is removed from the set C because it will no longer be at a distance 2 from another leaf (v will not be a leaf after the connection).
This function allows an incremental build of a tree by using the outputs T and C as inputs for the next iteration, together with the new K to be appended to the tree. For the first iteration, T can be a star, and C all its leaves.
Different methods can be used to select a vertex v from the set C. For instance, we consider three connection schemes: (1) The vertex with maximum degree, (2) the vertex with minimum degree, and (3) a randomly selected vertex. Figure 3 shows an example of the trees obtained with the three connection schemes in a simulation with 50 stars with five vertices each. We observe that the form of the tree obtained by selecting the vertex with minimum degree (Figure 3b) is similar to the tree for a randomly selected vertex (Figure 3c).
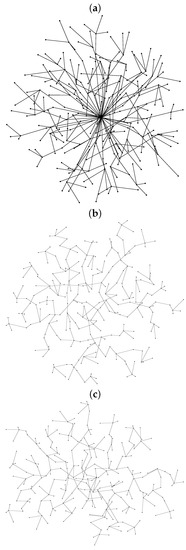
Figure 3.
Example of trees obtained using different strategies for choosing the vertex to connect a new star to the tree: (a) the vertex with maximum degree, (b) the vertex with minimum degree, and (c) a randomly selected vertex.
Calculating a minimum dominating set of a graph T is an NP-hard problem [6]. The computation of an isolating set can be done from the dominating set by exploring the connectivity of the graph obtained when a set of vertices is removed. When done this way, it is also a NP-hard problem. However, in Section 2, we have determined that the support set for a tree from the family is both a minimum dominating set and a minimum isolating set. In addition, when the graph is built using Algorithm 1, the supporting set can be incrementally constructed by adding the support of the star appended at each iteration to it.
Algorithm 1 can be used for building different trees from the family . In order to simplify the comparison among the results, we will show results obtained for stars with the same number of vertices. Figure 4 shows the ratio when the tree is obtained by connecting two stars while varying the number of vertices in each star from 3 to 50. The maximum value corresponds to a path of three vertices, that is, to a graph from the family . This is the same result obtained in Section 3.
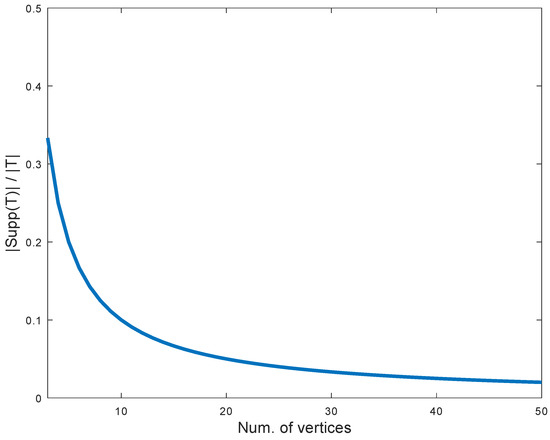
Figure 4.
Values of for two stars and a number of vertices in each star between 3 to 50.
In order to compare the strategies for building the tree, we have characterized each tree considering the degree and the diameter. These measures have a great importance in a large number of applications (see, for instance [7,8]): Vertices with high degrees tend to play central roles in many graphs and are considered by many to be the focal points of graph functionality; on the other hand, the diameter provides information about the cost associated to send information between vertices of a graph. Figure 5 compares the graph parameters for trees constructed by connecting from 2 to 30 stars with five vertices. The size of the supporting set is the same for all strategies because it is equal to the number of stars used to construct the tree. From the results in Figure 5 corresponding to the degree, we show the value obtained by averaging the degree of all vertices in the tree, the minimum degree and the maximum degree. For all the strategies, the average degree is similar, but the maximum value increases with the number of stars for the approach where the vertex with the maximum degree is chosen. This is a reasonable result, because this procedure produces a centralized graph where only one vertex is chosen for all the connections. For the other two approaches, the method produces a wide area network. Finally, in the results in Figure 5 corresponding to the diameter, we can see that the first strategy produces a tree with a short diameter, while in the other strategies the diameter increases with the number of stars. We also observe that the results obtained when choosing the vertex with a minimum degree (Figure 5b) are similar to those obtained when the vertex is randomly selected (Figure 5c).
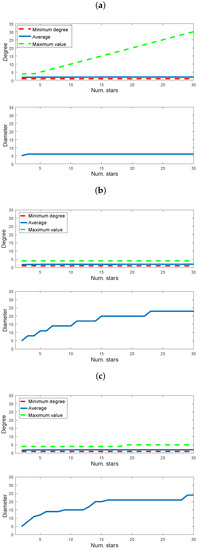
Figure 5.
Degree (minimum, average, and maximum value) and diameter obtained using different strategies for choosing the vertex to connect a new star to the tree: (a) The vertex with maximum degree, (b) the vertex with minimum degree, and (c) a randomly selected vertex.
5. Conclusions
We have studied the characterization of trees taking into account the relationship between the isolation number and the domination number. We have found conditions to guarantee the equality of both numbers. For such trees, a minimum dominating set can be found by computing the supporting set. We have also determined extremal trees for which the maximum bound of the isolation number is achieved.
Author Contributions
M.L. and M.J.S.-S. developed the theory; A.D. and F.J.V.-A. designed the algorithms, performed the simulations and analyzed the results; M.L. and M.J.S.-S. wrote the paper; M.J.S.-S. head the research. All authors have read and agreed to the published version of the manuscript.
Funding
CITIC, as Research Center accredited by Galician University System, is funded by "Consellería de Cultura, Educación e Universidade from Xunta de Galicia", supported in an 80% through ERDF Funds, ERDF Operational Programme Galicia 2014-2020, and the remaining 20% by "Secretaría Xeral de Universidades (Grant ED431G 2019/01). This research was also funded by Agencia Estatal de Investigación of Spain (PID2019-104958RB-C42 and TIN2017-85160-C2-1-R) and ERDF funds of the EU (AEI/FEDER, UE).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The code presented in the paper is available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Haynes, T.W.; Hedetniemi, S.T.; Slater, P.J. Fundamentals of Domination in Graphs; Marcel Dekker: New York, NY, USA, 1998. [Google Scholar]
- Distances and Domination in Graphs, 1st ed.; Ismael Gonzalez Yero: Cadiz, Spain, 2020; Available online: https://www.mdpi.com/books/pdfdownload/book/3089 (accessed on 15 May 2021).
- Hansberg, A.; Caro, Y. Isolation in graphs. Electron. Notes Discret. Math. 2015, 50, 465–470. [Google Scholar] [CrossRef]
- Caro, Y.; Hansberg, A. Partial Domination-the Isolation Number of a Graph. Filomat 2017, 31, 3925–3944. [Google Scholar] [CrossRef]
- Tokunaga, S.-I.; Jiarasuksakun, T.; Kaemawichanurat, P. Isolation number of maximal outerplanar graphs. Discret. Appl. Math. 2019, 267, 215–218. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S. Computers and Intractability. A Guide to the Theory of NP-Completeness; Freemann: New York, NY, USA, 1979. [Google Scholar]
- Alzoubi, K.M.; Wan, P.J.; Frieder, O. Distributed heuristics for connected dominating set in wireless ad hoc networks. IEEE J. Commun. Netw. 2002, 4, 22–29. [Google Scholar] [CrossRef]
- Kajdanowicz, T.; Morz, M. Using graph and vertex entropy to compare empirical graphs with theoretical graph models. Entropy 2016, 18, 320. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).