1. Introduction
In the automotive industry, productivity is a primary indicator for measuring vehicle assembly plant performance (along with quality and work-in-process inventory). Therefore, one of the overriding concerns for management teams in the industry is how to accurately assess productivity and identify productivity improvement opportunities to close the competitive gap between their actual practice and competitive best practices.
Regarding productivity assessment in the automotive industry, the idea of using hour per unit (HPU) as a performance metric is relatively well-accepted (HPU-based productivity may not be an ideal performance measure if the financial performance of manufacturing systems is available because financial performance is more directly aligned with the underlying goal of the company, that is, profit maximization. However, as financial performance is generally reported to the public at the company level, it is difficult to estimate the profitability of an individual manufacturing shop or line. Given the lack of publicly-available financial performance data, HPU as a metric of productivity is a reasonable index for assessing manufacturing performance.) and has been used in similar studies [
1,
2]. HPU is the total working hours spent at a plant divided by the total produced vehicle volume. The total working hours includes paid lunches, breaks, leaves and overtime. Note that HPU is an inverse measure of productivity, that is, a greater value for HPU indicates lower productivity, and vice-versa. One distinct advantage of using HPU is that it can account for production volume increases or decreases (denominator part) and labor efficiency changes (numerator part) simultaneously.
The current practice for assessing productivity is a simple HPU-based comparison between competitive plants without consideration of different manufacturing operation conditions among them, which can cause misleading assessments in identifying the competitive productivity gap. As an alternative to potentially inaccurate comparisons, a statistical regression model can be created for manufacturing plants within a particular industrial sector, which is used to benchmark a particular plant in relation to competing plants that perform the best practice in regard to HPU. This study uses stochastic frontier analysis (SFA) as a base model to account for different operation conditions exposed by influencing factors of HPU.
Since Aigner et al. (1977) [
3] and Meeusen and Broeck (1977) [
4] proposed SFA models independently, SFA has been used as a statistical benchmarking tool to provide a bird’s-eye view of industry or plant-level efficiency analysis. Through SFA-enabled benchmarking, inefficient distributions of productivity can be identified, from which the best theoretical level of productivity can be estimated for a given plant, thereby providing an answer to the practical question: “how competitive would my plant be compared with everyone else’s, if all other plants wear the same shoes as mine?” Although the original specification of the SFA model has been maintained by preserving its error term divided into two components–one to account for random effects (or measurement errors) and the other to account for technical inefficiency–the inefficiency component has been altered or extended in several ways. The survey on alternation and extension will be discussed in
Section 2. It is worth noting that Data Envelopment Analysis (DEA) [
5] is also proven an extremely useful tool based on non-parametric and deterministic modeling concept in the benchmarking study. However, this study suggests to use SFA because it provides parametric properties required to integrate shop-level stochastic models. Further, SFA provides useful modeling settings to address measurement errors that are caused by missing variables like cultural difference by company, varying weather condition by region and diverse local union contract which are likely to play a significant role in labor productivity study.
A general form of SFA for HPU-based productivity benchmarking is as follows:
where
is hour per unit of plant
i, which is the fraction of total labor hours over total vehicle production;
and
are control and external variables (Control variables typically consist of the variables that a plant can manipulate by their tactical strategies. External variables are factors lying outside the decision scope of a plant, such as a new vehicle model allocated by headquarters as per the company’s long-term manufacturing capacity planning. Examples of control variables include automation levels in the Bodyshop and Paintshop, in/outsourcing levels in the Bodyshop and General Assembly (GA). Examples of external variables are the number of models (or market segments) that the plant produces, frame styles (unibody vs body-on-frame), welding contents in the Bodyshop, or total parts attached in GA. The choice of variables to include (or exclude) for the model is determined by subject matter experts’ priory knowledge and expectations about what factors will have significant influence on productivity and statistical causality analysis results.), respectively;
includes the parameters to be estimated;
is the inefficiency or competitiveness gap in HPU use, which is distributed according to one-sided distribution; and
denotes the measurement error. Note that the sign of
is plus because the actual
will be higher than the “best practice” plant. The role of the function
is to normalize for different operation conditions by the plant, converting an “apples-to-oranges” comparison into an “apple-to-apple” comparison. Given a set of plant data, the distribution of the competitiveness gap (
) can be estimated as follows:
From the distribution of
, the percentile ranking of
i-plant’s productivity can be calculated as
where
is the probability density function (pdf) for the inefficiency, which is assumed to be supported in
, and
is the cumulative distribution function (cdf).
Note that the percentile ranking depicted by (
3) becomes 100% if
= 0, meaning that plant
i is ranked as the best in the automotive industry for a given operation condition. If the productivity of plant
i is poor, then the value of (
3) is close to 0%. This study uses the percentile ranking as a percentage performance metric for measuring plant productivity. For clarification between productivity and efficiency, what is usually analyzed in SFA is the efficiency score (as being
, where efficiency is defined relative to some benchmark of performance as known as “best practice”. However, in the labor study context, this concept must also consider the minimum labor resource required to produce the particular goods or services. From the managerial viewpoint, it must also help set a realistic goal based on best observable performance. Therefore, this paper defines the percentile ranking of
i-plant’s productivity from the inefficiency distribution. Using the defined productivity, it is straightforward for a plant to set a percentile target from an industrial performance distribution that has a specific curve shape representing what the industrial competition for operational efficiency looks like and then find a HPU target according to the percentile target. To highlight the difference between HPU competitiveness gap and the labor producibility concept, in fact, the interpretation of HPU competitiveness gap depends on how well a plant performs. The lower ranked plants (i.e., lower percentage performance) have higher potentials to further improvement so that the reducing one unit of HPU competitiveness gap is relatively easy for the lower ranked plants. Meanwhile, the plants that are already closer to their best practice level (i.e., higher percentage performance) tend to reach a point of diminishing returns and so the higher ranked plants should spend more efforts to lessen one unit of HPU competitiveness gap.
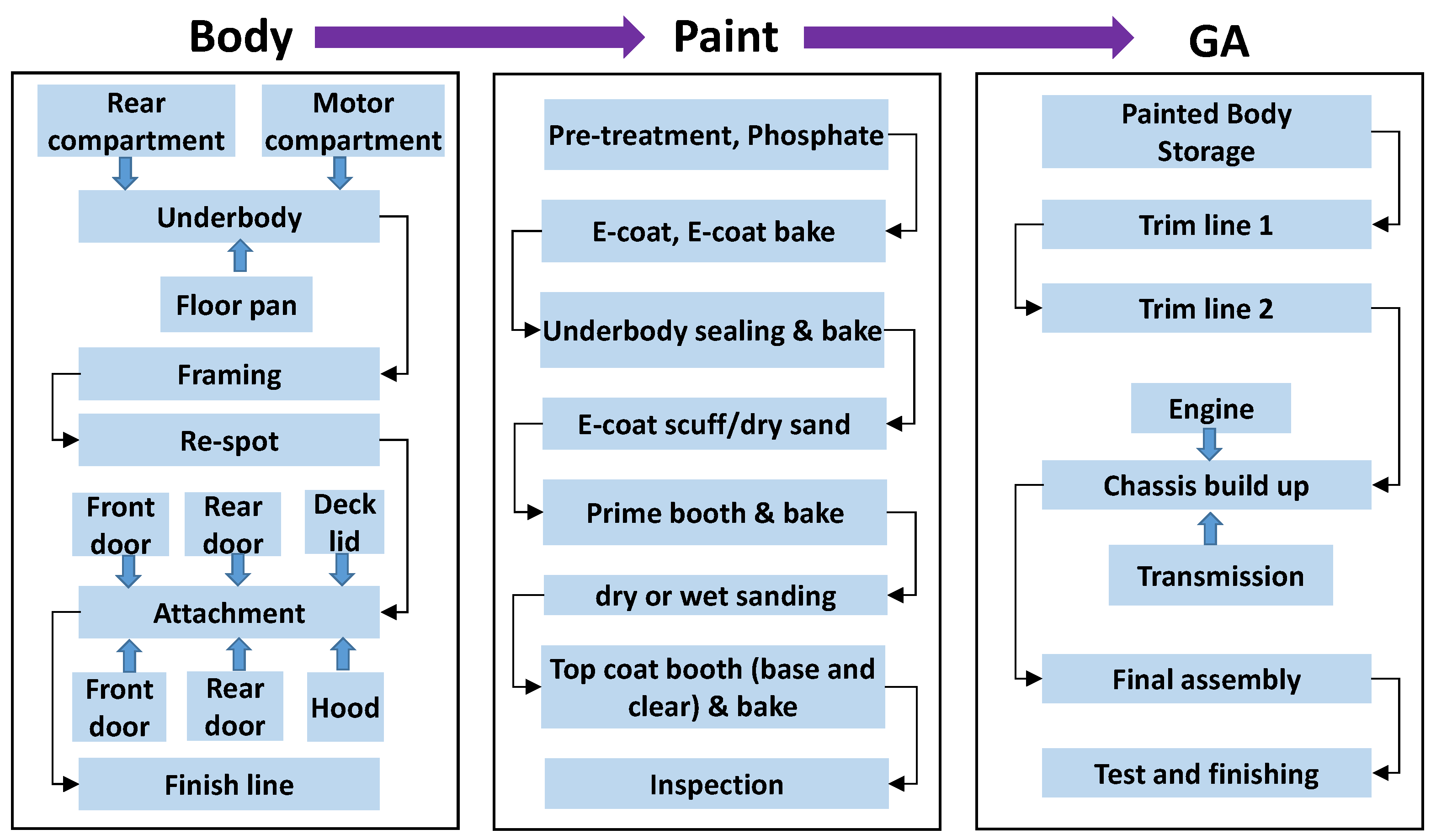
However, there is a modeling challenge in applying a multivariate SFA model to assess complex manufacturing systems, such as the vehicle assembly process. A typical automobile manufacturing process consists of many processes that can be grouped into the three main processes of Bodyshop, Paintshop, and GA, as depicted in
Figure 1. The Bodyshop transforms raw materials into the structure of a vehicle. Next, the Paintshop applies a protective and visual coating to the product. Finally, GA assembles all subcomponents, such as the engine, tires, and seats, into the vehicle. Although these three processes can be executed sequentially and simultaneously in the same plant, they are practically independent of each other in terms of technology, operation and staffing. This is the reason many car companies are able to leverage their inner network of manufacturing facilities that are located remotely, to produce (or paint) parts and pieces alternatively and then, ship them to another plants for other processes like final assembly.
In general, assessing a vehicle plant’s productivity should require a multivariate model, including many explanatory variables, to account for the complex car manufacturing system. A multivariate model is a valuable tool in dealing with the interaction of multiple variables; however, with many intercorrelated explanatory variables, it may have the problem of suppressor variable (A suppressor variable may inflate the predictive validity of another variable (or set of variables) by its inclusion in a regression equation. Multicollinearity is the usual suspect of suppressor variables. Suppressors are present when too many variables are used in one model and some of input variables are positively correlated. Its effect is to flip the coefficient sign of suppressor variables because a suppressor variable suppresses itself, but boosts the other positively correlated variables. Suppressors tend to remain even after passing a variance inflation factor test.) presence, which has the potential to significantly limit findings that can be reported because the obvious solution for suppressor variables is omitting the problem variables, resulting in useful datasets being passed over. Note that the gain effort of competitors’ data in the context of automotive industry benchmarking is highly expensive and time-consuming. The collected but neglected useful datasets could have been used to conduct analysis to find an effective productivity improvement path. Therefore, the data omission due to the inability in modeling complex manufacturing systems is rather frustrating.
This study will propose a systematic approach to assessing a plant’s productivity, where the problem of suppressor variable presence caused by multicollinearity is relieved. The overall approach is to execute the following steps: (1) decompose a vehicle assembly plant into three shops–Bodyshop, Paintshop and GA; (2) build SFA models for these shops; and (3) reintegrate the general plant system by the appropriate combination of the shops’ inefficiency distribution, which is part of the shop-level SFA model.
In this procedure, it is required to derive a probability density function from three different inefficiency distributions to aggregate shop-level assessment results to evaluate the plant-level productivity. We represent the density function as an integral of a common function and provide a computational error as well.
The objective of this paper is to provide the following contributions to researchers and practitioners from the proposed method. First, we provide insights into the use of SFA for accurate and objective assessment of plant productivity and the identification of productivity improvement opportunities. Second, we provide a step-by-step procedure for deriving a composite pdf and cdf from three half-normal inefficiency distributions for HPU in SFA. In particular, our study shows how to mitigate the problem of suppressor variable presence in assessing the productivity of highly complex vehicle assembly plants in such a way that the overall process is divided into shops (i.e., Bodyshop, Paintshop, and GA). Third, this paper shows an illustrative example that demonstrates the application of the proposed approach for assessing hypothetical vehicle assembly plants where the total labor hours are split into Bodyshop, Paintshop and GA, exclusively and collectively. At last, this study offers a solution process to clarify the reasons for underperforming plants in terms of labor productivity and identify the course of actions to cure the issues with some managerial insights emphasizing the balanced approach incorporating people, process and technology.
The remainder of this paper is organized as follows. In
Section 2, we review the existing literature.
Section 3 deals with the theoretical development of the SFA model focused on a mathematical solution for the composition of multiple stochastic frontier distributions. An application of the developed SFA model to the automotive industry is discussed in
Section 4 with some remarks relevant to practitioners. Some concluding remarks are drawn in the last section.
2. Literature Review
This work is motivated by two streams of extant research: (1) productivity analysis in manufacturing systems; and (2) efficiency assessment via SFA models.
In the first stream of studies, the productivity of manufacturing systems related to quality, flexibility and inventory is analyzed. A methodology that measures the efficiency of vehicle assembly plants in terms of productivity and quality was described by Krafcik (1988) [
6]. This study cites an earlier empirical study that assesses productivity to identify superior manufacturing practices because a comprehensive comparative analysis was performed based on real visits to 38 automotive assembly plants in 13 countries around the world. The automotive industry has attracted significant attention from researchers in management science and decision optimization due to its significant impact on the real world economy and its data availability. The mechanism for the achievement of high productivity via efficient labor utilization was studied by Lieberman et al. [
7]. Regarding the impact of flexibility on productivity, a study was undertaken to analyze how the increased complexity of parts involved in car manufacturing can result in a negative effect on productivity [
1]. In addition, a similar study showed that an increased number of vehicle options has a negative impact on both productivity and quality [
8]. By a comparison of US and Japanese automobile producers, it was shown that there is a strong relationship between higher productivity and inventory reduction [
9]. Gopal et al. (2013) showed that launch events can disrupt manufacturing operations, resulting in productivity losses [
2]. In their study, ordinary least squares regression was applied, but various sample selection methods were utilized to test their hypothesis. For example, a series of matched sample methodologies or an instrument variable was used to ascertain whether a plant hosting a launch suffers a decline in productivity, and the Heckman sample selection methodology [
10] was used to examine how experience and flexibility can mitigate productivity losses. Alden et al. (2006) reported how analytics can contribute to the improvement of plant productivity, with assembly plants of General Motors taken as examples [
11].
The studies in the second stream focus on the one-sided distributional form assumption of the efficiency component in SFA models. As the inefficiency component is widely assumed to be a half-normal distribution in many applications, we consider integrating different half-normal distributions here. We remark that a truncated normal distribution or an exponential distribution is also assumed for the inefficiency component. In particular, for the truncated normal distribution [
12,
13,
14], the first parameter can capture firm characteristics in representing heterogeneous efficiency effects, and the half-normal distribution can be transformed from the truncated normal distribution. Meesters (2014) also showed that the exponential distribution is a special limiting case of the truncated normal distribution, as is the half-normal distribution [
15].
Although practical experience with frontier analysis using SFA models has shown that such standard models are sufficiently accurate (see also [
16]), some researchers have developed complicated but more realistic distribution models by using the Gamma distribution. Green (1990) proposed the use of the gamma distribution to estimate the inefficiency term, although the likelihood function for the convolution of the two error components of the SFA model is not available in closed form because the likelihood function involves an integral that cannot be evaluated analytically [
17]. However, Beckers and Hammond (1987) showed that the likelihood can be computed using special functions in this context [
18]. Subsequently, Greene (2003) proposed a simulation-based method to address this issue [
19]. Tsionas (2012) showed that the fast Fourier transform of the characteristic function can be used to address the troublesome term in the likelihood function [
20]. It is worth noting that Kumbhakar et al. (2013) introduced the zero inefficiency stochastic frontier model which can accommodate the presence of both efficient and inefficient units [
21] and Makieła (2017) included more than one random inefficiency terms [
22].
For the purpose of this study, it is necessary to compute the distribution of the sum of inefficiency random variables for standard one-sided distributions. Indeed, in probability theory and statistics, the computation of the distribution of the sum of independent of random variables has been widely studied. For example, Moschopoulos (1985) showed that the distribution of the sum of independent gamma variates with different parameters can be represented as a gamma series [
23] and Bibingera (2013) provided a closed form of the distribution of the sum of independent exponentially distributed random variables [
24,
25]. In addition, Krenek et al. (2016) studied the sum of distributions for the case of truncated distributions [
26].
In particular, this work focuses on the derivation as well as numerical computation of the probability density function from three independent half-normal distributions. In Bayesian SFA, numerical tools such as Gibbs sampling can be used to approximate the multivariate probability distribution. On the other hand, it is required to obtain a closed form of the probability density function for non-Bayesian SFA. We notice that the half-normal distribution is a limit of a skewed normal distribution [
27] and the density function of the sum of independent skew normal random variables is given in a closed form [
28]. However, the expression involves a special function, the Kampé de Fériet function, which is not easy to evaluate. In contrast to Nadarajah and Li’s work [
28], we present the required pdf and cdf in the form of the integral of the error function and estimate the computational errors.
SFA is the most commonly used efficient frontier measures in the productivity analysis in econometrics [
29,
30]. However, in context of the automotive industry, few researchers have studied the application of SFA. Boyd (2008, 2014) [
31,
32] and Oh and Hildreth (2014, 2016) [
33,
34] worked to address the topic of energy intensity and its influencing factors. Besides, a few literatures dealing with productivity and Research and Development (R&D) efficiency in automotive industry with SFA were found [
35,
36].
Added to SFA, DEA [
5] is also an extremely useful tool developed in operations research community based on non-parametric modeling concept. There are plenty of literatures reporting DEA application to benchmarking studies (e.g., bank branch productivity study [
37], warehouse performance study [
38]). However, this study uses SFA because this study needs parametric modeling approach to integrate shop-level inefficiency distributions.
3. Composition of Multiple Stochastic Frontier Distributions
The goal of plant productivity analysis is to measure the overall plant productivity. However, due to the complexity of the manufacturing system, the multivariate model representing a whole plant may include too many explanatory variables intercorrelated with each other, resulting in the presence of suppressor variables. For example, let and denote the number of car platforms and the number of car models, respectively. Both and are used for the same purpose of indicating the complexity level of a given plant. Therefore, they are positively intercorrelated and have a negative relation with HPU. When both variables are introduced together into one multivariate model, the coefficient sign of one of the two variables is likely to flip over owing to the effect of suppression such that one variable takes a plus sign while the other variable takes a minus sign. In fact, mainly affects the Bodyshop process only, but the impact of is limited to the GA area. In other words, although and can cause the suppressor variable problem if combined, by separating them into different SFA models ( for Bodyshop and for GA), the problem can be avoided. This study proposes to build separate SFA models by shop and then compose their inefficiency distributions to estimate the overall plant productivity. In this section, a mathematical solution for the composition of multiple stochastic frontier distributions is built.
To this end, it is required to integrate inefficiency distributions of Bodyshop, Paintshop, and GA. As discussed earlier in explaining
Figure 1, the three processes are independent of each other and therefore, the competitiveness gap of those processes can be assumed to be independent. We denote
,
, and
as the competitiveness gap of Bodyshop, Paintshop, and GA, respectively. Then, the overall inefficiency for plant
i is given by
As the percentile ranking of
i-plant’s productivity is calculated from (
3), it is required to compute the associated probability density function. It is well-known that the probability density for the sum of independent random variables is given by the convolution of each density function. Thus, the distribution of the overall inefficiency
can be represented as the convolution of the distributions
for Bodyshop, Paintshop, and GA, respectively,
where
Here, we compute
under the assumption that the inefficiency components are distributed half-normally. The use of half-normal distribution to represent the inefficiency components is in fact pretty reasonable in the context of the automotive industry. When Kernel distribution estimate [
39] is applied to predict the shape of HPU competitiveness distribution in the automotive industry, it turned out that the distribution shape was far skewed to the left. The skewed shape to the left means that the industrial competition for labor productivity is highly intensive and many companies are already reaching out to their best practice, in which case the half-normal distribution can be introduced to account for the shape of HPU competitiveness distribution at its high rate observed in the far left side. To be sure, this study carried out LR (likelihood-ratio) tests [
40] for
,
, and
where two models were compared: (1) Ordinary Least Square (OLS) and (2) SFA with the half-normal distribution used for the inefficiency component. All three tests told that the LR statistic exceeds 99%, indicating that the choice of half normal distribution to represent inefficiency in Body shop, Paint shop and GA is a correct decision.
Thus, for some
,
where
is a Gaussian distribution function with mean 0 and variance
; and
is the characteristic function. Next, we state a technical lemma:
Lemma 1. Let be the probability density functions for the normal distributions with mean 0, and variances and , respectively. Then If only two independent variables are considered, the distribution of their sum can be easily computed by the convolution integral (
5). By considering the supports of
and
, we have
It follows from (
6) and Lemma 1 that
However, we are interested in the probability distribution function for the sum of three independent random variables. Unfortunately, we cannot compute it from convolution theorem (
5) as in the case of the sum of two independent variables.
Let
be normally distributed random variables with mean 0 and variances
. Then
and the density function
for
satisfies
On the other hand, the region
in the three-dimensional
space is bounded by the eight plains
, and
. Therefore,
Together with (
8),
is obtained from Lemma 1 and the derivatives of the integrals in (
9) with respect to
x;
The detailed derivation of (
10) is given in
Appendix B. We remark that
can be rewritten in terms of
for any permutation operator
P due to the symmetry of
.
Now, we compute the cumulative distribution function, that is,
To reduce the mathematical expression of (
10), let us define
as
Using the change of variables with
, we rewrite (
10) as
Substitution of
into (
11) together with changing the order of integration yields
We summarize our findings in Theorem 1.
Theorem 1. Assume that and are independent random variables that are half-normally distributed with parameters , and , respectively. Then the probability density function and the cumulative distribution function for are given by (10) and (12), respectively. It should be noted that one can compute
in a different form, using the result of Krenek et al. [
26]. However, it is not suitable for our numerical implementation as it is created via induction.
4. Illustrative Example
This section discusses the application of pdf (Equation (
10)) and cdf (Equation (
12)) developed in the previous section. The example discussed in this section deals with HPU data from the automotive industry. Since (
10) and (
12) are expressed in integrals of common functions, they can be easily implemented in Microsoft Excel and therefore all implemented works in this section was done in Microsoft Excel.
The data source for HPU data can be found in the Harbour Report (Oliver Wyman consulting firm, US), which is an annual survey of all automotive manufacturing plants in the world. Currently, most automotive manufacturers voluntarily provide data for the survey. To prove the data integrity, Oliver Wyman consultants visit each plant and audit the data. They publish an annual report that documents and compares the performance of plants based on HPU comparisons by market segment. In addition to HPU, the Harbour Report includes plant-specific operational data, including capacity, production volume, complexity, automation, souring, contents, and labor. However, due to the non-disclosure agreement signed by auto companies participating in the Harbour Report, the data in the report cannot be publicly shared (Before 2007, the Harbour report data was in the public domain. Gopal et al. (2013) [
2] reported that when they used publicly available data from the years 1999–2007 from North American automotive plants, the average annual production was 186,000 per plant and the average HPU was 27.1.).
Therefore, for the illustration purpose, the authors generated five similar plants that are competing in the luxury car market segment. The datasets for plants were generated to resemble real-world data as close as possible. The dataset is a set of values of explainable variables listed in
Table A1. From the datasets, SFA models for Bodyshop (
13), Paintshop (14) and GA (15) were constructed. The Bodyshop SFA model includes production volumes, the number of platforms, body-on-frame, total welds, and welding automation. Turning to Paintshop, the SFA model takes production volumes, the number of models, sealer automation, paint content automation, and paint content outsourcing as explanatory variables. GA’s SFA model uses production volumes, the number of models, body-on-frame, part numbers, GA outsourcing, logistic outsourcing, and the parts received as explanatory variables. Then,
and
for each plant was calculated.
It is worth noting that the global market is divided into several markets based on car size and price (The car industry generally uses the standard for the global market segments set by IHS Markit, UK). Among the market segments, E1 and E2 segments represent large & luxury class and high luxury class, respectively. In detail, Segment E1 counts car models with sizes of 4700–5100 mm and prices between $50K and $85K. For example, BMW 5 Series, Mercedes-Benz E-Class, Audi A6, Chrysler 300 and Toyota Crown belong to the E1 segment. The E2 segment contains car models having sizes greater than 4500 mm and prices of $85K–$170K. For example, Lincoln Town Car, Mercedes-Benz S-Class, BMW 7 Series, Chevrolet Corvette, and Lexus LS match the standards of the E2 segment. This study observed real plants producing either E1 or E2, or both car segments, and generated five synthetic plants. Overall, the plants producing models belonging to E1 and E2 segments are characterized by higher HPU than low class segment cars because of special efforts to maintain high quality and the high rate of in-house workload with small production volume, different from regular mass production models.
The authors believe that the use of synthetic datasets will not be detrimental to the overall purpose of this study because they are generated to close to the real-world data. Each plant’s HPU gaps for each theoretical best and the performance gaps are calculated in
Table 1. Recall that
,
, and
denote the competitiveness gap of Bodyshop, Paintshop and GA, respectively, where
,
, and
. When maximum likelihood estimation was applied to estimate the parameters in (
1), we obtained
,
and
.
inefficiency cdf for Bodyshop ( = )
inefficiency cdf for Paintshop ( = )
inefficiency cdf for GA ( = )
inefficiency cdf for overall plant (= )
Note that the cdf curve of the overall plant is obtained from Theorem 1, but using a numerical approach (because (
12) cannot be solved analytically). This study uses the trapezoidal rule to calculate (
12) numerically. First, the uniform grid for numerical calculation of
is defined as follows:
Then, Theorem 1 and the trapezoidal rule yield
where we adopt
.
Although the trapezoidal rule always finds an approximation for
, we estimate the error of the numerical integration compared with the actual
in order to provide the accuracy for our simulation. Fix
. Then it is known [
41] that the error for the trapezoidal rule is given by
or asymptotically,
Direct calculation shows that
As obviously
for any
u, it follows that for a sufficiently small
,
In our simulation, we take
and thus
which gives a tolerance of our simulation results.
Figure 3,
Figure 4 and
Figure 5 show the performance of competing plants with respect to their competitiveness gaps.
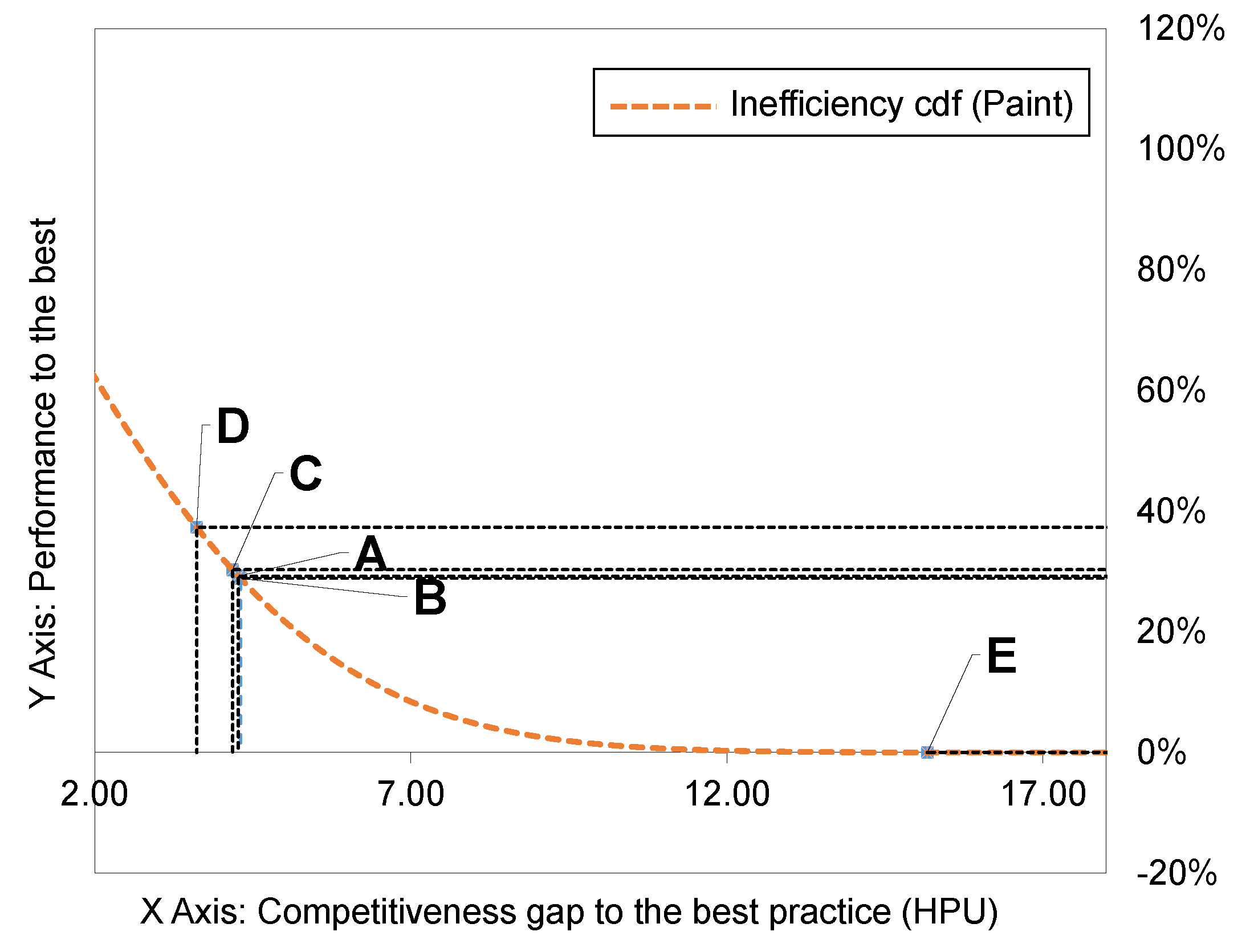
Figure 3 shows the order of performance ranking in Bodyshop, where plant B is ranked first, followed by plants E, A, D, and C. In Paintshop,
Figure 4 indicates that plant D is ranked first, followed by plants C, A, B and E. In GA, plant A outperforms other plants, followed by plants C, B, D, and E, as shown in
Figure 5. In terms of overall performance, as shown in
Figure 6, plant A has the best performance, followed by plants B, C, D, and E. Note that plant A, which is the best in GA performance, becomes the best in overall plant-wise performance. This result seems reasonable in the sense that assembling parts in GA takes up the largest portion of the plant-wise HPU; furthermore, cars belonging to the E1 and E2 market segments require more labor hours in GA because of higher parts attachment and various factory fit options compared to ordinary car models. Therefore, plant A becomes the best in overall plant-wise performance competition, although it has mediocre performance in Bodyshop and Paintshop. Based on the competitiveness gap disclosed from the performance assessment, each plant can set up their feasible performance improvement target. For example, plant B needs to catch up plant A in
Figure 6, where plant B can set up its target performance to be 79% to go after plant A, because plant A already shows that 79% achievement in the respective segment is possible.
Figure 7 and
Figure 8 show the pdfs and the reflected cdfs for our integrated model and the standard half-normal model for total HPU. We obtained
from the maximum likelihood estimation with the half-normal model.
Normally, the logical next step after a series of data-driven studies, including benchmarking, performance assessment, and feasible target setting, is to clarify the reasons why the outperforming (underperforming) plants show the best (worst) results, and what course of actions the underperforming plants should take to enhance their performance. While the data-driven studies can be done by techniques offered in this paper, it is people’s role to clarify the reasons and identify the course of actions. To help activate and facilitate the people’s role, this study offers a systematic solution process as shown in
Figure 9 where a description of each step is as follows.
The first step is data-driven assessment of labor productivity. This step is about performance assessment, identification of best practice plant, and feasible target setting, which this paper has delivered thus far.
The second step is a cross comparison with internal benchmarking results. Typically, a manufacturing company has used its standard time-and-motion study tool to estimate workload, based on which the company practices an internal benchmarking study. At this step, the external benchmarking study executed in the first step can be cross compared with the internal benchmarking study results to figure out the similarity or difference between the two benchmarking studies, being able to confirm the areas of opportunity for further improvement. One advantage of this step comes from the plenty of internal data and knowledge available within the company and so it is possible to further split the labor hours into the core areas to fine tune a further segmentation of the functional area for allocating labor hours. The core areas include manufacturing (i.e., all preparation and processing tasks associated with joining, stamping, machining, loading, fabricating, painting, and fastening), maintenance (i.e., planned/preventive/breakdown maintenance, Die/jig maintenance, conveyor system maintenance, etc.), support (i.e., labor required to support production, engineering/IT, various reporting, and etc.), logistics (parts receiving, checking, repacking/sequencing, line side delivery, material handling, etc.), quality (i.e., inspection, audits/checks, rework, test, measurement, reporting, etc.), and central site services (i.e., medical, training, finance, management, house keeping, etc.)
The third step is internal benchmarking visit. In case of a company which has a global manufacturing footprint, it is highly possible to select a peer group consisting of comparable plants with similar manufacturing operation parameters inside the company. In such a case, underperforming plants in the peer group may visit the best practice plant (identified from the first step) to learn how well the target plant performs and why the target plant is successful, and to adapt specific best practices.
The fourth step is brainstorming to identify the course of actions. Even after executing the third step, an underperforming plant may not discover enough actions for improvement to fill the competitiveness gap identified in the first step. In the case, turning to brainstorming ideas would be a solution. The typical brainstorming means the efforts of a group of people to generate new ideas and solutions around a specific problem of interest. Under the brainstorming scheme, subject matter experts, plant managers, and engineers hold a meeting where individuals can freely suggest as many spontaneous new ideas for labor productivity improvement as possible with no fear of being criticised.
The final step is external benchmarking visit. When the fourth step does not discover a complete solution set for labor productivity improvement due to lack of knowledge and experience, visiting a competitor’s plant directly may be a last resort but can be an effective solution. In general, with a non-disclosure agreements concluded, two competing companies can agree to mutually exchange information beneficial to both companies and visit each other to identify leading edge practices. Since the best practice plant was already identified at the first step, it is clear which competitor’s plant to aim to engage.
Further, this study also provide some managerial insights to practitioners that may increase the adoption and usage of the proposed methods in this paper as follows. Although every global manufacturer is driving its own version of a manufacturing production system in its local and regional facilities, it is possible to share common insights and ideas for clarification. While there are multiple reasons for underperformance, but the two reasons rated most important are overcapacity and the labor/operational competitiveness gap to best practices in HPU. The overcapacity issues are likely to be an expected challenge to face during the process of implementing the company’s long-term product portfolio strategy (e.g., car makers in North America keep traditional passenger car portfolio even though the sales of passenger cars in North America have been declining for the past years and continue on a downward trend). Since it is too early to judge the success or failure of the strategy, a directional change in the strategy is not expected. Indeed, a strategy change may produce a whole series of changes in objectives through the hierarchical arrangement with cost and confusion resulting from any major reconstruction. Meanwhile, the competitiveness gap in labor and operational efficiency is considered to be something that a company can address in the time and space of the present-day world if right decisions are made for assessment of current competitiveness, target setting, and the identification of areas of opportunities or a course of action to take. It is worth noting that at present, the improvement of labor and operational efficiency is tight, but even more important than ten years ago, as the theme of “doing more with less” continues to dominate the automotive manufacturing culture. Nowadays, nearly half of the North American and Europe plants operate on a three-shift or three-crew model, drastically increasing capacity utilization and capital efficiency with far fewer factories, as existed before the downturn in 2008. With this three-shift pattern, even if the next downturn arrives, the plants will not be closed, but just reduced to two shifts. However, this shift pattern means that factories are being asked to add more and more vehicles, which are growing in terms of features and complexity. In addition, much higher content with upgraded standards for safety and emissions and shifting consumer demands due to the change of traditional personal transportation methods are impacting both production complexity and vehicle costs, which add extreme challenges to the production environment.
As the three-shift pattern with high complexity has become the new standard in the industry, marginal productivity growth opportunities and an increase in competition for better operational efficiency have been observed, resulting in marginal productivity growth between competitors. In this environment, the improvement of labor and operational efficiency is becoming more important because performance improvements only driven by technology and automation investments are often masked by increasing product complexity, washing away much of the productivity gains. In general, higher operational efficiency is displayed by more flexible manufacturing. For example, in 2016, Honda transferred the Acura MDX from its Alabama plant to the East Liberty plant in Ohio to allow for more truck production in the Alabama plant, which also increased the utilization of car production in the Ohio plant in a very short period without a decline in production.
Regarding the identification of a course of action for labor and operational efficiency, one surprising discovery is that many of the newest factories with less automation equipment built in China, India, and Eastern Europe have shown incredible performance from young and eager workforces. This discovery is different from the general belief that the robots and automation inspired by Industry 4.0 are taking over the role of human workers, outperforming the labor-intensive traditional manufacturing system. Contrary to expectations, the best plants are not the automated plants, but the plants that display a good balance of people and technology, working in harmony. In fact, significant levels of automation may increase downtime which hinders production flows, driving more highly paid, skilled labor to keep the factory running, while avoiding throughput losses and quality problems. Rather, high-performance plants are commonly demonstrating less capital investment to full automation, but strong workforces at all levels, from the plant manager to the plant floor. These plants integrate automation technology more selectively, yet foster improvements with relatively low-budget technologies, such as small cobots to assist with unsafe or ergonomically difficult tasks, automated guided vehicles incorporated to bring materials, simple means of error proofing, visual controls to highlight potential problems, and improved part presentation (i.e., the use of specific part kits).