Improving the Teaching of Real Valued Functions Using Serious Games. Binary Who Is Who?
Abstract
1. Introduction
Statement of the Problem
- -
- Do the creation and use of games in the classroom improve the mathematical skills of the students?
- -
- Can mathematical contents of the curriculum be reinforced with the use of games?
2. Materials and Methods
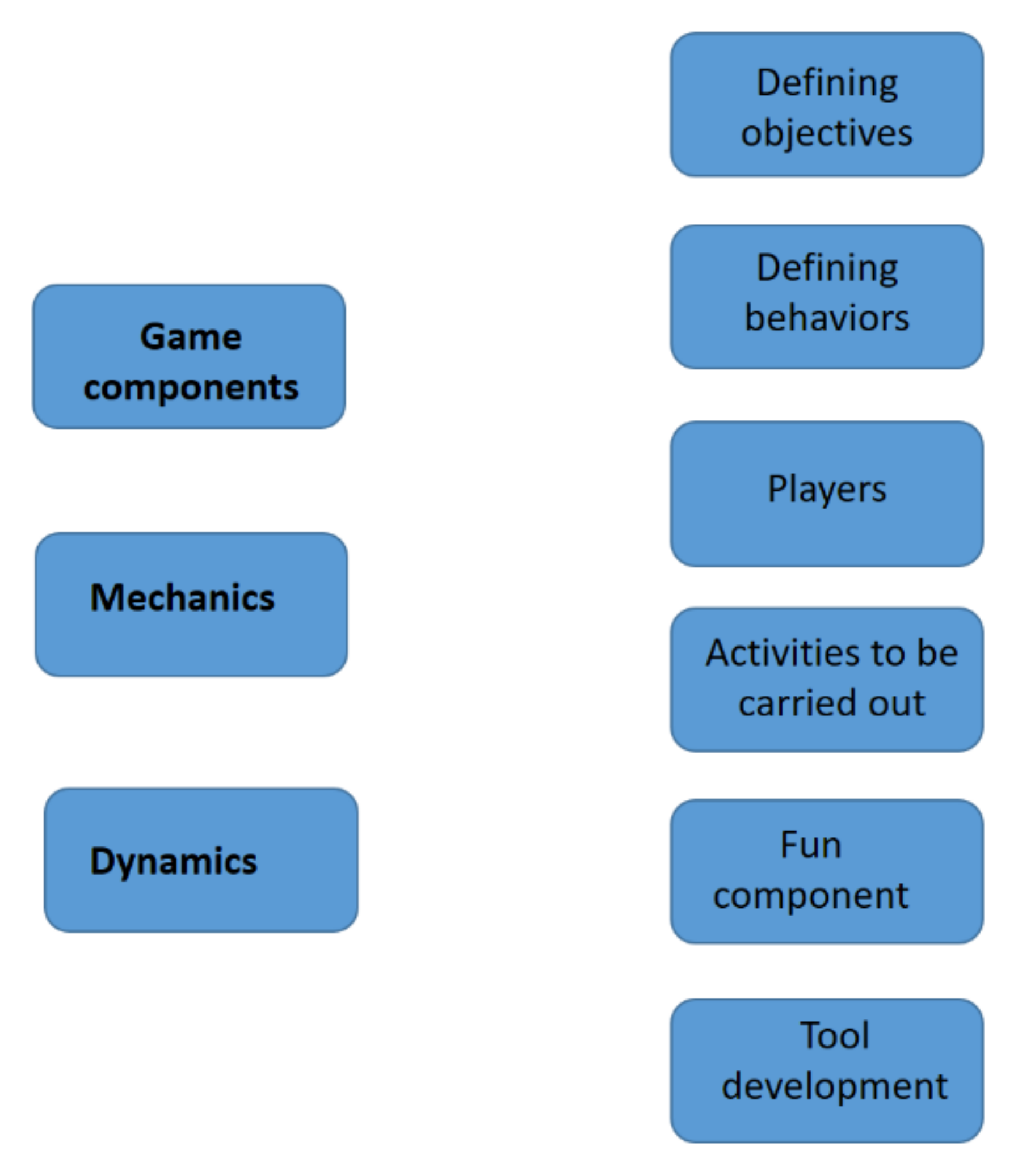
2.1. Theoretical Framework
- Search for board games existing in the market that can be suitable from a mathematical point of view and adapted for teaching and learning of various topics. The choice of games which are familiar to students means that the game mechanics are already familiar to them.
- Creation of the new adaptations and proposals.
- Proposal of collaboration, to a group of students, in the physical creation of the game and rules.
- Approach and implementation in the classroom. The students play with the proposals and they are guided in their resolution through the mathematical approach.
- Development of a video game based on the proposal.
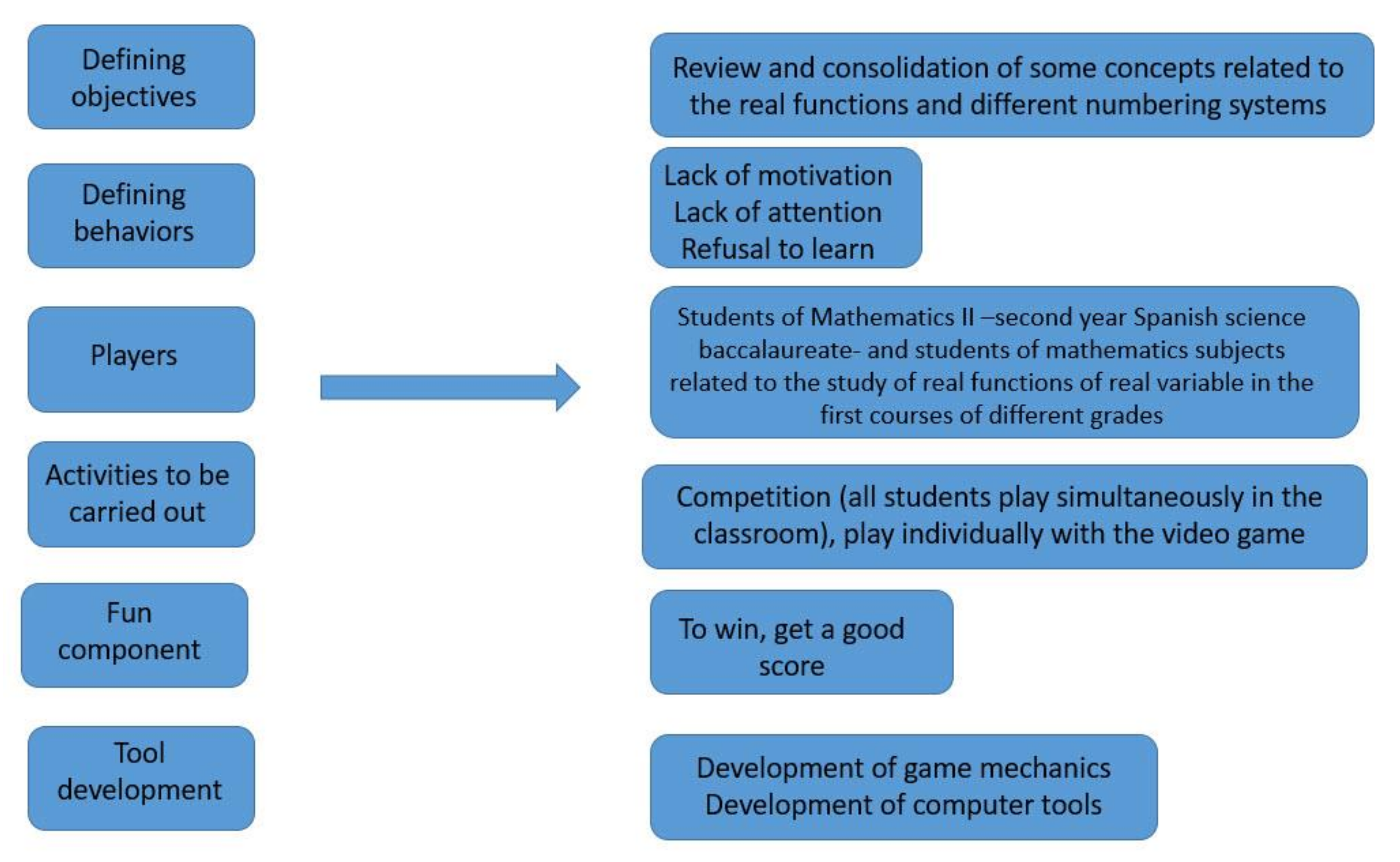
- Students of Mathematics II–second year Spanish science baccalaureate.
- Numerical systems: decimal and binary.
- Didactic unit: real functions of real variables: domain, asymptotes, growth, decrease, maximum and minimum, among others.
2.2. Procedure: How Do You Work with Students?
2.3. Methodological Design
2.3.1. Adaptation of the Game
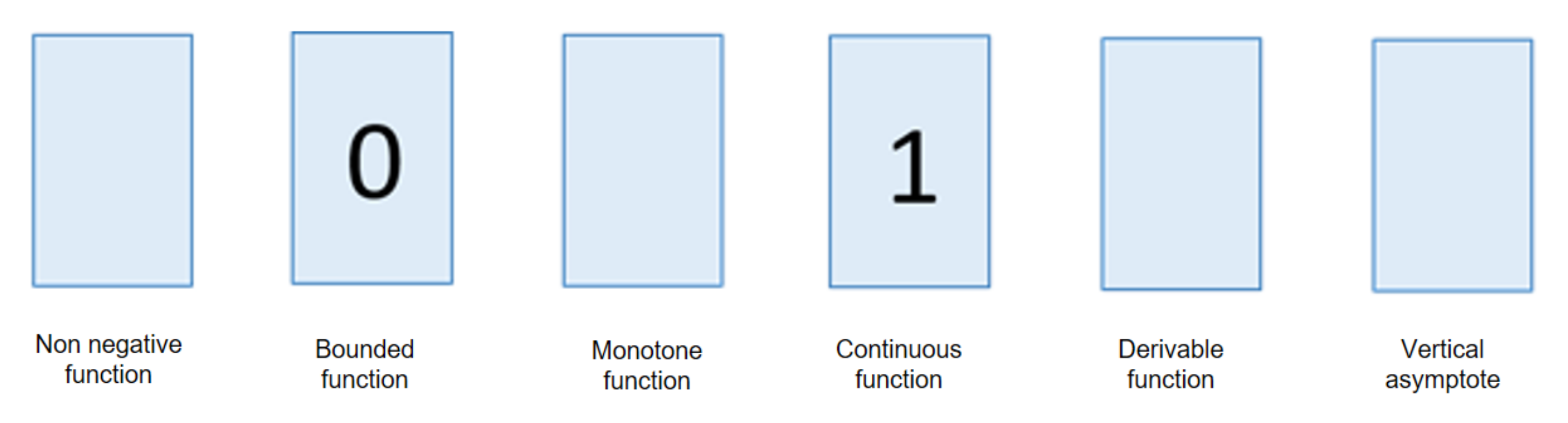
- Is it a non-negative function?
- Is it bounded?
- Is it monotone?
- Is it continuous?
- Is it derivable?
- Does it have a vertical asymptote?
2.3.2. Creation of the Game and Its Collaborations
2.3.3. Development of the Competition
- The students can see all the functions which make up the game. The teacher will select one of them (its associated number in the decimal system will be written on a piece of paper that will be saved without any participant seeing it).
- An orderly question time begins for the students. Each student will cross out the functions that do not match the indicated characteristic and, in addition, will be completing the vector of six positions with the answers that are obtained and applying their knowledge (some answers may implicitly give answers to other unasked questions).
- The moment that one of the students thinks that he/she knows the chosen function, he/she will select it on the screen and will give the number in the decimal system that corresponds to it. This means that the participant must change the vector of zeros and ones, corresponding to the answers to the questions asked, to the number in the corresponding decimal system.
- First, the tab of the chosen function will be flipped.
- If the numbers do not coincide, the student is eliminated and the game continues.
- If the numbers match, the teacher will see if it is the number saved at the beginning. If it is, there will be a winner of the game. Otherwise the student is eliminated and the game continues.
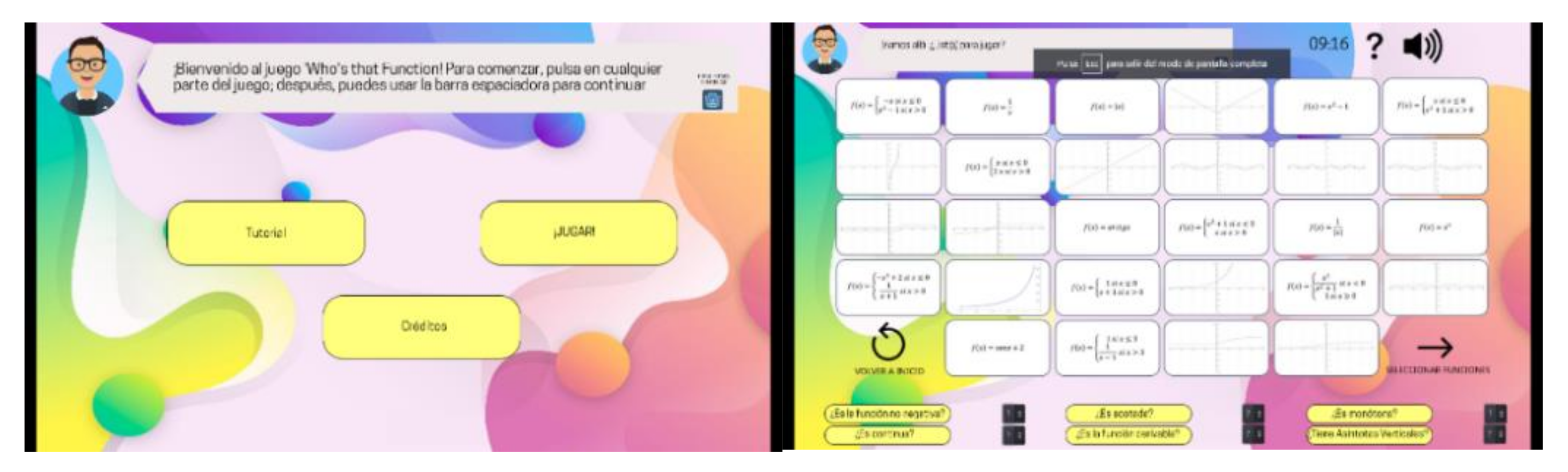
2.4. Video Game
Technical Description:
- Programming language:
- Operative environment:
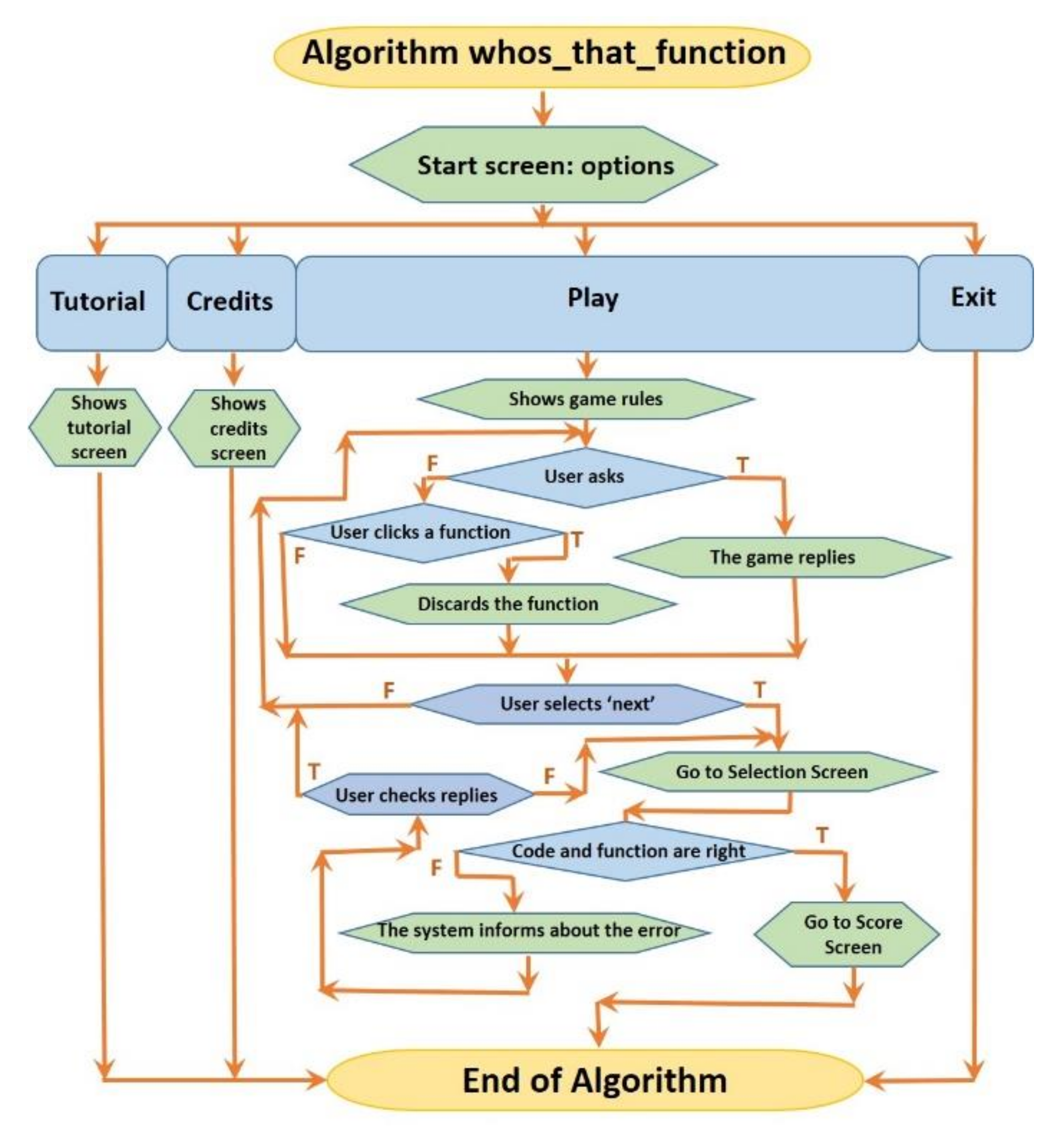
- Flow chart (see Figure 8):
2.5. Educational Content
- Limits of functions
- Calculation of asymptotes of a function
- Continuity
- Derivability
- Growth and decay
- Concavity and points of inflection
- Domain and range
- Monotonicity
- Intervals of constant sign, regions
- Graphical representation
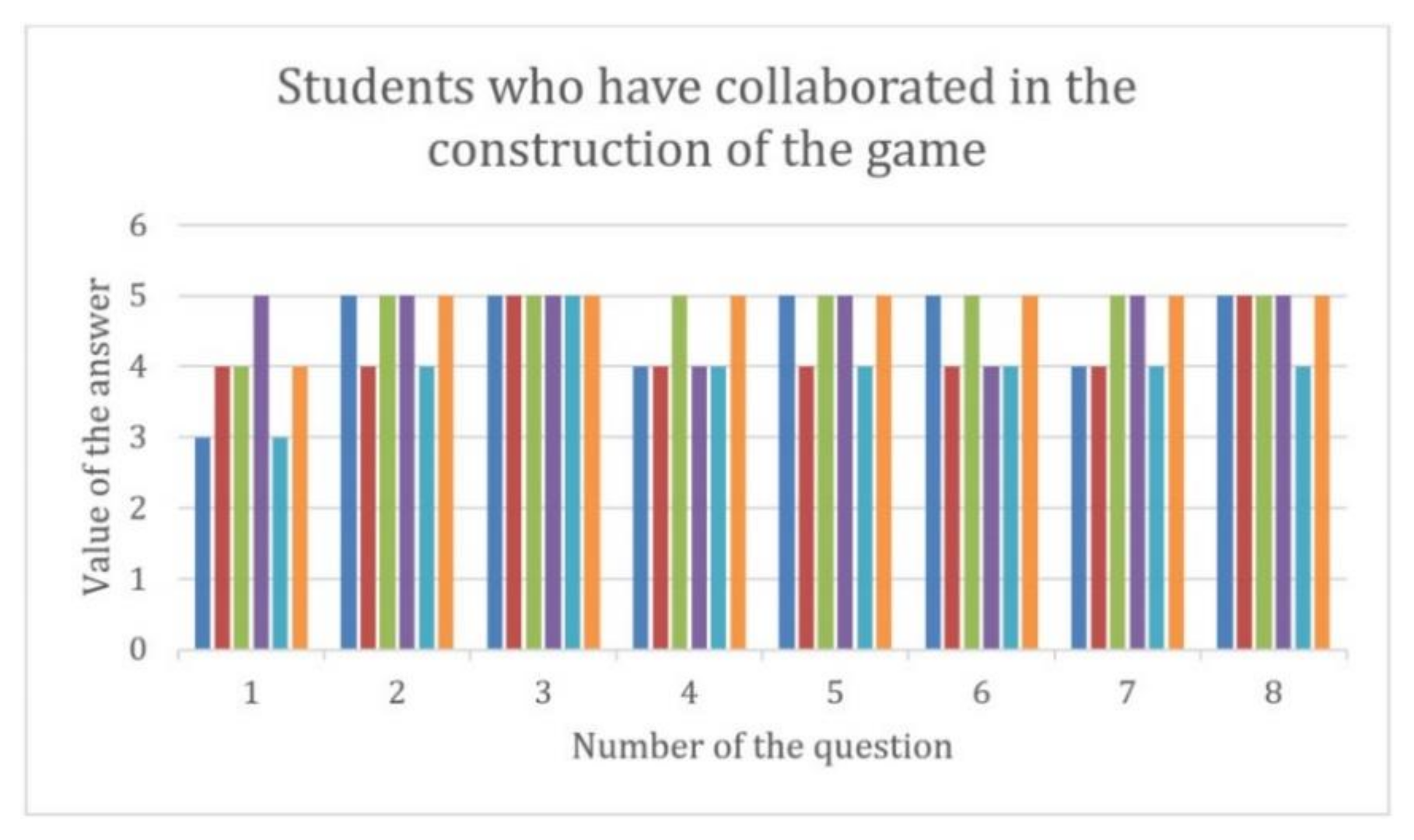
3. Results
- -
- four groups of eighty students each in their first year majoring in civil and territorial engineering at the Polytechnic University of Madrid (UPM) taking Calculus I.
- -
- eight workshops with a capacity for twenty students of the 2nd year of high school in various educational centers of the Community of Madrid (Spain).
- 92% say it has helped them to review the concepts.
- 84% consider it appropriate or very appropriate for their level.
- 85% would use more of these types of games in the course.
- 86% would find it appropriate to use these types of games in other subjects.
- 87% have increased their interest in mathematics.
- 90% would recommend the game.
- Awaken the interest in learning mathematics.
- To enable students to apply the acquired concepts.
- Enhance skills based on mathematical reasoning: strategy, planning, decision making, etc.
- Apply the dynamics and principles of games to improve the motivation, interest and involvement of students in subjects with mathematical content.
- Create a series of playful proposals (games) that promote mathematical knowledge and the playful approach to this science.
4. Discussion and Conclusions
5. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Survey on the activity “Binary Who is Who” |
| 1. Rate from 1 to 5 your level of interest towards the Mathematics subject, where 1 is nothing and 5 is a lot. |
| Mark only one box. |
| 1 2 3 4 5 |
| 2. Do you think that this game has helped you to better understand the functions? Rate from 1 to 5, where 1 is not useful and 5 very useful. |
| Mark only one box. |
| 1 2 3 4 5 |
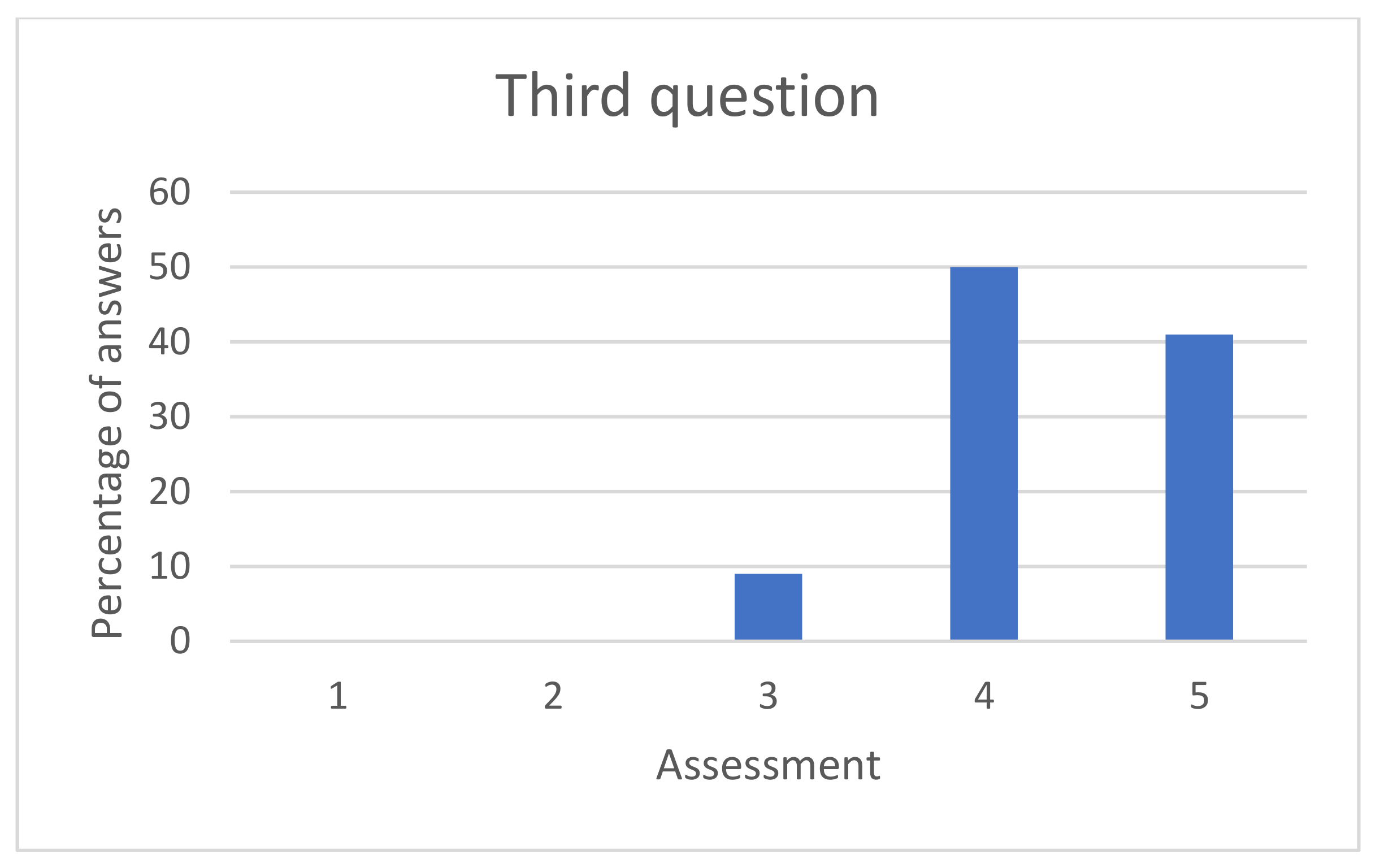
| 3. Do you think this game has helped you to review the contents of the subject? Rate from 1 to 5, where 1 is not useful and 5 very useful. |
| Mark only one box. |
| 1 2 3 4 5 |
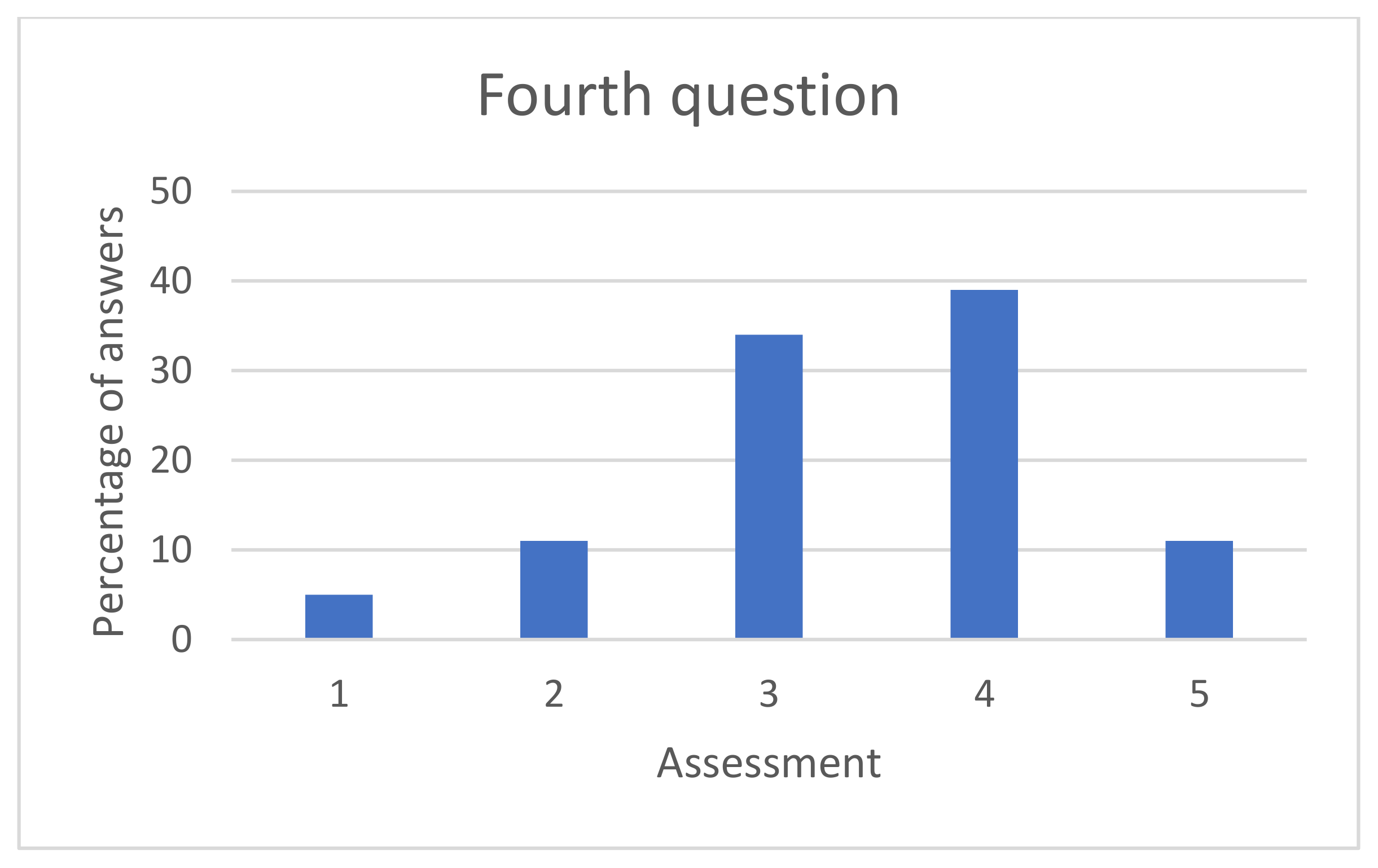
| 4. Do you think the difficulty of the game is appropriate to your level? Rate from 1 to 5, where 1 is not adequate and 5 is very adequate. |
| Mark only one box. |
| 1 2 3 4 5 |
| 5. Would you like to be able to have games of this style for other subjects of Mathematics? Rate from 1 to 5, where 1 is I would not like it and 5 I would like it very much. |
| Mark only one box. |
| 1 2 3 4 5 |
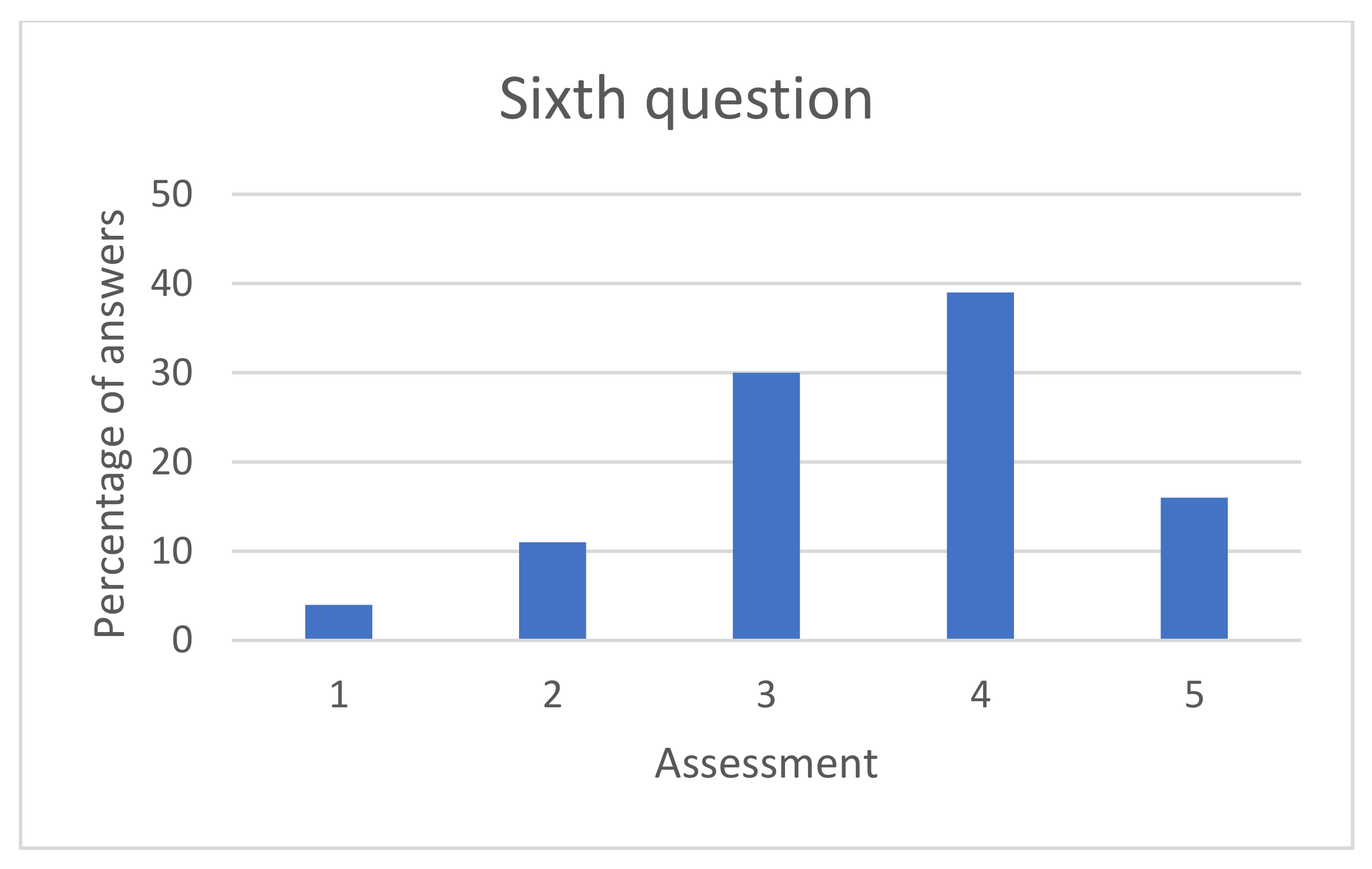
| 6. Would you like to be able to have games of this style for other subjects? Rate from 1 to 5, where 1 is I would not like it and 5 I would like it very much. |
| Mark only one box. |
| 1 2 3 4 5 |
| 7. Do you think this game has contributed to increasing your interest in Mathematics? Rate from 1 to 5, where 1 is nothing and 5 a lot. |
| Mark only one box. |
| 1 2 3 4 5 |
| 8. Would you recommend this game for students of your same level? Rate from 1 to 5 where 1 is not recommended and 5 highly recommended. |
| Mark only one box. |
| 1 2 3 4 5 |
- (a)
- Students who participated in the making of the game.
- (b)
- Students who have played “Binary Who is Who”.





References
- Huizinga, J. Homo Ludens; Rowohlt Taschenbuch Verlag GmbH: Hamburg, Germany, 1987. [Google Scholar]
- Sánchez, D.R.; Langer, M.; Kaur, R. Gamification in the classroom: Examining the impact of gamified quizzes on student learning. Comput. Educ. 2020, 144, 103666. [Google Scholar] [CrossRef]
- Kapp, K.M. The Gamification of Learning and Instruction: Game-Based Methods and Strategies for Training and Education; Pfeiffer: San Francisco, CA, USA, 2012. [Google Scholar]
- Ouariachi, T.; Olvera-Lobo, M.D.; Gutiérrez-Pérez, J. Evaluación de juegos online para la enseñanza y aprendizaje del cambio climático. Enseñanza Cienc. 2017, 35, 193–214. [Google Scholar]
- Martí-Parreño, J.; Méndez-Ibáñez, E.; Giménez-Fita, E.; Queiro-Ameijeiras, C. El uso de la gamificación en la educación superior: Propuesta de una ficha de análisis ludológico-narratológico. In Actas de las XII Jornadas Internacionales de Innovación Universitaria Educar para Transformar: Aprendizaje Experiencial; Rosillo, M., Ed.; Universidad Europea de Madrid: Madrid, Spain, 2015; pp. 103–111. [Google Scholar]
- Michael, D.; Chen, S. Serious Games: Games that Educate, Train and Inform; Thomson: Boston, MA, USA, 2005. [Google Scholar]
- Gee, J.P. Being a lion and being a soldier: Learning and games. In Handbook of Research on New Literacies; Coiro, J., Knobel, M., Lankshear, C., Leu, D.J., Eds.; Routledge: New York, NY, USA, 2008; pp. 1023–1036. [Google Scholar]
- Katsaliaki, K.; Mustafee, N. Edutainment for Sustainable Development: A survey of Games in the Field. Simul. Gaming 2014, 46, 647–672. [Google Scholar] [CrossRef]
- Suh, A.; Wagner, C.; Liu, L. Enhancing User Engagement through Gamification. J. Comput. Inf. Syst. 2018, 58, 204–213. [Google Scholar] [CrossRef]
- Kalogiannakis, M.; Papadakis, S.; Zourmpakis, A.-I. Gamification in Science Education. A Systematic Review of the Literature. Educ. Sci. 2021, 11, 22. [Google Scholar] [CrossRef]
- Gallagher, K. Problem solving through recreational mathematics. In Problem Solving in School Mathematics; Yearbook; Krulik, S., Reys, R.E., Eds.; NCTM: Reston, VA, USA, 1980; pp. 169–177. [Google Scholar]
- Sailer, M.; Hense, J.U.; Mayr, S.K.; Mandl, H. How gamification motivates: An experimental study of the effects of specific game design elements on psychological need satisfaction. Comput. Hum. Behav. 2017, 69, 371–380. [Google Scholar] [CrossRef]
- Marín, V. La Gamificación educativa. Una alternativa para la enseñanza creativa. Digit. Educ. Rev. 2015, 27, 1–4. [Google Scholar]
- Liarakou, G.; Sakka, E.; Gavrilakis, C.; Tsolakidis, C. Evaluation of serious games, as a tool for education for sustainable development. EURODL 2012, 15, 96–110. [Google Scholar]
- Chamoso, J.M.; Durán, J.; García, F.; Martín, J.; Rodríguez, M. Análisis y experimentación de juegos como instrumento para enseñar matemáticas. Suma 2004, 47, 47–58. [Google Scholar]
- Dele-Ajayi, O.; Sanderson, J.; Strachan, R.; Pickard, A. Learning Mathematics through Serious Games: An Engagement Framework. In Proceedings of the 2016 IEEE Frontiers in Education Conference (FIE), Erie, PA, USA, 12–15 October 2016; pp. 1–5. [Google Scholar]
- Moreno-Guerrero, A.J.; Rondón García, M.; Martínez Heredia, N.; Rodríguez-García, A.M. Collaborative Learning Based on Harry Potter for Learning Geometric Figures in the Subject of Mathematics. Mathematics 2020, 8, 369. [Google Scholar] [CrossRef]
- Lantarón, S.; López, M.; Merchán, S.; Rodrigo, J. Gamification actions in the teaching of mathematics at every educational level. In EDULEARN18 Proceedings; IATED: Palma, Spain, 2018; pp. 304–312. [Google Scholar]
- Lantarón, S.; López, M.; Merchán, S.; Rodrigo, J. Cajas Lógicas. In Proceedings of the Jornadas: Tendencias en Innovación Educativa y su Implantación en la UPM, Madrid, Spain, 20 November 2018. [Google Scholar]
- Lantarón, S.; López, M.; Merchán, S.; Rodrigo, J. Analysis of logical and strategical games as a tool for the teaching and approach to mathematical concepts. In INTED2019 Proceedings; IATED: Valencia, Spain, 2019; pp. 7963–7969. [Google Scholar]
- Edo, M.; Deulofeu, J. Investigación sobre juegos, interacción y construcción de conocimientos matemáticos. Enseñanza Cienc. 2006, 24, 257–268. [Google Scholar]
- González, A.G.; Molina, J.G.; Sánchez, M. La matemática nunca deja de ser un juego: Investigaciones sobre los efectos del uso de juegos en la enseñanza de las matemáticas. Educ. Matemática 2014, 26, 109–133. [Google Scholar]
- Queiruga-Dios, A.; Santos Sánchez, M.J.; Queiruga Dios, M.; Gayoso Martínez, V.; Hernández Encinas, A. A Virus Infected Your Laptop. Let’s Play an Escape Game. Mathematics 2020, 8, 166. [Google Scholar] [CrossRef]
- Iriondo-Otxotorena, J. Mejora Didáctica en la Transición de la Aritmética al Álgebra en el Primer Ciclo de la ESO Basada en la Ludificación. 2016. Available online: https://reunir.unir.net/handle/123456789/3538?show=full (accessed on 11 March 2021).
- Yung, O.C.; Junaini, S.N.; Kamal, A.; Ibharim, L.F. Slash 100%: Gamification of mathematics with hybrid QR-based card game. Indones. J. Electr. Eng. Comput. Sci. 2020, 20, 1453–1459. [Google Scholar] [CrossRef]
- Novak, N.; Tassell, J. Using video game play to improve education majors’ mathematical performance: An experimental study. Comput. Hum. Behav. 2015, 53, 124–130. [Google Scholar] [CrossRef]
- Contreras-Espinosa, R.S. Juegos digitales y gamificación aplicados en el ámbito de la educación. RIED 2016, 19, 27–33. [Google Scholar] [CrossRef]
- Guzmán, M. Tendencias Innovadoras en Educación Matemática; Editorial Popular: Madrid, España, 1993. [Google Scholar]
- Brull, S.; Finlayson, S. Importance of Gamification in Increasing Learning. J. Contin. Educ. Nurs. 2016, 47, 372–375. [Google Scholar] [CrossRef]
- Chu, C.; Hung, C.H. Effects of the Digital Game-Development Approach on Elementary School Students’ Learning Motivation, Problem Solving, and Learning Achievement. Int. J. Distance Educ. Technol. 2015, 13, 87–102. [Google Scholar] [CrossRef]
- Werbach, K.; Hunter, D. For the Win: How Game Thinking Can Revolutionize Your Business; Wharton Digital Press: Philadelphia, PA, USA, 2012. [Google Scholar]
- Oliva, H.A. La gamificación como estrategia metodológica en el contexto educativo universitario. Real. Reflexión 2017, 44, 29. [Google Scholar] [CrossRef]
- López, D.; Calonge, A.; Rodríguez, T.; Ros, G.; Lebron, J.A. Using gamification in a teaching innovation project at the University of Alcala: A new approach to experimental science practices. Electron. J. Learn 2019, 17, 93–106. [Google Scholar]
- Mansureh, K.; Atsusi, H.; Haiyan, B. The effects of modern mathematics computer games on mathematics achievement and class motivation. Comput. Educ. 2010, 55, 427–443. [Google Scholar]
- Ke, F. An implementation of design-based learning through creating educational computer games: A case study on mathematics learning during design and computing. Comput. Educ. 2014, 73, 26–39. [Google Scholar] [CrossRef]
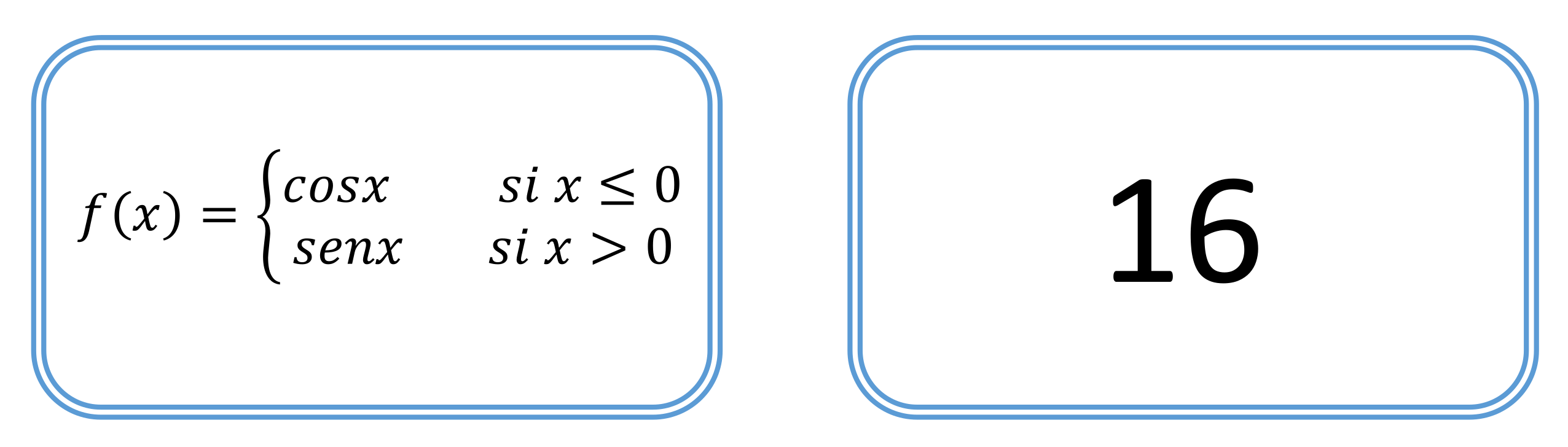
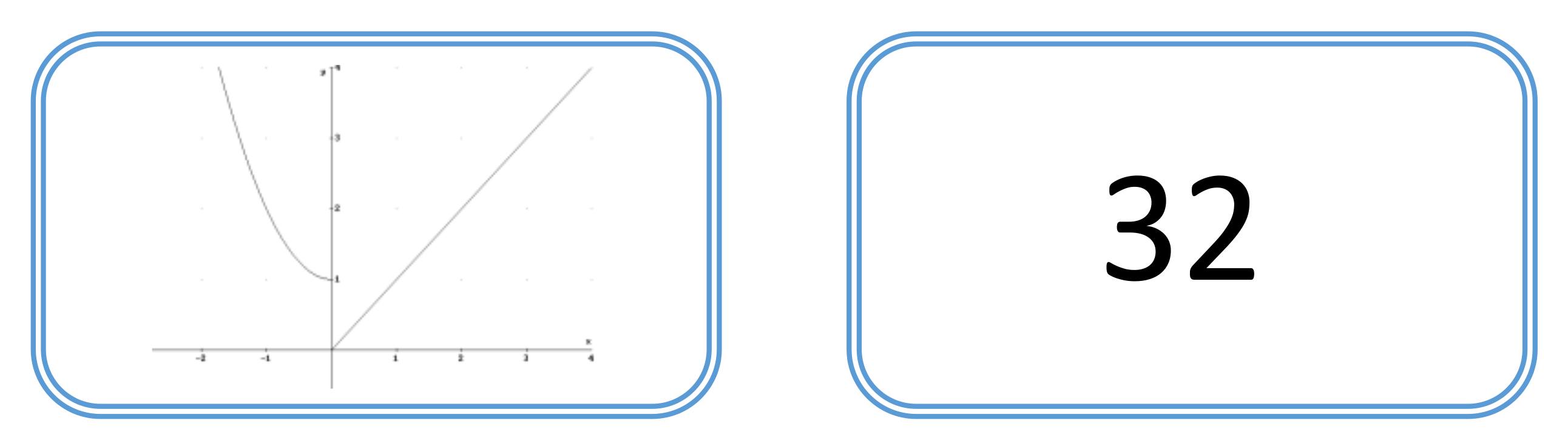

| (0,0,0,0,0,0) | (0,1,0,0,0,0) | (0,0,0,1,0,0) | (0,1,0,1,0,0) | (0,0,0,0,0,1) | (0,1,0,0,0,1) |
| (1,0,0,0,0,0) | (1,1,0,0,0,0) | (1,0,0,1,0,0) | (1,1,0,1,0,0) | (1,0,0,0,0,1) | (1,1,0,0,0,1) |
| (0,0,1,0,0,0) | (0,1,1,0,0,0) | (0,0,1,1,0,0) | (0,1,1,1,0,0) | (0,0,1,0,0,1) | (0,1,1,0,0,1) |
| (1,0,1,0,0,0) | (1,1,1,0,0,0) | (1,0,1,1,0,0) | (1,1,1,1,0,0) | (1,0,1,0,0,1) | (1,1,1,0,0,0) |
| (0,0,0,0,1,0) | (0,1,0,0,1,0) | (0,0,0,1,1,0) | (0,1,0,1,1,0) | (0,0,0,0,1,1) | (0,1,0,0,1,1) |
| (1,0,0,0,1,0) | (1,1,0,0,1,0) | (1,0,0,1,1,0) | (1,1,0,1,1,0) | (1,0,0,0,1,1) | (1,1,0,0,1,1) |
| (0,0,1,0,1,0) | (0,1,1,0,1,0) | (0,0,1,1,1,0) | (0,1,1,1,1,0) | (0,0,1,0,1,1) | (0,1,1,0,1,1) |
| (1,0,1,0,1,0) | (1,1,1,0,1,0) | (1,0,1,1,1,0) | (1,1,1,1,1,0) | (1,0,1,0,1,1) | (1,1,1,0,1,1) |
| (0,0,0,1,0,1) | (0,1,0,1,0,1) | (1,0,0,1,0,1) | (1,1,0,1,0,1) | (0,0,1,1,0,1) | (0,1,1,1,0,1) |
| (1,0,1,1,0,1) | (1,1,1,1,0,1) | (0,0,0,1,1,1) | (0,1,0,1,1,1) | (1,0,0,1,1,1) | (1,1,0,1,1,1) |
| (0,0,1,1,1,1) | (0,1,1,1,1,1) | (1,0,1,1,1,1) | (1,1,1,1,1,1) |
| (0,0,0,0,0,0) | (0,1,0,0,0,0) | (0,0,0,1,0,0) | (0,1,0,1,0,0) | (0,0,0,0,0,1) | (1,0,0,0,0,0) |
| (1,1,0,0,0,0) | (1,0,0,1,0,0) | (1,1,0,1,0,0) | (1,0,0,0,0,1) | (0,0,1,0,0,0) | (0,1,1,0,0,0) |
| (0,0,1,1,0,0) | (0,1,1,1,0,0) | (0,0,1,0,0,1) | (1,0,1,0,0,0) | (1,1,1,0,0,0) | (1,0,1,1,0,0) |
| (1,1,1,1,0,0) | (1,0,1,0,0,1) | (0,0,0,1,1,0) | (0,1,0,1,1,0) | (1,0,0,1,1,0) | (1,1,0,1,1,0) |
| (0,0,1,1,1,0) | (0,1,1,1,1,0) | (1,0,1,1,1,0) | (1,1,1,1,1,0) |
| Key Mathematical Concept | Game Design Element | Final Score |
|---|---|---|
| Being able to analyze the continuity of a function. | In the game, the student answers the question: Is it continuous? | In the video game, getting the function correct scores points. The number of points decreases as the number of attempts increases. |
| Being able to analyze the derivability of a function. | In the game, the student answers the question: Is it derivable? | |
| Being able to calculate limits of functions and asymptotes. Recognizing these concepts through the visualization of the graph of a function. | In the game, the student answers the question: Is there a vertical asymptote? | |
| Being able to analyze the range of a function. | In the game, the student answers the question: Is it bounded? | |
| Being able to recognize the growth and decay of a function and its monotonicity. | In the game, the student answers the question: Is it monotonous? | |
| Being able to analyze regions of constant sign for a function. | In the game, the student answers the question: Is it a non-negative function? | |
| Being able to study a function through its analytical or graphical representation. | The function cards are offered in one of two ways, mixing both in the set. | |
| Being able to recognize implications of different characteristics of the function. | The game allows the student to get the function without answering all the questions. | Extra points will be given to the player who gets the correct function without having needed all the answers. |
| Being able to change the base of a number representation. | Each function is assigned a number in base 10, which must be guessed from a number in base 2 obtained from the answers of the game. | In the video game, if the numbering is correct, the player gets points. The number of points decreases as the number of attempts increases. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lantarón, S.; López, M.; Merchán, S.; Rodrigo, J. Improving the Teaching of Real Valued Functions Using Serious Games. Binary Who Is Who? Mathematics 2021, 9, 1239. https://doi.org/10.3390/math9111239
Lantarón S, López M, Merchán S, Rodrigo J. Improving the Teaching of Real Valued Functions Using Serious Games. Binary Who Is Who? Mathematics. 2021; 9(11):1239. https://doi.org/10.3390/math9111239
Chicago/Turabian StyleLantarón, Sagrario, Mariló López, Susana Merchán, and Javier Rodrigo. 2021. "Improving the Teaching of Real Valued Functions Using Serious Games. Binary Who Is Who?" Mathematics 9, no. 11: 1239. https://doi.org/10.3390/math9111239
APA StyleLantarón, S., López, M., Merchán, S., & Rodrigo, J. (2021). Improving the Teaching of Real Valued Functions Using Serious Games. Binary Who Is Who? Mathematics, 9(11), 1239. https://doi.org/10.3390/math9111239






