1. Introduction
By , we denote the space of continuous functions defined on , and by , the space of all functions defined on , which are Lebesgue integrable. Let be the set of all positive integers.
We consider for , .
In order to prove Weierstrass’s approximation theorem [
1], S.N. Bernstein introduced the Bernstein operators in paper [
2], which, for
, are defined as:
where
, for every
, and
if
or
.
Let
and
. D. D. Stancu introduced in paper [
3] the following operators, which are a generalization of the well-known Bernstein operators (see [
2]),
defined as:
where
,
, are defined as before, and
.
The Bernstein operators have been intensively studied, and many generalizations were considered, one of which is the Kantorovich variant, due to L.V. Kantorovich, from 1930 (see [
4]). The Kantorovich operators
are positive linear operators and can be defined as:
where
,
, are the Bernstein basis, and
.
Following the generalization of Bernstein operators proposed by Stancu, D. Bărbosu introduced in paper [
5] the Kantorovich variant of Stancu–Bernstein operators, which, for
, is defined as:
with
,
, for every
and
The study of Kantorovich operators is still in the spotlight of many recent research papers (see [
6,
7,
8]). Among the numerous generalizations of the Kantorovich–Bernstein type operators, we mention the one by Indrea et al., (see [
9]), which introduces a new general class which preserves the test functions
and
.
In [
10], J.P. King introduced a new class of positive linear Bernstein-type operators which reproduce constant functions (
) and
. These operators are a generalization of the Bernstein operators, but they are not polynomial-type operators. With the results introduced by King, a new direction of research was initiated, which concerns the construction of new operators with better approximation properties, obtained by modifying existing sequences of linear positive operators. This subject has been one of great interest. Gonska and Piţul (see [
11]) studied estimates in terms of the first and second moduli of continuity for the operators introduced by King. Among the first generalizations of King’s result, we mention those of Agratini (see [
12]), Cardena-Morales et al., (see [
13]), Duman and Özarslan (see [
14,
15]) and Gonska et al., (see [
16]). The subject is still of interest. Among the more recent studies, we mention the one by Popa (see [
17]) where Voronovskaja-type theorems for King operators are studied. A recent extensive review of King type operators is that of Acar et al. (see [
18]).
Based on the results in [
3,
9,
19,
20], we introduce three new classes of King-type approximation operators. The aim of our paper is to obtain convergence properties of the uniform approximation of continuous functions using a Korovkin-type theorem(see [
21]). Our results are a generalization of previous results on the topic.
The article is structured as follows.
Section 2 presents some known results and notions that are to be used throughout the paper. In
Section 3, we introduce the general form of our operators and some properties they satisfy. In
Section 4,
Section 5 and
Section 6, we introduced three new classes of operators, which preserve exactly two of the test functions
. These operators are particular variants of the operator considered in
Section 3.
4. Stancu–Kantorovich Type Operators Which Preserve the Functions and
In this section, we shall construct an operator of Stancu–Kantorovich type as in (
3), that preserves the test functions
and
, i.e., an operator that satisfies
Now, from the conditions in (
7) and relations (
4), (
5) we get
and
for any
and
.
In order to have a positive operator, we shall assume that the functions
and
are positive. This condition yields the following inequality
Lemma 2. For and any integers , we have Proof. Let us consider the sequences
,
and
,
Imposing the condition we have that is a decreasing sequence, and is an increasing sequence, thus implying that our inclusion holds for any . □
Remark 2. From now on, we will consider .
Remark 3. Since on the interval we have that , for every , we will consider , where is a positive integer which is arbitrarily fixed. Note that for any , if we make sufficiently large, then .
Now, taking into account the sequences
and
obtained in (
8) and (
9), the operator in (
3) will be
for any
.
Lemma 3. The operator from (10) satisfiesfor . Proof. The first two relations from (
11) are obvious, and the third follows by applying relations (
5), (
8) and (
9) and after some computations. □
Lemma 4. The following relations hold Proof. Using the previous lemma and relation (
2), we get
and
which, after some calculations, yields (
14). □
Lemma 5. We haveuniformly with respect to . Consequently, for any , there exists an integer , sufficiently large, such thatfor any and such that . Proof. The relation (
15) follows from (
12) and (
14). The existence of
follows from the definition of the limit of a function and the inequality (
16) follows from (
15) by applying the inequality
, which is true for every
. □
Theorem 2. Let be a continuous function on . Then, we haveuniformly on I and for every there exists such thatfor any and such that . Proof. The Theorem from above follows from Theorem 1 by taking . □
Graphic Properties of Approximation
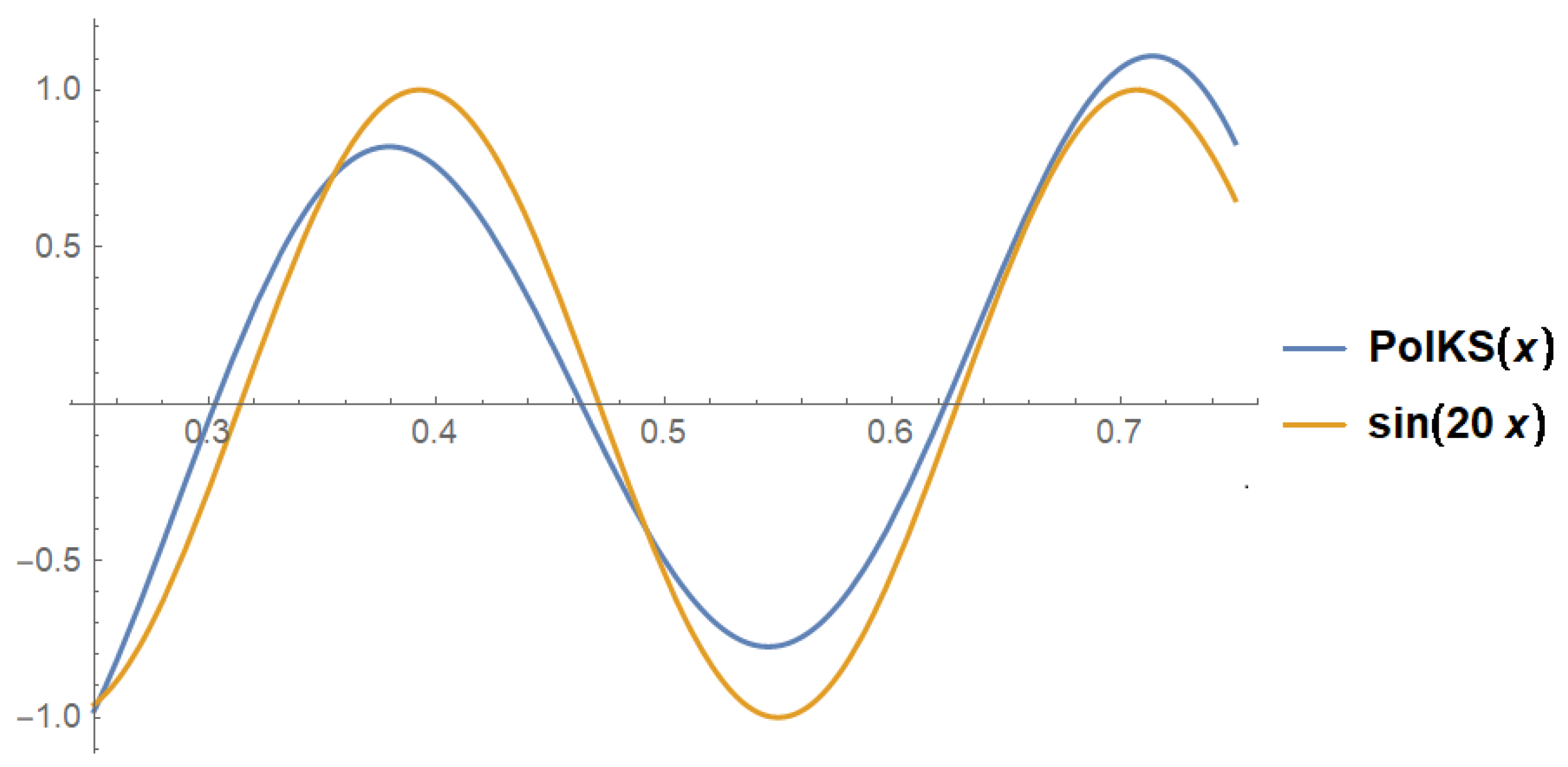
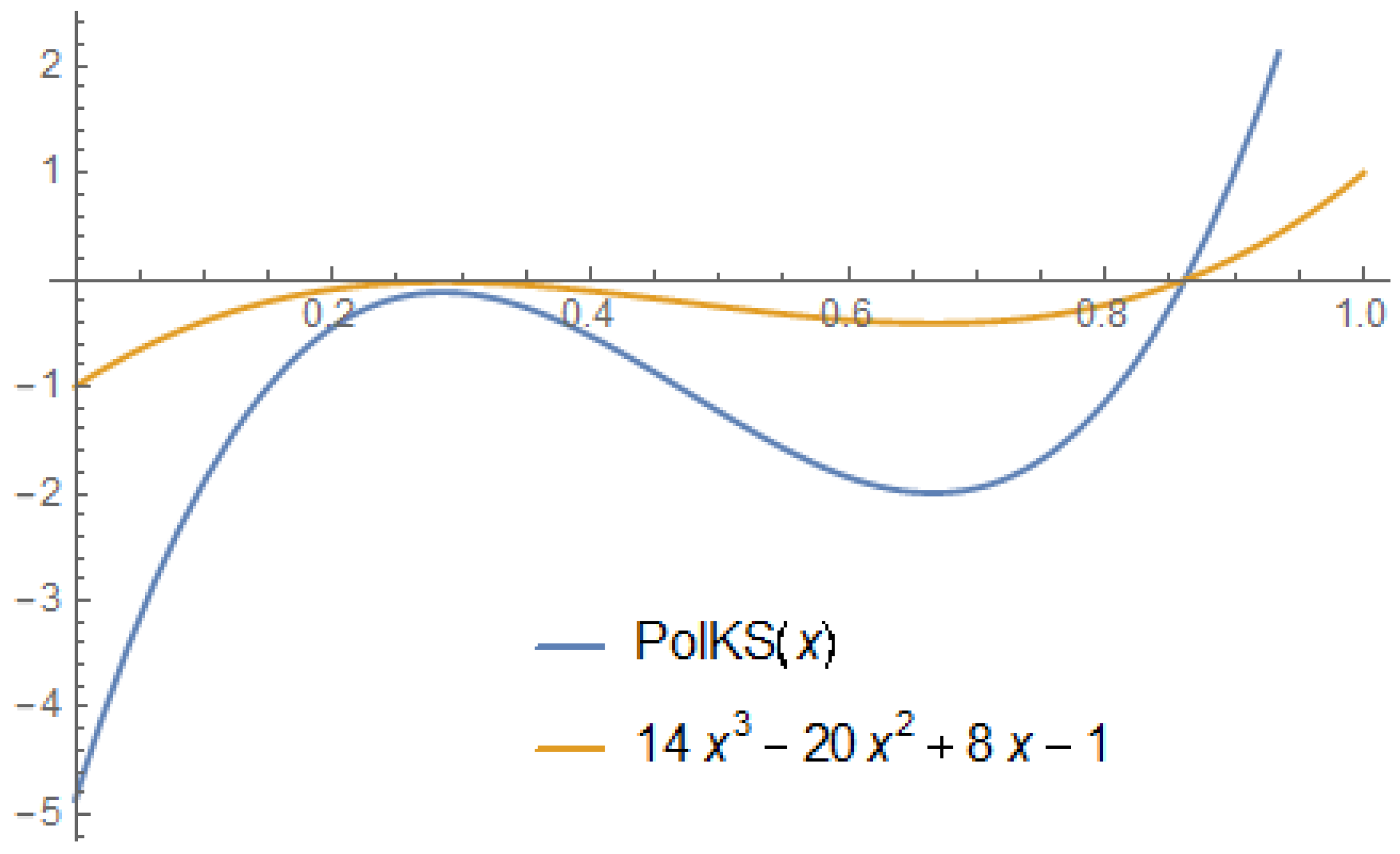
Remark 4. It can be seen in both Figure 1 and Figure 2 that our operators approximate the given functions for α and β chosen such that . 5. Stancu–Kantorovich-Type Operators Which Preserve the Functions and
In this section, we shall construct an operator of Stancu–Kantorovich-type, as in (
3), that preserves the test functions
and
, i.e., an operator that satisfies
Now, imposing the condition (
17) and the Equations (
4) and (
6), we get:
and the following quadratic equation, in
:
Note that for
,
, the discriminant
of the quadratic Equation (
19) is positive.
We make the following notation:
Now, solving Equation (
19) we obtain, for
:
and, from relation (
18) we get
In order to have positive linear operators, we shall impose that the functions
and
from (
21) and (
22) are positive. In this case, we obtain the following inequalities:
Lemma 6. Let be fixed. There is an integer such thatfor every such that and α, β, satisfying . Proof. We have that
and
therefore, for all
, the inclusion (
23) holds. □
Remark 5. Since the functions and are positive on the interval considered in (23), from now on, we will consider , for all and . Now, taking into account the sequences
and
obtained in (
21) and (
22), the operator in (
3) will be
for any
and
.
Lemma 7. The operator from (24) satisfiesfor and . Proof. The first and last relation from (
25) are obvious, and the second follows by applying relations (
5) and (
21). □
Now, we can obtain the following result.
Lemma 8. The following relations holdfor any and . Proof. Using the previous lemma and the definition of the operator
from (
2), we get the results after some calculations. □
Lemma 9. We have:uniformly with regard to . For any , there exists such thatfor any and such that Proof. We have:
and after some calculations, we get:
Now, replacing the right hand side term in (
27) and (
28) with (
32), we will get the convergences in (
29) and (
30). Using the definition of the limit of a function and the inequality
, we have that for every
, there exists
such that the inequality (
31) holds, for every
. □
Now, using the above results we obtain the following theorem.
Theorem 3. Let be a continuous function on Then, we haveuniformly on I and for every , there exists such thatfor any and such that . Proof. The Theorem follows from relation (
31) and from Theorem 1 by taking
. □
Graphic Properties of Approximation
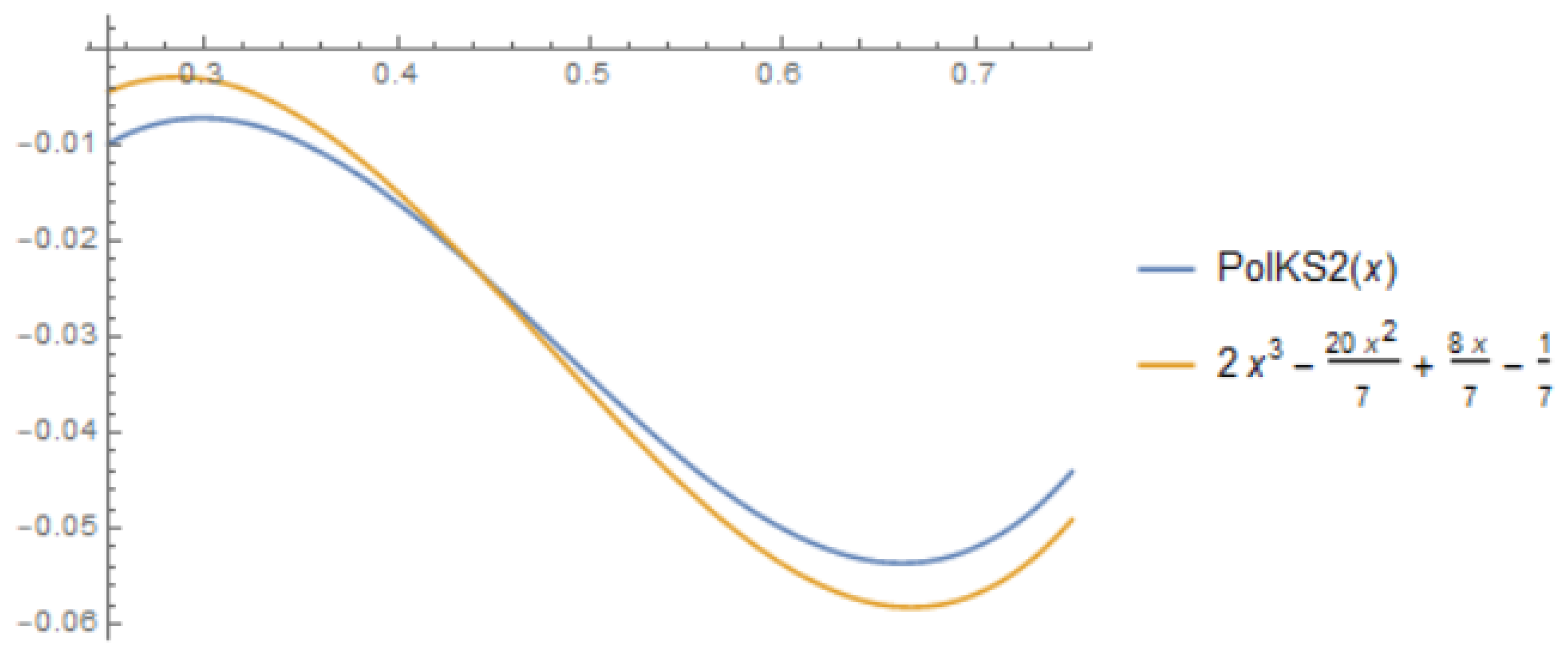
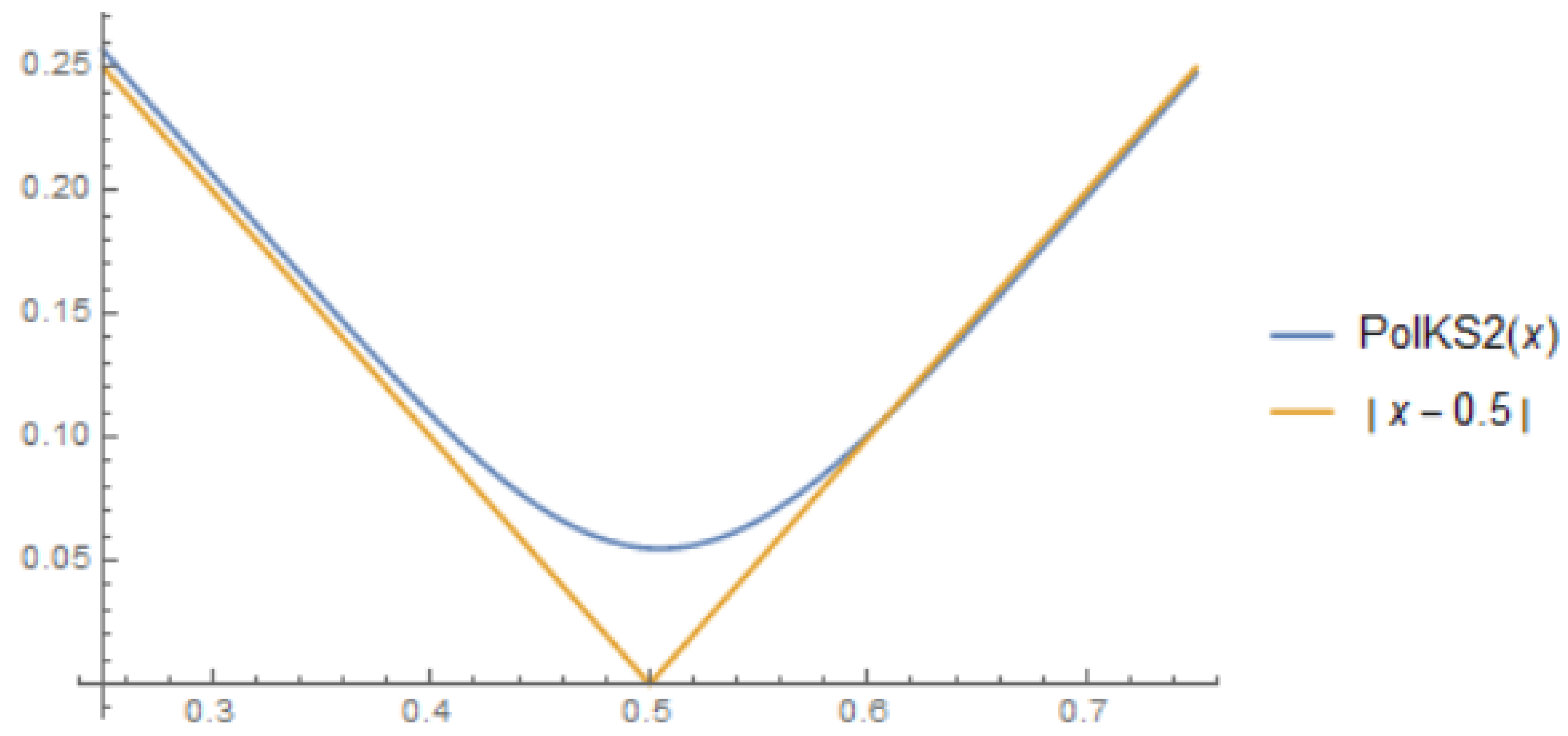
Remark 6. Furthermore, in this case, it can be seen in Figure 3 and Figure 4 that our operators approximate the given functions. 6. Stancu–Kantorovich Type Operators Which Preserve the Functions and
In this section, we shall construct an operator of Stancu–Kantorovich type as in (
3), that preserves the test functions
and
, i.e., an operator that satisfies
In order to obtain the main results of this section, we shall consider the following notation
where
and
.
With the previous notation, we have the following remark.
Remark 7. In order to have positive operators and for the relation (
34)
to hold, we shall impose that which implies From (
34), we get
which implies
Now, from the above considerations and imposing the conditions
and
we will obtain the following lemma.
Proof. Equaling relations (
5) and (
38) , we get
Now, using the Equation (
37), we have
which gives relation (
40).
Now, using relations (
37) and (
40), by direct computation, we will get Formula (
41). □
Imposing the condition (
39), we will obtain the following quadratic equation in
:
which has the following solutions:
where
Remark 8. It is easy to verify that and uniformly for .
From now on, in this section we will consider .
In order to have a positive operator, the quantities
and
from relations (
40) and (
41) shall be positive. With that condition, we get the following inequalities:
and
for all
and
which lead to
for all
and
.
Lemma 11. Let . Then, there exists such that relation (
42)
holds for any and ,
.
Proof. We have
, uniformly on
, and
uniformly for
. □
From now on, we will consider , with fixed .
We can write the operators in (
3) as
Lemma 12. For and , we have Proof. The proof follows immediately from relation (
2) and from the conditions (
38), (
39). □
Theorem 4. We haveuniformly on I for every . Proof. By applying Theorem 1. □
Remark 9. It was proved in [24] that there is no sequence of positive, linear and analytic operators that preserves the test functions and Therefore, we have operators Graphic Properties of Approximation
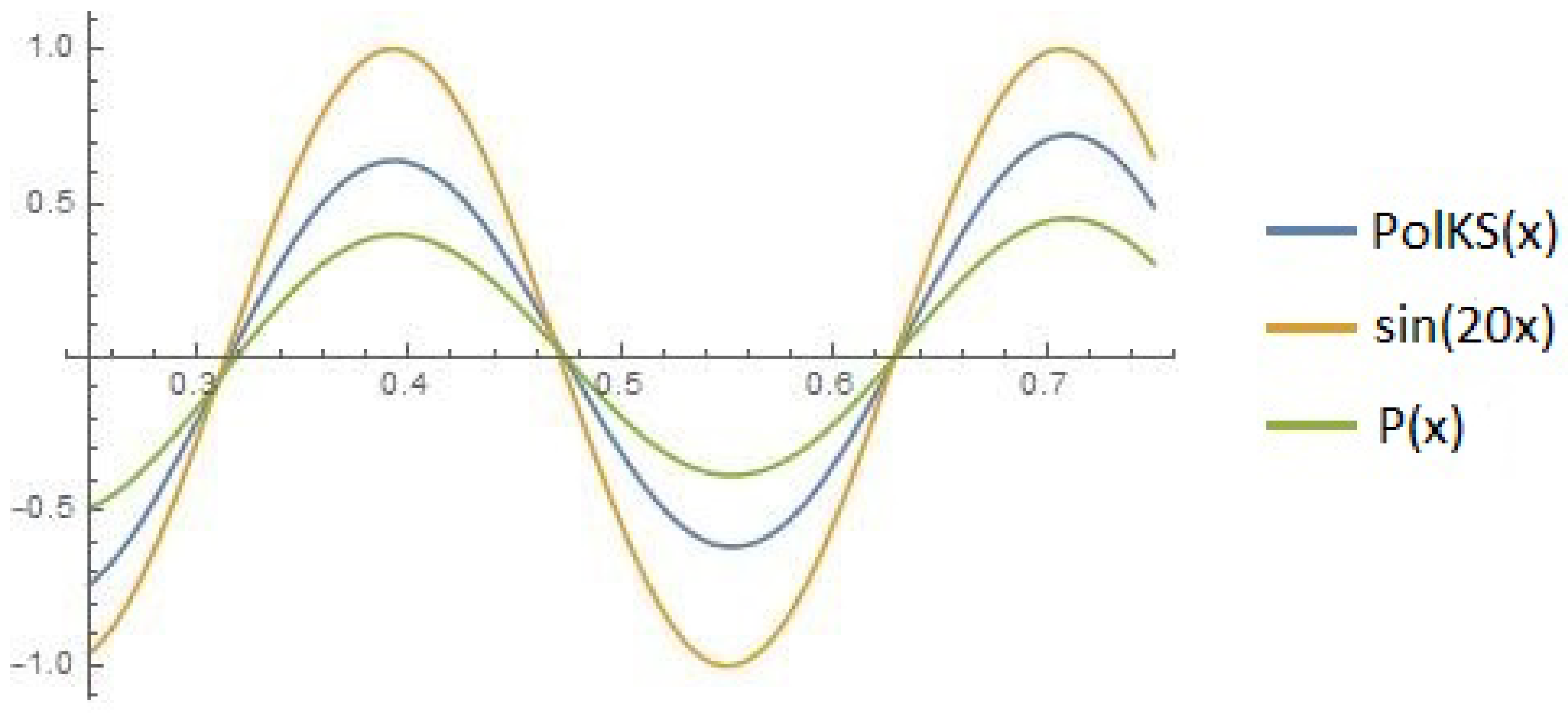
As a first comparison, we considered the function
, and we obtained the following graphics,
Figure 5, where
represents our operators that preserve
and
, and
is the operator obtained by Indrea et al. in [
9], which is also a particular case of our operators considered in the third section for
.
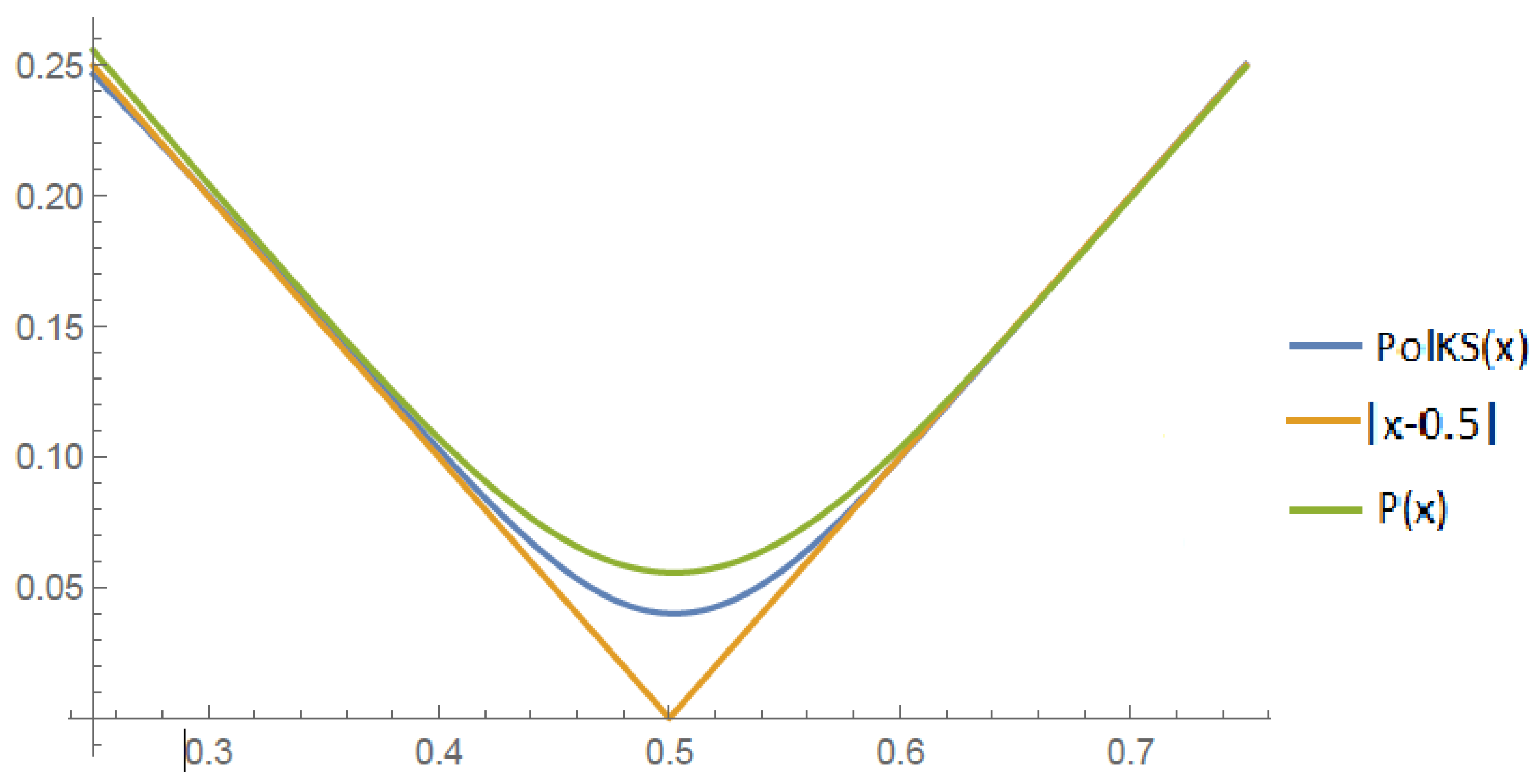
Now, we considered the function
and we obtained
Figure 6: