Robust Passivity Cascade Technique-Based Control Using RBFN Approximators for the Stabilization of a Cart Inverted Pendulum
Abstract
1. Introduction
- A robust model-free control design formulated using RBFN approximators and passivity framework.
- A design that enhances the performance of the closed-loop system by augmenting its dynamics with virtual states and an adaptive robustifying signal.
- An approach that guarantees the boundedness of all the states via the output of strictly passive (OSP) property.
2. Preliminaries and Control Objectives
2.1. RBFN Approximator
2.2. Passivity Theorem
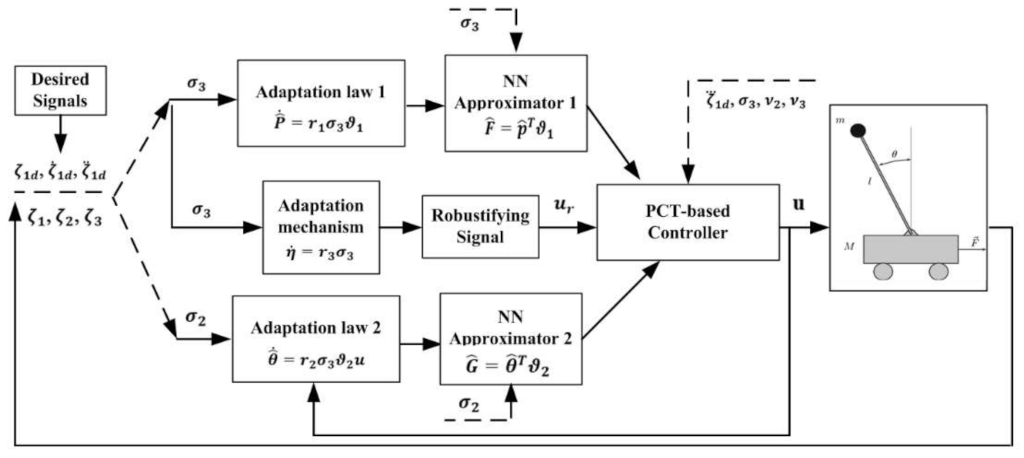
3. Proposed PCT-Based Control Design
3.1. State-Space Model of the System
3.2. The PCT-Based Control
3.3. Stability Analysis
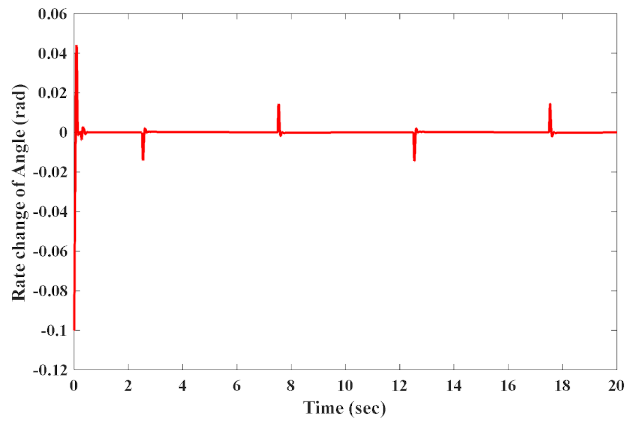
4. Simulation Results
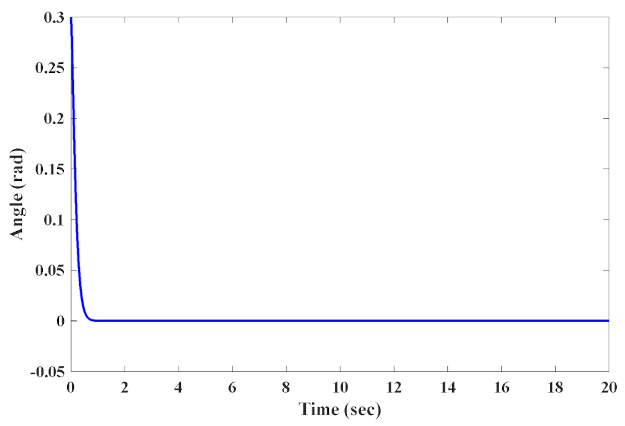
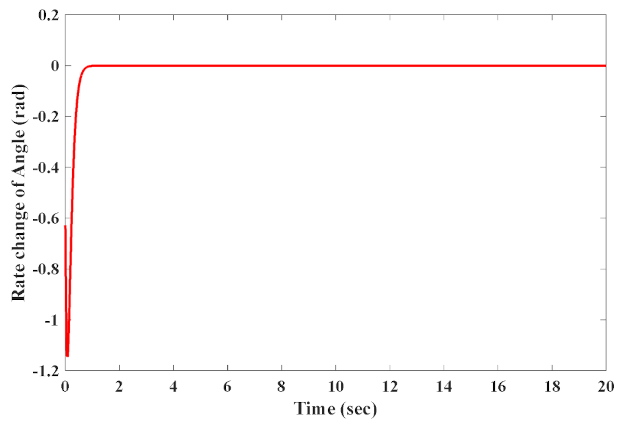
4.1. Normal Case
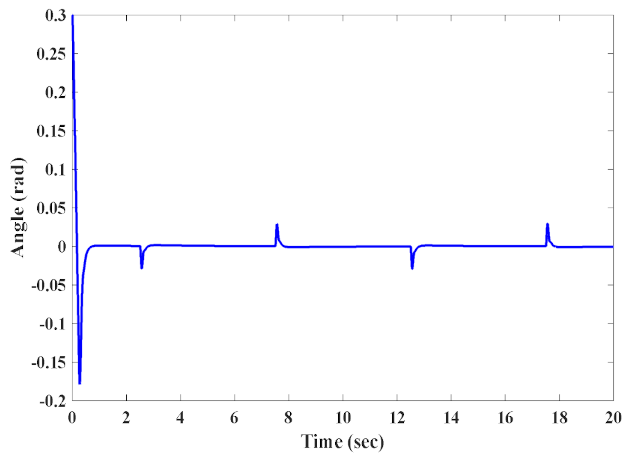
4.2. Abnormal Case (Existence of External Disturbances)
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mehedi, I.M.; Ansari, U.; Al-Saggaf, U. Three degrees of freedom rotary double inverted pendulum stabilization by using robust generalized dynamic inversion control: Design and experiments. J. Vib. Control. 2020, 26, 2174–2184. [Google Scholar] [CrossRef]
- Ben Hazem, Z.; Fotuhi, M.J.; Bingül, Z. Development of a Fuzzy-LQR and Fuzzy-LQG stability control for a double link rotary inverted pendulum. J. Frankl. Inst. 2020, 357, 10529–10556. [Google Scholar] [CrossRef]
- Pujol-Vazquez, G.; Mobayen, S.; Acho, L. Robust control design to the furuta system under time delay measurement feedback and exogenous-based perturbation. Mathematics 2020, 8, 2131. [Google Scholar] [CrossRef]
- Marinca, V.; Herisanu, N. Optimal auxiliary functions method for a pendulum wrapping on two cylinders. Mathematics 2020, 8, 1364. [Google Scholar] [CrossRef]
- Mobayen, S.; Tchier, F. Synchronization of A Class of Uncertain Chaotic Systems with Lipschitz Nonlinearities Using State-Feedback Control Design: A Matrix Inequality Approach. Asian J. Control. 2018, 20, 71–85. [Google Scholar] [CrossRef]
- Barkat, A.; Hamayun, M.T.; Ijaz, S.; Akhtar, S.; Ansari, E.A.; Ghous, I. Model identification and real-time implementation of a linear parameter–varying control scheme on lab-based inverted pendulum system. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2021, 235, 30–38. [Google Scholar] [CrossRef]
- Mobayen, S.; Tchier, F. Composite nonlinear feedback control technique for master/slave synchronization of nonlinear systems. Nonlinear Dyn. 2016, 87, 1731–1747. [Google Scholar] [CrossRef]
- Jacknoon, A.; Abido, M.A. Ant Colony based LQR and PID tuned parameters for controlling Inverted Pendulum. In Proceedings of the 2017 International Conference on Communication, Control, Computing and Electronics Engineering (ICCCCEE), Khartoum, Sudan, 16–18 January 2017; Institute of Electrical and Electronics Engineers (IEEE); Piscataway, NJ, USA, 2017; pp. 1–8. [Google Scholar]
- Mishra, S.K.; Chandra, D. Stabilization and Tracking Control of Inverted Pendulum Using Fractional Order PID Controllers. J. Eng. 2014, 2014, 1–9. [Google Scholar] [CrossRef]
- Elsayed, B.A.; Hassan, M.A.; Mekhilef, S. Fuzzy swinging-up with sliding mode control for third order cart-inverted pendulum system. Int. J. Control. Autom. Syst. 2014, 13, 238–248. [Google Scholar] [CrossRef]
- Mahjoub, S.; Mnif, F.; Derbel, N. Second-order sliding mode control applied to inverted pendulum. In Proceedings of the 14th International Conference on Sciences and Techniques of Automatic Control & Computer Engineering, Sousse, Tunisia, 20–22 December 2013; pp. 269–273. [Google Scholar]
- El-Nagar, A.M.; El-Bardini, M.; El-Rabaie, N.M. Intelligent control for nonlinear inverted pendulum based on interval type-2 fuzzy PD controller. Alex. Eng. J. 2014, 53, 23–32. [Google Scholar] [CrossRef]
- Jia, X.; Dai, Y.; Memon, Z.A. Adaptive Neuro-fuzzy Inference System Design of Inverted Pendulum System on an Inclined Rail. In Proceedings of the 2010 Second WRI Global Congress on Intelligent Systems, Wuhan, China, 16–17 December 2010; pp. 137–141. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, H.; Gu, D.; Wang, J. Cascaded control for balancing an inverted pendulum on a flying quadrotor. Robotica 2017, 35, 1263–1279. [Google Scholar] [CrossRef]
- Ding, Z.; Li, Z. A cascade fuzzy control system for inverted pendulum based on Mamdani-Sugeno type. In Proceedings of the 2014 9th IEEE Conference on Industrial Electronics and Applications, Hangzhou, China, 9–11 June 2014; Institute of Electrical and Electronics Engineers (IEEE); Piscataway, NJ, USA, 2014; pp. 792–797. [Google Scholar]
- Byrnes, C.I.; Isidori, A.; Willems, J.C. Feedback Equivalence to Passive Nonlinear Systems. In Analysis of Controlled Dynamical Systems; J.B. Metzler: Lyon, France, 1991; pp. 118–135. [Google Scholar]
- Jiang, Z.-P.; Hill, D.J.; Fradkov, A.L. A passification approach to adaptive nonlinear stabilization. Syst. Control. Lett. 1996, 28, 73–84. [Google Scholar] [CrossRef]
- Balachandran, R.; Jorda, M.; Artigas, J.; Ryu, J.-H.; Khatib, O. Passivity-based stability in explicit force control of robots. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Marina Bay Sands, Singapore, 29 May–3 June 2017; pp. 386–393. [Google Scholar]
- Focchi, M.; Medrano-Cerda, G.A.; Boaventura, T.; Frigerio, M.; Semini, C.; Buchli, J.; Caldwell, D.G. Robot impedance control and passivity analysis with inner torque and velocity feedback loops. Control. Theory Technol. 2016, 14, 97–112. [Google Scholar] [CrossRef]
- Kostarigka, A.K.; Rovithakis, G.A. Approximate Adaptive Output Feedback Stabilization via Passivation of MIMO Uncertain Systems Using Neural Networks. IEEE Trans. Syst. Man Cybern. Part B (Cybernetics) 2009, 39, 1180–1191. [Google Scholar] [CrossRef] [PubMed]
- Kuntanapreeda, S. Adaptive control of fractional-order unified chaotic systems using a passivity-based control approach. Nonlinear Dyn. 2016, 84, 2505–2515. [Google Scholar] [CrossRef]
- Leite, A.C.; Lizarralde, F. Passivity-based adaptive 3D visual servoing without depth and image velocity measurements for uncertain robot manipulators. Int. J. Adapt. Control. Signal Process. 2016, 30, 1269–1297. [Google Scholar] [CrossRef]
- Haddad, N.K.; Chemori, A.; Belghith, S. Robustness enhancement of IDA-PBC controller in stabilising the inertia wheel inverted pendulum: Theory and real-time experiments. Int. J. Control. 2018, 91, 2657–2672. [Google Scholar] [CrossRef]
- Sanner, R.M.; Slotine, J.-J.E. Direct adaptive control using Gaussian networks. Nonlinear Systems Lab., MIT. Tech. Rep. SL-910303 1991.
- Vidyasagar, M. Nonlinear Systems Analysis; SIAM: Philadelphia, PA, USA, 2002. [Google Scholar]
- Lin, W. Global asymptotic stabilization of general nonlinear systems with stable free dynamics via passivity and bounded feedback. Automatica 1996, 32, 915–924. [Google Scholar] [CrossRef]




| Symbol | Parameter | Value |
|---|---|---|
| Mass of pendulum | 0.2 | |
| Mass of cart | 0.5 | |
| Half-length of pendulum | 0.5 | |
| Gravity acceleration | 9.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahmani, R.; Mobayen, S.; Fekih, A.; Ro, J.-S. Robust Passivity Cascade Technique-Based Control Using RBFN Approximators for the Stabilization of a Cart Inverted Pendulum. Mathematics 2021, 9, 1229. https://doi.org/10.3390/math9111229
Rahmani R, Mobayen S, Fekih A, Ro J-S. Robust Passivity Cascade Technique-Based Control Using RBFN Approximators for the Stabilization of a Cart Inverted Pendulum. Mathematics. 2021; 9(11):1229. https://doi.org/10.3390/math9111229
Chicago/Turabian StyleRahmani, Reza, Saleh Mobayen, Afef Fekih, and Jong-Suk Ro. 2021. "Robust Passivity Cascade Technique-Based Control Using RBFN Approximators for the Stabilization of a Cart Inverted Pendulum" Mathematics 9, no. 11: 1229. https://doi.org/10.3390/math9111229
APA StyleRahmani, R., Mobayen, S., Fekih, A., & Ro, J.-S. (2021). Robust Passivity Cascade Technique-Based Control Using RBFN Approximators for the Stabilization of a Cart Inverted Pendulum. Mathematics, 9(11), 1229. https://doi.org/10.3390/math9111229









