The Novel Integral Homotopy Expansive Method
Abstract
1. Introduction
2. IHEM Method
3. Case Studies
3.1. Case Study 1
3.2. Case Study 2
3.3. Case Study 3
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zill, D.G. A First Course in Differential Equations with Modeling Applications; Cengage Learning: Hong Kong, China, 2012. [Google Scholar]
- Filobello-Nino, U.; Vazquez-Leal, H.; Khan, Y.; Perez-Sesma, A.; Diaz-Sanchez, A.; Herrera-May, A.; Pereyra-Diaz, D.; Castaneda-Sheissa, R.; Jimenez-Fernandez, V.; Cervantes-Perez, J. A handy exact solution for flow due to a stretching boundary with partial slip. Rev. Mex. FÃsica E 2013, 59, 51–55. [Google Scholar]
- Azam, M.; Xu, T.; Khan, M. Numerical simulation for variable thermal properties and heat source/sink in flow of Cross nanofluid over a moving cylinder. Int. Commun. Heat Mass Transf. 2020, 118, 104832. [Google Scholar] [CrossRef]
- Azam, M.; Xu, T.; Shakoor, A.; Khan, M. Effects of Arrhenius activation energy in development of covalent bonding in axisymmetric flow of radiative-Cross nanofluid. Int. Commun. Heat Mass Transf. 2020, 113, 104547. [Google Scholar] [CrossRef]
- Azam, M.; Mabood, F.; Xu, T.; Waly, M.; Tlili, I. Entropy optimized radiative heat transportation in axisymmetric flow of Williamson nanofluid with activation energy. Results Phys. 2020, 19, 103576. [Google Scholar] [CrossRef]
- Assas, L.M.B. Approximate solutions for the generalized KdV–Burgers’ equation by He’s variational iteration method. Phys. Scr. 2007, 76, 161–164. [Google Scholar] [CrossRef]
- Kazemnia, M.; Zahedi, S.; Vaezi, M.; Tolou, N. High—Order Differential Equations. J. Appl. Sci. 2008, 8, 4192–4197. [Google Scholar] [CrossRef][Green Version]
- Noorzad, R.; Poor, A.T.; Omidvar, M. Variational iteration method and homotopy-perturbation method for solving Burgers equation in fluid dynamics. J. Appl. Sci. 2008, 8, 369–373. [Google Scholar] [CrossRef]
- Evans, D.J.; Raslan, K.R. The tanh function method for solving some important non-linear partial differential equations. Int. J. Comput. Math. 2005, 82, 897–905. [Google Scholar] [CrossRef]
- Xu, F. A Generalized Soliton Solution of the Konopelchenko-Dubrovsky Equation using He’s Exp-Function Method. Z. FüR Naturforschung 2007, 62, 685–688. [Google Scholar] [CrossRef]
- Mahmoudi, J.; Tolou, N.; Khatami, I.; Barari, A.; Ganji, D. Explicit solution of nonlinear ZK-BBM wave equation using Exp-function method. J. Appl. Sci. 2008, 8, 358–363. [Google Scholar] [CrossRef][Green Version]
- Adomian, G. A review of the decomposition method in applied mathematics. J. Math. Anal. Appl. 1988, 135, 501–544. [Google Scholar] [CrossRef]
- Babolian, E.; Biazar, J. On the order of convergence of Adomian method. Appl. Math. Comput. 2002, 130, 383–387. [Google Scholar] [CrossRef]
- Kooch, A.; Abadyan, M. Efficiency of modified Adomian decomposition for simulating the instability of nano-electromechanical switches: Comparison with the conventional decomposition method. Trends Appl. Sci. Res. 2012, 7, 57. [Google Scholar] [CrossRef]
- Koochi, A.; Abadyan, M. Evaluating the ability of modified Adomian decomposition method to simulate the instability of freestanding carbon nanotube: Comparison with conventional decomposition method. J. Appl. Sci. 2011, 11, 3421–3428. [Google Scholar] [CrossRef]
- Vanani, S.K.; Heidari, S.; Avaji, M. A low-cost numerical algorithm for the solution of nonlinear delay boundary integral equations. J. Appl. Sci. 2011, 11, 3504–3509. [Google Scholar] [CrossRef]
- Chowdhury, S.H. A comparison between the modified homotopy perturbation method and Adomian decomposition method for solving nonlinear heat transfer equations. J. Appl. Sci. 2011, 11, 1416–1420. [Google Scholar] [CrossRef]
- Zhang, L.N.; Xu, L. Determination of the Limit Cycle by He’s Parameter-Expansion for Oscillators in a u3/(1 + u2) Potential. Z. FüR Naturforschung 2007, 62, 396–398. [Google Scholar] [CrossRef]
- Aminikhah, H.; Hemmatnezhad, M. A novel effective approach for solving nonlinear heat transfer equations. Heat Transf. Asian Res. 2012, 41, 459–467. [Google Scholar] [CrossRef]
- Filobello-Nino, U.; Vazquez-Leal, H.; Herrera-May, A.L.; Ambrosio-Lazaro, R.C.; Jimenez-Fernandez, V.M.; Sandoval-Hernandez, M.A.; Alvarez-Gasca, O.; Palma-Grayeb, B.E. The study of heat transfer phenomena by using modified homotopy perturbation method coupled by Laplace transform. Therm. Sci. 2020, 24, 1105–1115. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method for solving boundary value problems. Phys. Lett. A 2006, 350, 87–88. [Google Scholar] [CrossRef]
- He, J.H. Recent development of the homotopy perturbation method. Topol. Methods Nonlinear Anal. 2008, 31, 205–209. [Google Scholar]
- Beléndez, A.; Pascual, C.; Álvarez, M.L.; Méndez, D.I.; Yebra, M.S.; Hernández, A. Higher order analytical approximate solutions to the nonlinear pendulum by He’s homotopy method. Phys. Scr. 2008, 79, 015009. [Google Scholar] [CrossRef][Green Version]
- He, J.H. A coupling method of a homotopy technique and a perturbation technique for non-linear problems. Int. J. Non-Linear Mech. 2000, 35, 37–43. [Google Scholar] [CrossRef]
- El-Shahed, M. Application of He’s Homotopy Perturbation Method to Volterra’s Integro-differential Equation. Int. J. Nonlinear Sci. Numer. Simul. 2005, 6, 163–168. [Google Scholar] [CrossRef]
- HE, J.H. Some asymptotic methods for strongly nonlinear equations. Int. J. Mod. Phys. B 2006, 20, 1141–1199. [Google Scholar] [CrossRef]
- Ganji, D.; Babazadeh, H.; Noori, F.; Pirouz, M.; Janipour, M. An application of homotopy perturbation method for non-linear Blasius equation to boundary layer flow over a flat plate. Int. J. Nonlinear Sci. 2009, 7, 399–404. [Google Scholar]
- Vazquez-Leal, H.; Hernandez-Martinez, L.; Khan, Y.; Jimenez-Fernandez, V.; Filbello-Nino, U.; Diaz-Sanchez, A.; Herrera-May, A.; Castaneda-Sheissa, R.; Marin-Hernandez, A.; Rabago-Bernal, F.; et al. HPM method applied to solve the model of calcium stimulated, calcium release mechanism. Am. J. Appl. Math. 2014, 2, 29–35. [Google Scholar] [CrossRef][Green Version]
- Fereidoon, A.; Rostamiyan, Y.; Akbarzade, M.; Ganji, D.D. Application of He’s homotopy perturbation method to nonlinear shock damper dynamics. Arch. Appl. Mech. 2010, 80, 641–649. [Google Scholar] [CrossRef]
- Vazquez-Leal, H.; Sarmiento-Reyes, A.; Khan, Y.; Filobello-Nino, U.; Diaz-Sanchez, A. Rational biparameter homotopy perturbation method and laplace-padé coupled version. J. Appl. Math. 2012, 2012, 923975. [Google Scholar] [CrossRef]
- Aminikhah, H. Analytical approximation to the solution of nonlinear Blasius’ viscous flow equation by LTNHPM. ISRN Math. Anal. 2012, 2012, 957473. [Google Scholar] [CrossRef]
- Filobello-Nino, U.; Vazquez-Leal, H.; Sarmiento-Reyes, A.; Cervantes-Perez, J.; Perez-Sesma, A.; Jimenez-Fernandez, V.; Pereyra-Diaz, D.; Huerta-Chua, J.; Morales-Mendoza, L.; Gonzalez-Lee, M.; et al. Laplace transform–homotopy perturbation method with arbitrary initial approximation and residual error cancelation. Appl. Math. Model. 2017, 41, 180–194. [Google Scholar] [CrossRef]
- Filobello-Nino, U.; Vazquez-Leal, H.; Rashidi, M.; Sedighi, H.M.; Perez-Sesma, A.; Sandoval-Hernandez, M.; Sarmiento-Reyes, A.; Contreras-Hernandez, A.; Pereyra-Diaz, D.; Hoyos-Reyes, C.; et al. Laplace transform homotopy perturbation method for the approximation of variational problems. SpringerPlus 2016, 5, 1–33. [Google Scholar] [CrossRef] [PubMed]
- Tripathi, R.; Mishra, H.K. Homotopy perturbation method with Laplace transform (LT-HPM) for solving Lane–Emden type differential equations (LETDEs). SpringerPlus 2016, 5, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Filobello-Nino, U.; Vazquez-Leal, H.; Sarmiento-Reyes, A.; Perez-Sesma, A.; Hernandez-Martinez, L.; Herrera-May, A.; Jimenez-Fernandez, V.; Marin-Hernandez, A.; Pereyra-Diaz, D.; Diaz-Sanchez, A. The study of heat transfer phenomena using PM for approximate solution with Dirichlet and mixed boundary conditions. Appl. Comput. Math. 2013, 2, 143–148. [Google Scholar] [CrossRef][Green Version]
- Filobello-Nino, U.; Vazquez-Leal, H.; Khan, Y.; Yildirim, A.; Jimenez-Fernandez, V.; Herrera-May, A.; Castaneda-Sheissa, R.; Cervantes-Perez, J. Using perturbation methods and Laplace–Padé approximation to solve nonlinear problems. Miskolc Math. Notes 2013, 14, 89–101. [Google Scholar] [CrossRef]
- Filobello-Nino, U.; Vazquez-Leal, H.; Benhammouda, B.; Hernandez-Martinez, L.; Khan, Y.; Jimenez-Fernandez, V.M.; Herrera-May, A.L.; Castaneda-Sheissa, R.; Pereyra-Diaz, D.; Cervantes-Perez, J.; et al. A handy approximation for a mediated bioelectrocatalysis process, related to Michaelis-Menten equation. SpringerPlus 2014, 3, 1–6. [Google Scholar] [CrossRef]
- Filobello-Nino, U.; Vazquez-Leal, H.; Araghi, F.; Huerta-Chua, J.; Sandoval-Hernandez, M.; Hernandez-Mendez, S.; Muñoz-Aguirre, E. A novel distribution and optimization procedure of boundary conditions to enhance the classical perturbation method applied to solve some relevant heat problems. Discret. Dyn. Nat. Soc. 2020, 2020, 1303701. [Google Scholar] [CrossRef]
- Vazquez-Leal, H.; Sandoval-Hernandez, M.; Castaneda-Sheissa, R.; Filobello-Nino, U.; Sarmiento-Reyes, A. Modified Taylor solution of equation of oxygen diffusion in a spherical cell with Michaelis-Menten uptake kinetics. Int. J. Appl. Math. Res. 2015, 4, 253. [Google Scholar] [CrossRef]
- Filobello-Nino, U.; Vazquez-Leal, H.; Perez-Sesma, A.; Cervantes-Perez, J.; Hernandez-Martinez, L.; Herrera-May, A.; Jimenez-Fernandez, V.; Marin-Hernandez, A.; Hoyos-Reyes, C.; Diaz-Sanchez, A.; et al. On a practical methodology for optimization of the trial function in order to solve bvp problems by using a modified version of Picard method. Appl. Math. Inf. Sci 2016, 10, 1355–1367. [Google Scholar] [CrossRef]
- Vazquez-Leal, H.; Sarmiento-Reyes, A. Power series extender method for the solution of nonlinear differential equations. Math. Probl. Eng. 2015, 2015, 717404. [Google Scholar] [CrossRef]
- Vazquez-Leal, H.; Garcia-Gervacio, J.; Filobello-Nino, U.; Sandoval-Hernandez, M.; Herrera-May, A. PSEM Approximations for Both Branches of Lambert W Function with Applications. Discret. Dyn. Nat. Soc. 2019, 2019, 8267951. [Google Scholar] [CrossRef]
- Filobello-Nino, U.; Vazquez-Leal, H.; Herrera-May, A.; Ambrosio-Lazaro, R.; Castaneda-Sheissa, R.; Jimenez-Fernandez, V.; Sandoval-Hernandez, M.; Contreras-Hernandez, A. A handy, accurate, invertible and integrable expression for Dawson’s function. Acta Univ. 2020, 29, e2124. [Google Scholar] [CrossRef]
- Sandoval-Hernandez, M.A.; Vazquez-Leal, H.; Filobello-Nino, U.; Hernandez-Martinez, L. New handy and accurate approximation for the Gaussian integrals with applications to science and engineering. Open Math. 2019, 17, 1774–1793. [Google Scholar] [CrossRef]
- Shijun, L. Homotopy analysis method: A new analytic method for nonlinear problems. Appl. Math. Mech. 1998, 19, 957–962. [Google Scholar] [CrossRef]
- Rashidi, M.; Mohimanian Pour, S.; Hayat, T.; Obaidat, S. Analytic approximate solutions for steady flow over a rotating disk in porous medium with heat transfer by homotopy analysis method. Comput. Fluids 2012, 54, 1–9. [Google Scholar] [CrossRef]
- Kazemi, M.; Jafari, S.; Musavi, S.; Nejati, M. Analytical solution of convective heat transfer of a quiescent fluid over a nonlinearly stretching surface using Homotopy Analysis Method. Results Phys. 2018, 10, 164–172. [Google Scholar] [CrossRef]
- Vahdati, S.; Zulkifly, A.; Ghasemi, M. Application of homotopy analysis method to Fredholm and Volterra integral equations. Math. Sci. 2010, 4, 164–172. [Google Scholar]
- He, J.H.; Wu, X.H. Variational iteration method: New development and applications. Comput. Math. Appl. 2007, 54, 881–894. [Google Scholar] [CrossRef]
- Ma, W.X. N-soliton solutions and the Hirota conditions in (1 + 1)-dimensions. Int. J. Nonlinear Sci. Numer. Simul. 2021. Preprint. [Google Scholar] [CrossRef]
- Ma, W.X. N-soliton solutions and the Hirota conditions in (2+1)-dimensions. Opt. Quant. Electron. 2021, 52. [Google Scholar] [CrossRef]
- Ma, W.X.; Zhou, Y. Lump solutions to nonlinear partial differential equations via Hirota bilinear forms. J. Differ. Equ. 2018, 264, 2633–2659. [Google Scholar] [CrossRef]
- Vazquez-Leal, H. Exploring the Novel Continuum-Cancellation Leal-Method for the Approximate Solution of Nonlinear Differential Equations. Discret. Dyn. Nat. Soc. 2020, 2020, 4967219. [Google Scholar] [CrossRef]
- Vazquez-Leal, H.; Sandoval-Hernandez, M.A.; Filobello-Nino, U.; Huerta-Chua, J. The novel Leal-polynomials for the multi-expansive approximation of nonlinear differential equations. Heliyon 2020, 6, e03695. [Google Scholar] [CrossRef] [PubMed]
- Marinca, V.; Herisanu, N. Nonlinear Dynamical Systems in Engineering: Some Approximate Approaches; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Anandaram, M. Emden’s Polytropes: Gas Globes In Hydrostatic Equilibrium. Mapana J. Sci. 2013, 12, 99–127. [Google Scholar] [CrossRef]
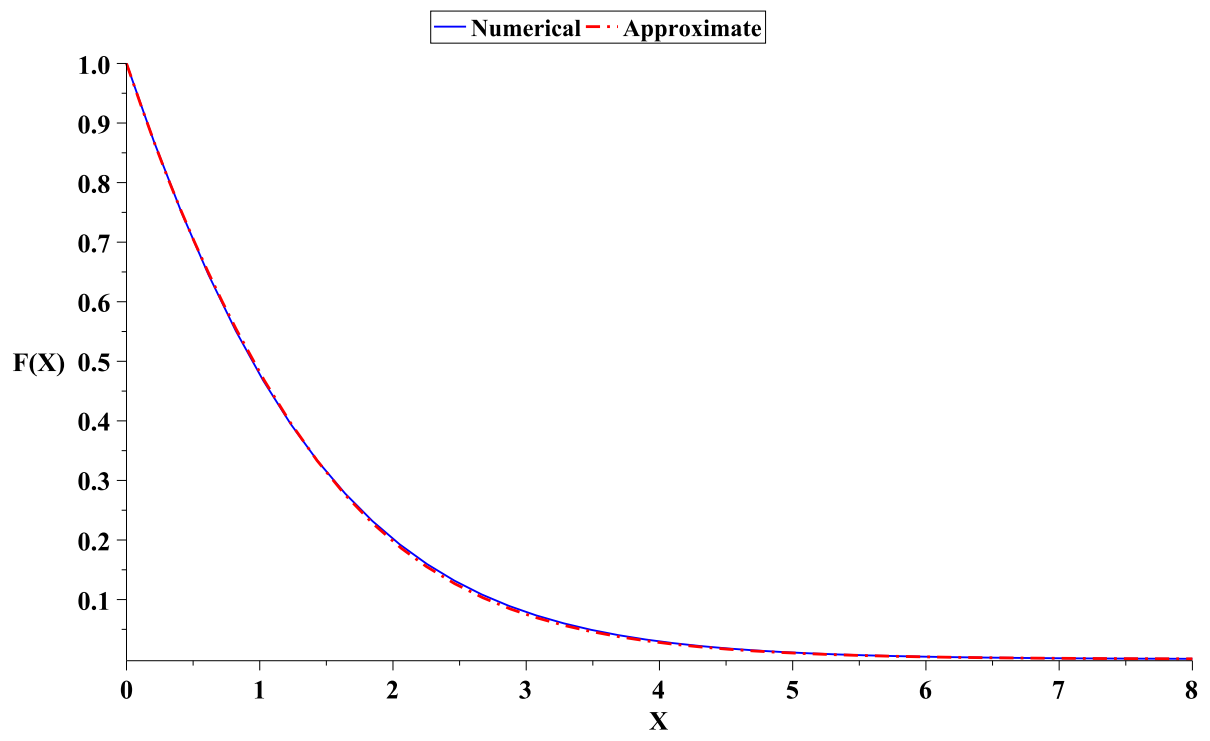
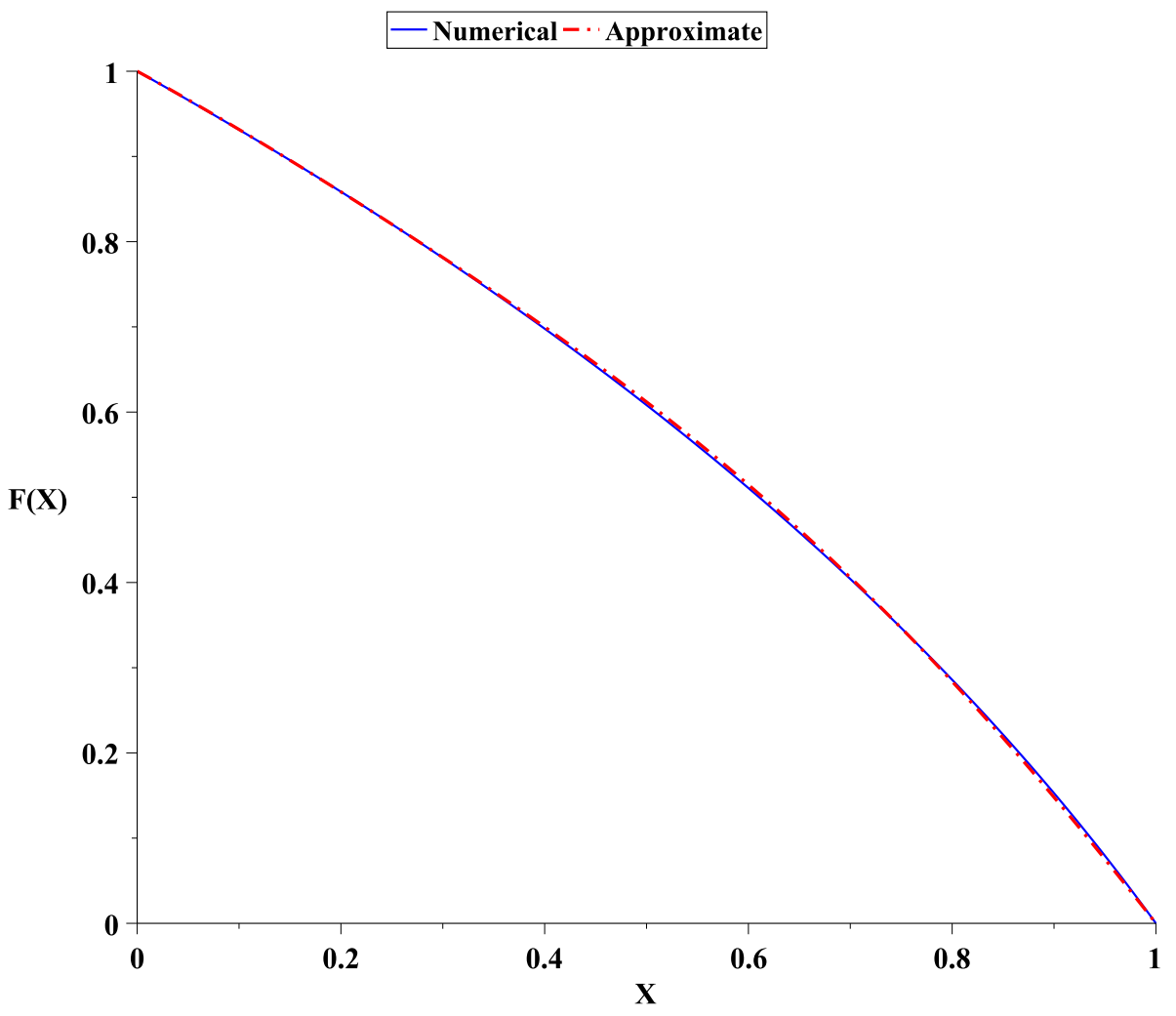
| x | y(x) (26) | Relative Error Using (26) | MHPMLT [20] | Relative Error Using MHPMLT [20] |
|---|---|---|---|---|
| 0 | 1 | 0 % | 1 | 0 % |
| 0.1 | 0.9233688 | 0.399% | 0.8999999 | 2.9226% |
| 0.2 | 0.8422068 | 0.7989% | 0.8439883 | 0.5901% |
| 0.3 | 0.7570558 | 1.10% | 0.7625396 | 0.3855% |
| 0.4 | 0.6680062 | 1.22% | 0.6769718 | 0.0970% |
| 0.5 | 0.5746978 | 1.11% | 0.5859061 | 0.8149% |
| 0.6 | 0.4763148 | 0.7042% | 0.4879678 | 1.7249% |
| 0.7 | 0.371595 | 0.0392% | 0.3817826 | 2.7815% |
| 0.8 | 0.258824 | 1.11% | 0.2659759 | 3.9355% |
| 0.9 | 0.135832 | 2.60% | 0.1391731 | 5.1314% |
| 1.0 | 0 | 0% | 0 | 0% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Filobello-Nino, U.; Vazquez-Leal, H.; Huerta-Chua, J.; Ramirez-Angulo, J.; Mayorga-Cruz, D.; Callejas-Molina, R.A. The Novel Integral Homotopy Expansive Method. Mathematics 2021, 9, 1204. https://doi.org/10.3390/math9111204
Filobello-Nino U, Vazquez-Leal H, Huerta-Chua J, Ramirez-Angulo J, Mayorga-Cruz D, Callejas-Molina RA. The Novel Integral Homotopy Expansive Method. Mathematics. 2021; 9(11):1204. https://doi.org/10.3390/math9111204
Chicago/Turabian StyleFilobello-Nino, Uriel, Hector Vazquez-Leal, Jesus Huerta-Chua, Jaime Ramirez-Angulo, Darwin Mayorga-Cruz, and Rogelio Alejandro Callejas-Molina. 2021. "The Novel Integral Homotopy Expansive Method" Mathematics 9, no. 11: 1204. https://doi.org/10.3390/math9111204
APA StyleFilobello-Nino, U., Vazquez-Leal, H., Huerta-Chua, J., Ramirez-Angulo, J., Mayorga-Cruz, D., & Callejas-Molina, R. A. (2021). The Novel Integral Homotopy Expansive Method. Mathematics, 9(11), 1204. https://doi.org/10.3390/math9111204







