Abstract
The uncertainty of the engineering system increases with its complexity, therefore, the tolerance to the uncertainty becomes important. Even under large variations of design parameters, the system performance should achieve the design goal in the design phase. Therefore, engineers are interested in how to turn a bad design into a good one with the least effort in the presence of uncertainty. To improve a bad design, we classify design parameters into key parameters and non-key parameters based on engineering knowledge, and then seek the maximum solution hyper-box which already includes non-key parameters of this bad design. The solution hyper-box on which all design points are good, that is, they achieve the design goal, provides target intervals for each parameter. The bad design can be turned into a good one by only moving its key parameters into their target intervals. In this paper, the PSO-Divide-Best method is proposed to seek the maximum solution hyper-box which is in compliance with the constraints. This proposed approach has a considerably high possibility to find the globally maximum solution hyper-box that satisfies the constraints and can be used in complex systems with black-box performance functions. Finally, case studies show that the proposed approach outperforms the EPCP and IA-CES methods in the literature.
1. Introduction
With the rapid development of technology in recent years, the engineering system has become increasingly complex. The growing complexity of the system provides a new source of uncertainty. Uncertainty arises because some design parameters may be changed over the course of development, or they cannot yet exactly be specified [1,2,3]. The uncertainty appears as a deviation between the desired and realized parameter settings, which may bring in design failure, therefore it is essential to improve design under the uncertainty for complex systems.
Design points that achieve their design goals are called good, otherwise they are called bad. However, if there is already a bad design point, engineers are interested in how to turn it into a good design with the least effort. It can be fulfilled by modifying as few parameters from the existing bad design as possible.
Traditional optimization [4], sensitivity analysis [5,6], robust design optimization [7,8,9], and reliability-based design optimization [10,11,12] are some classical approaches to improve designs. Traditional optimization seeks an optimum design point in the design space, which does not take uncertainty into account. Sensitivity analysis computes the effect of variability of input design parameters on variability of output performance value. Unfortunately, sensitivity analysis does not provide information on how the parameters of a bad design need to be changed in order to turn it into a good design. Robust design optimization seeks a design point in a deterministic neighborhood with small output variation. However, robust design optimization only deals with the case where the variability of design parameters is given. If the variability of the design parameters is not completely known, it has to be estimated, which is not always possible. Reliability-based design optimization is a method to determine optimal designs which are characterized by a low probability of failure. Unfortunately, it is established under the assumption that the complete information of the design uncertainty is known.
Evolutionary algorithms are often used to solve design optimization problems in the presence of uncertainties [13,14,15,16]. The non-dominated sorting genetic algorithm II is combined with reliability-based optimization for handling uncertainty in design parameters in [13]. Six-sigma robust design optimization is solved by the many-objective decomposition-based evolutionary algorithm in [14]. Evolutionary algorithms have some specific advantages, which include the ability to self-adapt the search for optimum solutions on the fly, as well as the flexibility of the procedures.
Besides, swarm intelligence-based algorithms are frequently-used techniques in design optimization problems [17,18,19,20]. The uncertainty is directly incorporated into optimization using particle swarm, and a deterministic Pareto front of optimal designs is found in [17]. The ant colony optimization is combined with reliability-based design optimization to achieve the global optimal design of a crane metallic structure under parametric uncertainty in [18]. Against the uncertainty of cost and traffic, a mathematical model is established using robust optimization method, and the corresponding optimal design is obtained by ant colony algorithm in [19]. Swarm intelligence-based algorithms often find an optimal solution when appropriate parameters are determined and sufficient convergence stage is achieved.
The solution hyper-box on which all design points are good is expressed by independent target intervals for each design parameter. The widths of target intervals quantify the robustness to uncertainty. Furthermore, the solution hyper-box can help to improve a bad design. More precisely, a bad design can be turned into a good one by only moving its design parameters into their target intervals. To make it easy to reach the target intervals, the solution hyper-box should be as large as possible.
There are two categories of approaches which seek for a solution hyper-box with the maximum volume in the literature. The first category is based on machine learning and data mining techniques [21,22,23]. A stochastic method is presented in [21], which combines online learning and query. It probes a candidate solution hyper-box by stochastic sampling, and then readjusts its boundaries in order to remove bad designs and explores more design space that has not been probed before. Because the locations of good and bad designs are estimated by Monte Carlo sampling, the obtained solution hyper-box may not have the maximum size. The second category is based on an analytical technique [24,25,26]. The algorithm presented in [24] applies interval arithmetic within an iterative optimization scheme to check whether the candidate hyper-box is a solution hyper-box. However, interval arithmetic limits the applicability of the algorithm, as the accuracy of the interval arithmetic depends on the problem. Besides, the interval arithmetic cannot handle the black-box performance function. The algorithm proposed in [26] combines the DIRECT algorithm [27] with evolutionary algorithms, where the former is a checking technique to guarantee that the obtained hyper-box is indeed a solution hyper-box and the latter is to seek the maximum size of hyper-box. Unfortunately, the DIRECT algorithm requires very high computational effort for its work.
This paper aims to turn a bad design into a good one with comparatively little effort in the presence of uncertainty. To this end, instead of focusing on an optimal design point, an approach based on the optimization of the solution hyper-box is proposed in this paper. Specifically, design parameters are classified into key parameters and non-key ones based on engineering knowledge firstly. Secondly, by adding proper constraints on non-key parameters, we seek the maximum solution hyper-box which already includes non-key parameters of the bad design. The maximum solution hyper-box provides the target intervals for each design parameter. Finally, the bad design is turned into a good one by only moving its key parameters to their target intervals. Obviously, the wider the target interval is, the stronger the robustness is against unintended variations.
Therefore, we focus on seeking for the maximum solution hyper-box which is in compliance with constraints. Fender et al. [28] extended the algorithm in [21] to account for constraints. However, the algorithm in [28] produces a hyper-box that may not have the largest size and may contain some bad designs, because the locations of good and bad designs are estimated by the Monte Carlo sampling. In this paper, the proposed PSO-Divide-Best method combines particle swarm optimization (PSO) [29] with the Divide-the-Best algorithm in [30], where the former is to evolve the solution hyper-box towards larger volume and the latter is to guarantee that the obtained solution hyper-box only includes good designs. The PSO-Divide-Best method is established based on black-box performance functions, so it is appropriate for most engineering problems.
The paper is organized as follows. The next section explains the motivation of this paper and gives a mathematical problem statement for optimizing the solution hyper-box with constraints. Section 3 introduces the Divide-the-Best algorithm and particle swarm optimization. Section 4 presents the proposed approach in detail. In Section 5, we apply the proposed approach to complex systems. In Section 6, we provide some concluding remarks.
2. Motivation and Problem Statement
2.1. Motivation
A voltage divider shown in Figure 1 is considered. The terminal voltage is expressed as and the resistance as .
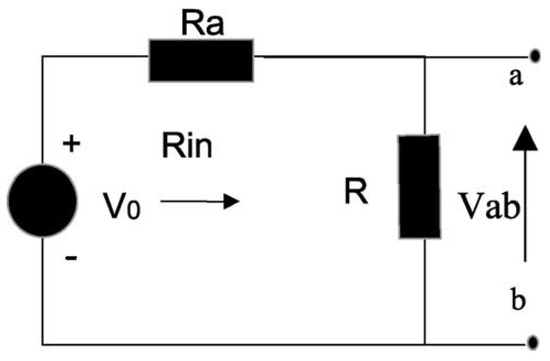
Figure 1.
Voltage divider example.
Good designs fulfilling the design goals should satisfy:
The complete solution space defined by Expression (1) is shown in Figure 2 as a grey region.
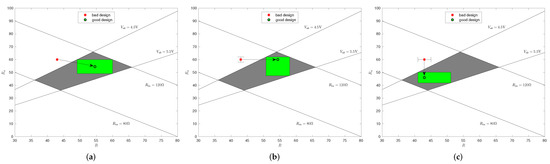
Figure 2.
Changes necessary to achieve the design goals: (a) R and ; (b) only R; and (c) only .
Now, a design with and is considered. It violates Equation (1a) and therefore is a bad design. To improve this bad design with the least effort, three scenarios are considered:
- (a)
- Figure 2a shows a solution hyper-box with the maximum volume. Both R and are changed so as to achieve the design goals.
- (b)
- Figure 2b shows a solution hyper-box that includes . To achieve the design goals, only R needs to be modified. The solution hyper-box is obtained by requiring a minimum safety margin of for . This is essential, because is subject to uncertainty and cannot be controlled exactly. The realized lower safety margin is larger than the required minimum safety margin, thus more tolerance to uncertainty is provided.
- (c)
- Figure 2c shows a solution hyper-box that includes . To realize the design goals, only needs to be modified. The same minimum safety margin as in Scenario (b) is required.
The solution hyper-box of Scenario (a) is much larger than those of Scenarios (b) and (c). In this sense, the solution hyper-box of Scenario (a) is the most robust one. However, Scenario (a) requires redesigning two design parameters, while Scenarios (b) and (c) only require redesigning one design parameter. If there is already a bad design, Scenarios (b) and (c) are recommended, because they only change one parameter. Otherwise, Scenario (a) is more appropriate, because it provides more tolerance to the uncertainty. To choose among Scenarios (b) and (c), two different strategies are possible. If there is no information on which design parameter is easier to redesign, the scenario with the maximum solution hyper-box is chosen, because it provides a larger target region and is easier to reach. This would be Scenario (a) with R as the key parameter. As alternative approach, engineers can take advantage of their engineering knowledge and choose Scenario (b) where is regarded as the key parameter, if they know that design parameter is easier to redesign than R.
This procedure can described by seeking the maximum solution hyper-boxes under the constraint that certain parameters should be included with a specified safety margin.
2.2. Problem Statement
Let represent the design point or design, which is composed of m design parameters. The output performance at is given by
where is the performance function. The performance is sufficient by satisfying the performance criterion
where is a predefined threshold value.
Designs or design points are called good if their performance satisfies (3), otherwise they are called bad. The lower and upper bounds of the design parameters, and , define the continuous design space. The region consisting of all good design points is the complete solution space.
To obtain interval boundaries of each parameter that are independent of other parameters, hyper-boxes are considered. The hyper-box is expressed by
where and are the upper bound and lower bound of the hyper-box, respectively. Furthermore, let denote the bounds of the hyper-box, that is,
We see that the first m components of are the lower bound and the last m ones are the upper bound . The volume of the hyper-box is thus given by
A hyper-box which only includes good design points is called a solution hyper-box.
The design parameter which can be modified easily with low modification cost is called the key parameter. The design parameter which is hard to be modified is called the non-key parameter.
As mentioned in Section 2.1, to turn a bad design into a good one with the least effort, a solution hyper-box which already includes non-key parameters of the bad design is sought. Formally, the problem we focus on is formulated as the following constrained optimization problem:
where k is the number value that corresponds to the dimension of a non-key parameter, K is the set of the indices of non-key parameters, and and are the lower and upper limit values, respectively. The constraints and ensure that the non-key parameter is included in the obtained hyper-box with a specified safety margin.
It can be seen from (7) that the aim of this paper is to seek for the largest solution hyper-box satisfying the constraints. The proposed problem is fundamentally different from robust design optimization in that it is to seek the intervals of a permissible design range, and interval boundaries are used as degrees of freedom rather than design parameters.
If the explicit expressions of and are analytically known, the problem (7) can be solved by classical optimization methods. However, the performance function is not analytically known in most engineering problems, thus cannot be explicitly expressed by and . Therefore, it is necessary to propose an approach which aims at black-box performance function.
3. Preliminaries
3.1. Divide-the-Best Algorithm
The problem (7) in Section 2.2 involves the following box-constrained global optimization sub-problem:
where is an m-dimensional hyper-box (hyper-rectangle) and is a performance function.
Numerous algorithms have been proposed (see, e.g., [27,30,31,32,33,34,35,36,37,38,39]) for solving the problem (8), under the assumption that the performance function satisfies the Lipschitz condition over the hyper-box with an unknown Lipschitz constant. The Divide-the-Best approach is the most well-known partitioning-based one. Particularly, the Divide-the-Best method in [30] has very promising performance, which uses the multiple estimates of the Lipschitz constant and an efficient diagonal partition. Therefore, the Divide-the-Best method in [30] is adopted in this paper to solve the problem (8). Figure 3 shows the flow chart of the Divide-the-Best algorithm in [30]. Given a vector of the method parameters, at each iteration k, the admissible region is adaptively partitioned into a collection of the finite number of robust subsets .
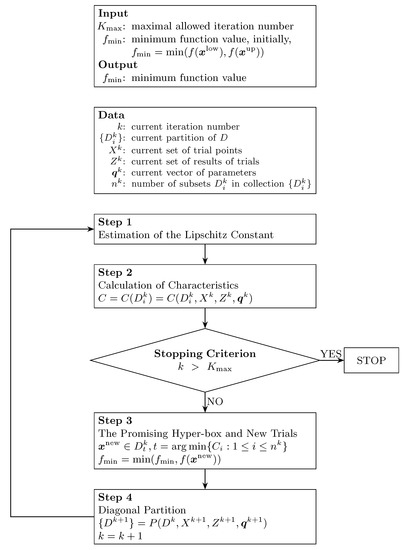
Figure 3.
Flow chart of Divide-the-Best algorithm in [30].
More precisely, in Step 1, several possible Lipschitz constants are chosen from a set of values varying from zero to infinity, denoted by . Then, the “merit” (called characteristic) of each hyper-box is calculated by the following formula (see Step 2 in Figure 3). The hyper-box over which characteristic is the minimum is called the “promising hyper-box”. It has higher possibility to find the global minimizer within the “promising hyper-box” (see Step 3). Subsequently, the new sample points are obtained from the old ones by adding and subtracting the two-thirds-side length of the longest edge of the “promising hyper-box”. Then, the evaluation of performance function at the new sample point is performed. Finally, in Step 4, the “promising hyper-box” is subdivided by an efficient diagonal partition strategy for performing the next iteration (see [30] for more details). Naturally, more than one “promising hyper-box” can be partitioned at every iteration. The stopping criterion is that the number of iteration reaches the pre-defined maximal allowed number. The evaluation of the performance function at a point is referred to as a trial.
To better demonstrate how the Divide-the-Best algorithm performs, its first three iterations on a two-dimensional function in [30] are shown in Figure 4.

Figure 4.
An example of subdivisions by an efficient partition strategy in [30]. The top, middle, and bottom rows are the first, second, and third iterations, respectively. The grey hyper-boxes are the promising ones. They are selected in Step 3 of the current iteration and divided in Step 4. The trial points where the performance function is evaluated are red points.
The Divide-the-Best algorithm in [30] balances global and local search in a more sophisticated way and provides a faster convergence to the global minimizers of difficult multi-extremal black-box performance functions.
3.2. Particle Swarm Optimization (PSO)
Particle swarm optimization (PSO) is a population-based meta-heuristics technique [29,40]. The population consists of potential solutions, called particles, which are a metaphor of birds in bird flocking. The particles are randomly initialized and then freely fly across the multidimensional search space. In social science context, a PSO system combines a social-only model and a cognition-only model [41]. The social-only component suggests that particles ignore their own experience and adjust their behavior according to the successful beliefs of particles in the neighborhood. On the other hand, the cognition-only component treats individuals as isolated beings. One advantage of PSO is that it often locates near optimal solutions significantly more quickly than evolutionary optimization [42].
Each particle is equivalent to a candidate solution of the problem (7). The particle moves according to an adjusted velocity, which is based on the corresponding particle’s experience and the experience of its companions. The velocity of the ith particle is modified under the following equation in the PSO algorithm:
where t is the current iteration number, is the velocity of the ith particle at iteration t, is the position of the ith particle at iteration t, is the best position of the particle i until iteration t, is the best position among all particles until iteration t, is the inertia weight at iteration t, is the allowed maximum iteration number, and are weight factors, and and are random numbers between 0 and 1. Naturally, according to Equation (5), represents the bounds of the ith hyper-box at iteration t.
It is worth mentioning that the second term of Equation (9) represents the cognitive part of PSO where the particle changes its velocity based on its own thinking and memory. The third term represents the social part of PSO where the particle changes its velocity based on the social-psychological adaptation of knowledge.
Each particle moves from the current position to the next one by the modified velocity in (9) using the following equation:
4. The Proposed Particle Swarm Optimization Divide-the-Best Algorithm
The particle swarm optimization algorithm does not rely on mathematical properties for application. The Divide-the-Best algorithm in [30] is an efficient algorithm to calculate the global minimum of a black-box performance function over a hyper-box. Therefore, an innovative approach which combines the particle swarm optimization algorithm with the Divide-the-Best algorithm is proposed to solve the problem (7), referred to as the particle swarm optimization divide-the-best algorithm (PSO-Divide-Best).
Specifically, particle swarm optimization drives the evolution toward increasing the volume of hyper-box. The Divide-the-Best algorithm solves the optimization sub-problem (8), and thus ensures that the obtained hyper-box only includes good designs.
The PSO-Divide-Best algorithm is illustrated in Algorithm 1. Initially, it generates randomly a group of particles satisfying constraints. During the process of optimization, at iteration t, firstly, the velocity and position of the ith particle are updated according to Equations (9) and (10), respectively. Then, if the conditions , , and are not satisfied, the re-updating is performed. Otherwise, the value of is evaluated by the Divide-the-Best algorithm in Figure 3 and denoted by . If the constraint is met, we calculate the corresponding volume according to Equation (6), otherwise the particle is re-updated. Next, and are updated.
| Algorithm 1 The particle swarm optimization divide-the-best algorithm (PSO-Divide-Best) |
|
Finally, to verify whether the best particle satisfies the constraints, the Divide-the-Best algorithm with more iterative times is performed. If the constraints are satisfied, PSO-Divide-Best outputs the best particle. Otherwise, it goes back to Step 2.
PSO is derivative-free and global search [43]. The Divide-the-Best algorithm in [30] can converge to the global minimum with any degree of accuracy provided there are enough iterations. Therefore, the proposed PSO-Divide-Best method in this paper has the following advantages:
- (1)
- PSO-Divide-Best has great possibility to reach the globally maximum solution hyper-box satisfying the constraints.
- (2)
- Due to the discrete nature of the trial points in the Divide-the-Best algorithm, the PSO-Divide-Best method can be applied to both analytically known and black-box performance functions.
- (3)
- PSO-Divide-Best guarantees that any point selected within the obtained hyper-box is a good design provided that the performance function is continuous.
In most engineering problems, the performance function is continuous whether it is analytically known or black-box. Therefore, the PSO-Divide-Best approach has strong applicability in engineering problems.
5. Case Studies
A stochastic approach based on Monte Carlo sample is discussed in [28]. This approach consists of two phases: exploration phase and consolidation phase. The purpose of the exploration phase is to identify a solution box as large as possible. The consolidation phase includes an algorithm which shrinks the hyper-box such that it contains only good designs. Therefore, we denote this method by “EPCP” hereafter (an abbreviation for “exploration phase and consolidation phase”). Besides, a method in [24] which combines interval arithmetic with cellular evolutionary strategies is denoted by “IA-CES” hereafter.
To compare the proposed PSO-Divide-Best method with the EPCP and IA-CES ones, two cases are considered. The first case is the vehicle structure design problem which has been studied by Fender et al. in [28]. The second case is the power-shift steering transmission control system (PSSTCS) with a price of approximately 500,000 USD.
In the proposed PSO-Divide-Best method, the weight factors and are set to 2, the maximum number of iterations is 2000, , , and the number of particles N is set to 160.
All experiments were performed in MATLAB R2016b on a windows platform with Intel Core i7-4790 CPU 3.60 GHz, 16 GB RAM.
5.1. Vehicle Structure Design Problem
The vehicle structure design problem in [28] consists of two structural components. The design parameters are the two deformation forces and . The performance functions are as follows:
where , kg is the mass, g is a critical threshold level, m/s is the speed, and m are the limits of the deformation measures. The design goals are achieved if for all .
A design with kN and kN is considered in [28]. It violates Equation (11a) and therefore is a bad design. To improve this bad design with the least effort, three scenarios are performed. In Scenario (a), both and are key parameters, that is, both and need to be modified. In Scenario (b), only is the key parameter. More precisely, is included in the solution hyper-box that is obtained by requiring a minimum safety margin of . In Scenario (c), only is the key parameter.
Since each performance function in Equation (11) is monotone, the exact solution is obtained by the penalty method [44], as shown in Table 1. The results in [28] obtained by the EPCP method are listed in Table 1. Due to the stochastic nature of the PSO, as adopted in [24], we ran the PSO-Divide-Best algorithm 20 times for each scenario, and the best solutions among the 20 runs are shown in Table 1. The results obtained by the IA-CES method are also shown in Table 1. The deviations between the lower boundaries computed numerically and the exact solutions are given by . The relative error is given by . Besides, the relative error for the upper boundaries of the hyper-box are defined in a similar way. The row entitled “volume” is the volume of hyper-box, and the row entitled “error” is the relative error between the volume of hyper-box computed numerically and the exact one.

Table 1.
The hyper-boxes obtained by the exact, EPCP, IA-CES and PSO-Divide-Best methods in Scenarios (a), (b), and (c) for vehicle structure design problem.
Table 1 shows that the hyper-boxes obtained by the PSO-Divide-Best method are nearly identical to the exact ones, while the hyper-boxes obtained by the EPCP and IA-CES approaches have a high deviation from the exact ones. Besides, the hyper-boxes obtained by the PSO-Divide-Best method are significantly larger than those obtained by the EPCP and IA-CES methods.
Furthermore, a visualization of the results of the EPCP, IA-CES, and PSO-Divide-Best methods in Table 1 is shown in Figure 5, Figure 6 and Figure 7, respectively, where the grey region is the complete solution space. Figure 5, Figure 6 and Figure 7 also give some examples of how to turn the bad design into a good one.

Figure 5.
The hyper-boxes (blue) obtained by the EPCP method: (a) and are key parameters; (b) only ; and (c) only .

Figure 6.
The hyper-boxes (yellow) obtained by the IA-CES method: (a) and are key parameters; (b) only ; and (c) only .

Figure 7.
The hyper-boxes (green) obtained by the PSO-Divide-Best method: (a) and are key parameters; (b) only ; and (c) only .
In Scenarios (a) and (b), the blue hyper-boxes exceed the grey region. This implies that the hyper-boxes obtained by the EPCP method contain some bad designs. Based on the hyper-box obtained by the EPCP method, a bad design may fail to be turned into a good one (see Figure 5a). Consequently, the EPCP method should be used with great caution.
The yellow hyper-boxes obtained by the IA-CES method all lie within the grey region; however, they are not the largest ones. This implies that target intervals for each parameter determined by the IA-CES method are relatively shorter. Therefore, the good design point which is determined by the IA-CES method has relatively poor robustness against unintended variations.
The green hyper-boxes obtained by the PSO-Divide-Best method all locate within grey region, therefore they only include good designs. Actually, as long as the key parameters of the bad design are moved into their target intervals defined by our method, the bad design is turned into a good one. Taking Scenario (b) as an example, according to the solution hyper-box obtained by the PSO-Divide-Best method shown in Table 1, the bad design is turned into a good one by changing into any value within .
5.2. The Power-Shift Steering Transmission Control System (PSSTCS)
Figure 8 and Figure 9 show the structure principle drawing and the function constitutes of PSSTCS, respectively.
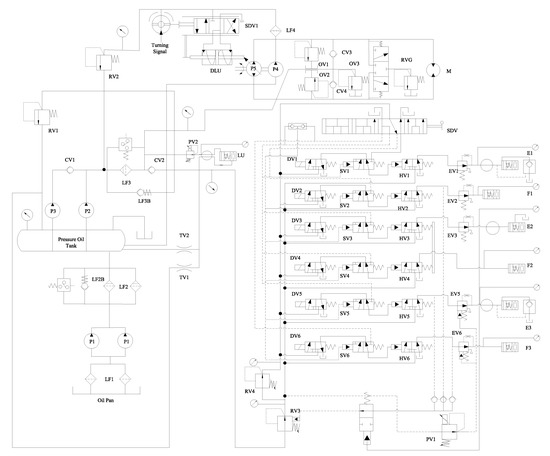
Figure 8.
Structure principle drawing of PSSTCS.
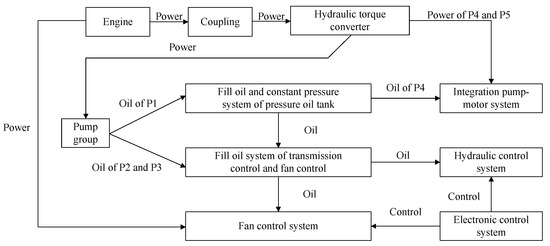
Figure 9.
Function constitutes of PSSTCS.
The PSSTCS is a non-monotonic coherent system which consists of 86 components. The design goal is that the system reliability should be higher than 0.9900. However, the system reliability function is not analytically known, so it is evaluated by the goal-oriented (GO) reliability assessment method in [45]. Now, we consider a design shown in Table A1 in Appendix A. Its system reliability is 0.9856; therefore, it is insufficient. To improve this bad design with the least effort, firstly, the engineers classify design parameters into key parameters and non-key ones according to modification difficulty degree. The key parameters (components) are marked with red color in Table A1. Secondly, we search the maximum solution hyper-box which already includes non-key parameters of this bad design. More precisely, in this PSSTCS case, the optimization problem (7) is formulated as follows:
where , , and are the lower and upper bounds of reliability for the ith component, , is the reliability for the ith component, , , , , , is the reliability threshold, and is the system reliability function which is evaluated by the GO method in [45]. Note that the volume here is replaced by the log-volume (logarithmic transformation of the volume) in order to calculate conveniently.
The IA-CES method is established based on analytically known function; therefore, it is not applicable to this complex system with black-box reliability function. The obtained hyper-boxes of the problem (12) by the EPCP and PSO-Divide-Best methods are listed in Table A2 in Appendix A. We see that the lower bounds obtained by the PSO-Divide-Best method are almost always smaller than those obtained by the EPCP method, and the upper bounds obtained by the PSO-Divide-Best method are almost always larger than those obtained by the EPCP method. This implies that the PSO-Divide-Best method provides much wider target intervals for most design parameters. Therefore, the PSO-Divide-Best method has stronger robustness against uncertainty.
Besides, the log-volume of the obtained hyper-box is listed in Table 2. We see that the log-volume of hyper-box obtained by the PSO-Divide-Best method is much larger than that by the EPCP method. This is further reflected that the PSO-Divide-Best method is more robust against variations.

Table 2.
The log-volume of the EPCP and PSO-Divide-Best hyper-boxes.
The hyper-box provides target intervals for each design parameter; therefore, the bad design can be turned into a good design by only moving its key parameters into their target intervals. Particularly, the good design for which the key parameters are located at the midpoints of their target intervals may be the most representative one. It provides the maximum robustness if the variation of design parameter is the same on both sides of a nominal value. These representative good designs obtained by the EPCP and PSO-Divide-Best methods are listed in Table A1. To verify whether these good designs satisfy the design goal, their system reliabilities were evaluated by the GO method, as also shown in Table A1. We can see these two good designs indeed achieve the design goal. Therefore, the system reliability for the PSSTCS can change from insufficient to sufficient by only modifying the reliabilities for key components according to Table A1.
To illustrate whether the obtained hyper-boxes meet the design goal, we use the Latin hypercube sampling to choose n designs from each hyper-box, and then calculate the rate of good designs as follows:
where is the indicator function, i.e., if and otherwise.
Figure 10 shows the rates of good designs under different sample sizes. We see that the rates of good designs of the PSO-Divide-Best method are all 1, while those of the EPCP method are all below 1. This implies that the hyper-box obtained by the PSO-Divide-Best method only includes good designs, while those obtained by the EPCP method includes some bad designs. Therefore, the EPCP method should be used cautiously, because it may fail to turn a bad design into a good one. However, the PSO-Divide-Best method is valid as it ensures any design within the obtained hyper-box is good.
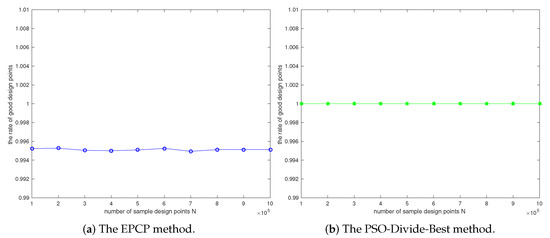
Figure 10.
The rate of good designs of the obtained hyper-boxes.
6. Conclusions
To improve a bad design with comparatively little effort in the presence of uncertainty, rather than changing all design parameters of this bad design, this paper only modifies its key parameters. To this end, the maximum solution hyper-box which already includes non-key parameters of a current bad design is sought. The solution hyper-box provides target intervals for each design parameter. A current bad design can be turned into a good one by only moving its key parameters into their target intervals. The volume of the solution hyper-box should be as large as possible for providing stronger robustness against unintended variations.
The PSO-Divide-Best algorithm combines the PSO and the Divide-the-Best algorithms [30] to seek a solution hyper-box which has the maximum volume and satisfies all the constraints. The case studies show the solution hyper-boxes obtained by the PSO-Divide-Best method only include good designs, and they are much larger than those obtained by the EPCP and IA-CES methods. This implies that a good design determined by the EPCP method may have stronger robustness against uncertainty. Therefore, our method is better than the EPCP and IA-CES methods.
Since the Divide-the-Best algorithm only evaluates the performance function at trial points, the PSO-Divide-Best method has strong application and can be applied to complex systems with black-box performance functions. As long as the performance function is continuous, our method can provide a solution hyper-box that is guaranteed to include only good designs. Therefore, a bad design can be turned into a good one provided that its key parameters are moved into the target intervals obtained by our method. This implies that our method is valid. Our method converges to the globally maximum solution hyper-box with very great probability. However, its convergence speed becomes slow as the number of design parameters increases. Therefore, the scalability of our method is relatively poor.
Author Contributions
Conceptualization, Y.C., J.S., and X.-J.Y.; methodology, Y.C.; and supervision, J.S. and X.-J.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grant 71801196, National Major Project from the Shanghai Nuclear Engineering Research and Design Institute under Grant 2017ZX06002006, and the Science Research Foundation of Capital University of Economics and Business under Grant XRZ2021043.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PSO | Particle Swarm Optimization |
| PSSTCS | Power-Shift Steering Transmission Control System |
| PSO-Divide-Best | Particle Swarm Optimization Divide-the-Best algorithm |
| EPCP | Approach in [28] including exploration phase and consolidation phase |
| IA-CES | Method in [24] which combines interval arithmetic with cellular evolutionary strategies |
Appendix A

Table A1.
The bad designs and the representative good designs.
Table A1.
The bad designs and the representative good designs.
| Bad Design | Good Design | Bad Design | Good Design | ||||
|---|---|---|---|---|---|---|---|
| EPCP | PSO-Divide-Best | EPCP | PSO-Divide-Best | ||||
| 0.9996 | 0.9998 | 0.9999 | 0.9996 | 0.9996 | 0.9996 | ||
| 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | ||
| 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9997 | 0.9999 | ||
| 0.9996 | 0.9996 | 0.9998 | 0.9996 | 0.9996 | 0.9996 | ||
| 0.9996 | 0.9997 | 0.9997 | 0.9996 | 0.9996 | 0.9996 | ||
| 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | ||
| 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9998 | 0.9996 | ||
| 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | ||
| 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | ||
| 0.9996 | 0.9997 | 0.9998 | 0.9996 | 0.9998 | 0.9999 | ||
| 0.9996 | 0.9998 | 0.9998 | 0.9996 | 0.9996 | 0.9996 | ||
| 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9997 | 0.9999 | ||
| 0.9996 | 0.9997 | 0.9998 | 0.9996 | 0.9996 | 0.9996 | ||
| 0.9996 | 0.9997 | 0.9999 | 0.9996 | 0.9996 | 0.9996 | ||
| 0.9996 | 0.9997 | 0.9998 | 0.9996 | 0.9996 | 0.9996 | ||
| 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | ||
| 0.9996 | 0.9997 | 0.9999 | 0.9996 | 0.9998 | 0.9999 | ||
| 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | ||
| 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | ||
| 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9998 | 0.9998 | ||
| 0.9996 | 0.9998 | 0.9998 | 0.9996 | 0.9996 | 0.9996 | ||
| 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9998 | 0.9999 | ||
| 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9998 | 0.9998 | ||
| 0.9996 | 0.9997 | 0.9999 | 0.9996 | 0.9998 | 0.9998 | ||
| 0.9996 | 0.9998 | 0.9999 | 0.9996 | 0.9997 | 0.9999 | ||
| 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9997 | 0.9998 | ||
| 0.9996 | 0.9998 | 0.9997 | 0.9996 | 0.9998 | 0.9999 | ||
| 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | ||
| 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9997 | ||
| 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9997 | ||
| 0.9996 | 0.9997 | 0.9999 | 0.9996 | 0.9997 | 0.9998 | ||
| 0.9996 | 0.9997 | 0.9995 | 0.9996 | 0.9997 | 0.9998 | ||
| 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | ||
| 0.9996 | 0.9997 | 0.9997 | 0.9996 | 0.9996 | 0.9996 | ||
| 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9995 | ||
| 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | ||
| 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9997 | 0.9996 | ||
| 0.9996 | 0.9997 | 0.9997 | 0.9996 | 0.9997 | 0.9998 | ||
| 0.9996 | 0.9997 | 0.9997 | 0.9996 | 0.9996 | 0.9998 | ||
| 0.9996 | 0.9997 | 0.9998 | 0.9996 | 0.9997 | 0.9995 | ||
| 0.9996 | 0.9997 | 0.9997 | 0.9996 | 0.9996 | 0.9996 | ||
| 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9997 | 0.9996 | ||
| 0.9996 | 0.9996 | 0.9995 | 0.9996 | 0.9998 | 0.9998 | ||
| 0.9856 | 0.9912 | 0.9940 | |||||

Table A2.
The lower and upper boundaries of hyper-boxes.
Table A2.
The lower and upper boundaries of hyper-boxes.
| Lower Bound | EPCP | PSO-Divide-Best | Upper Bound | EPCP | PSO-Divide-Best |
|---|---|---|---|---|---|
| 0.9997 | 0.9997 | 0.9999 | 1.0000 | ||
| 0.9995 | 0.9994 | 0.9998 | 1.0000 | ||
| 0.9996 | 0.9991 | 0.9998 | 1.0000 | ||
| 0.9995 | 0.9993 | 0.9998 | 1.0000 | ||
| 0.9995 | 0.9995 | 0.9998 | 1.0000 | ||
| 0.9997 | 0.9997 | 0.9998 | 1.0000 | ||
| 0.9995 | 0.9995 | 0.9997 | 1.0000 | ||
| 0.9995 | 0.9992 | 0.9998 | 1.0000 | ||
| 0.9996 | 0.9994 | 0.9998 | 1.0000 | ||
| 0.9995 | 0.9999 | 0.9999 | 1.0000 | ||
| 0.9990 | 0.9990 | 1.0000 | 1.0000 | ||
| 0.9990 | 0.9990 | 1.0000 | 1.0000 | ||
| 0.9991 | 0.9990 | 1.0000 | 1.0000 | ||
| 0.9997 | 0.9998 | 0.9999 | 1.0000 | ||
| 0.9995 | 0.9992 | 0.9998 | 1.0000 | ||
| 0.9996 | 0.9994 | 0.9998 | 1.0000 | ||
| 0.9997 | 0.9994 | 0.9999 | 1.0000 | ||
| 0.9995 | 0.9995 | 0.9999 | 1.0000 | ||
| 0.9995 | 0.9996 | 0.9999 | 1.0000 | ||
| 0.9997 | 0.9998 | 0.9999 | 1.0000 | ||
| 0.9997 | 0.9997 | 0.9999 | 1.0000 | ||
| 0.9997 | 0.9998 | 0.9999 | 1.0000 | ||
| 0.9990 | 0.9990 | 1.0000 | 1.0000 | ||
| 0.9995 | 0.9999 | 0.9998 | 1.0000 | ||
| 0.9995 | 0.9995 | 0.9999 | 1.0000 | ||
| 0.9997 | 0.9998 | 0.9999 | 1.0000 | ||
| 0.9995 | 0.9998 | 0.9999 | 1.0000 | ||
| 0.9990 | 0.9990 | 1.0000 | 1.0000 | ||
| 0.9995 | 0.9995 | 0.9999 | 1.0000 | ||
| 0.9997 | 0.9995 | 0.9999 | 1.0000 | ||
| 0.9990 | 0.9990 | 1.0000 | 1.0000 | ||
| 0.9990 | 0.9990 | 1.0000 | 1.0000 | ||
| 0.9995 | 0.9997 | 0.9999 | 1.0000 | ||
| 0.9997 | 0.9999 | 0.9999 | 1.0000 | ||
| 0.9990 | 0.9990 | 1.0000 | 1.0000 | ||
| 0.9991 | 0.9990 | 1.0000 | 1.0000 | ||
| 0.9991 | 0.9990 | 1.0000 | 1.0000 | ||
| 0.9992 | 0.9990 | 1.0000 | 1.0000 | ||
| 0.9990 | 0.9990 | 1.0000 | 1.0000 | ||
| 0.9997 | 0.9995 | 0.9999 | 1.0000 | ||
| 0.9997 | 0.9997 | 0.9999 | 1.0000 | ||
| 0.9995 | 0.9995 | 0.9999 | 1.0000 | ||
| 0.9997 | 0.9997 | 0.9999 | 1.0000 | ||
| 0.9997 | 0.9999 | 0.9999 | 1.0000 | ||
| 0.9998 | 0.9998 | 0.9999 | 1.0000 | ||
| 0.9997 | 0.9995 | 0.9999 | 1.0000 | ||
| 0.9995 | 0.9998 | 0.9999 | 1.0000 | ||
| 0.9997 | 0.9995 | 0.9999 | 1.0000 | ||
| 0.9997 | 0.9999 | 0.9999 | 1.0000 | ||
| 0.9995 | 0.9998 | 0.9999 | 1.0000 | ||
| 0.9996 | 0.9995 | 0.9998 | 1.0000 | ||
| 0.9995 | 0.9995 | 0.9998 | 1.0000 | ||
| 0.9997 | 0.9995 | 0.9999 | 1.0000 | ||
| 0.9997 | 0.9998 | 0.9999 | 1.0000 | ||
| 0.9997 | 0.9995 | 0.9999 | 1.0000 | ||
| 0.9997 | 0.9995 | 0.9999 | 1.0000 | ||
| 0.9996 | 0.9992 | 0.9998 | 1.0000 | ||
| 0.9995 | 0.9994 | 0.9998 | 1.0000 | ||
| 0.9996 | 0.9994 | 0.9998 | 1.0000 | ||
| 0.9995 | 0.9994 | 0.9998 | 1.0000 | ||
| 0.9996 | 0.9997 | 0.9998 | 1.0000 | ||
| 0.9996 | 0.9996 | 0.9998 | 1.0000 | ||
| 0.9995 | 0.9990 | 0.9998 | 1.0000 | ||
| 0.9996 | 0.9996 | 0.9998 | 1.0000 | ||
| 0.9996 | 0.9995 | 0.9998 | 1.0000 | ||
| 0.9995 | 0.9995 | 0.9998 | 1.0000 | ||
| 0.9995 | 0.9994 | 0.9998 | 1.0000 | ||
| 0.9996 | 0.9994 | 0.9998 | 1.0000 | ||
| 0.9996 | 0.9990 | 0.9998 | 1.0000 | ||
| 0.9995 | 0.9990 | 0.9998 | 1.0000 | ||
| 0.9995 | 0.9990 | 0.9998 | 1.0000 | ||
| 0.9995 | 0.9995 | 0.9998 | 1.0000 | ||
| 0.9996 | 0.9992 | 0.9998 | 1.0000 | ||
| 0.9995 | 0.9991 | 0.9998 | 1.0000 | ||
| 0.9995 | 0.9994 | 0.9998 | 1.0000 | ||
| 0.9996 | 0.9995 | 0.9998 | 1.0000 | ||
| 0.9995 | 0.9993 | 0.9998 | 1.0000 | ||
| 0.9995 | 0.9995 | 0.9998 | 1.0000 | ||
| 0.9996 | 0.9995 | 0.9998 | 1.0000 | ||
| 0.9996 | 0.9990 | 0.9998 | 1.0000 | ||
| 0.9996 | 0.9994 | 0.9998 | 1.0000 | ||
| 0.9996 | 0.9993 | 0.9998 | 1.0000 | ||
| 0.9996 | 0.9996 | 0.9998 | 1.0000 | ||
| 0.9996 | 0.9992 | 0.9998 | 1.0000 | ||
| 0.9995 | 0.9990 | 0.9998 | 1.0000 | ||
| 0.9997 | 0.9995 | 0.9999 | 1.0000 |
References
- Oberkampf, W.L. Uncertainty Quantification Using Evidence Theory; Stanford University: Stanford, CA, USA, 2005. [Google Scholar]
- Lim, D.; Ong, Y.S.; Sendhoff, B.; Lee, B.S. Inverse multi-objective robust evolutionary design optimization. Genet. Program. Evolvable Mach. 2007, 7, 383–404. [Google Scholar] [CrossRef][Green Version]
- Li, M.Y.; Zhang, W.D.; Hu, Q.P.; Guo, H.R.; Liu, J. Design and Risk Evaluation of Reliability Demonstration Test for Hierarchical Systems With Multilevel Information Aggregation. IEEE Trans. Reliab. 2017, 66, 135–147. [Google Scholar] [CrossRef]
- Zhao, Y.G.; Ono, T. A general procedure for first/second-order reliability method (FORM/SORM). Struct. Saf. 1999, 21, 95–112. [Google Scholar] [CrossRef]
- Saltelli, A.; Scott, M. Guest editorial: The role of sensitivity analysis in the corroboration of models and its link to model structural and parametric uncertainty. Reliab. Eng. Syst. Saf. 1997, 57, 1–4. [Google Scholar] [CrossRef]
- Pannier, S.; Graf, W. Sensitivity measures for fuzzy numbers based on artificial neural networks. In Applications of Statistics and Probability in Civil Engineering; CRC Press: London, UK, 2011; pp. 497–505. [Google Scholar]
- Taguchi, G.; Elsayed, E.; Hsiang, T. Quality Engineering in Production Systems; McGraw-Hill: New York, NY, USA, 1989. [Google Scholar]
- Hara, K.; Inoue, M. Gain-Preserving Data-Driven Approximation of the Koopman Operator and Its Application in Robust Controller Design. Mathematics 2021, 9, 949. [Google Scholar] [CrossRef]
- Lee, M.; Jeong, H.; Lee, D. Design Optimization of 3-DOF Redundant Planar Parallel Kinematic Mechanism Based Finishing Cut Stage for Improving Surface Roughness of FDM 3D Printed Sculptures. Mathematics 2021, 9, 961. [Google Scholar] [CrossRef]
- Gunawan, S.; Papalambros, P.Y. A Bayesian Approach to Reliability-Based Optimization With Incomplete Information. J. Mech. Des. 2006, 128, 909–918. [Google Scholar] [CrossRef]
- Stocki, R. A method to improve design reliability using optimal Latin hypercube sampling. Comput. Assist. Mech. Eng. Sci. 2005, 12, 393–411. [Google Scholar]
- Lehar, M.; Zimmermann, M. An inexpensive estimate of failure probability for high-dimensional systems with uncertainty. Struct. Saf. 2012, 36–37, 32–38. [Google Scholar] [CrossRef]
- Daum, D.A.; Deb, K.; Branke, J. Reliability-based optimization for multiple constraints with evolutionary algorithms. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007. [Google Scholar]
- Asafuddoula, M.; Singh, H.K.; Ray, T. Six-Sigma Robust Design Optimization Using a Many-Objective Decomposition-Based Evolutionary Algorithm. IEEE Trans. Evol. Comput. 2015, 19, 490–507. [Google Scholar] [CrossRef]
- Jin, Y.; Branke, J. Evolutionary optimization in uncertain environments—A survey. IEEE Trans. Evol. Comput. 2005, 9, 303–317. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Yang, S.; Branke, J. Evolutionary dynamic optimization: A survey of the state of the art. Swarm Evol. Comput. 2012, 6, 1–24. [Google Scholar] [CrossRef]
- Knight, J.T.; Zahradka, F.T.; Singer, D.J.; Collette, M. Multiobjective Particle Swarm Optimization of a Planing Craft with Uncertainty. J. Ship Prod. Des. 2018, 30, 194–200. [Google Scholar] [CrossRef]
- Fan, X.N.; Yue, X.Y.; Li, Y.Z. LHS applied to reliability-based design optimization of a crane metallic structure. J. Chem. Pharm. Res. 2015, 7, 2400–2406. [Google Scholar]
- Qin, Y.; Zhu, J.F.; Wei, Z. The robust optimization of the capacitated hub and spoke airline network design base on ant colony algorithms. In Proceedings of the 2010 International Conference on Intelligent Computing and Integrated Systems, Guilin, China, 22–24 October 2010; pp. 601–604. [Google Scholar]
- Chen, T.H.; Yeh, M.F.; Lee, W.Y.; Hsieh, W.H. Particle swarm optimization based networked control system design with uncertainty. Matec Web Conf. 2017, 119, 01051. [Google Scholar] [CrossRef]
- Zimmermann, M.; von Hoessle, J.E. Computing solution spaces for robust design. Int. J. Numer. Methods Eng. 2013, 94, 290–307. [Google Scholar] [CrossRef]
- Zimmermann, M. Vehicle Front Crash Design Accounting for Uncertainties. In Proceedings of the FISITA 2012 World Automotive Congress; Springer: Berlin/Heidelberg, Germany, 2013; Volume 197, pp. 83–89. [Google Scholar]
- Graff, L.; Harbrecht, H.; Zimmermann, M. On the computation of solution spaces in high dimensions. Struct. Multidiscip. Optim. 2016, 54, 811–829. [Google Scholar] [CrossRef][Green Version]
- Rocco, C.M.; Moreno, J.A.; Carrasquero, N. Robust design using a hybrid cellular-evolutionary and interval-arithmetic approach:a reliability application. Reliab. Eng. Syst. Saf. 2003, 79, 149–159. [Google Scholar] [CrossRef]
- Chen, Y.; Shi, J.; Yi, X.J. A New Reliable Operating Region Design Method. Math. Probl. Eng. 2020, 2020, 1–12. [Google Scholar] [CrossRef]
- Chen, Y.; Shi, J.; Yi, X.J. A globally optimal robust design method for complex systems. Complexity 2020, 2020, 1–25. [Google Scholar] [CrossRef]
- Jones, D.R.; Perttunen, C.D.; Stuckman, B.E. Lipschitzian optimization without the Lipschitz constant. J. Optim. Theory Appl. 1993, 79, 157–181. [Google Scholar] [CrossRef]
- Fender, J.; Graff, L.; Harbrecht, H.; Zimmermann, M. Identifying Key Parameters for Design Improvement in High-Dimensional Systems With Uncertainty. J. Mech. Des. 2014, 136, 041007. [Google Scholar] [CrossRef]
- Kennedy, J. The particle swarm: Social adaptation of knowledge. In Proceedings of the 1997 IEEE International Conference on Evolutionary Computation, Indianapolis, IN, USA, 13–16 April 1997. [Google Scholar]
- Sergeyev, Y.D.; Kvasov, D.E. Global search based on diagonal partitions and a set of Lipschitz constants. SIAM J. Optim. 2006, 16, 910–937. [Google Scholar] [CrossRef]
- Kvasov, D.E.; Sergeyev, Y.D. Multidimensional Global Optimization Algorithm Based on Adaptive Diagonal Curves. Comput. Math. Math. Phys. 2003, 43, 42–59. [Google Scholar]
- Strongin, R.G.; Sergeyev, Y.D. Global Optimization with Non-Convex Constraints. Sequential and Parallel Algorithms; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Sergeyev, Y.D.; Yaroslav, D. An Information Global Optimization Algorithm with Local Tuning. SIAM J. Optim. 2006, 5, 858–870. [Google Scholar] [CrossRef]
- Kvasov, D.E.; Sergeyev, Y.D. Deterministic approaches for solving practical black-box global optimization problems. Adv. Eng. Softw. 2015, 80, 58–66. [Google Scholar] [CrossRef]
- Sergeyev, Y.D.; Kvasov, D.E. A deterministic global optimization using smooth diagonal auxiliary functions. Commun. Nonlinear Sci. Numer. Simul. 2015, 21, 99–111. [Google Scholar] [CrossRef]
- Gablonsky, J.M. Modifications of the Direct Algorithm. Ph.D. Thesis, North Carolina State University, Raleigh, NC, USA, 2001. [Google Scholar]
- Paulavicius, R.; Chiter, L.; Žilinskas, J. Global optimization based on bisection of rectangles, function values at diagonals, and a set of Lipschitz constants. J. Glob. Optim. 2018, 71, 5–20. [Google Scholar] [CrossRef]
- Paulavičius, R.; Žilinskas, J.; Grothey, A. Investigation of selection strategies in branch and bound algorithm with simplicial partitions and combination of Lipschitz bounds. Optim. Lett. 2010, 4, 173–183. [Google Scholar] [CrossRef]
- Stripinis, L.; Paulavičius, R.; Žilinskas, J. Improved scheme for selection of potentially optimal hyper-rectangles in DIRECT. Optim. Lett. 2018, 12, 1699–1712. [Google Scholar] [CrossRef]
- Yan, J.; Hu, T.; Huang, C.C.; Wu, X. An improved particle swarm optimization algorithm. Adv. Mater. Res. 2009, 195–196, 1060–1065. [Google Scholar]
- Barrera, J.; Coello, C. A Review of Particle Swarm Optimization Methods Used for Multimodal Optimization. In Innovations in Swarm Intelligence; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Gandomi, A.H.; Yun, G.J.; Yang, X.S.; Talatahari, S. Chaos-enhanced accelerated particle swarm optimization. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 327–340. [Google Scholar] [CrossRef]
- Rao, S.S. Engineering Optimization Theory and Practice; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Kuhn, H.W.; Tucker, A.W. Nonlinear programming. In Proceedings of 2nd Berkeley Symposium; University of California Press: Berkeley, CA, USA, 1951; pp. 481–492. [Google Scholar]
- Yi, X.J.; Shi, J.; Dhillon, B.S.; Hou, P.; Dong, H.P. A new reliability analysis method for repairable systems with closed-loop feedback links. Qual. Reliab. Eng. Int. 2018, 34, 298–332. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).