Nonlinear-Observer-Based Design Approach for Adaptive Event-Driven Tracking of Uncertain Underactuated Underwater Vehicles
Abstract
1. Introduction
- (i)
- Contrary to the existing output-feedback tracking methods for 5-DOF or 6-DOF underwater vehicles [24,25,26,27], this study considers unknown system nonlinearities of the 6-DOF UUV dynamics. Thus, an adaptive velocity observer design strategy using state transformation and neural networks is proposed to estimate the velocity information of UUVs while compensating for the unknown system nonlinearities, where adaptive laws based on a scaling function are derived to learn weights of neural networks.
- (ii)
- Compared with the existing event-triggered control results for three-dimensional tracking [23,28], this study establishes the design methodology of the guaranteed-performance-based adaptive tracker and its event-triggering condition depending on only the position measurement of 6-DOF UUVs. Then, the stability of the proposed output-feedback event-triggered tracking system is analyzed in the Lyapunov sense.
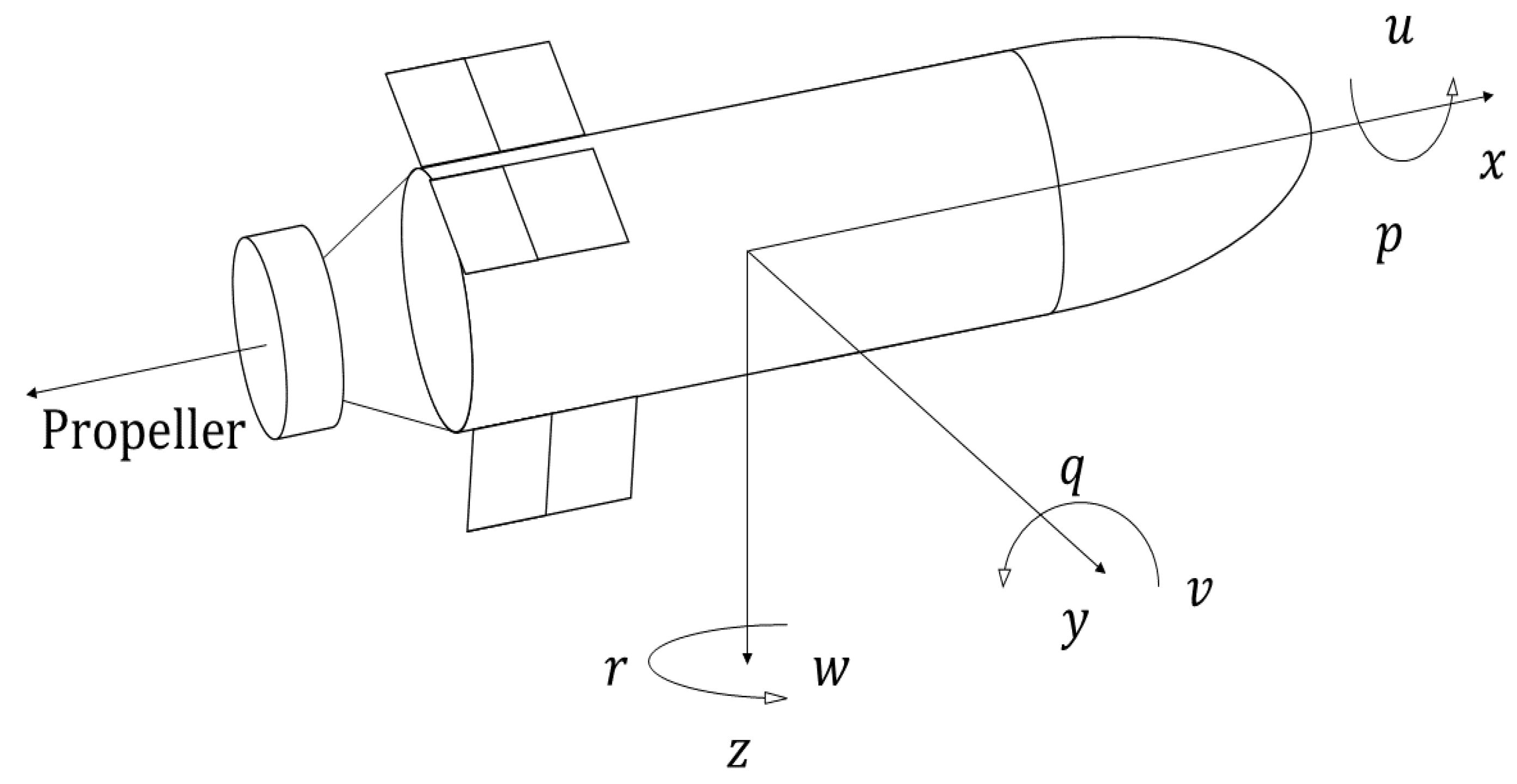
2. Problem Formulation
3. Nonlinear-Observer-Based Design Approach for Event-Driven Output- Feedback Control
3.1. Adaptive Nonlinear Observer Design Using Neural Networks
3.2. Output-Feedback Event-Driven Controller Design and Stability Analysis
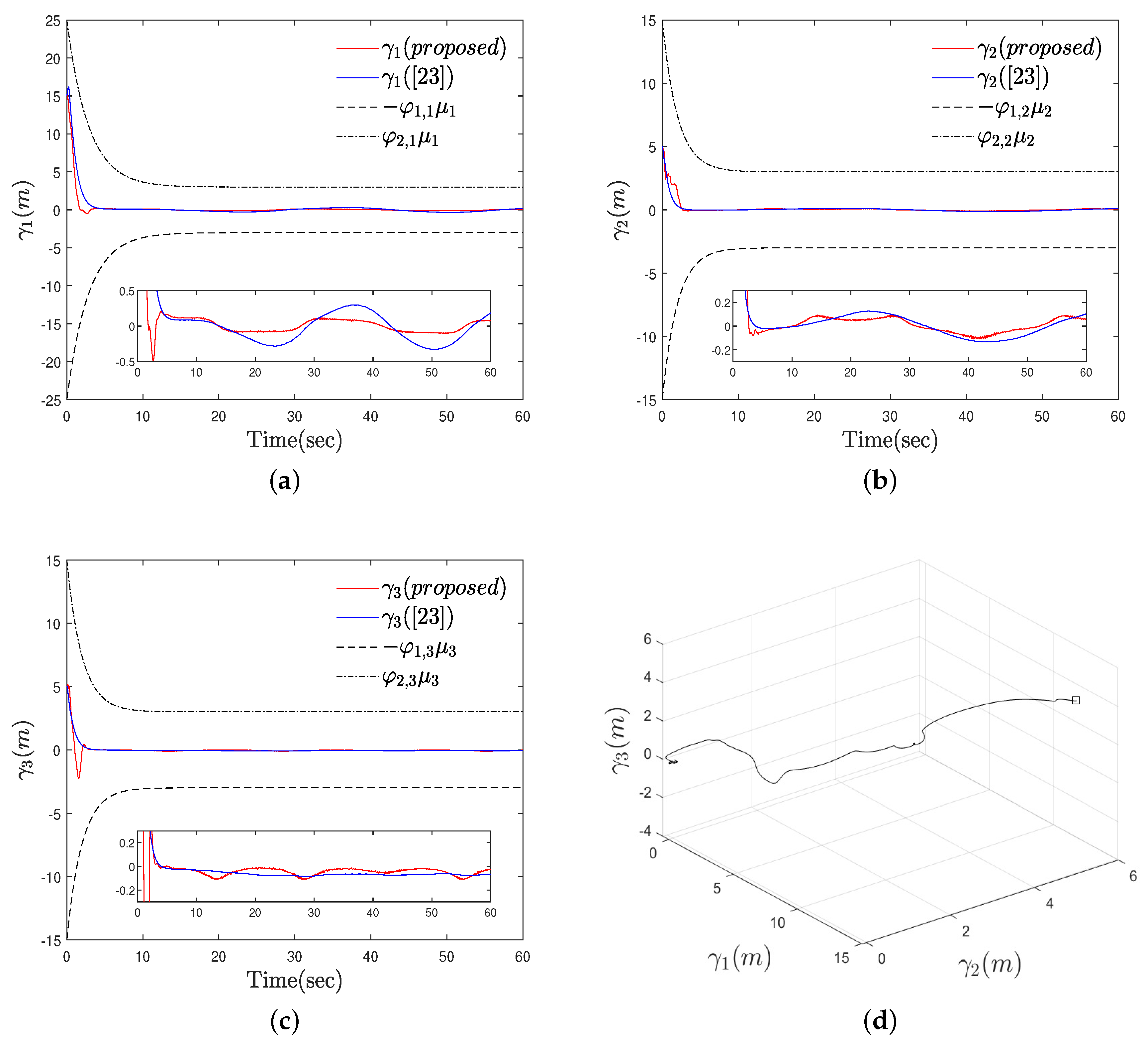
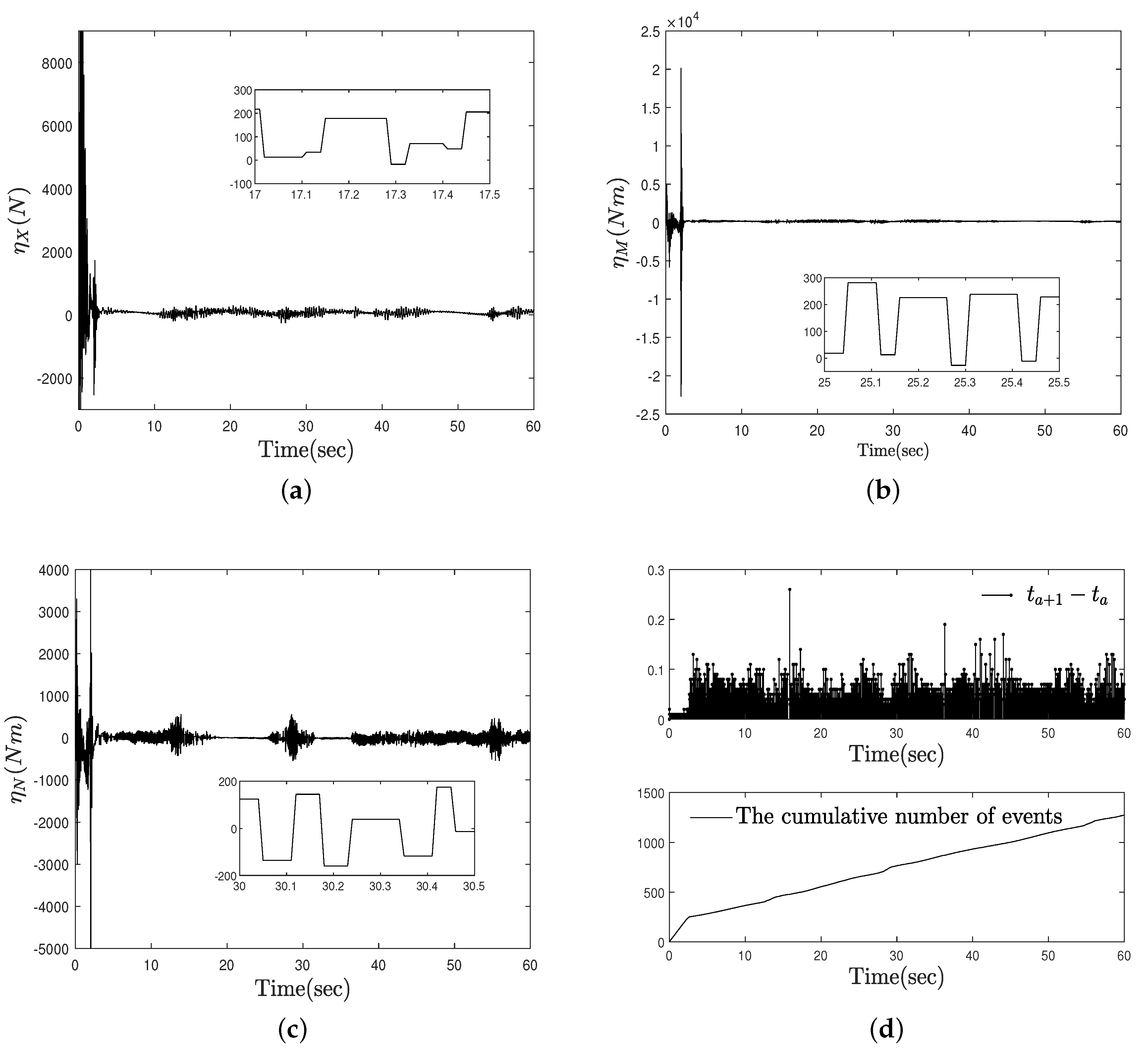
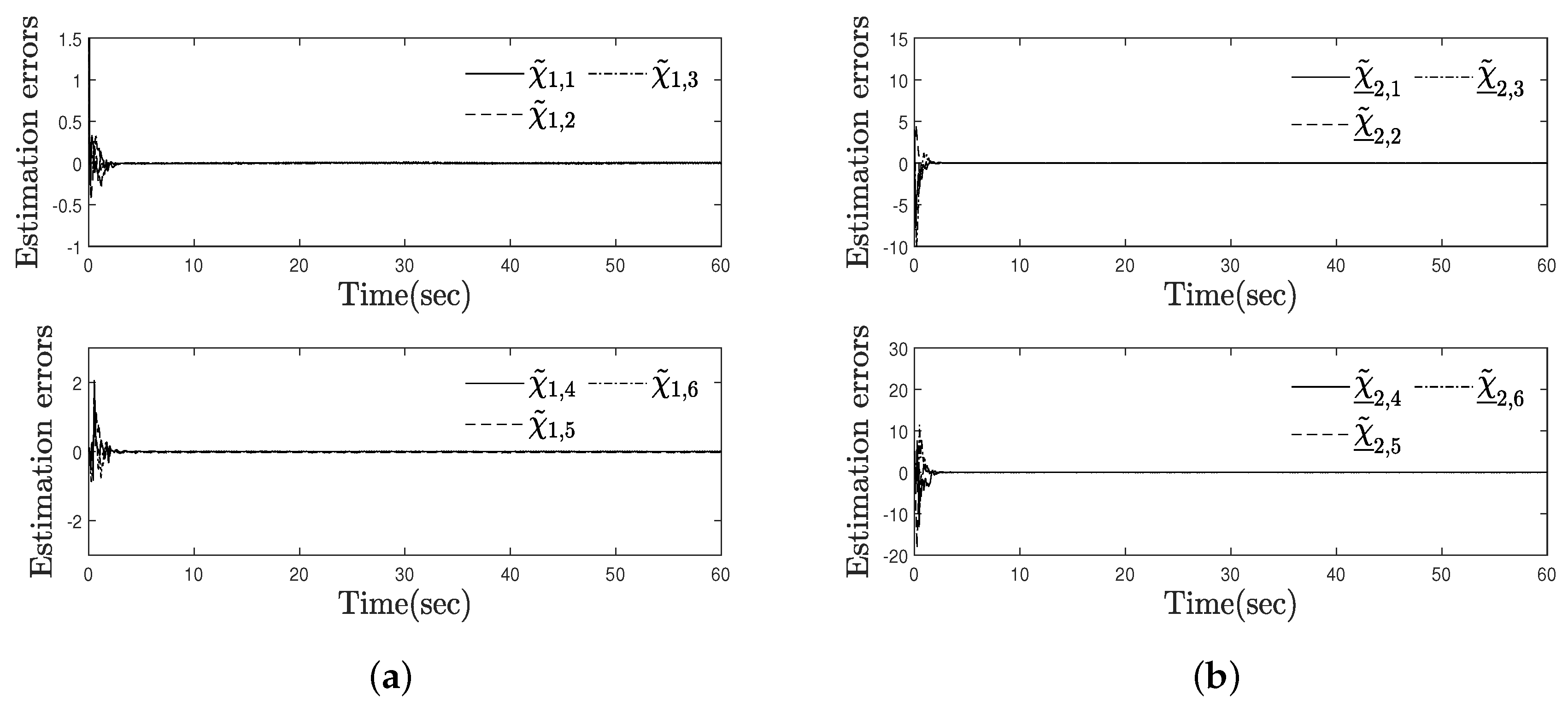
4. Simulation Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sahoo, A.; Dwivedy, S.K.; Robi, P. Advancements in the field of autonomous underwater vehicle. Ocean Eng. 2019, 181, 145–160. [Google Scholar] [CrossRef]
- Yuh, J. Design and control of autonomous underwater robots: A survey. Auton. Robot. 2000, 8, 7–24. [Google Scholar] [CrossRef]
- Xiang, X.; Yu, C.; Niu, Z.; Zhang, Q. Subsea cable tracking by autonomous underwater vehicle with magnetic sensing guidance. Sensors 2016, 16, 1335. [Google Scholar] [CrossRef]
- Bellingham, J.G.; Rajan, K. Robotics in remote and hostile environments. Science 2007, 318, 1098–1102. [Google Scholar] [CrossRef] [PubMed]
- Farrell, J.A.; Li, W.; Pang, S.; Arrieta, R. Chemical plume tracing experimental results with REMUS AUV. Oceans 2003, 2, 962–968. [Google Scholar]
- Peymani, E.; Fossen, T.I. Path following of underwater robots using lagrange multipliers. Robot. Auton. Syst. 2015, 67, 44–52. [Google Scholar] [CrossRef]
- Ribas, D.; Palomeras, N.; Ridao, P.; Carreras, M.; Mallios, A. Girona 500 auv: From survey to intervention. IEEE/ASME Trans. Mechatron. 2012, 17, 46–53. [Google Scholar] [CrossRef]
- Li, J.H.; Lee, P.M. Design of an adaptive nonlinear controller for depth control of an autonomous underwater vehicle. Ocean Eng. 2005, 32, 2165–2181. [Google Scholar] [CrossRef]
- Repoulias, F.; Papadopoulos, E. Planar trajectory planning and tracking control design for underactuated AUVs. Ocean Eng. 2007, 34, 1650–1667. [Google Scholar] [CrossRef]
- Taha, E.; Mohamed, Z.; Kamal, Y. Terminal sliding mode control for the trajectory tracking of underactuated Autonomous Underwater Vehicles. Ocean Eng. 2017, 129, 613–625. [Google Scholar]
- Shen, C.; Shi, Y.; Buckham, B. Trajectory tracking control of an autonomous underwater vehicle using lyapunov-based model predictive control. IEEE Trans. Indust. Elect. 2018, 65, 5796–5805. [Google Scholar] [CrossRef]
- Cho, G.R.; Li, J.H.; Park, D.; Jung, J.H. Robust trajectory tracking of autonomous underwater vehicles using back-stepping control and time delay estimation. Ocean Eng. 2020, 201, 107131. [Google Scholar] [CrossRef]
- Liang, X.; Qu, X.; Hou, Y.; Zhang, J. Three-dimensional path following control of underactuated autonomous underwater vehicle based on damping backstepping. Int. J. Adv. Robot. Syst. 2017, 14, 1729881417724179. [Google Scholar] [CrossRef]
- Liang, X.; Qu, X.; Hou, Y.; Ma, Q. Three-dimensional trajectory tracking control of an underactuated autonomous underwater vehicle based on ocean current observer. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418806811. [Google Scholar] [CrossRef]
- Wang, J.; Wang, C.; Wei, Y.; Zhang, C. Three-dimensional path following of an underactuated AUV based on neuro-adaptive command filtered backstepping control. IEEE Access 2018, 6, 74355–74365. [Google Scholar] [CrossRef]
- Shojaei, K. Three-dimensional neural network tracking control of a moving target by underactuated autonomous underwater vehicles. Neural Comput. Appl. 2019, 31, 509–521. [Google Scholar] [CrossRef]
- Rezazadegan, F.; Shojaei, K.; Sheikholeslam, F.; Chatraei, A. A novel approach to 6-DOF adaptive trajectory tracking control of an AUV in the presence of parameter uncertainties. Ocean Eng. 2015, 107, 246–258. [Google Scholar] [CrossRef]
- Karkoub, M.; Wu, H.M.; Hwang, C.L. Nonlinear trajectory-tracking control of an autonomous underwater vehicle. Ocean Eng. 2017, 145, 188–198. [Google Scholar] [CrossRef]
- Kumar, N.; Rani, M. An efficient hybrid approach for trajectory tracking control of autonomous underwater vehicles. Appl. Ocean Res. 2020, 95, 3627–3635. [Google Scholar] [CrossRef]
- Bechlioulis, C.P.; Karras, G.C.; Heshmati-Alamdari, S.; Kyriakopoulos, K.J. Trajectory tracking with prescribed performance for underactuated underwater vehicles under model uncertainties and external disturbances. IEEE Trans. Contr. Syst. Technol. 2017, 25, 429–440. [Google Scholar] [CrossRef]
- Elhaki, O.; Shojaei, K. Neural network-based target tracking control of underactuated autonomous underwater vehicles with a prescribed performance. Ocena Eng. 2018, 167, 239–256. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, M.; Wang, S. Adaptive region tracking control with prescribed transient performance for autonomous underwater vehicle with thruster fault. Ocena Eng. 2020, 196, 106804. [Google Scholar] [CrossRef]
- Kim, J.H.; Yoo, S.J. Adaptive event-triggered control strategy for ensuring predefined three-dimensional tracking performance of uncertain nonlinear underactuated underwater vehicles. Mathematics 2021, 9, 137. [Google Scholar] [CrossRef]
- Refsnes, J.E.; Sørensen, A.J.; Pettersen, K.Y. Model-based output feedback control of slender-body underactuated AUVs: Theory and experiments. IEEE Trans. Control Syst. Technol. 2008, 16, 930–946. [Google Scholar] [CrossRef]
- Yu, H.; Guo, C.; Shen, Z.; Yan, Z. Output feedback spatial trajectory tracking control of underactuated unmanned undersea vehicles. IEEE Access 2020, 8, 42924–42936. [Google Scholar] [CrossRef]
- Zhang, L.J.; Qi, X.; Pang, Y.J. Adaptive output feedback control based on DRFNN for AUV. Ocean Eng. 2009, 36, 716–722. [Google Scholar] [CrossRef]
- Elhaki, O.; Shojaei, K. A robust neural network approximation-based prescribed performance output-feedback controller for autonomous underwater vehicles with actuators saturation. Eng. Appl. Artif. Int. 2020, 88, 103382. [Google Scholar] [CrossRef]
- Batmani, Y.; Najafi, S. Event-triggered H∞ depth control of remotely operated underwater vehicles. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 1224–1232. [Google Scholar] [CrossRef]
- Bian, J.; Xiang, J. Three-dimensional coordination control for multiple autonomous underwater vehicles. IEEE Access 2019, 7, 63913–63920. [Google Scholar] [CrossRef]
- Prestero, T. Verification of a Six-Degree of Freedom Simulation Model for the REMUS Autonomous Underwater Vehicles. Ph.D. Thesis, Department of Mechanical Engineering at Massachusetts Institute of Technology, Cambridge, MA, USA, 2001. [Google Scholar]
- Fossen, T. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley and Sons Ltd.: Chichester, UK, 2011. [Google Scholar]
- Polycarpou, M.M. Stable adaptive neural control scheme for nonlinear systems. IEEE Trans. Autom. Control 1996, 41, 447–451. [Google Scholar] [CrossRef]
- Wang, C.; Hill, D.J.; Ge, S.S.; Ghen, G. An ISS-modular approach for adaptive neural control of pure-feedback sytems. Automatica 2006, 42, 723–731. [Google Scholar] [CrossRef]
- Swaroop, D.; Hedrick, J.; Yip, P.P.; Gerdes, J. Dynamic surface control for a class of nonlinear systems. IEEE Trans. Autom. Control 2000, 45, 1893–1899. [Google Scholar] [CrossRef]
- Sands, T. Development of deterministic artificial intelligence for unmanned underwater vehicles (UUV). Mar. Sci. Eng. 2020, 8, 578. [Google Scholar] [CrossRef]










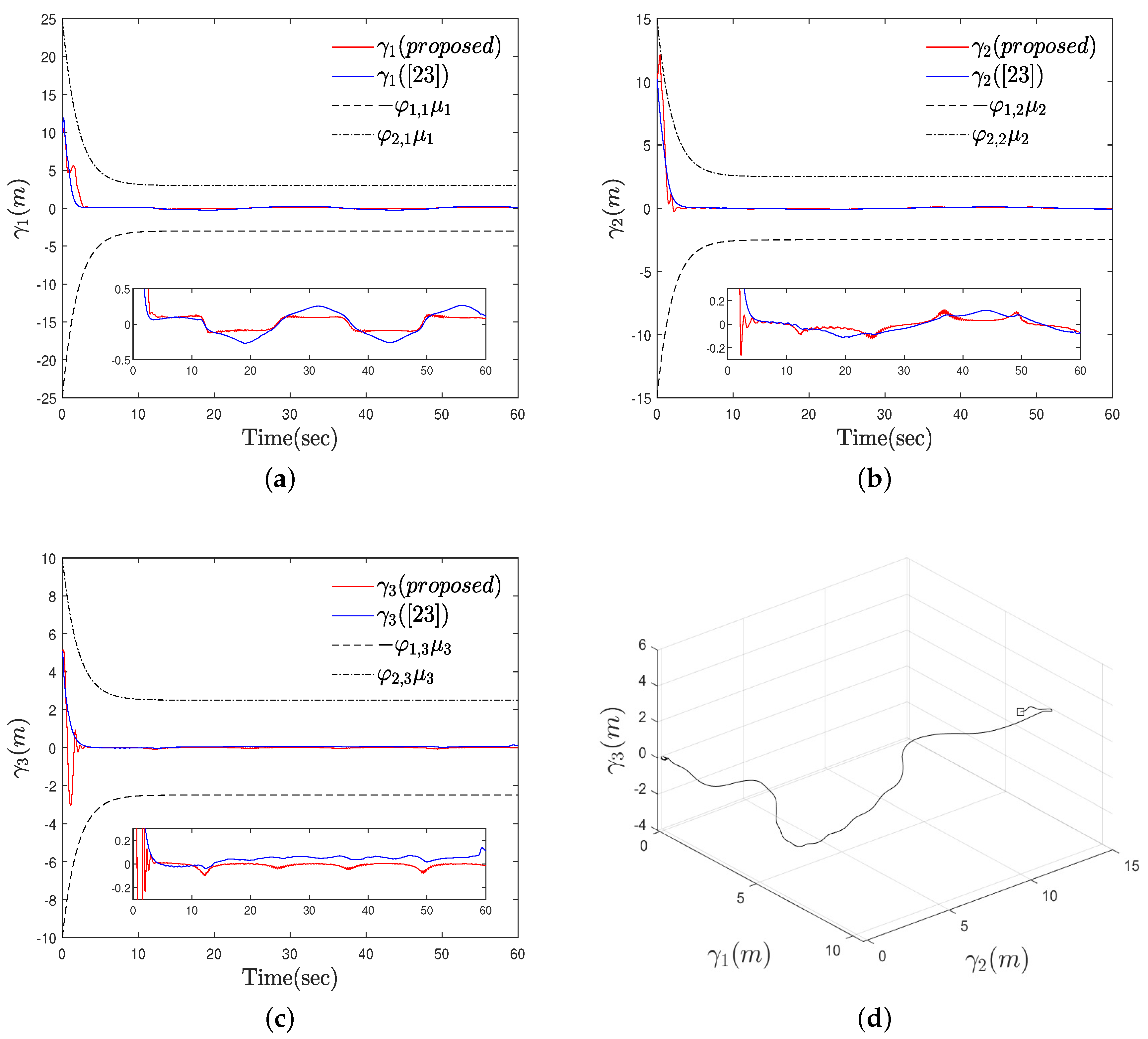
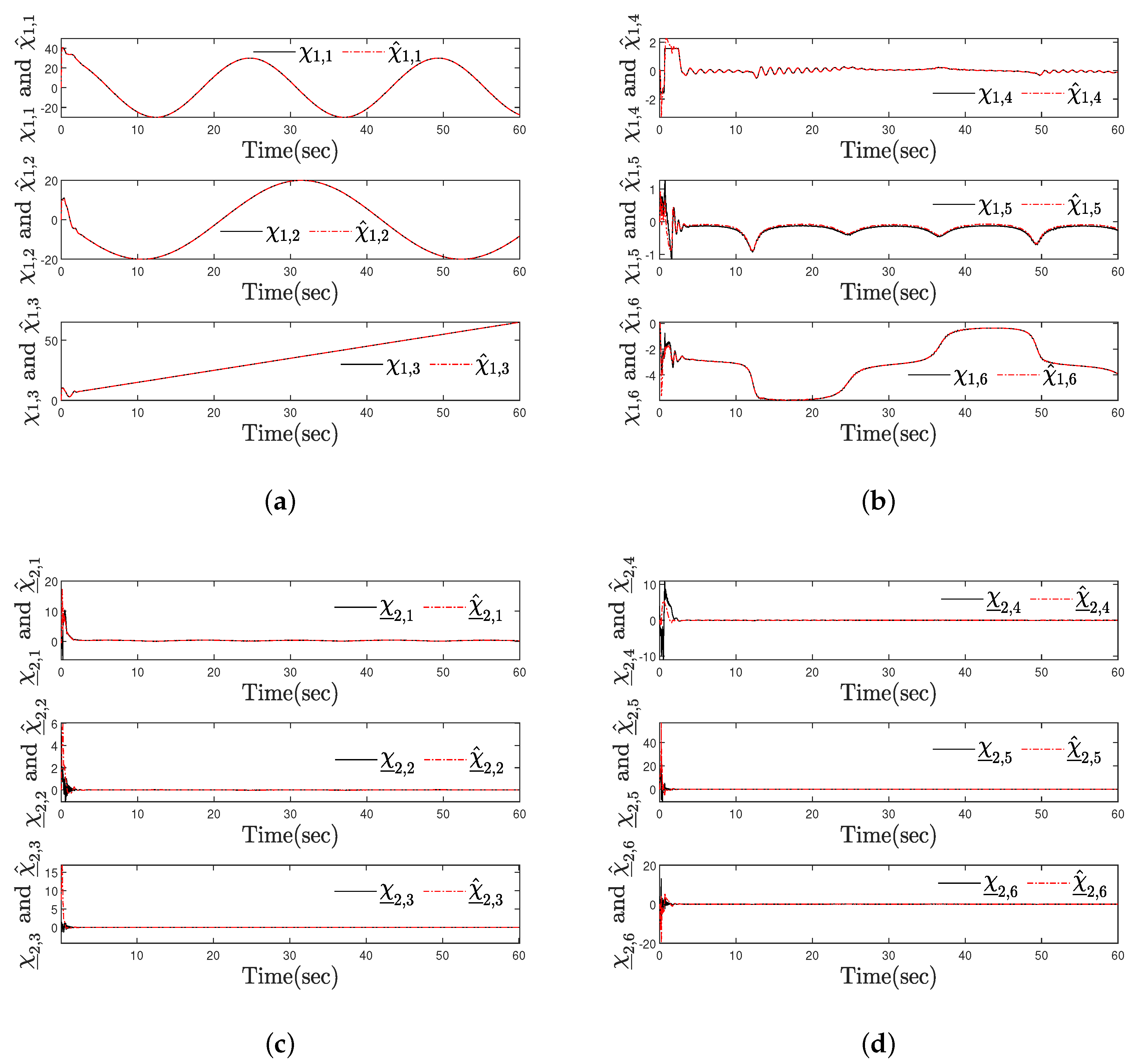
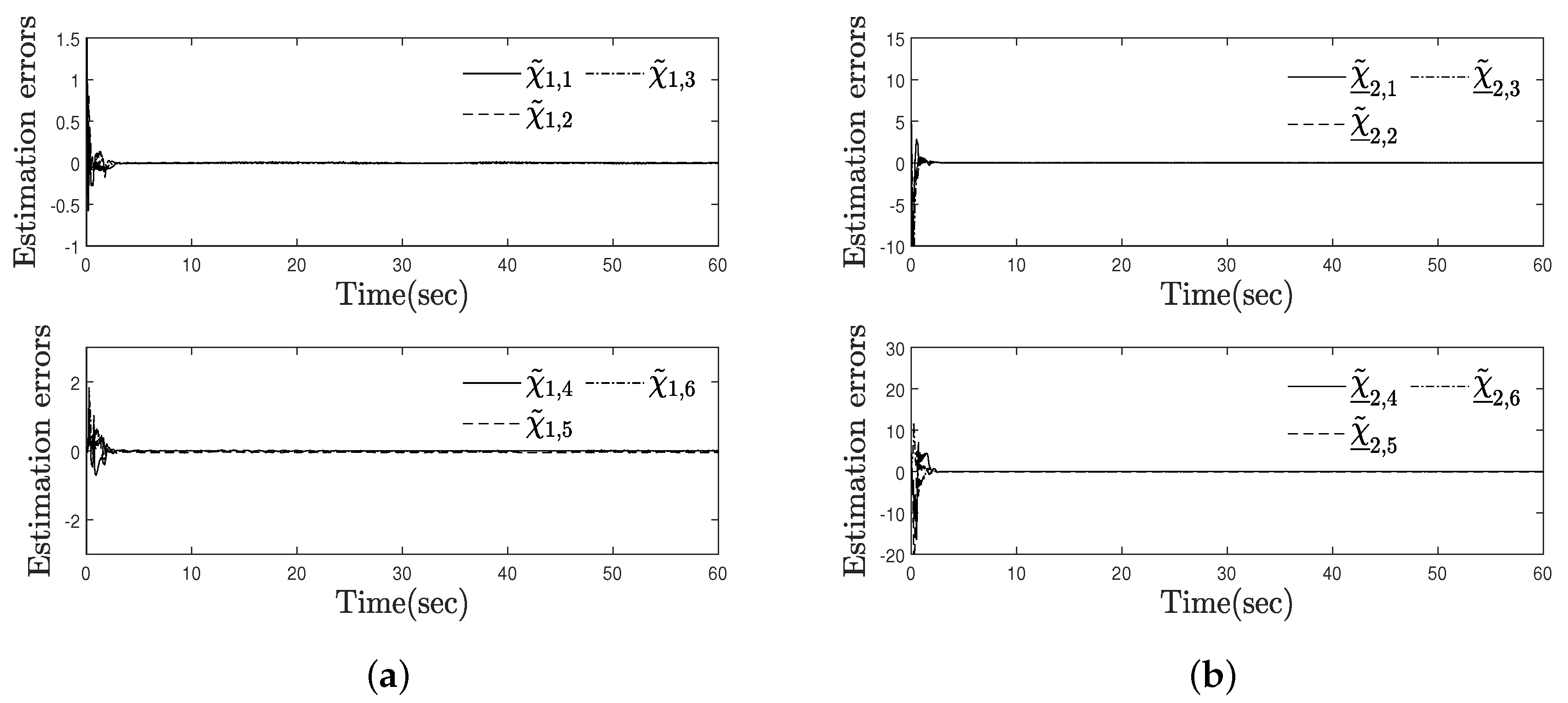
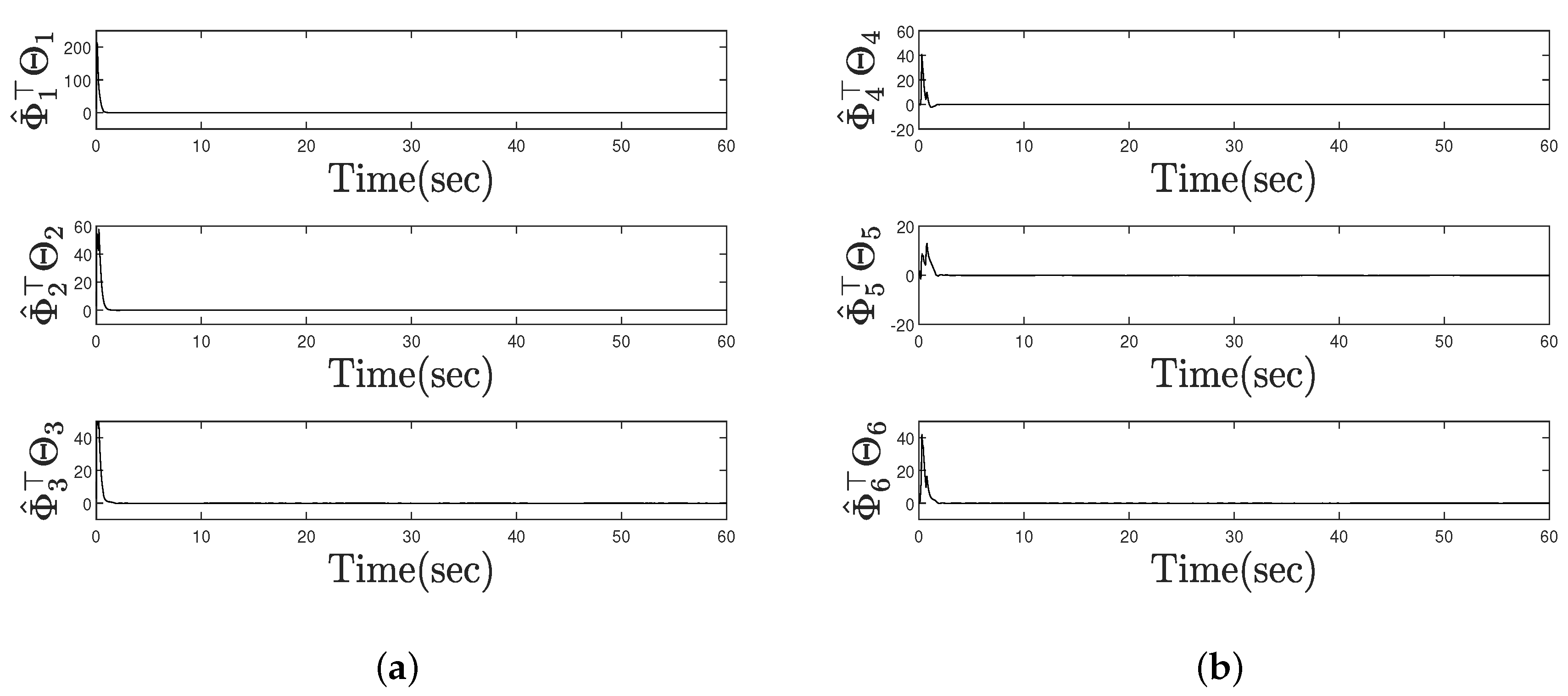

| Scenario 1 | initial conditions: , , , , |
| desired trajectory: , | |
| Scenario 2 | initial conditions: , , , , |
| desired trajectory: , | |
| Scenario 3 | initial conditions: , , , , |
| desired trajectory: , |
| Proposed | [23] | |||||
|---|---|---|---|---|---|---|
| Scenario | ||||||
| Scenario 1 | ||||||
| Scenario 2 | ||||||
| Scenario 3 |
| Scenario | ||||||
|---|---|---|---|---|---|---|
| Scenario 1 | ||||||
| Scenario 2 | ||||||
| Scenario 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.H.; Yoo, S.J. Nonlinear-Observer-Based Design Approach for Adaptive Event-Driven Tracking of Uncertain Underactuated Underwater Vehicles. Mathematics 2021, 9, 1144. https://doi.org/10.3390/math9101144
Kim JH, Yoo SJ. Nonlinear-Observer-Based Design Approach for Adaptive Event-Driven Tracking of Uncertain Underactuated Underwater Vehicles. Mathematics. 2021; 9(10):1144. https://doi.org/10.3390/math9101144
Chicago/Turabian StyleKim, Jin Hoe, and Sung Jin Yoo. 2021. "Nonlinear-Observer-Based Design Approach for Adaptive Event-Driven Tracking of Uncertain Underactuated Underwater Vehicles" Mathematics 9, no. 10: 1144. https://doi.org/10.3390/math9101144
APA StyleKim, J. H., & Yoo, S. J. (2021). Nonlinear-Observer-Based Design Approach for Adaptive Event-Driven Tracking of Uncertain Underactuated Underwater Vehicles. Mathematics, 9(10), 1144. https://doi.org/10.3390/math9101144






