1. Introduction
In 1971, Rosenfeld [
1] published an innovative paper on fuzzy subgroups. This article introduced the new field of abstract algebra and the new field of fuzzy mathematics. Many scientists and researchers worked in this field and obtained fruitful research. Liu [
2,
3] gave an important generalization in the field of fuzzy algebra by introducing fuzzy subrings of a ring and fuzzy ideals. Demirci [
4] firstly introduced the fuzzification of binary operation to group structure through fuzzy equality [
5] and introduced “vague groups.” After this work, many researchers used this concept and extended it to several other useful directions such as [
6,
7,
8,
9,
10]. In Demirci’s approach, the characteristic of the degree between the fuzzy binary operation is not used, and the identity and inverse element of an element are also not unique. Liu and Shi [
11] proposed a new approach to fuzzify the group structure by characterizing the degree of fuzzy binary operation, which is called
M-hazy groups. It is important to mention that
M-hazy associative law has been defined in order to obtain
M-hazy groups. Mehmood et al. [
12] extended this concept to the ring structure and gave a new method to the fuzzification of rings, which is defined by
M-hazy rings. It is also worth mentioning that an
M-hazy distributive law has been proposed so as to define
M-hazy rings. Furthermore, Mehmood et al. [
13] also provided the homomorphism theorems of
M-hazy rings with its induced fuzzifying convexities. Liu and Shi [
14] proposed
M-hazy lattices. Fan et al. [
15] introduced an
M-hazy
-semigroup.
Vector space has been the most widely studied and used in linear algebra theory. A vector space is a set of elements with a binary addition operator and a multiplication operator that has closure under these two operations over a field, all while satisfying a set of axioms. Vector spaces are the realm of linear combinations, also known as superpositions, weighted sums, and sums with coefficients. Such sums occur throughout mathematics, both pure and applied, including statistics, science, engineering, and economics. The key word is “linear”. Even when studying nonlinear phenomena, it is often useful to approximate with a simpler linear model. You can say that vector spaces are one of the great organizing tools of mathematics, helping reveal a structural similarity in a wide variety of topics found in such different contexts that they may seem completely different. Suppose you stand in front of a house. It is rather old but beautifully constructed of masonry that exhibits excellent craftsmanship. You point at a brick in one of the lower layers and ask “What is the need for this brick?” Short answer: it helps the structure. Long answer: it can be missed in the sense that the building won’t fall apart if you take it away, but it will damage it in various ways that will become clear if you live there for a couple of years. This house is a metaphor for mathematics. A vector space is a lot more than just a brick. It is one of the fundamental notions, and so is part of the foundation. The most fundamental notion is “Set,” and a vector space is one notch higher, a set with a specific structure. Can you do without it? Not if you want to do any serious mathematics. You can refine the structure to get topological vector space, metric vector space, complete vector space, normed vector space, and inner product vector space, each a refinement of the former. The beauty of this is that a refinement inherits all properties of its ancestor, so you are saved a lot of groundwork and can explore additional properties. The need for refinement is usually triggered by questions from physics or engineering. A nice example is Fourier analysis that fits smoothly in a Hilbert space structure.
Since Katsaras and Liu [
16] presented the notion of fuzzy vector spaces, many scientists and researchers explored its properties and obtained fruitful research such as [
17,
18,
19,
20,
21]. Mordeson [
22] defined bases of fuzzy vector spaces. Shi and Huang [
23] defined fuzzy bases and fuzzy dimension of fuzzy vector spaces. Nanda [
24,
25] introduced fuzzy fields and linear spaces. Malik and Mordeson [
26] defined fuzzy subfield of a field. Fang and Yan [
27] introduced the notion of
L-fuzzy topological vector spaces. Zhang and Xu [
28,
29] presented the concept of topological
L-fuzzifying neighborhood structures. Furthermore, Yan and Wu [
30] extended this concept by introducing fuzzifying topological vector spaces on completely distributive lattices. Wen et al. [
31] gave the degree to which an
L-subset of a vector space is an
L-convex set.
In the past few years, theory of convexity has emerged more and more important study for exceptional problems in many fields of applied mathematics. Since the 1950s, convexity theory has developed into several related theories. Van de Vel [
32] conducted an inventive investigation. His work was praised as excellence. An interesting question about the application part of convex theory attempts to include determining the computational complexity of convexity, pattern recognition problems, optimization, etc. Fuzzy set theory is an emerging discipline in different fields of abstract algebra such as topology and convexity theory, etc. Rosa [
33] firstly presented the notion of fuzzy convex spaces. Shi and Xiu [
34] proposed a new technique for the fuzzification of convex structures, which is described as
M-fuzzifying convex structures. In this technique, each subset of a set
X has a certain degree of convexity. Furthermore, Shi and Xiu [
35] gave the generalization of
L-convex structure and
M-fuzzifying convex structure by introducing
-fuzzy convex structure. In their approach, every
L-fuzzy subset can be considered as an
L-convex set to some extent. With repeated progress in the area of convexity theory, fuzzy convex structures have become a major research area such as [
36,
37,
38,
39,
40,
41,
42,
43,
44,
45,
46,
47,
48,
49,
50,
51,
52]. Pang and Xiu [
53] introduced the notion of lattice-valued interval operators and described their connection between
L-fuzzifying convex structures. Liu and Shi [
54] proposed
M-fuzzifying median algebra, which is obtained through fuzzy binary operation. This study provided the characteristics of
M-fuzzifying median algebra and
M-fuzzifying convex spaces. This work provided motivation to extend it on more algebraic structures like groups, rings, lattices, and vector spaces. Liu and Shi [
11] introduced
M-hazy groups by using the
M-hazy binary operation. Mehmood et al. [
12,
13] extended this idea by defining
M-hazy rings and obtained its induced fuzzifying convexities. By getting the motivations of these new proposed concepts through M-hazy operations, we proposed a new generalization of vector spaces over field based on
M-hazy binary operation, which is denoted as
M-hazy vector spaces over
M-hazy field.
The paper is organized as follows:
Section 2 consists of fundamental notions about completely residuated lattices, field and vector spaces,
M-hazy groups,
M-hazy rings, and
M-fuzzifying convex spaces. In
Section 3, the concept of
M-hazy vector space is defined and obtained its fundamental properties. In
Section 4, the concept of
M-hazy subspaces is introduced, and it has been shown that all the
M-hazy subspaces of
M-hazy vector space form a convex structure. In
Section 5, the linear transformation of
M-hazy vector spaces is introduced. Finally,
M-fuzzifying convex spaces are induced by
M-hazy subspaces of
M-hazy vector spaces.
Section 6 concludes the paper.
2. Preliminaries
This section contains the fundamental definitions about completely residuated lattices, fields, vector spaces, vector subspaces, M-hazy groups, M-hazy rings, and M-fuzzifying convexity.
All through this paper, represents a completely residuated lattice, and ≤ denotes the partial order of M. Assume P is a nonempty set and then denotes the least upper bound of K and the greatest lower bound of (resp., ) denotes the collection of all subsets (resp., M-subsets) on P. A family is up-directed provided for each that there exists a third element such that and are denoted by:
Definition 1 ([
55])
. Assume that is a function. ⋄ is defined to be a triangular norm (for short, t-norm) on if the following conditions holds:- (1)
- (2)
- (3)
implies
- (4)
for all
Definition 2 ([
55])
. Assume that is a function, and ⋄ is a t-norm in Then, → is defined to be the residuum of ⋄, if, for all Definition 3 ([
56])
. Assume that is a bounded lattice, where ⊥ represents the least element, ⊤ the greatest element, ⋄ is a t-norm on M, and → denotes the residuum of ⋄. Then, is said to be a residuated lattice. A residuated lattice is defined to be a completely residuated lattice if the primary lattice is complete. In addition, we define The proposition below shows properties of the implication operation.
Proposition 1 ([
57,
58])
. Assume is a completely residuated lattice. Then, for every , the below statements are valid:- (1)
- (2)
- (3)
- (4)
Definition 4 ([
11])
. Assume that is a function; then, * is defined to be an M-hazy operation on P, if the conditions given below hold:- (MH1)
we have
- (MH2)
Definition 5 ([
11])
. Assume is an M-hazy operation on a nonempty set Then, is defined to be an M-hazy group (in short, MHG) if the following conditions hold:- (MG1)
i.e., the M-hazy associative law holds.
- (MG2)
An element is said to be the left identity element of P, if for all
- (MG3)
An element is said to be the left inverse of u, if for each , and is denoted by
is defined to be an abelian MHG if the following condition holds:
- (MG4)
for all
Definition 6 ([
12])
. Assume and are the M-hazy addition operation and M-hazy multiplication operation on R, respectively. Then, is defined to be an M-hazy ring (in short, MHR) if the below conditions hold:- (MHR1)
is an abelian MHG.
- (MHR2)
is an M-hazy semigroup.
- (MHR3)
We now give the definition of
M-fuzzifying convex space, and we refer to Vel [
32] for all of the background on the convexity theory that may be required.
Definition 7 ([
34])
. A function is said to be an M-fuzzifying convexity on a nonempty set P if the below conditions hold:- (1)
;
- (2)
If is nonempty, then ;
- (3)
If , then .
Then, is said to be an M-fuzzifying convex space.
A function is defined as M-fuzzifying convexity preserving (M-CP, in short) given that for each ; is called M-fuzzifying convex-to-convex (M-CC, in short) provided that for each .
Definition 8 ([
22])
. A field is a set F with two operations, called addition and multiplication, which satisfy the following conditions:- (F1)
,
- (F2)
,
- (F3)
F contains an element 0 such that ,
- (F4)
For each , there is an element such that ,
- (F5)
,
- (F6)
,
- (F7)
,
- (F8)
F contains an element and such that ,
- (F9)
For each , there is an element such that ,
- (F10)
.
Definition 9 ([
22])
. A vector space is a nonempty set V over a field F, whose objects are called vectors equipped with two operations, called addition and scalar multiplication: for any two vectors in V and a scalar a in F defined by the mappings and , the following conditions are satisfied:- (V1)
,
- (V2)
There is a vector 0, called the zero vector, such that ,
- (V3)
For any vector u, there is a vector such that ,
- (V4)
,
- (V5)
,
- (V6)
,
- (V7)
,
- (V8)
3. M-Hazy Vector Spaces
In this section, we introduce the concept of M-hazy vector spaces over the M-hazy field.
We first introduce the concept of M-hazy field and give its properties, which are necessary to present the concept of M-hazy vector space.
Definition 10. Assume and are the M-hazy addition operation and M-hazy multiplication operation on F, respectively. Then, the 3-tuple is defined to be an M-hazy field (in short, MHF) if the below conditions hold:
- (MHF1)
is an abelian MHG.
- (MHF2)
is an abelian MHG.
- (MHF3)
Proposition 2. Assume that is an M-hazy field, and o and e are the additive and multiplicative identity elements of F, respectively. Then, ;
- (1)
.
- (2)
.
Proof. The proof is similar to the proof of Proposition 3.8 in [
11] so it is omitted. □
Proposition 3. In an M-hazy field , the left additive inverse of u is also the right additive inverse of u in . In addition, the left multiplicative inverse of u is also the right multiplicative inverse of u in . That is, the following conditions hold:
- (1)
- (2)
.
Proof. The proof is similar to the proof of Proposition 3.7 in [
11] so it is omitted. □
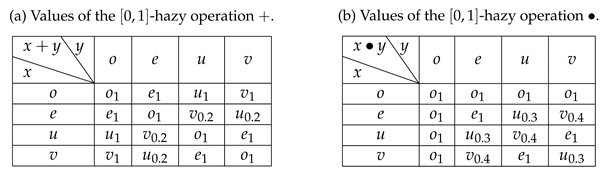
Example 1. Assume that is a set and assume . The mappings and are defined by the following tables:
It is easy to verify (MHF1), (MHF2), and (MHF3) analogous to Example 3.3 in [12]. Proposition 4. Assume that is an M-hazy field; then, the following equations hold:
- (1)
- (2)
Proof. The proof is similar to the proof of Proposition 3.11 and Corollary 3.12 in [
11] so it is omitted. □
We now present the concept of M-hazy vector space.
Definition 11. Assume is an M-hazy field and is an abelian M-hazy group. We define an M-hazy vector space over F as a quadruple , where ∘ is a mapping such that the following conditions hold:
- (MHV1)
and
- (MHV2)
and
- (MHV3)
and ,
- (MHV4)
and ,
Proposition 5. Assume and are the M-hazy operations under addition and under scalar multiplication on V, respectively; then, the following statements are equivalent for all , and .
- (MHV1)
, and , - (MHV1)
, and ,and - (MHV1)
then and - (MHV1)
If , , , , , then
Proof. (MHV1) ⇒ (MHV1) The proof is simple so it is omitted.
(MHV1
) ⇒ (MHV1
)
and
, we have
that is,
. A similar argument shows the other inequality.
(MHV1) ⇒ (MHV1) We need to only verify . According to (MHV1), we have , that is, , whence by (MH2), .
(MHV1
) ⇒ (MHV1)
and
, we have
and, by (MH2), we can complete the proof. □
Example 2. - (1)
The Euclidean space is an M-hazy vector space under the addition and scalar multiplication.
- (2)
The set of all polynomials of degree less than or equal to n is an M-hazy vector space under the addition and scalar multiplication of polynomials.
- (3)
The set of all matrices is an M-hazy vector space under the addition and scalar multiplication of matrices.
In the following discussion, we assume that the operation ⋄ in the completely residuated lattice M is ∧; that is, the lattice valued environment M is degenerated to complete Heyting algebra. We also assume that the smallest element ⊥ is prime in M.
Theorem 1. Assume that is an M-hazy vector space over an M-hazy field . Then, and :
- (1)
- (2)
- (3)
If then or .
Proof. We only prove (1). Assume
. By (MHV1)
and
, we have
When
, we have,
If , then by the condition (1) of Proposition 4, which is a contradiction. Hence, . □
4. M-Hazy Subspaces
In this section, we introduce the concept of M-hazy subspaces of M-hazy vector space.
Definition 12. Assume that is an M-hazy vector space over an M-hazy field . A nonempty subset W of V is called an M-hazy subspace of V if W itself is an M-hazy vector space over F.
Theorem 2. Assume W is a nonempty subset of an M-hazy vector space over an M-hazy field ; then, is an M-hazy subspace of over if and only if the following conditions hold:
- (1)
, we have ,
- (2)
and , we have ,
- (3)
, we have .
Proof. The proof is simple and omitted. □
Theorem 3. Assume W is a nonempty subset of an M-hazy vector space over an M-hazy field ; then, is an M-hazy subspace of over if and only if the following conditions hold:
- (1)
, we have ,
- (2)
and , we have .
Proof. The proof is similar to the proof of Theorem 4.4 in [
12] so it is omitted. □
Theorem 4. Assume W is a nonempty subset of an M-hazy vector space over an M-hazy field ; then, is an M-hazy subspace of over if and only if and , we have Proof. Assume that
W is an
M-hazy subspace of
V over an
M-hazy field
F. Suppose that
On the other hand,
and
by Theorem 3. Hence,
, which is a contradiction. Hence,
Conversely, suppose Since W is a nonempty subset of V and we know that (MH1) and (MH2) holds in V, thus it holds in W. Hence, and , we have and . Hence, In addition, and , we have by statement (1) of Theorem 1. Since and , we have ; thus, . Hence, by (MG2). Now, we already know that (MG3) holds in V, so it holds in W. Hence, , we have . Hence, W is an M-hazy subspace of V over F. □
Proposition 6. The intersection of a family of M-hazy subspace of an M-hazy vector space over an M-hazy field is an M-hazy subspace of .
Proof. Assume is an index set and is an M-hazy subspace of . Assume
(1) Since for each and K is a nonempty subset of V, we have .
(2) For every and for every , we obtain . Since W is an M-hazy subspace of V, we obtain and by Theorem 3. Since . This implies that there exists such that . This implies, for all , . Thus, we can obtain . Hence, . Similarly, . Hence, is an M-hazy subspace of . □
Proposition 7. The union of a nonempty up-directed family of M-hazy subspace of M-hazy vector space over an M-hazy field is an M-hazy subspace of . In particular, the union of a nonempty chain of M-hazy subspace of M-hazy vector space is an M-hazy subspace of .
Proof. Assume is an index set and is an M-hazy subspace of , where is an up-directed subfamily of . Let
(1) Clearly, N is a nonempty subset of V.
(2) For every and , there exists such that and . Since N is an up-directed family, then there exists such that ; this implies that . As is an M-hazy subspace of , we obtain and by Theorem 3. Hence, and . Hence, is an M-hazy subspace of . □
Based on the above results, we can draw an important and interesting conclusion; that is, we have the following result.
Proposition 8. All of the M-hazy subspaces of M-hazy vector space and the empty set form a convex structure.
5. Linear Transformation of M-Hazy Vector Spaces
In this section, we introduce the linear transformation of M-hazy vector spaces. We have also shown that M-fuzzifying convex spaces are induced by M-hazy subspace of M-hazy vector space.
Definition 13. Assume that and are two M-hazy vector spaces over an M-hazy field . Then, the mapping is called a linear transformation if the following conditions hold:
- (1)
- (2)
Definition 14. Assume V and W are two M-hazy vector spaces over an M-hazy field F, is a linear transformation, and is the additive identity element of W. Then, the kernel of τ, is determined by Example 3. - (1)
Assume that is an M-hazy vector space over an M-hazy field , the set and the whole M-hazy vector space V are M-hazy subspaces of V; they are called the trivial M-hazy subspaces of V.
- (2)
Assume and are the Euclidean spaces and is a linear transformation. The imageof τ is an M-hazy subspace of , and the inverse imageis an M-hazy subspace of .
Proposition 9. Assume the mapping is a linear transformation, and are two M-hazy vector spaces over an M-hazy field . Then, the following statements are valid:
- (1)
If J is an M-hazy subspace of V, then is an M-hazy subspace of W.
- (2)
If K is an M-hazy subspace of W, then is an M-hazy subspace of V containing .
Proof. (1) For all
, we have
. Then,
Then, by Theorem 3, it follows that is an M-hazy subspace of W.
(2) For all
, we have
. We find that
and
, since
K is an
M-hazy subspace of
W. Furthermore,
Consequently, is an M-hazy subspace of V.
Now, assume Since K is an M-hazy subspace of W, then , and so Hence, □
Proposition 10. Assume V and W are two M-hazy vector spaces over an M-hazy field F and is a linear transformation. Then, is an M-hazy subspace of V.
Proof. It is easy to see that is an M-hazy subspace of W. Then, by Proposition 9, we have that is an M-hazy subspace of V. □
The theorems below give an approach to induce M-fuzzifying convex spaces using M-hazy subspace of M-hazy vector space.
Theorem 5. Assume is an M-hazy vector space over an M-hazy field and define as follows: Then, is an M-fuzzifying convex space.
Proof. The proof is similar to the proof of Theorem 7 in [
13] so it is omitted. □
Theorem 6. Assume that the mapping is a linear transformation, and are two M-hazy vector spaces over an M-hazy field ; then, is an M-CP mapping.
Proof. The proof is similar to the proof of Theorem 8 in [
13] so it is omitted. □
Theorem 7. Assume the mapping is a linear transformation, and are two M-hazy vector spaces over an M-hazy field ; then, is an M-CC mapping.
Proof. Since the mapping is a linear transformation if the following conditions hold:
- (1)
- (2)
Then, for all
, we have
This implies that is an M-CC mapping. □
6. Conclusions
Liu and Shi [
11] introduced
M-hazy groups by using the
M-hazy binary operation. Mehmood et al. [
12,
13] extended this idea by defining
M-hazy rings and obtained its induced fuzzifying convexities. By getting the motivations of these new proposed concepts through M-hazy operations, we proposed a new generalization of vector spaces over field based on
M-hazy binary operation, which is denoted as
M-hazy vector spaces over
M-hazy field. In addition, by using the completely residuated lattice valed logic, some important properties of
M-hazy field,
M-hazy vector space, and
M-hazy subspace are introduced. Based on these properties, it is shown that an
M-hazy subspace of
M-hazy vector space forms a convex structure. In addition, the linear transformation of
M-hazy vector space is defined and proves its important results. The convexity of the
M fuzzy set on the set
P is the
M fuzzy set on the power set with certain properties. Therefore, to a certain extent, each subset of
P can be regarded as a convex set. Finally, considering the importance of this fact, a method is given that uses the
M-hazy subspace of
M-hazy vector space to induce the
M-fuzzifying convex space.
The possible directions for the future work could be M-hazy modules, bases, dimensions of M-hazy vector spaces, M-hazy topological vector spaces, and other fuzzy algebra.