Analysis of Re-Tensioning Time of Anchor Cable Based on New Prestress Loss Model
Abstract
1. Introduction
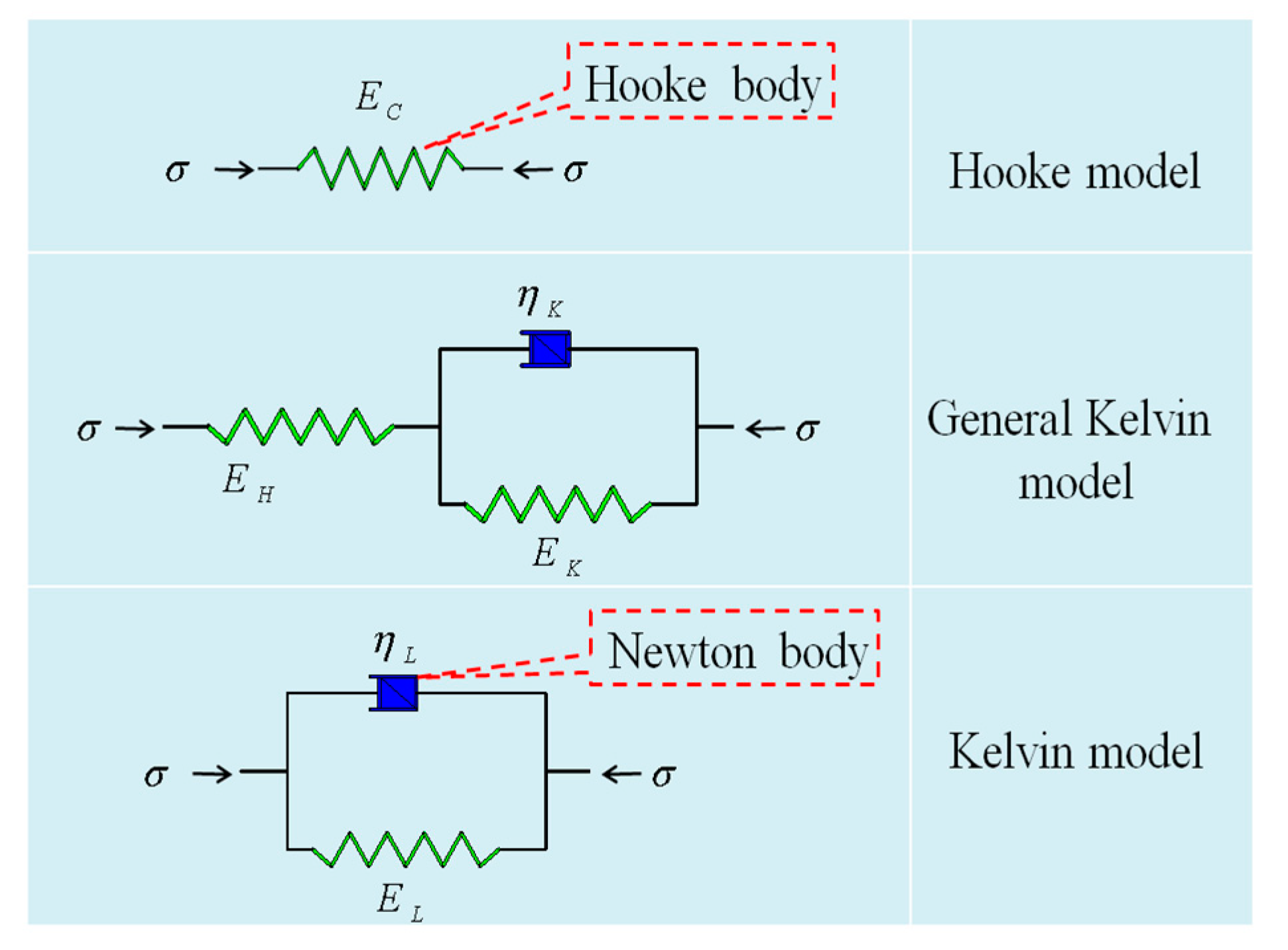
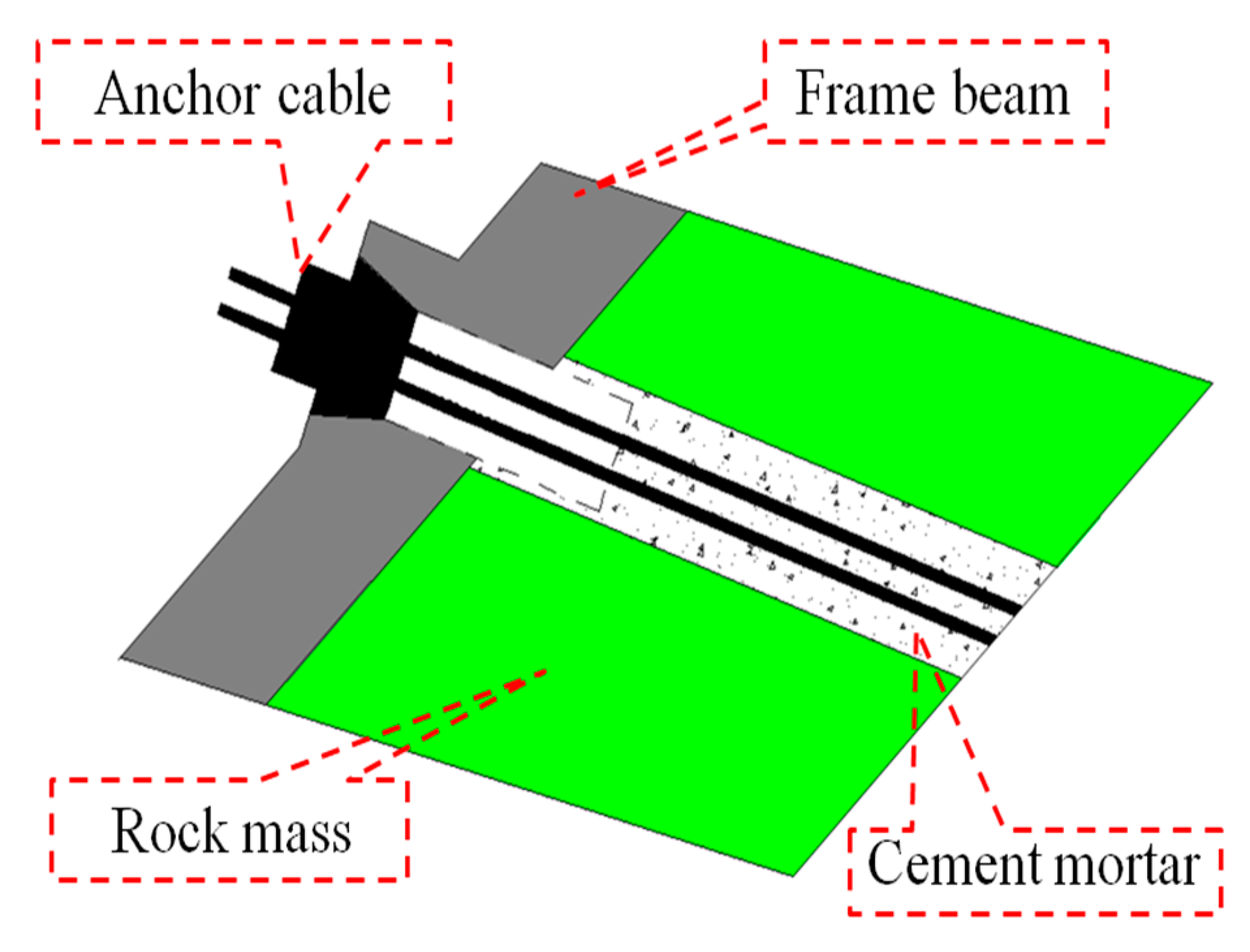
2. Prestress Loss Model of Anchor Cable Considering the Action of Frame Beam
2.1. Analysis Model of Anchor Cable
2.2. Analysis Model of Rock Mass
2.3. Analysis Model of Frame Beam
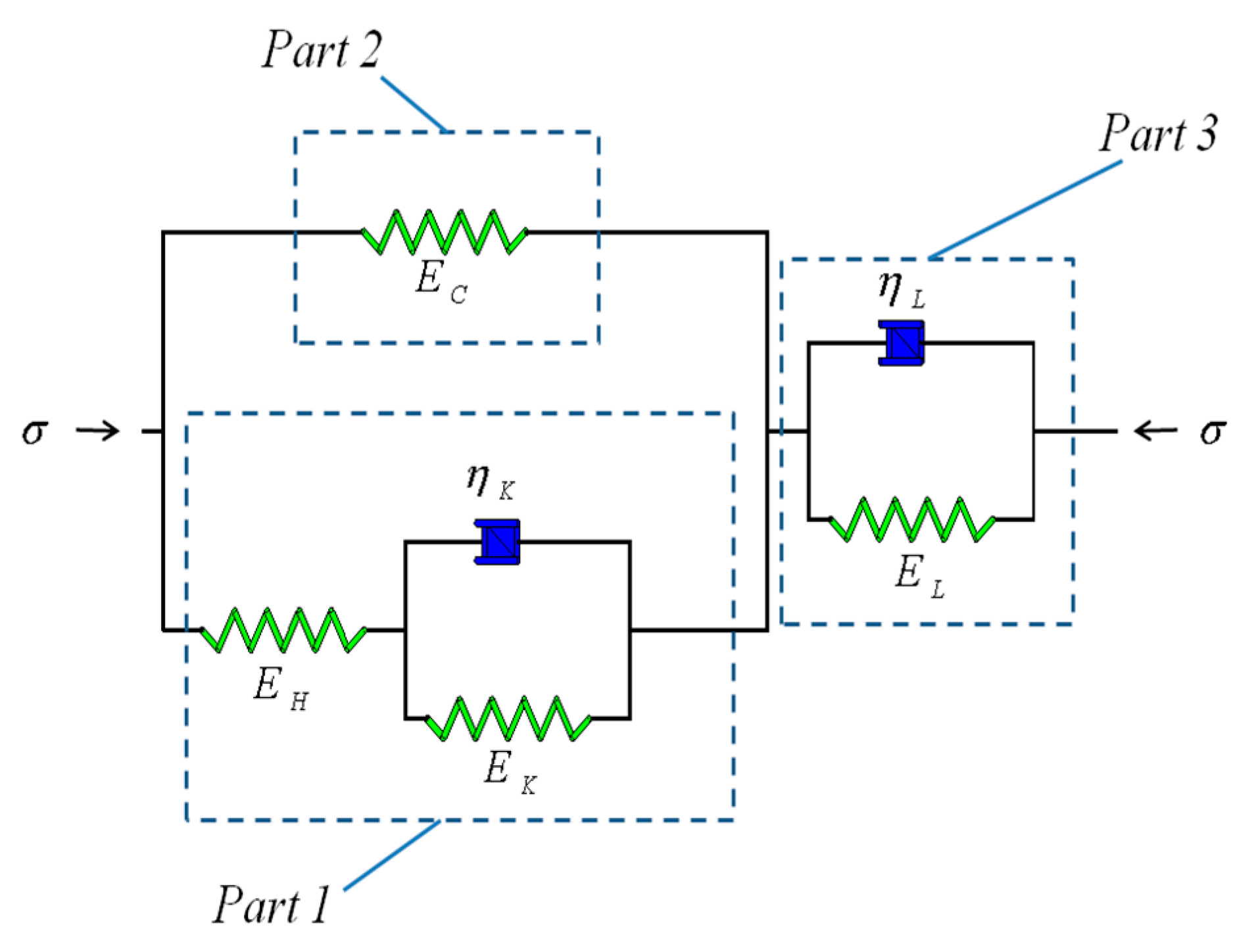
2.4. Establishment of Prestress Loss Model of Anchor Cable
2.5. Derivation of Model Calculation Formula
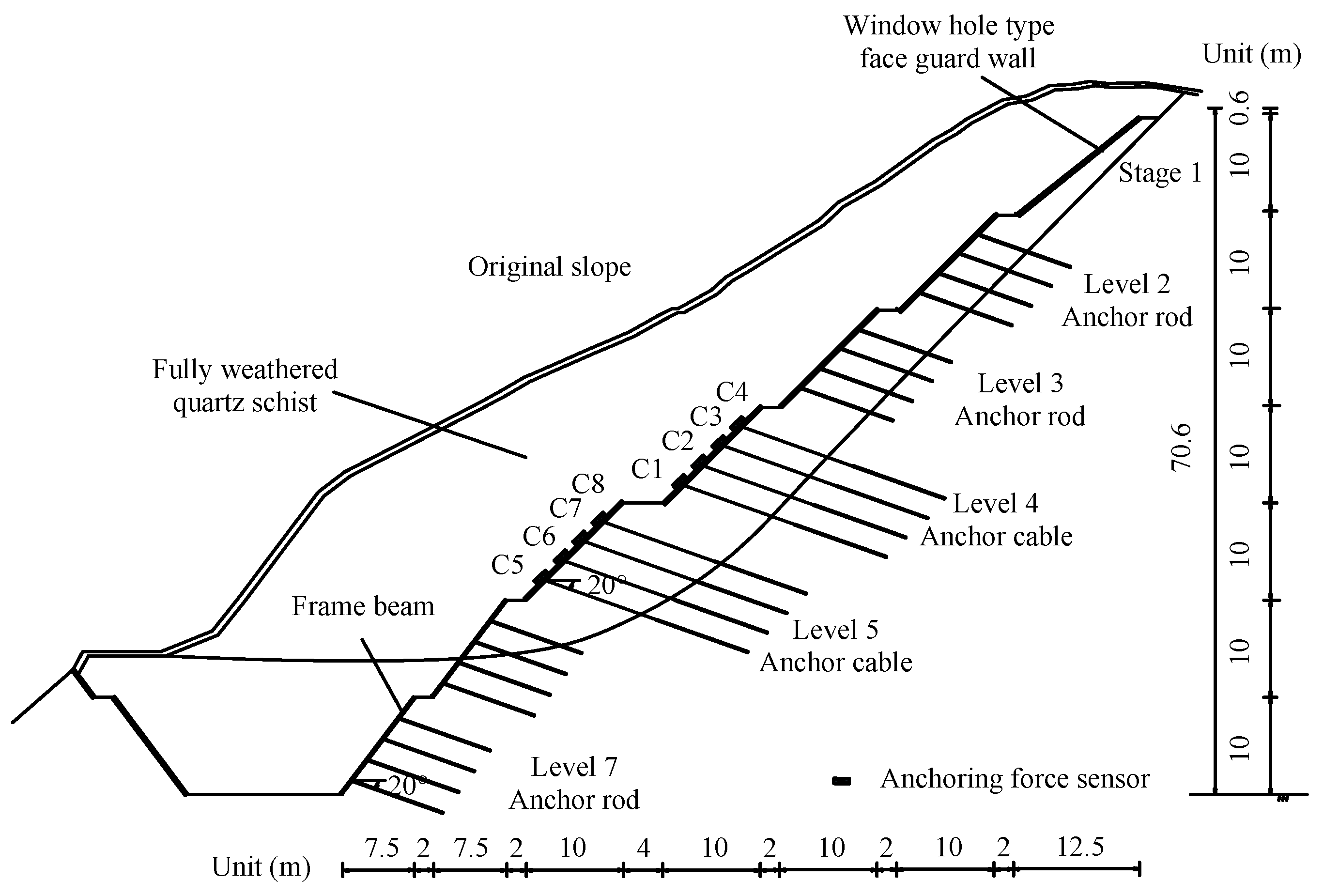
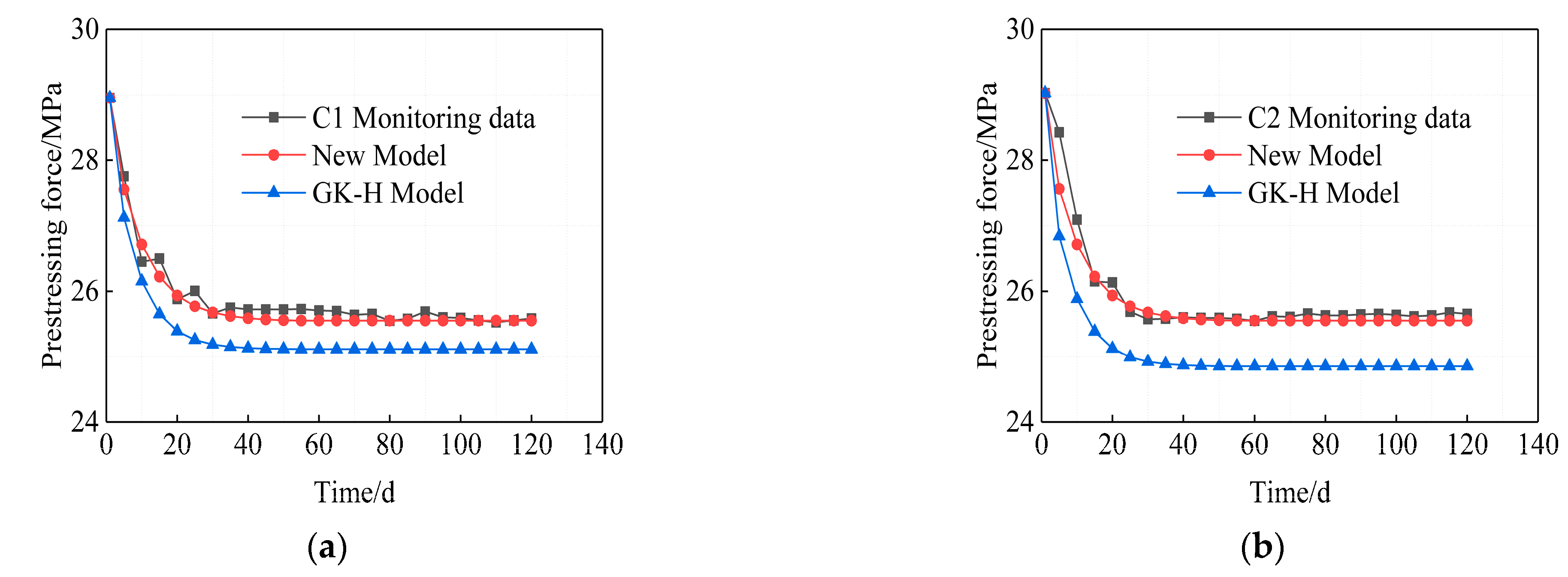
3. Model Validation Based on On-Site Monitoring Data
3.1. On-Site MonitoringTest
3.2. Model Validation
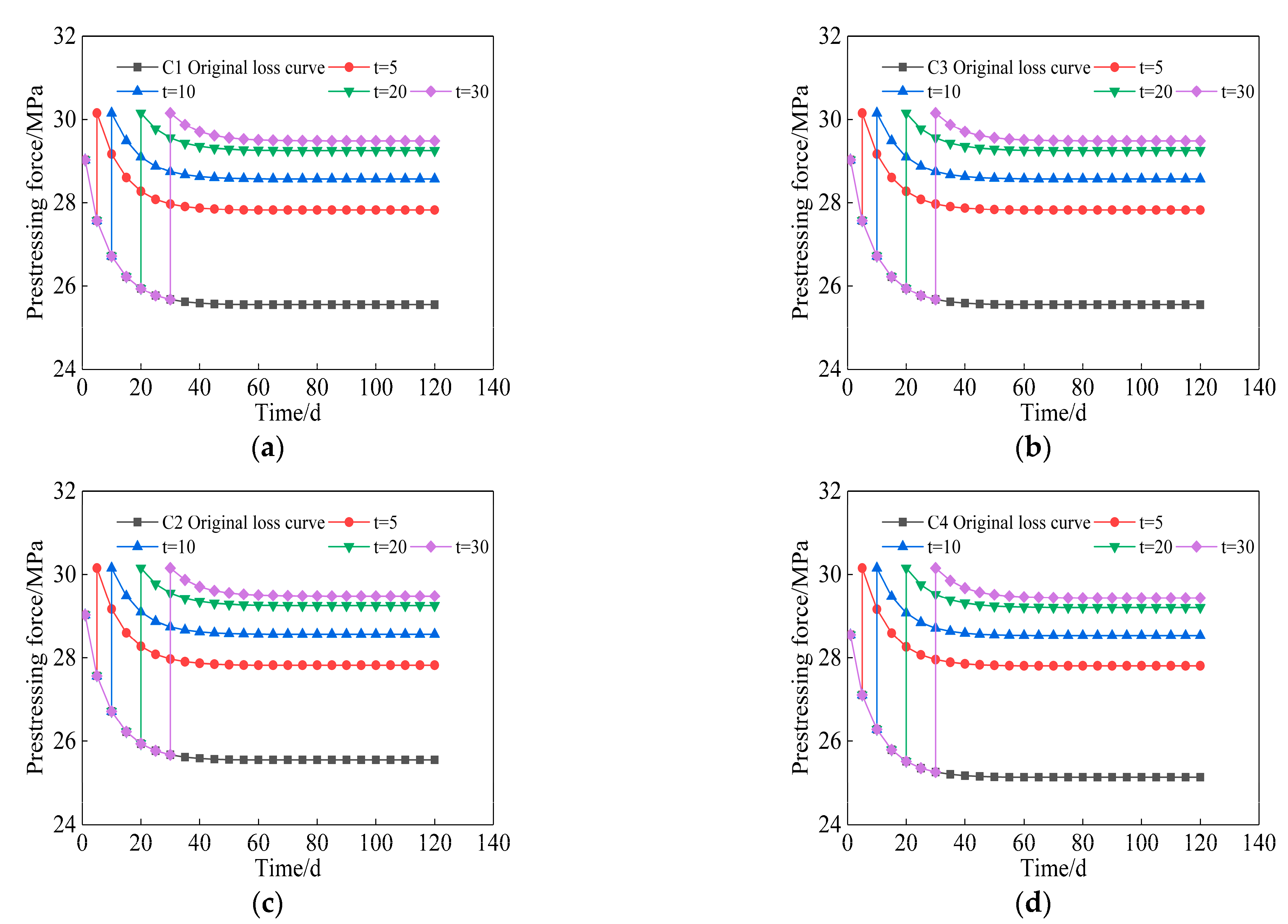
4. Re-Tensioning Time of Anchor Cable Prestress
5. Conclusions
- (1)
- The frame beam is the guarantee for the uniform stress of the rock mass of the anchored slope, and the role of the frame beam should not be ignored in the stress analysis of the anchored slope, in view of the interaction among the anchor cable, the frame beam and the rock mass, the new prestress loss model of the anchor cable is established, and compared with the field monitoring data and existing model, the accuracy of the new model is verified.
- (2)
- Based on the new established prestress loss model of the anchor cable, the prestress compensation time of anchor cable is studied. Although theoretically speaking, the later the re-tensioning time is, the greater the stable value of prestress after the re-tensioning of anchor cable is, however, there is little difference in the stable value of prestress when the anchor cable is re-tensioned at each time point after 20 days of the construction completed. It can be considered that the ideal effect of prestress compensation all can be achieved when the anchor cable is re-tensioned at each time point after 20 days of the construction completed.
- (3)
- In the multi-anchor supporting slope, the loss of prestress of each anchor cable is not the same, when the anchor cables with different prestress loss are re-tensioned, the effect of prestress compensation will also be different. The greater the original loss of the anchor cable is, the greater the prestress compensation ratio is, which means the better the prestress compensation effect is.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ersoz, T.; Topal, T. Assessment of rock slope stability with the effects of weathering and excavation by comparing deterministic methods and slope stability probability classification (SSPC). Environ. Earth Sci. 2018, 77. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Y.M.; Zhang, K.B.; Yu, H.; Tao, Z.Y. Field investigation and numerical study of a siltstone slope instability induced by excavation and rainfall. Landslides 2020, 17, 1485–1499. [Google Scholar] [CrossRef]
- Ma, K.; Xu, N.W.; Liang, Z.Z. Stability Assessment of the Excavated Rock Slope at the Dagangshan Hydropower Station in China Based on Microseismic Monitoring. Adv. Civ. Eng. 2018, 2018. [Google Scholar] [CrossRef]
- Najib, N.; Fukuda, D.; Kodama, J.-I.; Fujii, Y. The Deformation Modes of Rock Slopes due to Excavation in Mountain-Type Mines. Mater. Trans. 2015, 56, 1159–1168. [Google Scholar] [CrossRef]
- Xu, P.; Hatami, K.; Bao, J.J.; Li, T. Bearing capacity and failure mechanisms of two-tiered reinforced soil retaining walls under footing load. Comput. Geotech. 2020, 128, 17. [Google Scholar] [CrossRef]
- Wang, X.; Shrestha, R.; Li, X.; Mandal, A.K. Design Theory and Method of Geo-Synthetic Reinforced Soil Retaining Wall Combined with a Gravity Retaining Wall or Full Height Rigid Facing. Geotech. Geol. Eng. 2021, 39, 2075–2086. [Google Scholar] [CrossRef]
- Munoz-Medina, B.; Ordonez, J.; Romana, M.G.; Lara-Galera, A. Typology Selection of Retaining Walls Based on Multicriteria Decision-Making Methods. Appl. Sci. 2021, 11, 1457. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, G.; Chang, Z.; Wen, L.; Gao, W. Failure Analysis of a Highway Cut Slope with Anti-Slide Piles. Geofluids 2021, 2021. [Google Scholar] [CrossRef]
- Zhang, J.W.; Wang, X.J.; Wang, H.; Qin, H.Y. Model Test and Numerical Simulation of Single Pile Response under Combined Loading in Slope. Appl. Sci. 2020, 10, 6140. [Google Scholar] [CrossRef]
- Yuan, C.; Fan, L.; Cui, J.F.; Wang, W.J. Numerical Simulation of the Supporting Effect of Anchor Rods on Layered and Nonlayered Roof Rocks. Adv. Civ. Eng. 2020, 2020, 14. [Google Scholar] [CrossRef]
- Puccinelli, M. Considerations on the bond strenght value in the anchor rods design. Gallerie Gd. OpereSotter. 2018, 127, 29–35. [Google Scholar]
- An, C.-L.; Liang, Y.; Wang, L.-Q.; Deng, S.; Sun, Z.-H.; Fan, B.-Q.; Zheng, L.-B. Three-dimensional optimization design for the direction angle of anchor cable reinforcement in wedge rock slope. Rock Soil Mech. 2020, 41, 2765–2772. [Google Scholar] [CrossRef]
- Li, J.; Chen, S.X.; Yu, F.; Jiang, L.F.; Dai, Z.J. Discussion on mechanism of reinforcing high and steep slope with prestressed anchor cable. Rock Soil Mech. 2020, 41, 707–713. [Google Scholar] [CrossRef]
- Fan, Q.; Zhu, H.; Geng, J. Monitoring result analyses of high slope of five-step ship lock in the Three Gorges Project. J. Rock Mech. Geotech. Eng. 2015, 7, 199–206. [Google Scholar] [CrossRef]
- Sung, H.-J.; Tan Manh, D.; Kim, J.-M.; Kim, Y.-S. Long-term monitoring of ground anchor tensile forces by FBG sensors embedded tendon. Smart Struct. Syst. 2017, 19, 269–277. [Google Scholar] [CrossRef]
- Kim, Y.-S.; Sung, H.-J.; Kim, H.-W.; Kim, J.-M. Monitoring of tension force and load transfer of ground anchor by using optical FBG sensors embedded tendon. Smart Struct. Syst. 2011, 7, 303–317. [Google Scholar] [CrossRef]
- Lu, G.R.; Wang, Q.B.; Li, X.; Wang, L. Study and Practice of Controlling Anchorage Force Loss of Prestressed Anchor Rope. Appl Mech Mater. 2012, 166–169, 1663–1668. [Google Scholar] [CrossRef]
- Wang, Q.B.; Zhang, C.; Wang, H. Study of coupling effect between anchorage force loss of prestressed anchor cable and rock and soil creep. Rock Soil Mech. 2014, 35, 2150–2156. (In Chinese) [Google Scholar] [CrossRef]
- Chen, G.; Chen, T.; Chen, Y.; Huang, R.; Liu, M. A new method of predicting the prestress variations in anchored cables with excavation unloading destruction. Eng. Geol. 2018, 241, 109–120. [Google Scholar] [CrossRef]
- Chen, T.; Chen, G.Q.; Huang, R.Q.; Liu, M. A model of anchorage force loss of anchor cable during high slope strong unloading. Rock Soil Mech. 2018, 39, 4125–4132. (In Chinese) [Google Scholar] [CrossRef]
- Wang, G.F.; Qing, L.; Lu, L.; Cao, Z.; Wang, W. A Coupled Model Research of Anchor Prestress Loss Considering the Relaxation Characteristics of Anchor. Chin. J. Undergr. Space Eng. 2017, 13, 1585–1591. (In Chinese) [Google Scholar]
- Trzeciak, M.; Sone, H.; Dabrowski, M. Long-term creep tests and viscoelastic constitutive modeling of lower Paleozoic shales from the Baltic Basin, N Poland. Int. J. Rock Mech. Min. Sci. 2018, 112, 139–157. [Google Scholar] [CrossRef]
- Liu, H.Z.; Xie, H.Q.; He, J.D.; Xiao, M.L.; Zhuo, L. Nonlinear creep damage constitutive model for soft rocks. Mech. Time-Depend. Mater. 2017, 21, 73–96. [Google Scholar] [CrossRef]
- Zhu, W.; Dai, G.; Gong, W. Study on Cyclic Cumulative Deformation Characteristics and the Equivalent Cyclic Creep Model of Soft Clay. Math. Probl. Eng. 2021, 2021. [Google Scholar] [CrossRef]
- Zhang, Q.; Song, Z.; Wang, J.; Zhang, Y.; Wang, T. Creep Properties and Constitutive Model of Salt Rock. Adv. Civ. Eng. 2021, 2021. [Google Scholar] [CrossRef]
- Shi, K.Y.; Wu, X.P.; Liu, Z.; Dai, S.L. Coupled calculation model for anchoring force loss in a slope reinforced by a frame beam and anchor cables. Eng. Geol. 2019, 260, 9. [Google Scholar] [CrossRef]

/GPa | /GPa | /GPa | /GPa | /GPa.day |
|---|---|---|---|---|
| 8.23 | 28 | 41.91 | 57.5 | 597 |
| Anchor Cable Number | Time /d | Stable Value of Original Anchor Cable Prestress /MPa | Stable Value of Anchor Cable Prestress after Re-tensioning /MPa | Prestress Compensation Ratio |
|---|---|---|---|---|
| C1 | 5 | 25.55 | 27.76 | 1.086 |
| 10 | 25.55 | 28.50 | 1.115 | |
| 20 | 25.55 | 29.18 | 1.142 | |
| 30 | 25.55 | 29.41 | 1.151 | |
| C2 | 5 | 25.75 | 27.82 | 1.080 |
| 10 | 25.75 | 28.57 | 1.110 | |
| 20 | 25.75 | 29.25 | 1.136 | |
| 30 | 25.75 | 29.48 | 1.144 | |
| C3 | 5 | 25.16 | 27.80 | 1.105 |
| 10 | 25.16 | 28.54 | 1.134 | |
| 20 | 25.16 | 29.21 | 1.161 | |
| 30 | 25.16 | 29.44 | 1.170 | |
| C4 | 5 | 25.13 | 27.81 | 1.107 |
| 10 | 25.13 | 28.53 | 1.135 | |
| 20 | 25.13 | 29.21 | 1.162 | |
| 30 | 25.13 | 29.43 | 1.171 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, K.; Wu, X.; Tian, Y.; Xie, X. Analysis of Re-Tensioning Time of Anchor Cable Based on New Prestress Loss Model. Mathematics 2021, 9, 1094. https://doi.org/10.3390/math9101094
Shi K, Wu X, Tian Y, Xie X. Analysis of Re-Tensioning Time of Anchor Cable Based on New Prestress Loss Model. Mathematics. 2021; 9(10):1094. https://doi.org/10.3390/math9101094
Chicago/Turabian StyleShi, Keyou, Xiaoping Wu, Yurong Tian, and Xiaotian Xie. 2021. "Analysis of Re-Tensioning Time of Anchor Cable Based on New Prestress Loss Model" Mathematics 9, no. 10: 1094. https://doi.org/10.3390/math9101094
APA StyleShi, K., Wu, X., Tian, Y., & Xie, X. (2021). Analysis of Re-Tensioning Time of Anchor Cable Based on New Prestress Loss Model. Mathematics, 9(10), 1094. https://doi.org/10.3390/math9101094






