Orbit Entropy and Symmetry Index Revisited

Abstract

The size of the orbits or similar vertices of a network provides important information regarding each individual component of the network. In this paper, we investigate the entropy or information content and the symmetry index for several classes of graphs and compare the values of this measure with that of the symmetry index of certain graphs.

1. Introduction

Graph entropy measures were first introduced in the study of biological and chemical systems, with Rashevsky [1] and Mowshowitz [2,3,4,5] making the main contributions. In particular, Mowshowitz [5] interpreted the topological information content of a graph, such as its entropy measure. Since then, various graph entropy measures have been defined to investigate the structural properties of graphs [6,7,8] as well as [9,10,11,12,13].

A small-world graph [14,15] is a special type of graph in which the neighbors of any given vertex are likely to be neighbors of each other, but the probability that a vertex is the neighbor of another one is low and most vertices can be reached from each other by a few steps.

Adaptive networks are suitable to model the complex treatment represented by various real-world systems as well as to carry out decentralized information processing tasks such as drifting conditions and learning from online streaming data, see [16]. On the other hand, signal processing on graphs extends concepts and techniques from traditional signal processing to data indexed by generic graphs, see [17]. For example, neural networks and graph signal processing have emerged as important actors in data-science applications dealing with complex datasets, see [18].

This paper has two objectives. In Section 1, we investigate the automorphism group of some classes of graphs and verify their entropies and symmetry indices. In this way, some practical graph automorphism group decompositions are created that constitute the whole structure of graph automorphism groups.

In Section 2, we state concepts we use tp perform our analysis. We prove that there are several classes of graphs whose symmetry index is greater or equal than the orbit-entropy measure, while many other classes have a greater orbit entropy.

2. Entropy Measure and Symmetry Index of Graphs

Let $G=(V(G),E(G))$ be a connected graph. An automorphism is a permutation $\alpha$ on the set of vertices of G with the property that both $\alpha$ and ${\alpha }^{-1}$ preserve the vertex adjacency. In other words, for two vertices $u,v\in V(G)$ a permutation $\alpha$ on $V(G)$ is an automorphism, when $uv\in E(G)$ if and only if $\alpha (u)\alpha (v)\in E(G)$, where $\alpha (u)$ is the image of vertex u. The set of all automorphisms under the composition of maps forms a group denoted by $\mathrm{Aut}(\mathrm{G})$.

For example consider the cycle graph $C_3$ in Figure 1. The line of symmetry colored by red is denoted by permutation $(2,3)$. Hence, the permutations correspond to blue and green lines are respectively denoted by $(1,2)$ and $(1,3)$. A clockwise rotation equal ${120}^{\circ }$ around the middle point of $C_3$ is denoted by $(1,2,3)$ and equal ${240}^{\circ }$ by $(1,3,2)$. All of these permutations preserve the vertex adjacency and thus are automorphisms. Note that a ${360}^{\circ }$ rotation preserves the figure unchanged and we denote this permutation by $()$. Hence, the automorphism group of $C_3$ has 6 elements which is $Aut(C_3)=\{(),(1,2),(1,3),(2,3),(1,2,3),(1,3,2)\}$.

For any vertex $u\in V(G)$ an orbit of G containing u is defined as $u^G=\mathcal{O}(u)=\{\alpha (u):\alpha \in Aut(G)\}$. We say G is vertex-transitive if it has only one orbit. Equivalently, a graph is vertex-transitive if for two vertices $u,v\in V(G)$ there is an automorphism $\sigma \in Aut(G)$ such that $\sigma (u)=v.$

The orbits of the automorphism group of a graph form a partition of the vertices of the graph. This decomposition introduces the symmetry structure of the graph, and the orbit entropy measure obtained from the automorphism group provides an index of the complexity of the graph relative to the symmetry structure.

Mowshowitz [2] defined the topological information content, which is a classical graph entropy measure, as

$${\displaystyle {\mathrm{I}}_{\mathrm{a}}(\mathrm{G})=-\sum _{\mathrm{i}=1}^{\mathrm{k}}\frac{|{\mathrm{O}}_{\mathrm{i}}|}{|\mathrm{V}|}log(\frac{|{\mathrm{O}}_{\mathrm{i}}|}{|\mathrm{V}|}),}$$

where $O_i$ ($1\le i\le k$) are orbits of G under the action of automorphism group on the set of vertices. The collection of k orbits $\{O_1,\dots ,O_k\}$ defines a finite probability scheme in an obvious way. This measure is addressed to the problem of measuring the relative complexity of graphs. The idea of measuring the information content of a graph was first presented in [1]. Mowshowitz and Dehmer [19] defined the symmetry index $S(\mathrm{G})$ as

$$\begin{array}{ccc}\hfill \mathrm{S}(\mathrm{G})& =& (logn-{\mathrm{I}}_{\mathrm{a}}(\mathrm{G}))+log|\mathrm{Aut}(\mathrm{G})|\hfill \\ & =& {\displaystyle \frac{1}{n}(\sum _{i=1}^k|O_i|log|O_i|)+log|\mathrm{Aut}(\mathrm{G})|.}\hfill \end{array}$$

2.1. Relationship between Symmetry Index and Orbit Entropy

Consider a permutation $\sigma$ on the set $X=\{x_1,\dots ,x_n\}$. Then the set of all elements that $\sigma$ moves is called the support of $\sigma$. Two permutations $\sigma$ and $\gamma$ are disjoint if their supports have no intersection. Consider S to be a set of generators of $\mathrm{Aut}(\mathrm{G})$, $e\notin S$ and $S=S_1\cup \dots \cup S_m$ to be the partition of S, where $S_i$ cannot be decomposed into smaller support-disjoint subsets. Therefore, we have the following.

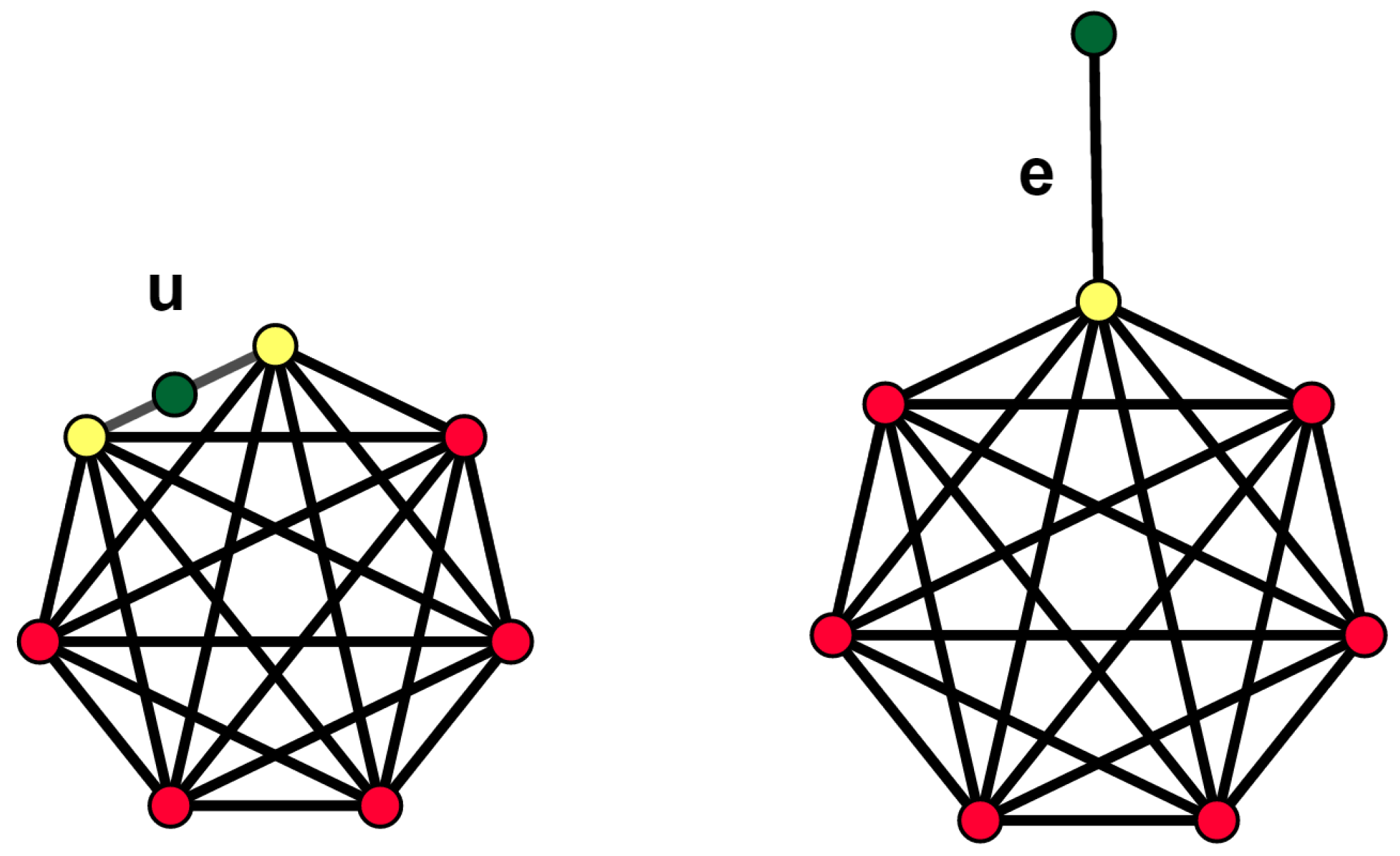
Theorem 1.

Ref. [20] If $A_i=\langle S_i\rangle$, then $\mathrm{Aut}(\mathrm{G})\cong {\mathrm{A}}_1\times {\mathrm{A}}_2\times \dots \times {\mathrm{A}}_{\mathrm{m}}$.

Consider $A=\mathrm{Aut}(\mathrm{G})$. For a vertex v in $V(G)$, $A_v$ denotes the stabilizer subgroup of G containing all automorphisms that fix the vertex v. Similarly, for a vertex u of G, its orbit is a set containing all $\alpha (u)$, where $\alpha$ is an automorphism of $Aut(G)$.

Theorem 2.

Ref. [21] (Orbit-stabilizer Theorem) Let A be a permutation group acting on a set Ω and u be an arbitrary point in the set Ω. Then $|A|=|A_u||u^A|$.

Definition 1.

Harary [22] defined the corona product $G_1\circ G_2$ of two graphs $G_1$ and $G_2$ as a new graph G obtained by taking one copy of $G_1$ (which has $p_1$ vertices) together with $p_1$ copies of $G_2$ and then joining the ith vertex of $G_1$ to all vertices in the ith copy of $G_2$; see Figure 2.

Suppose A and B are two finite groups in which B acts on the set X. The wreath product of A and B (denoted by $A\wr B$) is a group with the underline set

$$A\wr B=\{(f;h)|f:X\to Aisafunction,h\in B\}.$$

The group operation can be defined as $(f_1;h_1)(f_2;h_2)=(g;h_1{h}_2)$, where for each element $i\in X$, we obtain

$$g(i)=f_1(i)f_2(i^{h_1}).$$

Wreath product is one of the most significant combinatorial buildings in the field of permutation group theory. The next theorem shows that the automorphism group of a big graph can be constructed from wreath product of automorphism groups of its subgraphs.

Theorem 3.

Ref. [22] The automorphism group of the corona product $G_1\circ G_2$ of two graphs is isomorphic to the wreath product $\mathrm{Aut}({\mathrm{G}}_1)\wr \mathrm{Aut}({\mathrm{G}}_2)$ if and only if either $G_1$ or $G_2$ has no isolated vertices.

Let G and H be two disjoint graphs, where $V(G)=\{u_1,\dots ,u_n\}$, and let $u\in V(G)$ and $v\in V(H)$. The splice of two graphs G and H by vertices u and v, denoted by $G•H(u,v)$, is a new graph constructed by identifying two vertices u and v in the union of G and H [23]. Similarly, let K be a graph constructed by G and n copies of graph H and then splicing vertex $u_i$ of G by vertex v of the ith copy of H. The following result is contained in [24,25,26,27,28].

Theorem 4. (Balasubramanian)

Let K be as defined above. Then $\mathrm{Aut}(\mathrm{K})\cong \mathrm{Aut}(\mathrm{G})\wr \mathrm{Aut}(\mathrm{H})$.

Here, the orbit-entropy measure and the symmetry index of some classes of well-known graphs are determined, followed by a comparison of these measures for all the graphs. The results show that whether a measure is greater or smaller cannot be predicted in advance, and it depends on the structure of the graph or equivalently the structure of its automorphism group.

Example 1.

It is demonstrated that the orbit entropy of the path graph $P_n$ is greater than its symmetry index, whereas for the wheel graph $W_n$, the star graph $S_n$, and the complete bipartite graph $K_{m,n}$, the orbit entropy is less than the symmetry index. To do this, consider the following cases:

(a) 

If n is odd, then $\mathrm{Aut}({\mathrm{P}}_{\mathrm{n}})\cong {\mathcal{Z}}_2$ and $P_n$ has $\frac{n-1}{2}$ orbits of size two and a singleton orbit. Hence, $\mathrm{S}({\mathrm{P}}_{\mathrm{n}})=\frac{2\mathrm{n}-1}{\mathrm{n}}$ and ${\mathrm{I}}_{\mathrm{a}}({\mathrm{P}}_{\mathrm{n}})=log\mathrm{n}-\frac{\mathrm{n}-1}{\mathrm{n}}$. This means that if $n\ge 7$, then ${\mathrm{I}}_{\mathrm{a}}({\mathrm{P}}_{\mathrm{n}})>\mathrm{S}({\mathrm{P}}_{\mathrm{n}})$.

(b) 

If n is even, then $\mathrm{Aut}({\mathrm{P}}_{\mathrm{n}})\cong {\mathcal{Z}}_2$ and G has $n/2$ orbits of order 2. Hence, $\mathrm{S}(\mathrm{G})=2$ and ${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})=log\mathrm{n}-1$.

(c) 

If $G=S_n$, then $\mathrm{Aut}(\mathrm{G})\cong {\mathcal{S}}_{\mathrm{n}-1}$ and G has a singleton orbit together with an orbit of size $n-1$. Thus,

$$\mathrm{S}(\mathrm{G})=\frac{\mathrm{n}-1}{\mathrm{n}}log(\mathrm{n}-1)+log((\mathrm{n}-1)!)$$

and

$${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})=log\mathrm{n}-\frac{\mathrm{n}-1}{\mathrm{n}}log(\mathrm{n}-1).$$

(d) 

For the wheel graph $W_n$, it is well known that $\mathrm{Aut}({\mathrm{W}}_{\mathrm{n}})\cong {\mathrm{D}}_{2(\mathrm{n}-1)}$, and consequently it has a singleton orbit and an orbit of size $n-1$. Hence,

$$\mathrm{S}({\mathrm{W}}_{\mathrm{n}})=\frac{2\mathrm{n}-1}{\mathrm{n}}log(\mathrm{n}-1)+1\mathrm{and}{\mathrm{I}}_{\mathrm{a}}({\mathrm{W}}_{\mathrm{n}})={\mathrm{I}}_{\mathrm{a}}({\mathrm{S}}_{\mathrm{n}}).$$

(e) 

If $G=K_{m,n}$, then $\mathrm{Aut}(\mathrm{G})\cong {\mathcal{S}}_{\mathrm{n}}\times {\mathcal{S}}_{\mathrm{m}}$, and consequently G has two orbits of sizes m and n. Thus,

$$\mathrm{S}(\mathrm{G})=\frac{\mathrm{m}}{\mathrm{n}+\mathrm{m}}log\mathrm{m}+\frac{\mathrm{n}}{\mathrm{n}+\mathrm{m}}log\mathrm{n}+log(\mathrm{m}!\mathrm{n}!)$$

and

$$\begin{array}{ccc}\hfill I_a(G)& =& log(m+n)-\frac{m}{n+m}log(\frac{m}{n+m})\hfill \\ & -& \frac{n}{n+m}log(\frac{n}{n+m}).\hfill \end{array}$$

This completes the proof.

Theorem 5.

Let G be a graph with an automorphism group containing the identity element alone. Then ${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})>\mathrm{S}(\mathrm{G})$.

Proof. 

Assume that G is a graph on n vertices and $\mathrm{Aut}(\mathrm{G})\cong \mathrm{id}$. Hence, G has n orbits, giving

$${\displaystyle \mathrm{S}(\mathrm{G})=\frac{1}{\mathrm{n}}\sum _{\mathrm{i}=1}^{\mathrm{n}}1log1+log1=0}$$

and ${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})=log\mathrm{n}$. □

If the automorphism group of G acts transitively on $V(G)$, then it is concluded that G is vertex-transitive. Equivalently, a vertex-transitive graph has only one orbit. Similarly, an edge-transitive graph can be defined.

Theorem 6.

If G is vertex-transitive, then ${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})<\mathrm{S}(\mathrm{G})$.

Proof. 

Because G has only one orbit, $\mathrm{S}(\mathrm{G})=log(\mathrm{n}|\mathrm{Aut}(\mathrm{G})|)$ and $I_a(G)=-\frac{n}{n}log1=0$. Therefore, ${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})<\mathrm{S}(\mathrm{G})$. □

The Cayley graph $G=Cay(A,S)$ is a graph constructed from a group A and a subset $\varnothing \ne S\subseteq A$, where $e\notin S$ and $S^{-1}=S$. The vertex set of graph G comprises the elements of A, and two vertices a and b are adjacent if and only if $b^{-1}a\in S$.

Corollary 1.

If G is a Cayley graph or $G\cong C_n,K_n$, then the symmetry index of G is greater than its orbit-entropy measure.

Proof. 

It is well known that each Cayley graph is vertex-transitive [29], and the assertion follows. On the other hand, it is well known that $\mathrm{Aut}({\mathrm{C}}_{\mathrm{n}})\cong {\mathrm{D}}_{2\mathrm{n}}$, where $D_{2n}$ denotes the dihedral group of order $2n$ with the following presentation:

$$D_{2n}=〈x,y:x^n=y^2=1,y^{-1}xy=x^{-1}〉.$$

Also, $\mathrm{Aut}({\mathrm{K}}_{\mathrm{n}})\cong {\mathcal{S}}_{\mathrm{n}}$, which implies that both $C_n$ and $K_n$ are vertex-transitive, and we are done. □

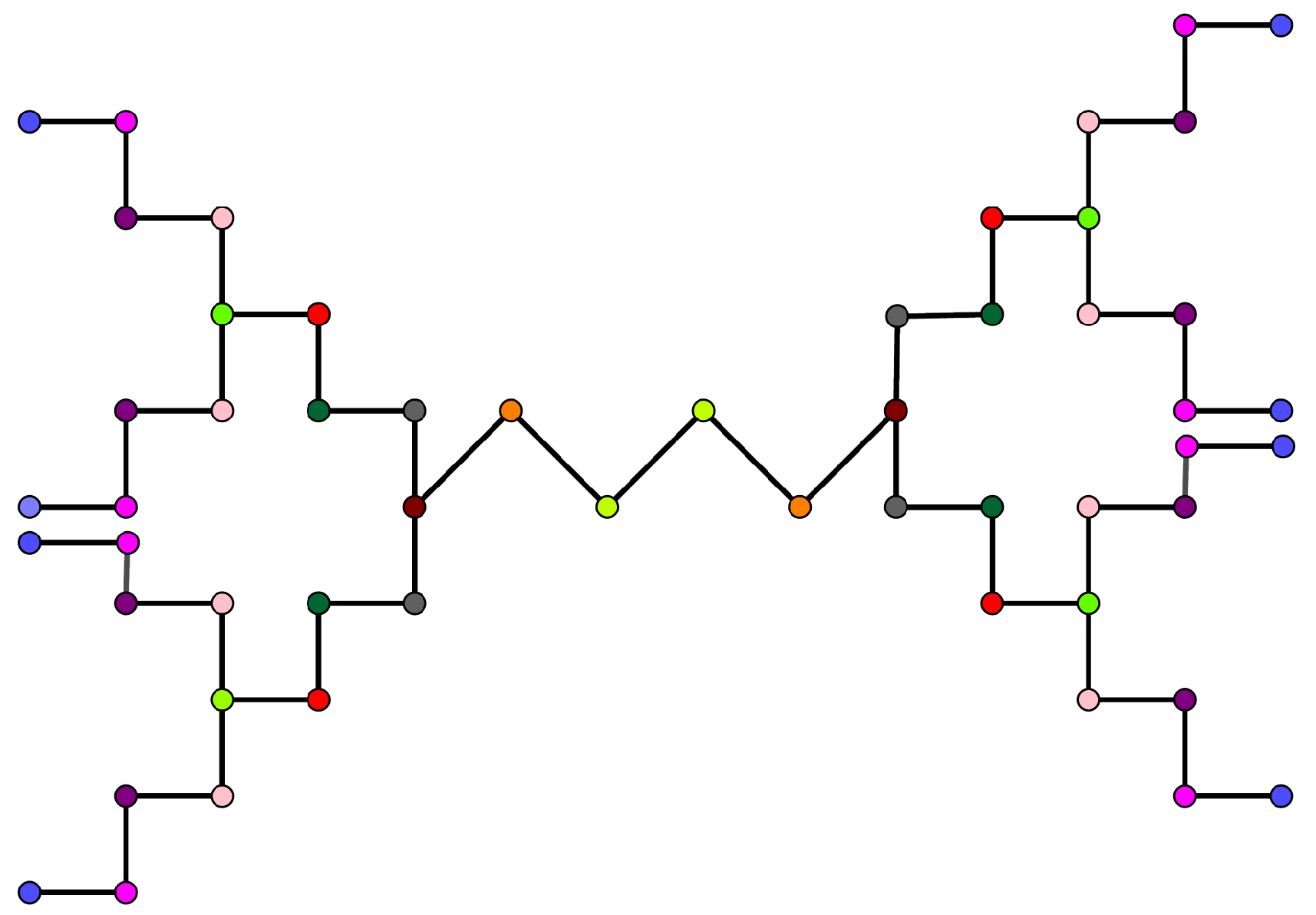
Two vertices u and v of a graph G are said to be similar if there is an automorphism $\alpha \in \mathrm{Aut}(\mathrm{G})$ such that $\alpha (u)=v$. Herein, all similar vertices have the same color.

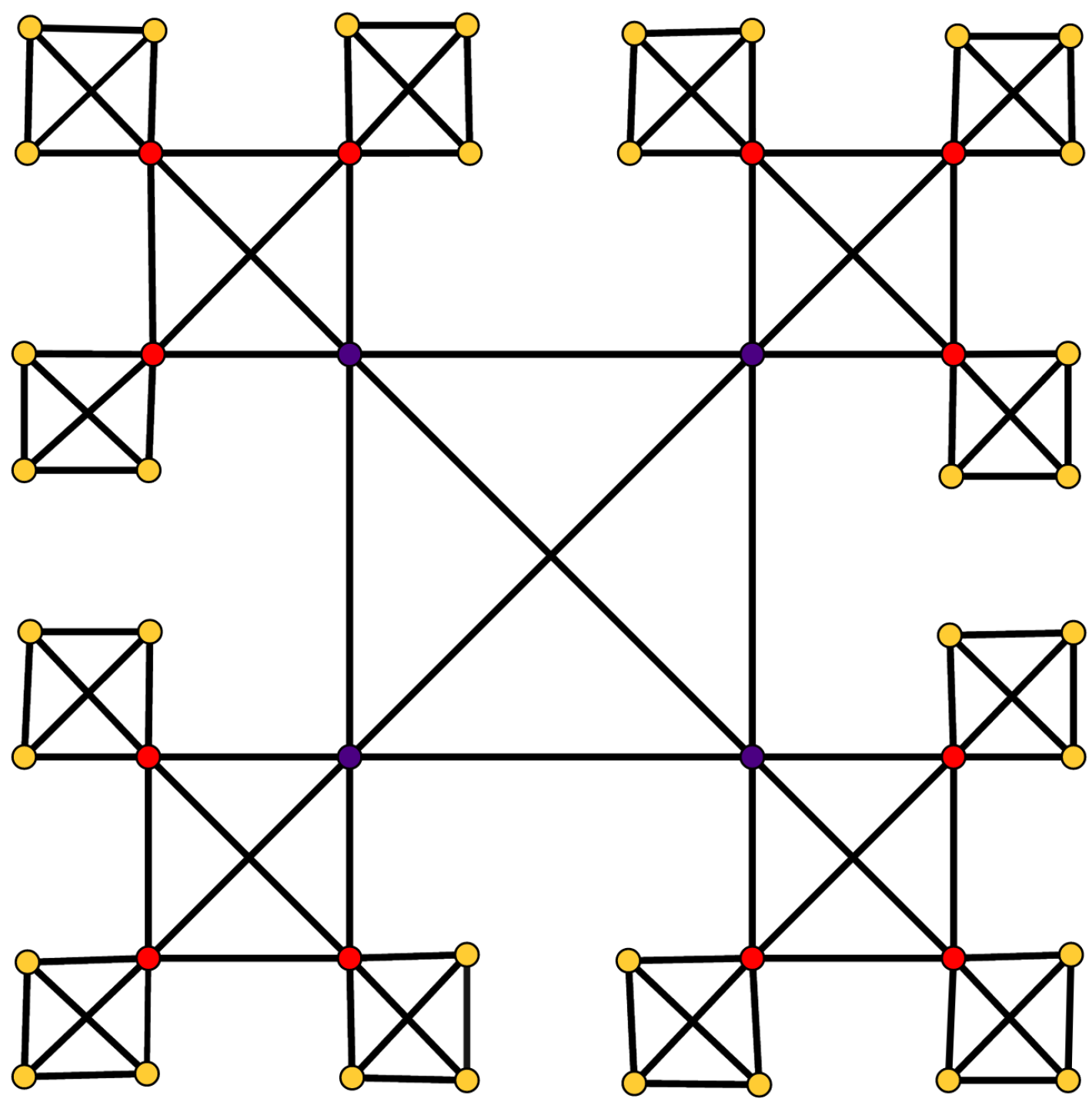
Corollary 2.

For the MacPherson graph $G=M(s,t)$ as shown in Figure 3, $\mathrm{Aut}(\mathrm{M}(\mathrm{s},\mathrm{t}))\cong {\mathcal{S}}_{\mathrm{s}}\wr {\mathcal{S}}_{\mathrm{s}-1}\wr {\mathcal{S}}_{\mathrm{s}-1}\wr \dots \wr {\mathcal{S}}_{\mathrm{s}-1}$ and $S(M(s,t))>{\mathrm{I}}_{\mathrm{a}}(\mathrm{M}(\mathrm{s},\mathrm{t}))$.

Proof. 

It is obvious that G is constructed by $K_s$ and n copies of graph $K_{s-1}$ and then by splicing each vertex $v_i$ of $K_s$ by vertex u of the ith copy of $K_{s-1}$. This means that $\mathrm{Aut}(\mathrm{M}(\mathrm{s},\mathrm{t}))\cong {\mathcal{S}}_{\mathrm{s}}\wr {\mathcal{S}}_{\mathrm{s}-1}\wr {\mathcal{S}}_{\mathrm{s}-1}\wr \dots \wr {\mathcal{S}}_{\mathrm{s}-1}$. In [30], it is proved that G is vertex-transitive. Considering this fact and Theorem 6, we may conclude the assertion. □

Theorem 7.

If G is a regular edge-transitive graph, then ${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})<\mathrm{S}(\mathrm{G})$.

Proof. 

Note first that if G is vertex-transitive, then ${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})<\mathrm{S}(\mathrm{G})$ from Theorem 6. Thus, we can assume that G is not vertex-transitive. Therefore, it is bipartite, and because G is regular, two independent sets are exactly the orbits of $\mathrm{Aut}(\mathrm{G})$ on $V(G)$. This means that $G\cong K_{m,m}$, and by Example 1, the required result is obtained. □

Theorem 8.

Let G be a graph of order $n\ne 3$, with $n-2$ singleton orbits and an orbit of order two. Then ${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})\ge \mathrm{S}(\mathrm{G})$, and for $n=3$, we have $\mathrm{S}(\mathrm{G})>{\mathrm{I}}_{\mathrm{a}}(\mathrm{G})$. In addition, if G has $n-3$ singleton orbits and an orbit of order three, then ${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})\ge \mathrm{S}(\mathrm{G})(\mathrm{n}\ge 8)$.

Proof. 

Suppose that $n=3$ and G has an orbit of size two. Then $G\cong P_3$ and thus $\mathrm{S}(\mathrm{G})>{\mathrm{I}}_{\mathrm{a}}(\mathrm{G})$. If $n>3$, then $\mathrm{Aut}(\mathrm{G})\cong {\mathcal{Z}}_2$ and so $\mathrm{S}(\mathrm{G})=\frac{\mathrm{n}+2}{\mathrm{n}}$, and ${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})=log\mathrm{n}-\frac{2}{\mathrm{n}}$. If $n=4$, then ${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})=\mathrm{S}(\mathrm{G})=\frac{3}{2}$. If $n\ge 5$, then $\mathrm{S}(\mathrm{G})=\frac{\mathrm{n}+2}{\mathrm{n}}\le \frac{7}{5}$ and ${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})=log\mathrm{n}-\frac{2}{\mathrm{n}}\ge \frac{8}{5}$. This gives ${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})>\mathrm{S}(\mathrm{G})$, and the assertion follows. If G has $n-3$ singleton orbits and an orbit of order three, then $\mathrm{Aut}(\mathrm{G})\cong {\mathcal{S}}_3$ or $\mathrm{Aut}(\mathrm{G})\cong {\mathcal{Z}}_3$. If $\mathrm{Aut}(\mathrm{G})\cong {\mathcal{S}}_3$, then $\mathrm{S}(\mathrm{G})=(\frac{\mathrm{n}+3}{\mathrm{n}})log(3)$ and ${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})=log\mathrm{n}-\frac{3}{\mathrm{n}}log3$. One can see that for $n\ge 8$, $\mathrm{S}(\mathrm{G})\le log9$ and thus ${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})>\mathrm{S}(\mathrm{G})$. If $\mathrm{Aut}(\mathrm{G})\cong {\mathcal{S}}_3$, then $\mathrm{S}(\mathrm{G})=1+\frac{\mathrm{n}+3}{\mathrm{n}}log3$ and ${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})=log\mathrm{n}-\frac{3}{\mathrm{n}}log3$. Thus we have ${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})\ge \mathrm{S}(\mathrm{G})$ for $n\ge 11$. □

Theorem 9.

Consider G to be a graph of order n, with $n-k$ singleton orbits and an orbit of order k. Consider the size of the automorphism group to be less than or equal to $\frac{n}{\sqrt[n]{k^{2k}}}$. Then $\mathrm{S}(\mathrm{G})\le {\mathrm{I}}_{\mathrm{a}}(\mathrm{G})$.

Proof. 

The following arise by definition:

$$\begin{array}{ccc}\hfill \mathrm{S}(\mathrm{G})& =& log(|\mathrm{Aut}(\mathrm{G})|)+\frac{\mathrm{k}}{\mathrm{n}}=log(|(\mathrm{Aut}(\mathrm{G})|{\mathrm{k}}^{\frac{\mathrm{k}}{\mathrm{n}}}),\hfill \\ \hfill {\mathrm{I}}_{\mathrm{a}}(\mathrm{G})& =& logn+\frac{k}{n}logk=log(\frac{n}{\sqrt[n]{k^{2k}}}).\hfill \end{array}$$

Therefore, if $|\mathrm{Aut}(\mathrm{G})|\le \frac{\mathrm{n}}{\sqrt[\mathrm{n}]{{\mathrm{k}}^{2\mathrm{k}}}}$, then $\mathrm{S}(\mathrm{G})\le {\mathrm{I}}_{\mathrm{a}}(\mathrm{G})$. □

Theorem 10.

Assume that G is a graph on n vertices and that the orbits of $A=\mathrm{Aut}(\mathrm{G})$ are of equal size. Thus for $n\ge s$, we have $\mathrm{S}(\mathrm{G})\le {\mathrm{I}}_{\mathrm{a}}(\mathrm{G})$, where v is an arbitrary vertex in $V(G)$ and $s=\frac{{|A|}^3}{|A_v{|}^2}$.

Proof. 

Suppose that G has k orbits. Then $\mathrm{S}(\mathrm{G})=log(\mathrm{m}|\mathrm{A}|)$ and ${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})=log(\frac{\mathrm{n}}{\mathrm{m}})=log\mathrm{k}$, where m is the orbit size. Thus, $\mathrm{S}(\mathrm{G})\le {\mathrm{I}}_{\mathrm{a}}(\mathrm{G})$ if and only if $m|\mathrm{Aut}(\mathrm{G})|\le \mathrm{k}$ if and only if $n\ge \frac{{|A|}^3}{|A_v{|}^2}=s$. For a given automorphism $\sigma$ of graph G, the fix point of $\sigma$ is defined by $fix(\sigma )=\{v\in V(G):\sigma (v)=v\}$. □

Theorem 11.

Let G be a graph on n vertices and $A=\mathrm{Aut}(\mathrm{G})$. If ${\displaystyle \sum _{\sigma \in \mathrm{Aut}(\mathrm{G})}|fix(\sigma )|<\frac{nalog(|A|)}{logn}}$, then $\mathrm{S}(\mathrm{G})>{\mathrm{I}}_{\mathrm{a}}(\mathrm{G})$.

Proof. 

Suppose that $O_1,\dots ,O_r$ are all orbits of A. Because $|O_i|\ge 1$, we obtain $\frac{|O_i|}{n}log\frac{|O_i|}{n}\ge \frac{1}{n}log\frac{1}{n}$, thus ${\displaystyle -\sum _{i=1}^r\frac{|O_i|}{n}log\frac{|O_i|}{n}\le \frac{r}{n}logn}$. Hence, ${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})\le \frac{\mathrm{r}}{\mathrm{n}}log(\mathrm{n})$. From the Burnside Lemma [21], the number of orbits is ${\displaystyle r=\frac{1}{|A|}\sum _{\sigma \in A}|fix(\sigma )|}$. This yields ${\displaystyle {\mathrm{I}}_{\mathrm{a}}(\mathrm{G})\le \frac{1}{\mathrm{n}|\mathrm{A}|}\sum _{\sigma \in \mathrm{A}}|\mathrm{fix}(\sigma )|log(\mathrm{n})}$. Now if ${\displaystyle \sum _{\sigma \in A}|fix(\sigma )|<\frac{nalog(|A|)}{logn}}$, then ${\displaystyle log(|A|)>\frac{log(n)}{n|A|}\sum _{\sigma \in A}|fix(\sigma )|}$. Thus, $log(|A|)>{\mathrm{I}}_{\mathrm{a}}(\mathrm{G})$ and so

$${\displaystyle \frac{1}{n}\sum _{\sigma \in A}|O_i|log(|O_i|)+log(|A|)>I_a(G)+\frac{1}{n}\sum _{\sigma \in A}|O_i|log|O_i|.}$$

This leads to $\mathrm{S}(\mathrm{G})>{\mathrm{I}}_{\mathrm{a}}(\mathrm{G})$. □

Theorem 12.

Suppose that $G_1\cong K_n+\{u\}$ and $G_2\cong K_n+\{e\}$; see Figure 4. Then ${\mathrm{I}}_{\mathrm{a}}({\mathrm{G}}_1)<\mathrm{S}({\mathrm{G}}_1)$ and ${\mathrm{I}}_{\mathrm{a}}({\mathrm{G}}_2)<\mathrm{S}({\mathrm{G}}_2)$.

Proof. 

Clearly, $G_1$ has n vertices of degree $n-1$ and a vertex of degree two. This leads to $\mathrm{Aut}({\mathrm{G}}_1)\cong {\mathcal{S}}_{\mathrm{n}-2}\times {\mathcal{Z}}_2$. Hence $G_1$ has three orbits of sizes one, two, and $n-2$, respectively, which means that

$$\begin{array}{ccc}\hfill \mathrm{S}({\mathrm{G}}_1)& =& \frac{n+3}{n+1}+\frac{n-2}{n+1}log(n-2)+log((n-2)!),\hfill \\ \hfill {\mathrm{I}}_{\mathrm{a}}({\mathrm{G}}_1)& =& log(n+1)-\frac{n-2}{n+1}log(n-2)-\frac{2}{n+1}.\hfill \end{array}$$

Meanwhile, $G_2$ has $n-1$ vertices of degree $n-1$, a vertex of degree n, and a vertex of degree one. This together with the fact that $\mathrm{Aut}({\mathrm{G}}_2)\cong {\mathcal{S}}_{\mathrm{n}-1}$ leads us to assume that $G_2$ has three orbits of sizes one, one, and $n-1$, respectively, and therefore

$$\begin{array}{ccc}\hfill \mathrm{S}({\mathrm{G}}_2)& =& \frac{n-1}{n+1}log(n-1)+log((n-1)!),\hfill \\ \hfill {\mathrm{I}}_{\mathrm{a}}({\mathrm{G}}_2)& =& log(n+1)-\frac{n-1}{n+1}log(n-1).\hfill \end{array}$$

This completes the proof. □

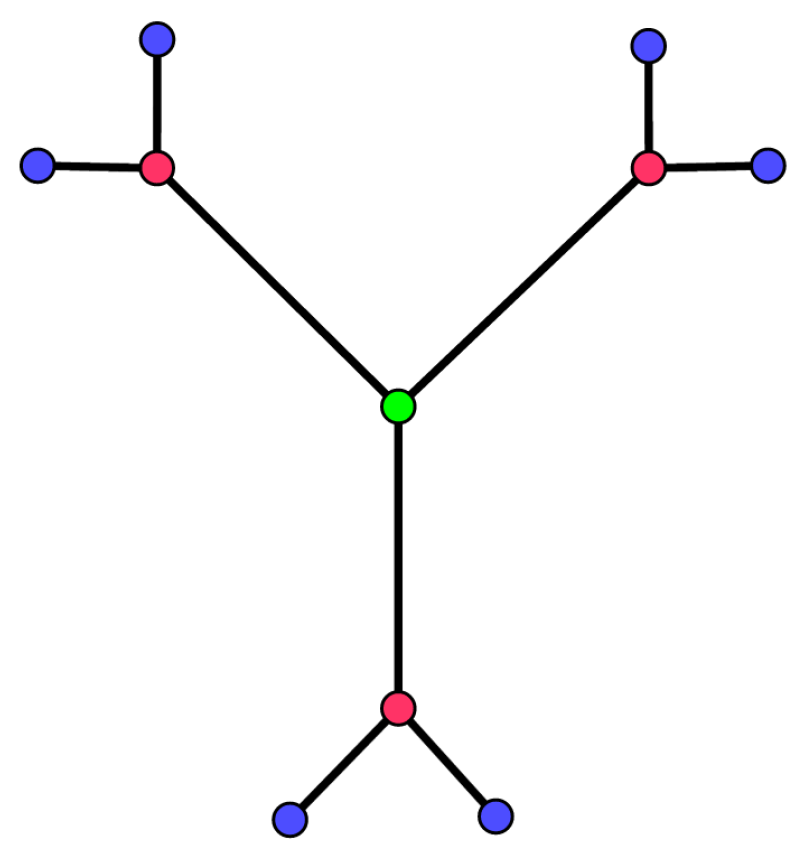
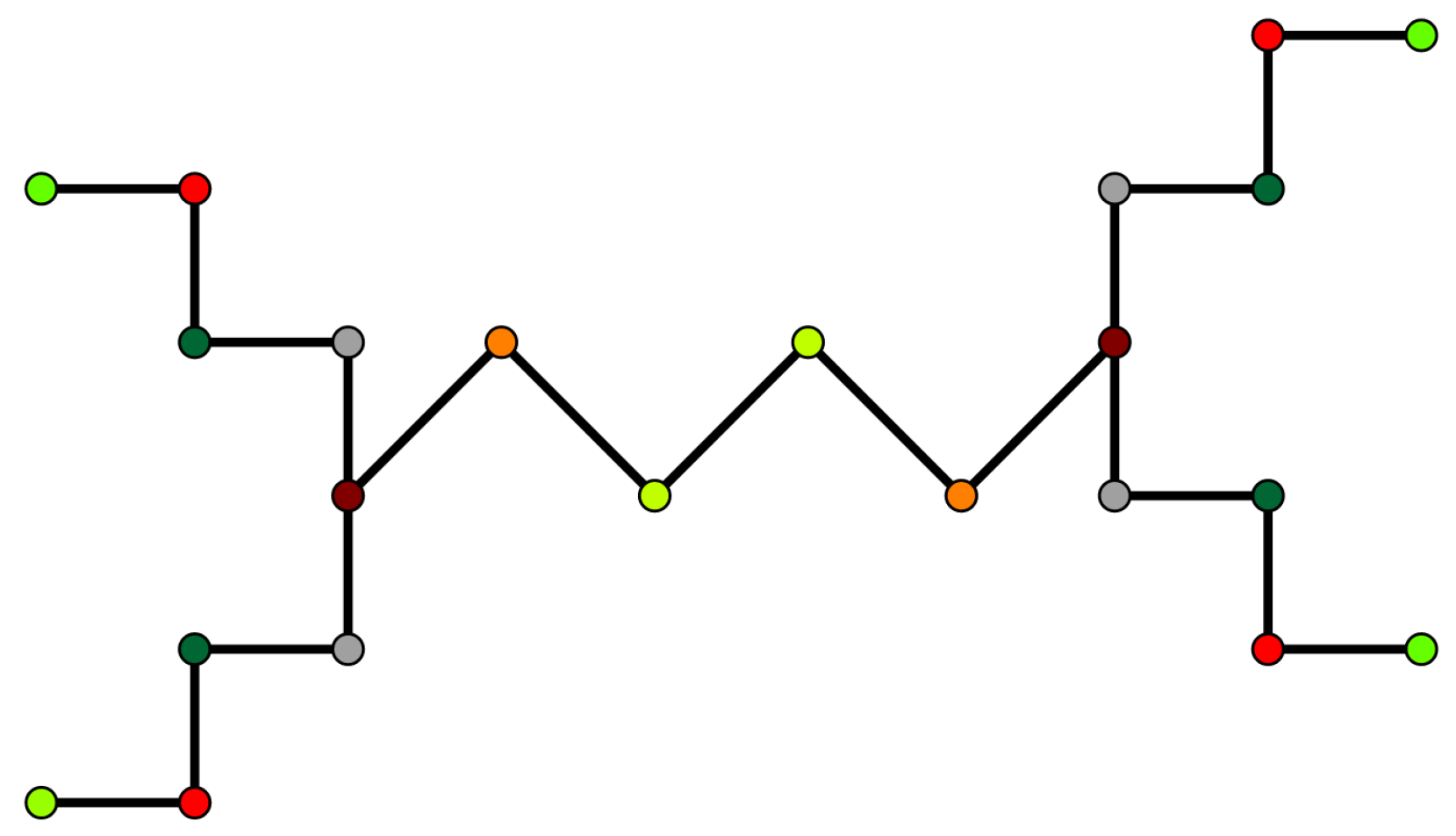
A caterpillar tree is a tree in which all the vertices are within distance one of a central path. In other words, the caterpillar tree $C(n_1,n_2,\dots ,n_r)$ consists of a path with r vertices in which $n_i$ pendent edges are attached to the ith vertex of $P_r$; see Figure 5.

Theorem 13.

Let $G=C(n_1,n_2,\dots ,n_r)$ be a caterpillar tree, where $n_1\ne n_r$. Then $I_a(G)<\mathrm{S}(\mathrm{G})$.

Proof. 

The graph G has ${\displaystyle \sum _{i=1}^r{n}_i+r=n}$ vertices, and from Theorem 1 we have that $\mathrm{Aut}(\mathrm{G})\cong {\mathcal{S}}_{{\mathrm{n}}_1}\times {\mathcal{S}}_{{\mathrm{n}}_2}\times \dots \times {\mathcal{S}}_{{\mathrm{n}}_{\mathrm{r}}}$. This leads to the conclusion that G has $2r$ orbits, and thus

$${\displaystyle \mathrm{S}(\mathrm{G})=\frac{1}{\mathrm{n}}\sum _{\mathrm{i}=1}^{\mathrm{r}}{\mathrm{n}}_{\mathrm{i}}log({\mathrm{n}}_{\mathrm{i}})+log({\mathrm{n}}_1!\dots {\mathrm{n}}_{\mathrm{r}}!)}$$

and

$${\displaystyle {\mathrm{I}}_{\mathrm{a}}(\mathrm{G})=log\mathrm{n}-\sum _{\mathrm{i}=1}^{\mathrm{r}}\frac{{\mathrm{n}}_{\mathrm{i}}}{\mathrm{n}}log{\mathrm{n}}_{\mathrm{i}}.}$$

Hence, $I_a(G)<\mathrm{S}(\mathrm{G})$. □

Theorem 14.

If T is a tree with two orbits, then $I_a(G)<\mathrm{S}(\mathrm{G})$.

Proof. 

Let T be a tree with two orbits. It is well known that $T\cong S_n$ or $T\cong B_{n,n}$ [22]; see Figure 6. If $T\cong B_{n,n}$, then $\mathrm{Aut}(\mathrm{G})\cong {\mathcal{S}}_{\mathrm{n}}\times {\mathcal{S}}_{\mathrm{n}}\times {\mathcal{Z}}_2$, and thus $\mathrm{S}(\mathrm{G})=2log(\mathrm{n}!)+\frac{\mathrm{n}}{\mathrm{n}+1}log(\mathrm{n})+2$. Meanwhile, ${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})=log(\mathrm{n}+1)-\frac{\mathrm{n}}{\mathrm{n}+1}log(\mathrm{n})$. Hence, ${\mathrm{I}}_{\mathrm{a}}({\mathrm{B}}_{\mathrm{n},\mathrm{n}})<\mathrm{S}({\mathrm{B}}_{\mathrm{n},\mathrm{n}})$. If $T\cong S_n$, then from Example 1 we obtain ${\mathrm{I}}_{\mathrm{a}}({\mathrm{S}}_{\mathrm{n}})<\mathrm{S}({\mathrm{S}}_{\mathrm{n}})$. □

Theorem 15.

If T is a tree with three orbits, then ${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})<\mathrm{S}(\mathrm{G})$.

Proof. 

It is well known that each tree has either a central vertex or a central edge [31]. First, suppose that T has a central vertex. The central vertex gives rise to a singleton orbit, and the leaf vertices are in the second orbit. If the leaf vertices give rise to at least two orbits, then T has at least four orbits, which is a contradiction. Hence, the leaf vertices necessarily lie in the same orbit. The other vertices are in the same orbit, therefore they all have the same degree. On the other hand, the leaf vertices are adjacent to the central vertex because there are only three orbits. This leads us to investigate $T\cong T_{n,r}$; see Figure 7. Clearly, T has $1+n+nr$ vertices, and Theorem 4 gives $\mathrm{Aut}(\mathrm{T})\cong {\mathcal{S}}_{\mathrm{n}}\wr {\mathcal{S}}_{\mathrm{r}}$, where the sizes of the orbits of T are one, n, and $nr$, respectively. This means that

$$\begin{array}{ccc}\hfill \mathrm{S}(\mathrm{T})& =& \frac{n(1+r)}{n(1+r)+1}logn+\frac{nr}{n(1+r)+1}logr\hfill \\ & +& log(n!r{!}^n),\hfill \\ \hfill {\mathrm{I}}_{\mathrm{a}}(\mathrm{T})& =& log(n(1+r)+1)-\frac{n(1+r)}{n(1+r)+1}logn\hfill \\ & -& \frac{nr}{n(1+r)+1}logr.\hfill \end{array}$$

Assume that T has a central edge. By a similar argument, it can be proved that T is isomorphic with graph $D{T}_{n,n}$, as shown in Figure 8. Theorem 4 gives $\mathrm{Aut}(\mathrm{T})\cong ({\mathcal{S}}_2\wr {\mathcal{S}}_{\mathrm{n}})\wr {\mathcal{S}}_{\mathrm{r}}$, and thus T has three orbits of sizes two, $2n$, and $2nr$, respectively. Therefore, we have that

$$\begin{array}{ccc}\hfill \mathrm{S}(\mathrm{T})& =& 2log(n(1+r)+1)-\frac{2n(1+r)}{n(1+r)+1}logn\hfill \\ & -& \frac{2nr}{n(1+r)+1}logr+2,\hfill \\ \hfill {\mathrm{I}}_{\mathrm{a}}(\mathrm{T})& =& log(n(1+r)+1)-\frac{n(1+r)}{n(1+r)+1}logn\hfill \\ & -& \frac{nr}{n(1+r)+1}logr.\hfill \end{array}$$

This completes the proof. □

2.2. Orbit Entropy and Symmetry Index of Dendrimers

A dendrimer is a molecular graph associated with a dendrimer molecule. In this section, we determine the entropy or information content of some dendrimers. In the case of organic molecules, the lower the information content (or the greater the symmetry), the fewer the possibilities for different interactions with other molecules. If all the atoms are in the same equivalence classes, then it makes no difference which one interacts with an atom of another molecule.

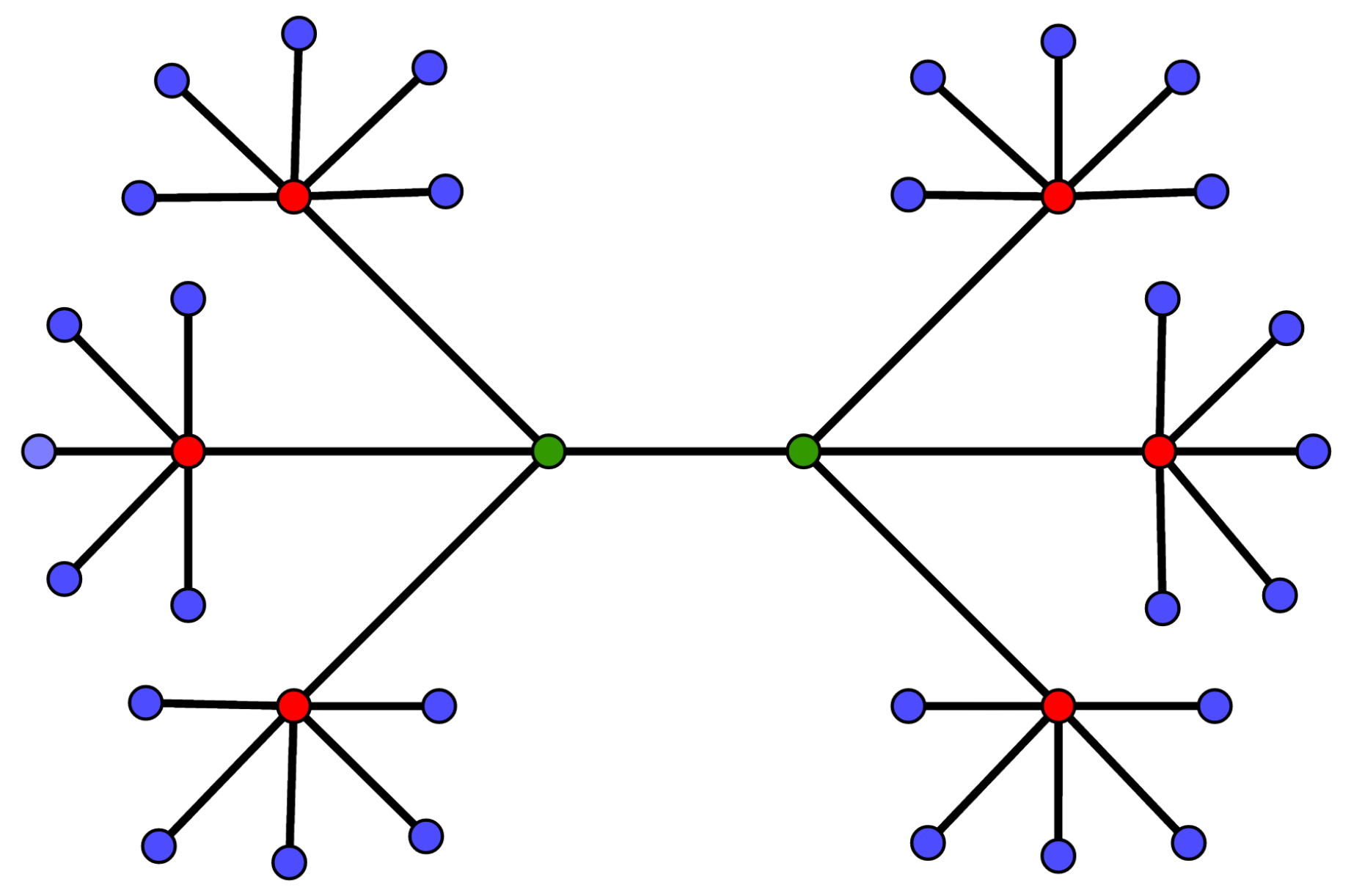
Theorem 16.

For the dendrimer ${\mathcal{G}}_n$ shown in Figure 9, we obtain $S({\mathcal{G}}_n)>{\mathrm{I}}_{\mathrm{a}}({\mathcal{G}}_{\mathrm{n}})$.

Proof. 

The fact that

$${\displaystyle |V({\mathcal{G}}_n)|=6+4\sum _{i=2}^{n+1}{2}^i=6+4(2^{n+2}-4)=2^{n+4}-10}$$

can be verified from Figure 9 and Figure 10. It is not difficult to prove that $\mathrm{Aut}({\mathcal{G}}_{\mathrm{n}})\cong \mathrm{Aut}({\mathcal{G}}_{\mathrm{n}-1})\wr {\mathcal{Z}}_2$. Using induction on n yields $\mathrm{Aut}({\mathcal{G}}_{\mathrm{n}})\cong {\mathcal{Z}}_2:({\underbrace{{\mathcal{Z}}_2\times {\mathcal{Z}}_2\times \dots \times {\mathcal{Z}}_2}}_{(2^{\mathrm{n}+1}-2)-\mathrm{times}})$, where “:” denotes the semi-direct product [22]. It is clear that ${\mathcal{G}}_n$ has three orbits of size two and four orbits of size $2^m$, $2\le m\le n+1$. Hence, the symmetry index and the orbit-entropy measure of dendrimer ${\mathcal{G}}_n$ are given by

$$\begin{array}{ccc}\hfill S({\mathcal{G}}_n)& =& log(2^{n+2}-4)+\frac{{\displaystyle 6+\sum _{m=2}^{n+1}m{2}^{m+2}}}{2^{n+4}-10},\hfill \\ \hfill {\mathrm{I}}_{\mathrm{a}}({\mathcal{G}}_{\mathrm{n}})& =& -(\frac{6}{2^{n+4}-10}log(\frac{2}{2^{n+4}-10})\hfill \\ & +& {\displaystyle \sum _{m=2}^{n+1}\frac{2^{m+2}}{2^{n+4}-10}log(\frac{2^m}{2^{n+4}-10}))}\hfill \\ & =& log(2^{n+4}-10)-\frac{{\displaystyle 6+\sum _{m=2}^{n+1}m{2}^{m+2}}}{2^{n+4}-10}.\hfill \end{array}$$

□

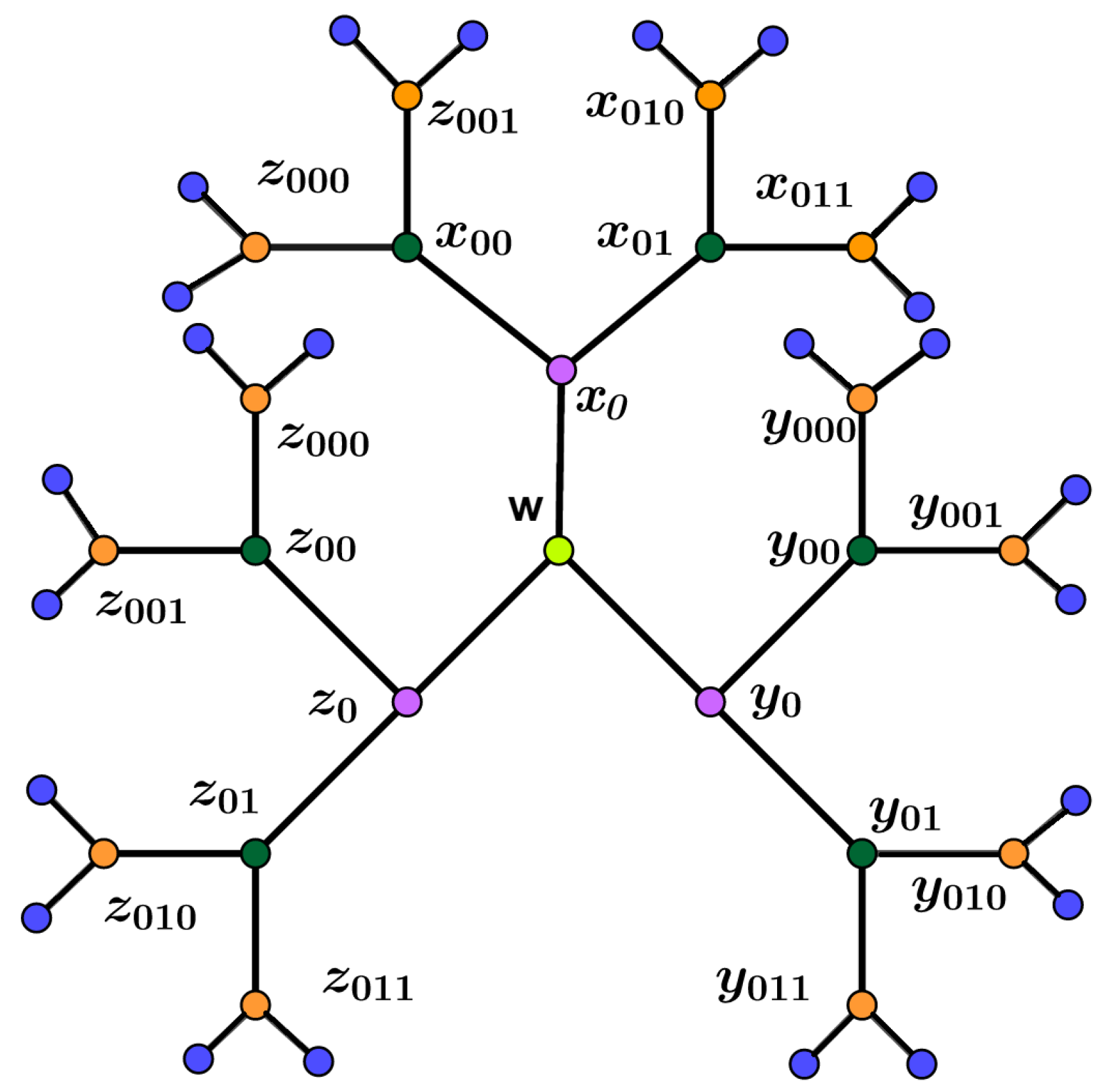
Here, we study the orbit-entropy measure and the symmetry index of another class of dendrimers, namely ${\mathcal{H}}_n$, shown in Figure 11. For a given vertex $v\in V(G)$, suppose that $N_G(v)=\{u\in V(G);uv\in V(G)\}$ and X is a subset of vertices of graph G. By $\langle X\rangle$, we mean the induced subgraph of G with vertex set X, and two vertices in X are adjacent if and only if they are adjacent in G. The central vertex t has degree three and $N_G(w)=\{x_0,y_0,z_0\}$. There are three branches rooted at vertices $x_0$, $y_0$, and $z_0$. For two vertices $u,v\in V(G)$, the distance between them is the length of the shortest path connecting them, denoted by $d(u,v)$. By the ith level of ${\mathcal{H}}_n$, we mean the set of vertices at distance i from the central vertex w.

Theorem 17.

For the dendrimer graph ${\mathcal{H}}_n$, we have $S({\mathcal{H}}_n)>I_a({\mathcal{H}}_n)$.

Proof. 

It is obvious that ${\displaystyle |V({\mathcal{H}}_n)|=4+3\sum _{i=1}^{n-1}{2}^i=3(2^n)-2}$. Similarly, $\mathrm{Aut}({\mathcal{H}}_1)\cong {\mathcal{S}}_3$, and if $n\ge 2$, then we have $\mathrm{Aut}({\mathcal{H}}_{\mathrm{n}})\cong \mathrm{Aut}({\mathcal{H}}_{\mathrm{n}-1})\wr {\mathcal{Z}}_2$ from the structure of ${\mathcal{H}}_n$. Now, using induction on n shows that $\mathrm{Aut}({\mathcal{H}}_{\mathrm{n}})\cong {\mathcal{S}}_3:({\underbrace{{\mathcal{Z}}_2\times {\mathcal{Z}}_2\times \dots \times {\mathcal{Z}}_2}}_{3(2^{\mathrm{n}-1}-1)-\mathrm{times}})$.

Hence, ${\mathcal{H}}_n$ has $n+1$ orbits as follows. $O_1$ is a singleton set containing the central vertex w. For $i\ge 2$, the ith orbit contains all vertices at distance i from the central vertex. Hence, the vertices of the kth level of this graph are the vertices of the form $a=xw$, $a=yw$, or $a=zw$ of length k, where $w\in {\{0,1\}}^{k-1}$. Therefore, we have that

$${\displaystyle S({\mathcal{H}}_n)=log(3^2(2^n-2))+\frac{1}{3(2^n)-2}\sum _{i=0}^{n-1}3(2^i)log3(2^i),}$$

$$\begin{array}{ccc}\hfill I_a({\mathcal{H}}_n)& =& {\displaystyle -(\sum _{i=0}^{n-1}\frac{3(2^i)}{3(2^n)-2}log(\frac{3(2^i)}{3(2^n)-2)})}\hfill \\ & +& \frac{1}{3(2^n)-2}log(\frac{1}{3(2^n)-2}))\hfill \\ & =& log(3(2^n)-2)\hfill \\ & -& {\displaystyle \frac{1}{3(2^n)-2}\sum _{i=0}^{n-1}3(2^i)log(3(2^i)).}\hfill \end{array}$$

□

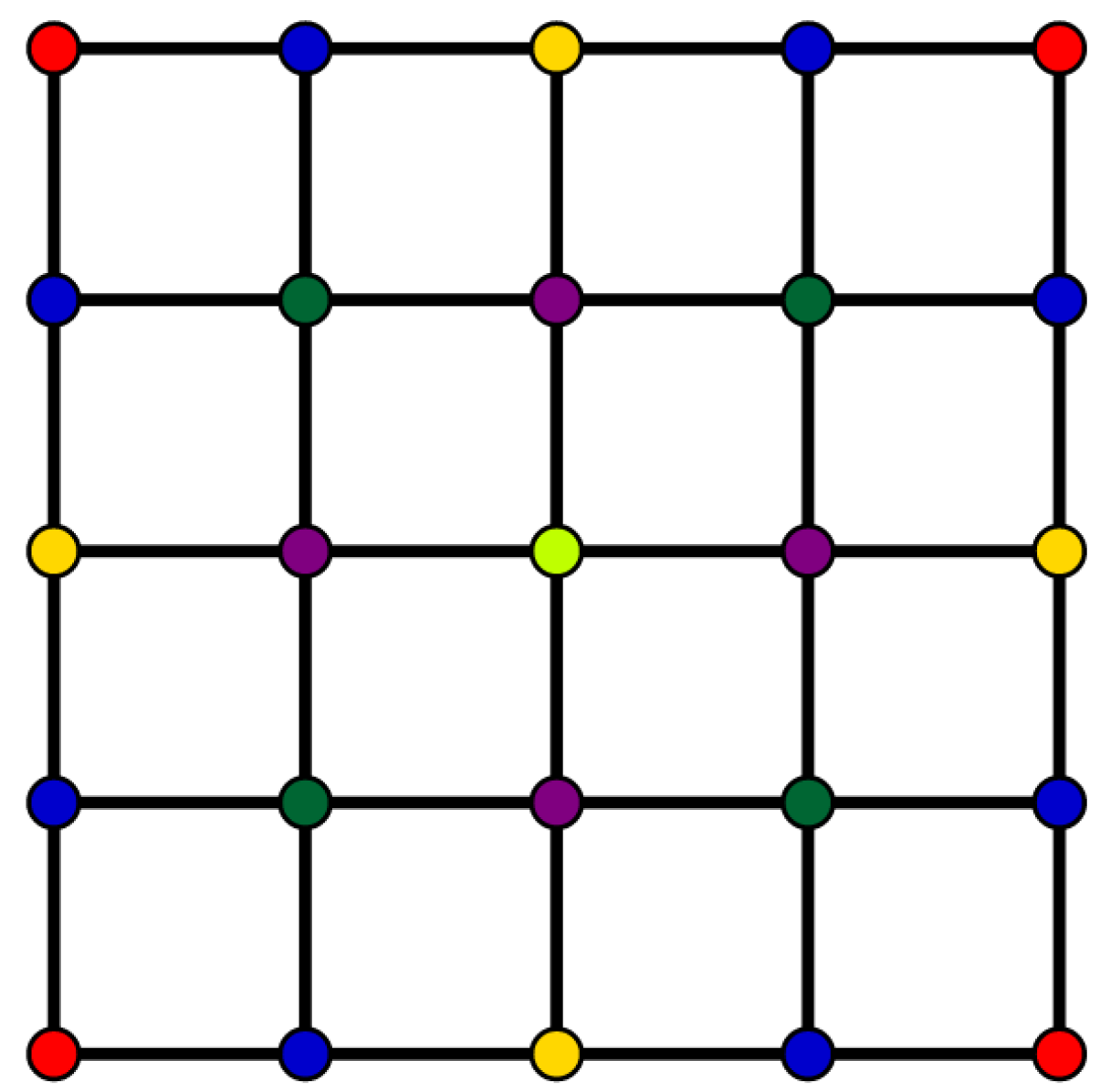
Consider the lattice graph $\mathcal{L}(m,n)$ that is the Cartesian product of two graphs $P_n$ and $P_m$, see Figure 12. Thus, we have the following.

Theorem 18.

Let $G=\mathcal{L}(m,n)$. If $n=m$, then we have $\mathrm{S}(\mathrm{G})<{\mathrm{I}}_{\mathrm{a}}(\mathrm{G})$ for $n\ge 21$. If $n\ne m$, then we have $\mathrm{S}(\mathrm{G})<{\mathrm{I}}_{\mathrm{a}}(\mathrm{G})$ for $(m+1)(n+1)\ge 64$.

Proof. 

• Consider $m=n$. Thus, G has ${(n+1)}^2$ vertices and $Aut(G)\cong D_8$, and the following two cases hold.

  (a)

  If n is odd, then G has $\frac{n+1}{2}$ orbits of size four and $\frac{n^2-1}{8}$ orbits of size eight. Thus, $\mathrm{S}(\mathrm{G})=\frac{6\mathrm{n}+4}{\mathrm{n}+1}$ and ${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})=2log(\mathrm{n}+1)-\frac{3\mathrm{n}+1}{\mathrm{n}+1}$. For $n\ge 21$, we obtain $log(n+1)>\frac{9n+7}{2(n+1)}$, thus $\mathrm{S}(\mathrm{G})<{\mathrm{I}}_{\mathrm{a}}(\mathrm{G})$.

  (b)

  If n is even, then G has n orbits of size four, $\frac{n(n-2)}{8}$ orbits of size eight, and a singleton orbit. Hence, $\mathrm{S}(\mathrm{G})=\frac{6{\mathrm{n}}^2+8\mathrm{n}+3}{{(\mathrm{n}+1)}^2}$ and ${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})=2log(\mathrm{n}+1)-\frac{3{\mathrm{n}}^2+2\mathrm{n}}{{(\mathrm{n}+1)}^2}$. For $n\ge 20$, $log(n+1)>\frac{9n^2+10n+3}{2{(n+1)}^2}$, and thus $\mathrm{S}(\mathrm{G})<{\mathrm{I}}_{\mathrm{a}}(\mathrm{G})$.

• Consider $m\ne n$. Thus, $Aut(G)={\mathcal{Z}}_2\times {\mathcal{Z}}_2$, and the following four cases hold.

  (a)

  If m and n are odd, then G has $\frac{(m+1)(n+1)}{4}$ orbits of size four. Thus, $\mathrm{S}(\mathrm{G})=4$ and ${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})=log((\mathrm{m}+1)(\mathrm{n}+1))-2$. Therefore, if $(m+1)(n+1)\ge 64$, then $\mathrm{S}(\mathrm{G})\le {\mathrm{I}}_{\mathrm{a}}(\mathrm{G})$.

  (b)

  If m is even and n is odd, then G has $\frac{m(n+1)}{4}$ orbits of size four and $\frac{n+1}{2}$ orbits of size two. Thus, $\mathrm{S}(\mathrm{G})=\frac{4\mathrm{m}+3}{\mathrm{m}+1}$ and ${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})=log((\mathrm{m}+1)(\mathrm{n}+1))-\frac{2\mathrm{m}+1}{\mathrm{m}+1}$. Therefore, if $(m+1)(n+1)\ge 64$, then $\mathrm{S}(\mathrm{G})<{\mathrm{I}}_{\mathrm{a}}(\mathrm{G})$.

  (c)

  If m is odd and n is even, then G has $\frac{n(m+1)}{4}$ orbits of size four and $\frac{m+1}{2}$ orbits of size two. Thus, $\mathrm{S}(\mathrm{G})=\frac{4\mathrm{n}+3}{\mathrm{n}+1}$ and ${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})=log((\mathrm{m}+1)(\mathrm{n}+1))-\frac{2\mathrm{n}+1}{\mathrm{n}+1}$. For $(m+1)(n+1)\ge 64$, we obtain $\mathrm{S}(\mathrm{G})<{\mathrm{I}}_{\mathrm{a}}(\mathrm{G})$.

  (d)

  If m and n are both even, then G has $\frac{nm}{4}$ orbits of size four, $\frac{n+m}{2}$ orbits of size two, and one singleton orbit. Thus, $\mathrm{S}(\mathrm{G})=\frac{4\mathrm{mn}+3\mathrm{m}+3\mathrm{n}+2}{(\mathrm{m}+1)(\mathrm{n}+1)}$ and

  $${\mathrm{I}}_{\mathrm{a}}(\mathrm{G})=log((\mathrm{m}+1)(\mathrm{n}+1))-\frac{\mathrm{mn}+\mathrm{m}+\mathrm{n}}{(\mathrm{m}+1)(\mathrm{n}+1)}.$$

  Therefore, if $(m+1)(n+1)\ge 32$, then $\mathrm{S}(\mathrm{G})<{\mathrm{I}}_{\mathrm{a}}(\mathrm{G})$.

□

3. Summary and Conclusions

Quantitative measures of graph complexity, defined in terms of Shannon entropy, are often based on vertex partitions [2,7]. For instance, partitions of the vertices of a graph are related to symmetry structure if they are based on vertex orbit cardinalities. In this paper, we investigated the orbit entropy [2] and the symmetry index [19] for several classes of graphs. We compared the values of these measures based on inequalities. As a result, we found several classes of graphs whose symmetry index was greater or equal to the orbit-entropy measure, while many other classes had a greater orbit entropy.

We also obtained useful and novel measures based on automorphism group decompositions. These measures should be compared with other existing graph complexity measures, which is left as future work.