On the Direct Limit from Pseudo Jacobi Polynomials to Hermite Polynomials
Abstract
1. Introduction
2. Basic Properties of Hermite and Pseudo-Jacobi Polynomials
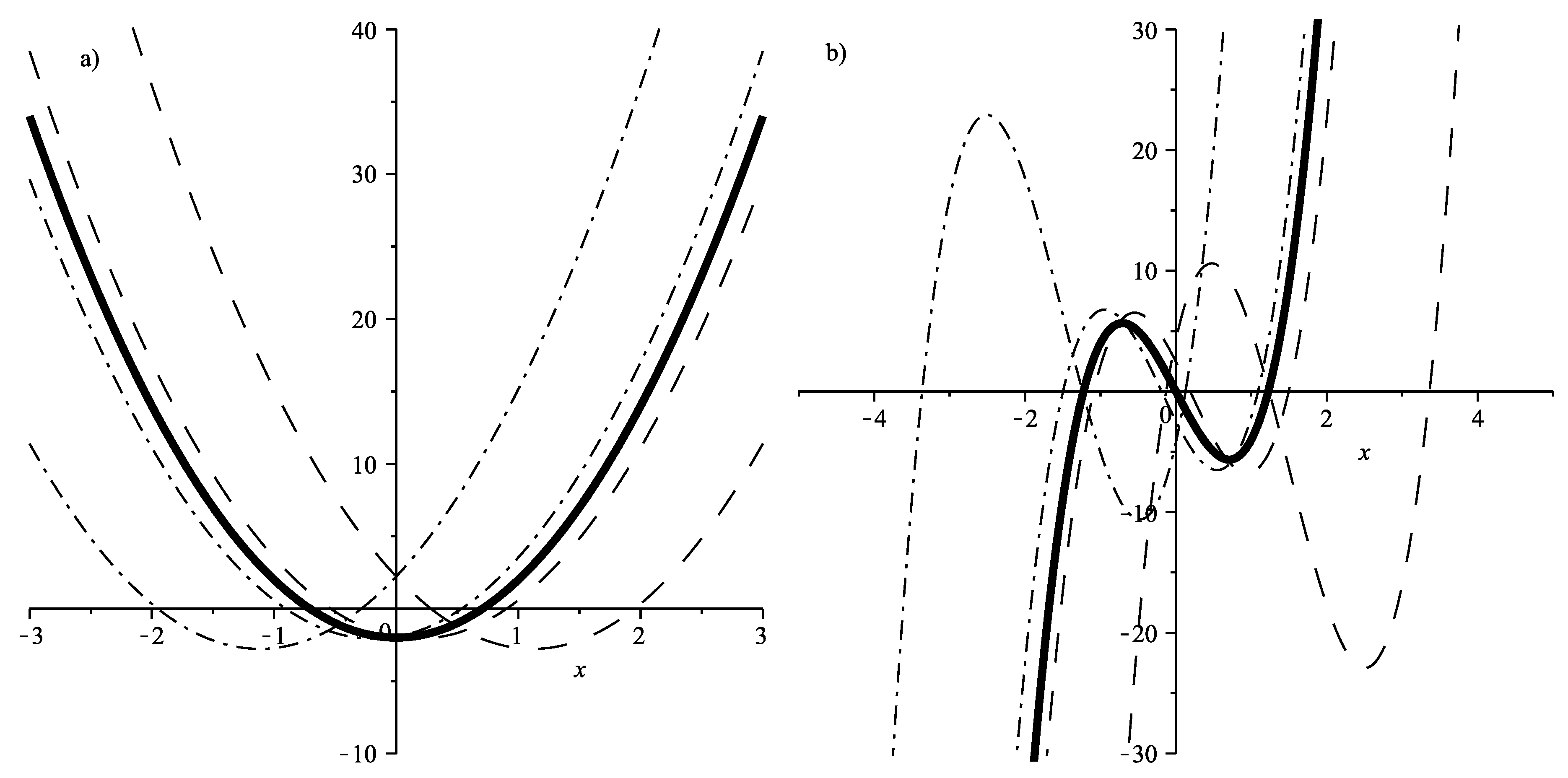
3. Direct Limit Relation between Pseudo-Jacobi and Hermite Polynomials
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Schoutens, W. Stochastic Processes and Orthogonal Polynomials; Springer: New York, NY, USA, 2000. [Google Scholar]
- Koekoek, R.; Lesky, P.A.; Swarttouw, R.F. Hypergeometric Orthogonal Polynomials and Their q-Analogues; Springer: Berlin, Germany, 2010. [Google Scholar]
- Chen, K.Y.; Srivastava, H.M. A limit relationship between Laguerre and Hermite polynomials. Integral Transform. Spec. Funct. 2005, 16, 75–80. [Google Scholar] [CrossRef]
- Koepf, W.; Masjed-Jamei, M. A generic polynomial solution for the differential equation of hypergeometric type and six sequences of orthogonal polynomials related to it. Integral Transform. Spec. Funct. 2006, 17, 559–576. [Google Scholar] [CrossRef]
- Labelle, J. Tableau d’Askey. Lect. Notes Math. 1985, 1171, xxxvi–xxxvii. [Google Scholar]
- Askey, R.; Wilson, J. Some basic hypergeometric orthogonal polynomials that generalize Jacobi polynomials. Mem. Am. Math. Soc. 1985, 54, 319. [Google Scholar] [CrossRef]
- Routh, E.J. On some properties of certain solutions of a differential equation of the second order. Proc. Lond. Math. Soc. 1884, 16, 245–261. [Google Scholar] [CrossRef]
- Romanovski, V.I. Sur quelques classes nouvelles de polynomes orthogonaux. CR Acad. Sci. Paris 1929, 188, 1023–1025. [Google Scholar]
- Masjed-Jamei, M.; Saad, N.; Koepf, W.; Soleyman, F. On the Finite Orthogonality of q-Pseudo-Jacobi Polynomials. Mathematics 2020, 8, 1323. [Google Scholar] [CrossRef]
- Lesky, P.A. Einordnung der Polynome von Romanovski-Bessel in das Askey-Tableau. Z. Angew. Math. Mech. 1998, 78, 646–648. [Google Scholar] [CrossRef]
- Jafarov, E.I.; Nagiyev, S.M.; Oste, R.; Van der Jeugt, J. Exact solution of the position-dependent effective mass and angular frequency Schrödinger equation: Harmonic oscillator model with quantized confinement parameter. J. Phys. A Math. Theor. 2020, 53, 485301. [Google Scholar] [CrossRef]
- Erdelyi, A.; Magnus, W.; Oberhettinger, F.; Tricomi, F.G. Higher Transcendental Functions; McGraw-Hill Book Company, Inc.: New York, NY, USA; Toronto, ON, Canada; London, UK, 1953; Volume I. [Google Scholar]
- Olver, F.W.J.; Daalhuis, A.B.O.; Lozier, D.W.; Schneider, B.I.; Boisvert, R.F.; Clark, C.W.; Miller, B.R.; Saunders, B.V.; Cohl, H.S.; McClain, M.A. (Eds.) NIST Digital Library of Mathematical Functions. Available online: http://dlmf.nist.gov/ (accessed on 15 December 2020).
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics: Non-Relativistic Theory; Pergamon Press: Oxford, UK, 1982. [Google Scholar]
- Ohnuki, Y.; Kamefuchi, S. Quantum Field Theory and Parastatistics; Springer: New York, NY, USA, 1982. [Google Scholar]
- Bouzeffour, F.; Jedidi, W. Fractional Supersymmetric Hermite Polynomials. Mathematics 2020, 8, 193. [Google Scholar] [CrossRef]
- Atakishiyev, N.M.; Suslov, S.K. The Hahn and Meixner polynomials of an imaginary argument and some of their applications. J. Phys. A Math. Gen. 1985, 18, 1583–1596. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jafarov, E.I.; Mammadova, A.M.; Van der Jeugt, J. On the Direct Limit from Pseudo Jacobi Polynomials to Hermite Polynomials. Mathematics 2021, 9, 88. https://doi.org/10.3390/math9010088
Jafarov EI, Mammadova AM, Van der Jeugt J. On the Direct Limit from Pseudo Jacobi Polynomials to Hermite Polynomials. Mathematics. 2021; 9(1):88. https://doi.org/10.3390/math9010088
Chicago/Turabian StyleJafarov, Elchin I., Aygun M. Mammadova, and Joris Van der Jeugt. 2021. "On the Direct Limit from Pseudo Jacobi Polynomials to Hermite Polynomials" Mathematics 9, no. 1: 88. https://doi.org/10.3390/math9010088
APA StyleJafarov, E. I., Mammadova, A. M., & Van der Jeugt, J. (2021). On the Direct Limit from Pseudo Jacobi Polynomials to Hermite Polynomials. Mathematics, 9(1), 88. https://doi.org/10.3390/math9010088





