Abstract
DP-coloring as a generalization of list coloring was introduced by Dvořák and Postle recently. In this paper, we prove that every planar graph in which the distance between 6-cycles is at least 2 is DP-3-colorable, which extends the result of Yin and Yu [Discret. Math. 2019, 342, 2333–2341].
1. Introduction
All graphs are finite and simple in this paper. Let G be a plane graph and V, E, and F be sets of vertices, edges, and faces of G, respectively. Two faces are adjacent if they have a common edge. For a face , we write when the vertices on f in a cyclic order are . A k-vertex (-vertex, -vertex) is a vertex of degree k (at most k, at least k). A k-face (-face, -face) is a face of degree k (at most k, at least k). The notation will be same for cycles. A triangle is a 3-cycle in G. A vertex or an edge of G is triangular when it is on a triangle. We say a chord is triangular in a cycle C if it splits the cycle C into at least one triangle. Let an ()-face be a k-face with . Let ()-edge be an edge with . Let be the length (number of edges) of the cycle C. Let be the number of edges incident with f. Let and denote the sets of vertices lying outside and inside of C, respectively. A cycle C is called separating if and . The distance between two vertices u and v in G is the length (number of edges) of the shortest path between them. The distance between two cycles C and in G is the minimum of the distances between vertices and . A matching of G is a set of independent edges in G.
A proper k-coloring of G is a function such that for every edge . Let , the chromatic number of G, be the smallest k such that G is k-colorable. A list assignment of G is a mapping L that assigns to each vertex a list of colors. An L-coloring of G is a function such that for every and for every edge . A graph G is k-choosable if G has a L-coloring for every assignment L with . Let , the choice number of G, be the smallest k such that G is k-choosable.
It is well known that 3-COLORING is NP-complete for planar graphs. This provides motivation for finding some sufficient conditions for 3-coloring of planar graphs. In 1959, Grötzsch [1] proved that planar graphs with no triangles are 3-colorable. In 1969, Havel [2] asked whether there exists or not a constant d such that if G is a planar graph with the distance of triangles at least d, then G is 3-colorable. Borodin and Glebov [3] proved that every planar graph with no 5-cycles and is 3-colorable. Dvor̂ák, Kral, and Thomas [4] showed that for every planar graph suffices.
List coloring was introduced as a generalization of proper coloring by Vizing [5] and independently by Erdos, Rubin, and Taylor [6]. Thomassen [7] showed that planar graphs with girth at least 5 are 3-choosable. Dvor̂ák [8] proved that planar graphs with the distance of 4-cycles from each other at least 26 are 3-choosable.
There are fewer techniques to approach list problems than ordinary coloring. Identifications of vertices are involved in the reduction configurations for ordinary coloring. However, in list coloring, because different vertices have different lists, it is not possible to use identification of vertices. The concept of DP-coloring as a generalization of list coloring, was introduced by Dvořák and Postle [9].
Definition 1.
Let G be a simple graph, and L be a list assignment of . For each vertex , let . For each edge in G, let be a partial matching between the sets and and let , called the matching assignment. The matching assignment is called a k-matching assignment if for each .
Definition 2.
A -coloring of G is a function ϕ that assigns each vertex a color , such that for every , the vertices and are not adjacent in . We say that G is -colorable if such a -coloring exists.
Definition 3.
The graph G is DP-k-colorable if, for each k-list assignment L and each matching assignment over L, it has an -coloring. The minimum k such that G is DP-k-colorable is the DP-chromatic number of G, denoted by .
If every satisfies , then is straight in a k-matching assignment . Dvořák and Postle [9] proved that planar graphs with no cycles of length from 4 to 8 are 3-choosable and noted that if G is a planar graph with no 4-cycles. Liu and Li [10] proved that planar graphs without adjacent cycles of length at most 8 are 3-choosable. Zhao and Miao [11] proved that every planar graph in which the distance between 5-cycles is at least 2 is DP-3-colorable. Bernshteyn et al. [12,13,14,15,16] gave some results on DP-coloring. DP-3-colorable planar graphs can be found in [17,18] and DP-4-colorable planar graphs can be found in [19,20,21]. Yin and Yu [22] proved planar graphs with no -cycles in which the distance between triangles is at least 2 are DP-3-colorable. We present the following result in this paper.
Theorem 1.
Let G be a planar graph in which the distance between 6-cycles is at least 2. Let be a -cycle in G. Then, for every DP-3-coloring of , there exists a DP-3-coloring of G whose restriction to is .
Corollary 1.
Every planar graph in which the distance between 6-cycles is at least 2 is DP-3-colorable.
Proof.
Let G be a planar graph. By Dvořák and Postle [9], if G is 4-cycle free then G is DP-3-colorable. So, we may assume that G contains a -cycle and the -cycle can be precolored. Then, G has a DP-3-coloring extended from the coloring of the -cycle by Theorem 1 when the distance between 6-cycles is at least 2 in G. □
2. Proof of Theorem 1
To prove Theorem 1, we use the reductio ad absurdum. Let G be a counterexample with the least number of vertices to Theorem 1. If G is 10-cycle free then G is DP-3-colorable by Dvořák and Postle [9]. So, we may assume that G contains a -cycle .
The following Lemma 1 to Lemma 8 are about some crucial properties of the minimal counterexample G.
Lemma 1.
If , then .
Proof.
Let and . Because G is a minimal counterexample, we can first extend of to . Then we can select a color for v such that for each neighbor u of v. Therefore, G has been colored, a contradiction. □
Lemma 2.
is the boundary of the outer face.
Proof.
First, we show that is not separating. For otherwise, if is separating, G can be colored by extending the coloring of to both and , a contradiction. Therefore, either or is empty. Then we may assume that is empty without loss of generality. So is the boundary of the outer face. □
Lemma 3.
There exist no separating -cycles.
Proof.
By Lemma 2, is not a separating -cycle. Let be a separating -cycle in G. Because G is a minimal counterexample, we can first extend of to . Then the coloring of the cycle C can be extended to . Therefore, G has been colored, a contradiction. □
Lemma 4.
Let C be a cycle in G. If , then C has no chord. If C, , has a chord e, then either e is triangular, or e splits C into a 7-cycle and a 4-cycle when , or e splits C into a 8-cycle and a 4-cycle when , or e splits C into a 7-cycle and a 5-cycle when .
Proof.
As the distance between cycles is at least 2 in G, C cannot have a chord if . If , then C can only have a triangular chord. If , then either e is triangular or e splits C into a 7-cycle and a 4-cycle. If , then either e is triangular or e splits C into an 8-cycle and a 4-cycle, or e splits C into a 7-cycle and a 5-cycle. □
Lemma 5.
has no chord.
Proof.
If has a chord e, then e must be one of the cases described in Lemma 4. Because G has no separating -cycles by Lemma 3, G has no other vertices except the vertices on . Then the coloring of is a coloring of G, a contradiction. □
Lemma 6
([18]). Let and H be a subgraph of G. If the vertices of H can be ordered as such that the following hold
- (1)
- , andhas no neighbor in,
- (2)
- and has at least one neighbor outside of H,
- (3)
- for each,has at mostneighbors in,then a DP-k-ofcan be extended to a DP-k-of G.
A vertex is internal if it is not incident with and a face is internal if it contains no vertex on .
Lemma 7.
Let f be an internal 7-face in G. If all vertices on f are vertices with degree 3, then f cannot be adjacent to an internal -face such that all vertices on are 3-vertices.
Proof.
Let and such that is the common edge of f and , and all vertices on f and are vertices with degree 3. Let . Order the vertices in H as . Since f and are internal faces, no vertex in H is on . Because G is a minimal counterexample, we can first extend of to . Then by Lemma 6, the coloring of can be extended to a coloring of G, a contradiction. □
Lemma 8.
Let f be an internal 7-face in G. Let be an internal -face which is adjacent to f. If except one vertex of f, all other vertices on f and are 3-vertices, then each of following holds:
- (a)
- If f contains a (3, 4)-edge and is adjacent to another internal -face with the common (3, 4)-edge, then has another vertex with degree at least 4.
- (b)
- f cannot be adjacent to another internal -face such that all vertices on are 3-vertices.
Proof.
Let and with the common (3, 3)-edge . Since the -cycles in G are at a distance of at least 2 from each other, by symmetry we may assume that the edge is on and .
- (a)
- Suppose otherwise that all vertices in are vertices with degree 3. If , then Let H be the set of vertices listed as: and . If , then Let H be the set of vertices listed as: and . Since f, and are internal faces, no vertex in H is on . Because G is a minimal counterexample, we can first extend of to . Then by Lemma 6, the coloring of can be extended to a coloring of G, a contradiction.
- (b)
- Suppose otherwise that is an internal -face and that all vertices on are 3-vertices. Since f has six vertices with degree 3, by symmetry we assume that . Let u be the neighbor of not on . We can rename the lists of vertices in such that each edge in is straight. Consider the graph obtained from by identifying and u. We claim that no new loops, multiple edges or cycles with length 3, 4, 5 or 6 are created. Otherwise, there is a -path from to u in G, which together with forms a cycle C, . Since is a -face, C cannot be a -cycle.
- If is in see Figure 1a, then C is a separating -cycle, it is a contradiction to Lemma 3.
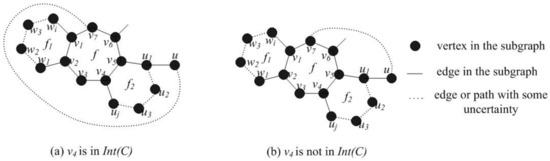 Figure 1. The identification of u and .
Figure 1. The identification of u and . - If is not in see Figure 1b. Since f is a 7-cycle and , by Lemma 3 and 4, must be incident with an edge e in . The other end vertex of e is either on C or not. If it is on C, then e is a chord of C. By Lemma 4, and e is on a -cycle . Then the distance between and is at most 1, a contradiction. If it is not on C, then it is in . So C must be a separating -cycle, it is a contradiction to Lemma 3. Because none of and u is on a -cycle, the -cycles in are at a distance of at least 2 from each other. Now, we claim that no new chord in is formed in . For otherwise, u is on and is adjacent to a vertex on , then there is a path between and u on with length at most five, which forms a -cycle with . Similar to the proof above, it does not occur.Since is still the boundary of the outer face of the embedding of , the coloring of can be extended to by minimality of G. Now keep the colors of all vertices in and color and u with the color of the identified vertex. Now color , and then color with the color of . We can do this because the edges in are straight and the color of is different from the color of and u. If , then we color in the order. If or 6, then we color in the order. Then we obtain a coloring of G, a contradiction.
□
Let be the outer face of the embedding of G. We are now ready to present a discharging procedure. We set the initial charge of every vertex to be , of every face in our fixed plane drawing of G to be , and set . Then by Euler’s Formula.
let and f be a k-face}. A 7-face f is special when f is in and adjacent to two internal -faces. We say a vertex v is rich to a -face f when v is on f and not on a -face which is adjacent to f.
The discharging rules:
(R1): If v is an internal 4-vertex and on a -face f, then v gives to f.
(R2): If v is an internal -vertex, then v gives to its incident -face if any and to its incident 7-face if any.
(R3): Each -face f () gives to its adjacent internal -face if any, to its adjacent internal -face if any, 1 to its adjacent internal -face if any, to its adjacent internal -face if any and to its adjacent internal -face if any.
(R4): Each internal 7-face receives from its incident rich 4-vertex.
(R5): After (R3) and (R4), each -face gives all its remaining charge to .
(R6): The outer face receives from each , gives 1 to each special 7-face if any, 3 to each face in if any, 2 to each face in if any and 1 to each face in if any.
Let denote the final charge of . To lead to a contradiction, we will prove that for all and .
Lemma 9.
For all , .
Proof.
Since receives from each by (R6) whether is positive or not, when v is on . Let v be an internal vertex in G, then by Lemma 1 . If , then .
Because the -cycles in G are at a distance of at least 2 from each other, each vertex can be incident with at most one -face. Let . If v is on a -face f, then v gives to f and to its incident 7-face when v is rich to the 7-face by (R1) and (R4). If v is not on a -face, then by (R4) v gives at most to each incident face. Thus, .
Let . By (R2), v gives to its incident -face if any and at most to each other incident face. Thus, . □
Lemma 10.
For all , .
Proof.
Let . If , then by (R6) f receives 3 from , so . Now let . If contains at least two -vertices, then by (R1) and (R2) f receives from each of the -vertices. So . If contains exactly one -vertex, then f receives from the -vertex and receives from each of its adjacent -faces by (R1), (R2) and (R3). So . If f is an internal -face, then f receives 1 from each of the adjacent -faces by (R3). So .
Let . If , then by (R6) f receives 2 from , so . Now let . If contains at least two -vertices, then f receives from each of the -vertices by (R1) and (R2). So . If contains exactly one -vertex, then f receives from the -vertex and receives from each adjacent -face by (R1), (R2) and (R3). So . If f is an internal -face, then f receives from each adjacent -face by (R3). So .
Let . If , then by (R6) f receives 1 from , so . Now let . If contains a -vertex, then f receives from the -vertex by (R1) and (R2). So . If f is an internal (3, 3, 3, 3, 3)-face, then f receives from each adjacent -face by (R3). So .
Let , by our rules f sends out nothing, so .
Let . By (R3) f needs to give to its adjacent internal -faces if any, to its adjacent internal -faces if any, 1 to its adjacent internal -faces if any, to its adjacent internal -faces if any and to its adjacent internal -faces if any. Since the distance between -cycles is at least 2, f is adjacent to at most internal -faces. If , then .
Let . Since the distance between -cycles is at least 2, f is adjacent to at most 2 internal -faces. Let . If f is adjacent to at most one internal -face, then by R(3) f gives at most 1 to the adjacent -face if any. So . If f is special, then f gives at most 1 to the adjacent -faces and receives 1 from , so . Now let . If f is adjacent to at most one internal -face, then by R(3) f gives at most 1 to the adjacent -face if any. So . Let f be adjacent to two internal -faces. If none of the -faces is a -face, then by R(3) f gives at most to the -faces, so . If one of the -faces has at least two -vertices, then the -face receives nothing from f by (R3), so . So, we assume that f is adjacent to a -face and another -face that has at most one -vertex. By Lemma 7, f has at least one -vertex.
- If shares a -edge with f, then f contains another -vertex . For otherwise, has at least two -vertices by Lemma 8(1), a contradiction. Since and the distance between -cycles is at least 2, f can be adjacent to at most two -faces. So, if , then must be rich and gives to f by (R4). If , then gives to f by (R2). So .
- If shares a -edge with f. If all vertices on are 3-vertices, then f contains at least two -vertices. For otherwise, cannot be a -face that all vertices on are 3-vertices by Lemma 8(2). Since and the distance between -cycles is at least 2, f can be adjacent to at most two -faces. So, if one of the -vertices is a 4-vertex, then it must be rich and gives to f by (R4). If one of the -vertices is a -vertex, then it gives to f by (R2). So . If contains a -vertex, then f has a -vertex because is a (3, 3, 3)-face by Lemma 7. Since and the distance between -cycles is at least 2, f can be adjacent to at most two -faces. So, if , then must be rich and gives to f by (R4). If , then gives to f by (R2). So .
□
Lemma 11.
.
Proof.
Suppose otherwise that . Let denote the set of edges between and . Let be the set of edges which are in but not on -faces. Let be the number of edges in . Let x be the charges that receives by (R5), so . Let be the number of faces in . Since has no chord by Lemma 5, each face in , , and has at least two edges in . Let be the number of special 7-faces. By (R5) and (R6),
Equality holds when each -face in , , and contains two edges in .
We consider the cases.
Case 1. If G has a special 7-face f, then and . Because f is adjacent to two internal -faces and the distance between -cycles is at least 2, so each edge in is in and f shares exactly one vertex or one edge with . So .
- Let. If f is a special 7-face, then each edge in is in and . So . For otherwise if is a -face in , then there must be two -faces adjacent to and containing vertices of , then , a contradiction. Since each special 7-face shares exactly one vertex or one edge with , . By (1), , a contradiction.
- Let. By (1), . If, then , a contradiction. If, then . Since , . Recall , so . Because and , so and . It follows that is adjacent to a -face f which has at least 7 consecutive 2-vertices. So by (R3), a contradiction. If , then . Since , . If , because and , then and . If , then and is adjacent to a -face f which has at least 3 consecutive 2-vertices and is adjacent to the 3-face in . So by (R3), a contradiction. If , then , and is adjacent to a -face f which has at least 8 consecutive 2-vertices. So by (R3), a contradiction. If , because and and , then and . Thus, the two 7-faces in must share an edge in . Then is adjacent to a -face f which has at least 7 consecutive 2-vertices. So by (R3), a contradiction.
Case 2. If G has no special 7-faces, then . Recall that
- Let. By (1), , . Since and the distance between -cycles is at least 2, .
Let. By (1), . If, then , a contradiction. If, then and is adjacent to a -face f which has at least one 2-vertex and is adjacent to two 3-faces in . So by (R3), a contradiction. If , then and . It follows that is adjacent to three -faces and each -face f contains at least one 2-vertex and is adjacent to two 3-faces in . So by (R3), a contradiction.
Let. By (1), . If, then , a contradiction. If, then and is adjacent to a -face f which has at least 2 consecutive 2-vertices and is adjacent to two 3-faces in . So by (R3), a contradiction. If , then and . It follows that is adjacent to two -faces that each -face f contains at least one 2-vertex and is adjacent to two 3-faces in . So by (R3), a contradiction. If , then and . If , then and is adjacent to a -face f which has at least one 2-vertex and is adjacent to two 3-faces in . So by (R3), a contradiction. If , then . It follows that is adjacent to a -face which has at least one 2-vertex and is adjacent to two 3-faces in , and a -face which has at least three 2-vertices and is adjacent to two 3-faces in . So by (R3), a contradiction.
Let. By (1), . If, then , a contradiction. If, then and is adjacent to a -face f which has at least 5 consecutive 2-vertices and is adjacent to the 3-face in . So by (R3), a contradiction. If , then and . It follows that is adjacent to a -face which has at least 6 consecutive 2-vertices and is adjacent to the 3-face in . So by (R3), a contradiction. If , then . If , then then . It follows that is adjacent to a -face f which has at least 2 consecutive 2-vertices and is adjacent to the 3-face in and the 4-face in . So by (R3), a contradiction. If , then and . It follows that is adjacent to a -face which has at least 7 consecutive 2-vertices and is adjacent to the 3-face in . So by (R3), a contradiction. If , then and . If , then . It follows that is adjacent to a -face f which has at least 2 consecutive 2-vertices and is adjacent to the 3-face in and the 5-face in . So by (R3), a contradiction. If , then . If , then . It follows that is adjacent to two -faces and each -face f contains at least one 2-vertex and is adjacent to the 3-face in and the 4-face in . So by (R3), a contradiction. If , then and is adjacent to a -face f which has at least 8 consecutive 2-vertices and is adjacent to the 3-face in . So by (R3), a contradiction.
Let, then . For otherwise that . Since and , .
Let . By (1), . If , then , a contradiction. If , then and is adjacent to a -face f which has at least 2 consecutive 2-vertices and is adjacent to the 4-faces in . Thus, by (R3), a contradiction.
Let. By (1), . If, then , a contradiction. If, then and is adjacent to a -face f which has at least 5 consecutive 2-vertices and is adjacent to the 4-face in . So by (R3), a contradiction. If , then , and is adjacent to a -face f which has at least 6 consecutive 2-vertices and is adjacent to the 4-face in . So by (R3), a contradiction. If , then , and is adjacent to a -face f which has at least 7 consecutive 2-vertices and is adjacent to the 4-face in . So by (R3), a contradiction.
Let, then . For otherwise that . Since and , .
Let. By (1), . If, then , a contradiction. If, then and is adjacent to a -face f which has at least 5 consecutive 2-vertices and is adjacent to the 5-face in . So by (R3), a contradiction. If , then , and is adjacent to a -face f which has at least 6 consecutive 2-vertices and is adjacent to the 5-face in . So by (R3), a contradiction.
Let, then . For otherwise that . Since and , . If , then , a contradiction. If , then and is adjacent to a -face f which has at least 5 consecutive 2-vertices and is adjacent to the 6-face in . So by (R3), a contradiction.
- Let. By (1), , . Since , .
Let. By (1), . If, then , a contradiction. If, then . It follows that is adjacent to a -face f which has at least 4 consecutive 2-vertices. So by (R3), a contradiction.
Let. By (1), . If, then , a contradiction. If, then . It follows that is adjacent to a -face f which has at least 7 consecutive 2-vertices. So by (R3), a contradiction. If , then . So . If , then and is adjacent to a -face f which has at least 3 consecutive 2-vertices and is adjacent to the 3-face in . So by (R3), a contradiction. If , then and . It follows that is adjacent to a -face f which has at least 8 consecutive 2-vertices. So by (R3), a contradiction. If , then . So . If , then and is adjacent to a -face f which has at least one 2-vertex and is adjacent to the 3-faces in . So by (R3), a contradiction. If , then and . It follows that is adjacent to two -faces. If one of the -faces f is a -face and contains at least 5 consecutive 2-vertices, then by (R3), a contradiction. For otherwise that all of -faces contain at least 3 consecutive 2-vertices and are adjacent to the 3-face in , then by (R3), a contradiction. If , then . So . If , then and is adjacent to a -face f which has at least 3 consecutive 2-vertices and is adjacent to the 4-face in . So by (R3), a contradiction. If , then , and is adjacent to a -face f which has at least 9 consecutive 2-vertices. So by (R3), a contradiction. □
Proof
(Proof of Theorem 1). From Lemmas 9–11, , a contradiction to Euler’s Formula. Thus, the counterexample G cannot exist. So, Theorem 1 is true. □
3. Conclusions
The coloring theory of graphs is useful in many fields, such as discrete mathematics, allocation of wireless communication channels, combinatorial optimization, computer theory.
It is well known that 3-COLORING is NP-complete for planar graphs. This provides motivation for finding some sufficient conditions for 3-coloring of planar graphs. DP-coloring is a stronger version of list coloring. Proving a planar graph to be DP-3-colorable is harder than proving a planar graph to be 3-colorable.
It is unknown if there exists a planar graph in which the distance between 6-cycles at least 1 is not DP-3-colorable.
Author Contributions
Y.Z. designed the problem and wrote the paper. L.M. validates the results. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (No.11771443 and 12071265).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Grötzsch, H. Ein Dreifarbensatz für dreikreisfreie Netze auf der Kugel. Math.-Natur. Reihe 1959, 8, 109–120. [Google Scholar]
- Havel, I. On a Conjecture of B. Grünbaum. J. Comb. Theory 1969, 7, 184–186. [Google Scholar] [CrossRef]
- Borodin, O.V.; Glebov, A. Planar Graphs with Neither 5-Cycles Nor Close 3-Cycles Are 3-Colorable. J. Graph Theory 2010, 66, 1–31. [Google Scholar] [CrossRef]
- Dvořák, Z.; Kral, D.; Thomas, R. Three-coloring triangle-free graphs on surfaces V. Coloring planar graphs with distant anomalies. J. Comb. Theory Ser. B 2020. [Google Scholar] [CrossRef]
- Vizing, V. Vertex colorings with given colors. Metody Diskret. Analiz Novosib. 1976, 29, 3–10. [Google Scholar]
- Erdos, P.; Rubin, A.; Taylor, H. Choosability in graphs. Congr. Numer. 1979, 26, 125–157. [Google Scholar]
- Thomassen, C. 3-list-coloring planar graphs of girth 5. J. Comb. Theory Ser. B 1995, 64, 101–107. [Google Scholar] [CrossRef]
- Dvořák, Z. 3-choosability of planar graphs with(≥4)-cycles far apart. J. Comb. Theory Ser. B 2014, 104, 28–59. [Google Scholar] [CrossRef]
- Dvořák, Z.; Postle, L. Correspondence coloring and its application to list-coloring planar graphs without cycles of length 4 to 8. J. Comb. Theory Ser. B 2018, 129, 38–54. [Google Scholar] [CrossRef]
- Liu, R.; Li, X. Every planar graph without adjacent cycles of length at most 8 is 3-choosable. Eur. J. Combin. 2019, 82, 102995. [Google Scholar] [CrossRef]
- Zhao, Y.; Miao, L. Every Planar Graph with the Distance of 5□-Cycles at Least 3 from Each Other Is DP-3-Colorable. Mathematics 2020, 8, 1920. [Google Scholar] [CrossRef]
- Bernshteyn, A. The asymptotic behavior of the correspondence chromatic number. Discret. Math. 2016, 339, 2680–2692. [Google Scholar] [CrossRef]
- Bernshteyn, A.; Kostochka, A. Sharp Dirac’s Theorem for DP-critical graphs. J. Graph Theory 2018, 88, 521–546. [Google Scholar] [CrossRef]
- Bernshteyn, A.; Kostochka, A.; Zhu, X. DP-colorings of graphs with high chromatic number. Eur. J. Combin. 2017, 65, 122–129. [Google Scholar] [CrossRef]
- Bernshteyn, A.; Kostochka, A. On differences between DP-coloring and list coloring. Sib. Adv. Math. 2018, 21, 62–71. [Google Scholar] [CrossRef]
- Bernshteyn, A.; Kostochka, A.; Pron, S. On DP-coloring of graphs and multigraphs. Sib. Math. J. 2017, 58, 28–36. [Google Scholar] [CrossRef]
- Liu, R.; Loeb, S.; Rolek, M.; Yin, Y.; Yu, G. DP-3-coloring of planar graphs without 4, 9-cycles and cycles of two lengths from {6; 7; 8}. Graphs Combin. 2019, 35, 695–705. [Google Scholar] [CrossRef]
- Liu, R.; Loeb, S.; Yin, Y.; Yu, G. DP-3-coloring of some planar graphs. Discret. Math. 2019, 342, 178–189. [Google Scholar] [CrossRef]
- Kim, S.J.; Ozeki, K. A Sufficient condition for DP-4-colorability. Discret. Math. 2018, 341, 1983–1986. [Google Scholar] [CrossRef]
- Chen, L.; Liu, R.; Yu, G.; Zhao, R.; Zhou, X. DP-4-colorability of two classes of planar graphs. Discret. Math. 2019, 342, 2984–2993. [Google Scholar] [CrossRef]
- Liu, R.; Li, X.; Nakprasit, K.; Sittitrai, P.; Yu, G. DP-4-colorability of planar graphs without adjacent cycles of given length. Discret. Appl. Math. 2020, 277, 245–251. [Google Scholar] [CrossRef]
- Yin, Y.; Yu, G. Planar graphs without cycles of lengths 4 and 5 and close triangles are DP-3-colorable. Discret. Math. 2019, 342, 2333–2341. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).