2. MABPSP Model and Its Semi-Markov MARBP Reformulation
A decision-maker ponders how to prioritize the allocation of effort to M dynamic and stochastic projects that are labelled by , one of which must be engaged (active) at each of a sequence of decision periods , with and as , while others are rested (passive). Switching projects on and off entails setup and setdown delays and costs, respectively. A setup (resp. setdown) delay on a project is necessarily followed by a period in which the project is worked on (resp. rested), i.e., the times at which a setup or a setdown delay are completed are not decision periods. We will say that a project is “active” when it is either being engaged (worked upon) or undergoing a setup or a setdown delay. Let and denote the prevailing state, which belongs to the finite state space , and action for project m at time t (: active; : passive), and let denote the previously chosen action, with indicating the initial setup status.
While project
m is passive, it neither accrues rewards nor changes state. Switching it on when it lies in state
entails a lump setup cost
, followed by a random setup delay of duration
periods, whose
z-transform is
, over which no rewards are earned. After such a setup, the project must be engaged, yielding a reward
, after which its state moves at the next period to
with transition probability
. After at least one period in which the project is engaged, it may be decided to switch it off. If this is done when the project lies in state
, then a lump setdown cost
is incurred, followed by a random setdown delay of duration
with
z-transform
, over which no rewards accumulate. Subsequently, the project remains passive for one or more periods. Note that setup delay distributions are allowed to be state-dependent, whereas setdown delay’s are not (cf.
Section 2.1). Rewards and costs are geometrically time-discounted with factor
. We write, in what follows, the above
z-transforms evaluated at
simply as
and
.
Actions are prescribed through a
scheduling policy , which is chosen from the class
of policies that are
admissible, i.e., nonanticipative with respect to the history of states and actions, and engaging one project at a time. The MABPSP (cf.
Section 1) is concerned with finding an admissible scheduling policy that attains the maximum expected total discounted reward net of switching costs.
This problem can be cast into the framework of
semi-Markov decision problems (SMDPs) by including into the state of each project
m the last action taken, i.e., by using the
augmented state , which belongs to the
augmented state space . Thus, one obtains a multidimensional SMDP having
joint state and
joint action . This is a special type of semi-Markov MARBP (cf.
Section 1), as the constituent projects become restless in such a reformulation.
Rewards and dynamics for the reformulated project
m are as follows, where
and
denote the
one-stage (i.e., from
to
) expected reward and transition probability, which results from taking action
in state
. On the one hand, if, in period
, the project lies in state
and it is again engaged, it yields the reward
and its state transitions at
to
with probability
. If, instead, the project is switched off, it gives the reward
and its state moves at
to
with probability 1, i.e.,
. On the other hand, if the project occupies at time
the state
and is then switched on, it yields the expected reward
until the following decision time
, in which the project state transitions to
with probability
. If the project is kept idle, then it gives no reward, i.e.,
, and its state remains frozen up to
, so
.
Thus, the MABPSP of concern is formulated as the semi-Markov MARBP
where
is expectation under policy
conditioned on starting from the joint state
.
2.1. Reduction to the Case with No Setdown Penalties
We next show that one can restrict attention with no loss of generality to the case that there are no setdown penalties, which will allow for us to simplify subsequent analyses. Imagine that, say, at time
, a passive project is set up and is then worked on for a random number of periods determined by a stopping time
, after which it is set down. Dropping the label
m, denote, by
,
, and
, the active reward vector, and the setup and setdown cost vectors. Denote, by
, the setup delay
z-transform vector and by
the constant setdown delay transform, both evaluated at
. The total discounted expected net reward that is obtained from the project over such a time interval, starting from the augmented state
, is
where
is the setup delay. The corresponding discounted
active time expended on the project is
where, as pointed out above, the setup and setdown delays
and
are both considered to be active time.
In the next result, which extends Lemma 3.4 of [
27] to the present setting,
is the identity matrix indexed by
,
,
is a vector of zeros, and
.
Lemma 1. - (a)
.
- (b)
.
Proof. (a) Use the identity
to write
(b) This part follows by writing
□
Lemma 1 can be used in order to eliminate setdown penalties: it suffices to incorporate them into new setup costs, setup delay transforms, and active rewards, while using the transformations
Note that such a reduction would not have been accomplished had the setdown delay transform not been constant. In the case
and
, we obtain
and
.
Accordingly, we will focus henceforth on the normalized case without setdown penalties , .
2.2. The AT Index
We next consider the AT index of a project with setup penalties—dropping again the label
m—extending the original definitions in [
10]. The continuation AT index is
where
is a stopping time for engaging the project starting in state
i when it is already set up; hence,
is just the project’s Gittins index. As for the switching AT index, it is given by
where now
is a stopping-time rule that is followed after the project has been set up in state
i.
The following requirements will be assumed henceforth on setup costs and setup delay transforms, which extend the corresponding conditions in [
10].
Assumption 1. The following holds:
- (i)
non-negative setup costs: for .
- (ii)
non-negative rewards: If some setup delay can be positive, i.e., , then for .
The next result shows that Assumption 1 ensures the satisfaction of the hysteresis property in (
1).
Lemma 2. Under Assumption 1, for .
Proof. For a given state
and stopping-time rule
as above, write
and
. Now, Assumption 1 ensures that
and
, and hence
Further, (
9), (
7), and (
8) immediately yield that
, which completes the proof. □
3. New Methodological Results on Restless Bandit Indexation
This section presents new results on restless bandit indexation, which, besides having an intrinsic interest, are required and form the basis for the approach to non-restless bandits with switching times that is deployed in later sections.
3.1. Indexable Restless Bandits and the Whittle Index
Consider a semi-Markov restless bandit, representing a dynamic and stochastic project whose state transitions over time periods through the finite state space . The project’s evolution is governed by a policy that is taken from the class of nonanticipative randomized policies, which, at each of an increasing sequence of decision periods with and as , prescribes an action that determines the status during the ensuing stage until the next decision period (1: active; 0: passive). Taking action at time when the project occupies state has the following consequences over the following stage, relative to a given one-period discount factor : an expected total discounted amount of reward and of a generic resource is earned and expended, respectively; further, the joint distribution of the stage’s duration and its final state is given through the discounted transition transform , where denotes an event indicator.
It will be convenient to partition
into the (possibly empty) set of
uncontrollable states
where both actions entail identical resource consumptions and dynamics, and the remaining set
of
controllable states, which is assumed to consist of
elements. The notation
is meant to reflect the convention that the passive action
is chosen in uncontrollable states.
The value of the rewards earned and amount of resource expended by a policy
starting from state
y is evaluated, respectively, by the discounted reward and resource consumption metrics
Let us introduce a parameter
representing the resource unit price, and consider the
λ-price problem
which concerns finding a policy that maximizes the value of rewards earned minus the cost of resources expended. Because (
10) is an infinite-horizon finite-state and -action SMDP, by standard results it is solved by stationary deterministic policies that are characterized by the solutions to the following DP equations, where
denotes the optimal value starting from
y under price
:
Such a project is said to be
indexable (cf. [
29]), if, for each controllable state
, there exists a unique break-even price
, such that: it is optimal to engage the project in state
y if and only if
, and it is optimal to rest it if and only if
. Or, in terms of the DP Equation (
11),
and
We will refer to the mapping
as the project’s
Whittle index. See [
29].
3.2. Exploiting Special Structure: Indexability Relative to a Family of Policies
While one can readily numerically test whether a given restless bandit instance is indexable, a researcher investigating a particular restless bandit model will instead be concerned with analytically establishing its indexability under an appropriate range of model parameters. The key to achieving such a goal is—as in optimal-stopping problems—to exploit special structure by
guessing a family of policies (stationary deterministic), among which there exists an optimal policy for (
10) for every resource price
.
We represent a stationary deterministic policy by its
active (state) set, consisting of those controllable states where it prescribes engaging the project. Thus, a family of such policies is given as a family
of active sets
, and, hence, we will refer to the family of
-policies. Relative to such a family, we will call the project
-indexable if (i) it is indexable, and (ii)
-policies are optimal for
-price problem (
10) for every resource price
.
We will impose the following connectivity requirements on .
Assumption 2. The active-set family satisfies the following conditions:
- (i)
- (ii)
for any , with , there exist such that
- (iii)
for any ,
Note that condition (iii) in Assumption 2 means that is a lattice relative to set inclusion. As for condition (ii), it ensures that any two nested active sets with can be connected by an increasing chain of adjacent (i.e., differing by one state) sets in . Further, condition (i) ensures that one can connect in such a fashion ∅ with . We will call a set family satisfying Assumption 2(ii, iii) a monotonically connected lattice.
3.3. New Sufficient Conditions for -Indexability and Adaptive-Greedy Index Algorithm
Suppose that, for a particular restless bandit model, a suitable active-set family
, as above, has been posited relative to which one aims to analytically establish
-indexability. While, in the aforementioned earlier work of the author, sufficient conditions for
-indexability are given, which further ensure that the project’s Whittle index can be computed by using an adaptive-greedy index algorithm that was introduced in such work, we next introduce new sufficient conditions that are significantly less restrictive.The new conditions are motivated by the model of concern in this paper, as we will see that it need not satisfy the former conditions, as mentioned in
Section 1.
In order to formulate the new conditions and the index algorithm we need to define certain
marginal metrics, as follows. Given an action
and active set
, write, as
, the policy that initially chooses action
a, and then follows the
S-active policy. For a given state
y and active set
S, consider the
marginal work metric
which represents the marginal increase in the amount of resource expended resulting from taking first the active rather than the passive action and, then, following the
S-active policy. Note that such a marginal work metric vanishes at uncontrollable states:
Further, define the
marginal reward metric
which represents the marginal increase in rewards earned. Finally, for
, define the
marginal productivity metricWe will consider the adaptive-greedy index algorithm that is given in Algorithm 1 in its top-down version, where index values are meant to be computed from highest to lowest; one could similarly consider the symmetric bottom-up version. Such an algorithm has a very simple structure, as it constructs in n steps (recall that ), an increasing chain of successive active sets in , proceeding at each step in a greedy fashion. Thus, once active set has been obtained, the next active set is constructed by augmenting with a controllable state that maximizes marginal productivity metric , restricting attention to states y for which the following active set is in , so . Ties are broken arbitrarily.
Note that Algorithm 1 only shows an algorithmic scheme, as it is not specified how to compute the metrics that are required for computations. A complete fast-pivoting implementation of such an algorithm is given by the author in [
49].
Additionally, note that the algorithm’s input consists of all the project’s primitive parameters, namely states, rewards, transition probabilities, and discount factor.
The same considerations apply to Algorithm 2.
| Algorithm 1: Top-down adaptive-greedy index algorithm . |
Output: for to N do choose ; end { for } |
The main result of this section, giving the new indexability conditions and ensuring the validity of the adaptive-greedy index algorithm for computing the Whittle index, is stated next.
| Algorithm 2: Geometrically intuitive reformulation of adaptive-greedy index algorithm . |
Output: for to N do choose ; end { for } |
Theorem 1. The following holds:
- (a)
Suppose that the project satisfies the following conditions:
- (i)
for every active set or, equivalently, for every nested active-set pair with , - (ii)
for every resource price , there exists an optimal -policy for λ-price problem (
10).
Then, the project is -indexable and algorithm computes its Whittle index in non-increasing order.
- (b)
If the project is indexable, then it satisfies conditions (i) and (ii) in part (a) for some nested family of adjacent active sets of the form with .
In order to prove Theorem 1, we need to establish a number of preliminary results. Before doing so, let us clarify the improvement that the new sufficient
-indexability conditions (i) and (ii) in Theorem 1(a) represent over those that were introduced in Niño-Mora [
30,
31] based on PCLs, which are:
- (i)
for every , for ;
- (ii)
algorithm computes index in non-increasing order: .
Thus, the new condition (i) in Theorem 1(a), as formulated in (
16), is significantly less stringent than the old condition (i). Further, the reformulation in (
17) clarifies its intuitive meaning: it means that resource consumption metric
is monotone non-decreasing in the active set
S within the domain
, and that two nested active sets
in
give different resource consumption vectors
and
.
As for the old condition (ii), the author has found that, in complex models with a multidimensional state, it can be elusive to establish it analytically. In contrast, the new condition (ii) in Theorem 1(a) allows one either to draw on the rich literature available on optimality of structured policies for special models, or to deploy ad hoc DP arguments to prove the optimality of -policies for the model at hand.
Note that [
50] has proposed sufficient
-indexability conditions, which are, however, significantly more restrictive than those herein. Thus, the conditions in [
50] require, among further assumptions, including (i) and (ii) in Theorem 1(a), that the resource metric be submodular and reward metric be supermodular in the active set. Theorem 1(a) shows that such extra assumptions are unnecessary.
Theorem 1(b) further assures that the new conditions are also necessary for indexability, in the sense that any indexable restless bandit satisfies them relative to some nested active-set family , as stated.
We start by establishing the equivalence between the formulations in (
16) and (
17) of condition (i) in Theorem 1(a), by drawing on the results in Niño-Mora (Sect. 6 of [
31]) (for Markovian restless bandits) and in Niño-Mora (Sect. 4 of [
32]) for semi-Markov restless bandits. These refer to relations between resource and reward metrics and their marginal counterparts, via
state-action occupancy measuresNote that
measures the expected total discounted number of decision periods, in which action
a is chosen in state
while using policy
, starting from state
y. In the present notation, the relevant relations are
and
Lemma 3. Conditions (
16)
and (
17)
in Theorem 1(a)
are equivalent. Proof. Suppose that (
16) holds for a certain
. We then have, on the one hand, that
for
such that
, along with
for any
y, implies, via the first identity in (
19), that
; further, by taking
, we obtain
, since
. Hence, we have
, for such
. On the other hand, we have that
for
such that
, along with
for any
y, implies, via the second identity in (
19), that
; further, by taking
, we obtain
, since
. Hence, we have
for such
. Now, the proven relations imply (
17) via Assumption 2(ii).
Conversely, suppose that (
17) holds for a certain
. Then, on the one hand, we have
for
such that
. This, along with
for every
y implies, via the first identity in (
19), that
for such
. On the other hand, we have
for
such that
. This, along with
for every
y implies, via the second identity in (
19), that
for such
. Therefore, (
16) holds, which completes the proof. □
3.4. Proving Theorem 1: Achievable Resource-Reward Performance Region Approach
We next deploy an approach in order to prove Theorem 1, which draws on first principles via an intuitive geometric and economic viewpoint introduced in [
31,
32]. We will find it convenient to consider, instead of (
10), the
-price problem that is obtained by using the averaged resource and reward metrics where the initial project state
is drawn from a distribution
p with positive probability mass
at every state
,
i.e.,
Relative to such metrics, consider the project’s
achievable resource-reward performance region
which is defined as the region in the resource-reward plane that consists of all the performance points
that can be achieved under admissible project operating policies
. The optimality of stationary deterministic policies for infinite-horizon finite-state and -action SMDPs ensures that
is the
closed convex polygon spanned as the
convex hull of points
for active sets
. Thus, we can reformulate
-price problem (
22) as the
linear programming (LP) problem
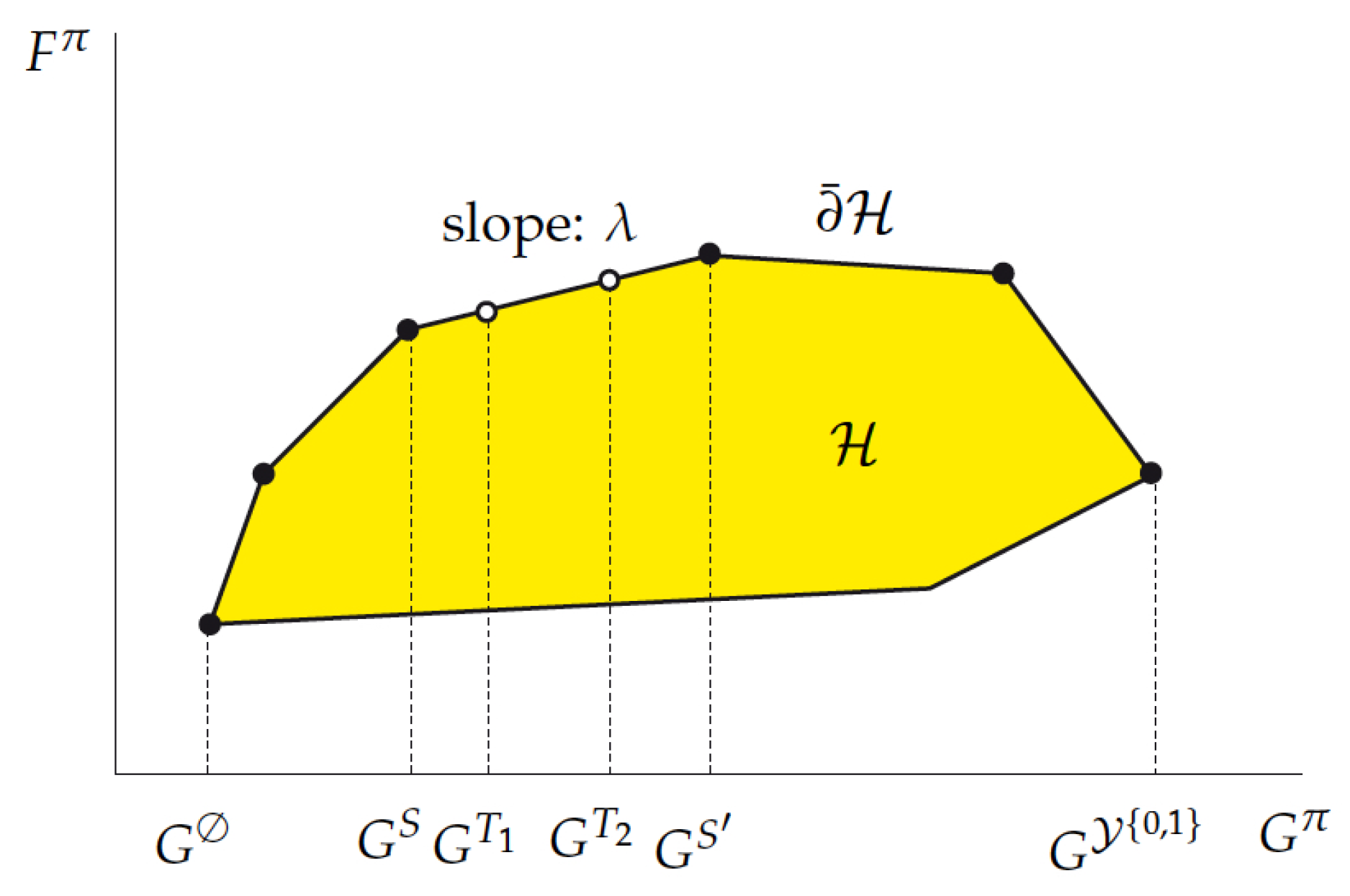
In order to illustrate and clarify such an approach, consider the concrete example of a certain restless bandit having state space
that is discussed in (Sec. 2.2 of [
34]) For such a project,
Figure 1, in that paper, plots the achievable resource-reward performance region
, with points
being labeled by their active sets
S.
The fact that such a project is indexable is apparent from the structure of the
upper boundary of
,
as this is determined from left to right by an
increasing nested family of adjacent active sets connecting ∅ to :
. Thus, the Whittle indices of the states are given by the successive
slopes measuring the
marginal reward versus resource trade-off rates:
In this example, the geometry of the top-down adaptive-greedy algorithm
corresponds to traversing the upper boundary
from left to right, proceeding, at each step, by augmenting the current active set by a new state in a locally greedy fashion, as the slopes in (
26) are equivalently formulated as
The insights that are conveyed by such an example extend to the general setting of concern herein, as elucidated in Niño-Mora [
31,
32,
34]. Thus, the indexability of a project is recast as a property of the upper boundary
of region
, whereby it is determined by a nested active-set family as in the example. Note that the equivalence between the geometric slopes in (
27) and the marginal productivity rates (
26) in follow from (
19) and (
20) or, more precisely, from the corresponding relations for the averaged metrics,
and
where
is the state-action occupancy measure that is obtained by drawing the initial state according to the probabilities
. Thus, assuming condition (i) in Theorem 1(a), we have, for
,
Such relations allow for us to reformulate the adaptive-greedy algorithm in Algorithm 1 into the geometrically intuitive form that is shown in Algorithm 2. Such a reformulation clarifies that this algorithm seeks to traverse, from left to right, the upper boundary , proceeding at each step by augmenting the current active set by a new state in a locally greedy fashion, while only using active sets in .
We next proceed to establish a number of preliminary results, on which the proof of Theorem 1 will draw. The first shows that the family of optimal active sets for the -price problem is a lattice that contains its intervals.
Lemma 4. If S and are optimal active sets for (
22)
, then so is any satisfying Proof. The result is an immediate property of the DP Equations (
11) characterizing the optimal stationary deterministic policies (i.e., the optimal active sets) for the
-price problem. □
The following result shows that, under condition (i) in Theorem 1(a), resource consumption metric is strictly increasing relative to active-set inclusion in the domain .
Lemma 5. Suppose that condition (i) in Theorem 1(a) holds. Then, for , .
Proof. The result follows immediately from the formulation of such a condition (i) in (
17), along with the assumption of positive initial state probabilities
for
. □
The next result establishes, under conditions (i) and (ii) in Theorem 1(a), the non-degeneracy of the extreme points of in upper boundary , showing that each is achieved by a unique active set in .
Lemma 6. Suppose that conditions (i) and (ii) in Theorem 1(a) hold. Then, for every that is an extreme point of , there exists a unique active set achieving it, i.e., with .
Proof. Because
is an extreme point of
in
, there exists a resource price
, such that
is the unique solution to the LP problem (
24) for
. Now, condition (ii) in Theorem 1 ensures that there exists an active set
that is optimal for
-price problem (
22), i.e., such that
. Let us argue, by contradiction, that such an active set is unique, assuming that there exists a different active set
, for which
. Then, by Assumption 2(iii) and Lemma 4, both
and
would belong in
and be optimal for the
-price problem. Therefore,
Now, since it is assumed that
, there are two cases to consider: in the first case, if it were
, then it would be
and, hence, by Lemma 5,
, which contradicts (
31). In the second case, if it were
, then it would be
and, hence, by Lemma 5,
, which again contradicts (
31). Therefore, there cannot exist such an
, which completes the proof. □
We can now prove Theorem 1.
Proof of Theorem 1. (a) We will show that the project is
-indexable by using the geometric characterization of indexability that is reviewed in the present section. Namely, by showing that the upper boundary
is determined by an increasing nested family of adjacent active sets in
connecting ∅ to
. We refer the reader to the plot shown in
Figure 1 for a geometric illustration of the following arguments.
Let us start by showing that the extreme points of
, which determine
, are attained, from left to right, by a unique increasing chain of active sets in
—not necessarily adjacent. Thus, consider two adjacent extreme points of
in
, i.e., joined by a line segment in
. By Lemma 6, there exist two unique and distinct active sets
, whose performance points
and
achieve such extreme points, where we assume, without loss of generality, that
. We will show that it must be
. Letting
be the slope of the line segment joining such extreme points we have that both
S and
solve the
-price problem and, hence, by Lemma 4, so do
and
. Now, from the stated properties of
S and
, it follows that points
and
must lie in the line segment joining
and
and, hence,
. Further, since, by Assumption 2(iii)
, Lemma 5 gives that
and
. Therefore,
We next argue, by contradiction, that
: if such were not the case, i.e.,
, then it would follow that
and, hence, by Lemma 5,
, contradicting (
32).
Let us next show that, if any two adjacent extreme points and in , with , are determined by active sets in such a chain that are not adjacent, they can be connected from left to right by points in that are attained by an increasing chain of adjacent active sets in . On the one hand, Assumption 2(ii) ensures the existence of an increasing chain of active sets in that are adjacent and connect S to : . On the other hand, if is the slope of the line segment joining such extreme points, then we have that both S and solve the -price problem and, hence, by Lemma 4, so does every intermediate active set in such a chain. Hence, Lemma 5 ensures that , as required.
In order to establish -indexability, it only remains to show that the leftmost (resp. rightmost) extreme point of in is that attained by active set (resp. ). This follows from Assumption 2(i), condition (ii) in Theorem 1(a), and Lemma 5 (ensuring that for , ).
Having established -indexability, the result that algorithm computes the project’s Whittle index follows immediately from the algorithm’s geometric interpretation, as revealed by its reformulation in Algorithm 2.
(b) Suppose now that the project is indexable. Then, is determined by some increasing chain of adjacent active sets connecting ∅ to : . Letting , it is readily seen that such an active-set family satisfies conditions (i) and (ii) in part (a). This completes the proof. □
4. Application to Projects with Setup Delays and Costs
This section deploys the framework and results above on restless bandit indexation in our motivating model: the restless bandit reformulation of a non-restless bandit with setup costs and delays (and no setdown penalties: cf.
Section 2.1), as discussed in
Section 2. The project label
m is dropped thereafter from the notation.
In this reformulation, all of the augmented states are controllable, i.e.,
, and an active-state subset of the augmented state space
representing a stationary deterministic policy is given by specifying the original-state subsets
, such that the project is engaged when it was rested (resp. engaged) previously if the state
belongs to
(resp. in
). We will denote such an active set/policy, as in [
27], by
We next address the issue of guessing an appropriate family
of active sets
, which contains optimal active sets for the
-price problem of concern (cf. (
10)), which is now formulated as
where
and
are the reward and resource (work) metrics that are given by
The intuition that, under Assumption 1, if engaging the project is optimal when it was not set up, then engaging it should also be optimal when it was set up, leads us to posit the following choice of
:
Such an represents a family of policies that satisfies Assumption 2. If , policy has the hysteresis region , i.e., when the original state lies in the policy sticks to the previously chosen action. We will seek to prove indexability with respect to such a family of policies, i.e., -indexability.
Note that the marginal work, reward, and productivity metrics defined in general by (
12)–(
15) now take the form
and, for
,
We next adapt to the present setting the general top-down adaptive-greedy algorithm
in Algorithm 1, which yields the algorithm in Algorithm 3, where
is now the number of project states in the non-restless formulation. The output of the algorithm has been decoupled, noting that, at every step, the algorithm expands the current active set
by adding a state that can be either of the form
or
. Thus, instead of using a single counter
k, ranging from 0 to
, two counters
are used, with such counters being related by
. Henceforth, we use a more algorithm-like notation, writing, e.g.,
as
. Note that the active sets
and
that are generated in the algorithm are given by
and
, and satisfy
, for
, consistently with (
35). Thus, the algorithm produces a decoupled output consisting of two augmented-state strings strings
and
, which jointly span
, along with corresponding switching and continuation index values
and
.
| Algorithm 3: Adaptation of index algorithm to the present model. |
Output: , ; ; ; while do if choose if choose if or ; ; ; else ; ; ; end { if } end { while } |
4.1. Proving That -Policies Are Optimal
We next aim to establish that condition (ii) in Theorem 1(a) is satisfied by the present model, i.e., that
-policies, i.e., those with active sets
that are defined by (
35), suffice to solve the
-price problem (
33) for any price
. We will use the DP optimality equations that characterize the optimal value function
for problem (
33), starting from each augmented state
: thus, for each original state
,
We start by showing that the optimal value function is non-negative.
Lemma 7. .
Proof. Because no setdown penalties are assumed (cf.
Section 2.1), a possible course of action incurring zero net reward is to set down the project and keep it that way, which yields the result. □
We can now prove the optimality of -policies.
Lemma 8. For every , there exists an optimal active set for λ-price problem (
33).
Proof. Fix
and
. It suffices to show that, if resting the project is optimal in state
, then it is also optimal doing so in state
. Let us formulate that hypothesis, as
We aim to show that, then, it is optimal resting the project in state
, so
Consider first the case
. We will argue, by contradiction, that hypothesis (
40) then cannot hold, i.e., it cannot be optimal to rest the project once it is active. Drawing on non-restless bandit theory, note that, when the project is active, it is optimal to rest it only if it ever reaches an original state
at which
, where
is the original (non-restless) bandit’s Gittins index. Assumption 1(ii) now assures us that
for each
, and, therefore, it is optimal to keep the project active forever.
Next, consider the case
. Then, the following chain of inequalities holds:
where the fact that the second inequality holds is apparent by reformulating it as
and noting that Assumption 1(ii) and Lemma 7, ensure that the latter inequality left-hand side is non-negative, and, further, Assumption 1(i) and
ensure non-positivity of its right-hand side. This completes the proof. □
4.2. Work Metric Analysis and -Indexability Proof
We now consider how to calculate work and marginal work metrics and , by relating them to the corresponding metrics and for the underlying non-restless project. We will further use such analyses to establish that condition (i) in Theorem 1(a) holds for the model of concern, thus allowing for us to apply such a theorem.
For each
, the
are characterized by the unique solution to the evaluation equations
Further, the marginal work metric
is evaluated by
Note that (
41) and (
42) imply that
We now go back to the project’s restless bandit reformulation. The next result, whose proof is omitted, as it is immediate, gives the evaluation equations for work metric under a given active set.
The following result represents work metric in terms of the .
Lemma 10. For :
- (a)
, for .
- (b)
, for .
- (c)
, for .
- (d)
, for .
Proof. (a) The result follows readily from the definition of .
(b) For
, we have
while using Lemma 9 and part (a). Thus, the
satisfy the equations in (
41) characterizing the
for
, which gives the result.
(c) We have, for
,
using Lemma 9, the inclusion
, and (a, b).
(d) The result follows readily from the definition of . □
Concerning the marginal work metric
, (
36) and Lemma 9, they readily give that
The following result represents marginal work metric in terms of the .
Lemma 11. For every :
- (a)
, for .
- (b)
, for .
- (c)
, for .
- (d)
, for .
- (e)
, for .
- (f)
, for .
Proof. (a) We have, for
,
using (
44), Lemma 10(a,b), and (
42).
(b) We can write, for
,
while using (
44), Lemma 10(a,b), and (
42).
(c) We have, for
,
using (
44),
, Lemma 9, Lemma 10(b,c), and (
42).
(d) We obtain, for
,
while using Lemma 9,
, Lemma 10(b,c), and (
42).
(e) We have, for
,
using (
44), Lemma 9, Lemma 10(d), and (
42).
(f) We have, for
,
using (
44), Lemma 9, Lemma 10(b), and (
42). □
It must be now remarked that, at the corresponding point in the analysis of [
27]—for the case with no setup delays
—one could establish the positivity of the marginal work metric, i.e.,
for
,
, which is the first PCL-indexability condition and it implies the less stringent condition (i) in Theorem 1(a). However, here, it is apparent from Lemma 11(c) that, for
,
can be negative for
that is close to 1. This is why we cannot use here the same line of argument that is given in [
27] to show indexability.
As mentioned above, we will use, instead, for such a purpose, Theorem 1(a). The following result shows that condition (i) in that theorem holds for the model of concern.
Proof. First, consider the case
. Then, using Lemma 11(a–d), along with
, gives that, for
,
Now, consider the case
. Then, again using Lemma 11(a–d) along with
gives that, for
,
Finally, consider
, which is different from
and
. Then, Lemma 11 and (
35) imply that it could only happen that marginal work metric
be negative if
and
. However, such a case is not included in the required conditions, since
(due to
), yet
(since
). This completes the proof. □
We are now ready to deploy Theorem 1(a) in the present model.
Proposition 1. The present restless bandit model is -indexable and Algorithm 3 computes its Whittle index.
Proof. Lemmas 8 and 12 show that conditions (i) and (ii) in Theorem 1(a) hold, respectively, which implies the result. □
4.3. The AT Index Is the Whittle Index
We next use the results above in order to prove the identity between the Whittle index and the AT index. We will reformulate the AT index formulae in (
7)–(
8) while using active sets
, rather than stopping times
. Thus, we can reformulate the continuation and switching AT indices, as
and
Recall that we denote the Whittle index by .
Proposition 2. For , and .
Proof. We start by showing that
, while using the equivalences
drawing on the project’s
-indexability (Proposition 1), and so, if resting the project iin
is optimal, then resting it in
is also optimal, together with Lemmas 10(b) and 14(b).
We next prove that
, through the chain of equivalences
drawing on the result that the project is
-indexable, together with Lemmas 10(c) and 14(c). □
4.4. Reward Metric Analysis
We proceed by considering how to calculate the reward and marginal reward metrics and , by relating them to the metrics and for the corresponding non-restless project with no setup penalties.
For every active set
, the reward metric
is determined by the evaluation equations
and the marginal reward metric is given by
Going back to the semi-Markov restless bandit reformulation, the following result shows the evaluation equations for the reward metrics , for an active set .
The following result formulates the reward metric , in terms of the ’s.
Lemma 14. For :
- (a)
, for .
- (b)
, for .
- (c)
, for .
- (d)
, for .
Proof. (a) This part follows from the definition of .
(b) We have, for
,
while using Lemma 13 and part (a). Thus, the
’s, for
, satisfy (
47), which yields the result.
(c) We can write, for
,
using parts (a, b), Lemma 13, and (
47).
(d) The result follows from the definition of . □
Concerning the marginal reward metric
, we obtain, from (
37) and Lemma 13, that
The following result represents the marginal reward in terms of the .
Lemma 15. For :
- (a)
, for .
- (b)
, for .
- (c)
, for .
- (d)
, for .
- (e)
, for .
- (f)
, for .
Proof. (a) We have, for
,
using (
49), Lemmas 13 and 14(a,b), (
47), and (
48).
(b) We can write, for
,
using (
49), (
48), and Lemma 14(a,b).
(c) We have, for
,
using (
49),
, Lemmas 13 and 14(b,c), and (
48).
(d) We can write, for
,
while using Lemmas 13 and 14(b,c),
, and (
48).
(e) We have, for
,
using (
49), Lemmas 13 and 14(d), and (
48).
(f) We obtain, for
,
using (
49), Lemmas 13 and 14(b), and (
48). This completes the proof. □
6. How Does the Index Depend on Switching Penalties?
We next present and discuss properties on the index dependence on the switching penalties, when considering the case where the latter are constant across states: , and for . The notation below will make explicit the prevailing penalties, writing , and .
We write, as
, the Gittins index, and as
, the reward metric of the original project with no switching penalties. We will draw on the following expression for the switching index:
where
Note that (
51) uses the transformation that is considered in
Section 2.1, together with the switching-index formulation in (
46), while using the result that the original non-restless project’s reward metric with transformed rewards
, for
, is
.
We will further use the following preliminary result.
Lemma 17. - (a)
If , then and .
- (b)
If , then is monotone increasing in F and in G.
Proof. (a) The results follows from the interpretation of work and reward metrics, using Assumption 1(ii) for the latter.
(b) This part follows from the following results:
□
We have the following result.
Proposition 4. - (a)
.
- (b)
If , then .
- (c)
is convex and piecewise linear in , decreasing in c and non-increasing in d.
- (d)
For , or for small enough and , or for , is convex and non-decreasing in ϕ and in ψ.
- (e)
.
- (f)
, as .
Proof. (a) The result follows from noting that
is the Gittins index of the project with modified active rewards
(cf.
Section 2.1), which is related to the project Gittins index
(with unmodified rewards
) by the stated expression.
(b) Using Lemma 17(b) and
, we obtain
(c) The result follows by noting that (
51) formulates
as the maximum of linear functions in
that decrease in
c and are non-increasing in
d.
(d) Concerning the dependence on
, when
the result follows by (b). Furthermore,
where the inequalities hold for
small enough, using that
so that
, and for
. Hence,
is a maximum of convex non-decreasing functions, which is also convex non-decreasing.
The same argument can be applied to dependence on
, while using that
Parts (e) and (f) follow straightforwardly. □
We conjecture that Lemma 4(c) should hold without the qualifications considered above.
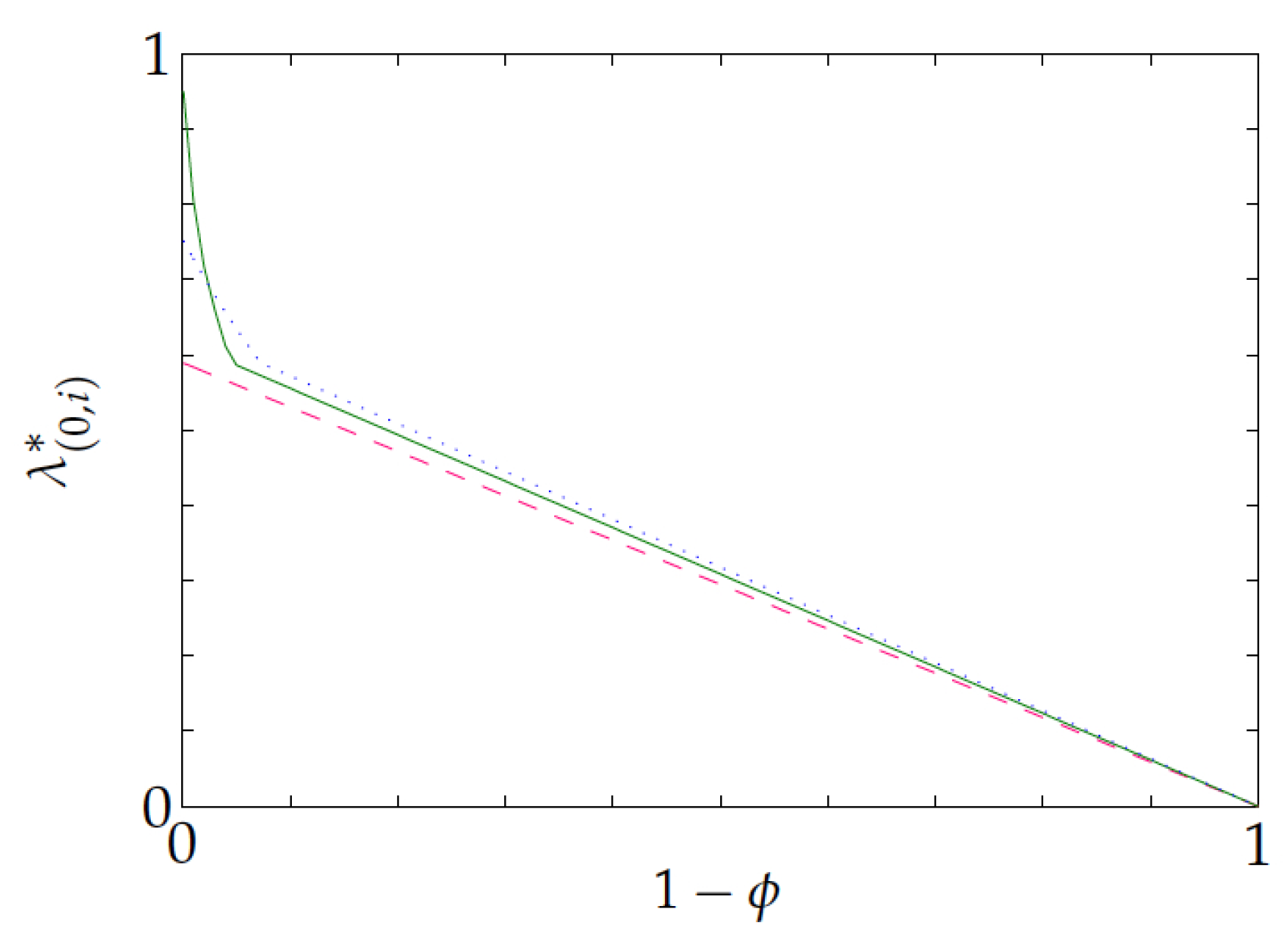
Now, consider the following examples to illustrate the results above. The first example concerns a three-state project with no setdown penalties or setup costs, setup delay transform
,
,
Figure 2 plots the project’s switching index for each of the three states versus
. Note that each of the lines shown corresponds to one of the project states. The plot agrees with Proposition 4(d, e). It also illustrates that the relative ordering of states that is induced by the switching index can vary with
.
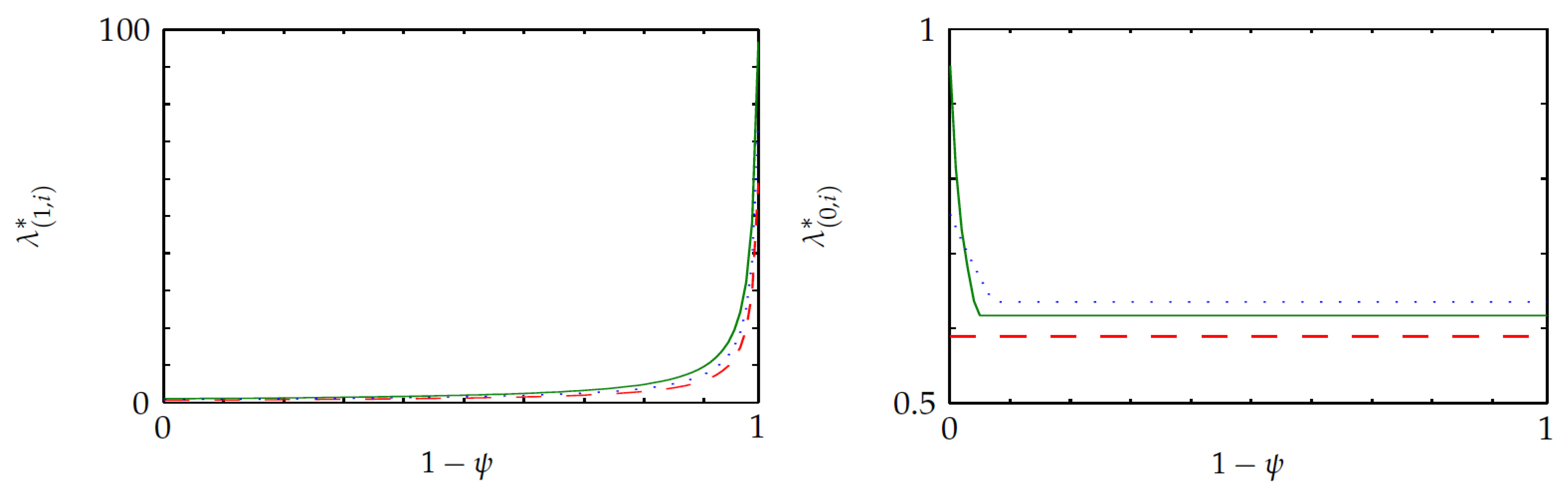
The following example is based on the same project, but with no setup delays and with setdown delay transform
.
Figure 3 displays the continuation and switching indices for each of the three states versus
. Note that each of the lines shown corresponds to one of the project states. The plots agree with Proposition 4(a,d,f). Note that the continuation index
increases to infinity as
vanishes, as the incentive of sticking to a project increases steeply as the setdown delay becomes larger. The plot for the switching index further shows that the relative ordering of states can vary with
.
7. Numerical Study
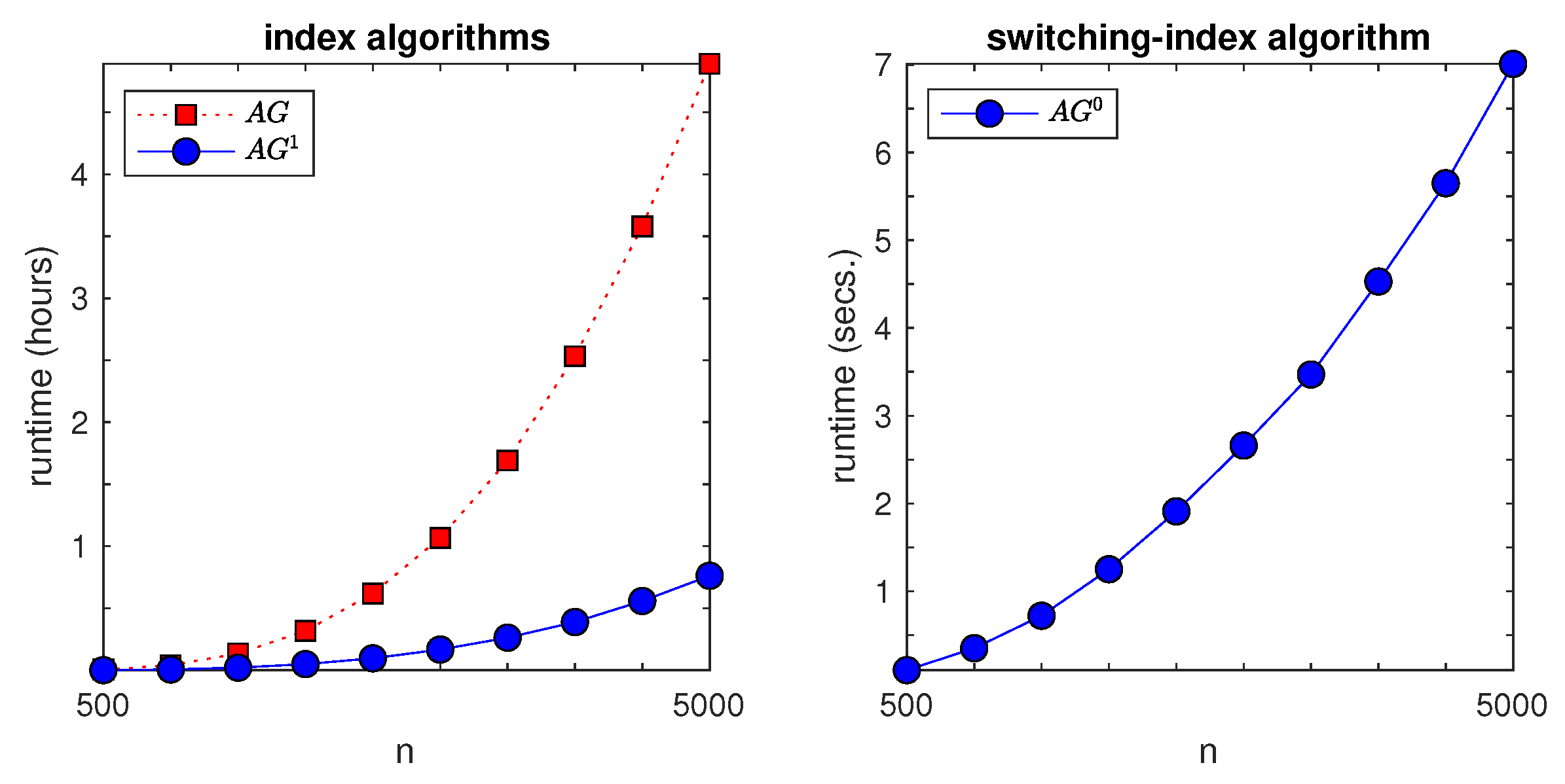
We next report on the results of a numerical study, which is based on MATLAB implementations of the algorithms that are discussed here developed by the author.
The first experiment addressed the runtime of the decoupled index computing method. A random project instance with setup delays and costs was randomly generated for each of the following numbers of states:
. For each such
n, the time to compute the continuation index and required extra quantities while using the fast-pivoting algorithm with extended output in [
28] was recorded, as well as the time for computing the switching index by algorithm
, and the time for jointly computing both indices by using the simplex-based implementation that is given in [
49] of the adaptive-greedy algorithm
. This experiment was run on a 2.8 GHz PC with 4 GB of memory.
Figure 4 shows the results. The left pane plots total runtimes (measured in hours) to compute both indices versus
n. Red squares represent the
joint-computing scheme, and blue circles represent the two-stage scheme. We see that the latter attained approximately a fourfold speed-up over the former. The right pane plots runtimes (measured in seconds), for the switching index algorithm versus the number of states
n. The timescale change from hours to seconds highlights the order-of-magnitude speed-up attained.
The following experiments were designed in order to evaluate the average relative performance of the Whittle index policy in randomly generated two- and three-project instances, both versus the optimal problem value, and versus the benchmark Gittins index policy, which does not take setups into account. For each problem instance, the optimal value was calculated by solving with the CPLEX LP solver the LP formulation of the DP optimality equations. The Whittle index and benchmark scheduling policies were evaluated by solving, with MATLAB, the appropriate systems of linear evaluation equations.
The second experiment was designed to assess the dependence of the relative performance of Whittle’s index policy for two-project instances on a constant setup-time transform and discount factor —with no setdown penalties. A sample of 100 randomly generated instances with 10-state projects was obtained with MATLAB. In each instance, the parameters for each project were independently drawn: transition probabilities (by scaling a matrix with uniform entries) and uniform (between 0 and 1) active rewards. For every instance and parameters —with a 0.1 grid—the optimal value and the values of the Whittle index () and benchmark () policies were calculated, together with the relative optimality of the Whittle index policy , and the optimality-gap ratio of the Whittle index over the benchmark policy . The latter were then averaged over the 100 instances for each pair, in order to obtain the average values and .
Values
,
and
were computed, as follows. The corresponding value functions
,
and
were calculated. Subsequently, the values were calculated when considering that both projects start out being passive, as
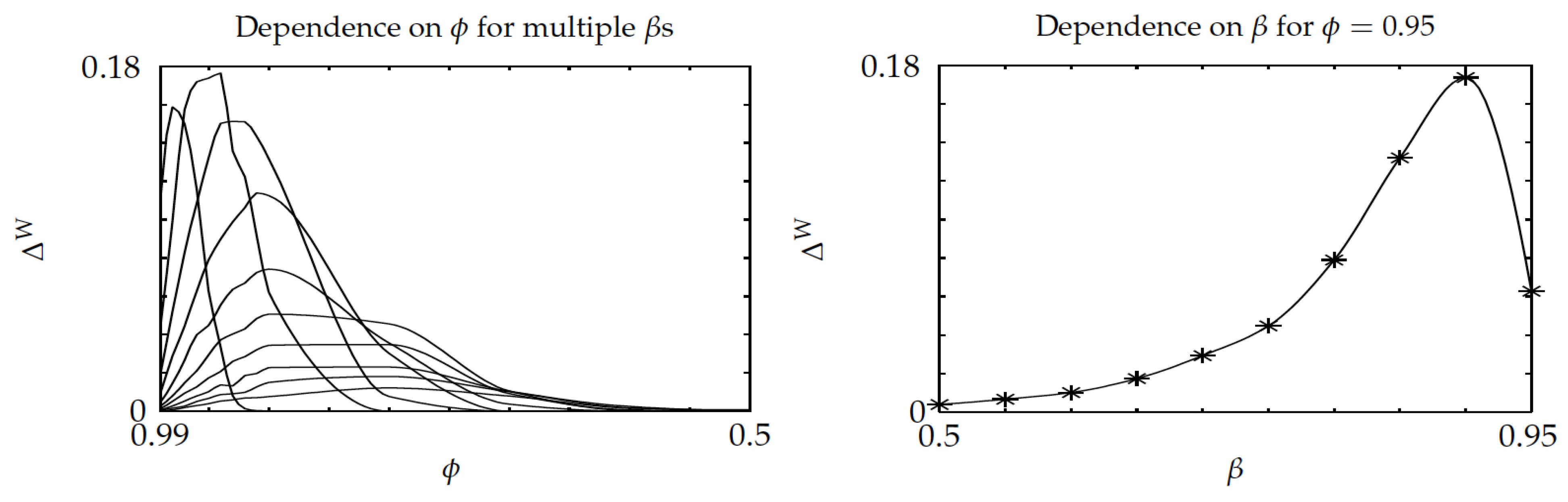
Figure 5 displays, in its left pane, the relative gap
versus
—note the inverted
-axis used throughout—for multiple
, while using cubic interpolation. The gap starts at 0 as
approaches 1 (as the optimal policy is then obtained), and then grows up to a maximum, which is below
, and then decreases to 0 as
gets smaller. That pattern agrees with intuition: for small enough
, both the optimal and Whittle index policies initially pick a project and stick to it. Because the best such project can be determined by single-project evaluations, the Whittle index policy will correctly choose it. The right pane shows that
is not monotonic in
, as it is increasing for small
and then decreases for
closer to 1. Hence, in the left pane, the higher peaks typically correspond to larger values of
.
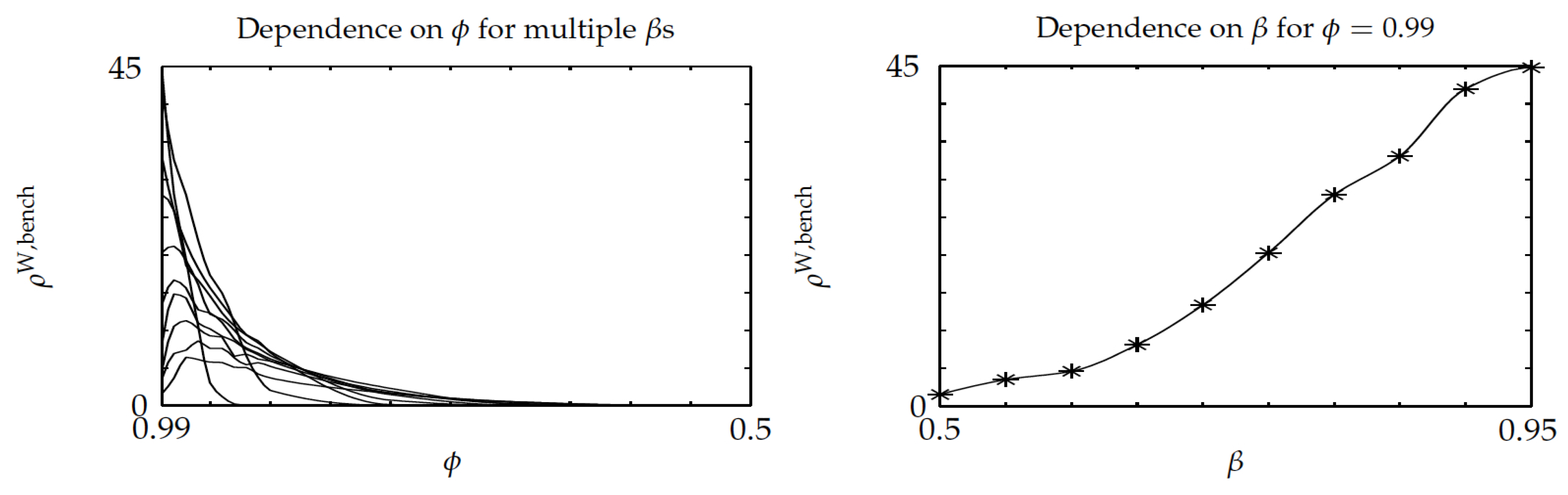
Figure 6 shows similar plots for the optimality-gap ratio
of the Whittle index over the benchmark policy. They highlight that the average optimality gap for the Whittle index policy remains below
of that for the benchmark policy. The left pane shows that the ratio vanishes for
that is small enough, as the Whittle index policy is then optimal. Additionally, the right pane shows that the ratio is increasing with
. Thus, in the left pane, for fixed
, higher values correspond to larger
.
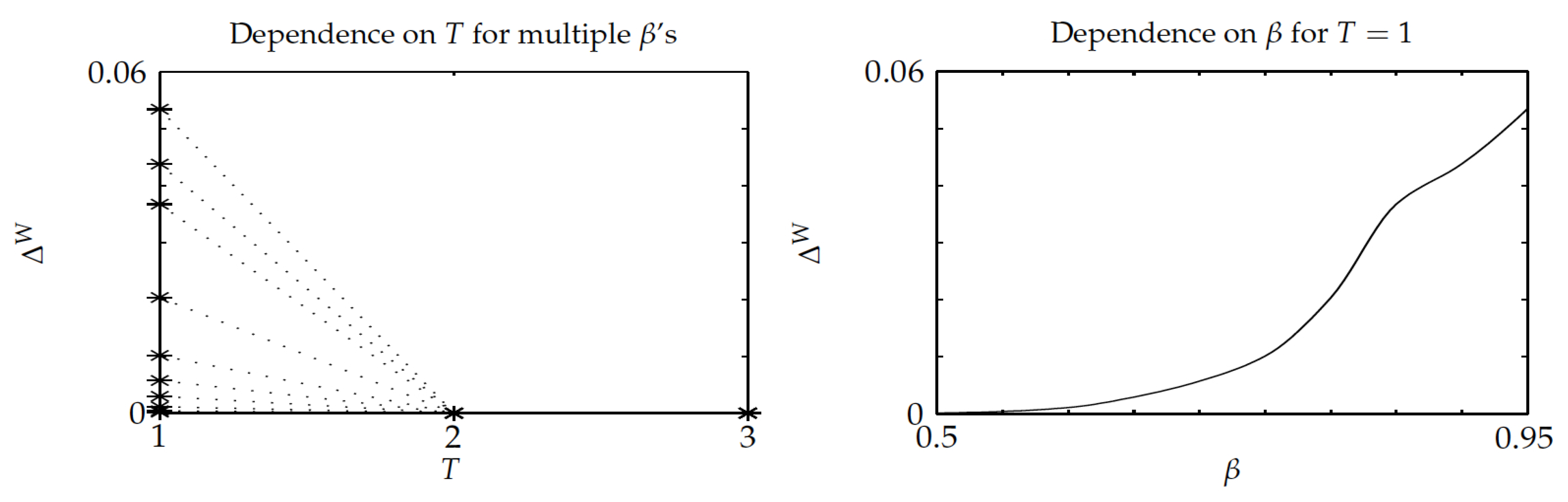
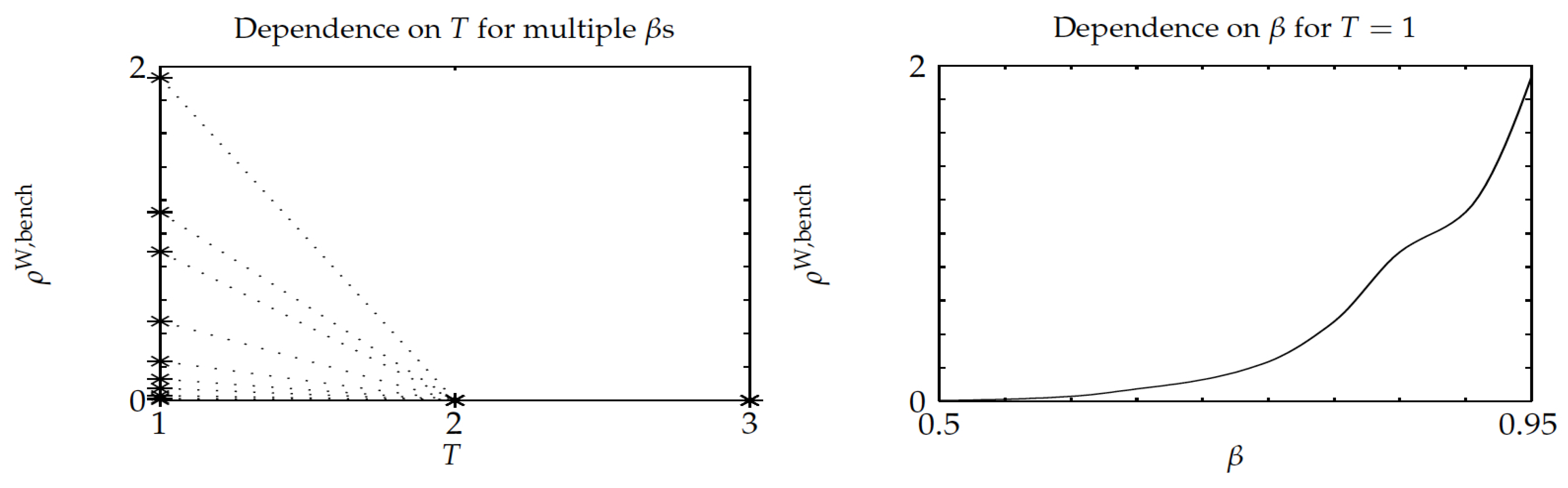
The third experiment was similar in nature as the previous one, but, when considering instead a constant setup delay
T for each project,
.
Figure 7 and
Figure 8 show the results, which highlight that Whittle’s index policy was optimal for
, its relative optimality gap did not exceed
, and it substantially outperformed the benchmark Gittins-index policy, as the optimality-gap ratio stays below
.
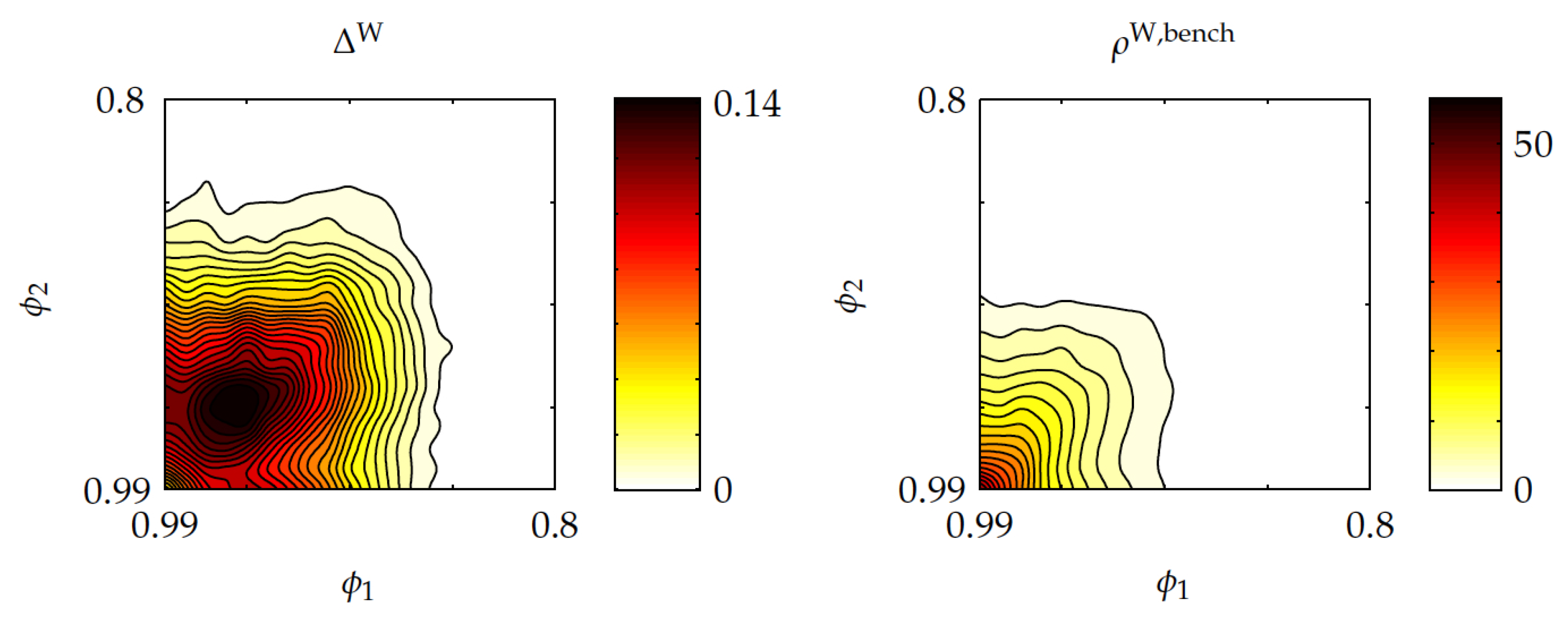
The fourth experiment addressed the effect of asymmetric (and constant) setup delay transforms, with these varying over the range
, in two-project instances with discount factor
. In the left contour plot in
Figure 9 it is shown that the average relative optimality gap of Whittle’s index policy,
, reaches a maximum of approximately
, and it vanishes as both
and
get close to unity, and as either of them becomes small enough. The right contour plot shows that the optimality-gap ratio
reaches the maximum values of nearly
, then vanishing as either
or
becomes sufficiently small.
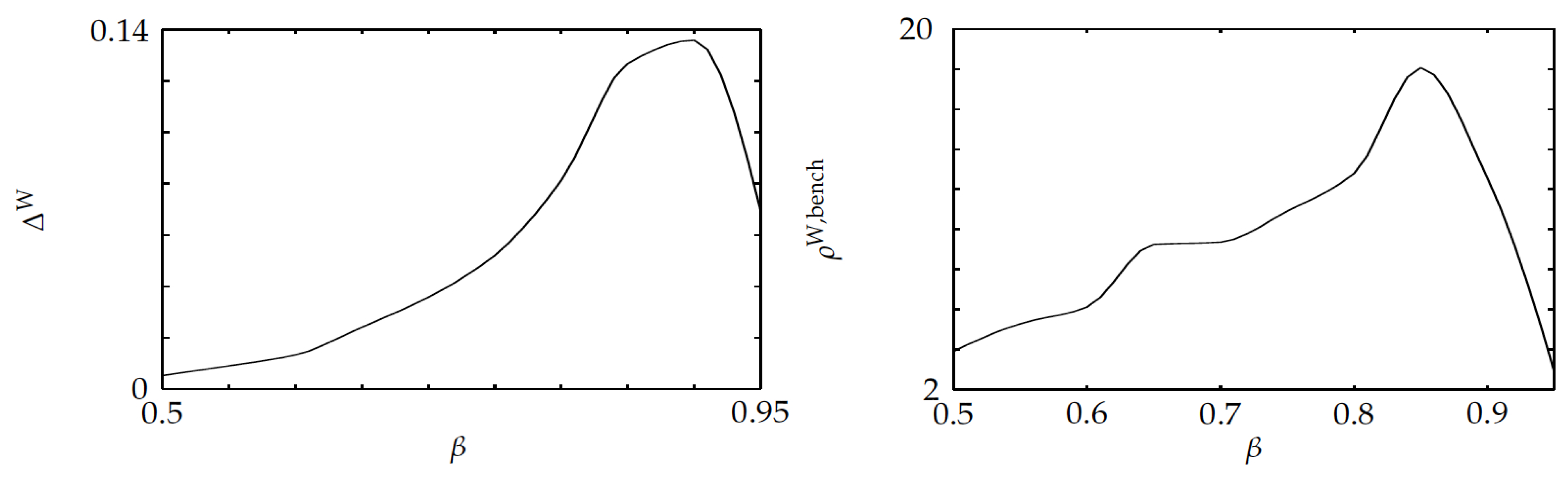
The fifth experiment studied the effect of state-dependent setup delay parameters
, as the discount factor is changed. Uniform[0.9, 1] i.i.d. state-dependent setup costs were randomly generated for every instance. The left pane shown in
Figure 10 displays the average relative optimality gap versus the discount factor, showing that such a gap stays below
. The right pane highlights that the average optimality-gap ratio
stays below
.
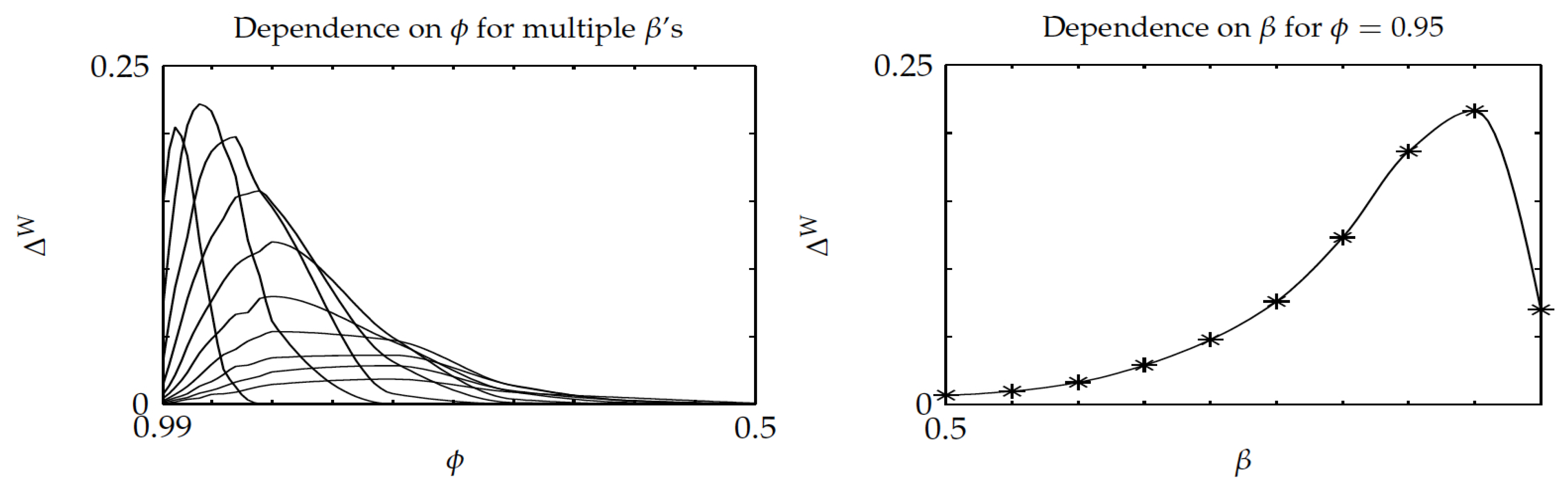
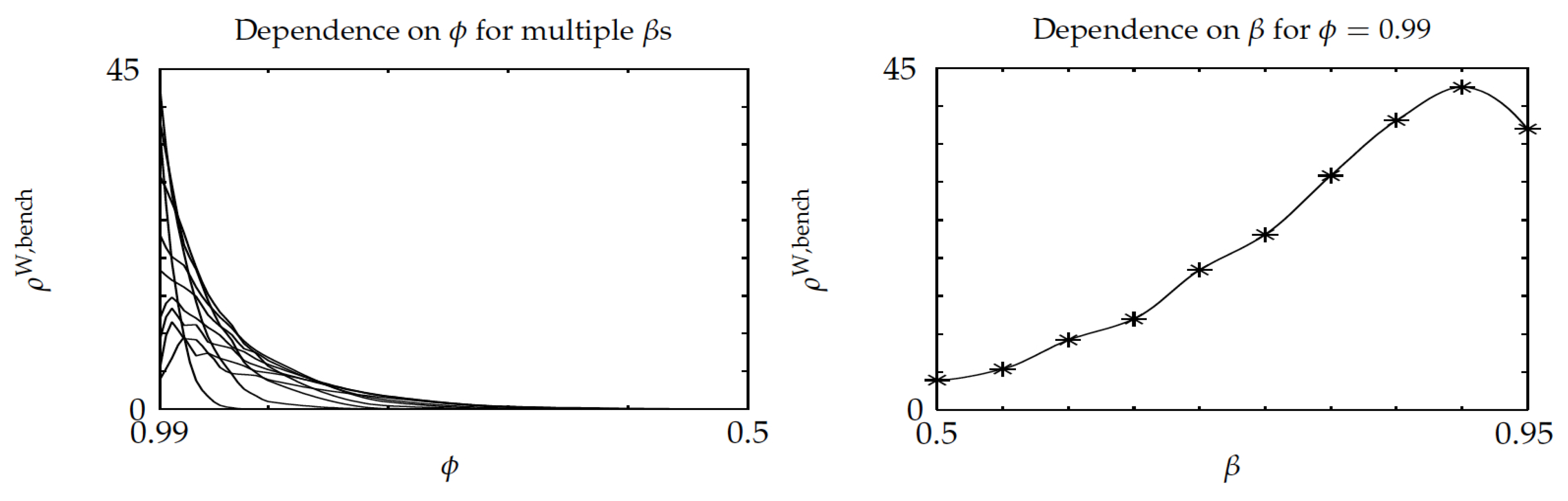
The sixth experiment considered the relative performance of Whittle’s index policy on three-project instances in terms of a setup delay parameter
and discount factor, while using a random sample of 100 instances of three eight-state projects. For each instance, the parameters varied over the range
. The results are displayed in
Figure 11 and
Figure 12, which are the counterparts of
Figure 5 and
Figure 6. Comparing
Figure 5 and
Figure 11 shows a slight degradation of performance for Whittle’s index policy in the latter, although the average gap
stays small, beneath
. Comparing
Figure 6 and
Figure 12 shows similar values for the ratio
.