Fundamentals of Synthesized Optimal Control

Abstract

This paper presents a new formulation of the optimal control problem with uncertainty, in which an additive bounded function is considered as uncertainty. The purpose of the control is to ensure the achievement of terminal conditions with the optimal value of the quality functional, while the uncertainty has a limited impact on the change in the value of the functional. The article introduces the concept of feasibility of the mathematical model of the object, which is associated with the contraction property of mappings if we consider the model of the object as a one-parameter mapping. It is shown that this property is sufficient for the development of stable practical systems. To find a solution to the stated problem, which would ensure the feasibility of the system, the synthesized optimal control method is proposed. This article formulates the theoretical foundations of the synthesized optimal control. The method consists in making the control object stable relative to some point in the state space and to control the object by changing the position of the equilibrium points. The article provides evidence that this approach is insensitive to the uncertainties of the mathematical model of the object. An example of the application of the method for optimal control of a group of robots is given. A comparison of the synthesized optimal control method with the direct method on the model without disturbances and with them is presented.

1. Introduction

Object control in the classical mathematical sense is to qualitatively change the right-hand sides of the differential equations describing the mathematical model of the control object, due to the control vector included in them. Thus, the problem of optimal control [1] consists in finding such a control function, as a function of time, which will make the required changes in the right-hand sides of the model of the control object so that, for given initial conditions, the partial solution of the system of differential equations achieves the control goal with the optimal value of the quality criterion.

There are two main directions for solving the problem of optimal control: direct and indirect approaches. The indirect approach based on the Pontryagin’s maximum principle [2,3,4] solves optimal control by formulating it as a boundary-value problem, in which it is necessary to find the initial conditions for a system of differential equations for conjugate variables. Its optimal solution is highly accurate, however, very sensitive to the formulation of additional conditions that the control must satisfy, along with ensuring the maximum of the Hamiltonian, which are generally very difficult to set in practice for problems with complex phase constraints. The direct approach reduces the optimal control problem to a nonlinear programming problem [5,6,7], that provides the transition from the optimization problem in the infinite-dimensional space to the optimization problem in the finite-dimensional space, so it is more convenient and can be readily solved within a wider convergence region.

However, these works generally focus on the nominal trajectory performance without considering possible uncertainties. In practice, in the right-hand sides of the models, there are objectively some uncertainties of various nature. As a rule, they are not taken into account, but the presence of such uncertainties can lead to the loss of optimality of the obtained control.

There are also approaches when the impact of uncertainties is taken into account during the reference trajectory design beforehand [8,9]. For example, desensitized optimal control [10], modifies the nominal optimal trajectory such that it is less sensitive with respect to uncertain parameters. This involves constructing an appropriate sensitivity cost which, when penalized, provides solutions that are relatively insensitive to parametric uncertainties.

Although in practice such solutions do not guarantee the stability and still require construction of the feedback stabilization control system to eliminate errors [8].

In control theory, there is a field of robust control [11,12,13,14], which provides a certain stability coefficient of the control system. Robust control methods generally move the eigenvalues of the linearized system as far as possible to the left of the imaginary axis of the complex plane, so that uncertainties and perturbations do not make the system unstable. These methods are not aimed at solving the optimal control problem.

In practical control system design, the existing uncertainties of the mathematical model of the object, which subsequently cause the discrepancy between the real trajectory of the object and the obtained optimal one, are compensated by the synthesis of a feedback motion stabilization system relative to the optimal trajectory [8,15,16,17]. But construction of the stabilization system changes the mathematical model of the object and the received control might be not optimal for the new model.

In this paper, uncertainties are included in the problem statement as an additive bounded function. And the optimal control problem is supposed to be solved after ensuring stability to the plant in the state space. This approach was called the method of synthesized optimal control. A control function is found such that the system of differential equations will always have a stable equilibrium point in the state space. With that, the control system contains parameters that affect the position of the equilibrium point. Consequently, the object is controlled by changing the position of the equilibrium point. In this paper, it is shown that such control can also provide the required value of the quality criterion, but the mathematical model of the control object turns out to be insensitive to the existing uncertainties and external disturbances. The approach of synthesized optimal control is new, but we have already managed to obtain good experimental results [18,19] confirming the effectiveness of such control. In this paper, we provide mathematical formulations of the approach and give a theoretical substantiation of the efficiency of the synthesized optimal control. A comparative numerical example of solving the problem of optimal control of two robots under phase constraints by the indirect method of synthesized optimal control and by the direct method based on piecewise linear approximation is given.

2. Problem Statement

The mathematical model of control object with uncertainty is given

$$\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x},\mathbf{u})+\mathbf{y}\left(t\right),$$

(1)

where $\mathbf{x}\in {\mathbb{R}}^n$, $\mathbf{u}\in \mathrm{U}\subseteq {\mathbb{R}}^m$, $\mathrm{U}$ is a compact set, $m\le n$, $\mathbf{y}$ is a uncertainty function, $\mathbf{y}\left(t\right)\in {\mathbb{R}}^n$,

$${\mathbf{y}}^{-}\le \mathbf{y}\left(t\right)\le {\mathbf{y}}^{+}$$

(2)

${\mathbf{y}}^{-}$, ${\mathbf{y}}^{+}$ are set constant vectors.

Initial conditions are set

$$\mathbf{x}\left(0\right)={\mathbf{x}}^0.$$

(3)

Terminal condition is set

$$\mathbf{x}\left(t_f\right)={\mathbf{x}}^f,$$

(4)

where time $t_f$ of hitting terminal conditions $t_f$ is not given, but is limited

$$t_f\le t^{+},$$

(5)

$t^{+}$ is a given positive value.

The functional is given

$$J=\underset{0}{\overset{t_f}{\int }}{f}_0(\mathbf{x}\left(t\right),\mathbf{u}\left(t\right))dt+p_1\parallel {\mathbf{x}}^f-\mathbf{x}\left(t_f\right)\parallel \to \underset{\mathbf{u}(·)\in \mathrm{U}}{min},$$

(6)

where $p_1$ is a given positive value.

It is necessary to find a control function

$$\mathbf{u}=\mathbf{h}(\mathbf{x},t)$$

(7)

such that for any partial solution

$$\mathbf{x}(t,{\mathbf{x}}^0)$$

(8)

of the system

$$\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x},\mathbf{h}(\mathbf{x},t))+\mathbf{y}\left(t\right)$$

(9)

from initial conditions (3) for any uncertainty function (2) value of the functional (6) satisfies inequation

$$J(\mathbf{x}(t,{\mathbf{x}}^0),\mathbf{y}\left(t\right))\le J(\mathbf{x}(t,{\mathbf{x}}^0),0)+{\Delta }_y,$$

(10)

where $J(\mathbf{x}(t,{\mathbf{x}}^0),\mathbf{y}\left(t\right))$ is a value of functional (6) for the solution (8) with perturbation (2), $J(\mathbf{x}(t,{\mathbf{x}}^0),0)$ is a value of functional (6) for the same solution (8) without perturbations, $\mathbf{y}(·)\equiv 0$, ${\Delta }_y$ is a given positive value.

Among possible solutions in the form (7) we consider only such that possess the following properties. Let $\mathbf{x}(t,{\mathbf{x}}^0)$ be some partial solution of the system (9) with $\mathbf{y}\left(t\right)\equiv 0$ and $J\left(0\right)$ be a value of criterion (10) for it. Let us denote

$$\tilde{\mathbf{x}}=\mathbf{x}(t,{\mathbf{x}}^0)+\tilde{\mathbf{z}}\left(t\right),$$

(11)

$$\widetilde{\tilde{\mathbf{x}}}=\mathbf{x}(t,{\mathbf{x}}^0)+\widetilde{\tilde{\mathbf{z}}}\left(t\right),$$

(12)

and

$$\tilde{\delta }=\underset{t\in [0;t_f]}{max}\parallel \mathbf{x}(t,{\mathbf{x}}^0)-\tilde{\mathbf{x}}\left(t\right)\parallel ,$$

(13)

$$\tilde{\tilde{\delta }}=\underset{t\in [0;t_f]}{max}\parallel \mathbf{x}(t,{\mathbf{x}}^0)+\widetilde{\tilde{\mathbf{x}}}\left(t\right)\parallel .$$

(14)

Then $\tilde{\delta }>0$ exist, such that $\forall \tilde{\tilde{\delta }}\le \tilde{\delta }$ conditions are met

$$\tilde{\tilde{\Delta }}\le \tilde{\Delta },$$

(15)

where

$$\tilde{\Delta }=|J(\mathbf{x}(t,{\mathbf{x}}^0),0)-J(\tilde{\mathbf{x}}\left(t\right),0)|,$$

(16)

$$\tilde{\tilde{\Delta }}=|J(\mathbf{x}(t,{\mathbf{x}}^0),0)-J(\widetilde{\tilde{\mathbf{x}}}\left(t\right),0)|.$$

(17)

The condition (15) is called the continuous dependence of the functional on perturbations.

The goal is to look for solutions in form (7) so that they satisfy condition (15).

3. Theoretical Background and Justifications for the Synthesized Optimal Control Method

Problems with uncertainties are often considered in optimal control, since the question is relevant in the practical implementation of obtained systems. As a rule, uncertain parameters of the right-hand sides or initial conditions are considered as uncertainties, or some random perturbations are introduced. The main direction of solving problems with perturbations is to ensure the stability of the obtained solution. So, firstly, the problem of optimal control is solved without uncertainties, and then, using the stabilization system, an attempt is made to ensure the stability of motion relative to the optimal trajectory. In fact, the creation of a stabilization system is an attempt to ensure the stability of the differential equation solution according to Lyapunov.

Theorem 1.

To perform the condition (10) it is enough that a partial solution (8) of the system (9) without perturbations $\mathbf{y}\left(t\right)\equiv 0$

$$\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x},\mathbf{h}(\mathbf{x},t)),$$

(18)

was stable according to Lyapunov.

Proof. 

From differential Equation (1) follows

$$\mathbf{x}(t+\Delta t)=\mathbf{x}\left(t\right)+\Delta t\mathbf{f}(\mathbf{x},\mathbf{h}(\mathbf{x},t\left)\right)+\Delta t\mathbf{y}\left(t\right),$$

(19)

or

$$\overline{\mathbf{x}}\left(t\right)=\mathbf{x}(t,{\mathbf{x}}^0)+\mathbf{v}\left(t\right),$$

(20)

where

$$\mathbf{v}\left(t\right)=\underset{0}{\overset{t}{\int }}\mathbf{y}\left(t\right)dt.$$

(21)

Let ${\Delta }_y$ be given. Then according to condition (15) you can always define $\tilde{\Delta }$ and value $\overline{\delta }$ for perturbed solution $\overline{\mathbf{x}}$ such that according to condition of stability on Lyapunov [20,21]

$$\parallel \mathbf{x}(t,{\mathbf{x}}^0)-\overline{\mathbf{x}}\left(t\right)\parallel <\overline{\delta },\forall t\in [0;t_f].$$

(22)

For this it is enough to satisfy the inequality

$$0\le \parallel \mathbf{v}\left(t\right)\parallel \le \overline{\delta }/2,\forall t\in [0;t_f].$$

(23)

 □

However, to find control function (7) such that partial solution (8) was stable according to Lyapunov is rather difficult and, in fact, it is not always necessary. According to Lyapunov’s theorem, a stable solution to a differential equation must have the property of an attractor [20,22], and, therefore, from the mathematical point of view the synthesis of stabilization system is an attempt to give an attractor property to the found optimal trajectory [21,23]. The main problem of unstable solutions is that they are difficult to implement, since small perturbations of the model lead to large errors of the functional, in other words, the solution does not have the attractor property. But in fact, the requirement for the optimal solution to obtain the attractor property or be Lyapunov stable is a fairly strict one and it could be redundant, and other weaker requirements may be enough to implement the resulting solution. For example, the motion of a pendulum is not Lyapunov stable if it is not the zero rest point, but it is physically feasible, since its small perturbations lead to small perturbations of the functional.

In this concern let us introduce the concept of feasibility.

4. Feasibility Property

Based on a qualitative analysis [24] of the solutions of systems of differential equations, the feasibility means that small changes in the model do not lead to a loss of quality. In other words, it is necessary that the solution has the contraction property.

Hypothesis 1.

A mathematical model is feasible, if its errors do not increase in time.

Definition 1.

The system of differential equations is practically feasible, if this system as a one-parametric mapping obtains a contraction property in the implementation domain.

Consider a system of differential equations

$$\dot{\mathbf{x}}=\mathbf{f}\left(\mathbf{x}\right),$$

(24)

where $\mathbf{x}\in {\mathbb{R}}^n$.

Any ordinary differential equation is a recurrent description of a time function. A solution of the differential equation is a transformation from a recurrent form to a usual time function.

Computer calculation of the differential Equation (24) has a form

$$\mathbf{x}(t+\Delta t)=\mathbf{x}\left(t\right)+\Delta t\mathbf{f}\left(\mathbf{x}\right(t\left)\right),$$

(25)

where t is an independent parameter, $\Delta t$ is a constant parameter, and it is called a step of integration.

The right side of the Equation (25) is a one-parametric mapping from space ${\mathbb{R}}^n$ to itself

$$F(\mathbf{x},t)=\mathbf{x}\left(t\right)+\Delta t\mathbf{f}\left(\mathbf{x}\left(t\right)\right):{\mathbb{R}}^n\to {\mathbb{R}}^n.$$

(26)

Let a compact domain $\mathrm{D}$ be set in the space ${\mathbb{R}}^n$. All solutions of the differential Equations (24), that are of our interest, belong to this domain. Therefore, for the differential Equations (24) the initial and terminal conditions belong to this domain

$$\mathbf{x}\left(0\right)\in \mathrm{D}\subseteq {\mathbb{R}}^n,\mathbf{x}\left(t_f\right)\in \mathrm{D}\subseteq {\mathbb{R}}^n,$$

(27)

where $\mathbf{x}\left(t_f\right)$ is a terminal point of the solution (24).

Theorem 2.

In domain $\mathrm{D}$ for the mapping (26), the following property is performed

$$\rho ({\mathbf{x}}^a\left(t\right),{\mathbf{x}}^b\left(t\right))\le \rho ({F(\mathbf{x}}^a\left(t\right),t),F({\mathbf{x}}^b\left(t\right),t)),$$

(28)

where ${\mathbf{x}}^a\left(t\right)\in \mathrm{D}$, ${\mathbf{x}}^b\left(t\right)\in \mathrm{D}$, $\rho ({\mathbf{x}}^a,{\mathbf{x}}^b)$ is a distance between two points in the space ${\mathbb{R}}^n$

$$\rho ({\mathbf{x}}^a,{\mathbf{x}}^b)=∥{\mathbf{x}}^a-{\mathbf{x}}^b∥.$$

(29)

Then the mathematical model (24) is feasible if the domain $\mathrm{D}\subseteq {\mathbb{R}}^n$ according to the hypothesis.

Proof. 

Let $\mathbf{x}\left(t\right)\in \mathrm{D}$ be a known state of the system in the moment t and $\mathbf{y}\left(t\right)\in \mathrm{D}$ be a real state of the system in the same moment. The error of the state is

$$\delta \left(t\right)=\rho \left(\mathbf{x}\right(t),\mathbf{y}(t\left)\right).$$

(30)

According to the mapping (26)

$$\delta (t+\Delta t)=\rho \left(F\right(\mathbf{x}\left(t\right),t),F(\mathbf{y}\left(t\right)\left)\right).$$

(31)

And according to the condition (28) of the theorem

$$\delta \left(t\right)\le \delta (t+\Delta t).$$

(32)

This proves the theorem. □

The condition (28) shows that the system of differential equations as a one-parametric mapping has contraction property.

Assume that the system (24) in the neighborhood of the domain $\mathrm{D}$ has one stable equilibrium point, and there is no other equilibrium point in this neighborhood

$$\mathbf{f}\left(\tilde{\mathbf{x}}\right)=0,$$

(33)

$$det(\lambda \mathbf{E}-\mathbf{A}\left(\tilde{\mathbf{x}}\right))={\lambda }^n+a_{n-1}{\lambda }^{n-1}+\dots +a_1\lambda +a_0=\prod _{j=1}^n(\lambda -{\lambda }_j)=0,$$

(34)

where $\mathbf{E}$ is a unit $n\times n$ matrix,

$$\mathbf{A}\left(\tilde{\mathbf{x}}\right)=\frac{\partial \tilde{\mathbf{f}}\left(\mathbf{x}\right)}{\partial \mathbf{x}},$$

(35)

$${\lambda }_j={\alpha }_j+i{\beta }_j,$$

(36)

${\alpha }_j<0$,$i=\sqrt{-1}$, $j=1,\dots ,n$.

Theorem 3.

If for the system (24) there is a domain $\mathrm{D}$ that includes one stable equilibrium point (33)–(36), then the system (24) is practically feasible.

Proof. 

According to the Lyapunov’s stability theorem on the first approximation the trivial solution of the differential Equation (24)

$$\mathbf{x}\left(t\right)=\tilde{\mathbf{x}}=\mathrm{constant}$$

(37)

is stable. This means, that, if any solution begins from other initial point ${\mathbf{x}}^0\ne \tilde{\mathbf{x}}$, then it will be approximated to the stable solution asymptotically

$$\rho (\mathbf{x}(t+\Delta t,{\mathbf{x}}^a),\tilde{\mathbf{x}})\le \rho (\mathbf{x}(t,{\mathbf{x}}^a),\tilde{\mathbf{x}}),$$

(38)

where $\mathbf{x}(t,{\mathbf{x}}^a)$ is a solution of the differential Equation (24) from initial point ${\mathbf{x}}^a$.

The same is true for another initial condition ${\mathbf{x}}^b$

$$\rho (\mathbf{x}(t+\Delta t,{\mathbf{x}}^b),\tilde{\mathbf{x}})\le \rho (\mathbf{x}(t,{\mathbf{x}}^b),\tilde{\mathbf{x}}).$$

(39)

From here, it follows that the domain D has a fixed point $\tilde{\mathbf{x}}$ of contraction mapping [24], therefore distance between solutions $\mathbf{x}(t,{\mathbf{x}}^a)$ and $\mathbf{x}(t,{\mathbf{x}}^b)$ also tends to zero or

$$\rho (\mathbf{x}(t+\Delta t,{\mathbf{x}}^a),\mathbf{x}(t+\Delta t,{\mathbf{x}}^b))\le \rho (\mathbf{x}(t,{\mathbf{x}}^a),\mathbf{x}(t,{\mathbf{x}}^b)).$$

(40)

This proves the theorem. □

Following the principle of feasibility, an approach is proposed in which the optimal control problem is solved after ensuring the stability of the object in the state space. This approach is called the method of synthesized optimal control. It includes two stages. In the first stage, the system without perturbations is made stable in some point of the state space. This stage of synthesis of the stabilization system allows to embed the control in the object so that the system of differential equations would have the necessary property of feasibility. In this case, the equilibrium point can be changed after some time, but the object maintains equilibrium at every moment in time. Then we control the position of the stable equilibrium point, as an attractor, to solve the optimal control problem.

5. The Synthesized Optimal Control

According to this approach, it is necessary to find such a control function (7) that the system without perturbations would always have a stable equilibrium point in the state space. Together with that, in the control function a parameter vector is introduced. The value of this parameter vector affects on position of the equilibrium point in the states space

$$\mathbf{u}=\mathbf{g}(\mathbf{x},{\mathbf{q}}^{*}),$$

(41)

where ${\mathbf{q}}^{*}$ is a parameter vector.

Control function (41) provides for the system without perturbations

$$\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x},\mathbf{g}(\mathbf{x},{\mathbf{q}}^{*}))$$

(42)

existence of the equilibrium point

$$\mathbf{f}({\mathbf{x}}^{*}\left({\mathbf{q}}^{*}\right),\mathbf{g}({\mathbf{x}}^{*}\left({\mathbf{q}}^{*}\right),{\mathbf{q}}^{*}))=0,$$

(43)

where ${\mathbf{x}}^{*}\left({\mathbf{q}}^{*}\right)$ is a vector of coordinates of equilibrium point, depending on the parameter vector ${\mathbf{q}}^{*}$. The system (42) satisfies conditions (34)–(36) in the point ${\mathbf{x}}^{*}\left({\mathbf{q}}^{*}\right)$.

Algorithmically, the method of synthesized optimal control first solves the problem of stabilization system synthesis. For solving the synthesis problem, the functional (6) is not used. Purpose of the control synthesis problem is to receive such control function (41) to provide existence of the stable equilibrium point in the state space.

Once the function (41) is found, the optimal control problem is solved next for the mathematical model (42) with the initial conditions (3) and the terminal conditions (4), and with the quality criterion

$$J_1=\underset{0}{\overset{t_f}{\int }}{f}_0(\mathbf{x}\left(t\right),\mathbf{g}(\mathbf{x}\left(t\right),{\mathbf{q}}^{*}\left(t\right)))dt+p_1\parallel {\mathbf{x}}^f-\mathbf{x}\left(t_f\right)\parallel \to \underset{{\mathbf{q}}^{*}\in \mathrm{Q}}{min},$$

(44)

where Q is a compact set in the space of parameters.

In general case, the vector of parameters ${\mathbf{q}}^{*}$ can be some function ${\mathbf{q}}^{*}\left(t\right)$. The properties of this function and methods for finding it requires additional studies. In this work this function is found for the original optimal control problem (1)–(6) as a piece-wise constant one.

Thus, in the synthesized optimal control approach, the uncertainty in the right parts is compensated by the stability of the system relative to a point in the state space. Near the equilibrium point, all solutions converge and feasibility principle is satisfied. This first step of stabilization system synthesis is a key idea of the approach, it provides achievement of better results in the tasks with complex environment and noise. However, this approach could not be previously presented as a single computational method, since there was no general numerical approach for solving the problem of control synthesis. Formally, the problem of synthesis of stabilization system involves the construction of such a feedback control module described by some functions that produces control basing on the received data about the object’s state and this control makes the object achieve the terminal goal with the optimal value of some given criterion. In the overwhelming majority of cases, the control synthesis problem is solved analytically or technically taking into account the specific properties of the mathematical model. But now modern numerical methods of symbolic regression can be applied to find a solution without reference to specific model equations. Let us consider the issue in more details.

6. The Problem of Control System Synthesis

Consider the problem statement of the general numerical synthesis of the control system.

The mathematical model is

$$\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x},\mathbf{u}),$$

(45)

where $\mathbf{x}\in {\mathbb{R}}^n$, $\mathbf{u}\in \mathrm{U}\subseteq {\mathbb{R}}^m$.

The domain of initial conditions is given

$${\mathrm{X}}_0=\{{\mathbf{x}}^{0,1},\dots ,{\mathbf{x}}^{0,K}\}\subseteq {\mathbb{R}}^n.$$

(46)

The terminal condition is given

$${\mathbf{x}}^{*}={[x_1^{*}\dots x_n^{*}]}^T\in {\mathbb{R}}^n.$$

(47)

The quality criterion is given

$$J_3=\sum _{i=1}^K{t}_{f,i}+p_1\parallel {\mathbf{x}}^{*}-\mathbf{x}(t_{f,i},{\mathbf{x}}^{0,i})\parallel \to \underset{\mathbf{u}}{min},$$

(48)

where $t_{f,i}$ is a time of achieving the terminal condition from the initial condition ${\mathbf{x}}^{0,i}$. It is necessary to find a control in the form (41).

The general formulation of the synthesis problem was posed by V.G. Boltyanskiy in the 60s of the last century [25]. One of the ways to solve it is to reduce the problem to the partial differential equation of Bellman [26,27], who also proposed a method for its solution in the form of a dynamic programming method [26,28]. Bellman’s equation in the general case has no solution; therefore, most often it is solved numerically for one initial condition, which in our case is not enough to ensure stability.

To solve the synthesis problem and obtain an equilibrium point, methods of modal control [29] can be applied for linear systems, as well as other analytical methods such as backstepping [30], analytical design of aggregated controllers [31,32], or synthesis based on the application of the Lyapunov function [21,33]. Note that all known analytical synthesis methods for nonlinear systems, when implemented, are associated with a specific type of model, therefore they cannot be considered universal. In practice, linear controllers, such as PID or PI controllers, are often used to ensure stability. Their use is also associated with a specific model, which is linearized in the neighbourhood of the equilibrium point, and their use is not related to the formal statement of the considered synthesis problem.

To solve the synthesis problem in the considered mathematical formulation, it is necessary to find the control function in the form (41). Most of the known methods specify the control function with an accuracy of the parameter values, for example, methods associated with the solution of the Bellman equation, like analytical design of optimal controllers [34], as well as the use of various controllers, including controllers based on very popular now artificial neural networks [35].

This paper proposes to solve the addressed problem numerically. For a solution of the synthesis problem we apply numerical methods of symbolic regression. These methods can look for a structure of the function in the form a special code by some genetic algorithm and also search for the optimal values of parameters in the desired function.

7. Symbolic Regression Methods

To encode a mathematical expression, it is necessary to define sets of arguments of the mathematical expression and elementary functions. To decode a code of the mathematical expression it is enough to know how many arguments has each elementary function. For encoding elementary function, it is enough to use integer vector with two components. The first component is the number of arguments of the elementary function. The second component is the function number. Arguments of mathematical expression are elementary functions without arguments, therefore the first component of an argument code is zero.

For the control synthesis problem (45)–(48) it is necessary to find a mathematical expression of the control function (41).

Let us define sets of elementary functions.

A set of mathematical expression arguments or elementary functions without arguments includes variables, parameters, and unit elements for elementary functions with two arguments,

$${\mathrm{F}}_0=\{f_{0,1}=x_1,\dots ,f_{0,n}=x_n,f_{0,n+1}=c_1,\dots ,f_{0,n+p},f_{0,n+p+1}=e_1,\dots ,f_{0,n+p+r}=e_V\},$$

(49)

where $x_i$ is a component of the state vector, $i=1,\dots ,n$, $\mathbf{x}={[x_1\dots x_n]}^T$, $c_i$ is a component of the parametric vector, $i=1,\dots ,p$, $\mathbf{c}={[c_1\dots c_p]}^p$, $e_i$ is a unit element for function with two arguments.

A set of functions with one argument includes an identity function

$${\mathrm{F}}_1=\{f_{1,1}\left(z\right)=z,f_{1,2}\left(z\right),\dots ,f_{1,W}\left(z\right)\}.$$

(50)

A set of functions with two arguments includes such functions, that are associative, commutative and have a unit element

$${\mathrm{F}}_2=\{f_{2,1}(z_1,z_2),\dots ,f_{2,V}(z_1,z_2)\},$$

(51)

where each element from the set $F_2$ has the following properties:

-

associative

$$f_{2,j}(f_{2,j}(z_1,z_2),z_3)=f_{2,j}(z_1,f_{2,j}(z_2,z_3)),j=1,\dots ,V,$$

(52)

-

commutative

$$f_{2,j}(z_1,z_2)=f_{2,j}(z_2,z_1),j=1,\dots ,V,$$

(53)

-

existing of a unit element

$$f_{2,j}(z_1,e_j)=z_1,f_{2,j}(e_j,z_2)=z_2,j=1,\dots ,V.$$

(54)

To describe the most common mathematical expressions, it is enough functions with one and two arguments. Functions with three and more arguments may not be used.

Any element of the sets (49)–(51) is encoded by integer vector with two arguments

$$\mathbf{s}={\left[s_1{s}_2\right]}^T,$$

(55)

where $s_1$ is the number of arguments, $s_2$ is a function number.

A code of the mathematical expression is a set of codes of elementary functions

$$\mathrm{S}={\mathbf{s}}^1\dots {\mathbf{s}}^L,$$

(56)

where ${\mathbf{s}}^j={\left[s_1^j{s}_2^j\right]}^T$, $s_1^j\in \{0,1,2\}$,

$$s_2^j\in \left\{\begin{array}{c}\{1,\dots ,n+p+V\},\mathrm{if}{s}_1^j=0\hfill \\ \{1,\dots ,W\},\mathrm{if}{s}_1^j=1\hfill \\ \{1,\dots ,V\},\mathrm{otherwise}\hfill \end{array}\right.$$

(57)

Theorem 4.

For the mathematical expression code (57) with L elements to be correct, it is necessary and enough that the following formulas are valid

$$1+\sum _{i=1}^j{s}_1^i\le L,j=1,\dots ,L-1,$$

(58)

$$1-L+\sum _{i=1}^L{s}_1^i=0.$$

(59)

Proof. 

Consider the Formula (58) and add there $-j$ in the left and right sides

$$-j+1+\sum _{i=1}^j{s}_1^i\le L-j.$$

(60)

Consider left side of the inequation (60)

$$T\left(j\right)=-j+1+\sum _{i=1}^j{s}_1^i.$$

(61)

This equation calculates how many elements from the set of arguments (49) should be after element j. The value $T\left(j\right)$ is increasing on 1 after each $s_1^j=2$, it is not changing after each $s_1^j=1$, and it is decreasing on 1 after $s_1^j=0$.

At $j=L$, we receive the Equation (59). After the last element $j=L$ it must be no elements on the right from element L.

Assume that the inequation (57) fails. Then from (61) we receive for $j=L$

$$T\left(j\right)=-L+1+\sum _{i=1}^j{s}_1^i>0.$$

(62)

This means, that after the last element there are some elements. This does not allow to decode the code. Therefore conditions (57) and (58) are necessary.

Let the inequation (57) and Equation (58) be satisfied. If the element after the element j is an argument from the set (49), then $T\left(j\right)$ is decreasing on 1, if it is the function number with one argument, then $T\left(j\right)$ is not changed, if it is the function number with two arguments, then $T\left(j\right)$ increases on 1. Equation (58) shows that the last element from the set (49) does not need arguments. The formula is decoded. Therefore, performing the Formulas (57) and (58) is enough. QED. □

From Equation (58) it follows

$$\sum _{i=1}^L{s}_1^i=L-1.$$

(63)

Such direct encoding is in the genetic programming [36]. This method of symbolic regression does not include extra elements, therefore codes of different mathematical expressions have different lengths. It is not very comfortable for programming and implementing crossover in genetic programming. For crossover it is necessary to find in the code (55) the sub-code of mathematical expression with the properties (57) and (58). Crossover operation in genetic programming is performed as exchanging sub-codes of mathematical expressions. Searching for sub-codes and exchanging them takes significant time of the algorithm. Other symbolic regression methods that can be effectively used to find a mathematical expression, such as the network operator method [37,38], or Cartesian genetic programming [39,40] have codes of equal length for different mathematical expressions due to redundant elements.

An effective tool in the search for an optimal mathematical expression is the principle of small variations of the basic solution [41]. According to this principle, the search for the mathematical expression can begin in the neighbourhood of one given basic solution. This solution is coded by some symbolic regression method. Other possible solutions are obtained using sets of codes of small variations of the basic solution. Each small variation slightly modifies the basic solution code so that a new code corresponds to some kind of mathematical expression.

To find the optimal mathematical expression by any method of symbolic regression, a special genetic algorithm is used. Depending on the code of symbolic regression, this genetic algorithm has its own crossover and mutation operations. Using the principle of small variations of the basic solution, crossover and mutation operations are performed on the sets of small variations.

In the numerical solution of control synthesis problems by symbolic regression methods, together with the search of the structure of the mathematical expression, it is advisable to look for the optimal values of the parameter vector $\mathbf{c}={[c_1\dots c_p]}^T$, which is included in this mathematical expression in the form of its additional arguments (49). For this purpose, it is convenient to use the same genetic algorithm as for finding the structure. In this case, a possible solution is a pair including the code for structure of the mathematical expression and the vector of parameters. When performing a crossover operation, we get not two, but four offsprings. Two offsprings have new mathematical expression structures and new parameter values, and two others inherit parent structures and have only new parameter values. The crossover operation for parameters is performed as in the classical genetic algorithm, by exchanging codes after the crossover point.

It can be seen that the methods of symbolic regression can automate the process of synthesis of control systems, but very little of them are used in this direction. Only few scientific groups [42,43,44] are developing these approaches for solving the problem of control system synthesis in view of a number of difficulties, such as non-numerical search space and the absence of a metric on it, the complexity of the program code and the absence of publicly available software packages, and so forth.

8. A Computational Example

Let us consider the optimal control problem for two mobile robots. They have to exchange its position on the plane with obstacles.

Mathematical models of mobile robots [45] are given

$$\begin{array}{ccc}\hfill {\dot{x}}^j& =& 0.5(u_1^j+u_2^j)cos\left({\theta }^j\right),\hfill \\ \hfill {\dot{y}}^j& =& 0.5(u_1^j+u_2^j)sin\left({\theta }^j\right),\hfill \\ \hfill {\dot{\theta }}^j& =& 0.5(u_1^j-u_2^j),\hfill \end{array}$$

(64)

where ${\mathbf{u}}^j=[u_1^j{u}_2^j]$ is a vector of control, $j=1,2$.

Control is restricted

$$-10=u_i^{-}\le u_i^j\le u_i^{+}=10,j=1,2,i=1,2.$$

(65)

The initial conditions are set

$$x^1\left(0\right)=0,y^1\left(0\right)=0,{\theta }^1\left(0\right)=0,x^2\left(0\right)=10,y^2\left(0\right)=10,{\theta }^2\left(0\right)=0.$$

(66)

The terminal conditions are set

$$x^1\left(t_f\right)=10,y^1\left(t_f\right)=10,{\theta }^1\left(t_f\right)=0,x^2\left(t_f\right)=0,y^2\left(t_f\right)=0,{\theta }^2\left(t_f\right)=0,$$

(67)

where

$$t_f=\left\{\begin{array}{c}t ,\mathrm{if}t<t^{+}\mathrm{and}{\Delta }_f\left(t\right)\le \epsilon \hfill \\ t^{+},\mathrm{otherwise}\hfill \end{array}\right.$$

(68)

$${\Delta }_f\left(t\right)=\sqrt{{(10-x^1\left(t\right))}^2+{(10-y^1\left(t\right))}^2+{\left({\theta }^1\left(t\right)\right)}^2+{\left(x^2\left(t\right)\right)}^2+{\left(y^2\left(t\right)\right)}^2+{\left({\theta }^2\left(t\right)\right)}^2},$$

(69)

$t^{+}=2.4$ s, $\epsilon =0.01$.

The quality functional includes the time to reach the terminal state and penalty functions for violation of the accuracy of reaching the terminal state and for violation of static and dynamic phase constraints

$$J_e=t_f+w_1{\Delta }_f\left(t_f\right)+w_2\underset{0}{\overset{t_f}{\int }}\sum _{i=1}^2\sum _{j=1}^2\vartheta \left({\phi }_{i,j}\left(t\right)\right)dt+$$

$$w_3\underset{0}{\overset{t_f}{\int }}\vartheta (d^2-{(x^1\left(t\right)-x^2\left(t\right))}^2-{(y^1\left(t\right)-y^2\left(t\right))}^2)dt\to \underset{{\mathbf{u}}^1,{\mathbf{u}}^2}{min}$$

(70)

where $w_1=2.5$, $w_2=3$, $w_3=3$,

$$\vartheta \left(\alpha \right)=\left\{\begin{array}{c}1,\mathrm{if}\alpha >0\hfill \\ 0,\mathrm{otherwise}\hfill \end{array}\right.,$$

(71)

$${\phi }_{i,j}\left(t\right)=r_i-\sqrt{{(x_i-x^j\left(t\right))}^2+{(y_i-y^j\left(t\right))}^2},i=1,2,j=1,2,$$

(72)

$r_1=3$, $r_2=3$, $x_1=5$, $x_2=5$, $y_1=9$, $y_2=1$, $d=2$.

It is necessary to find such a control to move all robots from its initial conditions (66) to the terminal conditions (67) with the minimal value of the quality criterion (70).

To solve the optimal control problem (64)–(72) by the proposed synthesized optimal control method it is necessary to initially solve the control synthesis problem (45)–(48) for each robot. Since robots are similar, it is enough to solve the control synthesis problem once for one robot. For the solution of this problem, the symbolic regression method of Cartesian genetic programming is used.

In the result, the following control function was obtained:

$$u_i^j=\left\{\begin{array}{c}{u}_i^{+}=10,\mathrm{if}{u}_i^{+}\le {\tilde{u}}_i^j\hfill \\ u_i^{-}=-10,\mathrm{if}{\tilde{u}}_i^j\le u_i^{-}\hfill \\ {\tilde{u}}_i^j,\mathrm{otherwise}\hfill \end{array}\right.,i=1,2,j=1,2,$$

(73)

where

$${\tilde{u}}_1^j=A+B+{\rho }_{\#}\left(A\right),j=1,2,$$

(74)

$${\tilde{u}}_1^j=B-A-{\rho }_{\#}\left(A\right),j=1,2,$$

(75)

$$A=c_1({\theta }^{*}-{\theta }^j)+{\sigma }_{\#}\left((x^{*}-x^J)(y^{*}-y^J)\right),$$

(76)

$$B=2(x^{*}-x^j)+\mathrm{sgn}(x^{*}-x^J)c_2,$$

(77)

$${\rho }_{\#}\left(\alpha \right)=\left\{\begin{array}{c}\mathrm{sgn}\left(\alpha \right)B^{+},\mathrm{if}\left|\alpha \right|>-log\left({\delta }^{-}\right)\hfill \\ \mathrm{sgn}\left(\alpha \right)(exp(\left|\alpha \right|)-1)\hfill \end{array}\right.,{\sigma }_{\#}\left(\alpha \right)=\mathrm{sgn}\left(\alpha \right)\sqrt{\left|\alpha \right|},$$

(78)

$c_1=3.1094$, $c_2=3.6289$, $B^{+}={10}^8$, ${\delta }^{-}={10}^{-8}$.

For solution of the synthesis problem eight initial conditions were used and the quality criterion took into account the speed and the accuracy of terminal position achievement

$${\mathbf{x}}^{*}={\left[x^{*}{y}^{*}{\theta }^{*}\right]}^T.$$

(79)

In the result of the solution of control synthesis problem a stable equilibrium point in the state space is appeared. Position of the equilibrium point depends on the terminal vector (79).

In the second stage the set of four points (79) were searched for each robot on criterion (70)

$${\mathrm{X}}^{*}=\{{\mathbf{x}}^{*,1,1},\dots ,{\mathbf{x}}^{*,1,4},{\mathbf{x}}^{*,2,1},\dots ,{\mathbf{x}}^{*,2,4}\}.$$

(80)

These points were switching in some time interval $\Delta t=0.6$ s for control function (73) of each robot.

To search for the points the evolutionary algorithm of Grey wolf optimizer [46,47] was used. In result, after more than one hundred tests the following best points were found:

$$\begin{array}{cccccc}\hfill {\mathbf{x}}^{*,1,1}& =& {\left[4.01591.89541.2397\right]}^T,\hfill & \hfill {\mathbf{x}}^{*,1,2}& =& {\left[7.08904.23410.5270\right]}^T,\hfill \\ \hfill {\mathbf{x}}^{*,1,3}& =& {[7.2194-0.44801.3042]}^T,\hfill & \hfill {\mathbf{x}}^{*,1,4}& =& {\left[11.97229.46630.1866\right]}^T,\hfill \\ \hfill {\mathbf{x}}^{*,2,1}& =& {[5.38994.0791-0.1208]}^T,\hfill & \hfill {\mathbf{x}}^{*,2,2}& =& {[-0.64014.3126-0.0176]}^T,\hfill \\ \hfill {\mathbf{x}}^{*,2,3}& =& {\left[0.31030.89550.6335\right]}^T,\hfill & \hfill {\mathbf{x}}^{*,2,4}& =& {[-0.0791-0.15180.0195]}^T.\hfill \end{array}$$

(81)

The algorithm simulated the system (64) with the control (73) for calculation of criterion values (70) in one test more than 500,000 times.

When searching for points, the following constraints were used

$$-2\le x^{*}\le 12,-2\le y^{*}\le 12,-\pi /2\le {\theta }^{*}\le \pi /2.$$

(82)

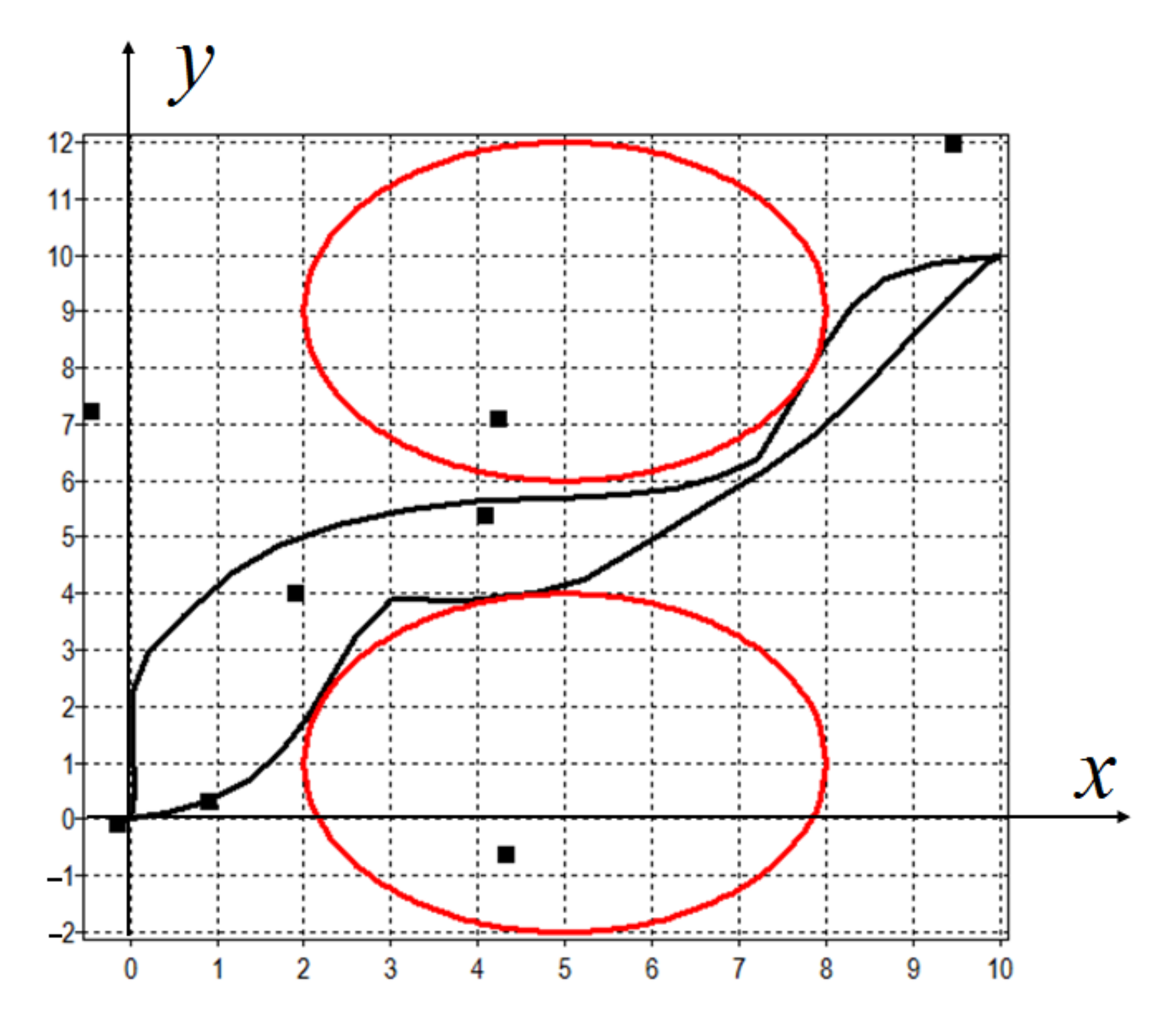
In the Figure 1 the projections of optimal trajectories on the plane $\{x,y\}$ are presented. The trajectories are black lines, red circles are obstacles, small black squares are projections of found points (81).

The quality criterion (70) for found control was $J_e=2.8914$.

For comparative study of the obtained solution, the same optimal control problem was solved by a direct method. For this purpose control functions of robots were approximated by piece-wise linear functions of time. The interval of approximation was ${\Delta }_{d}t=0.4$ s, therefore a number of intervals was

$$K=⌊\frac{t^{+}}{{\Delta }_{d}t}⌋=⌊\frac{2.4}{0.4}⌋=6.$$

(83)

For the approximation of control function, the values of parameters on the boundaries of intervals were searched. For each one control function it was necessary to find $K+1=7$ parameters. Total vector of parameters had twenty eight components.

$$\mathbf{q}={[q_1\dots q_{28}]}^T.$$

(84)

The direct control has the following form

$$u_i^j=\left\{\begin{array}{c}10=u_i^{+},\mathrm{if}{u}_i^{+}\le {\overline{u}}_i^j\hfill \\ -10=u_i^{-},\mathrm{if}{\overline{u}}_i^j\le u_i^{-}\hfill \\ {\overline{u}}_i^j,\mathrm{otherwise}\hfill \end{array}\right.,i=1,2,j=1,2,$$

(85)

where

$${\overline{u}}_1^1=q_s+(q_{s+1}-q_s)\frac{(t-s{\Delta }_{d}t)}{{\Delta }_{d}t},$$

(86)

$${\overline{u}}_2^1=q_{s+L}+(q_{s+L+1}-q_{s+L})\frac{(t-s{\Delta }_{d}t)}{{\Delta }_{d}t},$$

(87)

$${\overline{u}}_1^2=q_{s+2K}+(q_{s+2L+1}-q_{s+2L})\frac{(t-s{\Delta }_{d}t)}{{\Delta }_{d}t},$$

(88)

$${\overline{u}}_2^2=q_{s+3L}+(q_{s+3L+1}-q_{s+3L})\frac{(t-s{\Delta }_{d}t)}{{\Delta }_{d}t},$$

(89)

$s{\Delta }_{d}t\le t\le (s+1){\Delta }_{d}t$, $s\in \{1,\dots ,6\}$, $L=K+1=7$.

To search for optimal parameters the same evolutionary algorithm of Grey wolf optimizer was used. In the result of more than one hundred tests the following best values of parameters were found:

$$\begin{array}{ccc}\hfill \mathbf{q}& =& [19.61255.43187.592119.40202.39282.16271.6976\hfill \\ \hfill & & 1.49415.182816.908711.2478-2.449917.7201-0.6297\hfill \\ \hfill & & -0.9093-1.6815-19.5283-16.4979-0.2321-11.4719-17.7372\hfill \\ \hfill & & {-1.4218-18.0214-3.7942-3.0899-13.3196-9.7212-0.3233]}^T\hfill \end{array}$$

(90)

The process of searching the parameters had restrictions

$$-20=q^{-}\le q_i\le q^{+}=20,i=1,\dots ,28.$$

(91)

In one test, the algorithm simulated the system (64) with the control (85) for calculation of criterion values (70) more than 500,000 times. A value of quality criterion (70) for found control was $J_e=2.5134$.

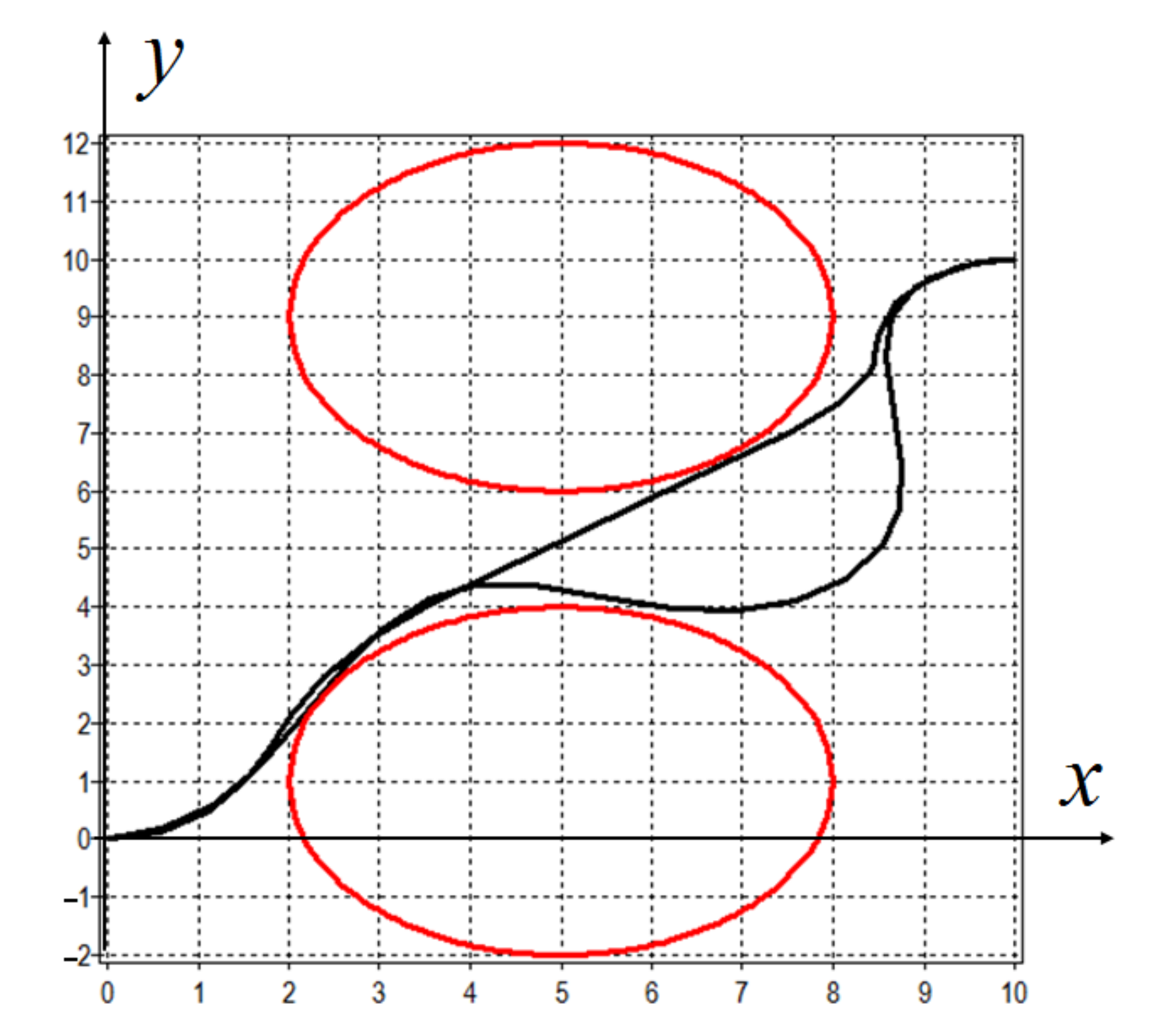
In Figure 2, the projection of optimal trajectories of mobile robots on the horizontal plane $\{x,y\}$ is presented.

To check the obtained solutions of sensitivity to perturbations, we included random functions of uncertainty into the model (64)

$$\begin{array}{ccc}\hfill {\dot{x}}^j& =& 0.5(u_1^j+u_2^j)cos\left({\theta }^j\right)+B\xi \left(t\right),\hfill \\ \hfill {\dot{y}}^j& =& 0.5(u_1^j+u_2^j)sin\left({\theta }^j\right)+B\xi \left(t\right),\hfill \\ \hfill {\dot{\theta }}^j& =& 0.5(u_1^j-u_2^j)+B\xi \left(t\right),\hfill \end{array}$$

(92)

where $j=1,2$, $\xi \left(t\right)$ generates new random value in interval from $-1$ to 1 at every call.

Results of simulations with the found optimal controls and different levels of perturbations of the model are presented in the

Table 1. The average values of functional (70).

Level of Noise B	Synthesized Control	Direct Control
0	2.8914	2.5134
0.1	3.0014	3.0260
0.2	3.0066	3.8571
0.5	3.2141	5.5497
0.8	3.3156	5.8968
1	3.4123	6.7952
1.5	3.6954	8.2654

. The Table 1 includes average values of functional (70) on ten tests. As we can see, the synthesized optimal control is less sensitive to the perturbation of model. For the synthesized control with the level of perturbation $B=1.5$, the average value of the functional is changed by no more than $30\%$ and, for the direct control with the same level of perturbations, the functional is changed by more than $200\%$.

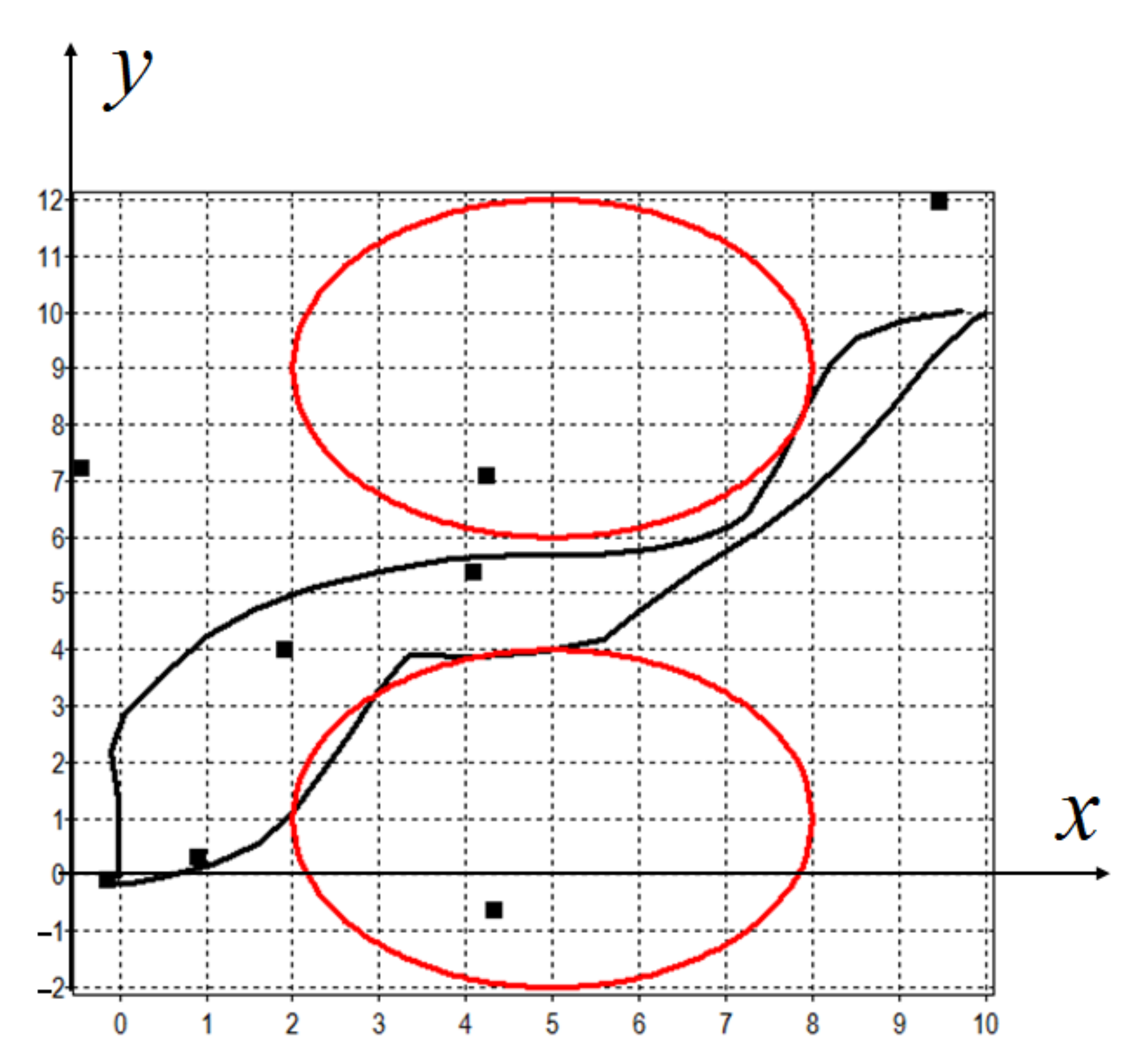
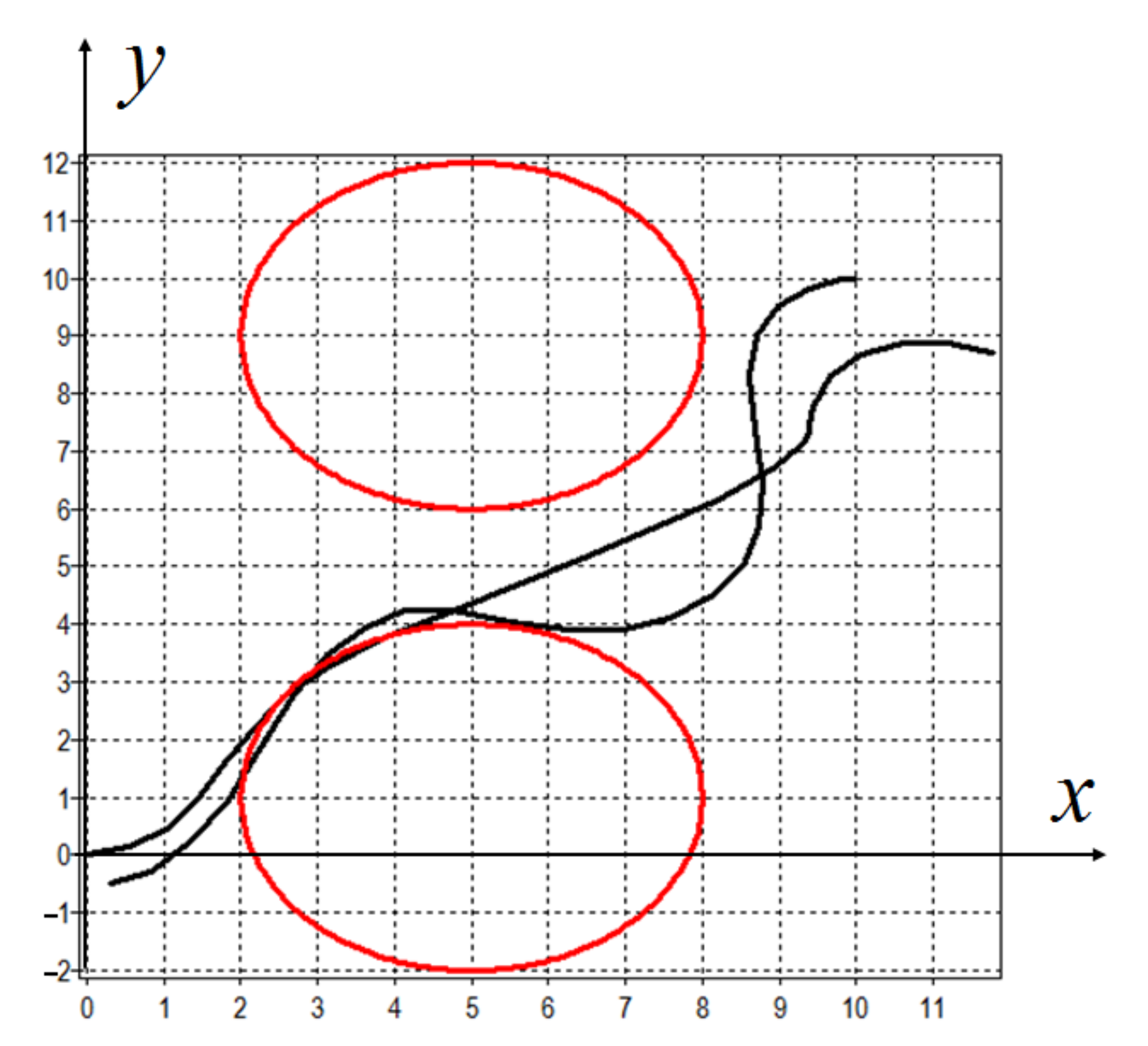
In Figure 3, the trajectories for synthesized optimal control with model perturbations of level $B=1.5$ are presented. In Figure 4, the trajectories for the direct control with the same level of perturbation $B=1.5$ are presented.

As can be seen from Figure 3 and Figure 4, the synthesized control does not change the nature of the motion of objects under large disturbances, and direct control first of all violates the accuracy of achieving the terminal conditions.

9. Conclusions

This work presents the statement of the new optimal control problem with uncertainty. In this problem, the mathematical model of the control object includes an additive limited perturbing function simulating possible model inaccuracies. It is necessary to find an optimal control function that provides for limited perturbations bounded variation of functional value. For this purpose, it is proposed to use the synthesized optimal control method. According to this method initially, the control synthesis problem is solved. After that, in the state space a stable equilibrium point appears. In the second stage, the original optimal control problem is solved by searching positions of some stable equilibrium points, which are a control for stabilization system, obtained in the first stage. It is shown that such an approach supplies the property of a contraction mapping for differential equations of the mathematical model of the plant. Such differential equations are quite feasible, and their solutions reduce the errors of determining the state vector. For the solution of the control synthesis problem it is proposed to apply symbolic regression methods. A comparative example is presented. Computational experiments showed that the obtained solution is very less sensitive to perturbations in the mathematical model of the control object than the direct solution of the optimal control problem.

10. Findings/Results

This paper presents a new formulation of the optimal control problem, taking into account the objectively existing uncertainties of the model. The concept of feasibility is introduced, which means that small changes in the model do not lead to a loss of quality. Given the theoretical substantiations (definitions and theorems) that a system of differential equations of the mathematical model is feasible if it obtains, as a one-parametric mapping, a contraction property in the implementation domain. This property is an alternative to Lyapunov stability; it is softer, but sufficient for the development of real stable practical systems. An approach based on the method of synthesized optimal control is proposed, which makes it possible to develop systems that have the property of feasibility.

11. Discussion

According to the method of synthesized optimal control, the stability of the object is first ensured, that is, an equilibrium point appears in the phase space. In the neighbourhood of the stability point, the phase trajectories contract, and this property determines the feasibility of the system. For this, it is necessary to numerically solve the problem of synthesizing the stabilization system in order to obtain expressions for the control and substitute them in the right-hand sides of the object model. The synthesis problem is quite difficult. This paper proposes using numerical methods of symbolic regression to solve it. There are several successful applications, but they are still not very popular due to the complexity of the search area on a non-numerical space of functions where there is no metric. This is the direction for future research.

In the applied method of synthesized optimal control in the second stage we searched positions of equilibrium points as a piece-wise constant function. It is necessary to investigate other types of functions to change the position of the equilibrium point, how many points should be and how often they should be switched.

In further studies it is also necessary to consider solutions of the new optimal control problem for different control objects.

With the numerical solution of the optimal control problem by evolutionary algorithm it was defined that these algorithms can find solutions for complex optimal control problems with static and dynamic phase constraints. It is necessary to continue to research different evolutionary algorithms for the solution of the optimal control problems.