Kähler–Einstein Metrics on Smooth Fano Symmetric Varieties with Picard Number One
Abstract
1. Introduction
2. Criterion for Existence of Kähler–Einstein Metrics on Symmetric Varieties
2.1. Spherical Varieties and Algebraic Moment Polytopes
2.2. Symmetric Spaces and Symmetric Varieties
2.3. Existence of Kähler–Einstein Metrics on Symmetric Varieties
3. Moment Polytopes of Smooth Fano Symmetric Varieties and Their Barycenters
3.1. Smooth Fano Embedding of with Picard Number One
3.2. Smooth Fano Embedding of with Picard Number One
3.3. Smooth Fano Embedding of with Picard Number One
3.4. Smooth Fano Embedding of with Picard Number One
3.5. Smooth Fano Embedding of with Picard Number One
3.6. Smooth Fano Embedding of with Picard Number One
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aubin, T. Équations du type Monge–Ampère sur les variétés kählériennes compactes. Bull. Sci. Math. 1978, 102, 63–95. [Google Scholar]
- Yau, S.-T. On the Ricci curvature of a compact Kähler manifold and the complex Monge–Ampère equation, I. Commun. Pure Appl. Math. 1978, 31, 339–411. [Google Scholar] [CrossRef]
- Matsushima, Y. Sur la structure du groupe d’homéomorphismes analytiques d’une certaine variété kählérienne. Nagoya Math. J. 1957, 11, 145–150. [Google Scholar] [CrossRef]
- Futaki, A. An obstruction to the existence of Einstein Kähler metrics. Invent. Math. 1983, 73, 437–443. [Google Scholar] [CrossRef]
- Tian, G. The K-energy on hypersurfaces and stability. Commun. Anal. Geom. 1994, 2, 239–265. [Google Scholar] [CrossRef]
- Tian, G. Kähler–Einstein metrics with positive scalar curvature. Invent. Math. 1997, 130, 1–37. [Google Scholar] [CrossRef]
- Donaldson, S.K. Scalar curvature and stability of toric varieties. J. Differ. Geom. 2002, 62, 289–349. [Google Scholar] [CrossRef]
- Chen, X.; Donaldson, S.; Sun, S. Kähler–Einstein metrics on Fano manifolds. I: Approximation of metrics with cone singularities. J. Am. Math. Soc. 2015, 28, 183–197. [Google Scholar] [CrossRef]
- Chen, X.; Donaldson, S.; Sun, S. Kähler–Einstein metrics on Fano manifolds. II: Limits with cone angle less than 2π. J. Am. Math. Soc. 2015, 28, 199–234. [Google Scholar] [CrossRef]
- Chen, X.; Donaldson, S.; Sun, S. Kähler–Einstein metrics on Fano manifolds. III: Limits as cone angle approaches 2π and completion of the main proof. J. Am. Math. Soc. 2015, 28, 235–278. [Google Scholar] [CrossRef]
- Tian, G. K-stability and Kähler–Einstein metrics. Commun. Pure Appl. Math. 2015, 68, 1085–1156. [Google Scholar] [CrossRef]
- Koszul, J.-L. Sur la forme hermitienne canonique des espaces homogènes complexes. Can. J. Math. 1955, 7, 562–576. [Google Scholar] [CrossRef]
- Matsushima, Y. Remarks on Kähler–Einstein manifolds. Nagoya Math. J. 1972, 46, 161–173. [Google Scholar] [CrossRef]
- Wang, X.-J.; Zhu, X. Kähler–Ricci solitons on toric manifolds with positive first Chern class. Adv. Math. 2004, 188, 87–103. [Google Scholar] [CrossRef]
- Mabuchi, T. Einstein–Kähler forms, Futaki invariants and convex geometry on toric Fano varieties. Osaka J. Math. 1987, 24, 705–737. [Google Scholar]
- Delcroix, T. Kähler–Einstein metrics on group compactifications. Geom. Funct. Anal. 2017, 27, 78–129. [Google Scholar] [CrossRef]
- Delcroix, T. K-stability of Fano spherical varieties. Ann. Sci. Éc. Norm. Supér. 2020, 53, 615–662. [Google Scholar] [CrossRef]
- Ruzzi, A. Smooth projective symmetric varieties with Picard number one. Int. J. Math. 2011, 22, 145–177. [Google Scholar] [CrossRef]
- Gandini, J. Embeddings of spherical homogeneous spaces. Acta Math. Sin. (Engl. Ser.) 2018, 34, 299–340. [Google Scholar] [CrossRef]
- Knop, F. The Luna–Vust theory of spherical embeddings. In Proceedings of the Hyderabad Conference on Algebraic Groups (Hyderabad, 1989); Manoj Prakashan: Madras, India, 1991; pp. 225–249. [Google Scholar]
- Timashev, D.A. Homogeneous spaces and equivariant embeddings. In Encyclopaedia of Mathematical Sciences; Springer: Heidelberg, Germany, 2011; Volume 138, p. 8. [Google Scholar]
- Luna, D.; Vust, T. Plongements d’espaces homogènes. Comment. Math. Helv. 1983, 58, 186–245. [Google Scholar] [CrossRef]
- Kirwan, F. Convexity properties of the moment mapping. III. Invent. Math. 1984, 77, 547–552. [Google Scholar] [CrossRef]
- Brion, M. Sur L’image de L’application Moment, Séminaire D’algèbre Paul Dubreil et Marie-Paule Malliavin (Paris, 1986); Lecture Notes in Mathematics; Springer: Berlin, Germany, 1987; Volume 1296, pp. 177–192. [Google Scholar]
- De Concini, C.; Procesi, C. Complete Symmetric Varieties. In Invariant Theory (Montecatini, 1982); Lecture Notes in Mathematics; Springer: Berlin, Germany, 1983; Volume 996, pp. 1–44. [Google Scholar]
- Steinberg, R. Endomorphisms of Linear Algebraic Groups. In Memoirs of the American Mathematical Society; No. 80; American Mathematical Society: Providence, RI, USA, 1968. [Google Scholar]
- Vust, T. Opération de groupes réductifs dans un type de cônes presque homogènes. Bull. Soc. Math. France 1974, 102, 317–333. [Google Scholar] [CrossRef]
- Ruzzi, A. Geometrical description of smooth projective symmetric varieties with Picard number one. Transform. Groups 2010, 15, 201–226. [Google Scholar] [CrossRef]
- Mihai, I.A. Odd symplectic flag manifolds. Transform. Groups 2007, 12, 573–599. [Google Scholar] [CrossRef][Green Version]
- Manivel, L. The Cayley Grassmannian. J. Algebra 2018, 503, 277–298. [Google Scholar] [CrossRef]
- Manivel, L. The double Cayley Grassmannian. arXiv 2020, arXiv:2004.00313. [Google Scholar]
- Kim, S.-Y.; Park, K.-D. On the deformation rigidity of smooth projective symmetric varieties with Picard number one. C. R. Math. Acad. Sci. Paris 2019, 357, 889–896. [Google Scholar] [CrossRef]
- Gagliardi, G.; Hofscheier, J. Gorenstein spherical Fano varieties. Geom. Dedic. 2015, 178, 111–133. [Google Scholar] [CrossRef]
- Brion, M. Groupe de Picard et nombres caractéristiques des variétés sphériques. Duke Math. J. 1989, 58, 397–424. [Google Scholar] [CrossRef]
- Brion, M. Curves and Divisors in Spherical Varieties, Algebraic Groups and Lie Groups; Australian Mathematical Society Lecture Notes; Cambridge University Press: Cambridge, MA, USA, 1997; Volume 9, pp. 21–34. [Google Scholar]
- Vust, T. Plongements d’espaces symétriques algébriques: Une classification. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 1990, 17, 165–195. [Google Scholar]
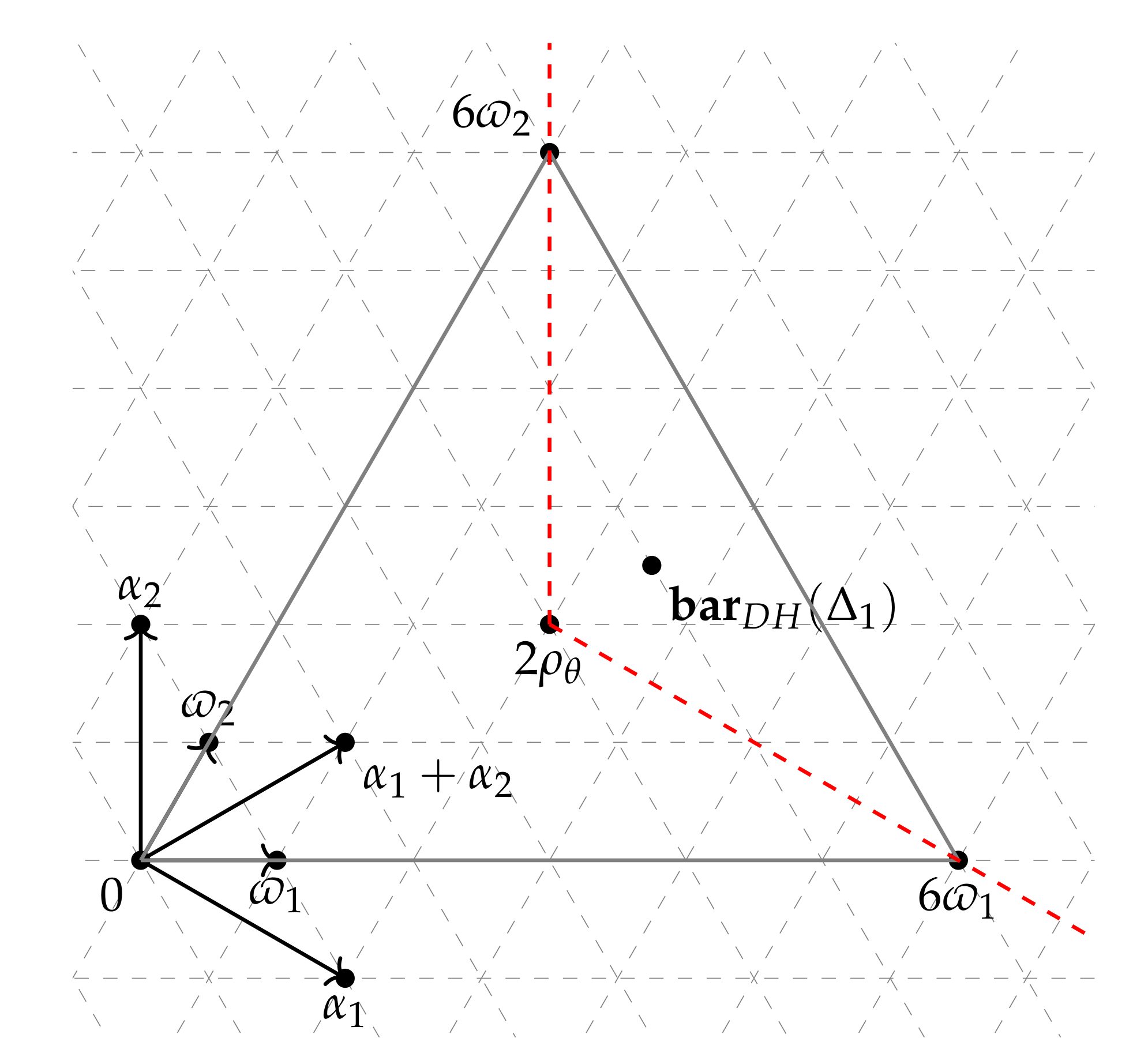
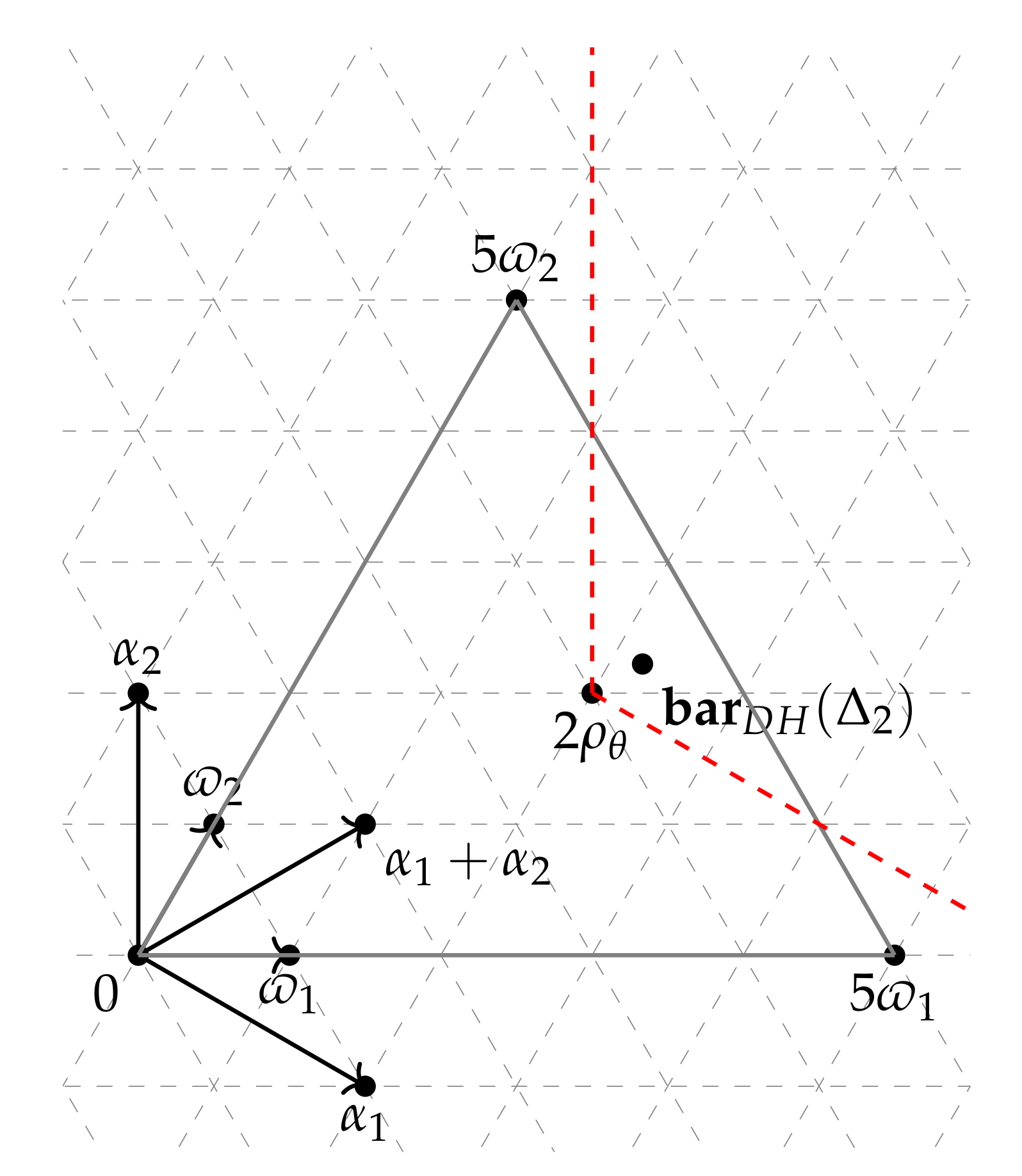
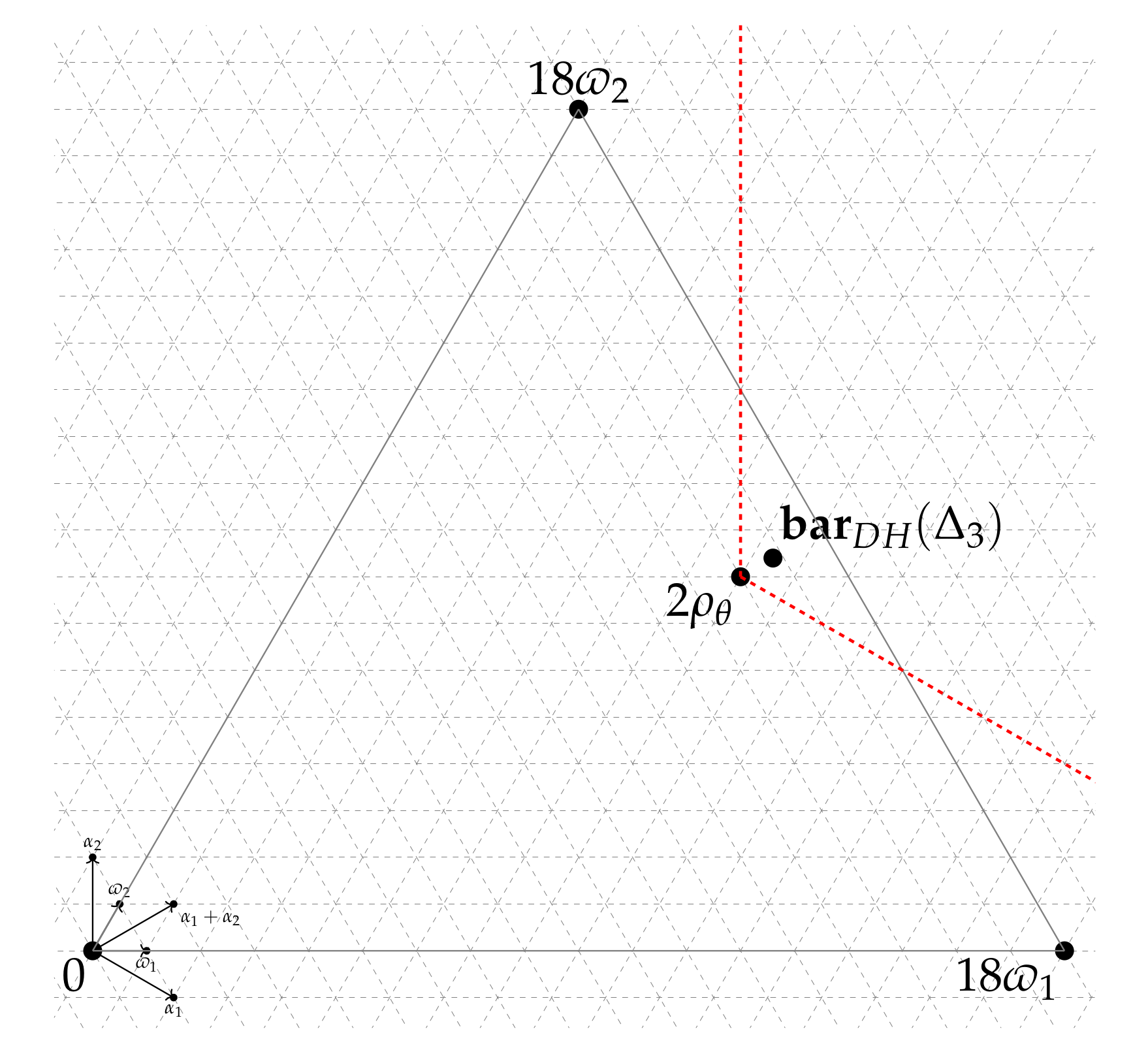
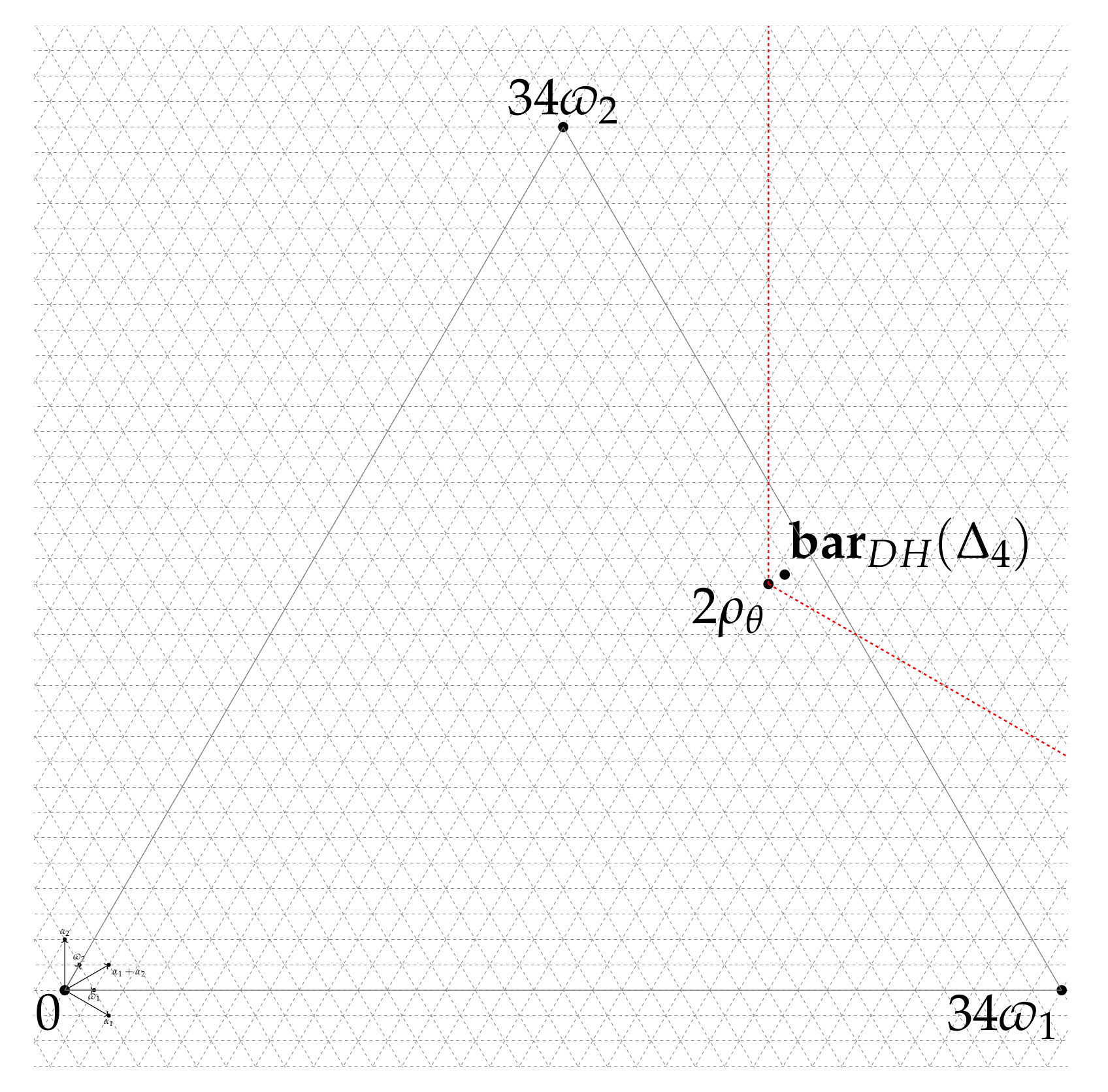
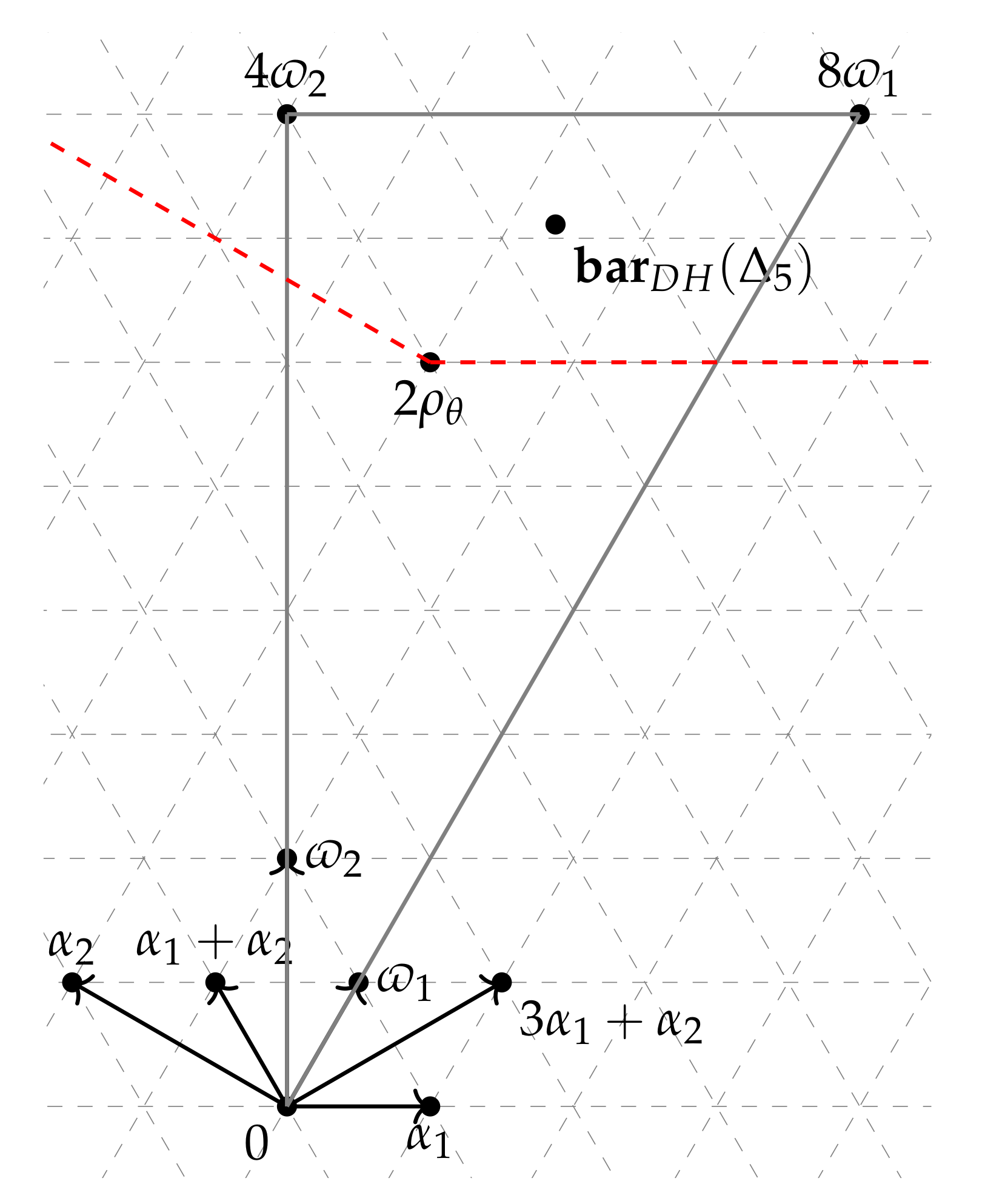
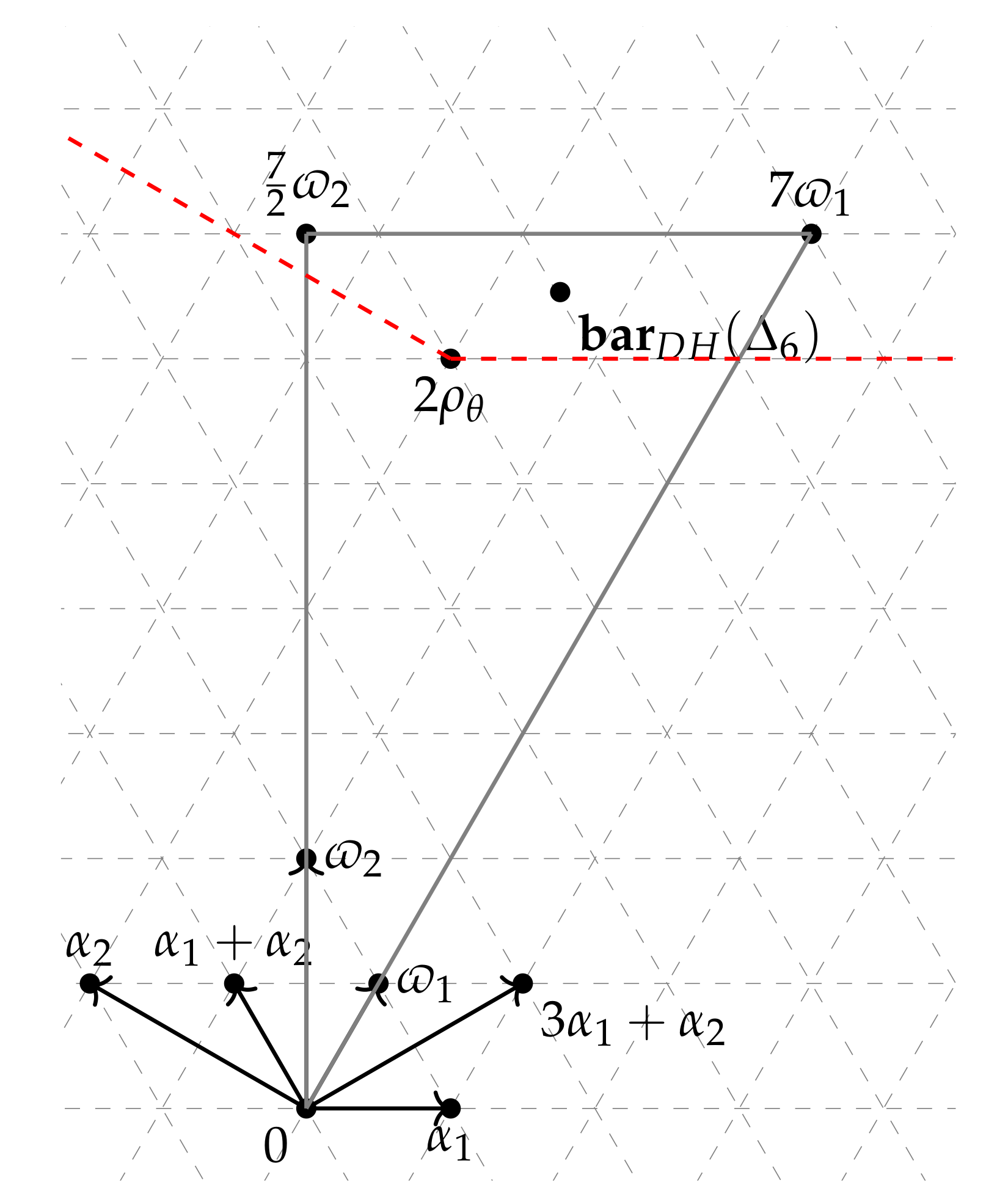
| Multiplicity | Geometric Description | |||||
|---|---|---|---|---|---|---|
| 1 | 5 | 3 | 1 | hyperplane section of | ||
| 2 | 8 | 5 | 2 | hyperplane section of | ||
| 3 | 14 | 9 | 4 | hyperplane section of | ||
| 4 | 26 | 17 | 8 | hyperplane section of | ||
| 5 | 8 | 4 | 1 | Cayley Grassmannian | ||
| 6 | 14 | 7 | 2 | double Cayley Grassmannian |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.-H.; Park, K.-D.; Yoo, S. Kähler–Einstein Metrics on Smooth Fano Symmetric Varieties with Picard Number One. Mathematics 2021, 9, 102. https://doi.org/10.3390/math9010102
Lee J-H, Park K-D, Yoo S. Kähler–Einstein Metrics on Smooth Fano Symmetric Varieties with Picard Number One. Mathematics. 2021; 9(1):102. https://doi.org/10.3390/math9010102
Chicago/Turabian StyleLee, Jae-Hyouk, Kyeong-Dong Park, and Sungmin Yoo. 2021. "Kähler–Einstein Metrics on Smooth Fano Symmetric Varieties with Picard Number One" Mathematics 9, no. 1: 102. https://doi.org/10.3390/math9010102
APA StyleLee, J.-H., Park, K.-D., & Yoo, S. (2021). Kähler–Einstein Metrics on Smooth Fano Symmetric Varieties with Picard Number One. Mathematics, 9(1), 102. https://doi.org/10.3390/math9010102




