Numerical Investigation of Freely Falling Objects Using Direct-Forcing Immersed Boundary Method
Abstract
1. Introduction
2. Mathematical Model and Numerical Method
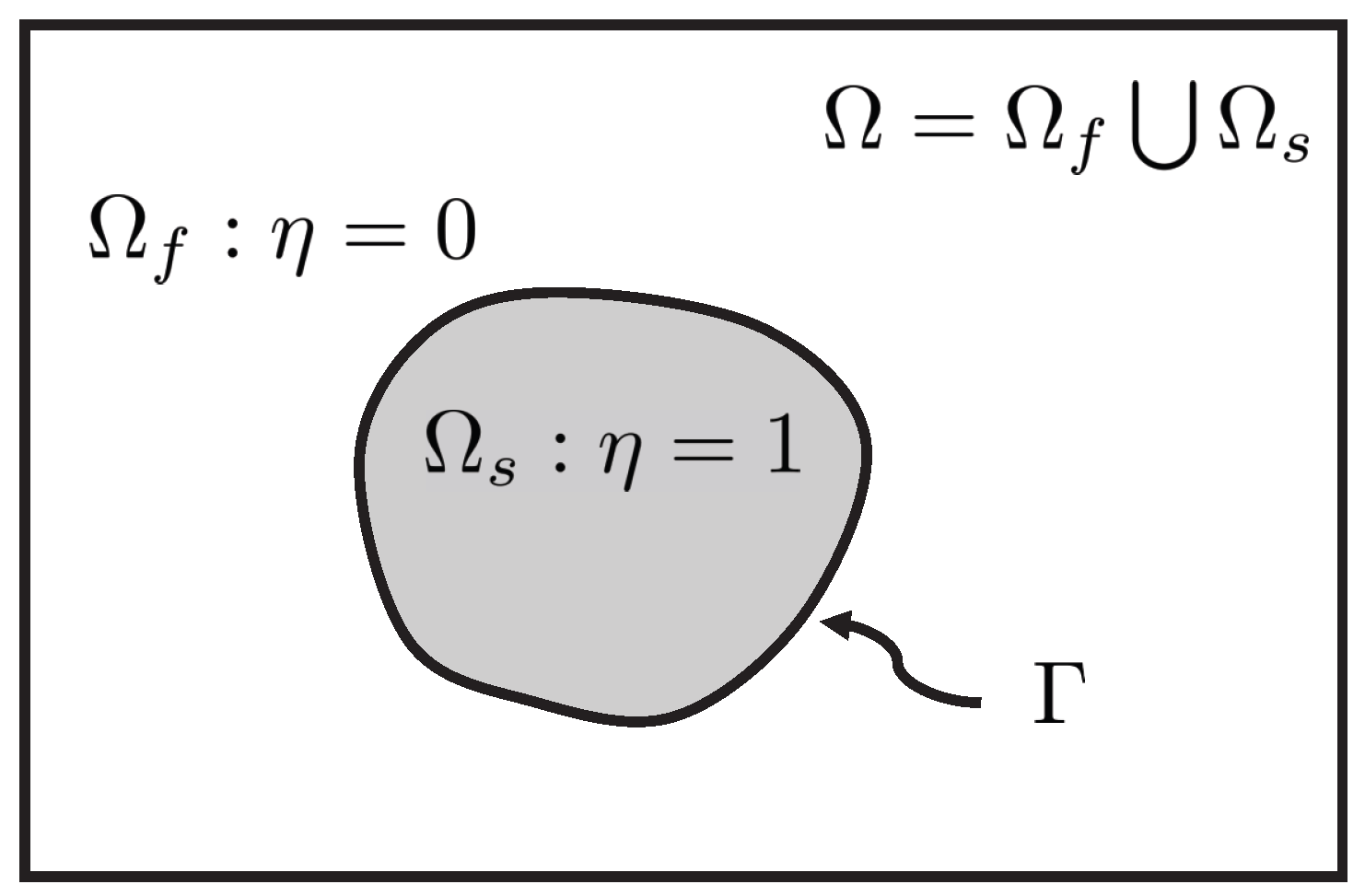
2.1. DFIB Method
2.2. Equations of Motion Governing the Movement of an Immersed Solid
2.3. Collision Model
2.4. Numerical Procedure
- Integrate and to obtain center-of-mass position and angle of rotation for solid object and then determine solid domain .
- Determine volume of solid function through .
- Calculate via projection method.
3. Numerical Validations
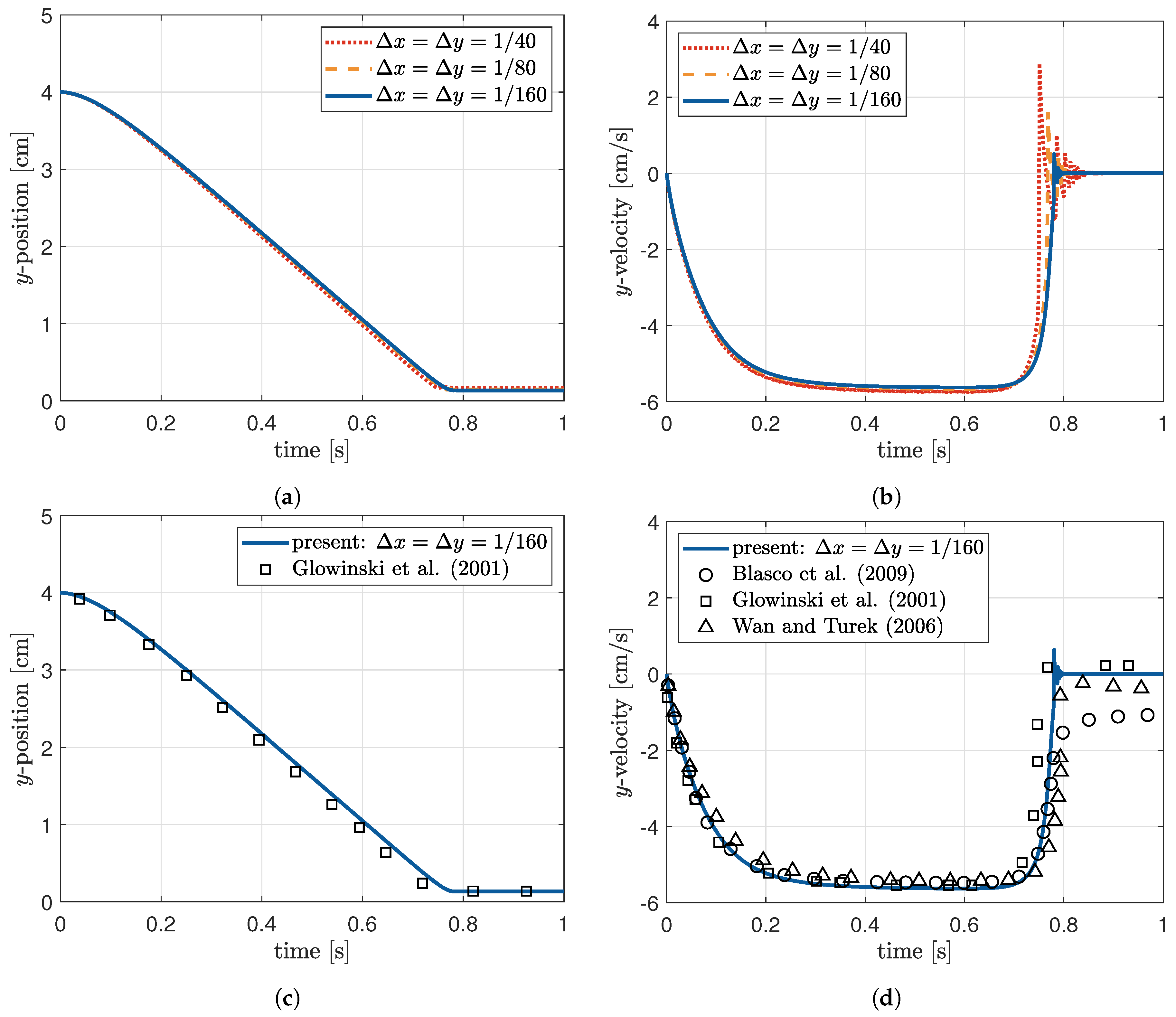
3.1. Sedimentation of a Circular Disk
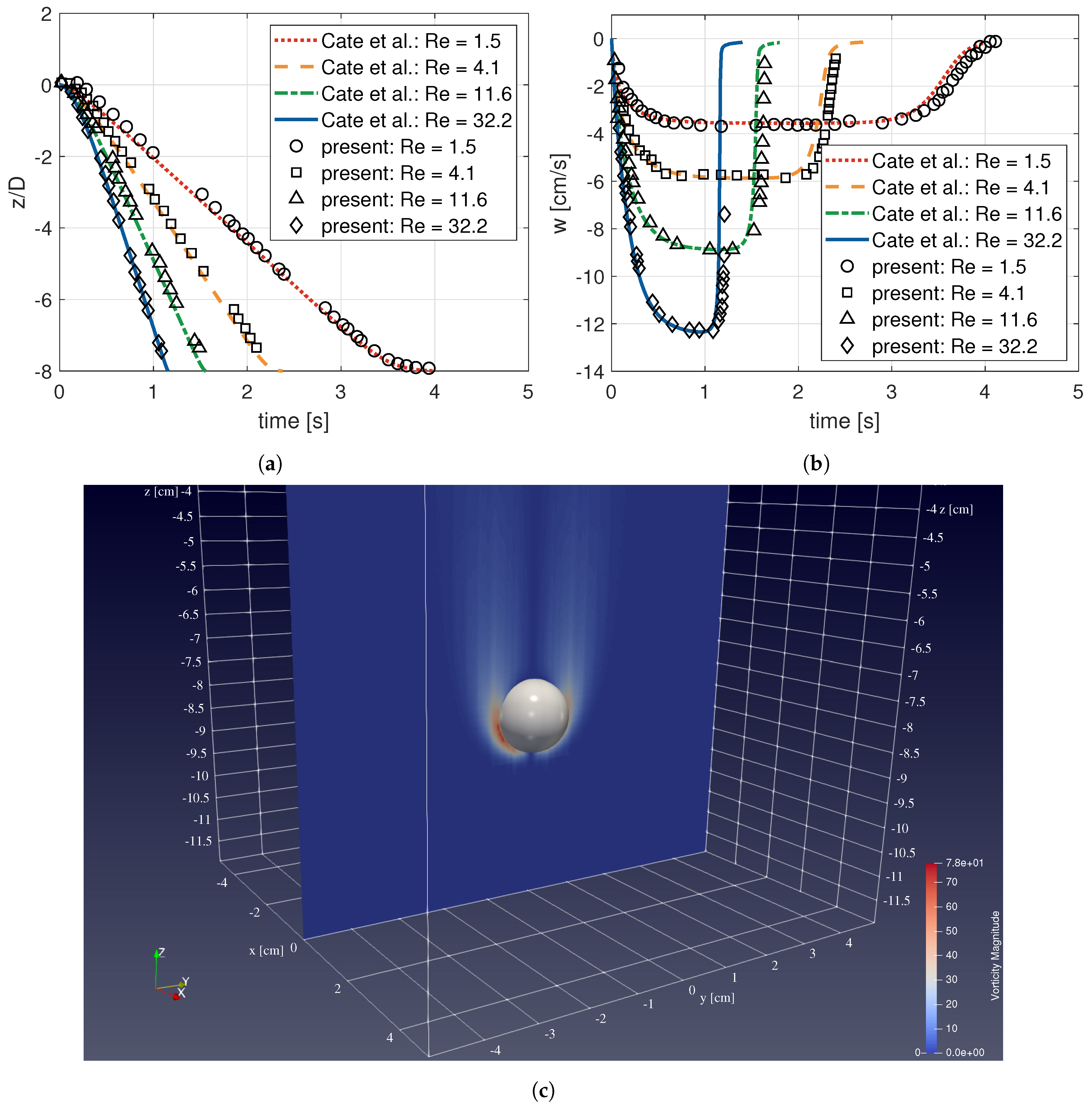
3.2. Sedimentation of a 3D Sphere
4. More Sedimentation Simulations by DFIB Method
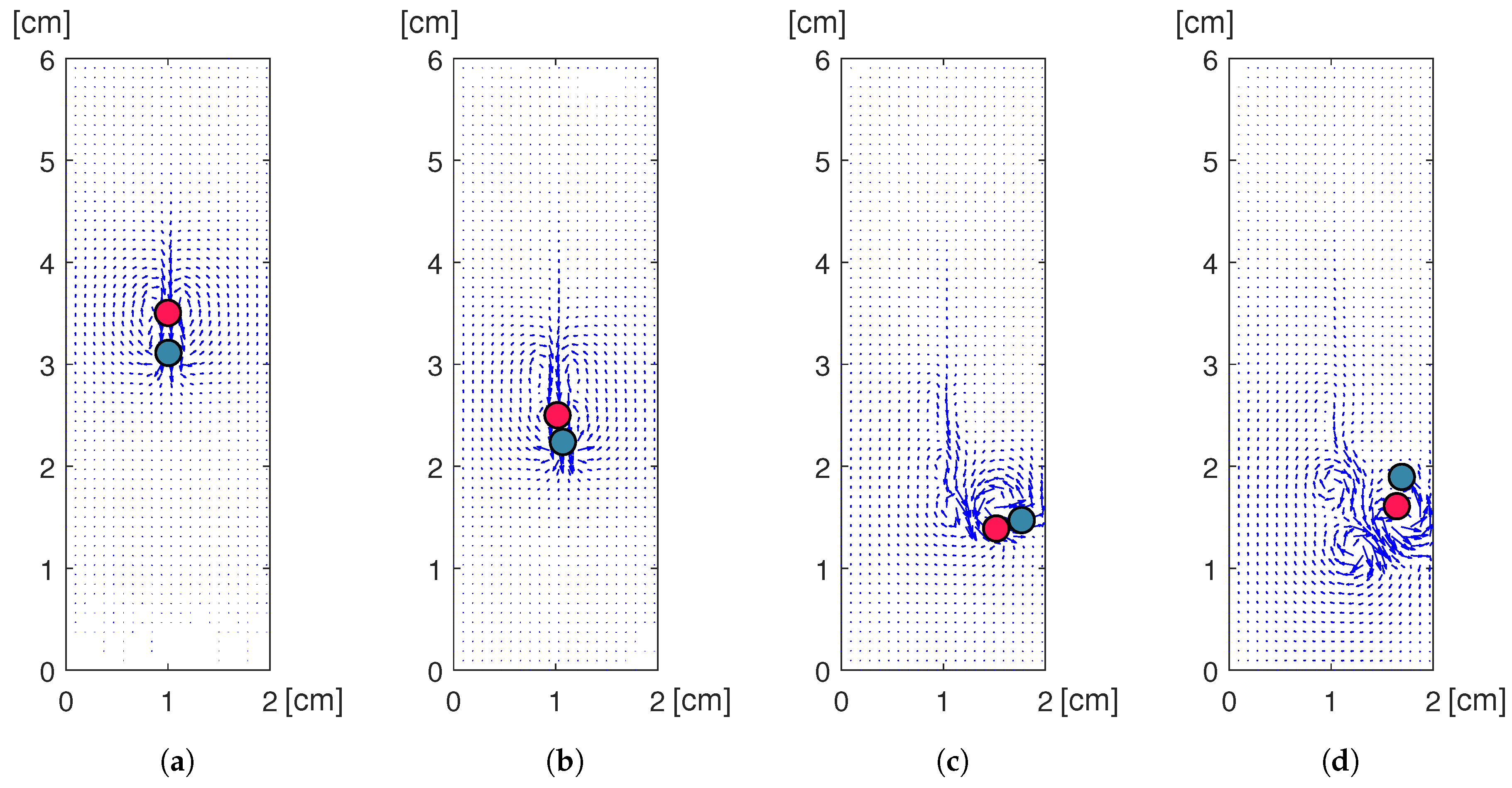
4.1. Sedimentation of Two Tandem Circular Disks
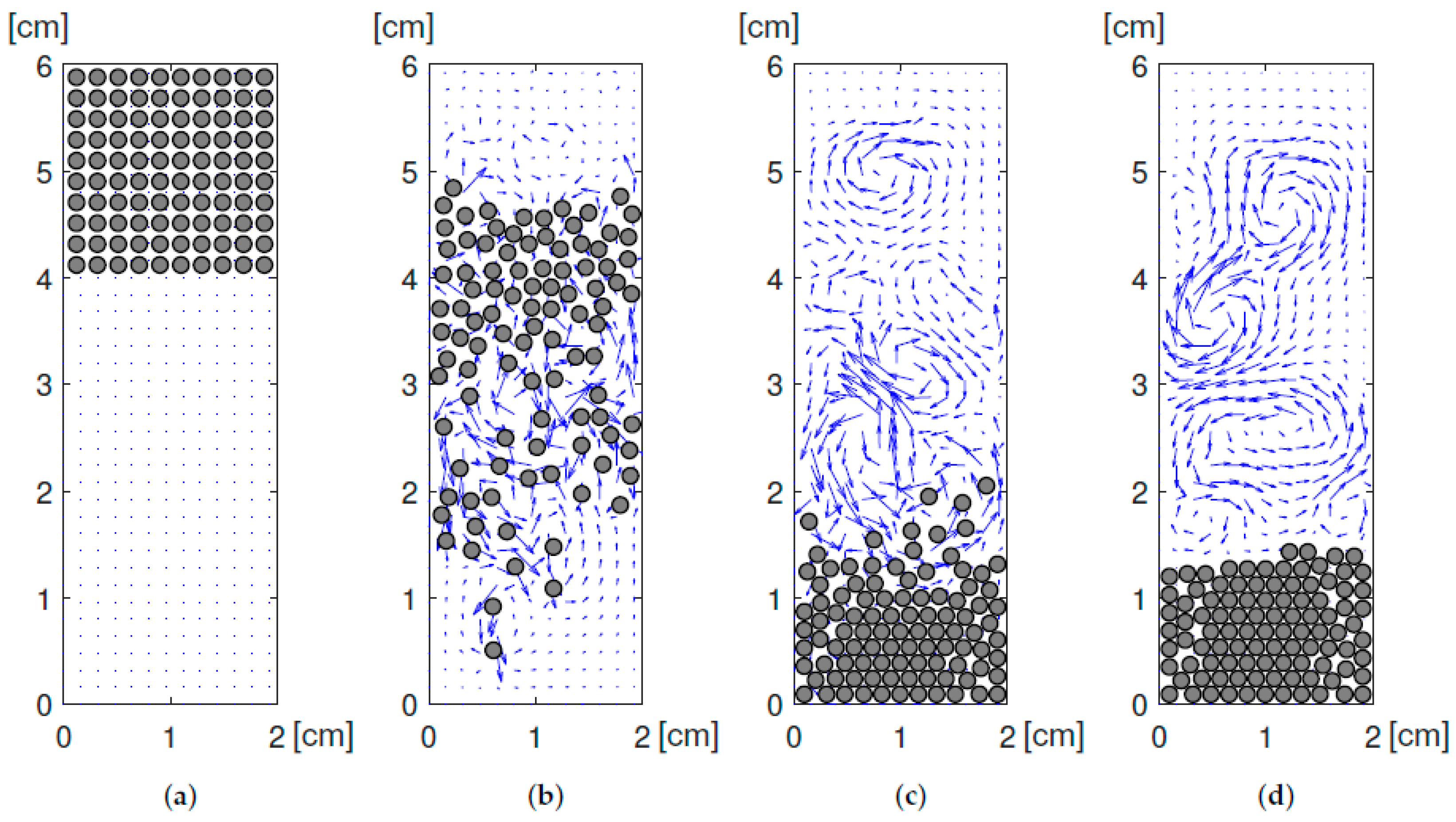
4.2. Sedimentation of Multiple Circular Disks
5. Sedimentation of Solid Objects without Rotational Symmetry
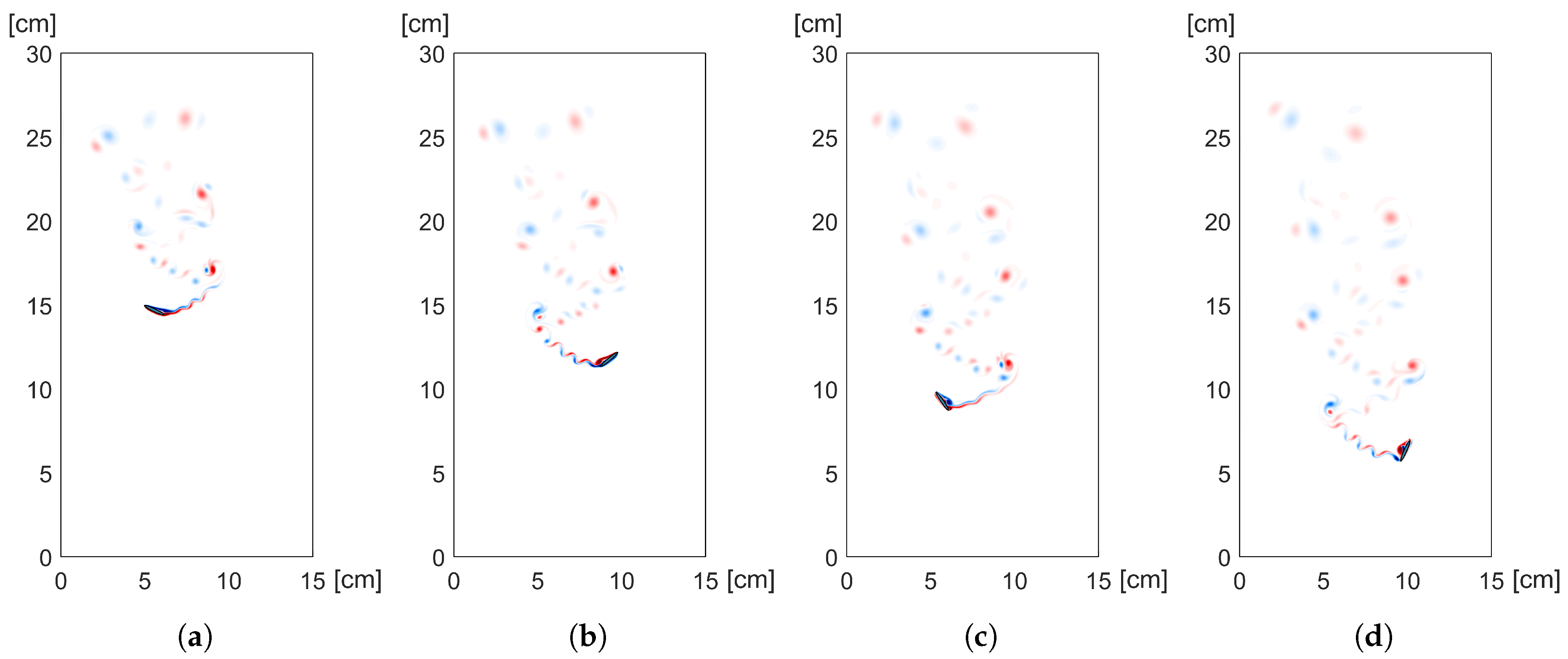
5.1. Sedimentation of a Regular Triangle
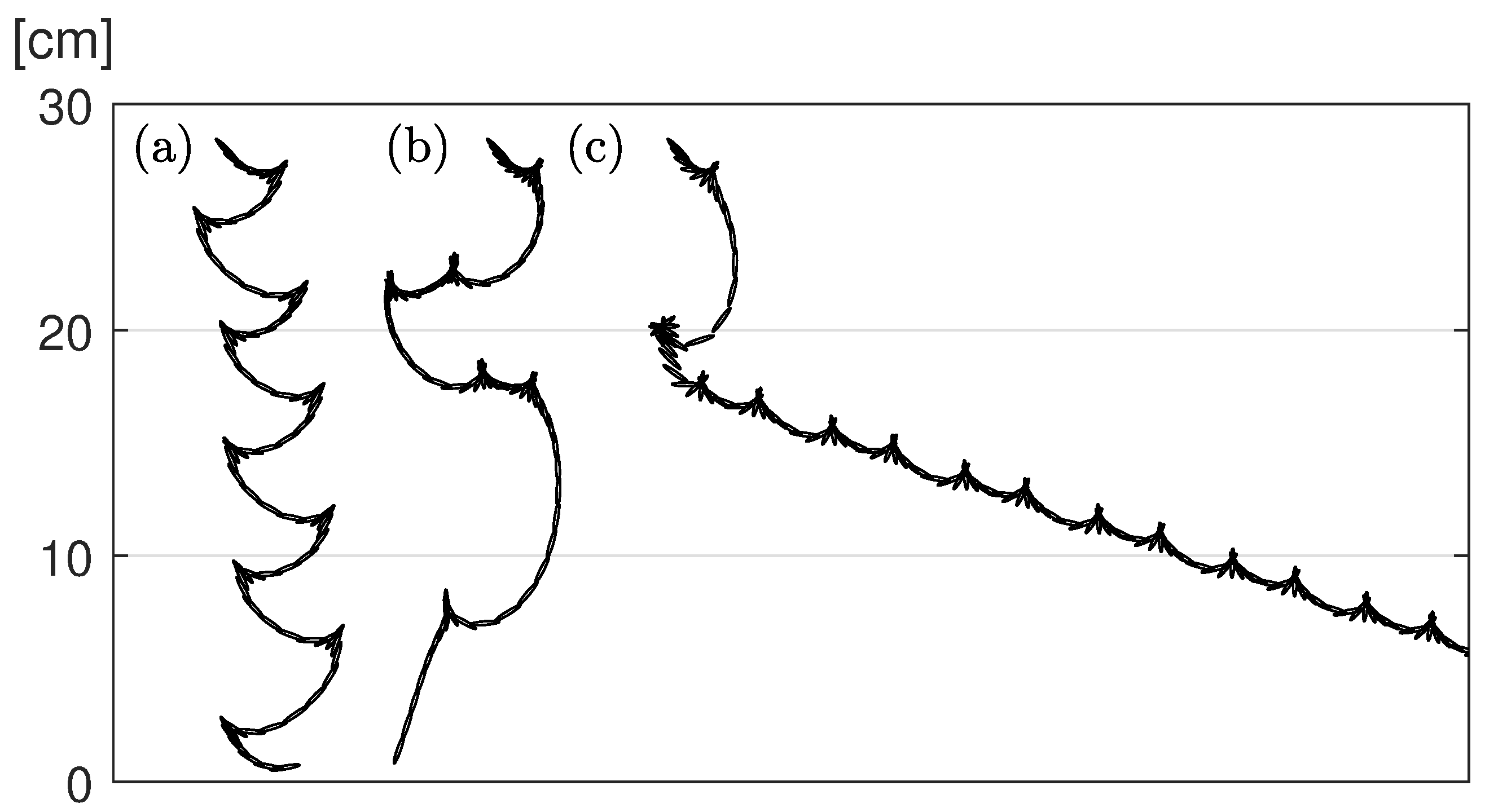
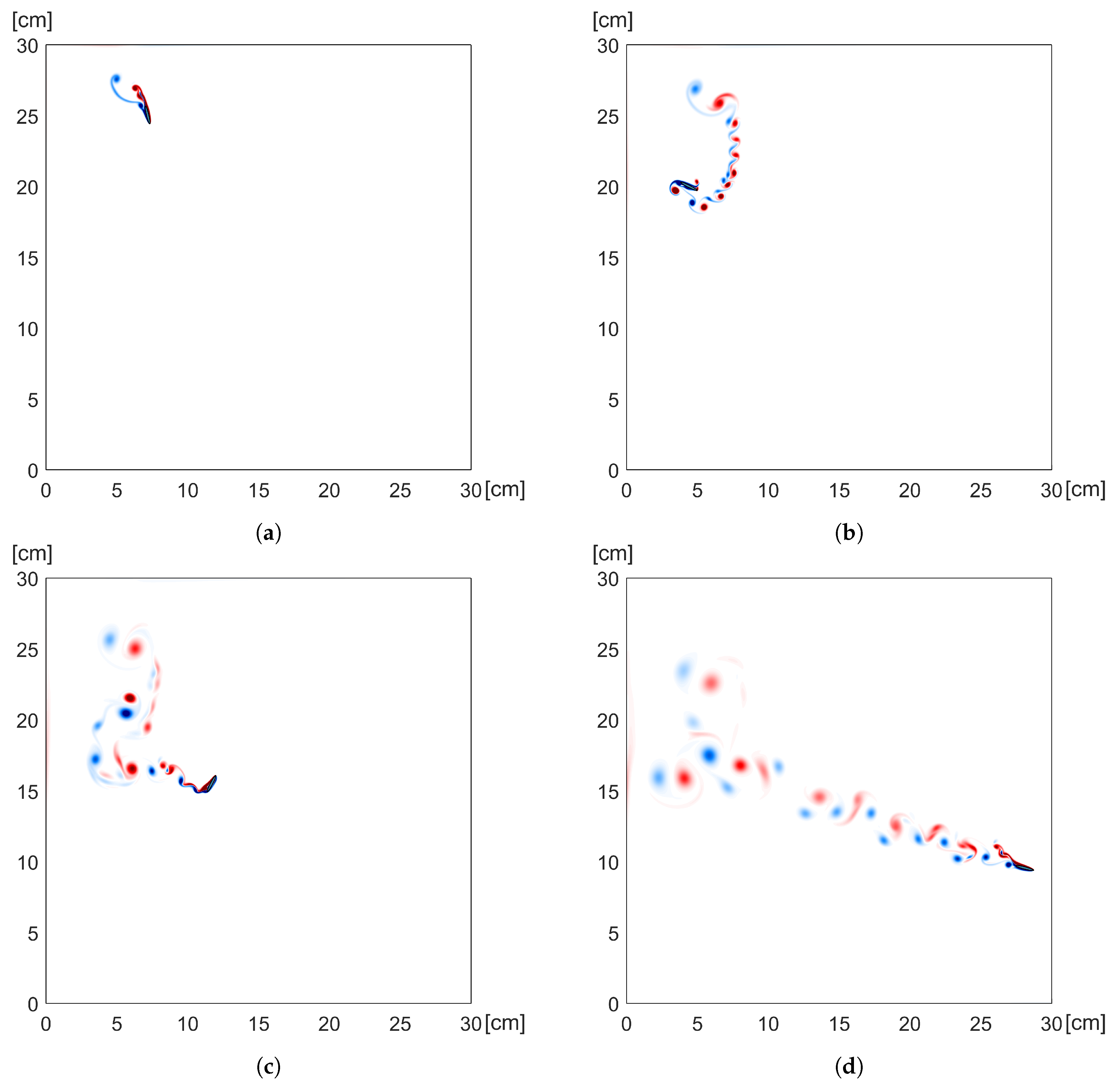
5.2. A Freely Falling Ellipse
- Reynolds number, , with ,
- the dimensionless moment of inertia, ,
- the aspect ratio of the ellipse, , where a and b are the width and thickness of the ellipse, respectively.
6. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
% Initiallize the parameters of the simulation nu = 0.01; % cm^2/s % Create the mesh lx = 30; ly = 30; n = 64; Th = RectangleMesh([0, lx, 0, ly], lx*n, ly*n); % Create the triangle object r = 0.5; % radius of the circumscribed circle edge_length = sqrt(3)*r; angle_of_attack = 5*pi/180; center_of_mass = [15, 28]; rho_s = 1.5; tri = TriangleObject(Th, center_of_mass, edge_length, r, angle_of_attack, rho_s); % Time setting dt = 1e-4; nt = 50000; % Boundary condition UN = 0; VN = 0; US = 0; VS = 0; UE = 0; VW = 0; UW = 0; VE = 0; % Initialize [u, v, p] = initialize(Th, UW, UE, US, UN, VW, VE, VS, VN); u_old = u; v_old = v; % DFIB curtime = 0; for iter = 1:nt curtime = curtime + dt; fprintf(‘current time: %f\n’, curtime) % Move the object to next time level tri.move(dt); % Preprocessing dpdx = diff(p, 1, 1)/Th.hx; dpdy = diff(p, 1, 2)/Th.hy; [H1, H2] = H(u, v, nu, Th.hx, Th.hy); [H1_old, H2_old] = H(u_old, v_old, nu, Th.hx, Th.hy); % Solve the intermediate velocity u_old = u; v_old = v; u(2:end-1, 2:end-1) = u(2:end-1, 2:end-1) + dt*(-dpdx + 1.5*H1 - 0.5*H1_old); v(2:end-1, 2:end-1) = v(2:end-1, 2:end-1) + dt*(-dpdy + 1.5*H2 - 0.5*H2_old); u = updateBC_u(u, UW, UE, US, UN); v = updateBC_v(v, VW, VE, VS, VN); % Solve the Poisson system S = diff(u(:, 2:end-1), 1, 1)/Th.hx + diff(v(2:end-1, :), 1, 2)/Th.hy; phi = FFT_Poisson_solver(S/dt, Th.hx, Th.hy); % Projection step u(2:end-1, 2:end-1) = u(2:end-1, 2:end-1) - dt*diff(phi, 1, 1)/Th.hx; v(2:end-1, 2:end-1) = v(2:end-1, 2:end-1) - dt*diff(phi, 1, 2)/Th.hy; % update pressure p = p + phi; % update virtual force tri.computeVirtualForce(u, v, dt); % update velocity u(:, 2:end-1) = tri.eta1 .* tri.us + (1-tri.eta1).*u(:, 2:end-1); v(2:end-1, :) = tri.eta2 .* tri.vs + (1-tri.eta2).*v(2:end-1, :); end
function [u, v, p] = initialize(Th, UW, UE, US, UN, VW, VE, VS, VN) u = zeros(Th.nx+1, Th.ny+2); v = zeros(Th.nx+2, Th.ny+1); p = zeros(Th.nx, Th.ny); u = updateBC_u(u, UW, UE, US, UN); v = updateBC_v(v, VW, VE, VS, VN); end
function [H1, H2] = H(u, v, nu, hx, hy) [uconv, vconv] = convection_div(u, v, hx, hy); ulap = laplacian(u, hx, hy); vlap = laplacian(v, hx, hy); H1 = nu*ulap - uconv; H2 = nu*vlap - vconv; end
function [Nu, Nv] = convection_div(u, v, hx, hy) uce = (u(1:end-1,2:end-1) + u(2:end,2:end-1))/2; uco = (u(:,1:end-1) + u(:,2:end))/2; vco = (v(1:end-1,:) + v(2:end,:))/2; vce = (v(2:end-1,1:end-1) + v(2:end-1,2:end))/2; uuce = uce.*uce; uvco = uco.*vco; vvce = vce.*vce; Nu = (uuce(2:end,:) - uuce(1:end-1,:))/hx ... + (uvco(2:end-1,2:end) - uvco(2:end-1,1:end-1))/hy; Nv = (vvce(:,2:end) - vvce(:,1:end-1))/hy ... + (uvco(2:end,2:end-1) - uvco(1:end-1,2:end-1))/hx; end
function lap = laplacian(f, hx, hy) [m, n] = size(f); i = 2:m-1; j = 2:n-1; lap = (f(i+1, j) + f(i-1, j) - 2*f(i,j))/(hx*hx) ... + (f(i, j+1) + f(i, j-1) - 2*f(i,j))/(hy*hy); end
function u = updateBC_u(u, UW, UE, US, UN) u(1, :) = UW; u(end, :) = UE; u(:, 1) = (8/3)*US - 2*u(:, 2) + (1/3)*u(:, 3); u(:, end) = (8/3)*UN - 2*u(:, end-1) + (1/3)*u(:, end-2); end
function v = updateBC_v(v, VW, VE, VS, VN) v(:, 1) = VS; v(:, end) = VN; v(1, :) = (8/3)*VW - 2*v(2, :) + (1/3)*v(3, :); v(end, :) = (8/3)*VE - 2*v(end-1, :) + (1/3)*v(end-2, :); end
function uh = FFT_Poisson_solver(fh, hx, hy) [M, N] = size(fh); demon = -(2*sin(pi*(0:M-1)’*ones(1, N)./(2*M))./hx).^2 ... -(2*sin(pi*ones(M, 1)*(0:N-1)./(2*N))./hy).^2; fhat = dct(dct(fh)’)’; uhat = fhat./demon; uhat(1,1) = 0; uh = idct(idct(uhat)’)’; end
classdef RectangleMesh < handle % RectangleMesh Mesh of the 2D rectangle (x0, y0) x (x1, y1) properties (SetAccess=‘private’) domain; x, y, xc, yc; Xu, Yu, Xv, Yv, Xc, Yc; nx, ny, hx, hy; end
methods function obj = RectangleMesh(domain, nx, ny) obj.domain = domain; obj.x = linspace(domain(1), domain(2), nx + 1); obj.y = linspace(domain(3), domain(4), ny + 1); obj.xc = avg(obj.x); obj.yc = avg(obj.y); obj.nx = nx; obj.ny = ny; obj.hx = (domain(2) - domain(1)) / nx; obj.hy = (domain(4) - domain(3)) / ny; [obj.Xu, obj.Yu] = ndgrid(obj.x, obj.yc); [obj.Xv, obj.Yv] = ndgrid(obj.xc, obj.y); [obj.Xc, obj.Yc] = ndgrid(obj.xc, obj.yc); end end end
classdef TriangleObject < handle % Class of Regular triangle properties Th, center_of_mass, edge_length, r, angle_of_attack, density; vx, vy, vel, vel_old; omega, omega_old; theta, theta_old, us, vs; eta0, eta1, eta2, eta0_old, eta1_old, eta2_old; forceX, forceY, forceX_old, forceY_old; gravity = [0, -981]; end
methods function obj = TriangleObject(Th, center_of_mass, edge_length, r, ... angle_of_attack, density) obj.Th = Th; obj.center_of_mass = center_of_mass; obj.edge_length = edge_length; obj.r = r; obj.angle_of_attack = angle_of_attack; obj.density = density; obj.initialize(); obj.updateEta(); end function move(obj, dt) % Compute translational motion obj.translational_motion(dt); % Compute rotation motion obj.rotational_motion(dt) % Compute center_of_mass at next time level obj.center_of_mass = obj.center_of_mass + 0.5*dt*(obj.vel + obj.vel_old); % Compute theta at next time level obj.theta = obj.theta + 0.5*dt*(obj.omega + obj.omega_old); % update velocity r1 = obj.Th.Xv - obj.center_of_mass(1); r2 = obj.Th.Yu - obj.center_of_mass(2); obj.us = obj.vel(1) - obj.omega*r2; obj.vs = obj.vel(2) + obj.omega*r1; % Update body position obj.update_position(); % Update eta obj.updateEta(); end function computeVirtualForce(obj, u, v, dt) obj.forceX_old = obj.forceX; obj.forceY_old = obj.forceY; obj.forceX = obj.eta1.*(obj.us - u(:, 2:end-1))/dt; obj.forceY = obj.eta2.*(obj.vs - v(2:end-1, :))/dt; end end
methods(Access=‘private’) function initialize(obj) obj.forceX = zeros(obj.Th.nx+1, obj.Th.ny); obj.forceY = zeros(obj.Th.nx, obj.Th.ny+1); obj.forceX_old = obj.forceX; obj.forceY_old = obj.forceY; vx0 = [-obj.r*cos(pi/6), obj.r*cos(pi/6), 0]; vy0 = [-obj.r*sin(pi/6), -obj.r*sin(pi/6), obj.r]; obj.vx = obj.center_of_mass(1) ... + (vx0.*cos(obj.angle_of_attack) - vy0.*sin(obj.angle_of_attack)); obj.vy = obj.center_of_mass(2) ... + (vx0.*sin(obj.angle_of_attack) + vy0.*cos(obj.angle_of_attack)); obj.vel = [0, 0]; obj.vel_old = [0, 0]; obj.omega = 0; obj.omega_old = 0; % rad/s obj.theta = 0; obj.theta_old = 0; obj.us = 0; obj.vs = 0; end function translational_motion(obj, dt) hx = obj.Th.hx; hy = obj.Th.hy; HFX = trapz(trapz(obj.forceX,1)*hx, 2)*hy; HFY = trapz(trapz(obj.forceY,1)*hx, 2)*hy; HFX_old = trapz(trapz(obj.forceX_old, 1)*hx, 2)*hy; HFY_old = trapz(trapz(obj.forceY_old, 1)*hx, 2)*hy; area = (sqrt(3)*obj.edge_length*obj.edge_length)/4; Ms = obj.density*area; Mf = 1.0*area; vel_1_ = obj.vel(1) + dt*((1-Mf/Ms)*obj.gravity(1) ... - (1.5*HFX - 0.5*HFX_old)/Ms ... + (Mf/Ms)*(obj.vel(1) - obj.vel_old(1))/dt); vel_2_ = obj.vel(2) + dt*((1-Mf/Ms)*obj.gravity(2) ... - (1.5*HFY - 0.5*HFY_old)/Ms ... + (Mf/Ms)*(obj.vel(2) - obj.vel_old(2))/dt); obj.vel_old = obj.vel; obj.vel = [vel_1_, vel_2_]; end function rotational_motion(obj, dt) hx = obj.Th.hx; hy = obj.Th.hy; r1 = obj.Th.Xc - obj.center_of_mass(1); r2 = obj.Th.Yc - obj.center_of_mass(2); torque = getTorque(avg(obj.forceX), avg(obj.forceY’)’, r1, r2); torque_old = getTorque(avg(obj.forceX_old), avg(obj.forceY_old’)’, r1, r2); HT = H(1, obj.eta0.*torque, hx, hy); HT_old = H(1, obj.eta0.*torque_old, hx, hy); If = sqrt(3)*obj.edge_length/48; Is = obj.density*If; omega_ = obj.omega + dt*(-1.5*HT + 0.5*HT_old)/Is ... + (If/Is)*(obj.omega - obj.omega_old); obj.omega_old = obj.omega; obj.omega = omega_; end function update_position(obj) aoa = obj.angle_of_attack; vx0 = [-obj.r*cos(pi/6), obj.r*cos(pi/6), 0]; vy0 = [-obj.r*sin(pi/6), -obj.r*sin(pi/6), obj.r]; obj.vx = obj.center_of_mass(1) ... + (vx0.*cos(aoa+obj.theta) - vy0.*sin(aoa+obj.theta)); obj.vy = obj.center_of_mass(2) ... + (vx0.*sin(aoa+obj.theta) + vy0.*cos(aoa+obj.theta)); end function updateEta(obj) obj.eta1 = inpolygon(obj.Th.Xu, obj.Th.Yu, obj.vx, obj.vy); obj.eta2 = inpolygon(obj.Th.Xv, obj.Th.Yv, obj.vx, obj.vy); obj.eta0 = inpolygon(obj.Th.Xc, obj.Th.Yc, obj.vx, obj.vy); end
end end % help funtion in this class function output = getTorque(Fx, Fy, rx, ry) output = rx.*Fy - ry.*Fx; end function output = H(rho, F, hx, hy) output = sum(sum(rho.*F))*hx*hy; end
References
- Belmonte, A.; Eisenberg, H.; Moses, E. From flutter to tumble: Inertial drag and froude similarity in falling paper. Phys. Rev. Lett. 1998, 81, 345–348. [Google Scholar] [CrossRef]
- Mahadevan, L.; Ryu, W.S.; Samuel, A.D. Tumbling cards. Phys. Fluids 1999, 11, 1–3. [Google Scholar] [CrossRef]
- Pesavento, U.; Wang, Z.J. Falling paper: Navier-Stokes solutions, model of fluid forces, and center of mass elevation. Phys. Rev. Lett. 2004, 93, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Andersen, A.; Pesavento, U.; Jane Wang, Z. Unsteady aerodynamics of fluttering and tumbling plates. J. Fluid Mech. 2005, 541, 65–90. [Google Scholar] [CrossRef]
- Jin, C.; Xu, K. Numerical study of the unsteady aerodynamics of freely falling plates. Commun. Comput. Phys. 2008, 3, 834–851. [Google Scholar]
- Chern, M.-J.; Noor, D.Z.; Liao, C.-B.; Horng, T.-L. Direct-forcing immersed boundary method for mixed heat transfer. Commun. Comput. Phys. 2015, 18, 1072–1094. [Google Scholar] [CrossRef]
- Horng, T.-L.; Hsieh, P.-W.; Yang, S.-Y.; You, C.-S. A simple direct-forcing immersed boundary projection method with prediction-correction for fluid-solid interaction problems. Comput. Fluids 2018, 176, 135–152. [Google Scholar] [CrossRef]
- Noor, D.Z.; Chern, M.J.; Horng, T.L. An immersed boundary method to solve fluid-solid interaction problems. Comput. Mech. 2009, 44, 447–453. [Google Scholar] [CrossRef]
- Fernandes, A.C.; Gomes, H.C.; Campello, E.M.; Müller, A.S.; Pimenta, P.M. A coupled FEM–DEM method for the modeling of fluids laden with particles. Comput. Part. Mech. 2020. [Google Scholar] [CrossRef]
- Hamid, A.; Arshad, A.B.; Mehdi, S.; Qasim, M.D.; Ullah, A.; Molina, J.J.; Yamamoto, R. A numerical study of sedimentation of rod like particles using smooth profile method. Int. J. Multiph. Flow 2020, 127, 103263. [Google Scholar] [CrossRef]
- Kwon, J.; Monaghan, J.J. Sedimentation in homogeneous and inhomogeneous fluids using SPH. Int. J. Multiph. Flow 2015, 72, 155–164. [Google Scholar] [CrossRef]
- Riazi, A.; Türker, U. The drag coefficient and settling velocity of natural sediment particles. Comput. Part. Mech. 2019, 6, 427–437. [Google Scholar] [CrossRef]
- Walayat, K.; Talat, N.; Jabeen, S.; Usman, K.; Liu, M. Sedimentation of general shaped particles using a multigrid fictitious boundary method. Phys. Fluids 2020, 32, 063301. [Google Scholar] [CrossRef]
- Walayat, K.; Zhang, Z.; Usman, K.; Chang, J.; Liu, M. Dynamics of elliptic particle sedimentation with thermal convection. Phys. Fluids 2018, 30, 103301. [Google Scholar] [CrossRef]
- Glowinski, R.; Pan, T.W.; Hesla, T.I.; Joseph, D.D.; Périaux, J. A fictitious domain approach to the direct numerical simulation of incompressible viscous flow past moving rigid bodies: Application to particulate flow. J. Comput. Phys. 2001, 169, 363–426. [Google Scholar] [CrossRef]
- Cate, A.T.; Nieuwstad, C.H.; Derksen, J.J.; Van den Akker, H.E.A. Particle imaging velocimetry experiments and lattice-Boltzmann simulations on a single sphere settling under gravity. Phys. Fluids 2002, 14, 4012–4025. [Google Scholar] [CrossRef]
- Aulisa, E.; Bnà, S.; Bornia, G. A monolithic ALE Newton–Krylov solver with Multigrid-Richardson–Schwarz preconditioning for incompressible fluid-structure interaction. Comput. Fluids 2018, 174, 213–228. [Google Scholar] [CrossRef]
- Saksono, P.H.; Dettmer, W.G.; Perić, D. An adaptive remeshing strategy for flows with moving boundaries and fluid–structure interaction. Int. J. Numer. Methods Eng. 2007, 71, 1009–1050. [Google Scholar] [CrossRef]
- Sahin, M.; Mohseni, K. An arbitrary Lagrangian-Eulerian formulation for the numerical simulation of flow patterns generated by the hydromedusa Aequorea victoria. J. Comput. Phys. 2009, 228, 4588–4605. [Google Scholar] [CrossRef]
- Blasco, J.; Calzada, M.C.; Marín, M. A Fictitious Domain, parallel numerical method for rigid particulate flows. J. Comput. Phys. 2009, 228, 7569–7613. [Google Scholar] [CrossRef]
- Wan, D.; Turek, S. Direct numerical simulation of particulate flow via multigrid FEM techniques and the fictitious boundary method. Int. J. Numer. Methods Fluids 2006, 51, 531–566. [Google Scholar] [CrossRef]
- Fortes, A.F.; Joseph, D.D.; Lundgren, T.S. Nonlinear mechanics of fluidization of beds of spherical particles. J. Fluid Mech. 1987, 177, 467–483. [Google Scholar] [CrossRef]
- Hu, H.H.; Joseph, D.D.; Crochet, M.J. Direct simulation of fluid particle motions. Theor. Comput. Fluid Dyn. 1992, 3, 285–306. [Google Scholar] [CrossRef]
- Choi, H.G. Splitting method for the combined formulation of the fluid-particle problem. Comput. Methods Appl. Mech. Eng. 2000, 190, 1367–1378. [Google Scholar] [CrossRef]
- Gazzola, M.; Chatelain, P.; van Rees, W.M.; Koumoutsakos, P. Simulations of single and multiple swimmers with non-divergence free deforming geometries. J. Comput. Phys. 2011, 230, 7093–7114. [Google Scholar] [CrossRef]
- Kolomenskiy, D.; Schneider, K. A Fourier spectral method for the Navier Stokes equations with volume penalization for moving solid obstacles. J. Comput. Phys. 2009, 228, 5687–5709. [Google Scholar] [CrossRef]



| [kg/m] | [Ns/ m] | [m/s] | ||
|---|---|---|---|---|
| Case 1 | 970 | 3.73 | 3.8 | 1.5 |
| Case 2 | 965 | 2.12 | 6.0 | 4.1 |
| Case 3 | 962 | 1.13 | 11.5 | 11.6 |
| Case 4 | 960 | 0.58 | 12.8 | 32.2 |
| e | [cm/s] | |||||
|---|---|---|---|---|---|---|
| fluttering | 1000 | 0.08 | 8 | 1.2603 | 0.0118 | 173.2413 |
| chaotic falling | 1000 | 0.16 | 8 | 2.5206 | 0.0285 | 71.6779 |
| tumbling | 1000 | 0.25 | 8 | 3.9385 | 0.0396 | 51.5626 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, C.-S.; Chern, M.-J.; Noor, D.Z.; Horng, T.-L. Numerical Investigation of Freely Falling Objects Using Direct-Forcing Immersed Boundary Method. Mathematics 2020, 8, 1619. https://doi.org/10.3390/math8091619
You C-S, Chern M-J, Noor DZ, Horng T-L. Numerical Investigation of Freely Falling Objects Using Direct-Forcing Immersed Boundary Method. Mathematics. 2020; 8(9):1619. https://doi.org/10.3390/math8091619
Chicago/Turabian StyleYou, Cheng-Shu, Ming-Jyh Chern, Dedy Zulhidayat Noor, and Tzyy-Leng Horng. 2020. "Numerical Investigation of Freely Falling Objects Using Direct-Forcing Immersed Boundary Method" Mathematics 8, no. 9: 1619. https://doi.org/10.3390/math8091619
APA StyleYou, C.-S., Chern, M.-J., Noor, D. Z., & Horng, T.-L. (2020). Numerical Investigation of Freely Falling Objects Using Direct-Forcing Immersed Boundary Method. Mathematics, 8(9), 1619. https://doi.org/10.3390/math8091619





