Cooperative and Non-Cooperative Frameworks with Utility Function Design for Intermediate Deadline Assignment in Real-Time Distributed Systems
Abstract
1. Introduction
- We develop the first non-cooperative distributed framework for intermediate deadline assignment in real-time distributed systems.
- We design the first utility function that regulates a trade-off between delay fairness and performance for intermediate deadline assignment in real-time distributed systems.
- We demonstrate the validity of the existing cooperative framework and the proposed non-cooperative framework associated with the designed utility function.
2. Target Problem and Related Work
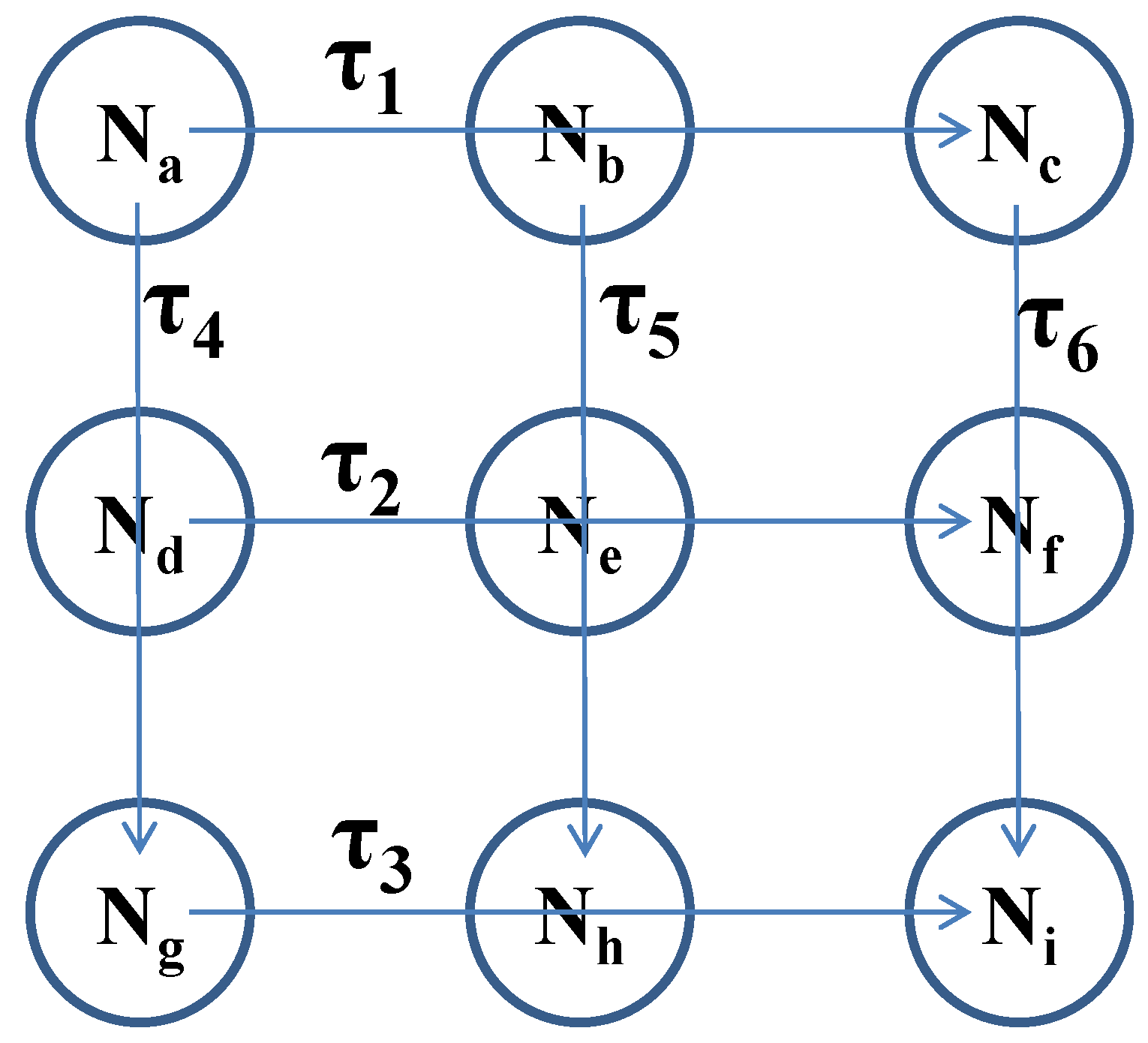
2.1. Intermediate Deadline Assignment Problem
2.2. Related Work
3. Distributed Framework for Intermediate Deadline Assignment
3.1. Existing Cooperative Distributed Framework
3.2. Proposed Non-Cooperative Distributed Framework
3.3. Deployment of Distributed Framework
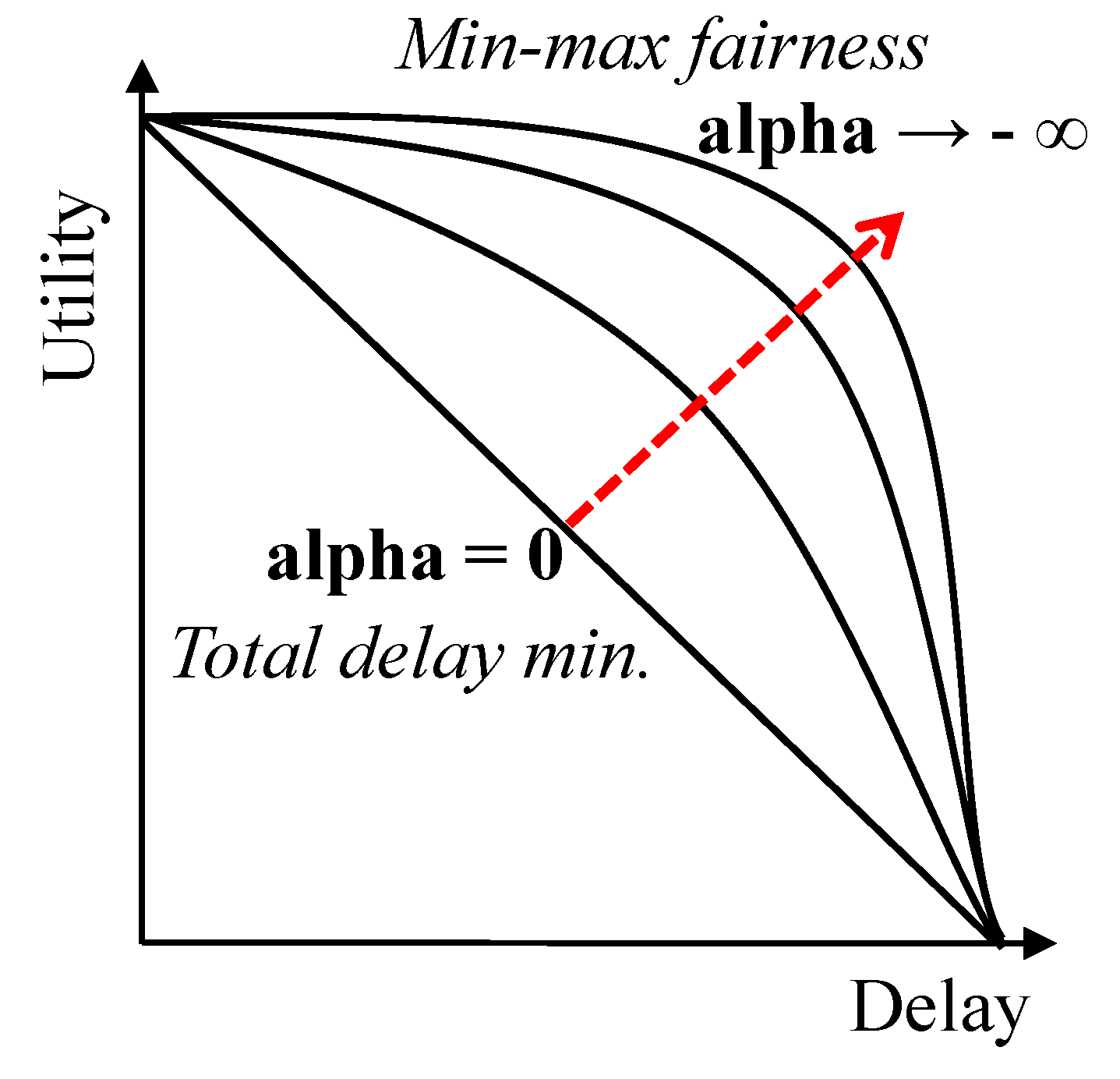
4. Utility Function Design
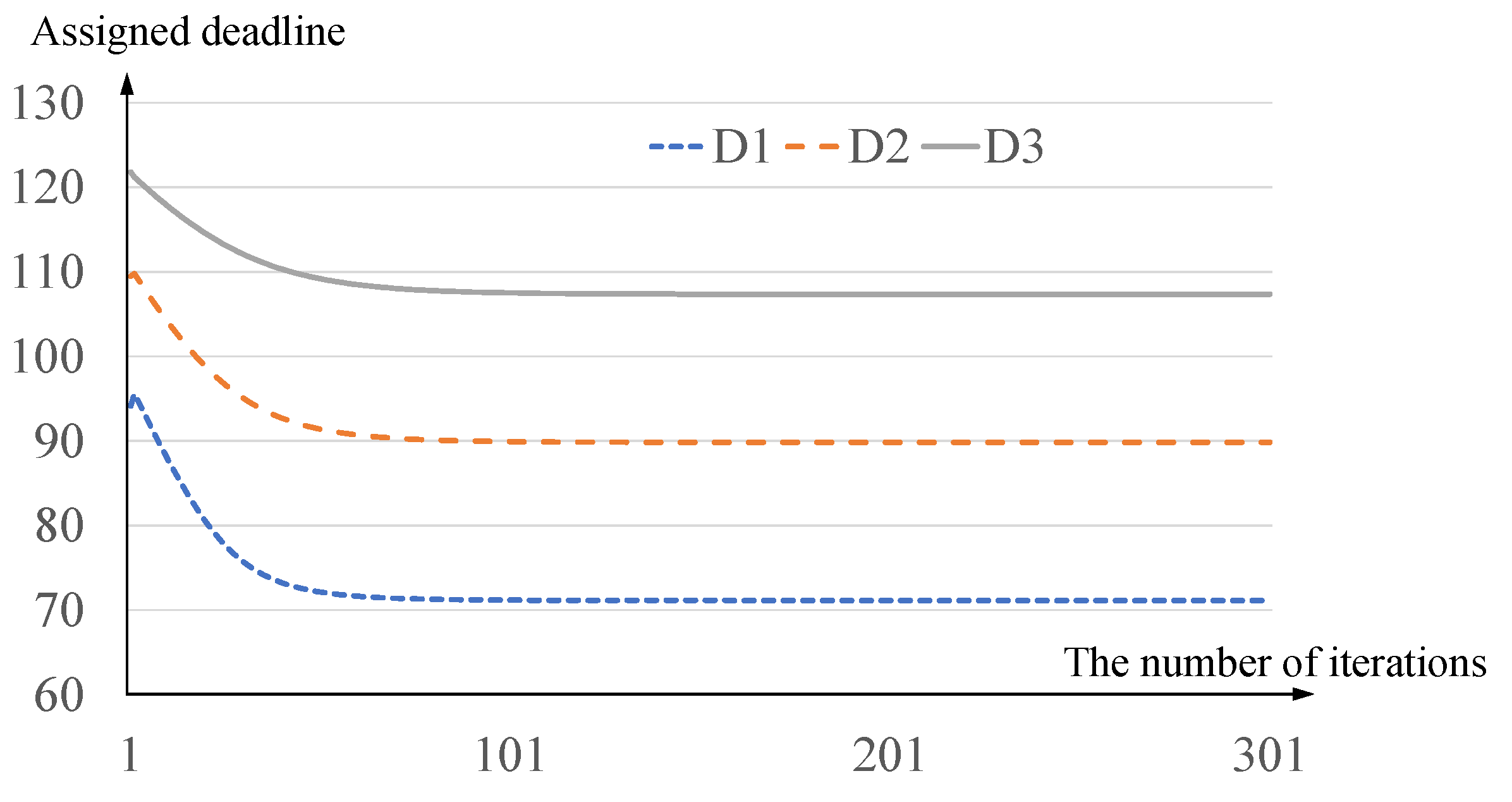
5. Experiments
6. Conclusions
Funding
Conflicts of Interest
References
- Singh, A.K.; Dziuzanski, P.; Mendis, H.R.; Indrusiak, L.S. A Survey and Comparative Study of Hard and Soft Real-Time Dynamic Resource Allocation Strategies for Multi-/Many-Core Systems. ACM Comput. Surv. 2017, 50, 24:1–24:40. [Google Scholar] [CrossRef]
- Steffens, L.; Agarwal, M.; van der Wolf, P. Real-Time Analysis for Memory Access in Media Processing SoCs: A Practical Approach. In Proceedings of the Euromicro Conference on Real-Time Systems (ECRTS), Prague, Czech Republic, 2–4 July 2008; pp. 255–265. [Google Scholar]
- Tian, W.; Zhao, Y.; Xu, M.; Zhong, Y.; Sun, X. A Toolkit for Modeling and Simulation of Real-Time Virtual Machine Allocation in a Cloud Data Center. IEEE Trans. Autom. Sci. Eng. 2015, 12, 153–161. [Google Scholar] [CrossRef]
- Wang, X.; Tushar, W.; Yuen, C.; Zhang, X. Promoting Users’ Participation in Mobile Crowdsourcing: A Distributed Truthful Incentive Mechanism (DTIM) Approach. IEEE Trans. Veh. Technol. 2020, 69, 5570–5582. [Google Scholar] [CrossRef]
- Garcia, J.; Harbour, M. Optimized priority assignment for tasks and messages in distributed hard real-time systems. In Proceedings of the IEEE Workshop on Parallel and Distributed Real-Time Systems, Santa Barbara, CA, USA, 25 April 1995; pp. 124–132. [Google Scholar]
- Saksena, M.; Hong, S. An Engineering Approach to Decomposing End-to-End Delays on a Distributed Real-Time System. In Proceedings of the IEEE International Workshop on Parallel and Distributed Real-Time Systems, Honolulu, HI, USA, 15–16 April 1996; pp. 244–251. [Google Scholar]
- Kao, B.; Garcia-Molina, H. Deadline Assignment in a Distributed Soft Real-Time System. In Proceedings of the International Conference on Distributed Computing Systems, Pittsburgh, PA, USA, 25–28 May 1993; pp. 428–437. [Google Scholar]
- Bettati, R.; Liu, J. End-to-End Scheduling to Meet Deadlines in Distributed Systems. In Proceedings of the International Conference on Distributed Computing Systems, Yokohama, Japan, 9–12 June 1992; pp. 452–459. [Google Scholar]
- Natale, M.D.; Stankovic, J. Dynamic End-to-End Guarantees in Distributed Real-Time Systems. In Proceedings of the IEEE Real-Time Systems Symposium (RTSS), San Juan, Puerto Rico, 7–9 December 1994; pp. 216–227. [Google Scholar]
- Jonsson, J.; Shin, K. Deadline Assignment in Distributed Hard Real-Time Systems with Relaxed Locality Constraints. In Proceedings of the International Conference on Distributed Computing Systems, Baltimore, MD, USA, 27–30 May 1997; pp. 432–440. [Google Scholar]
- Stavrinides, G.L.; Karatza, H.D. Scheduling multiple task graphs with end-to-end deadlines in distributed real-time systems utilizing imprecise computations. J. Syst. Softw. 2010, 83, 1004–1014. [Google Scholar] [CrossRef]
- Jayachandran, P.; Abdelzaher, T. Delay Composition Algebra: A Reduction-based Schedulability Algebra for Distributed Real-Time Systems. In Proceedings of the IEEE Real-Time Systems Symposium (RTSS), Barcelona, Spain, 30 November–3 December 2008; pp. 259–269. [Google Scholar]
- Jayachandran, P.; Abdelzaher, T. End-to-End Delay Analysis of Distributed Systems with Cycles in the Task Graph. In Proceedings of the Euromicro Conference on Real-Time Systems (ECRTS), Dublin, Ireland, 25 January 2009; pp. 13–22. [Google Scholar]
- Lee, J.; Shin, I.; Easwaran, A. Online Robust Optimization Framework for QoS Guarantees in Distributed Soft Real-Time Systems. In Proceedings of the 10th ACM International Conference on Embedded Software (EMSOFT), Scottsdale, AZ, USA, 24–29 October 2010; pp. 89–98. [Google Scholar]
- Lee, J.; Shin, I.; Easwaran, A. Convex Optimization Framework for Intermediate Deadline Assignment in Soft and Hard Real-Time Distributed Systems. J. Syst. Softw. 2012, 85, 2331–2339. [Google Scholar] [CrossRef]
- Hong, S.; Chantem, T.; Hu, X.S. Local-Deadline Assignment for Distributed Real-Time Systems. IEEE Trans. Comput. 2015, 64, 1983–1997. [Google Scholar] [CrossRef]
- Agrawal, M.; Manchanda, K.; Agarwal, A.; Saraswat, S.; Gupta, A.; Gupta, H.P.; Dutta, T. A Supervised Approach-based Job Scheduling Technique for Distributed Real-Time Systems. In Proceedings of the 2018 IEEE International Conference on Advanced Networks and Telecommunications Systems (ANTS), Indore, India, 16–19 December 2018; pp. 1–6. [Google Scholar]
- Rehman, H.U.; Kumam, P.; Argyros, I.K.; Shutaywi, M.; Shah, Z. Optimization Based Methods for Solving the Equilibrium Problems with Applications in Variational Inequality Problems and Solution of Nash Equilibrium Models. Mathematics 2020, 8, 822. [Google Scholar] [CrossRef]
- Inthakon, W.; Suantai, S.; Sarnmeta, P.; Chumpungam, D. A New Machine Learning Algorithm Based on Optimization Method for Regression and Classification Problems. Mathematics 2020, 8, 1007. [Google Scholar] [CrossRef]
- Manikantan, R.; Chakraborty, S.; Uchida, T.K.; Vyasarayani, C.P. Parameter Identification in Nonlinear Mechanical Systems with Noisy Partial State Measurement Using PID-Controller Penalty Functions. Mathematics 2020, 8, 1084. [Google Scholar] [CrossRef]
- Liu, C.; Layland, J. Scheduling Algorithms for Multi-programming in A Hard-Real-Time Environment. J. ACM 1973, 20, 46–61. [Google Scholar] [CrossRef]
- Audsley, N.; Burns, A.; Wellings, A. Deadline monotonic scheduling theory and application. Control. Eng. Pract. 1993, 1, 71–78. [Google Scholar] [CrossRef]
- Jeffay, K.; Stanat, D.F.; Martel, C.U. On non-preemptive scheduling of period and sporadic tasks. In Proceedings of the IEEE Real-Time Systems Symposium (RTSS), San Antonio, TX, USA, 4–6 December 1991; pp. 129–139. [Google Scholar]
- Burke, J.V.; Lewis, A.S.; Overton, M.L. The speed of Shor’s R-algorithm. IMA J. Numer. Anal. 2008, 28, 711–720. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Bertsekas, D.P.; Tsitsiklis, J.N. Parallel and Distributed Computation: Numerical Methods; Athena Scientific: Nashua, NH, USA, 1997. [Google Scholar]
- Low, S.H. Optimization flow control, I: basic algorithm and convergence. IEEE/ACM Trans. Netw. 1999, 7, 861–874. [Google Scholar] [CrossRef]
- Athuraliya, S.; Low, S.H. Optimization Flow Control II: Implementation; Technical Report; Caltech: Pasadena, CA, USA, 2000. [Google Scholar]
- Athuraliya, S.; Li, V.H.; Low, S.H.; Yin, Q. REM: Active Queue Management. IEEE Netw. 2001, 15, 48–53. [Google Scholar] [CrossRef]
- MATLAB: The Language of Technical Computing. Available online: http://www.mathworks.com/products/matlab/ (accessed on 13 September 2020).
| System Utility | Sum of Delay Upper-Bounds | Standard Deviation | |
|---|---|---|---|
| −5.348 × 10 | 534.8 | 20.1 | |
| −1.960 × 10 | 536.7 | 16.2 | |
| −1.539 × 10 | 539.8 | 13.5 | |
| −9.101 × 10 | 543.0 | 11.6 |
| System Utility | Sum of Delay Upper-Bounds | Standard Deviation | |
|---|---|---|---|
| −5.348 × 10 | 534.8 | 20.1 | |
| −1.960 × 10 | 536.7 | 16.2 | |
| −1.539 × 10 | 539.8 | 13.5 | |
| −9.101 × 10 | 543.0 | 11.6 |
| System Utility | Sum of Delay Upper-Bounds | Standard Deviation | |
|---|---|---|---|
| −5.601 × 10 | 560.1 | 25.3 | |
| −3.167 × 10 | 604.8 | 37.0 | |
| −2.854 × 10 | 611.2 | 39.0 | |
| −2.713 × 10 | 611.4 | 39.1 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J. Cooperative and Non-Cooperative Frameworks with Utility Function Design for Intermediate Deadline Assignment in Real-Time Distributed Systems. Mathematics 2020, 8, 1579. https://doi.org/10.3390/math8091579
Lee J. Cooperative and Non-Cooperative Frameworks with Utility Function Design for Intermediate Deadline Assignment in Real-Time Distributed Systems. Mathematics. 2020; 8(9):1579. https://doi.org/10.3390/math8091579
Chicago/Turabian StyleLee, Jinkyu. 2020. "Cooperative and Non-Cooperative Frameworks with Utility Function Design for Intermediate Deadline Assignment in Real-Time Distributed Systems" Mathematics 8, no. 9: 1579. https://doi.org/10.3390/math8091579
APA StyleLee, J. (2020). Cooperative and Non-Cooperative Frameworks with Utility Function Design for Intermediate Deadline Assignment in Real-Time Distributed Systems. Mathematics, 8(9), 1579. https://doi.org/10.3390/math8091579





