Abstract
In real-time distributed systems, it is important to provide offline guarantee for an upper-bound of each real-time task’s end-to-end delay, which has been achieved by assigning proper intermediate deadlines of individual real-time tasks at each node. Although existing studies have succeeded to utilize mathematical theories of distributed computation/control for intermediate deadline assignment, they have assumed that every task operates in a cooperative manner, which does not always hold for real-worlds. In addition, existing studies have not addressed how to exploit a trade-off between end-to-end delay fairness among real-time tasks and performance for minimizing aggregate end-to-end delays. In this paper, we recapitulate an existing cooperative distributed framework, and propose a non-cooperate distributed framework that can operate even with selfish tasks, each of which is only interested in minimizing its own end-to-end delay regardless of achieving the system goal. We then propose how to design utility functions that allow the real-time distributed system to exploit the trade-off. Finally, we demonstrate the validity of the cooperative and non-cooperative frameworks along with the designed utility functions, via simulations.
1. Introduction
In real-time distributed systems, each real-time task executes on several nodes in a sequential manner subject to timing constraints. Therefore, it is important to provide predictable performance for the end-to-end delay of each real-time task, which implies that an upper-bound of the end-to-end delay should be provided before the system starts [1]. An example of such a real-time distributed system is an LCD video player [2]. In the system, multiple media applications compete for processing units, and each media processing application is executed in the processing units in a sequential manner; also, QoS (Quality of Service) of each media processing application is dependent on end-to-end delays. Since each application’s QoS can be expressed as time-sensitive utility functions, the goal of the system is maximizing the collective utilities of individual applications in the worst-case. With this utility, the system can provide QoS at least as much as the collective utilities. More examples of real-time distributed systems can be found in some scenarios in cloud data center [3] and mobile crowdsourcing [4]; a delay-sensitive application is executed in a series of virtual machines and mobile devices, respectively for the former and latter, and QoS of the application is a function of its response time.
The end-to-end delay predictability required by a real-time distributed system has been achieved by assigning proper intermediate deadlines of individual real-time tasks executed on each node [1,5,6,7,8,9,10,11,12,13,14,15,16,17]. However, although existing studies for the intermediate deadline assignment have succeeded to utilize mathematical theories (including convex optimization [18,19,20]) of distributed computation/control for intermediate deadline assignment, they have assumed that every task operates in a cooperative manner, which does not always hold in real-world situations. In addition, existing studies have not addressed how to exploit a trade-off between end-to-end delay fairness among real-time tasks and performance for minimizing total end-to-end delays of the entire real-time distributed system.
In this paper, we address two important issues for the intermediate deadline assignment problem for real-time distributed systems, which are related to non-cooperative tasks and utility function design. First, after recapitulating an existing cooperative distributed framework, we propose a non-cooperative distributed framework that operates even with selfish tasks, each of which is only interested in minimizing its own end-to-end delay regardless of achieving the system goal. To this end, we propose a penalty function that makes each task spontaneously restrain itself from behaving in a selfish manner, and present how to apply the penalty function to each task. Second, we propose a design principle for utility functions that enable the real-time distributed system to exploit a trade-off between end-to-end delay fairness among individual tasks and performance for minimizing total end-to-end delays of the entire system. This can be achieved by adjusting a parameter to be detailed in Section 4. Then, our simulation results show the validity of the cooperative and non-cooperative frameworks in conjunction with the designed utility functions.
In summary, this paper makes the following contributions.
- We develop the first non-cooperative distributed framework for intermediate deadline assignment in real-time distributed systems.
- We design the first utility function that regulates a trade-off between delay fairness and performance for intermediate deadline assignment in real-time distributed systems.
- We demonstrate the validity of the existing cooperative framework and the proposed non-cooperative framework associated with the designed utility function.
The remainder of this paper is structured as follows. Section 2 presents our target problem and related work. Section 3 recapitulates an existing cooperative distributed framework and proposes a non-cooperative one with its deployment issues. Section 4 proposes a utility function design. Section 5 demonstrates the validity of the proposed techniques. Section 6 concludes the paper.
2. Target Problem and Related Work
In this section, we first explain our system model and then our target problem, which is the intermediate deadline assignment problem for real-time distributed systems. We next summarize existing studies related to the target problem.
2.1. Intermediate Deadline Assignment Problem
We target the intermediate deadline assignment problem for real-time distributed systems, which is defined in [14,15] as follows. We consider a real-time distributed system with a set of tasks and a set of nodes . Let denote the size of A; therefore and denote the number of tasks and nodes, respectively. Each task consists of a series of subtasks (numbered from 1 to ), each of which is executed on exactly one node in a sequential manner. Let denote the subtask of executed on node ; we may omit n in if n is irrelevant. Also, we use as the worst-case execution time of . Then, adjacent subtasks of (e.g., and ) execute in a sequential manner; that is, is ready to execute only after completes its execution. Each task is a sporadic task, meaning that its first subtask is released repeatedly with a minimum separation of time units.
Once we calculate the reponse time (i.e., the maximum local delay) that each subtask undergoes in its node (denoted by ), then we can calculate the maximum end-to-end delay by . Each task has its own delay-sensitive utility function that characterizes QoS (Quality-of-Service) level, and then the system utility is defined as follows:
Since it is difficult to calculate the maximum end-to-end delay before the system starts (i.e., offline as opposed to online), existing studies assign , the intermediate deadline for each task on each node (i.e., ). Then, as long as the following schedulability condition holds for all nodes, the local delay for each task executed on each node is guaranteed to be upper-bounded by the intermediate deadline, i.e., [21,22,23].
where denotes the utilization bound for node . It is known that , and , if subtasks in node are scheduled by preemptive EDF (Earliest Deadline) First [21], preemptive DM (Deadline Monotonic) [22], and non-preemptive EDF [23], respectively.
Then, considering that holds for all , the intermediate deadline assignment problem that we target is to maximize the system utility subject to the node schedulability conditions, which is formally stated in the following primal problem [14,15].
Note that it is straightforward that every intermediate deadline should be no smaller than the corresponding worst-case execution time (i.e., for every pair of ) to satisfy the node schedulability conditions in Equation (4).
2.2. Related Work
In the literature, several studies regarding the intermediate deadline assignment problem have also been proposed for real-time distributed systems. Several existing studies have addressed the intermediate deadline assignment problem; for example, straightforward deadline distribution technique [7], the critical scaling factor technique [6], and the excess of response time technique [5] have been proposed. In addition, there have been a few studies that focus on parallel subtasks; they usually aims at addressing how to handle interference between subtasks [9,10]. On the other hand, there have been some studies that handle pipelined tasks using end-to-end delay analysis techniques [12,13], and the end-to-end deadline guarantee has also been applied to utilizing optional (i.e., non-mandatory) execution parts [11]. A study has achieved improvement of the schedulability condition for the intermediate assignment problem [16]. Recently, a study has tried to solve the intermediate deadline assignment problem using the machine learning techniques [17]. While the above studies are well summarized in [1], they assumed that a centralized computing unit can control all tasks, and did not consider a distributed framework.
To solve the intermediate deadline assignment problem in a distributed manner, convex optimization has been utilized in some studies. That is, they applied a Lagrange dual function, and then found a sequence that converges to the optimal solution by utilizing the decomposition techniques with descent algorithms. Such decomposition has been applied to the intermediate assignment problem for real-time distributed systems [14,15]. However, all existing studies assume that all tasks are cooperative in achieving the system goal, which does not always hold for real-worlds. In addition, there has been no study about how to exploit a trade-off between delay fairness between individual tasks and performance of achievement of the system goal.
Different from existing studies, this paper (i) proposes the first non-cooperative distributed framework and (ii) designs a utility function that exploits a trade-off between delay fairness and system performance, both for the intermediate deadline assignment problem in real-time distributed systems.
3. Distributed Framework for Intermediate Deadline Assignment
In this section, we present how to solve the primal problem (defined in Section 2.1) in a distributed manner, assuming that the utility function for each task is given. To this end, we recapitulate the existing cooperative framework in which every task spontaneously collaborates on achieving the system goal (i.e., solving the primal problem). We then propose a non-cooperative framework, which can operate even when every task tries to maximize its own utility regardless of achieving the system goal. Finally, we discuss deployment issues for the cooperative and non-cooperative frameworks.
3.1. Existing Cooperative Distributed Framework
The primal problem in Section 2.1 can be solved using various techniques (e.g., Shor’s r-algorithm [24]), if a centralized computing unit has capability of controlling all tasks. However, in many real environments, a centralized computing/control is impossible or requires non-negligible overhead, which necessitates a framework with distributed computing/control. For the distributed framework, existing studies [14,15] utilize Lagrange Duality; the primal problem in Section 2.1 is transformed by its dual problem using Lagrange multipliers [25] as follows:
In the above dual problem, a node price is a Lagrange multiplier for the schedulability condition of a node n. If the primal problem is a convex optimization problem, strong duality is guaranteed by making node prices non-negative [25]. This means that the solution by the primal problem is equivalent to that by the dual problem. To make the primal problem in Section 2.1 convex, the utility functions and the schedulability constraints should be concave. Since holds for every pair of , the schedulability constraints in (4) are concave as follows [14,15]:
Therefore, if the utility functions are concave, we can solve the dual problem using the distributed computation/control without any loss of performance. That is, by applying the gradient projection algorithm [26,27], we can find the optimal solution iteratively. Node prices can be also calculated in an iterative manner, as follows [14,15]:
where denotes .
The constants are step sizes, which determine the rate of convergence of the iteration. If they are sufficiently small to satisfy Lipschitz continuity [26], they are able to guarantee the convergence. We can calculate the intermediate deadline of subtask , by solving the following differential equation in which for all [14,15]:
The condition for the iteration to halt is to satisfy the following inequalities for all :
where is a sufficiently small positive number; also it regulates a trade-off between the solution’s accuracy and the rate of convergence. The condition for the iteration to halt has been widely used in gradient algorithms [26].
Then, as long as every task follows Equation (8), the cooperative distributed framework operates correctly.
3.2. Proposed Non-Cooperative Distributed Framework
The dual problem presented in Section 3.1 assumes that all tasks are cooperative and collaborate on achieving the system goal (i.e., solving the primal problem). However, in many distributed systems, it is possible for each task to be only interested in maximizing its own utility regardless of achieving the system goal. In this case, the optimization goal for each task is as follows:
If each task tries to achieve the above optimization goal, each task no longer follows the distributed computing process explained in Section 3.1. Therefore, the node schedulability conditions in Equation (4) tend to be violated, as each task tries to monopolize the utilization (i.e., the left-hand-side of the node schedulability conditions in Equation (4)) by decreasing the intermediate deadline as much as possible. This means, the local delay for each task on each node cannot be upper-bounded by the intermediate deadline due to the violation of the node schedulability conditions; therefore, each task actually cannot have any guaranteed utility. To avoid the violation of the node schedulability conditions, we impose a penalty for each task in contributing the utilization to the node schedulablity conditions. Once we apply a penalty function to each task, the optimization problem for each task is as follows:
Then, the most important design guideline for the penalty function is to make each task meet the node schedulability conditions in Equation (4) when each task simply maximizes Equation (11) without considering the node schedulability conditions. Therefore, we apply the two following principles for designing the penalty function. First, the penalty increases as the remaining budget of the node schedulability (i.e., ) becomes close to zero; in addition, if the remaining budget converges to zero, the penalty increases infinitely, which can avoid the violation of the node schedulability conditions. Second, the penalty increases as the budget of the node schedulability used by each task (i.e., ) gets larger. Using the two principles, we design the penalty function for each task as follows:
Note that it is trivial that the above penalty function satisfies the first and second principles for designing the penalty function.
Then, instead of maximizing the system utility, each task can achieve Equation (11) with Equation (12). The advantage of this framework is to guarantee a certain amount of the system utility even if each task is non-cooperative in achieving the system utility. However, this framework cannot achieve the system utility as much as the one by the cooperative framework in Section 3.1, which is inevitable in applying the penalty functions. The next subsection will show how to impose the penalty to each task, and Section 5 will demonstrate the difference between the system utility achieved by the cooperative distributed framework explained in Section 3.1 and that by the non-cooperative one proposed in Section 3.2
3.3. Deployment of Distributed Framework
In this subsection, we first discuss an important deployment issue for the non-cooperative distributed framework, which is, how to apply the penalty function to each task. We then explain which information should be exchanged and how the information is exchanged for the cooperative distributed framework and then non-cooperative one.
As to the proposed non-cooperative distributed framework, we need to address an important issue for its deployment, which is how to apply the penalty function to each task. To this end, we appoint the node on which each task is executed in the latest, to an arbitrator node. The role of the arbitrator node is to impose a penalty to each task as much as the one in Equation (12). Since a utility for each task is a function of the end-to-end delay, the only way for each arbitrator node to impose a penalty is to add an artificial delay. To this end, the arbitrator node calculate that satisfies as follows.
where is given in Equation (12).
Once the last subtask of a task (i.e., ) is scheduled with other subtasks on a node , the node (as an arbitrator node for ) intentionally delays the execution of such that the total delay for is close to (but not larger than ). By this postponement, the arbitrator node can impose a penalty as much as Equation (12), which in turn, makes each task to voluntarily operate without monopolizing the node utilization.
We now explain the information exchange issue for the cooperative distributed framework. As shown in Equation (7), each node needs to know the current intermediate deadline of all tasks which are executed on the node, i.e., for all . In addition, as shown in Equation (8), each task needs to know the node price for all nodes that the task is executed on. The information needed for each node and each task can be piggybacked by each task itself or its control message [28,29].
When it comes to the non-cooperative distributed framework, the information exchange issue is similar to that of the cooperative one. That is, each arbitrator node needs to know all the intermediate deadlines of tasks, which are executed on the node in the latest, i.e., all satisfying , as shown in Equation (12). Also, each task needs to know (i) the current intermediate deadline of all subtasks for and (ii) the utilization for all nodes that is executed on. Similar to the cooperative distributed framework, this information can be piggybacked.
4. Utility Function Design
In Section 3, we explained that the cooperative and non-cooperative distributed frameworks can successfully work if a concave utility function for each task is given. Then, what if a system designer has a chance to determine utility functions for a real-time distributed system? Now, we propose a guideline in determining utility functions for a distributed real-time system, in order to help the system designer to exploit a trade-off between performance (i.e., the system utility) and fairness between the end-to-end delays of individual tasks. To this end, we define the following utility functions:
where , and .
Figure 1 illustrates the utility functions. With , the system goal is maximizing the sum of the utilities (that is equivalent to minimizing ). Therefore, this system goal is interpreted as minimizing the total sum of assigned deadlines, and does not pay attention to end-to-end delay upper-bound fairness among individual tasks. On the other hand, as becomes smaller, the system tries to achieve a higher degree of end-to-end delay fairness. Finally, with converging to , the system goal is equivalent to minimizing the longest end-to-end delay of a task (i.e., ), which achieves the highest degree of min-max fairness among end-to-end delay upper-bounds of individual tasks.
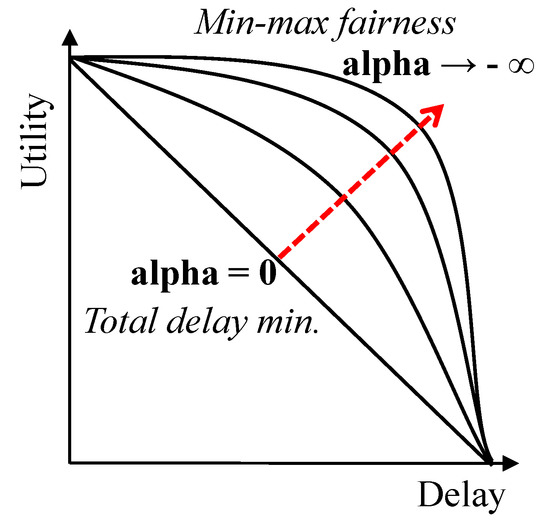
Figure 1.
The proposed utility functions with varying .
5. Experiments
In this section, we show how the cooperative distributed framework in Section 3.1 and the non-cooperative one in Section 3.2 operate with the utility function designed in Section 4. To this end, we target a typical real-time distributed system shown in Figure 2. The system consists of a set of 9 nodes and a set of 6 tasks . Each task executes on three different nodes sequentially; for example, is executed on , and in a sequential manner, and is executed on , and in a sequential manner, as shown in Figure 2. We set , , , , , , , , , , , , , , , , and to 10, 10, 10, 15, 15, 15, 20, 20, 20, 10, 10, 10, 15, 15, 15, 20, 20 and 20, respectively. We set the period of each task is 40. We apply each node employs preemptive EDF (Earliest Deadline First) scheduling, meaning that holds for all nodes. We plug in in Equation (14) into Equations (3), (5) and (11), respectively for the primal problem, the dual problem, and the individual-level optimization problem with penalty, where x means . We consider four options for : and , which means the utility functions are , , , and , respectively. For distributed computing, we use MATLAB [30] for the cooperative and non-cooperative frameworks as well as solving the primal problem directly.
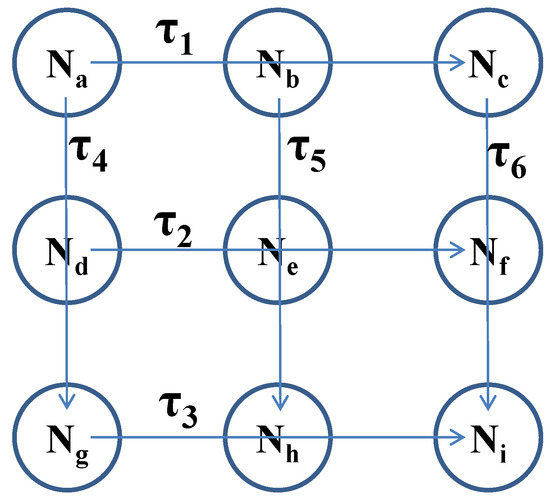
Figure 2.
A typical real-time distributed system.
Table 1, Table 2 and Table 3 show the system utility, the sum of the assigned intermediate deadlines (i.e., total delay upper-bound) and standard deviation among individual tasks’ end-to-end delay upper-bounds, respectively, by solving the primal problem directly (denoted by Primal), by the cooperative framework in Section 3.1 (denoted by Coop), and by the non-cooperative framework in Section 3.2 (denoted by Non-Coop). Then, Table 1, Table 2 and Table 3 show the results by the centralized framework, the distributed framework for cooperative tasks, and the distributed framework for non-cooperative tasks, respectively. We have three observations for the experimental results in the three tables.

Table 1.
The system utility, assigned intermediate deadline sum (i.e., total delay upper-bound) and standard deviation, with different utility functions, by solving the primal problem in Section 2.1.

Table 2.
The system utility, assigned intermediate deadline sum (i.e., total delay upper-bound) and standard deviation, with different utility functions, by the cooperative framework in Section 3.1.

Table 3.
The system utility, assigned intermediate deadline sum (i.e., total delay upper-bound) and standard deviation, with different utility functions, by the non-cooperative framework in Section 3.2.
First, for every utility function, the system utility achieved by Primal and that by Coop are exactly the same. For example, the system utility with under primal and that under Coop are −5.348 × 10; the intermediate deadlines under both are 20.0, 22.2, 24.1, 27.2, 30.0, 32.3, 34.1, 37.3, 40.0, 20.0, 22.2, 24.1, 27.2, 30.0, 32.3, 34.1, 37.3, and 40.0, respectively for , , , , , , , , , , , , , , , , , and . This comes from the fact that the primal problem in Section 2.1 is convex as long as the utility functions are concave, as we mentioned in Section 3.1. On the other hand, the system utility achieved by Coop is different from that by Non-Coop. For example, the system utility with under Coop and that under Non-Coop are −5.348 × 10 and −5.601 × 10, respectively. The difference is a cost to make the real-time distributed system operate correctly in the presence of selfish tasks.
Second, as in Equation (14) decreases, the sum of delay upper-bounds also increases and the standard deviation of individual task’s delay upper-bounds decreases under Primal and Coop. For example, under Primal and Coop, the sum of delay upper-bounds is 534.8 with (i.e., ), and increases up to 543.0 with (i.e., ). At the same time, the standard deviation of individual task’s delay upper-bounds is 20.1 with (i.e., ), and decreases down to 11.6 with (i.e., ). This demonstrates that the proposed utility function succeeds to exploit a trade-off between increasing the fairness of individual tasks’ end-to-end delay upper-bounds and decreasing the total end-to-end delay for all tasks.
Third, as in Equation (14) decreases, the sum of delay upper-bounds also increases under Non-Coop while the standard deviation of individual task’s delay upper-bounds does not decrease. For example, under Non-Coop, the sum of delay upper-bounds is 560.1 with (i.e., ), and increases up to 611.4 with (i.e., ). The reason why the standard deviation of individual task’s delay upper-bounds does not decrease as decreases is due to the penalty function. According to the observation, we suggest that the system designer does not decrease in the proposed utility function in order to achieve the fairness of end-to-end delays of individual tasks, for the non-cooperative framework. Therefore, it is better for the system designer to reduce the sum of delay upper-bounds as much as possible by assigning when the target real-time distributed system operates in a non-cooperative manner.
While we already presented the experimental results in terms of performance and fairness for delay upper-bounds, one may wonder the convergence issue for the distributed framework. Now, we present a representative case of how each assigned end-to-end deadline converges. In the case of the cooperative framework with (i.e., the second case in Table 2), Figure 3 shows the assigned end-to-end deadline for , and (i.e., , and ) according to the number of iterations (1 to 301 in the X-axis). Note that the results for , and are the same as , and , respectively, due to the topology symmetry. The initial values for , and are set to , and for every in Equation (7) is set to . As shown in the figure, the assigned end-to-end deadlines , and rapidly converge to , and , respectively. The difference between the final converged deadline and the assigned deadline with 64 iterations is smaller than for every , and that with 110 iterations is smaller than for every . This demonstrates the convergence rate for the distributed framework with the proposed utility function is high in the representative case, which can be observed in other cases.
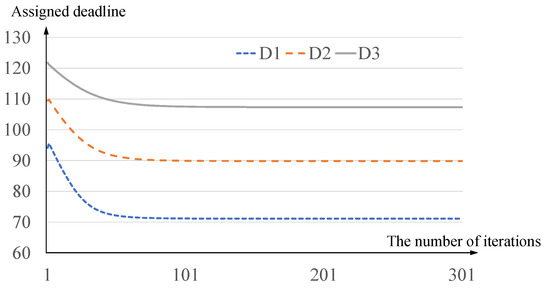
Figure 3.
The convergence of the assigned end-to-end deadline for , and (i.e., , and ).
6. Conclusions
In this paper, we focused on the intermediate deadline assignment problem in real-time distributed systems, and addressed two important issues. First, we developed a non-cooperative distributed framework that can operate with selfish tasks, each of which is only interested in maximizing its own utility. Second, we proposed a principle to design utility functions that can exploit a trade-off between minimizing the aggregate end-to-end delays of the entire system and maximizing fairness among end-to-end delays of individual tasks. In addition, we demonstrated the validity of the two techniques via simulations. By addressing the two important issues, we (i) enable real-time distributed systems to operate even in the presence of selfish nodes, and (ii) offer guidelines on how to design real-time distributed systems in consideration of a trade-off between performance and fairness.
Funding
This work was supported in part by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (2019R1A2B5B02001794, 2017H1D8A2031628).
Conflicts of Interest
The author declares no conflict of interest.
References
- Singh, A.K.; Dziuzanski, P.; Mendis, H.R.; Indrusiak, L.S. A Survey and Comparative Study of Hard and Soft Real-Time Dynamic Resource Allocation Strategies for Multi-/Many-Core Systems. ACM Comput. Surv. 2017, 50, 24:1–24:40. [Google Scholar] [CrossRef]
- Steffens, L.; Agarwal, M.; van der Wolf, P. Real-Time Analysis for Memory Access in Media Processing SoCs: A Practical Approach. In Proceedings of the Euromicro Conference on Real-Time Systems (ECRTS), Prague, Czech Republic, 2–4 July 2008; pp. 255–265. [Google Scholar]
- Tian, W.; Zhao, Y.; Xu, M.; Zhong, Y.; Sun, X. A Toolkit for Modeling and Simulation of Real-Time Virtual Machine Allocation in a Cloud Data Center. IEEE Trans. Autom. Sci. Eng. 2015, 12, 153–161. [Google Scholar] [CrossRef]
- Wang, X.; Tushar, W.; Yuen, C.; Zhang, X. Promoting Users’ Participation in Mobile Crowdsourcing: A Distributed Truthful Incentive Mechanism (DTIM) Approach. IEEE Trans. Veh. Technol. 2020, 69, 5570–5582. [Google Scholar] [CrossRef]
- Garcia, J.; Harbour, M. Optimized priority assignment for tasks and messages in distributed hard real-time systems. In Proceedings of the IEEE Workshop on Parallel and Distributed Real-Time Systems, Santa Barbara, CA, USA, 25 April 1995; pp. 124–132. [Google Scholar]
- Saksena, M.; Hong, S. An Engineering Approach to Decomposing End-to-End Delays on a Distributed Real-Time System. In Proceedings of the IEEE International Workshop on Parallel and Distributed Real-Time Systems, Honolulu, HI, USA, 15–16 April 1996; pp. 244–251. [Google Scholar]
- Kao, B.; Garcia-Molina, H. Deadline Assignment in a Distributed Soft Real-Time System. In Proceedings of the International Conference on Distributed Computing Systems, Pittsburgh, PA, USA, 25–28 May 1993; pp. 428–437. [Google Scholar]
- Bettati, R.; Liu, J. End-to-End Scheduling to Meet Deadlines in Distributed Systems. In Proceedings of the International Conference on Distributed Computing Systems, Yokohama, Japan, 9–12 June 1992; pp. 452–459. [Google Scholar]
- Natale, M.D.; Stankovic, J. Dynamic End-to-End Guarantees in Distributed Real-Time Systems. In Proceedings of the IEEE Real-Time Systems Symposium (RTSS), San Juan, Puerto Rico, 7–9 December 1994; pp. 216–227. [Google Scholar]
- Jonsson, J.; Shin, K. Deadline Assignment in Distributed Hard Real-Time Systems with Relaxed Locality Constraints. In Proceedings of the International Conference on Distributed Computing Systems, Baltimore, MD, USA, 27–30 May 1997; pp. 432–440. [Google Scholar]
- Stavrinides, G.L.; Karatza, H.D. Scheduling multiple task graphs with end-to-end deadlines in distributed real-time systems utilizing imprecise computations. J. Syst. Softw. 2010, 83, 1004–1014. [Google Scholar] [CrossRef]
- Jayachandran, P.; Abdelzaher, T. Delay Composition Algebra: A Reduction-based Schedulability Algebra for Distributed Real-Time Systems. In Proceedings of the IEEE Real-Time Systems Symposium (RTSS), Barcelona, Spain, 30 November–3 December 2008; pp. 259–269. [Google Scholar]
- Jayachandran, P.; Abdelzaher, T. End-to-End Delay Analysis of Distributed Systems with Cycles in the Task Graph. In Proceedings of the Euromicro Conference on Real-Time Systems (ECRTS), Dublin, Ireland, 25 January 2009; pp. 13–22. [Google Scholar]
- Lee, J.; Shin, I.; Easwaran, A. Online Robust Optimization Framework for QoS Guarantees in Distributed Soft Real-Time Systems. In Proceedings of the 10th ACM International Conference on Embedded Software (EMSOFT), Scottsdale, AZ, USA, 24–29 October 2010; pp. 89–98. [Google Scholar]
- Lee, J.; Shin, I.; Easwaran, A. Convex Optimization Framework for Intermediate Deadline Assignment in Soft and Hard Real-Time Distributed Systems. J. Syst. Softw. 2012, 85, 2331–2339. [Google Scholar] [CrossRef]
- Hong, S.; Chantem, T.; Hu, X.S. Local-Deadline Assignment for Distributed Real-Time Systems. IEEE Trans. Comput. 2015, 64, 1983–1997. [Google Scholar] [CrossRef]
- Agrawal, M.; Manchanda, K.; Agarwal, A.; Saraswat, S.; Gupta, A.; Gupta, H.P.; Dutta, T. A Supervised Approach-based Job Scheduling Technique for Distributed Real-Time Systems. In Proceedings of the 2018 IEEE International Conference on Advanced Networks and Telecommunications Systems (ANTS), Indore, India, 16–19 December 2018; pp. 1–6. [Google Scholar]
- Rehman, H.U.; Kumam, P.; Argyros, I.K.; Shutaywi, M.; Shah, Z. Optimization Based Methods for Solving the Equilibrium Problems with Applications in Variational Inequality Problems and Solution of Nash Equilibrium Models. Mathematics 2020, 8, 822. [Google Scholar] [CrossRef]
- Inthakon, W.; Suantai, S.; Sarnmeta, P.; Chumpungam, D. A New Machine Learning Algorithm Based on Optimization Method for Regression and Classification Problems. Mathematics 2020, 8, 1007. [Google Scholar] [CrossRef]
- Manikantan, R.; Chakraborty, S.; Uchida, T.K.; Vyasarayani, C.P. Parameter Identification in Nonlinear Mechanical Systems with Noisy Partial State Measurement Using PID-Controller Penalty Functions. Mathematics 2020, 8, 1084. [Google Scholar] [CrossRef]
- Liu, C.; Layland, J. Scheduling Algorithms for Multi-programming in A Hard-Real-Time Environment. J. ACM 1973, 20, 46–61. [Google Scholar] [CrossRef]
- Audsley, N.; Burns, A.; Wellings, A. Deadline monotonic scheduling theory and application. Control. Eng. Pract. 1993, 1, 71–78. [Google Scholar] [CrossRef]
- Jeffay, K.; Stanat, D.F.; Martel, C.U. On non-preemptive scheduling of period and sporadic tasks. In Proceedings of the IEEE Real-Time Systems Symposium (RTSS), San Antonio, TX, USA, 4–6 December 1991; pp. 129–139. [Google Scholar]
- Burke, J.V.; Lewis, A.S.; Overton, M.L. The speed of Shor’s R-algorithm. IMA J. Numer. Anal. 2008, 28, 711–720. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Bertsekas, D.P.; Tsitsiklis, J.N. Parallel and Distributed Computation: Numerical Methods; Athena Scientific: Nashua, NH, USA, 1997. [Google Scholar]
- Low, S.H. Optimization flow control, I: basic algorithm and convergence. IEEE/ACM Trans. Netw. 1999, 7, 861–874. [Google Scholar] [CrossRef]
- Athuraliya, S.; Low, S.H. Optimization Flow Control II: Implementation; Technical Report; Caltech: Pasadena, CA, USA, 2000. [Google Scholar]
- Athuraliya, S.; Li, V.H.; Low, S.H.; Yin, Q. REM: Active Queue Management. IEEE Netw. 2001, 15, 48–53. [Google Scholar] [CrossRef]
- MATLAB: The Language of Technical Computing. Available online: http://www.mathworks.com/products/matlab/ (accessed on 13 September 2020).
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).