Abstract
This article introduces an extension of the Power Muth (PM) distribution for modeling positive data sets with a high coefficient of kurtosis. The resulting distribution has greater kurtosis than the PM distribution. We show that the density can be represented based on the incomplete generalized integro-exponential function. We study some of its properties and moments, and its coefficients of asymmetry and kurtosis. We apply estimations using the moments and maximum likelihood methods and present a simulation study to illustrate parameter recovery. The results of application to two real data sets indicate that the new model performs very well in the presence of outliers.
1. Introduction
A symmetric extension of the normal distribution is the slash distribution. It is represented as the quotient between two independent random variables, one normal and the other a power of the uniform distribution (see Johnson et al. [1]). Thus, we say that X has a slash distribution if its representation is:
where , and Y is independent of U and .
This distribution presents heavier tails than the normal distribution, i.e., it has greater kurtosis. Properties are studied in Rogers and Tukey [2] and Mosteller and Tukey [3]. Maximum likelihood (ML) estimators are studied in Kafadar [4]. Gómez et al. [5] and Gómez and Venegas [6] extended the slash distribution by introducing the slash-elliptical family. Gómez et al. [7] used the slash-elliptical family to extend the Birnbaum–Saunders distribution. This slash methodology was used by Olmos et al. [8,9] in half-normal and generalized half-normal distributions; by Reyes et al. [10] in the Birnbaum–Saunders distribution; by Gómez et al. [11] in the Gumbel distribution, and by Segovia et al. [12] in the power Maxwell distribution, among others.
Muth [13] introduced a continuous probability distribution with application in reliability theory; and it is studied in Jodrá et al. [14]. A random variable Y is said to have a Muth (M) distribution with shape parameter if the probability density function (pdf) is given by
which we denote by .
An important function in the M distribution is the generalized integro-exponential function, which is defined by the following integral representation:
where , and is the gamma function. For further details, the reader is referred to Milgram [15] and Chiccoli et al. [16,17] and references therein.
Recently, Jodrá et al. [18] developed an extension of the M model, called PM, fixing the shape parameter in the M model. In this work, they incorporate a shape parameter , which makes the PM model more flexible than with the parameter . Thus, they obtain a two-parameter model which we consider below. A random variable X has a PM distribution with scale parameter and shape parameter if its pdf is given by
which we denote by .
Let , some properties of this distribution are:
- ,
- ,
where is the cumulative distribution function (cdf) of X, is the quantile function and denotes the negative branch of the Lambert W function (see Corless et al. [19]) and is the generalized integro-exponential function defined above.
For future developments, we define the incomplete generalized integro-exponential function as
where .
The principal object of the present article is to study an extension of the PM model with a greater range in its kurtosis coefficient, in order to use this new distribution to model data sets with atypical observations. In this work, we will show that the new distribution enables us to model more kurtosis than the PM distribution does. In addition, as we will see later, this new distribution can be represented as a scale mixture that allows us to carry out the simulation study.
The rest of the article is organized as follows. In Section 2, we give the representation of the model, generating the new density, basic properties, moments, and coefficients of asymmetry and kurtosis. In Section 3, we draw inferences using the moments and ML methods, carrying out a simulation study to observe the consistency of ML estimators. In Section 4, we show two illustrations in real data sets. In Section 5, we offer some conclusions.
2. Probability Density Function
2.1. Stochastic Representation
We consider that the random variable Z has a slash power Muth (SPM) distribution with parameters , and q if it can be represented as
where and are independent, , and . We denote this by writing .
2.2. Density Function
The following proposition presents the pdf for the SPM distribution that can be generated by using (3).
Proposition 1.
Let . Then, the pdf of Z is given by
where is the scale parameter, is the shape parameter, is the parameter related to the kurtosis of the distribution, , and is defined in (2).
Proof.
Consequently, by using the representation given in (3) and the transformation of variables method, we get
hence marginalizing we have
Finally, making the variable transformation and working inside the integral, the result follows. □
When , the canonic SPM distribution is obtained, denoted by . Then, the density function of Z is given by
We perform a brief comparison illustrating that the tails of the SPM distribution are heavier than those of the PM distribution.
Table 1 shows for different values of z in the distributions mentioned. We noted that the SPM distribution has much heavier tails than the PM distribution. Figure 1 depicts examples of the SPM distribution for different values the parameters.

Table 1.
Tails comparison for different SPM and PM distributions.
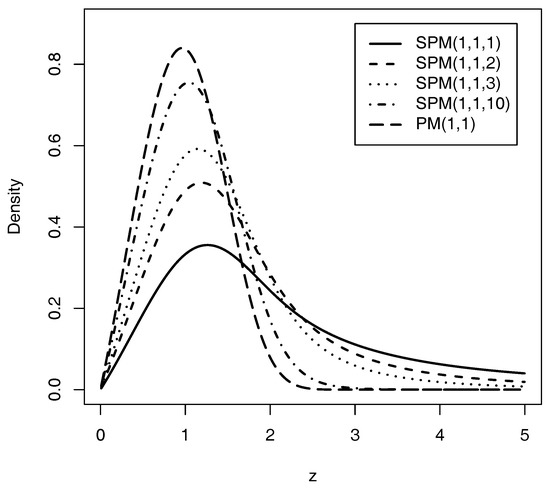
Figure 1.
Plot of the SPM distribution.
2.3. Probabilistic Properties
In this subsection, we study basic properties of the SPM distribution.
Proposition 2.
Let . Then, the cdf of Z is given by
where of and .
Proof.
Using cfd definition. □
Proposition 3.
Let . If , then Z converges in law to a random variable .
Proof.
Let . Then, Z can be represented as . First, we study the probability convergence of .
Since and if , then . Hence, we have that converges to 0 as , which implies that . Thus, applying Slutsky lemma finishes the proof of the proposition. □
Proposition 4.
If and , then .
Proof.
By noting that the marginal pdf of Z is given by
Then, marking the transformation variable where and , by some algebraic adjustments, we get (4). □
2.4. Moments
Proposition 5.
Let . Then, for and , it follows that the r-th moment of Z can be written as
where .
Proof.
Using the stochastic representation for the distribution given in (3), we have that
where and are the moments of the distribution. □
Corollary 1.
If , then it follows that
- 1.
- 2.
- 3.
- 4.
Corollary 2.
Let , then the asymmetry coefficient, () and the kurtosis coefficient () for and are, respectively,
where and
Remark 1.
The asymmetry and kurtosis coefficients were obtained using:
Figure 2 shows the skewness and kurtosis coefficients of the SPM model for different values of q and ; we can see that for small values of q the kurtosis coefficient increases in the SPM model. The ranges of both coefficients are larger than those of the PM model (see Jodrá et al. [18]). Thus, the SPM model is more flexible than the PM model for modeling data with larger coefficients of asymmetry and kurtosis.
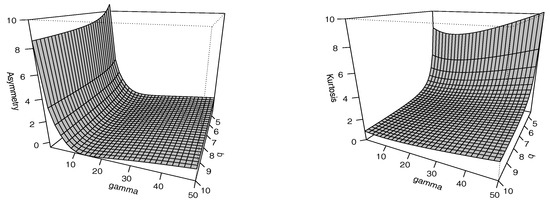
Figure 2.
Asymmetry coefficient (left) and kurtosis coefficient (right) for SPM distribution.
3. Inference
In this section, we address the problem of estimating parameters of the SPM distribution. In Section 3.1, we apply moment estimation and, in Section 3.2, we describe the ML method. Finally, in Section 3.3, we present some simulation results. For the following subsections, we consider be a random sample of size n from the distribution with parameters , , q and , , ..., the observed values of the sample.
3.1. Moment Method Estimators
Rewriting the first moment with isolated and replacing E(Z) by the sample mean , we have the equation
Therefore, using (5) and replacing the second and third population moments by the corresponding second and third sampling moments, we obtain the following equations:
3.2. Ml Estimation
The log-likelihood (ℓ) function can be written as follows:
where , and , . Then, the ML equations are given by
where is given in (1) and , with .
Solutions for Equations (8)–(10) can be obtained using numerical procedures such as the Newton–Raphson procedure.
3.3. Simulation Study
By using the stochastic representation given in (3), it is possible to generate random numbers of a random variable distribution with the following algorithm:
- Simulate
- Compute where W is the Lambert W function.
- Compute
It then follows that .
Table 2 shows the results of simulations studies illustrating the behavior of the ML estimates for 1000 generated samples of sizes 50, 100, 150, and 200 from a population with distribution. For each sample generated, ML estimates were computed numerically using a Newton–Raphson procedure. Means, standard deviations (SD), and empirical coverage (C) based on a confidence interval of 95%. It is observed that the bias becomes smaller as the sample size n increases, as one would expect.

Table 2.
Simulation of 1000 iterations for the model.
4. Applications
In this section, we consider two real data sets to illustrate that the SPM distribution may be more suitable than the PM distribution for modeling data with excess kurtosis.
4.1. Application I (Rubidium Concentration)
We consider Rubidium concentration data from 86 soil samples obtained by the Mining Department of Universidad de Atacama, Chile. Statistical measurements and the ML estimates of the SPM distribution were obtained and compared with the PM distribution with its standard errors.
Table 3 shows some descriptive statistics for the data set, where and denote the skewness and kurtosis coefficients, respectively, of the sample. In this respect, we highlight the high kurtosis of this data. Figure 3 presents a boxplot for the data, where an atypical observation is noted. From the results in Section 3.1, the moment estimates for the parameters of the SPM model are , and . These estimates are used as the initial values needed to implement estimation by the ML method using the numerical method.

Table 3.
Summary statistics for Rubidium concentration.
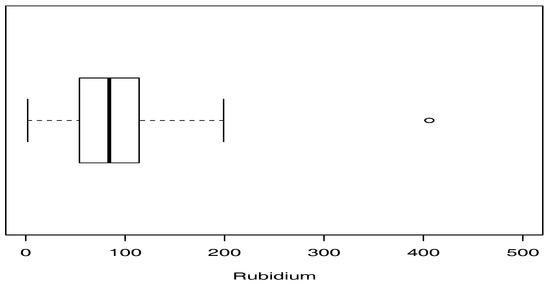
Figure 3.
Boxplot for rubidium dataset.
In Table 4, we compare the SPM and PM models. We calculated the Akaike information criterion AIC (see Akaike [20]) and the Bayesian information criterion BIC (see Schwartz [21]). It can be seen that AIC and BIC show a better fit of the SPM model, and the qqplots in Figure 4 show that the SPM model fits better than the PM model.

Table 4.
Parameter estimates, standard error (SE), and values for PM and SPM models for Rubidium concentration.
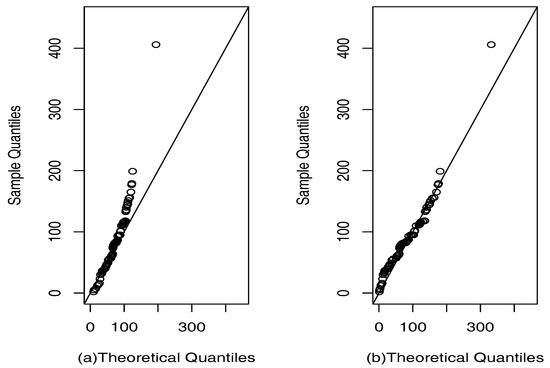
Figure 4.
qqplots for rubidium dataset: (a) PM model; (b) SPM model.
4.2. Application II (Dietary Retinol Consumed)
The real data were obtained from a cross-sectional study to investigate the relation between personal characteristics and dietetic factors dietéticos, and plasma concentrations of retinol, beta-carotene, and other carotenoids in 315 patients. The data set is available online at “http://lib.stat.cmu.edu/datasets/Plasma_Retinol” and contains 14 variables. The data consist of dietary retinol consumed by 315 patients (mcg per day). Table 5 shows some descriptive statistics for the data set, in which we highlight the very high kurtosis of the data. Figure 5 presents a boxplot for the data, which shows that there are several outliers. From the results in Section 3.1, the moment estimates for the parameters of the SPM model are , and . These estimates are used as initial values for calculating the ML estimates.

Table 5.
Summary statistics for the dietary retinol concentration.
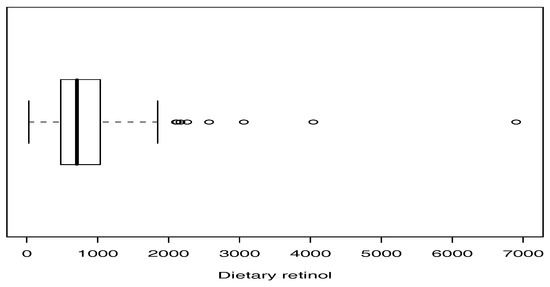
Figure 5.
Boxplot for retinol dataset.
Table 6 shows the ML estimates for the parameters of the SPM and PM models. For each model, we report the corresponding AIC and BIC values. It can be seen that AIC and BIC show better fit in the SPM model, and, when there are more atypical observations, the fit of the SPM model is much better. Finally, the qqplots in Figure 6 show that the SPM model fits better than the PM model.

Table 6.
Parameter estimates, (SE) indicates standard error estimates, and log-likelihood values for PM and SPM models for the dietary retinol concentration.
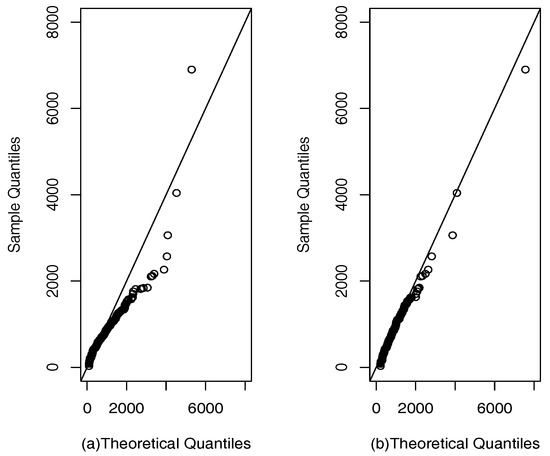
Figure 6.
qqplots for retinol dataset: (a) PM model; (b) SPM model.
5. Discussion
We have presented a new extension of the PM model, called the slash Power Muth model. It is defined on the basis of the principle used to produce the slash distribution, but using the PM model instead of the normal model. Thus, the PM model is a special case of the SPM model.
We studied properties of the SPM distribution including stochastic representation, moments, asymmetry, and kurtosis. Parameters are estimated using the moment method and ML method. The results of a simulation study show good parameter recovery. Some other characteristics of the new model are:
- The density of the SPM model has a closed-form and is expressed in terms of the incomplete generalized integro-exponential function.
- The SPM model presents more flexible coefficients of asymmetry and kurtosis than those of the PM model. Furthermore, as shown in Table 1, the tails become heavier when the parameter q is smaller.
- We discuss two stochastic representations for the SPM model: one is based on the quotient between two independent random variables, a PM in the numerator, and a power of a U in the denominator; the other is obtained as a mixture of the scale of a PM model and a U model.
- The moments and coefficients of asymmetry and kurtosis have closed-form expressions and are expressed in terms of the generalized integro-exponential function.
- In the applications, two criteria (AIC and BIC) were used to compare the models. In both data sets, the coefficient of kurtosis is high, indicating the presence of atypical observations. The criteria indicate that the SPM model provides the best fit to the data.
- The SPM distribution is a good alternative for modeling continuous positive data sets with atypical observations. These situations are common in all areas of knowledge, for example environmental science, economic, geo-chemistry, survival, reliability, etc. In the future, we will use this distribution in problems of regression, reliability, survival analysis, and Bayesian inference.
Author Contributions
Conceptualization, J.M.A. and H.W.G.; formal analysis, J.R., K.I.S., O.V. and H.W.G.; investigation, J.M.A., J.R., K.I.S. and O.V.; methodology, J.R. and H.W.G.; software, K.I.S.; supervision, H.W.G.; validation, J.M.A. and O.V.; visualization, O.V. All authors have read and agreed to the published version of the manuscript.
Funding
The research of J. Reyes and H.W. Gómez was supported by Semillero UA-2020.
Acknowledgments
We thank the anonymous referees for their very valuable comments and suggestions, which improved our manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions, 2nd ed.; Wiley-Interscience: New York, NY, USA, 1994; Volume 1. [Google Scholar]
- Rogers, W.H.; Tukey, J.W. Understanding some long-tailed symmetrical distributions. Statist. Neerl. 1972, 26, 211–226. [Google Scholar] [CrossRef]
- Mosteller, F.; Tukey, J.W. Data Analysis and Regression; Addison-Wesley: Boston, MA, USA, 1977. [Google Scholar]
- Kafadar, K. A biweight approach to the one-sample problem. J. Am. Stat. Assoc. 1982, 77, 416–424. [Google Scholar] [CrossRef]
- Gómez, H.W.; Quintana, F.A.; Torres, F.J. New Family of Slash-Distributions with Elliptical Contours. Stat. Probabil. Lett. 2007, 77, 717–725. [Google Scholar] [CrossRef]
- Gómez, H.W.; Venegas, O. Erratum to: A New Family of Slash-Distributions with Elliptical Contours. Stat. Probab. Lett. 2008, 78, 2273–2274. [Google Scholar] [CrossRef]
- Gómez, H.W.; Olivares-Pacheco, J.F.; Bolfarine, H. An extension of the generalized Birnbaum–Saunders distribution. Stat. Probab. Lett. 2009, 79, 331–338. [Google Scholar] [CrossRef]
- Olmos, N.M.; Varela, H.; Gómez, H.W.; Bolfarine, H. An extension of the half-normal distribution. Stat. Pap. 2012, 53, 875–886. [Google Scholar] [CrossRef]
- Olmos, N.M.; Varela, H.; Bolfarine, H.; Gómez, H.W. An extension of the generalized half-normal distribution. Stat. Pap. 2014, 55, 967–981. [Google Scholar] [CrossRef]
- Reyes, J.; Barranco-Chamorro, I.; Gallardo, D.I.; Gómez, H.W. Generalized modified slash Birnbaum–Saunders distribution. Symmetry 2018, 10, 724. [Google Scholar] [CrossRef]
- Gómez, Y.M.; Bolfarine, H.; Gómez, H.W. Gumbel distribution with heavy tails and applications to environmental data. Math. Comput. Simul. 2019, 157, 115–129. [Google Scholar] [CrossRef]
- Segovia, F.A.; Gómez, Y.M.; Venegas, O.; Gómez, H.W. A power Maxwell distribution with heavy tails and applications. Mathematics 2020, 8, 1116. [Google Scholar] [CrossRef]
- Muth, J.E. Reliability models with positive memory derived from the mean residual life function. In The Theory and Applications of Reliability; Tsokos, C.P., Shimi, I., Eds.; Academic Press: New York, NY, USA, 1977; Volume II, pp. 401–435. [Google Scholar]
- Jodrá, P.; Jiménez-Gamero, M.D.; Alba-Fernández, M.V. On the Muth Distribution. Math. Model. Anal. 2015, 20, 291–310. [Google Scholar] [CrossRef]
- Milgram, M.S. The generalized integro-exponential function. Math. Comput. 1985, 44, 443–458. [Google Scholar] [CrossRef]
- Chiccoli, C.; Lorenzutta, S.; Maino, G. A numerical method for generalized exponential integrals. Comp. Math. Applic. 1987, 14, 261–268. [Google Scholar] [CrossRef]
- Chiccoli, C.; Lorenzutta, S.; Maino, G. Recent results for generalized exponential integrals. Comp. Math. Applic. 1990, 19, 21–29. [Google Scholar] [CrossRef]
- Jodrá, P.; Gómez, H.W.; Jiménez-Gamero, M.D.; Alba-Fernández, M.V. The power Muth distribution. Math. Model. Anal. 2017, 22, 186–201. [Google Scholar] [CrossRef]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.G.; Jeffrey, D.J.; Knuth, D.E. On the Lambert W function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).