Dominating the Direct Product of Two Graphs through Total Roman Strategies

Abstract

Given a graph G without isolated vertices, a total Roman dominating function for G is a function $f:V\left(G\right)\to \{0,1,2\}$ such that every vertex u with $f\left(u\right)=0$ is adjacent to a vertex v with $f\left(v\right)=2$, and the set of vertices with positive labels induces a graph of minimum degree at least one. The total Roman domination number ${\gamma }_{tR}\left(G\right)$ of G is the smallest possible value of ${\sum }_{v\in V\left(G\right)}f\left(v\right)$ among all total Roman dominating functions f. The total Roman domination number of the direct product $G\times H$ of the graphs G and H is studied in this work. Specifically, several relationships, in the shape of upper and lower bounds, between ${\gamma }_{tR}(G\times H)$ and some classical domination parameters for the factors are given. Characterizations of the direct product graphs $G\times H$ achieving small values ($\le 7$) for ${\gamma }_{tR}(G\times H)$ are presented, and exact values for ${\gamma }_{tR}(G\times H)$ are deduced, while considering various specific direct product classes.

1. Introduction

The present investigation is devoted to describe several contributions to the theory of total Roman dominating functions while dealing with the direct (or tensor or Kronecker) product of two graphs. Studies concerning parameters in relation to domination in graphs are very frequently present in recent years. This might probably be caused by the popularity of some classical problems, like for instance Vizing’s conjecture [1,2] for domination in Cartesian products. The conjecture claims that the cardinality of the smallest dominating set of the Cartesian product of two graphs is at least equal to the product of the domination numbers of the factor graphs involved in the product. See [3], for a survey and recent results concerning this conjecture. Several other problems concerning domination parameters in product graphs have occupied the mind of a significant number of investigators. Works of that type concerning direct product graphs are [4,5,6,7].

The (total) Roman domination variants are among the most popular topics of domination in graphs. Both versions have had their birth in connection with some defense strategies related to the ancient Roman Empire (see [8,9]). Studies on (total) Roman domination in product graphs have not escaped from the researcher’s attention. For instance, [10,11,12,13] are aimed to these goals, although no works appear that considers the Roman domination parameters for the case of direct products. We hence continue with giving new contributions to the theory of parameters related to domination in graph products, specifically we center our attention on the total Roman domination version for the case of the direct product of graphs.

In this work, we consider simple graphs without isolated vertices. For a function $f:V\left(G\right)\to \{0,1,2\}$ and a set of vertices $S\subseteq V\left(G\right)$, the weight of S under f is $f\left(S\right)={\sum }_{v\in S}f\left(v\right)$. Moreover, the weight of f is $\omega \left(f\right)=f\left(V\right(G\left)\right)$. Since the function f generates three sets $V_0,V_1,V_2$ such that $V_i=\{v\in V\left(G\right):f\left(v\right)=i\}$, $i\in \{0,1,2\}$, we shall write $f=(V_0,V_1,V_2)$.

A function $f=(V_0,V_1,V_2)$ is known to be a Roman dominating function on G whenever all vertices $v\in V_0$ have at least one neighbor $u\in V_2$. In connection with this, the parameter of G called Roman domination number stands for the least weight among all functions that are proved to be Roman dominating on G. This parameter is usually represented as ${\gamma }_R\left(G\right)$. Such concepts in the theory of graphs were formally introduced in [14], motivated in part by some domination strategies which arose from the antique Roman Empire (see for instance [8,9]). A Roman dominating function $f=(V_0,V_1,V_2)$ is called a total Roman dominating function if $V_1\cup V_2$ induces a graph without isolated vertices. The total Roman domination number of G stands for the minimum possible weight among all total Roman dominating functions on G. This parameter is denoted ${\gamma }_{tR}\left(G\right)$. By a ${\gamma }_{tR}\left(G\right)$-function we mean a total Roman dominating function whose weight equals precisely ${\gamma }_{tR}\left(G\right)$. These concepts of total Roman domination were first introduced in [15] by using some more general settings. The concepts were further specifically introduced and first well studied in [16]. Some other recent studies on total Roman domination in graphs are for example [17,18,19].

A set $D=\{v_1,\dots ,v_r\}\subset V\left(G\right)$ is called a packing set of G, if $N\left[v_i\right]\cap N\left[v_j\right]=Ø$ for every two different integers $i,j\in \{1,\dots ,r\}$. The packing number of G is the cardinality of a largest possible packing set of G. We represent such cardinality as $\rho \left(G\right)$. A packing set induces a subgraph of maximum degree 0, i.e., a graph without edges. If we substitute the closed neighborhoods with open neighborhood in the definition above, then the concept of open packing sets arises. Hence, D is considered to be an open packing set whenever $N\left(v_i\right)\cap N\left(v_j\right)=Ø$ for any two distinct $i,j\in \{1,\dots ,r\}$. Similarly, the parameter called open packing number of G is the cardinality of the largest possible open packing set of G. We write this cardinality by using the notation ${\rho }_o\left(G\right)$. We recall that any open packing set represents a set of vertices of the graph which induces a graph with the maximum degree equal to one, and clearly, it could have some vertices whose degree equals zero.

A set $D\subseteq V\left(G\right)$ is total dominating if all the vertices of the whole graph G have at least a neighbor in the set D. The cardinality of the smallest total dominating set of G is known as the total domination number of G. This cardinality is then represented as ${\gamma }_t\left(G\right)$. A set being total dominating and with cardinality ${\gamma }_t\left(G\right)$ is said to be a ${\gamma }_t\left(G\right)$-set. The graph G is called an efficient open domination graph, if there is a total dominating set of G which is simultaneously also an open packing.

The direct product (also known as tensor product or Kronecker product) of two graphs G and H is the graph denoted by $G\times H$ whose vertex set is given by $V(G\times H)=V\left(G\right)\times V\left(H\right)$ and the edge set is the Cartesian product of the vertex sets of the factors, i.e., $E(G\times H)=\{(g,h)(g^{\prime },h^{\prime }):g{g}^{\prime }\in E\left(G\right),h{h}^{\prime }\in E\left(H\right)\}$. The example $P_6\times P_6$ is shown in Figure 1. As usual, we call the map $p_G:(g,h)\mapsto g$ a projection of $G\times H$ onto G and the map $p_H:(g,h)\mapsto h$ a projection of $G\times H$ onto H. The set $G^h=\{(g,h):g\in V\left(G\right)\}$ is called a G-layer through $h\in V\left(H\right)$ and contains all vertices that project to h. An H-layer $H^g=\{(g,h):h\in V\left(H\right)\}$ through $g\in V\left(G\right)$ is similarly defined. Please note that vertices from a G-layer and from an $H^g$-layer form an independent set of $G\times H$.

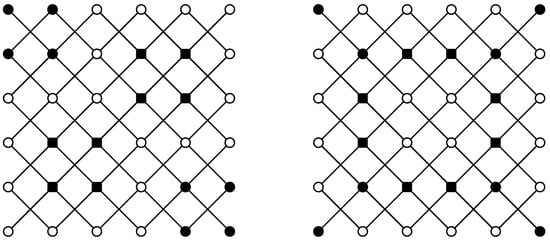
Figure 1. Two total Roman dominating functions on $P_6\times P_6$ where vertices in $V_0$ are white circles, vertices in $V_1$ are black circles and black squares represent vertices in $V_2$.

The direct product is a graph product (see the exhausting monograph on graph products [20]) in categorical sense, as the end vertices of every edge from $G\times H$ project to end vertices of edges in both factors. Consequently, one of the most natural products among all graph products is precisely the direct product, but on the other hand, this also makes this product the most elusive one in many perspectives. Therefore, the connectedness of both factors G and H does not imply the connectedness of the product $G\times H$. (Notice that $P_6\times P_6$ from Figure 1 is not connected.) To achieve this, one of the factors must also be non-bipartite, see Theorem 5.9 in [20]. One reason for this is that layers form independent sets in $G\times H$. On the other side, the open neighborhoods behave “nicely”, with respect to the factors, while making a direct product based on the fact

$$N_{G\times H}(g,h)=N_G\left(g\right)\times N_H\left(h\right).$$

(1)

Two different total Roman dominating functions on $P_6\times P_6$ are presented in Figure 1.

The degree ${\delta }_G\left(v\right)$ of the vertex v in G is represented as the cardinality of the open neighborhood of v, i.e., ${\delta }_G\left(v\right)=\left|N_G\left(v\right)\right|$. The maximum degree of a vertex in a graph G is denoted by $\Delta \left(G\right)$. Clearly, $1\le \Delta \left(G\right)\le \left|V\right(G\left)\right|-1$ as we consider only simple graphs with no isolated vertices. A leaf of G is a vertex $v\in V\left(G\right)$ with degree ${\delta }_G\left(v\right)=1$ and in contrast, if ${\delta }_G\left(v\right)=\left|V\left(G\right)\right|-1$, then the vertex v is called a universal vertex. For the specific case of the direct product of two graphs G and H, we recall that ${\delta }_{G\times H}(g,h)={\delta }_G\left(g\right){\delta }_H\left(h\right)$ and $\Delta (G\times H)=\Delta \left(G\right)\Delta \left(H\right)$ by (1).

2. General Bounds

We start our exposition with some lower and upper bounds for ${\gamma }_{tR}(G\times H)$ which are mainly depending on $\rho \left(G\right)$, $\rho \left(H\right)$, ${\gamma }_{tR}\left(G\right)$ and ${\gamma }_{tR}\left(H\right)$.

Theorem 1.

If $g=(A_0,A_1,A_2)$ is a ${\gamma }_{tR}\left(G\right)$-function (with maximum cardinality of $A_2$) and $h=(B_0,B_1,B_2)$ is a ${\gamma }_{tR}\left(H\right)$-function (with maximum cardinality of $B_2$), then

$$max\{\rho \left(H\right){\gamma }_{tR}\left(G\right),\rho \left(G\right){\gamma }_{tR}\left(H\right)\}\le {\gamma }_{tR}(G\times H)\le {\gamma }_{tR}\left(H\right){\gamma }_{tR}\left(G\right)-2|A_2\left|\right|B_2|.$$

Proof. 

We consider a function f on $G\times H$ defined as follows. If $(u,v)\in (A_2\times (B_1\cup B_2))\cup (A_1\times B_2)$, then $f(u,v)=2$; if $(u,v)\in (A_1\times B_1)$, then $f(u,v)=1$; and $f(u,v)=0$ otherwise. If $f(u,v)\ge 1$, then since $g\left(u\right)\ge 1$ and $h\left(v\right)\ge 1$, there exist two vertices $u^{\prime }\in N_G\left(u\right)$ and $v^{\prime }\in N_H\left(v\right)$ such that $g\left(u^{\prime }\right)\ge 1$ and $h\left(v^{\prime }\right)\ge 1$. Thus, it follows $(u^{\prime },v^{\prime })\in N_{G\times H}(u,v)$ and $f(u^{\prime },v^{\prime })\ge 1$. Now, consider a vertex $(u,v)\in V(G\times H)$ such that $f(u,v)=0$. If $(u,v)\in A_0\times V\left(H\right)$, then there exist two vertices $u^{″}\in N_G\left(u\right)$ and $v^{″}\in N_H\left(v\right)$ such that $g\left(u^{″}\right)=2$ and $h\left(v^{″}\right)\ge 1$. Thus, it follows $(u^{″},v^{″})\in N_{G\times H}(u,v)$ and $f(u^{″},v^{″})=2$. Finally, if $(u,v)\in A_i\times B_0$ with $i\in \{1,2\}$, then a symmetrical argument to the above one produce a similar conclusion.

Consequently, we deduce f is a total Roman dominating function on the direct product $G\times H$, which leads to

$$\begin{array}{cc}\hfill {\gamma }_{tR}(G\times H)& \le \omega \left(f\right)\hfill \\ \hfill & =2|A_2\times B_2|+2|A_2\times B_1|+2|A_1\times B_2|+|A_1\times B_1|\hfill \\ \hfill & =\left(2\right|A_2|+|A_1\left|\right)\left(\right|B_2|+|B_1\left|\right)+|A_1\left|\right|B_2|\hfill \\ \hfill & =\left(2\right|A_2|+|A_1\left|\right)\left(2\right|B_2|+|B_1\left|\right)-2|A_2\left|\right|B_2|\hfill \\ \hfill & ={\gamma }_{tR}\left(G\right){\gamma }_{tR}\left(H\right)-2|A_2\left|\right|B_2|.\hfill \end{array}$$

Now, in order we deduce the lower bound, a ${\gamma }_{tR}(G\times H)$-function f and a $\rho \left(G\right)$-set $S=\{u_1,\dots ,u_{\rho \left(G\right)}\}$ are considered. Hence, for any integer $i\in \{1,\dots ,\rho (G\left)\right\}$, we construct a function $h_i$ on H as follows: for any vertex $v\in V\left(H\right)$, we set $h_i\left(v\right)=max\{f(u,v):u\in N_G\left[u_i\right]\}$.

If $h_i\left(v\right)\ge 1$, then there is a vertex $(u,v)\in N_G\left[u_i\right]\times \left\{v\right\}$ for which $f(u,v)\ge 1$. If $f(u_i,v)=0$, then there exists a vertex $(x,y)\in N_G\left(u_i\right)\times N_H\left(v\right)$ such that $f(x,y)=2$ and $(x,y)\in N_{G\times H}(u_i,v)$. Moreover, note that in this case $h_i\left(y\right)=2$ and that $y\in N_H\left(v\right)$. Now, if $f(u_i,v)\ge 1$, then there exists a vertex $(x^{\prime },y^{\prime })\in N_{G\times H}(u_i,v)$ such that $f(x^{\prime },y^{\prime })\ge 1$. In such situation, we similarly get $h_i\left(y^{\prime }\right)\ge 1$ and $y^{\prime }\in N_H\left(v\right)$.

On the other hand, if $h_i\left(v\right)=0$, then for every vertex $(u,v)\in N_G\left[u_i\right]\times \left\{v\right\}$ we have $f(u,v)=0$. In particular, for the vertex $(u_i,v)$, there exists a vertex $(u_i^{\prime },v^{\prime })\in N_{G\times H}(u_i,v)$ with $v^{\prime }\ne v$ and $f(u_i^{\prime },v^{\prime })=2$. Hence, for the vertex $v^{\prime }\in V\left(H\right)$ it is satisfied $v^{\prime }\in N_H\left(v\right)$ and $h_i\left(v^{\prime }\right)=2$.

As a consequence of these arguments, we deduce that $h_i$ is a total Roman dominating function on H whose weight is less than or equal to $f(N_G\left[u_i\right]\times V\left(H\right))$, i.e., ${\gamma }_{tR}\left(H\right)\le f(N_G\left[u_i\right]\times V\left(H\right))$. Hence, we have the following.

$${\gamma }_{tR}(G\times H)\ge \sum _{i=1}^{\rho \left(G\right)}f(N_G\left[u_i\right]\times V\left(H\right))\ge \sum _{i=1}^{\rho \left(G\right)}{\gamma }_{tR}\left(H\right)=\rho \left(G\right){\gamma }_{tR}\left(H\right).$$

By the symmetry of the product, we also deduce that ${\gamma }_{tR}(G\times H)\ge \rho \left(H\right){\gamma }_{tR}\left(G\right)$, and this ends the proof for the case of the lower bound. ☐

Since every graph of order at least three contains at least one total Roman dominating function whose weight equals the total Roman domination number and at least one vertex labeled two, the following result is directly deduced from the result above.

Corollary 1.

For all graphs G and H of orders at least three,

$${\gamma }_{tR}(G\times H)\le {\gamma }_{tR}\left(G\right){\gamma }_{tR}\left(H\right)-2.$$

Notice that we can avoid the remarks about maximum cardinality of $A_2$ and $B_2$ in Theorem 1. However, the bound is better if we take a ${\gamma }_{tR}\left(G\right)$-function and a ${\gamma }_{tR}\left(H\right)$-function with maximum cardinality of $A_2$ and $B_2$, respectively. The proof of the upper bound from Theorem 1 remains valid for any total Roman dominating functions g and h of graphs G and H without isolated vertices, respectively, as long as we exchange ${\gamma }_{tR}\left(G\right)$ and ${\gamma }_{tR}\left(H\right)$ by $\omega \left(g\right)$ and $\omega \left(h\right)$, respectively, in the last step of the proof. Therefore, we can improve the upper bound of Theorem 1, as we next show.

Remark 1.

For every two graphs G and H,

$${\gamma }_{tR}(G\times H)\le min\{\omega \left(g\right)\omega \left(h\right)-2|A_2\left|\right|B_2\left|\right\},$$

where such minimum value is understood for every pair of total Roman dominating functions $g=(A_0,A_1,A_2)$ and $h=(B_0,B_1,B_2)$ on G and H, respectively.

Despite the fact that the bound above represents an advance with respect to the upper bound of Theorem 1, we have no knowledge of one pair of graphs G and H where the bound given in Remark 1 is better than the upper bound of Theorem 1.

Let $D_G$ be a ${\gamma }_t\left(G\right)$-set. Clearly, the function $g=(V\left(G\right)-D_G,Ø,D_G)$ total Roman dominating for G and the weight of g is $\omega \left(g\right)=2{\gamma }_t\left(G\right)$. Remark 1 yields the following connection.

Corollary 2.

For any graphs G and H,

$${\gamma }_{tR}(G\times H)\le 2{\gamma }_t\left(G\right){\gamma }_t\left(H\right).$$

If the graphs G and H represent efficient open domination graphs, then ${\rho }_o\left(H\right)={\gamma }_t\left(H\right)$ and ${\rho }_o\left(G\right)={\gamma }_t\left(G\right)$ (see [21], Observation 1.1), and Corollary 2 implies the following.

Corollary 3.

If the graphs G and H represent efficient open domination graphs, then ${\gamma }_{tR}(G\times H)\le 2{\rho }_o\left(G\right){\rho }_o\left(H\right)$.

A graph G is known to be a total Roman graph if it satisfies that ${\gamma }_{tR}\left(G\right)=2{\gamma }_t\left(G\right)$. In the case of two total Roman graphs we can develop the upper bound of Corollary 2 to the following result.

Corollary 4.

If G and H are two total Roman graphs, then

$${\gamma }_{tR}(G\times H)\le \frac{{\gamma }_{tR}\left(G\right){\gamma }_{tR}\left(H\right)}{2}.$$

Another consequence of Theorem 1 can be deduced by using open packings instead of packings, since $\rho \left(G\right)\ge \frac{{\rho }_o\left(G\right)}{2}$ for any graph G.

Corollary 5.

For any graphs G and H of orders at least three,

$${\gamma }_{tR}(G\times H)\ge max\left\{\frac{{\rho }_o\left(H\right){\gamma }_{tR}\left(G\right)}{2},\frac{{\rho }_o\left(G\right){\gamma }_{tR}\left(H\right)}{2}\right\}.$$

The bound given in Theorem 1 can be enhanced by a factor of 2, whenever one factor is bipartite and the other without triangles as shown next.

Theorem 2.

If G is a triangle free graph and H is a bipartite graph of order at least two without isolated vertices, then

$${\gamma }_{tR}(G\times H)\ge 2\rho \left(G\right){\gamma }_{tR}\left(H\right).$$

Proof. 

Let f and S be defined in a similar manner to that of the proof of Theorem 1 for the lower bound. Clearly, for any vertex $u_i\in S$, $N_G\left[u_i\right]\times V\left(H\right)$ induces a non-connected graph with at least two components. In this sense, for every $i\in \{1,\dots ,\rho (G\left)\right\}$ and for every component of the subgraph induced by $N_G\left[u_i\right]\times V\left(H\right)$, we can construct a total Roman dominating function in the same style as in the proof of Theorem 1. This means that $f(N_G\left[u_i\right]\times V\left(H\right))\ge 2{\gamma }_{tR}\left(H\right)$. A similar argument as the one used to prove Theorem 1 gives the stated bound. ☐

The bound of Corollary 5 can also be improved if we consider one bipartite factor and the other without triangles as next stated.

Theorem 3.

If G is a graph with no triangles and with a ${\rho }_o\left(G\right)$-set which induces a graph with all components isomorphic to $K_2$, and H is a bipartite graph of order at least two, then

$${\gamma }_{tR}(G\times H)\ge {\rho }_o\left(G\right){\gamma }_{tR}\left(H\right).$$

Proof. 

Let f be a ${\gamma }_{tR}(G\times H)$-function, and assume $S=\{u_1,v_1,\dots ,u_{{\rho }_o\left(G\right)/2},v_{{\rho }_o\left(G\right)/2}\}$ is a ${\rho }_o\left(G\right)$-set such that $u_i\sim v_i$ for every $i\in \{1,\dots ,{\rho }_o\left(G\right)/2\}$. Since H is bipartite and G is triangle free, the set $(N\left(u_i\right)\cup N\left(v_i\right))\times V\left(H\right)$ induces a non-connected graph with at least two components. In concordance with this fact, by using similar arguments as those ones in the proof for the lower bound of Theorem 1, we deduce that for every $i\in \{1,\dots ,{\rho }_o\left(G\right)/2\}$, we can construct two total Roman dominating functions $h_i,h_i^{\prime }$ on H satisfying that $2{\gamma }_{tR}\left(H\right)\le \omega \left(h_i\right)+\omega \left(h_i^{\prime }\right)\le f((N_G\left(u_i\right)\cup N_G\left(v_i\right))\times V\left(H\right))$. Therefore, we obtain that

$${\gamma }_{tR}(G\times H)\ge \sum _{i=1}^{{\rho }_o\left(G\right)/2}f((N_G\left(u_i\right)\cup N_G\left(v_i\right))\times V\left(H\right))=\frac{{\rho }_o\left(G\right)}{2}(\omega \left(h_i\right)+\omega \left(h_i^{\prime }\right))\ge {\rho }_o\left(G\right){\gamma }_{tR}\left(H\right),$$

and the proof is completed. ☐

3. Direct Product Graphs with Small ${\mathit{\gamma }}_{\mathit{tR}}(\mathit{G}\times \mathit{H})$

We concentrate our attention in this section on the case when ${\gamma }_{tR}(G\times H)$ is small. We shall characterize all the direct product graphs $G\times H$ for which ${\gamma }_{tR}(G\times H)\le 7$. For this we need the following class of graphs.

A graph G is called triangle centered if there exists a triangle $C_3=xyz$ in G such that every vertex of G is adjacent to at least two vertices of $C_3$. We call such $C_3$ the central triangle of a triangle centered graph. Notice that any two vertices of a central triangle form a total dominating set of a triangle centered graph G and we have ${\gamma }_t\left(G\right)=2$.

Theorem 4.

The following assertions holds for any two graphs G and H.

(i) 

There are no graphs G and H for which ${\gamma }_{tR}(G\times H)\in \{1,2,3,5\}$.

(ii) 

${\gamma }_{tR}(G\times H)=4$ if and only if G and H are both isomorphic to $K_2$.

(iii) 

${\gamma }_{tR}(G\times H)=6$ if and only if (G and H have at least two universal vertices each and at least one of them is of order at least three), or (one factor is $K_2$ and the other one is of order at least three and contains a universal vertex), or (the graphs G and H are triangle centered).

(iv) 

${\gamma }_{tR}(G\times H)=7$ if and only if both G and H have a universal vertex, one of the graph G and H has exactly one universal vertex, and the other one is different from $K_2$, and only one of G and H can be triangle centered.

(v) 

If at most one of the graphs G and H has a universal vertex, ${\gamma }_t\left(G\right)={\gamma }_t\left(H\right)=2$, and G and H are not both triangle centered, then ${\gamma }_{tR}(G\times H)=8$.

Proof. 

For $\left(i\right)$ notice that there must be at least two adjacent vertices $(g,h)$ and $(g^{\prime },h^{\prime })$ in $V_1\cup V_2$ for a ${\gamma }_{tR}(G\times H)$-function $f=(V_0,V_1,V_2)$. If $|V_1\cup V_2|=2$, then $(g,h^{\prime })$ and $(g^{\prime },h)$ have label 0 and no neighbor with label 2, a contradiction. This already shows that ${\gamma }_{tR}(G\times H)\ge 3$. If ${\gamma }_{tR}(G\times H)=3$, then either $|V_1\cup V_2|=2$, which is not possible, or $|V_1\cup V_2|=3$. In later case there are three vertices of label 1 and no vertex of label 2, a contradiction as we have $\left|V\right(G\times H\left)\right|\ge 4$. Hence ${\gamma }_{tR}(G\times H)>3$.

To end with $\left(i\right)$ suppose that ${\gamma }_{tR}(G\times H)=5$. Let first $|V_2|=2$ where $(g,h),(g_1,h_1)\in V_2$. If $g\ne g_1$ and $h\ne h_1$, then only one vertex from $(g,h_1)$ and $(g_1,h)$ can have label 1 and the other has label 0 and is not adjacent to a vertex of label 2, a contradiction. Therefore, either $g=g_1$ or $h=h_1$, say $g=g_1$. In $V_1$ is only one vertex, say $(g_2,h_2)$, and it must be adjacent to both vertices of $V_2$. This means that $h_2\ne h$ and $h_2\ne h_1$. But then $(g,h_2)$ possess label 0 and is not adjacent to a vertex of label 2, a contradiction.

So let $|V_2|=1$ where $(g,h)\in V_2$ and $(g^{\prime },h^{\prime })\in V_1$ is adjacent to $(g,h)$. There are only two more vertices in $V_1$ and these vertices must be $(g,h^{\prime })$ and $(g^{\prime },h)$ because they are not adjacent to $(g,h)$. If there exists any other vertex from the mentioned four, then such a vertex implies the existence of a vertex of label 0 in $G^h\cup H^g$, a contradiction. Hence we have only four vertices and $G\times H\cong K_2\times K_2$. But in this case we have ${\gamma }_{tR}(G\times H)\le 4$ as there exists a total Roman dominating function with $V_1=V\left(G\right)\times V\left(H\right)$. This is the final contradiction and ${\gamma }_{tR}(G\times H)\ne 5$.

The implication $(\Leftarrow )$ of item $\left(ii\right)$ follows from $\left(i\right)$ and the total Roman dominating function with $V_1=V\left(K_2\right)\times V\left(K_2\right)$. For $(\Rightarrow )$ of $\left(ii\right)$ suppose that at least one of G and H contains more than three vertices. Hence $\left|V\right(G)\times V(H\left)\right|\ge 6$ and if all vertices have label 1, then ${\gamma }_{tR}(G\times H)\ge 6>4$. Otherwise, if $V_0\ne Ø$, then also $V_2\ne Ø$. Let $(g,h)\in V_2$ and let $(g^{\prime },h^{\prime })\in V_1\cup V_2$ be a neighbor of $(g,h)$. If also $(g,h^{\prime }),(g^{\prime },h)\in V_1\cup V_2$, then we have ${\gamma }_{tR}(G\times H)>4$. On the other hand, if at least one of $(g,h^{\prime })$ and $(g^{\prime },h)$ has label 0, then there exists a vertex of label 2 different than $(g,h)$ and $(g^{\prime },h^{\prime })$, meaning that ${\gamma }_{tR}(G\times H)>4$ again and $\left(ii\right)$ is done.

For $\left(iii\right)$ we start with $(\Leftarrow )$. We know from $\left(i\right)$ and $\left(ii\right)$ that ${\gamma }_{tR}(G\times H)\ge 6$ whenever at least one of G and H contains more than two vertices, which is true in all three cases. Suppose first that each G and H have at least two universal vertices $g,g^{\prime }$ and $h,h^{\prime }$, respectively, and are of order at least three. If we set $V_2=\{(g,h),(g^{\prime },h^{\prime })\}$, $V_1=\{(g,h^{\prime }),(g^{\prime },h)\}$ and $V_0=V\left(G\right)-(V_1\cup V_2)$, then $f_1=(V_0,V_1,V_2)$ is a total Roman dominating function with $\omega \left(f\right)=6$. Assume now that one factor, say H, is $K_2$ and that G contains at least three vertices together with a universal vertex g. For $V\left(H\right)=\{h,h^{\prime }\}$ we define $f_2=(V_0^{\prime },V_1^{\prime },V_2^{\prime })$ by making $V_2^{\prime }=\{(g,h),(g,h^{\prime })\}$, $V_1^{\prime }=\{(g^{\prime },h^{\prime }),(g^{\prime },h)\}$ and $V_0^{\prime }=V\left(G\right)-(V_1\cup V_2)$ for an arbitrary neighbor $g^{\prime }$ of g in G. It is easy to check that $f_2$ is a total Roman dominating function with $\omega \left(f_2\right)=6$. The third possibility is that both G and H are triangle centered graphs with central triangles $g_1{g}_2{g}_3$ and $h_1{h}_2{h}_3$, respectively. We define $V_2^{″}=\{(g_1,h_1),(g_2,h_2),(g_3,h_3)\}$, $V_1^{″}=Ø$ and $V_0^{″}=V\left(G\right)-V_2$. We will show that $f_3=(V_0^{″},V_1^{″},V_2^{″})$ is a total Roman dominating function. First notice that $V_2$ induces a triangle in $G\times H$. Let $(g,h)\in V_0$. By the definition of the central triangle, g and h are adjacent to at least two vertices of $\{g_1,g_2,g_3\}$ and $\{h_1,h_2,h_3\}$, respectively. Hence, there exists $i\in \{1,2,3\}$ such that $g{g}_i\in E\left(G\right)$ and $h{h}_i\in E\left(H\right)$, and $(g,h)$ is adjacent to $(g_i,h_i)\in V_2$. Therefore, f is a total Roman dominating function on $G\times H$ with $\omega \left(f_3\right)=6$. In all three cases we have ${\gamma }_{tR}(G\times H)\le 6$ and by $\left(i\right)$ and $\left(ii\right)$ the equality ${\gamma }_{tR}(G\times H)=6$ follows.

For the opposite implication $(\Rightarrow )$ of $\left(iii\right)$ we have ${\gamma }_{tR}(G\times H)=6$ and analyze the different possibilities for the cardinalities of $V_1$ and $V_2$ for a ${\gamma }_{tR}(G\times H)$-function $f=(V_0,V_1,V_2)$. We start with $|V_1|=0$ and $|V_2|=3$ and let $(g_1,h_1),(g_2,h_2),(g_3,h_3)\in V_2$. As $V_1\cup V_2$ induces a graph without isolated vertices one vertex of these mentioned three, say $(g_2,h_2)$, must be adjacent to the other two. Hence $g_1{g}_2,g_2{g}_3\in E\left(G\right)$ and $h_1{h}_2,h_2{h}_3\in E\left(H\right)$. If $g_1{g}_3\notin E\left(G\right)$, then $(g_1,h_2)$ is a vertex of label 0 not adjacent to a vertex from $V_2$. Similar, if $h_1{h}_3\notin E\left(H\right)$, then $(g_2,h_1)$ is a vertex of label 0 not adjacent to a vertex from $V_2$. Hence $g_1{g}_2{g}_3$ and $h_1{h}_2{h}_3$ form a triangle in G and H, respectively. Suppose that there exists $g\in V\left(G\right)$ that is either adjacent to exactly one vertex of $\{g_1,g_2,g_3\}$, say to $g_1$, or to no vertex of $\{g_1,g_2,g_3\}$. In both cases we obtain $(g,h_1)$ must has label 0, and is not adjacent to any vertex of $V_1\cup V_2$, which is not possible for a total Roman dominating function f. Thus, every vertex $g\in V\left(G\right)$ must be adjacent to at least two vertices from $\{g_1,g_2,g_3\}$ and G is triangle centered. Similarly, one shows that H is triangle centered and the third option follows.

We continue with $|V_1|=2$ and $|V_2|=2$. Let $(g,h)$ and $(g^{\prime },h^{\prime })$ be vertices of label 2. Assume first that $(g,h)$ and $(g^{\prime },h^{\prime })$ are adjacent. Hence, the vertices $(g,h^{\prime })$ and $(g^{\prime },h)$ are not adjacent to $(g,h)$ nor to $(g^{\prime },h^{\prime })$ and must have label 1. All the other vertices are in $V_0$. Moreover, $V_0\ne Ø$ as the converse leads to a contradiction with f being a ${\gamma }_{tR}(G\times H)$-function. Every vertex $(g,x)$, $x\in V\left(H\right)-\{h,h^{\prime }\}$ has label 0 and is not adjacent to $(g,h)$. Therefore, they must be adjacent to $(g^{\prime },h^{\prime })$, which means that $h^{\prime }$ is a universal vertex of H. Similarly, every vertex $(g^{\prime },x)$, $x\in V\left(H\right)-\{h,h^{\prime }\}$ has label 0 and is not adjacent to $(g^{\prime },h^{\prime })$. So, they are adjacent to $(g,h)$, and h is a universal vertex of H. By symmetric arguments, also g and $g^{\prime }$ are universal vertices of G. Thus, both G and H have at least two universal vertices. If both have only two vertices, then we have a contradiction with $\left(ii\right)$. Therefore, we obtained the first possibility.

Let now $(g,h)$ and $(g^{\prime },h^{\prime })$ be nonadjacent. If they are not in the same (G- or H-) layer, then $(g,h^{\prime })$ and $(g^{\prime },h)$ are not adjacent to $(g,h)$ nor to $(g^{\prime },h^{\prime })$ and must have label 1. All the other vertices must be in $V_0$. However, this is a contradiction because $V_1\cup V_2$ induces four isolated vertices. Hence, $(g,h)$ and $(g^{\prime },h^{\prime })$ are in the same G- or H-layer, say in $H^g$. Therefore, $g=g^{\prime }$. If there exists different $h_1,h_2\in V\left(H\right)-\{h,h^{\prime }\}$, then $(g,h_1),(g,h_2)\in V_1$, since there are no edges between vertices of $H^g$. A contradiction again, due to no existing edges between vertices of $V_1\cup V_2$. If $V\left(H\right)|=3$, say $V\left(H\right)=\{h,h^{\prime },h_1\}$, then $f(g,h_1)=1$ and the other vertex $(a,b)$ from $V_1$ must be adjacent to all three vertices from $H^g$. This is not possible as $(a,b)$ is contained in one of the layers $G^h$, $G^{h^{\prime }}$ or $G^{h_1}$. Again, we have a vertex from $V_1\cup V_2$ that is not adjacent to any other vertex of $V_1\cup V_2$, a contradiction. Therefore, H contains only two vertices h and $h^{\prime }$, which are adjacent and therefore both universal vertices. If both vertices from $V_1$ belong to the same G-layer, say $G^h$, then $(g,h)$ is not adjacent to any vertex from $V_1\cup V_2$, which is not possible. Therefore, we may assume that $V_1=\{(g_1,h),(g_2,h^{\prime })\}$. Clearly $g{g}_1,g{g}_2\in E\left(G\right)$, so that $V_1\cup V_2$ induces a subgraph without isolated vertices. Also every vertex $(g_3,h)\in V_0$ must be adjacent to $(g,h^{\prime })$, which means that $g{g}_3\in E\left(G\right)$ and g is an universal vertex of G. (Notice also that in the case when $g_1=g_2$, there always exists $g_3\in V\left(G\right)-\{g,g_1\}$, because otherwise we have a contradiction with $\left(ii\right)$.) This yields the middle case of $\left(iii\right)$.

To end with $\left(iii\right)$ let $|V_1|=4$ and $|V_2|=1$, where $V_2=\left\{(g,h)\right\}$. Let $(g^{\prime },h^{\prime })\in V_1$ be a neighbor of $(g,h)$. Clearly all vertices from $G^h\cup H^g$ must be in $V_1\cup V_2$, meaning that one of the factors is $K_2$ and the other contains three vertices, say $H\cong K_2$. Moreover, g must be a universal vertex of G. Therefore, either $G\cong C_3$ or $G\cong P_3$, which is the middle case of $\left(iii\right)$ and the proof of $\left(iii\right)$ is completed.

We continue with $(\Leftarrow )$ of $\left(iv\right)$. We may assume that G has exactly one universal vertex g, and that H is different from $K_2$ with a universal vertex h, and that at most one of G and H is triangle centered. Furthermore, let $g^{\prime }$ and $h^{\prime }$ be arbitrary neighbors of g in G and of h in H, respectively. By $\left(i\right),\left(ii\right)$ and $\left(iii\right)$ we know that ${\gamma }_{tR}(G\times H)\ge 7$. If we set $V_2=\{(g,h),(g,h^{\prime }),(g^{\prime },h)\}$, $V_1=\left\{(g^{\prime },h^{\prime })\right\}$ and $V_0=V(G\times H)-(V_1\cup V_2)$, then $f=(V_0,V_1,V_2)$ is a total Roman dominating function with $\omega \left(f\right)=7$. Hence, ${\gamma }_{tR}(G\times H)\le 7$ and the equality follows.

For $(\Rightarrow )$ of $\left(iv\right)$, suppose that ${\gamma }_{tR}(G\times H)=7$ and that $f=(V_0,V_1,V_2)$ is a ${\gamma }_{tR}(G\times H)$-function. First assume that $|V_1|=1$ and $|V_2|=3$, where $V_1=\left\{(g_1,h_1)\right\}$ and $V_2=\{(g_2,h_2),(g_3,h_3),(g_4,h_4)\}$. We may also assume that $(g_1,h_1)(g_2,h_2),(g_3,h_3)(g_4,h_4)\in E(G\times H)$ as f is a ${\gamma }_{tR}(G\times H)$-function. Vertices $(g_3,h_4)$ and $(g_4,h_3)$ are not adjacent to $(g_3,h_3)$ nor to $(g_4,h_4)$. If $g_3\ne g_2\ne g_4$, then $(g_2,h_2)$ is adjacent to both $(g_3,h_4)$ and $(g_4,h_3)$ (even if one of them equals to $(g_1,h_1)$). As a consequence, we have $g_2{g}_3,g_2{g}_4\in E\left(G\right)$ and $h_2{h}_3,h_2{h}_4\in E\left(H\right)$. In other words, $g_2{g}_3{g}_4$ and $h_2{h}_3{h}_4$ form a triangle in G and H, respectively. Let g be an arbitrary vertex from $V\left(G\right)-\{g_2,g_3,g_4\}$ and let h be an arbitrary vertex from $V\left(H\right)-\{h_2,h_3,h_4\}$. The vertex $(g,h)$ is adjacent to at least one vertex from $V_2$ (even if $(g,h)=(g_1,h_1)$). Let $(g_i,h_i)$ be a neighbor of $(g,h)$ for some $i\in \{2,3,4\}$. Clearly, $(g_i,h)$ and $(g,h_i)$ are not adjacent to $(g_i,h_i)$. Hence they must be adjacent to $(g_j,h_j)$ for some $j\in \{2,3,4\}-\left\{i\right\}$, meaning that $g{g}_j\in E\left(G\right)$ and $h{h}_j\in E\left(H\right)$. We see that both G and H are triangle centered graphs, and by $\left(iii\right)$ we have ${\gamma }_{tR}(G\times H)=6$, a contradiction with ${\gamma }_{tR}(G\times H)=7$.

So, we can assume that either $g_2=g_3$ or $g_2=g_4$, say that $g_2=g_3$. Moreover, also $h_2=h_4$ as otherwise $(g_2,h_4)$ has no neighbor of label 2. If $h_2$ is not adjacent to some vertex $h\in V\left(H\right)$, then $(g_2,h)$ is not adjacent to a vertex of label 2, meaning that $h_2$ is a universal vertex of H. Similarly, we see that $g_2$ is a universal vertex of G. We have ${\gamma }_{tR}(G\times H)=6$ by $\left(iii\right)$ when both G and H have (at least) two universal vertices, or one is $K_2$ and the other contains a universal vertex, a contradiction. Hence, one of G or H has at most one universal vertex and the other is not $K_2$ and we are done in this case.

The second possibility is that $|V_1|=3$ and $|V_2|=2$, where $V_1=\{(g_1,h_1),(g_2,h_2),(g_3,h_3)\}$ and $V_2=\{(g_4,h_4),(g_5,h_5)\}$. If $(g_4,h_4)$ and $(g_5,h_5)$ are adjacent, then $(g_4,h_5),(g_5,h_4)\in V_1$, say $(g_4,h_5)=(g_2,h_2)$ and $(g_5,h_4)=(g_3,h_3)$. Suppose that $g_1\notin \{g_4,g_5\}$ and $h_1\notin \{h_4,h_5\}$. All the vertices of $G^{h_4}-\{(g_4,h_4),(g_5,h_4)\}$ must be in $V_0$ and adjacent to $(g_5,h_5)$, meaning that $g_5$ is a universal vertex of G. Similarly, all the vertices of $G^{h_5}-\{(g_4,h_5),(g_5,h_5)\}$ must be in $V_0$ and adjacent to $(g_4,h_4)$, meaning that $g_4$ is a universal vertex of G. This means that G is triangle centered with central triangle $g_1{g}_4{g}_5$. By symmetric arguments H is triangle centered with central triangle $h_1{h}_4{h}_5$. By $\left(iii\right)$ we have ${\gamma }_{tR}(G\times H)=6$, a contradiction. Therefore, either $h_1\in \{h_4,h_5\}$ or $g_1\in \{g_4,g_5\}$, say $h_1=h_4$. By the same arguments as above, we see that $g_4$ is a universal vertex of G, and that $h_4$ and $h_5$ are universal vertices of H. (Notice that $g_1$ is not adjacent to $g_5$, otherwise also $g_5$ is universal vertex, a contradiction with $\left(iii\right)$.) If $H\cong K_2$, then we have ${\gamma }_{tR}(G\times H)=6$ by $\left(iii\right)$, a contradiction. Otherwise $H\ncong K_2$ and we are done.

Now we can assume that $(g_4,h_4)$ and $(g_5,h_5)$ are not adjacent. If $g_4\ne g_5$ and $h_4\ne h_5$, then, as in the previous paragraph, we can choose the notation such that $(g_4,h_5)=(g_2,h_2)$ and that $(g_5,h_4)=(g_3,h_3)$. Moreover, $(g_1,h_1)$ must be adjacent to all other vertices from $V_1\cup V_2$ to avoid isolated vertices of positive label. Vertices $(g_5,h_1)$ and $(g_1,h_4)$ are from $V_0$ and must have a neighbor in $V_2$. The only possibility is that $(g_5,h_1)$ is adjacent to $(g_4,h_4)$ and $(g_1,h_4)$ is adjacent to $(g_5,h_5)$. The mentioned edges imply that $g_4{g}_5\in E\left(G\right)$ and $h_4{h}_5\in E\left(H\right)$, a contradiction with the not adjacency of $(g_4,h_4)$ and $(g_5,h_5)$. It remains that $(g_4,h_4)$ and $(g_5,h_5)$ belong to the same layer, say $H^{g_4}$, i.e., $g_4=g_5$. Every vertex from $H^{g_4}-\{(g_4,h_4),(g_4,h_5)\}$ is not adjacent to a vertex of label 2 and must poses label 1. We need also at least two vertices of label 1 outside of $H^{g_4}$ to assure non-isolated vertices in $V_1\cup V_2$. This means that $\left|V\right(H\left)\right|\le 3$. Every vertex from $G^{h_4}-\left\{(g_4,h_4)\right\}$ must be adjacent to $(g_4,h_5)$ and $g_4$ is a universal vertex of G. If $H\cong K_2$, then we have a contradiction with $\left(iii\right)$. So, either $H\cong P_3$ or $H\cong C_3$, meaning that also H has a universal vertex and the second possibility is done.

The last option is that $|V_1|=5$ and $|V_2|=1$, where $V_2=\left\{(g,h)\right\}$. Clearly all vertices from $G^h\cup H^g$ must be in $V_1\cup V_2$ and g and h must be universal vertices of G and H, respectively. We either obtain a contradiction with $\left(iii\right)$ (when one factor is $K_2$) or obtain that $G\cong H\cong K_{1,2}$ which yields the desired situation and the proof of $\left(iv\right)$ is completed.

We conclude this proof with $\left(v\right)$. We have ${\gamma }_{tR}(G\times H)\ge 8$ from assertions $\left(i\right)-\left(iv\right)$. Let $D_G=\{g,g^{\prime }\}$ be a ${\gamma }_t\left(G\right)$-set and $D_H=\{h,h^{\prime }\}$ be a ${\gamma }_t\left(H\right)$-set. We set $V_2=D_G\times D_H$, $V_1=Ø$ and $V_0=V(G\times H)-V_2$ and claim that $f=(V_0,V_1,V_2)$ is a total Roman dominating function on $G\times H$. Let $(g_1,h_1)\in V_0$. Clearly, $g_1$ is neighbor of g or of $g^{\prime }$, say of g, and $h_1$ is neighbor of h or $h^{\prime }$, say h. Therefore $(g_1,h_1)$ is neighbor of $(g,h)$ and f satisfies the conditions to be total Roman dominating for $G\times H$. Hence, the inequality ${\gamma }_{tR}(G\times H)\le 8$ is obtained, which leads to the claimed equality. ☐

A wheel graph $W_n$, $n\ge 4$, is a join of $K_1$ and $C_{n-1}$ and a fan graph $F_n$, $n\ge 2$, is a join of $K_1$ and $P_{n-1}$. Clearly $W_n$ and $F_n$ have exactly one universal vertex when $n>4$. In particular, $W_n$ and $F_n$ are triangle centered whenever $n\in \{4,5\}$. For a complete graph $K_n$ and a maximum matching M of it, the graph $K_n-M$, $n\ge 5$, is a triangle centered graph with a universal vertex whenever n is an odd number. By using Theorem 4 we directly obtain the next results (among others).

Corollary 6.

For integers $n,m>5$, $p\ge 1$, $q,s,t\ge 2$, $r>2$ and maximum matchings M and $M^{\prime }$ we have

(i) 

${\gamma }_{tR}(K_r\times K_s)=6$;

(ii) 

${\gamma }_{tR}(K_{1,s}\times K_{1,t})=7$;

(iii) 

${\gamma }_{tR}(K_{p,q}\times K_{s,t})=8$;

(iv) 

${\gamma }_{tR}(K_q\times K_{s,t})=8$;

(v) 

${\gamma }_{tR}(K_r\times W_n)=7$;

(vi) 

${\gamma }_{tR}(K_r\times F_n)=7$;

(vii) 

${\gamma }_{tR}(W_n\times F_m)=8$;

(viii) 

${\gamma }_{tR}(W_n\times W_m)=8$;

(ix) 

${\gamma }_{tR}(F_n\times F_m)=8$;

(x) 

${\gamma }_{tR}((K_n-M)\times (K_m-M^{\prime }))=6$.

With the help from Corollary 6, we can comment the sharpness for most of the bounds from Section 2. The upper bounds of Theorem 1, of Corollary 1 and of Remark 1 are sharp by $\left(ii\right)$ of Corollary 6. For instance that is, since the total Roman domination number of any star on at least two leaves is 3, with total Roman dominating functions of minimum weight assigning 2 to the center of the star, 1 to one of its leaves and 0 otherwise, we obtain that ${\gamma }_{tR}(K_{1,s}\times K_{1,t})={\gamma }_{tR}\left(H\right){\gamma }_{tR}\left(G\right)-2|A_2\left|\right|B_2|=7$, by using the notations of Theorem 1. For the remaining cases, similar computations can be easily made, as well as, for the next remarked tightness situations. The upper bound from Corollary 2 is sharp by $\left(iii\right),\left(iv\right),\left(vii\right),\left(viii\right)$ and $\left(ix\right)$ of Corollary 6. For $p=q=s=t=2$ we have ${\gamma }_{tR}(K_{2,2}\times K_{2,2})={\gamma }_{tR}(C_4\times C_4)=8$ by $\left(iii\right)$ of Corollary 6, and so for Corollary 4, its upper bound is sharp. The lower bound from Theorem 1 follows from ${\gamma }_{tR}(P_4\times P_4)=8=\rho \left(P_4\right){\gamma }_{tR}\left(P_4\right)$ which holds by $\left(v\right)$ of Theorem 4. By $\left(iii\right)$ of Corollary 6, we show the sharpness of the bounds from Theorems 2 and 3 and Corollary 3. In conclusion, only the tightness of the bound presented in Corollary 5 remains open.

We end this section with an alternative presentation with respect to Theorem 4, where we consider the number of vertices in $V_1\cup V_2$ of a total Roman dominating function. For the minimum cardinality of $V_1\cup V_2$, we need an additional condition that the cardinality of $V_2$ must be maximum to be able to characterize them.

Theorem 5.

Given two graphs G and H of orders at least three, the next items are equivalent.

(i) 

Graphs G and H are triangle centered.

(ii) 

${\gamma }_{tR}(G\times H)=6$.

(iii) 

For any ${\gamma }_{tR}(G\times H)$-function $f=(V_0,V_1,V_2)$ with the largest possible cardinality for $V_2$, it follows $|V_1\cup V_2|=3$.

Proof. 

The direction $\left(\right(i)\Rightarrow (ii\left)\right)$ follows from $\left(iii\right)$ of Theorem 4.

For the direction $\left(\right(ii)\Rightarrow (iii\left)\right)$, let ${\gamma }_{tR}(G\times H)=6$ where $f=(V_0,V_1,V_2)$ is a ${\gamma }_{tR}(G\times H)$-function with maximum cardinality of $V_2$. There exist vertices from $G\times H$ in $V_0$ as there are at least nine vertices in $G\times H$. Consequently $V_2\ne Ø$. Let $(g,h)\in V_2$ and let $(g^{\prime },h^{\prime })$ be a neighbor of $(g,h)$ with $f(g^{\prime },h^{\prime })>0$. There exists at least one vertex $(x,y)$ from $(G^h\cup H^g)-\left\{(g,h)\right\}$ of label 0, because ${\gamma }_{tR}(G\times H)=6$. Suppose that $(g^{″},h^{″})$ is a neighbor of $(x,y)$ of label 2. Assume first that $(g^{\prime },h^{\prime })=(g^{″},h^{″})$. The vertices $(g^{\prime },h)$ and $(g,h^{\prime })$ are not adjacent to $(g^{\prime },h^{\prime })$ nor to $(g,h)$. If they have label equal to 1, then all the other vertices have label 0 and every vertex is adjacent to $(g,h)$ or to $(g^{\prime },h^{\prime })$. Let $g_1$ and $h_1$ be a third vertex of G and H, respectively. Clearly, $(g_1,h^{\prime })$ and $(g^{\prime },h_1)$ are adjacent to $(g,h)$ and with this, we have $g{g}_1\in E\left(G\right)$ and $h{h}_1\in E\left(H\right)$. Similarly, $(g,h_1)$ and $(g_1,h)$ are adjacent to $(g^{\prime },h^{\prime })$, and with this we get $g^{\prime }{g}_1\in E\left(G\right)$ and $h^{\prime }{h}_1\in E\left(H\right)$. Let us define $f^{\prime }=(V_0^{\prime },V_1^{\prime },V_2^{\prime })$ where $V_0^{\prime }=(V_0\cup V_1)-\left\{(g_1,h_1)\right\}$, $V_1^{\prime }=Ø$ and $V_2^{\prime }=V_2\cup \left\{(g_1,h_1)\right\}$. Clearly, $f^{\prime }$ is a total Roman dominating function with $|V_2^{\prime }|>|V_2|$, a contradiction with the choice of f. Therefore, the label of $(g^{\prime },h)$ and $(g,h^{\prime })$ must be 0 and there exists a third vertex $(g_2,h_2)$ of label 2 that is adjacent to $(g^{\prime },h)$ and $(g,h^{\prime })$. From ${\gamma }_{tR}(G\times H)=6$ it follows that $|V_1\cup V_2|=3$.

Next we assume that $(g^{\prime },h^{\prime })\ne (g^{″},h^{″})$. If also $f(g^{\prime },h^{\prime })=2$, then $V_2=\{(g,h),(g^{\prime },h^{\prime }),(g^{″},h^{″})\}$ and $V_1=Ø$ and we are done. So, let $f(g^{\prime },h^{\prime })=1$. Because ${\gamma }_{tR}(G\times H)=6$ there exists a fourth vertex $(a,b)$ in $V_1\cup V_2$ with $f(a,b)=1$ and all other vertices are in $V_0$. Vertex $(g^{″},h^{″})$ is not from $G^h\cup H^g$, because $V_2$ contains only $(g,h)$ and $(g^{″},h^{″})$ and we have at least three vertices in every G- or H-layer. Hence, $g\ne g^{″}$ and $h\ne h^{″}$. Vertices $(g,h^{″})$ and $(g^{″},h)$ are not adjacent to $(g,h)$ nor to $(g^{″},h^{″})$, and must therefore have label 1. This leads to $\{(g^{″},h),(g,h^{″})\}=\{(g^{\prime },h^{\prime }),(a,b)\}$, and this is not possible since $(g^{\prime },h^{\prime })$ is adjacent to $(g,h)$. Hence, $|V_1\cup V_2|=3$ in all cases and this implication is done.

$\left(\right(iii)\Rightarrow (i\left)\right)$ Let $|V_1\cup V_2|=3$ and let $(g_1,h_1),(g_2,h_2),(g_3,h_3)\in V_1\cup V_2$. As $V_1\cup V_2$ induces a graph without isolated vertices, one vertex of these mentioned three, say $(g_2,h_2)$, must be adjacent to the other two. Thus, $g_1{g}_2,g_2,g_1\in E\left(G\right)$ and $h_1{h}_2,h_2,h_3\in E\left(H\right)$. If $g_1{g}_3\notin E\left(G\right)$, then $(g_1,h_2)$ is a vertex that is labeled with 0 being not neighbor of a vertex belonging to $V_2$. Similarly, if $h_1{h}_3\notin E\left(H\right)$, then $(g_2,h_1)$ is a vertex whose label is equal to 0 being not neighbor of one vertex from $V_2$. Hence $g_1{g}_2{g}_3$ and $h_1{h}_2{h}_3$ form a triangle in G and H, respectively. Suppose there is a vertex $g\in V\left(G\right)$ which is either neighbor of exactly one vertex of $\{g_1,g_2,g_3\}$, say to $g_1$, or to no vertex of $\{g_1,g_2,g_3\}$. In both cases the vertex $(g,h_1)$ has label 0 and is not adjacent to any vertex of $V_1\cup V_2$, which is not possible since f is a function which is total Roman dominating. Hence, every vertex $g\in V\left(G\right)$ is adjacent to two or more vertices from $\{g_1,g_2,g_3\}$ and G is triangle centered. Similarly, one shows that H is triangle centered. ☐

4. A General Lower Bound and Its Consequences on the Direct Product

The following lower bound for ${\gamma }_{tR}\left(G\right)$ depends on the order of G and its maximum degree $\Delta \left(G\right)$ as well as on a ${\gamma }_{tR}\left(G\right)$-function.

Theorem 6.

If $f=(V_0,V_1,V_2)$ is a ${\gamma }_{tR}\left(G\right)$-function of a graph G, then ${\gamma }_{tR}\left(G\right)\ge \left|V\left(G\right)\right|-(\Delta \left(G\right)-2)|V_2|$ and $|V_2|\ge \frac{\left|V\left(G\right)\right|-|V_1|}{\Delta \left(G\right)}$. Moreover, if in addition $\left|V\left(G\right)\right|=\Delta \left(G\right)|V_2|+|V_1|$, then the equality ${\gamma }_{tR}\left(G\right)=\left|V\left(G\right)\right|-(\Delta \left(G\right)-2)|V_2|$ holds.

Proof. 

Assume $g=(V_0,V_1,V_2)$ is a ${\gamma }_{tR}\left(G\right)$-function. Every vertex from $V_2$ must have one neighbor in $V_1\cup V_2$. This means that every vertex from $V_2$ has no more than $\Delta \left(G\right)-1$ adjacent vertices in $V_0$. With this we have

$$\left|V\left(G\right)\right|=|V_0|+|V_1|+|V_2|\le (\Delta \left(G\right)-1)|V_2|+|V_1|+|V_2|.$$

(2)

From (2) we extract $|V_2|$ and obtain the second inequality

$$|V_2|\ge \frac{\left|V\left(G\right)\right|-|V_1|}{\Delta \left(G\right)}.$$

Notice that from (2), it follows $|V_2|$ is maximum when $|V_1|=0$. Now we return to (2), and add $0=|V_2|-|V_2|$ on the right side to get

$$\left|V\left(G\right)\right|\le (\Delta \left(G\right)-2)|V_2|+2|V_2|+|V_1|=|V_2|(\Delta \left(G\right)-2)+{\gamma }_{tR}\left(G\right),$$

(3)

that yields the first inequality. Notice that from the additional condition $\left|V\left(G\right)\right|=\Delta \left(G\right)|V_2|+|V_1|$ we get

$$|V_0|+|V_1|+|V_2|=|V\left(G\right)|=\Delta \left(G\right)|V_2|+|V_1|$$

and consequently $|V_0|=(\Delta \left(G\right)-1)|V_2|$. This connection gives the equality in the lines (2) and (3) and the proof is completed. ☐

With respect to the condition $\left|V\left(G\right)\right|=\Delta \left(G\right)|V_2|+|V_1|$ in the theorem above, we see that there are several graphs satisfying it. For instance, consider a graph $G_k$, with $k\ge 3$, obtained as follows. We begin with a set of k disjoint stars $K_{1,k}$ on k leaves. Next, we add some edges between pairs of leaves belonging to different stars such that every leaf from all the stars will have at most one new neighbor. Observe that $G_k$ has maximum degree $\Delta \left(G_k\right)=k$ and that $|V\left(G_k\right)|=k(k+1)$. Also, we observe that a function $f=(V_0,V_1,V_2)$ that assigns 2 to the centers of the stars ($|V_2|=k$), 1 to exactly one neighbor of each center of the stars ($|V_1|=k$), and 0 otherwise, is a ${\gamma }_{tR}\left(G_k\right)$-function. Thus, $|V\left(G_k\right)|=k(k+1)=\Delta \left(G_k\right)|V_2|+|V_1|$.

If we rewrite the Theorem 6 for the direct product $G\times H$, then we have the following.

Corollary 7.

Let G and H be any two graphs. If $f=(V_0^{\prime },V_1^{\prime },V_2^{\prime })$ is a ${\gamma }_{tR}(G\times H)$-function, then ${\gamma }_{tR}(G\times H)\ge \left|V\left(G\right)\right|\left|V\left(H\right)\right|-(\Delta \left(H\right)\Delta \left(G\right)-2)|V_2^{\prime }|$ and $|V_2^{\prime }|\ge \frac{\left|V\left(G\right)\right|\left|V\left(H\right)\right|-|V_1^{\prime }|}{\Delta \left(H\right)\Delta \left(G\right)}$. Moreover, if in addition $\left|V\left(G\right)\right|\left|V\left(H\right)\right|=\Delta \left(H\right)\Delta \left(G\right)|V_2^{\prime }|+|V_1^{\prime }|$, then the equality ${\gamma }_{tR}(G\times H)=\left|V\left(G\right)\right|\left|V\left(H\right)\right|-(\Delta \left(H\right)\Delta \left(G\right)-2)|V_2^{\prime }|$ holds.

The lower bound from Theorem 6 is better when $|V_2|$ is small as possible. Also, one cannot expect that the mentioned bound behave well when there exists a small quantity of vertices with maximum number of neighbors in G. From this point of view, one can expect that Theorem 6 works at its best for regular graphs. To see this, the following known remark is necessary.

Remark 2. 

([21]) If S is an efficient open dominating set of an efficient open domination graph G, then S is a ${\gamma }_t\left(G\right)$-set.

Theorem 7.

If G is a regular efficient open domination graph, then ${\gamma }_{tR}\left(G\right)=2{\gamma }_t\left(G\right)$.

Proof. 

Let D be an efficient open dominating set of an r-regular graph G. By Remark 2 we have that D is a ${\gamma }_t\left(G\right)$-set. Hence, $f=(V_0,V_1,V_2)=(V\left(G\right)-D,Ø,D)$ is a total Roman dominating function on G of weight $\omega \left(f\right)=2{\gamma }_t\left(G\right)$ that clearly fulfills the condition $\left|V\left(G\right)\right|=\Delta \left(G\right)|V_2|+|V_1|=r|D|$. By Theorem 6 the result follows. ☐

For two graphs G and H, its direct product $G\times H$ represents an efficient open domination graph whenever both G and H contain efficient open dominating sets. This was proved in [22]. Moreover, for the two efficient open dominating sets $D_G$ and $D_H$ of G and H, respectively, the set $D_G\times D_H$ is an efficient open dominating set of $G\times H$. Hence we have the following result.

Corollary 8.

If G and H are regular graphs and they are also efficient open domination graphs, then ${\gamma }_{tR}(G\times H)$ = $2{\gamma }_t\left(H\right){\gamma }_t\left(G\right)$.

The relaxation of Corollary 8 and Theorem 7 without the condition of regular graphs is not true anymore as shown by $\left(ii\right)$ of Corollary 6. Clearly $K_{1,s}$ and $K_{1,t}$ are efficient open domination graphs that are not regular and we have ${\gamma }_{tR}(K_{1,s}\times K_{1,t})=7\ne 8=2{\gamma }_t\left(K_{1,s}\right){\gamma }_t\left(K_{1,t}\right)$.

A prism $P_G$ over a graph G is a graph obtained from two disjoint copies of the graph G by adding a perfect matching between analogous vertices of each copy (or the Cartesian product $G\square K_2$). All the prisms that are efficient open domination graphs are described in Theorem 4.3 from [21]. One 3-regular example is $P_{C_{3r}}$ and for them we have ${\gamma }_t\left(P_{C_{3r}}\right)=2r$.

It is well known that a cycle $C_n$ contains an efficient open dominating set whenever n is congruent with 0 modulo 4. Thus, the next result is clear by Corollary 8.

Corollary 9.

If m and n are positive integers divisible by 4 and $t\ge 2$ and $r\ge 1$ are any integers, then

(i) 

${\gamma }_{tR}(C_m\times C_n)=\frac{mn}{2}$;

(ii) 

${\gamma }_{tR}(C_m\times K_{t,t})=2m$;

(iii) 

${\gamma }_{tR}(C_m\times P_{C_{3r}})=2mr$;

(iv) 

${\gamma }_{tR}(K_{t,t}\times P_{C_{3r}})=8r$.