A Comparative Study of the Fractional-Order Clock Chemical Model
Abstract
1. Introduction, Definitions and Preliminaries
2. The Fractional-Order Logistic Equation
3. The Spectral Collocation Method (SCM)
4. Runge-Kutta Methods
4.1. Two-Stage Fractional Runge-Kutta Method
4.2. Four-Stage Fractional Runge-Kutta
5. Numerical Results and Discussion
- In Table 1, we notice that the order of the errors are small in all of the methods used here. Additionally, in the cases of the SCM and the FSFRK methods are much better than those in the cases of the TSFR and the LPI methods.
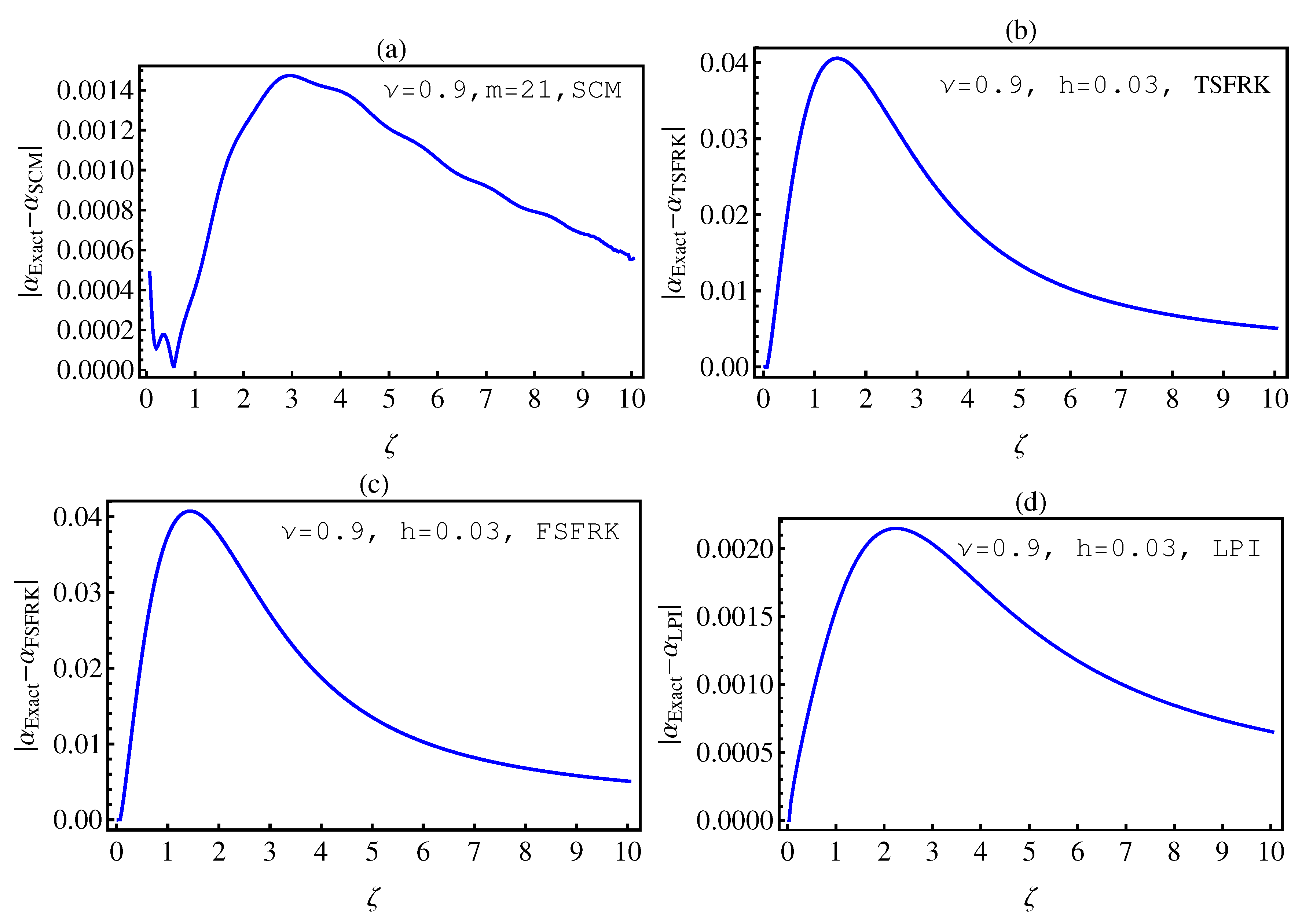
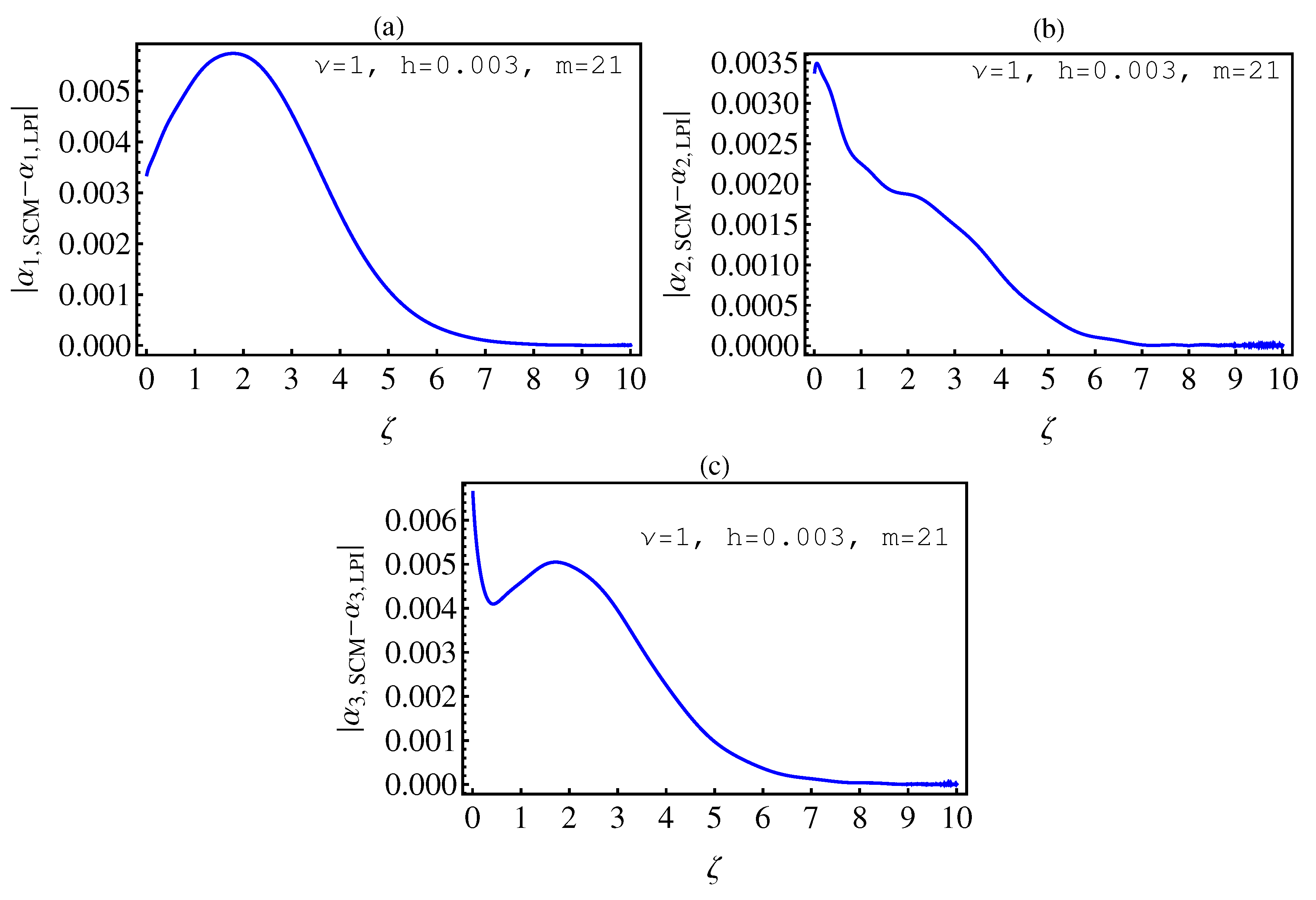
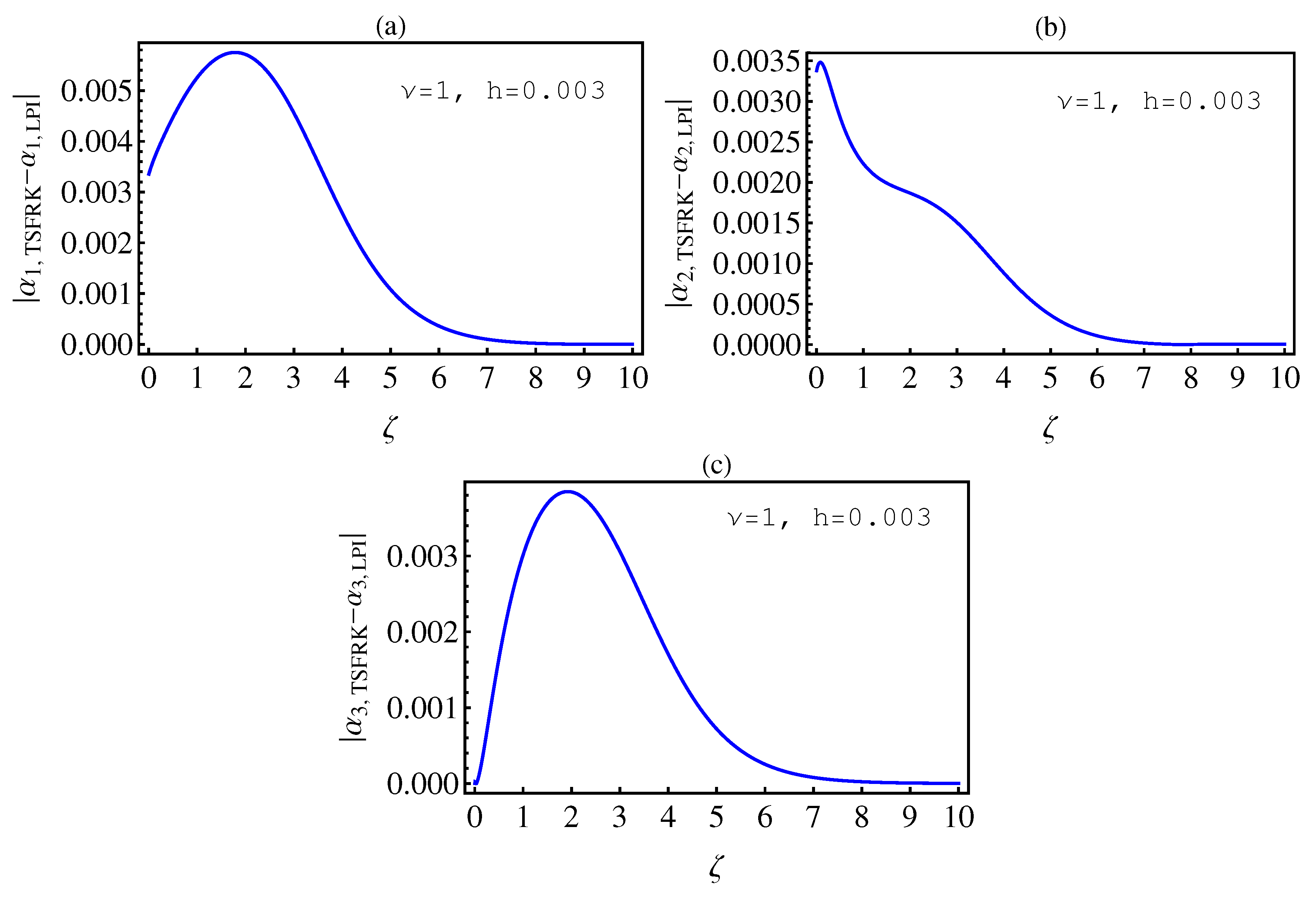
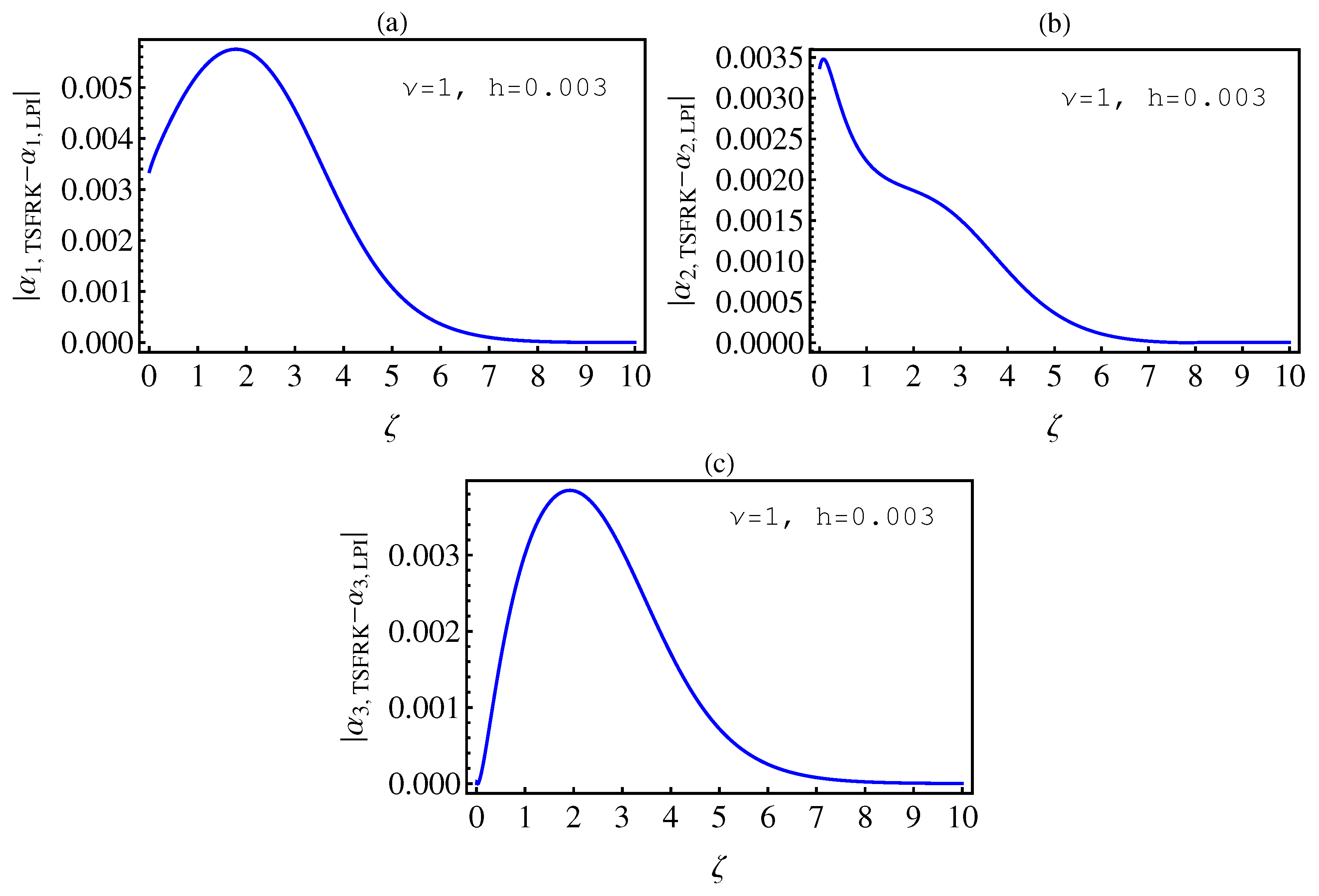
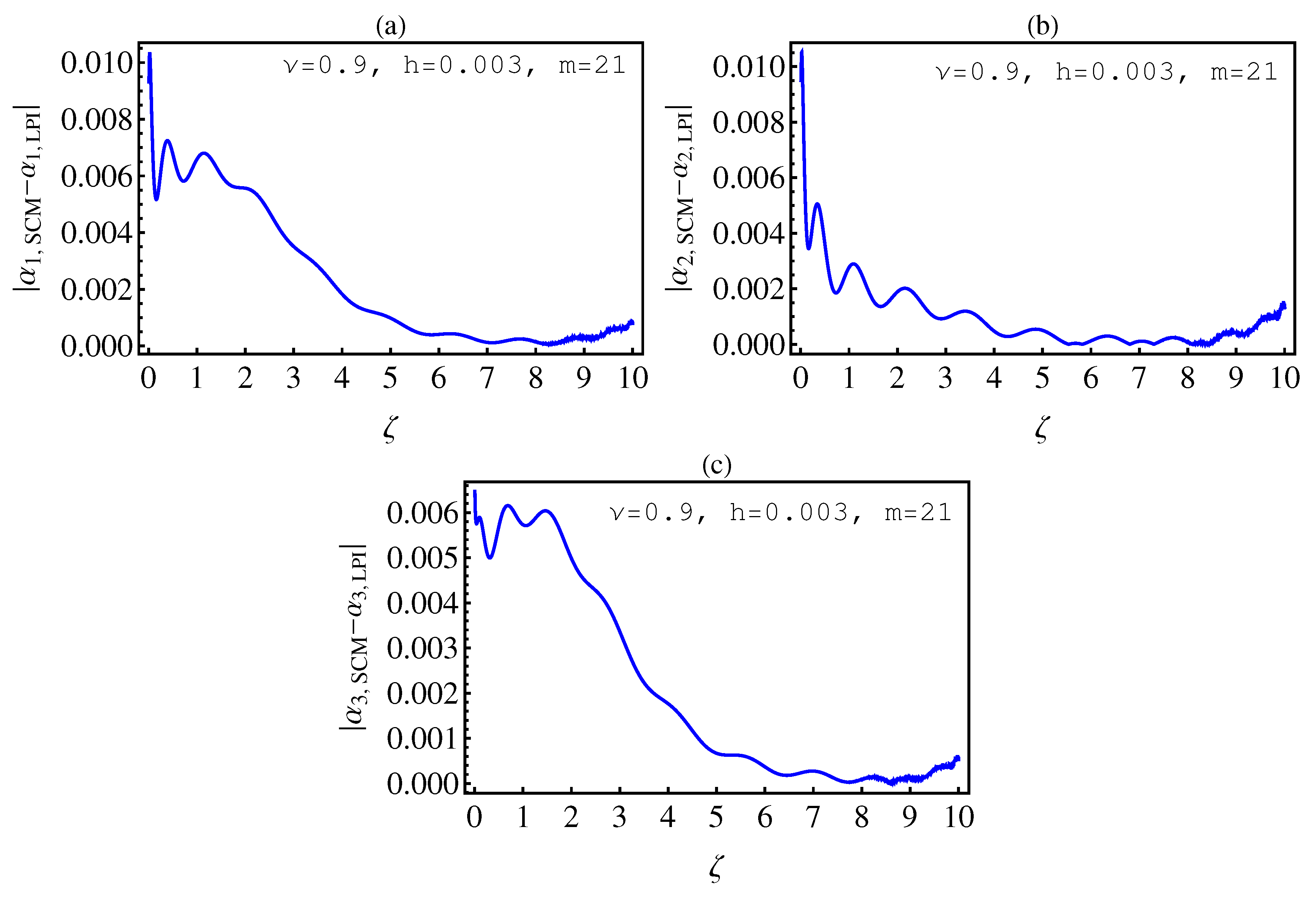
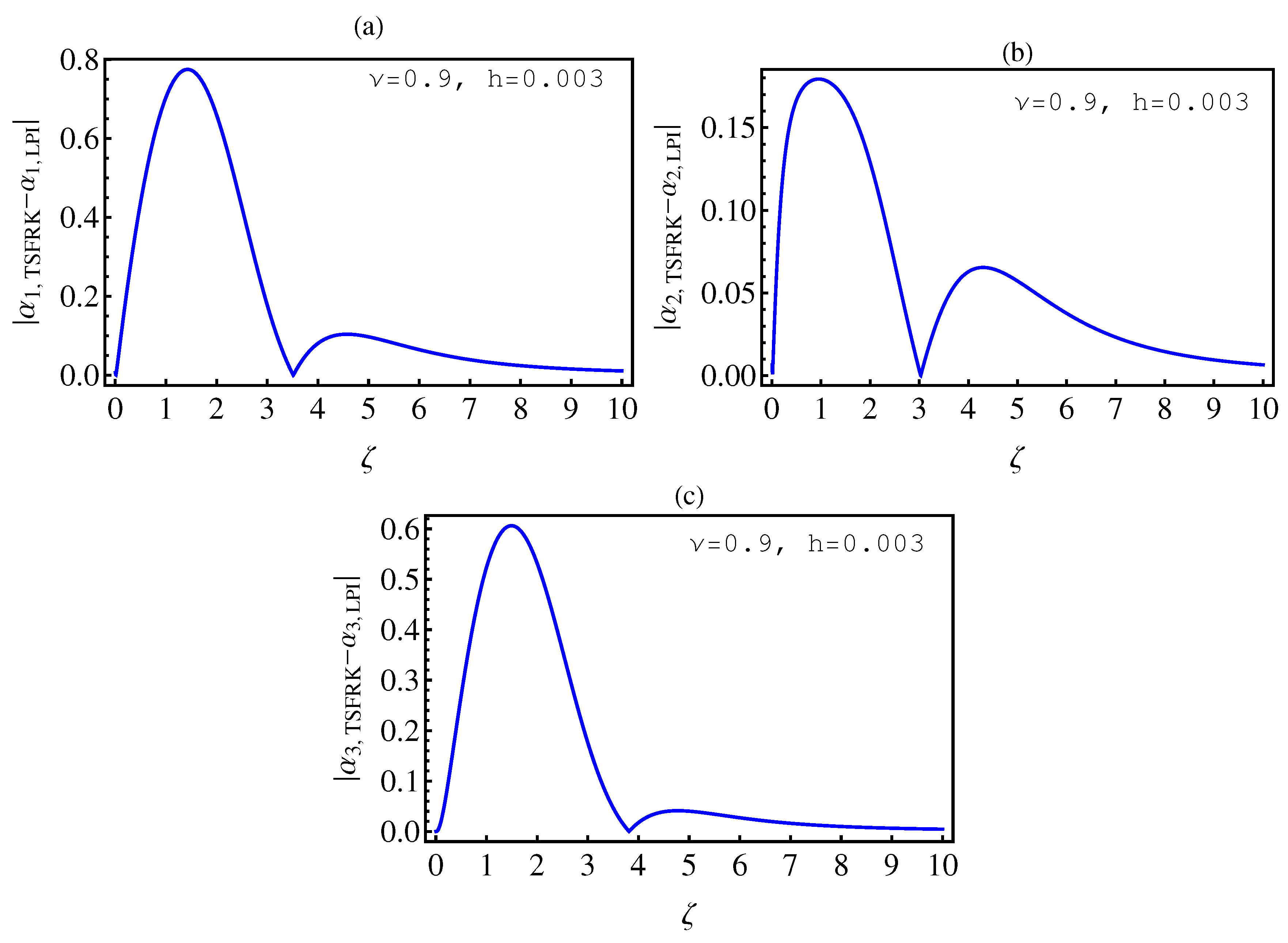
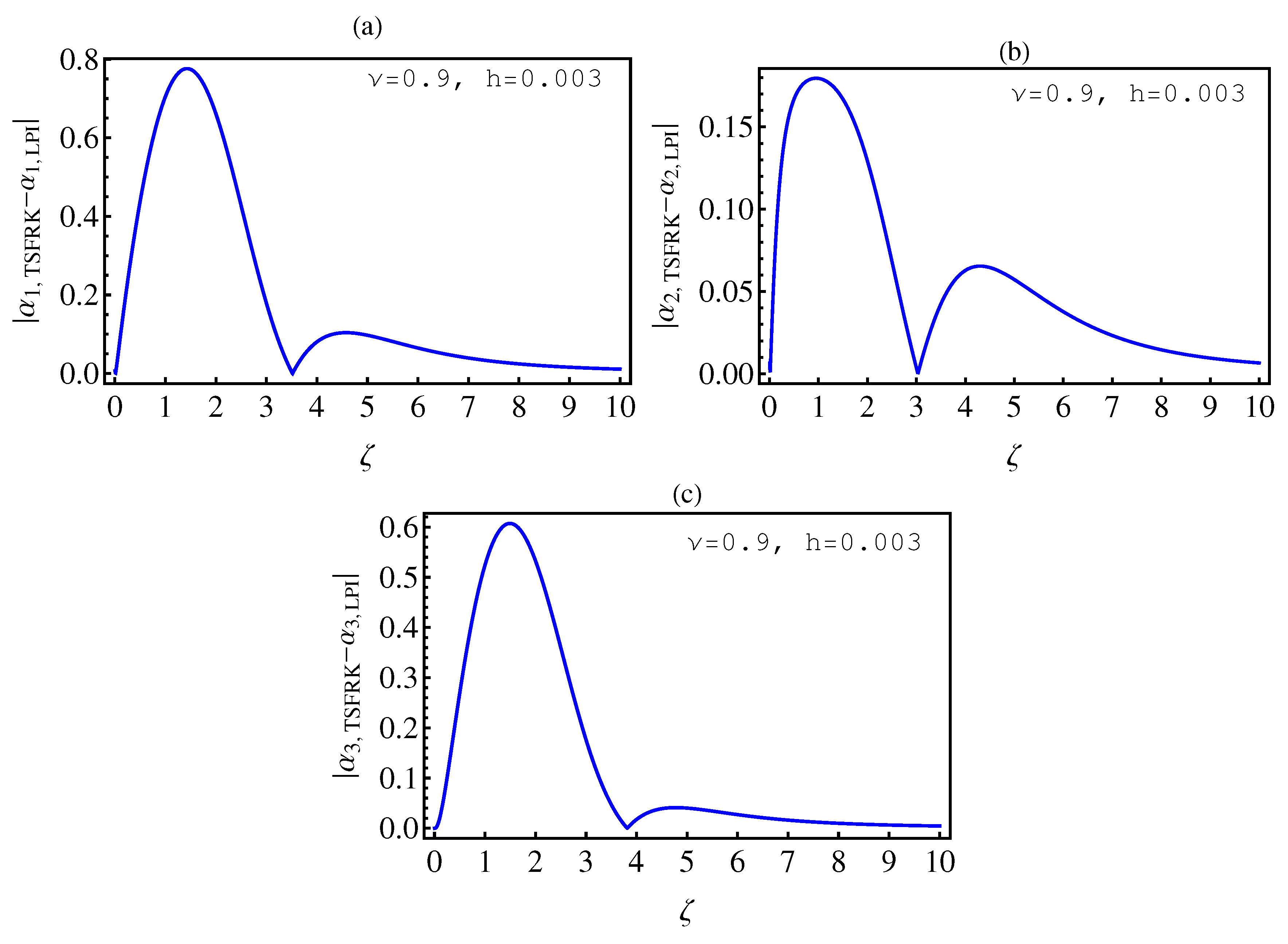
- In Table 2, we see that the orders of the errors for all of the methods are close to each other. However, the SCM and LPI methods are better than the TSFRK and FSFRK methods. Therefore, we cannot say here that one of the methods is the best absolutely, but we can say that some of the methods are better than the other methods. In Figure 3, Figure 4 and Figure 5, we compute the absolute error between LPI and SCM, TSFRK, and FSFRK, respectively. In these figures, we set and the initial values are set as and From these figures, we observe that the order of the error for the SCM, TSFRK, and FSFRK methods is . In Figure 6, Figure 7 and Figure 8, we find the absolute error for the same caption as those of Figure 3, Figure 4 and Figure 5, but with In the non-integer order, we have obtained the same results, as illustrated in Figure 2. The order of the error of the SCM is better than those of the TSFRK and FSFRK. From this investigation, we can say that the numerical solutions based upon the SCM and LPI methods are remarkably accurate and effective in the case of non-integer order.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Mathematics in Science and Engineering; Academic Press: New York, NY, USA; London, UK; Sydney, Australia; Tokyo, Japan; Toronto, ON, Canada, 1999; Volume 198. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematical Studies; Elsevier (North-Holland) Science Publishers: Amsterdam, The Netherlands; London, UK; New York, NY, USA, 2006; Volume 204. [Google Scholar]
- Saad, K.M.; Srivastava, H.M.; Gómez-Aguilar, J.F. A fractional quadratic autocatalysis associated with chemical clock reactions involving linear inhibition. Chaos Solitons Fract. 2020, 132, 1–9. [Google Scholar] [CrossRef]
- Srivastava, H.M. Fractional-order derivatives and integrals: Introductory overview and recent developments. Kyungpook Math. J. 2020, 60, 73–116. [Google Scholar]
- Khader, M.M.; Saad, K.M. Numerical treatment for studying the blood ethanol concentration systems with different forms of fractional derivatives. Int. J. Mod. Phys. C 2020, 31, 1–13. [Google Scholar] [CrossRef]
- Abdo, M.S.; Shah, K.; Wahash, H.A.; Panchal, S.K. On a comprehensive model of the novel corona-virus (COVID-19) under Mittag-Leffler derivative. Chaos Solitons Fract. 2020, 135, 109867. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Saad, K.M.; Gómez-Aguilar, J.F.; Almadiy, A.A. Some new mathematical models of the fractional-order system of human immune against IAV infection. Math. Biosci. Engrg. 2020, 17, 4942–4969. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Saad, K.M. New approximate solution of the time-fractional Nagumo equation involving fractional integrals without singular kernel. Appl. Math. Inform. Sci. 2020, 14, 1–8. [Google Scholar]
- Ghanbari, B.; Günerhan, H.; Srivastava, H.M. An application of the Atangana-Baleanu fractional derivative in mathematical biology: A three-species predator-prey model. Chaos Solitons Fract. 2020, 138, 109919. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Jena, R.M.; Chakraverty, S.; Jena, S.K. Dynamic response analysis of fractionally-damped generalized Bagley-Torvik equation subject to external loads. Russ. J. Math. Phys. 2020, 27, 254–268. [Google Scholar] [CrossRef]
- Area, I.; Ndairou, F.; Nieto, J.J.; Silva, C.J. Ebola model and optimal control with vaccination constraints. J. Ind. Manag. Optim. 2018, 14, 427–446. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Dubey, R.S.; Jain, M. A study of the fractional-order mathematical model of diabetes and its resulting complications. Math. Methods Appl. Sci. 2019, 42, 4570–4583. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Günerhan, H. Analytical and approximate solutions of fractional-order susceptible-infected-recovered epidemic model of childhood disease. Math. Methods Appl. Sci. 2019, 42, 935–941. [Google Scholar] [CrossRef]
- Baleanu, D.; Jajarmi, A.; Mohammad, H.; Rezapour, S. A new study on the mathematical modelling of human liver with Caputo-Fabrizio fractional derivative. Chaos Solitons Fract. 2020, 134, 1–13. [Google Scholar] [CrossRef]
- Saad, K.M.; Al-Sharif, E.H.F. Comparative study of a cubic autocatalytic reaction via different analysis methods. Discret. Contin. Dyn. Syst. Ser. S 2019, 12, 665–684. [Google Scholar]
- Singh, H.; Pandey, R.K.; Srivastava, H.M. Solving non-linear fractional variational problems using Jacobi polynomials. Mathematics 2019, 7, 224. [Google Scholar] [CrossRef]
- Khader, M.M.; Saad, K.M. A numerical study using Chebyshev collocation method for a problem of biological invasion: Fractional Fisher equation. Int. J. Biomath. 2018, 11, 1–15. [Google Scholar] [CrossRef]
- Saad, K.M. New fractional derivative with non-singular kernel for deriving Legendre spectral collocation method. Alex. Eng. J. 2019, 59, 1909–1917. [Google Scholar] [CrossRef]
- Preece, S.J.; Billingham, J.; King, A.C. Chemical clock reactions: The effect of precursor consumption. J. Math. Chem. 1999, 26, 47–73. [Google Scholar] [CrossRef]
- Billingham, J.; Needham, D.J. Mathematical-modeling of chemical clock reactions II. A class of autocatalytic clock reaction schemes. J. Eng. Math. 1993, 27, 113–145. [Google Scholar] [CrossRef]
- West, B.J. Exact solution to fractional logistic equation. Phys. A Stat. Mech. Appl. 2015, 429, 103–108. [Google Scholar] [CrossRef]
- Carleman, T. Application de la théorie des équations intégrales linéaires aux systmes d’équations différentielles non linéaires. Phys. A Stat. Mech. Appl. 1932, 59, 63–87. [Google Scholar]
- Khalil, H.; Khan, R.A.; Al-Smadi, M.H.; Freihat, A.A.; Shawagfeh, N. New Operational matrix for shifted Legendre polynomials and fractional differential equations with variable coefficients. Punjab Univ. J. Math. 2015, 47, 1–23. [Google Scholar]
- Mohammadi, F.; Cattani, C. A generalized fractional-order Legendre wavelet Tau method for solving fractional differential equations. J. Comput. Appl. Math. 2018, 339, 306–316. [Google Scholar] [CrossRef]
- Mohammadi, F.; Mohyud-Din, S.T. A fractional-order Legendre collocation method for solving the Bagley-Torvik equations. Punjab Univ. J. Math. 2016, 269, 2–14. [Google Scholar] [CrossRef]
- Lebedev, N.N. Special Functions and Their Applications; Silverman, R.A., Translator; Dover Publications: New York, NY, USA, 1972; pp. 43–60. [Google Scholar]
- Khader, M.M.; Hendy, A.S. The approximate and exact solutions of the fractional-order delay differential equations using Legendre pseudo-spectral method. Int. J. Pure Appl. Math. 2012, 74, 287–297. [Google Scholar]
- Lubich, C. Discretized fractional calculus. SIAM J. Math. Anal. 1986, 17, 704–719. [Google Scholar] [CrossRef]
- Arshad, M.S.; Baleanu, D.; Riaz, M.B.; Abbas, M. A novel 2-stage fractional Runge-Kutta method for a time fractional logistic growth model. Discrete Dyn. Nat. Soc. 2020, 2020, 1020472. [Google Scholar] [CrossRef]
- Milici, C.; Machado, J.A.T.; Drăgănescu, G. Application of the Euler and Runge-Kutta generalized methods for FDE and symbolic packages in the analysis of some fractional attractors. Int. J. Nonlinear Sci. Numer. Simul. 2020, 21, 159–170. [Google Scholar] [CrossRef]

| K | ||||
|---|---|---|---|---|
| K | ||||
|---|---|---|---|---|
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Srivastava, H.M.; Saad, K.M. A Comparative Study of the Fractional-Order Clock Chemical Model. Mathematics 2020, 8, 1436. https://doi.org/10.3390/math8091436
Srivastava HM, Saad KM. A Comparative Study of the Fractional-Order Clock Chemical Model. Mathematics. 2020; 8(9):1436. https://doi.org/10.3390/math8091436
Chicago/Turabian StyleSrivastava, Hari Mohan, and Khaled M. Saad. 2020. "A Comparative Study of the Fractional-Order Clock Chemical Model" Mathematics 8, no. 9: 1436. https://doi.org/10.3390/math8091436
APA StyleSrivastava, H. M., & Saad, K. M. (2020). A Comparative Study of the Fractional-Order Clock Chemical Model. Mathematics, 8(9), 1436. https://doi.org/10.3390/math8091436






