Nonlinear Systems of Volterra Equations with Piecewise Smooth Kernels: Numerical Solution and Application for Power Systems Operation
Abstract
:1. Introduction
2. Problem Statement
3. Description of the Iterative Approximate Method
The Convergence Theorem
- Equation (8) has a unique solution for , i.e., there exists ;
- where ;
- .
4. Discretization of the System of Linear Integral Equations
4.1. Problem Formulation
4.2. Piecewise Constant Approximation
4.3. Polynomial Collocation Method
4.3.1. Description of the Problem
4.3.2. Collocation
5. Numerical Results
5.1. System of Linear Integral Equations
5.2. Nonlinear Equations
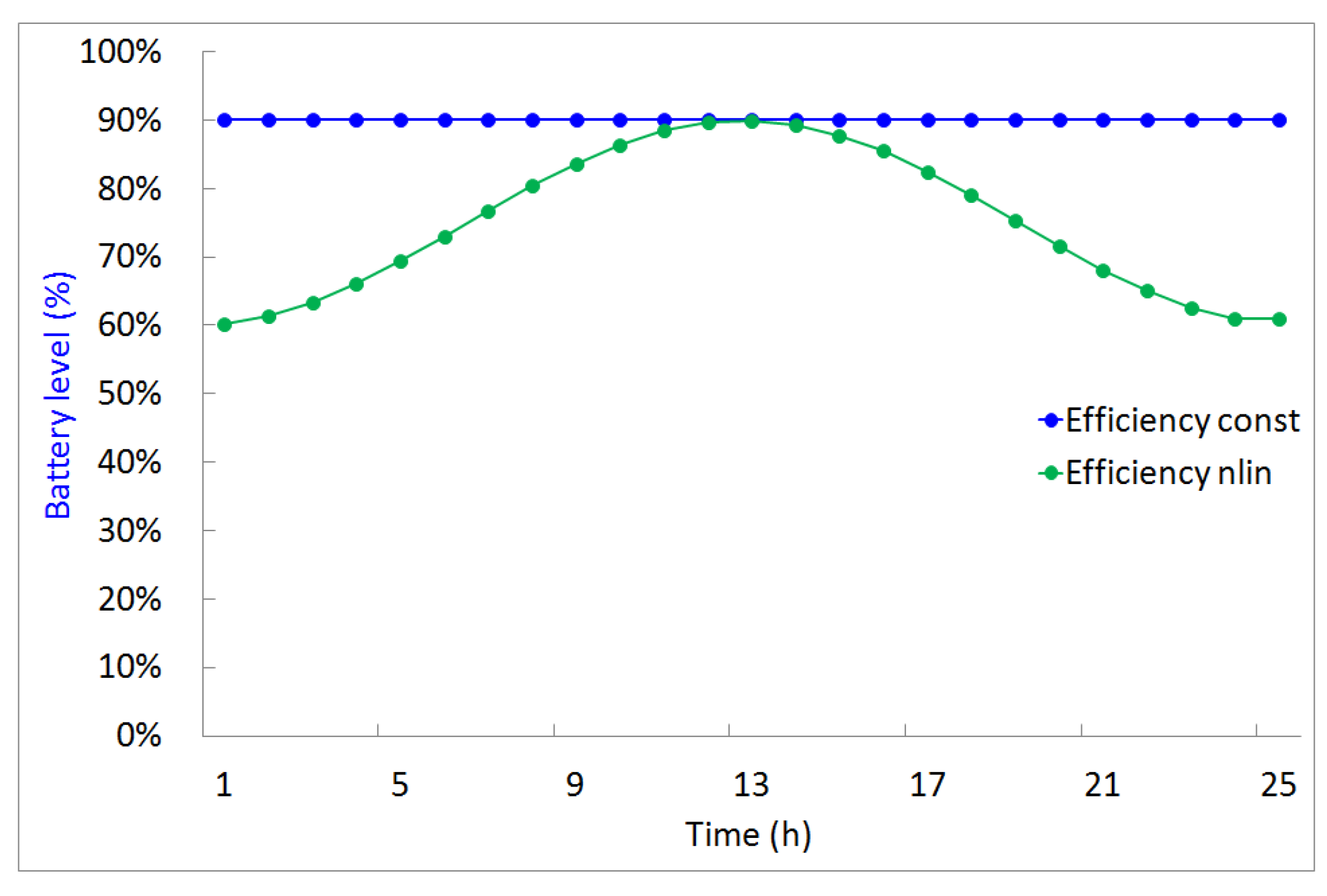
5.3. Nonlinear Systems of Equations
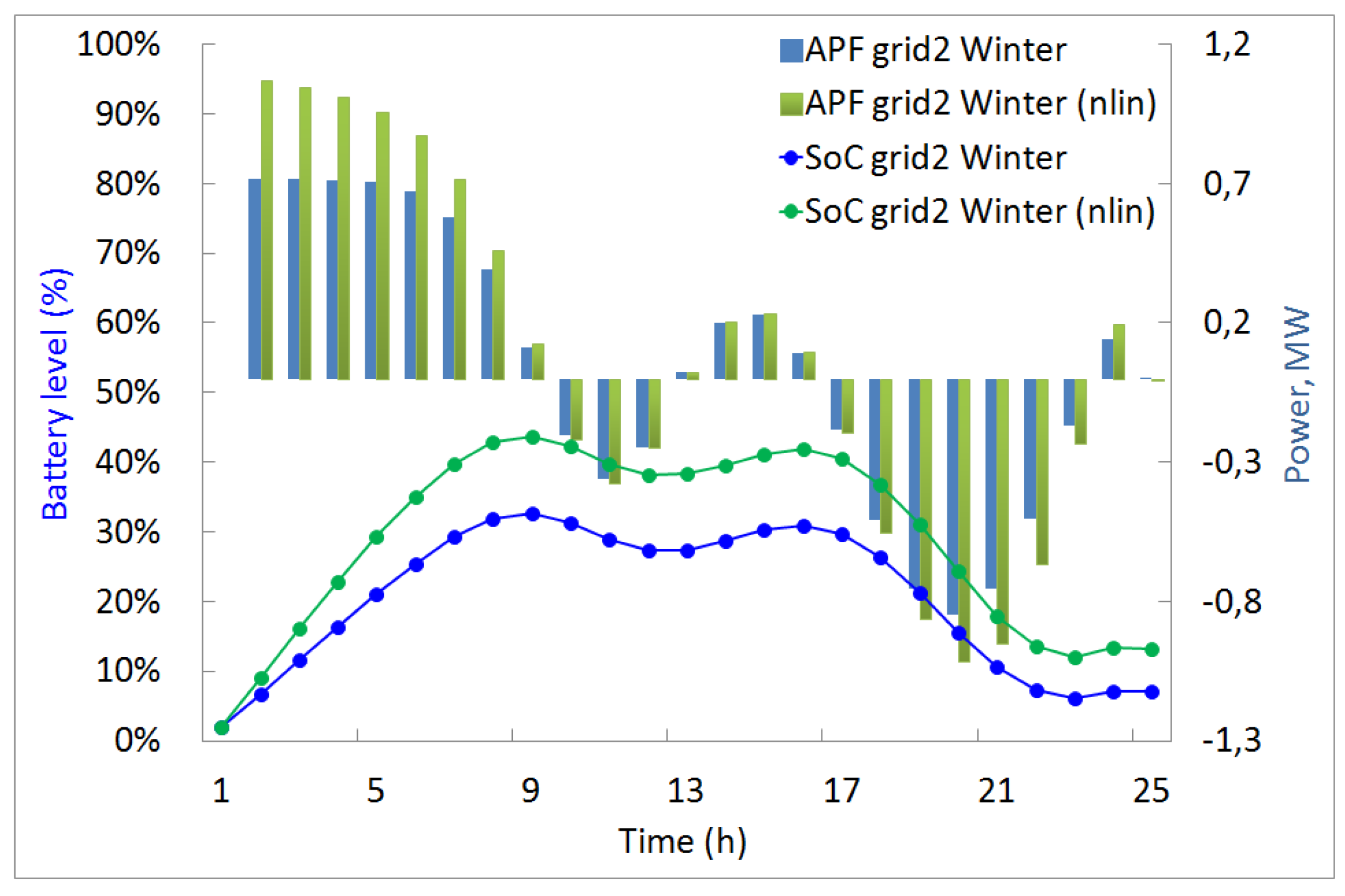
6. Storage System Analysis in Microgrid Using System of Volterra Equations
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Volterra, V. Theory of Functionals and of Integral and Integro-Differential Equations; Dover Publications: Mineola, NY, USA, 1959; Volume 4, 226p. [Google Scholar]
- Tikhonov, A.N.; Arsenin, V.Y. Solutions of Ill-Posed Problems; Winston: Washington, DC, USA, 1977; 258p. [Google Scholar]
- Evans, G.C. Integral equation of the second kind with discontinuous kernel. Trans. Am. Math. 1910, 11, 393–413. [Google Scholar] [CrossRef]
- Anselone, P.M. Uniform approximation theory for integral equations with discontinuous kernels. SIAM J. Numer. Anal. 1967, 4, 245–253. [Google Scholar] [CrossRef]
- Denisov, A.M.; Lorenzi, A. On a special Volterra integral equation of the first kind. Boll. U.M.I. 1995, 7, 443–457. [Google Scholar]
- Boikov, I.V.; Tynda, A.N. Approximate solution of nonlinear integral equations of developing systems theory. Differ. Equ. 2003, 39, 1214–1223. [Google Scholar] [CrossRef]
- Tynda, A.N.; Kudryashova, N.Y. Numerical methods for the problems of nonlinear macroeconomic integral models. Zhurnal SVMO 2017, 19, 79–94. [Google Scholar] [CrossRef] [Green Version]
- Tynda, A.N. Iterative numerical method for integral models of a nonlinear dynamical system with unknown delay. Proc. Appl. Math. Mech. 2009, 9, 591–592. [Google Scholar] [CrossRef]
- Hritonenko, N.; Yatsenko, Y. Mathematical Modeling in Economics, Ecology and the Environment, 2nd ed.; Springer: Berlin, Germany, 2013. [Google Scholar]
- Hritonenko, N.; Yatsenko, Y. Nonlinear integral models with delays: Recent developments and applications. J. King Saud Univ. Sci. 2020, 32, 726–731. [Google Scholar] [CrossRef]
- Ivanov, D.V.; Khamisov, O.V.; Karaulova, I.V.; Markova, E.V.; Trufanov, V.V. Control of power grid development: Numerical solutions. Autom. Remote Control 2004, 65, 472–482. [Google Scholar] [CrossRef]
- Botoroeva, M.N.; Bulatov, M.V. Applications and methods for the numerical solution of a class of integral-algebraic equations with variable limits of integration. In Bulletin of Irkutsk State University. Series “Mathematics”; Bulletin of Irkutsk State University: Irkutsk, Russia, 2017; Volume 20, pp. 3–16. [Google Scholar] [CrossRef]
- Apartsyn, A.S. Nonclassical Linear Volterra Equations of the First Kind, 2nd ed.; Series: Inverse and Ill-Posed Problems Series; Kabanikhin, S.I., Ed.; Walter de Gruyter: Berlin, Germany, 2011; Volume 39. [Google Scholar]
- Sidorov, D.N. On parametric families of solutions of Volterra integral equations of the first kind with piecewise smooth kernel. Differ. Equ. 2013, 49, 210–216. [Google Scholar] [CrossRef]
- Markova, E.V.; Sidorov, D.N. On one integral Volterra model of developing dynamical systems. Autom. Remote Control 2014, 75, 413–421. [Google Scholar] [CrossRef]
- Sidorov, D.N. Solvability of systems of Volterra integral equations of the first kind with piecewise continuous kernels. Russ. Math. 2013, 57, 54–63. [Google Scholar] [CrossRef]
- Sidorov, N.A.; Sidorov, D.N. On the solvability of a class of Volterra operator equations of the first kind with piecewise continuous kernels. Math. Notes 2014, 96, 811–826. [Google Scholar] [CrossRef]
- Sidorov, D.N. Generalized solution to the Volterra equations with piecewise continuous kernels. Bull. Malays. Math. Sci. Soc. 2014, 37, 757–768. [Google Scholar]
- Sidorov, D.N.; Sidorov, N.A. Convex majorants method in the theory of nonlinear Volterra equations. Banach J. Math. Anal. 2012, 6, 1–10. [Google Scholar] [CrossRef]
- Sidorov, D. Integral Dynamical Models: Singularities, Signals and Control; World Scientific Series on Nonlinear Sciences Series A; Chua, L.O., Ed.; World Scientific Press: Singapore, 2015; Volume 87. [Google Scholar]
- Sidorov, N.; Sidorov, D.; Sinitsyn, A. Toward General Theory of Differential-Operator and Kinetic Models; World Scientific Series on Nonlinear Sciences Series A; Chua, L.O., Ed.; World Scientific Press: Singapore, 2020; Volume 97. [Google Scholar]
- Sidorov, D.; Muftahov, I.; Tomin, N.; Karamov, D.; Panasetsky, D.; Dreglea, A.; Liu, F. A dynamic analysis of energy storage with renewable and diesel generation using Volterra equations. IEEE Trans. Ind. Inform. 2019. [Google Scholar] [CrossRef] [Green Version]
- Sidorov, D.; Tao, Q.; Muftahov, I.; Zhukov, A.; Karamov, D.; Dreglea, A.; Liu, F. Energy balancing using charge/discharge storages control and load forecasts in a renewable-energy-based grids. In Proceedings of the 38th China Control Conference, Guangzhou, China, 27–30 July 2019; IEEE: New York, NY, USA, 2019. [Google Scholar] [CrossRef] [Green Version]
- Sidorov, D.; Panasetsky, D.; Tomin, N.; Karamov, D.; Zhukov, A.; Muftahov, I.; Dreglea, A.; Liu, F.; Li, Y. Toward zero-emission hybrid AC/DC power systems with renewable energy sources and storages: A case study from lake Baikal region. Energies 2020, 13, 1226. [Google Scholar] [CrossRef] [Green Version]
- Muftahov, I.; Tynda, A.; Sidorov, D. Numeric solution of Volterra integral equations of the first kind with discontinuous kernels. J. Comput. Appl. Math. 2017, 313, 119–128. [Google Scholar] [CrossRef]
- Kantorovich, L.V.; Akilov, G.P. Functional Analysis, 2nd ed.; Pergamon: Oxford, UK, 1982; 589p. [Google Scholar]
- Noeiaghdam, S.; Sidorov, D.; Sizikov, V.; Sidorov, N. Control of accuracy on Taylor-collocation method to solve the weakly regular Volterra integral equations of the first kind by using the CESTAC method. Appl. Comput. Math. 2020, 19, 87–105. [Google Scholar]
| m | |||||
|---|---|---|---|---|---|
| 2 | 1.0 | 2.0 | |||
| 3 | 1.0 | 2.0 | |||
| 5 | 1.0 | 2.0 | |||
| 8 | 1.0 | 2.0 | |||
| 12 | 1.0 | 2.0 | |||
| 15 | 1.0 | 2.0 |
| m | |||||||
|---|---|---|---|---|---|---|---|
| 2 | 0.6(6) | 1.3(3) | 2.0 | ||||
| 3 | 0.6(6) | 1.3(3) | 2.0 | ||||
| 5 | 0.6(6) | 1.3(3) | 2.0 | ||||
| 8 | 0.6(6) | 1.3(3) | 2.0 | ||||
| 12 | 0.6(6) | 1.3(3) | 2.0 | ||||
| 15 | 0.6(6) | 1.3(3) | 2.0 |
| Piece-Wise Constant Approximation | |||||
| h | |||||
| m | 5 | 5 | 5 | 5 | 5 |
| 0.0286877 | 0.0152708 | 0.00730057 | 0.0044031 | 0.00386043 | |
| Piece-Wise Linear Approximation | |||||
| h | |||||
| m | 6 | 9 | 9 | 9 | 10 |
| 0.001496942 | 0.0008320731 | 0.0004604894 | 0.0002356853 | 0.0001186141 | |
| m | ||||
|---|---|---|---|---|
| 1 | 3 | |||
| 10 | 3 | |||
| 20 | 3 |
| m | ||||
|---|---|---|---|---|
| 1 | 5 | |||
| 5 | 5 | |||
| 10 | 5 | |||
| 20 | 5 |
| m | ||||
|---|---|---|---|---|
| 1 | 10 | |||
| 5 | 10 | |||
| 10 | 10 | |||
| 20 | 10 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sidorov, D.; Tynda, A.; Muftahov, I.; Dreglea, A.; Liu, F. Nonlinear Systems of Volterra Equations with Piecewise Smooth Kernels: Numerical Solution and Application for Power Systems Operation. Mathematics 2020, 8, 1257. https://doi.org/10.3390/math8081257
Sidorov D, Tynda A, Muftahov I, Dreglea A, Liu F. Nonlinear Systems of Volterra Equations with Piecewise Smooth Kernels: Numerical Solution and Application for Power Systems Operation. Mathematics. 2020; 8(8):1257. https://doi.org/10.3390/math8081257
Chicago/Turabian StyleSidorov, Denis, Aleksandr Tynda, Ildar Muftahov, Aliona Dreglea, and Fang Liu. 2020. "Nonlinear Systems of Volterra Equations with Piecewise Smooth Kernels: Numerical Solution and Application for Power Systems Operation" Mathematics 8, no. 8: 1257. https://doi.org/10.3390/math8081257
APA StyleSidorov, D., Tynda, A., Muftahov, I., Dreglea, A., & Liu, F. (2020). Nonlinear Systems of Volterra Equations with Piecewise Smooth Kernels: Numerical Solution and Application for Power Systems Operation. Mathematics, 8(8), 1257. https://doi.org/10.3390/math8081257









