Cu-Al₂O₃/Water Hybrid Nanofluid Stagnation Point Flow Past MHD Stretching/Shrinking Sheet in Presence of Homogeneous-Heterogeneous and Convective Boundary Conditions

Abstract

The intent of this research was to present numerical solutions to homogeneous–heterogeneous reactions of the magnetohydrodynamic (MHD) stagnation point flow of a Cu-Al₂O₃/water hybrid nanofluid induced by a stretching or shrinking sheet with a convective boundary condition. A proper similarity variable was applied to the system of partial differential equations (PDEs) and converted into a system of ordinary (similarity) differential equations (ODEs). These equations were solved using Matlab’s in-built function (bvp4c) for various values of the governing parameters numerically. The present investigation considered the effects of homogeneous–heterogeneous reactions and magnetic field in the hybrid nanofluid flow. It was observed that dual solutions were visible for the shrinking sheet, and an analysis of stability was done to determine the physically realizable in the practice of these solutions. It was also concluded that hybrid nanofluid acts as a cooler for some increasing parameters. The magnetohydrodynamic parameter delayed the boundary layer separation; meanwhile, the nanoparticle volume fraction quickened the separation of the boundary layer that occurred. In addition, the first solution of hybrid nanofluid was found to be stable; meanwhile, the second solution was not stable. This study is therefore valuable for engineers and scientists to get acquainted with the properties of hybrid nanofluid flow, its behavior and the way to predict it.

1. Introduction

Stagnation-point flow, describing the fluid motion near the stagnation region of a solid surface at the front of a blunt-nosed body, exists in both cases of a fixed or moving body in a fluid. The stagnation-point region offers the highest mass deposition, pressure and heat transfer rates. The idea of analyzing two-dimensional (2D) stagnation flows was first proposed by Hiemenz [1], where the Navier–Stokes equations were simplified to nonlinear ODEs using a similarity transformation. Afterwards, Homann [2] considered the axisymmetric case. Crane [3] was the first to solve the Newtonian fluid flow over the stretching of an elastic sheet and obtained an exact solution for the boundary layer 2D Navier–Stokes equations. The combination of stretching surface and stagnation flow was considered by Mahapatra and Gupta [4,5]. Stretching sheets have many important industrial applications such as the production of paper, polymeric sheets, liquid film in condensation processes, fine-fiber mattes and many more [6]. In contrast to stretching surfaces, the study of shrinking surfaces in which the fluid’s velocity on the boundary moves to a fixed point have been investigated by Miklavčič and Wang [7]. They found that this kind of flow depends on externally imposed mass suction. Afterwards, Wang [8] extended the work of Miklavčič and Wang [7] to the case of the stagnation region. Since then, the flow induced by stretching/shrinking surfaces has been extensively studied by other authors in varied geometric configurations [9,10,11,12,13].

Over the last few decades, numerous studies have focused on the use of nanoparticles in thermal systems to improve the heat transfer efficiency by dispersing a certain concentration of nanoparticles in base fluids. Such a mixture is known as nanofluid in the literature. Several studies have shown the effectiveness of using nanoparticles to enhance heat transfer in forced convection applications, but the efficacy of nanoparticles to enhance heat transfer in natural convection is still unclear. It is well understood that conventional working fluids, i.e., water, oil or ethylene glycol have poor thermal conductivity resulting in a low heat transfer performance. In an effort to improve it, Choi [14] and Khanafer et al. [15] dispersed metallic nanoparticles with high thermal conductivity into a base fluid to form so-called nanofluids. Later on, many authors discussed the effects of nanoparticles for different models of fluid, see for example, [16,17,18,19,20].

After Huminic and Huminic’s [21] research, hybrid nanofluids have become a new class of working fluids containing very small particles with sizes less than 100 nm and are important in applications involving heat transfer. Such fluids consist of two solid materials, for example, Al₂O₃–Cu, Al₂O₃–Ag, Cu–TiO₂ and Cu–CuO, in traditional liquids (water, kerosene, ethylene glycol and engine oil). The objective of using hybrid nanofluids is to further strengthen the heat transfer and to develop nanotechnology. Nowadays, these hybrid nanofluids are implemented in numerous heat transfer applications as mini channel heat sinks, air conditioning systems, micro channels, helical coil heat exchangers, tubulars and plate heat exchangers. Comprehensive investigations on hybrid nanofluids can be found in the literature [22,23,24,25].

The natural process of chemical reactions that occurs in biochemical, combustion and catalysis mechanisms involves both homogeneous and heterogeneous reactions. A fraction of the reactions has the capacity to either progress gradually or not progress at all unless a catalyst is present. It should be noted that a homogeneous reaction persists during the whole process, whereas heterogeneous reactions take place in a confined region or within the boundary of a phase. A simple isothermal model for homogeneous–heterogeneous reactions in boundary layer flow was studied by Merkin [26]. Later, Bachok et al. [27] investigated the problem of stagnation point flow towards a stretching sheet in the existence of homogeneous–heterogeneous reactions. Rashidi et al. [28] reported the effect of chemical reactions in the mixed convection boundary layer flow. Afterwards, Hayat et al. [29] considered the Oldroyd-B fluid flow with effects of homogeneous–heterogeneous reactions. Since then, many authors have become interested in focusing their studies on homogeneous and heterogeneous reactions with different aspects of flow [30,31].

In the current research, the homogeneous–heterogeneous reactions in the magnetohydrodynamic (MHD) stagnation point flow of a hybrid nanofluid induced by a stretching/shrinking surface with a convective boundary condition were numerically studied. The nanoparticles of alumina (Al₂O₃) were added to the base fluid (water) as nanofluid (Al₂O₃/water). Afterwards, copper (Cu) nanoparticles were mixed to this nanofluid to get hybrid nanofluid (Cu-Al₂O₃/water). The results obtained are original and new.

2. Flow Analysis

The steady 2D MHD stagnation point boundary layer flow of Cu-Al₂O₃/water hybrid nanofluid induced by a stretching or shrinking sheet was investigated, where the x-axis was measured along the plate and the y-axis was normal to it. The velocity at the sheet is assumed to be $u_w\left(x\right)=cx$ and that of the far flow from the plate is $u_e\left(x\right)=cx$, in which $c$ is a positive constant. Furthermore, the surface is assumed to be heated at the variable temperature $T_f\left(x\right)$, while $T_{\infty }$ is the ambient temperature. The magnetic field of strength $B_o$ is applied normal to the x-axis. The interaction of homogeneous and heterogeneous reactions is given as:

$$A+2B\to 3B,\mathrm{rate}=k_{c}a{b}^2$$

(1)

$$A\to B,\mathrm{rate}=k_{s}a$$

(2)

in which the concentration of chemical species $A$ and $B$ are denoted by $a$ and $b$, respectively, while $k_s$ and $k_c$ are the constant rates.

Based on the above assumption, the governing equations are given as [30,32]:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$

(3)

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=u_e\frac{d{u}_e}{dx}+\frac{{\mu }_{hnf}}{{\rho }_{hnf}}\frac{{\partial }^{2}u}{\partial y^2}-\frac{{\sigma }_{hnf}{B}_o^2}{{\rho }_{hnf}}\left(u-u_e\right)$$

(4)

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{k_{hnf}}{{\left(\rho C_p\right)}_{hnf}}\frac{{\partial }^{2}T}{\partial y^2}+\frac{{\mu }_{hnf}}{{\left(\rho C_p\right)}_{hnf}}{\left(\frac{\partial u}{\partial y}\right)}^2+\frac{{\sigma }_{hnf}{B}_o^2}{{\left(\rho C_p\right)}_{hnf}}{\left(u-u_e\right)}^2$$

(5)

$$u\frac{\partial a}{\partial x}+v\frac{\partial a}{\partial y}=D_A\frac{{\partial }^{2}a}{\partial y^2}-k_{c}a{b}^2$$

(6)

$$u\frac{\partial b}{\partial x}+v\frac{\partial b}{\partial y}=D_B\frac{{\partial }^{2}b}{\partial y^2}+k_{c}a{b}^2$$

(7)

subject to:

$$\begin{array}{c}v=0,u=u_w\left(x\right)\lambda ,-k_{hnf}\frac{\partial T}{\partial y}=h_f\left(T_f-T\right),D_B\frac{\partial b}{\partial y}=-k_{s}a,D_A\frac{\partial a}{\partial y}=k_{s}a\mathrm{at}y=0\\ u\to u_e\left(x\right),T\to T_{\infty },a\to a_o,b\to 0\mathrm{as}y\to \infty \end{array}$$

(8)

where $u$ and $v$ are the velocity components along the x- and y-axes; $D_A$ and $D_B$ are the diffusion coefficient; $T_f\left(x\right)=T_{\infty }+T_o{\left(x/L\right)}^2$, where $L$ and $T_o$ are the characteristic length and temperature, respectively; $T$ and $h_f$ are the temperature and heat transfer coefficient; $\lambda$ is the stretching and shrinking parameter with a positive constant of $\lambda$ corresponding to the stretching sheet, negative constant of $\lambda$ for a shrinking sheet and $\lambda =0$ corresponds to the static sheet, respectively. Furthermore, $\mu$ and $\rho$ are the dynamic viscosity and density, $k$ and $\sigma$ are the thermal conductivity and electrical conductivity, respectively, while $\left(\rho C_p\right)$ is the heat capacity where $\prime hnf\prime$ refers to hybrid nanofluid. These terms are given by [33]:

$$\begin{array}{c}{\rho }_{hnf}={\phi }_2{\rho }_{s2}+\left(1-{\phi }_2\right)\left[\left(1-{\phi }_1\right){\rho }_f+{\phi }_1{\rho }_{s1}\right],{\mu }_{hnf}=\frac{{\mu }_f}{{\left(1-{\phi }_1\right)}^{2.5}{\left(1-{\phi }_2\right)}^{2.5}},\\ {\left(\rho C_p\right)}_{hnf}={\phi }_2{\left(\rho C_p\right)}_{s2}+\left(1-{\phi }_2\right)\left[\left(1-{\phi }_1\right){\left(\rho C_p\right)}_f+{\phi }_1{\left(\rho C_p\right)}_{s1}\right],\\ \frac{k_{hnf}}{k_{bf}}=\frac{k_{s2}+2k_{bf}-2{\phi }_2\left(k_{bf}-k_{s2}\right)}{k_{s2}+2k_{bf}+{\phi }_2\left(k_{bf}-k_{s2}\right)}\mathrm{where}\frac{k_{bf}}{k_f}=\frac{k_{s1}+2k_f-2{\phi }_1\left(k_f-k_{s1}\right)}{k_{s1}+2k_f+{\phi }_1\left(k_f-k_{s1}\right)},\\ \frac{{\sigma }_{hnf}}{{\sigma }_{bf}}=\frac{{\sigma }_{s2}+2{\sigma }_{bf}-2\left({\sigma }_{bf}-{\sigma }_{s2}\right){\phi }_2}{{\sigma }_{s2}+2{\sigma }_{bf}+\left({\sigma }_{bf}-{\sigma }_{s2}\right){\phi }_2}\mathrm{where}\frac{{\sigma }_{bf}}{{\sigma }_f}=\frac{{\sigma }_{s1}+2{\sigma }_f-2\left({\sigma }_f-{\sigma }_{s1}\right){\phi }_1}{{\sigma }_{s1}+2{\sigma }_f+\left({\sigma }_f-{\sigma }_{s1}\right){\phi }_1}\end{array}$$

(9)

here, nanoparticle volume fraction denoted by $\phi$ and subscript $‘f’,‘s1’$ and $‘s2’$ represent the fluid, Al₂O₃ nanoparticle and Cu nanoparticle. The physical properties of the base fluid (water), alumina (Al₂O₃) and copper (Cu) hybrid nanofluids are given in

Table 1. Thermophysical properties of hybrid nanofluid [34].

Physical Properties	Water	Al2O3	Cu
$\rho \left(\mathrm{kg}{\mathrm{m}}^{-3}\right)$	997.0	3970	8933
$C_p\left(\mathrm{J}{\mathrm{kg}}^{-1}{\mathrm{K}}^{-1}\right)$	4180	765	385
$k\left({\mathrm{Wm}}^{-1}{\mathrm{K}}^{-1}\right)$	0.6071	40	400
$\sigma \left({\mathrm{\Omega }}^{-1}{\mathrm{m}}^{-1}\right)$	0.05	1 × 10−10	5.96 × 107

.

The following similarity variables are established [27,35]:

$$u=u_e\left(x\right)f^{\prime }\left(\eta \right),v=-\sqrt{c{\nu }_f}f\left(\eta \right),\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_f-T_{\infty }},g\left(\eta \right)=\frac{a}{a_o},h\left(\eta \right)=\frac{b}{a_o},\eta =y\sqrt{\frac{c}{{\nu }_f}}$$

(10)

Invoking the similarity variables (10), and taking $k_c=c/a_o^2$ (see Merkin [26]), Equations (3)–(7) with Conditions (8) are converted into the following:

$$\frac{{\mu }_{hnf}/{\mu }_f}{{\rho }_{hnf}/{\rho }_f}{f}^{‴}-{f^{\prime }}^2+1+f{f}^{″}-\frac{{\sigma }_{hnf}/{\sigma }_f}{{\rho }_{hnf}/{\rho }_f}M\left(f^{\prime }-1\right)=0$$

(11)

$$\begin{array}{r}\frac{1}{\mathrm{Pr}}\frac{k_{hnf}/k_f}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}{\theta }^{″}+f{\theta }^{\prime }-2f^{\prime }\theta +\frac{{\mu }_{hnf}/{\mu }_f}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}Ec{f^{″}}^2\\ +\frac{{\sigma }_{hnf}/{\sigma }_f}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}EcM{\left(f^{\prime }-1\right)}^2=0\end{array}$$

(12)

$$\frac{1}{Sc}{g}^{″}+f{g}^{\prime }-g{h}^2=0$$

(13)

$$\frac{\delta }{Sc}{h}^{″}+f{h}^{\prime }+g{h}^2=0$$

(14)

subject to:

$$\begin{array}{c}{f}^{\prime }\left(0\right)=\lambda ,f\left(0\right)=0,-\frac{k_{hnf}}{k_f}{\theta }^{\prime }\left(0\right)=Bi\left[1-\theta \left(0\right)\right],\delta h^{\prime }\left(0\right)=-K_{s}g\left(0\right),g^{\prime }\left(0\right)=K_{s}g\left(0\right),\\ f^{\prime }\left(\eta \right)\to 1,\theta \left(\eta \right)\to 0,h\left(\eta \right)\to 0,g\left(\eta \right)\to 1\mathrm{as}\eta \to \infty \end{array}$$

(15)

here, $Sc$ and $\mathrm{Pr}$ are the Schmidt and Prandtl numbers, respectively, and $M$, $Ec$ and $Bi$ are the magnetic parameter, Eckert and Biot number, respectively. Meanwhile, $K_s$ and $\delta$ are the heterogeneous reaction’s strength and the ratio of the coefficients of diffusion, respectively, which are given as:

$$\begin{array}{c}\mathrm{Pr}=\frac{{\nu }_f}{{\alpha }_f},Sc=\frac{{\nu }_f}{D_A},M=\frac{{\sigma }_f{B}_o^2}{c{\rho }_f},Ec=\frac{u_e^2}{C_p{}_f\left(T_f-T_{\infty }\right)},\\ Bi=\left(\frac{h_f}{k_f}\right)\sqrt{\frac{{\nu }_f}{c}},K_s=\left(\frac{k_s}{D_A}\right)\sqrt{\frac{{\nu }_f}{c}},\delta =\frac{D_B}{D_A}\end{array}$$

(16)

It is seen that for $Bi>>1$, Equation (15) for $\theta \left(\eta \right)$ reduces to $\theta \left(0\right)=1$ (isothermal stretching/shrinking surface). If we suppose further that diffusion coefficients $D_A$ and $D_B$ are equal, i.e., $\delta =1$, and by using these assumptions, the following relation is obtained:

$$g\left(\eta \right)+h\left(\eta \right)=1$$

(17)

so that Equations (13) and (14) become:

$$\frac{1}{Sc}{g}^{″}+f{g}^{\prime }-g{\left(1-g\right)}^2=0$$

(18)

subject to:

$$g^{\prime }\left(0\right)=K_{s}g\left(0\right),g\left(\eta \right)\to 1\mathrm{as}\eta \to \infty$$

(19)

It is necessary to identify the skin friction coefficient and local Nusselt number, which are denoted by $C_f$ and $N{u}_x$:

$$C_f=\frac{{\mu }_{hnf}}{{\rho }_f{u}_e^2}{\left(\frac{\partial u}{\partial y}\right)}_{y=0},N{u}_x=-\frac{x{k}_{hnf}}{k_f\left(T_f-T_{\infty }\right)}{\left(\frac{\partial T}{\partial y}\right)}_{y=0}$$

(20)

using (10), we get:

$${\mathrm{Re}}_x^{1/2}{C}_f=\frac{{\mu }_{hnf}}{{\mu }_f}{f}^{″}\left(0\right),{\mathrm{Re}}_x^{-1/2}N{u}_x=-\frac{k_{hnf}}{k_f}{\theta }^{\prime }\left(0\right)$$

(21)

where ${\mathrm{Re}}_x=u_e\left(x\right)x/{\nu }_f$ is the local Reynolds number.

3. Stability of Solutions

For various problems, literature on [36,37,38] have identified that ODEs admit multiple (dual) solutions. Hence, these features were tested by considering the unsteady form of PDEs (4)–(8). Therefore, a new dimensionless time variable $\tau =ct$ is introduced together with new similarity variables:

$$\begin{array}{c}u=u_e\left(x\right)\frac{\partial f}{\partial \eta }\left(\eta ,\tau \right),v=-\sqrt{c{\nu }_f}f\left(\eta ,\tau \right),\theta \left(\eta ,\tau \right)=\frac{T-T_{\infty }}{T_f-T_{\infty }},g\left(\eta ,\tau \right)=\frac{a}{a_o},\\ h\left(\eta ,\tau \right)=\frac{b}{a_o},\eta =y\sqrt{\frac{c}{{\nu }_f}},\tau =ct\end{array}$$

(22)

Implementing Variable (22), we have

$$\frac{{\mu }_{hnf}/{\mu }_f}{{\rho }_{hnf}/{\rho }_f}\frac{{\partial }^{3}f}{\partial {\eta }^3}+f\frac{{\partial }^{2}f}{\partial {\eta }^2}-{\left(\frac{\partial f}{\partial \eta }\right)}^2+1-\frac{{\sigma }_{hnf}/{\sigma }_f}{{\rho }_{hnf}/{\rho }_f}M\left(\frac{\partial f}{\partial \eta }-1\right)-\frac{{\partial }^{2}f}{\partial \eta \partial \tau }=0$$

(23)

$$\begin{array}{c}\frac{1}{\mathrm{Pr}}\frac{k_{hnf}/k_f}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}\frac{{\partial }^2\theta }{\partial {\eta }^2}-2\frac{\partial f}{\partial \eta }\theta +f\frac{\partial \theta }{\partial \eta }+\frac{{\mu }_{hnf}/{\mu }_f}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}Ec{\left(\frac{{\partial }^{2}f}{\partial {\eta }^2}\right)}^2\\ +\frac{{\sigma }_{hnf}/{\sigma }_f}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}EcM{\left(\frac{\partial f}{\partial \eta }-1\right)}^2-\frac{\partial \theta }{\partial \tau }=0\end{array}$$

(24)

$$\frac{1}{Sc}\frac{{\partial }^{2}g}{\partial {\eta }^2}+f\frac{\partial g}{\partial \eta }-g{h}^2-\frac{\partial g}{\partial \tau }=0$$

(25)

$$\frac{\delta }{Sc}\frac{{\partial }^{2}h}{\partial {\eta }^2}+f\frac{\partial h}{\partial \eta }+g{h}^2-\frac{\partial h}{\partial \tau }=0$$

(26)

subject to:

$$\begin{array}{c}\frac{\partial f}{\partial \eta }\left(0,\tau \right)=\lambda ,f\left(0,\tau \right)=0,-\frac{k_{hnf}}{k_f}\frac{\partial \theta }{\partial \eta }\left(0,\tau \right)=Bi\left[1-\theta \left(0,\tau \right)\right],\\ \delta \frac{\partial h}{\partial \eta }\left(0,\tau \right)=-K_{s}g\left(0,\tau \right),\frac{\partial g}{\partial \eta }\left(0,\tau \right)=K_{s}g\left(0,\tau \right),\\ \frac{\partial f}{\partial \eta }\left(\eta ,\tau \right)\to 1,\theta \left(\eta ,\tau \right)\to 0,g\left(\eta ,\tau \right)\to 1,h\left(\eta ,\tau \right)\to 0\mathrm{as}\eta \to \infty \end{array}$$

(27)

Then, Equations (25) and (26) are reduced to:

$$\frac{1}{Sc}\frac{{\partial }^{2}g}{\partial {\eta }^2}+f\frac{\partial g}{\partial \eta }-g{\left(1-g\right)}^2-\frac{\partial g}{\partial \tau }=0$$

(28)

subject to:

$$\frac{\partial g}{\partial \eta }\left(0,\tau \right)=K_{s}g\left(0,\tau \right),g\left(\eta ,\tau \right)\to 1\mathrm{as}\eta \to \infty$$

(29)

To determine the stability of the steady flow solution, $f=f_o\left(\eta \right),g=g_o\left(\eta \right)$ and $\theta ={\theta }_o\left(\eta \right)$ fulfilled the boundary value problem, and we write (see [34]):

$$\begin{array}{l}f\left(\eta ,\tau \right)=f_o\left(\eta \right)+e^{-\gamma \tau }F\left(\eta ,\tau \right),\\ g\left(\eta ,\tau \right)=g_o\left(\eta \right)+e^{-\gamma \tau }H\left(\eta ,\tau \right),\\ \theta \left(\eta ,\tau \right)={\theta }_o\left(\eta \right)+e^{-\gamma \tau }G\left(\eta ,\tau \right)\end{array}$$

(30)

where the unknown eigenvalue parameter denoted by $\gamma$ and functions $F\left(\eta \right),H\left(\eta \right)$ and $G\left(\eta \right)$ are relatively small compared to $f_o\left(\eta \right),g_o\left(\eta \right)$ and ${\theta }_o\left(\eta \right)$. Substitute Variables (30) into Equations (23), (24) and (28), and taking $\tau =0$ along with Conditions (27) and (29), the following equations are obtained:

$$\frac{{\mu }_{hnf}/{\mu }_f}{{\rho }_{hnf}/{\rho }_f}{F}_o{}^{‴}+f_o{F}_o{}^{″}+\left(\gamma -2f_o{}^{\prime }-\frac{{\sigma }_{hnf}/{\sigma }_f}{{\rho }_{hnf}/{\rho }_f}M\right)F_o{}^{\prime }+f_o{}^{″}{F}_o=0$$

(31)

$$\begin{array}{c}\frac{1}{\mathrm{Pr}}\frac{k_{hnf}/k_f}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}{G}_o{}^{″}+f_o{G}_o{}^{\prime }+\left(\gamma -2f_o{}^{\prime }\right)G_o+F_o{\theta }_o{}^{\prime }-2{\theta }_o{F}_o{}^{\prime }\\ +2\frac{{\mu }_{hnf}/{\mu }_f}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}Ec{f}_o{}^{″}{F}_o{}^{″}+2\frac{{\sigma }_{hnf}/{\sigma }_f}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}EcM\left(f_o{}^{\prime }-1\right)F_o{}^{\prime }=0\end{array}$$

(32)

$$\frac{1}{Sc}{H}_o{}^{″}+f_o{H}_o{}^{\prime }+F_o{g}_o{}^{\prime }-\left(1-4g_o+3g_o^2-\gamma \right)H_o=0$$

(33)

and the Boundary Conditions (27) and (29) become:

$$\begin{array}{c}{F}_o\left(0\right)=0,F_o{}^{\prime }\left(0\right)=0,-\frac{k_{hnf}}{k_f}{G}_o{}^{\prime }\left(0\right)=Bi{G}_o\left(0\right),H_o{}^{\prime }\left(0\right)=K_s{H}_o\left(0\right)\\ F_o{}^{\prime }\left(\eta \right)\to 0,G_o\left(\eta \right)\to 0,H_o\left(\eta \right)\to 0\mathrm{as}\eta \to \infty .\end{array}$$

(34)

When solving the eigenvalue problems (31)–(34), an infinite number of eigenvalues ${\gamma }_1<{\gamma }_2<{\gamma }_3<\dots$ can be obtained. The flow of a solution is said to be stable if the smallest eigenvalue $\gamma$ is positive (there is an initial decay of perturbation). However, when $\gamma$ is negative, there is an initial growth of perturbation, and thus we can conclude that the flow is unstable. Following Harris et al. [39], the boundary conditions can be relaxed either on $F_o{}^{\prime }\left(\eta \right)$ or $G_o\left(\eta \right)$ to determine the possible smallest eigenvalue. In this study, the condition $F_o{}^{\prime }\left(\eta \right)\to 0$ as $\eta \to \infty$ was relaxed and replaced by $F_o{}^{″}(0)=1$.

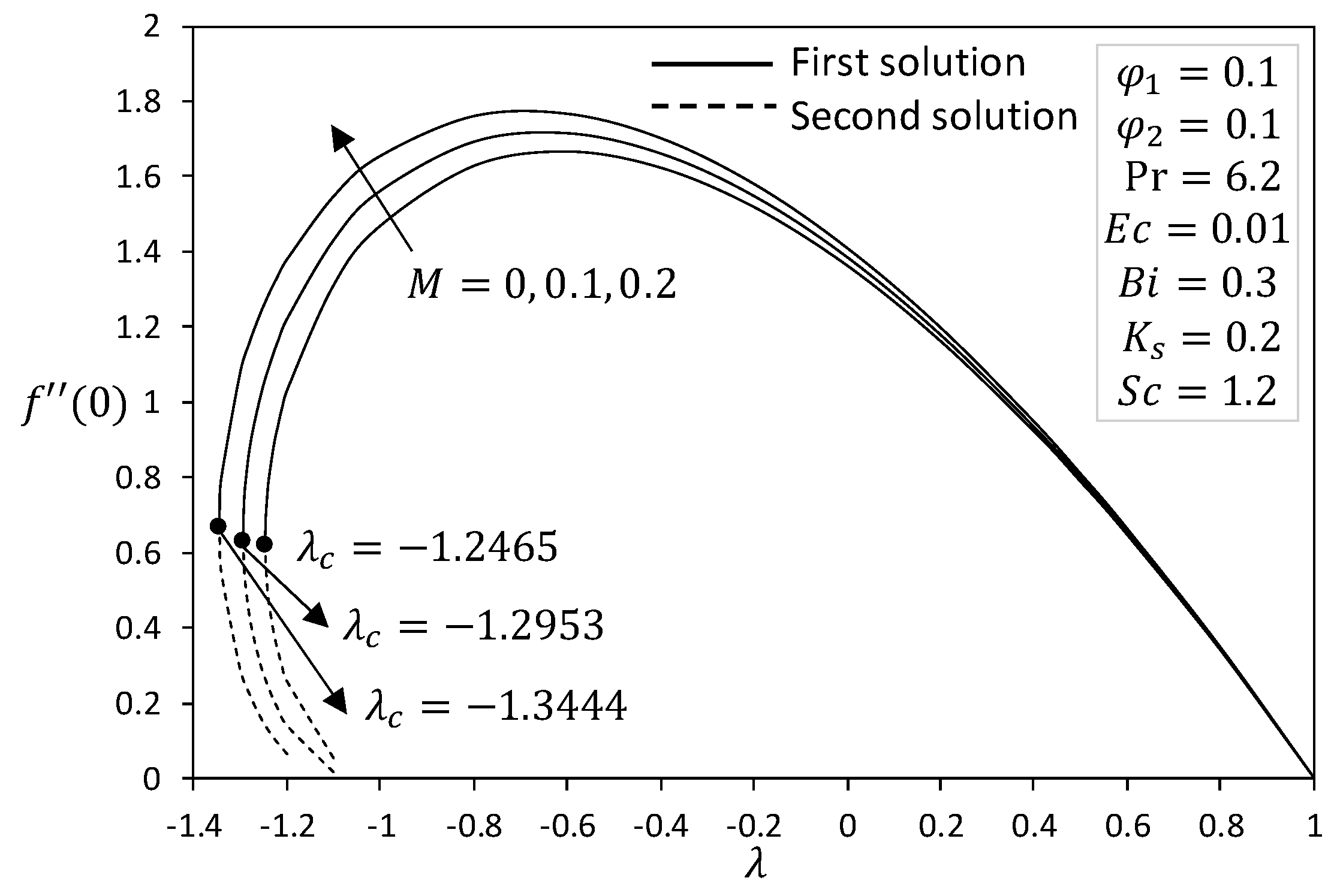
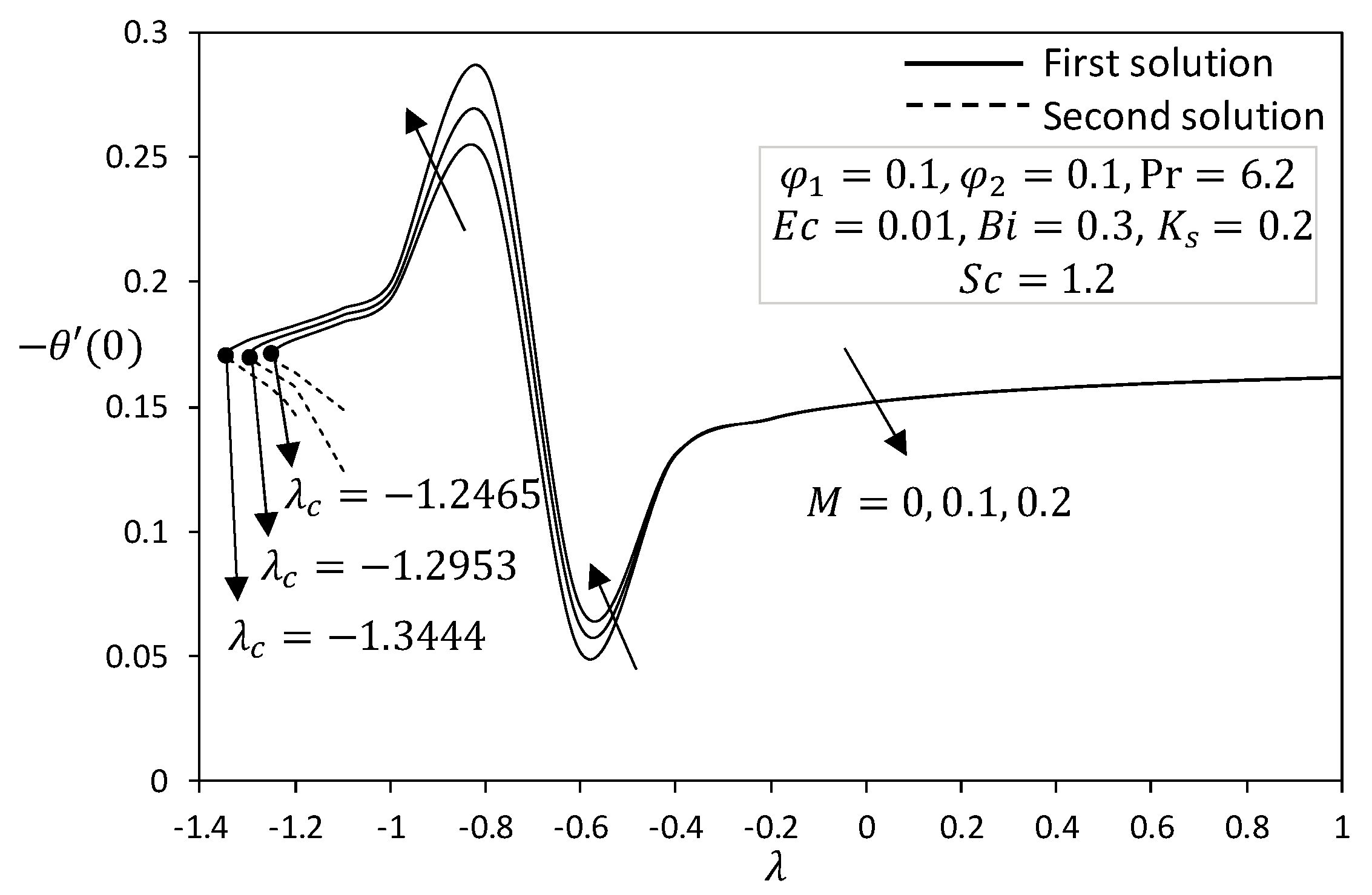
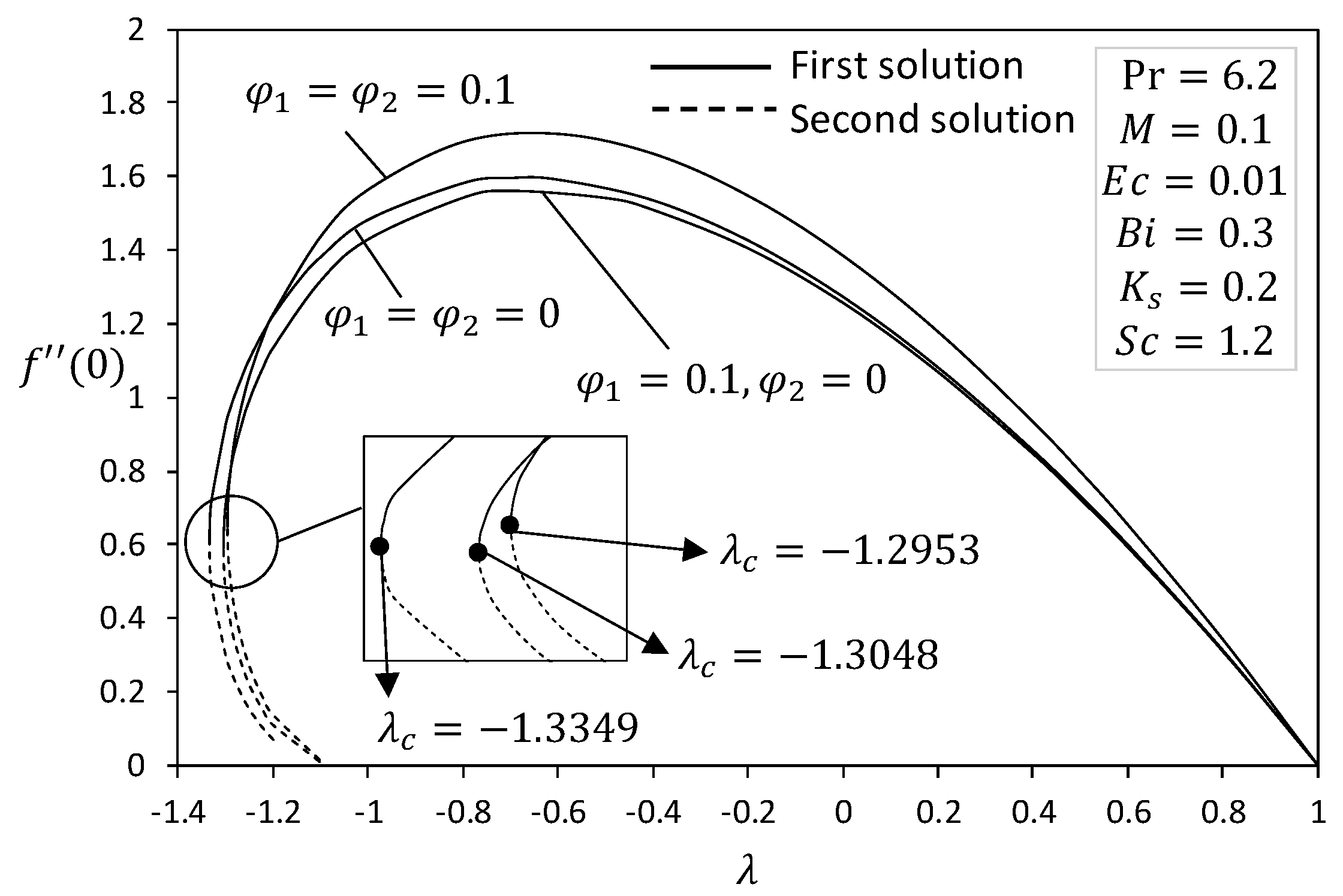
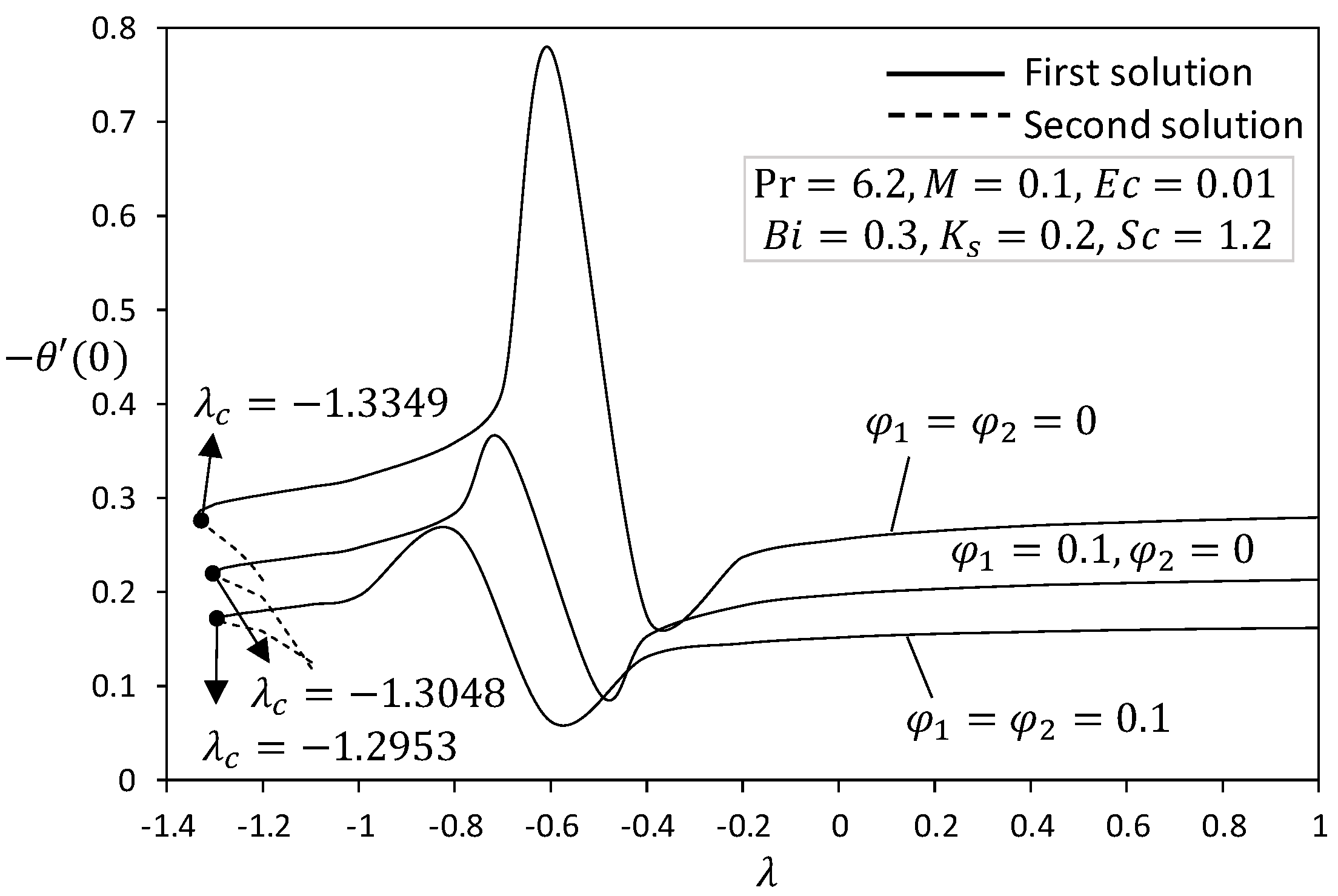
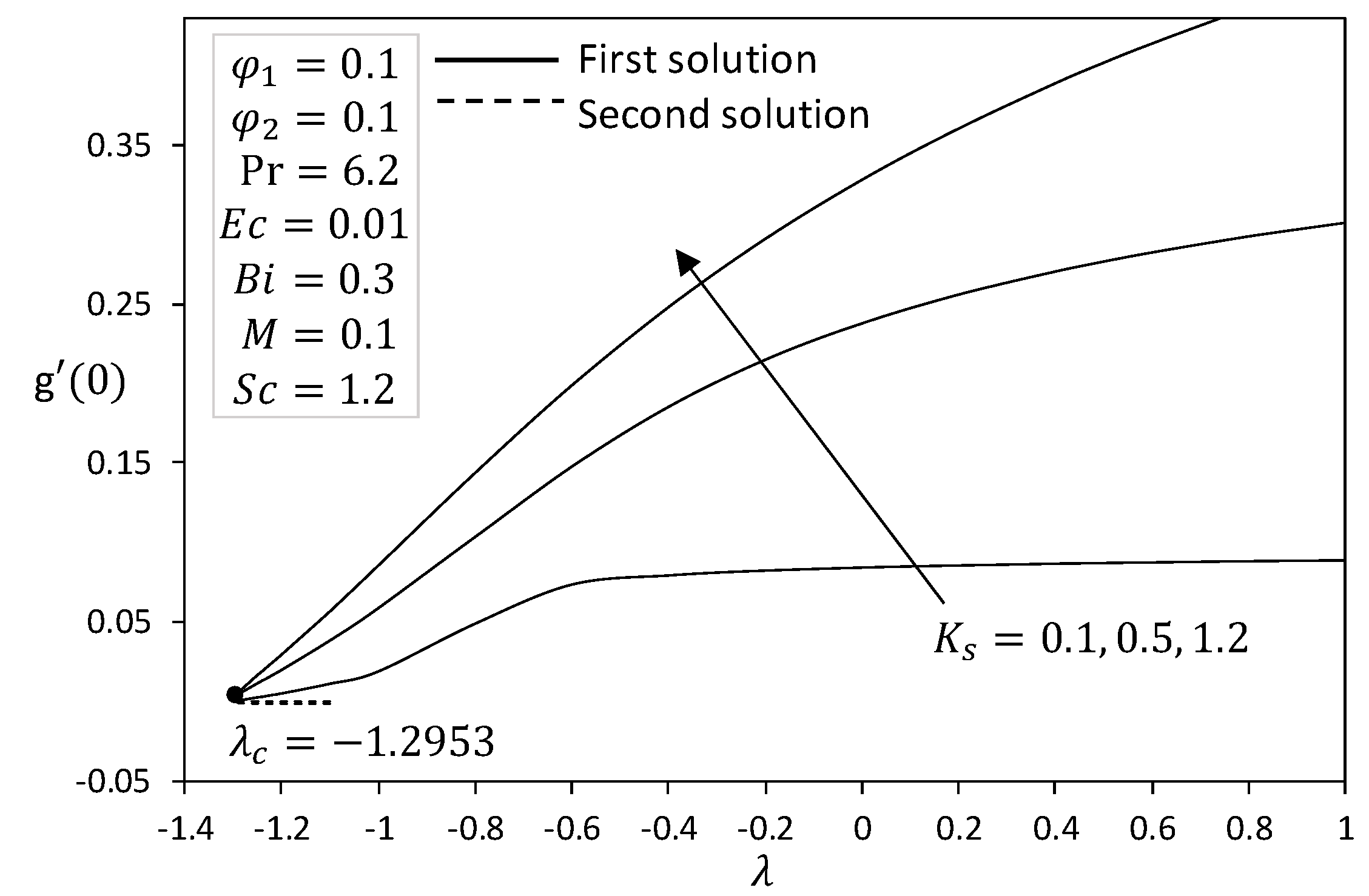
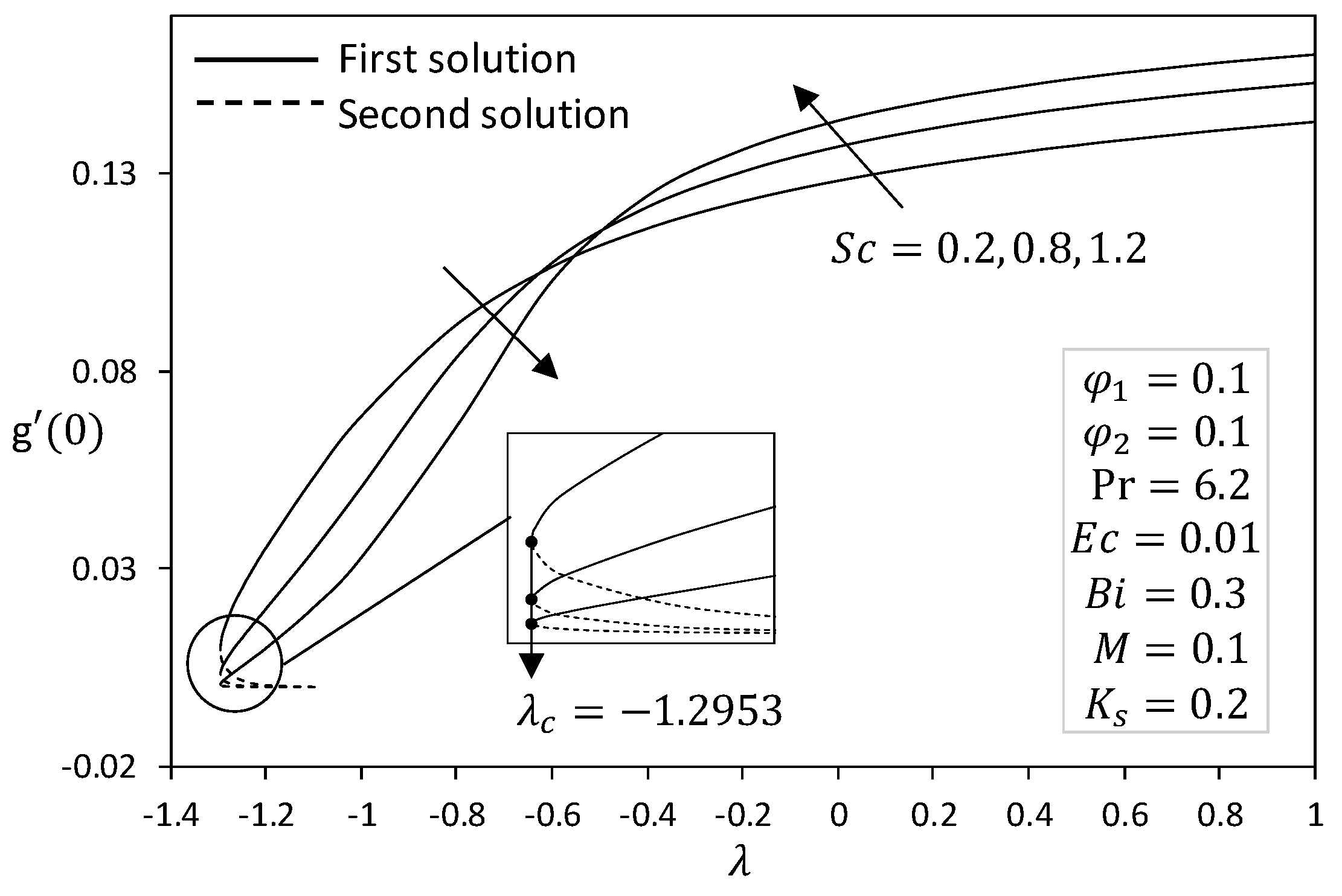
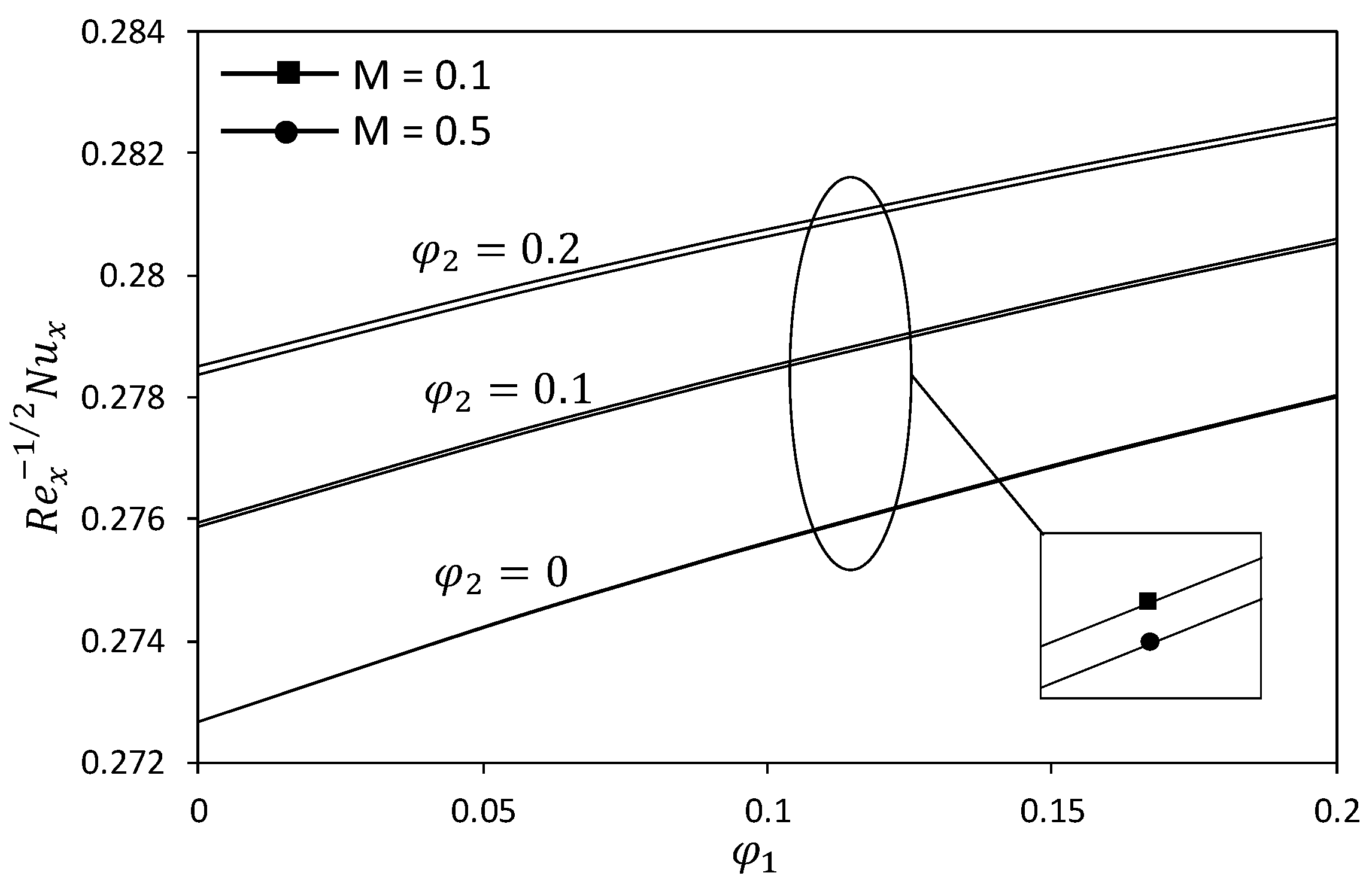
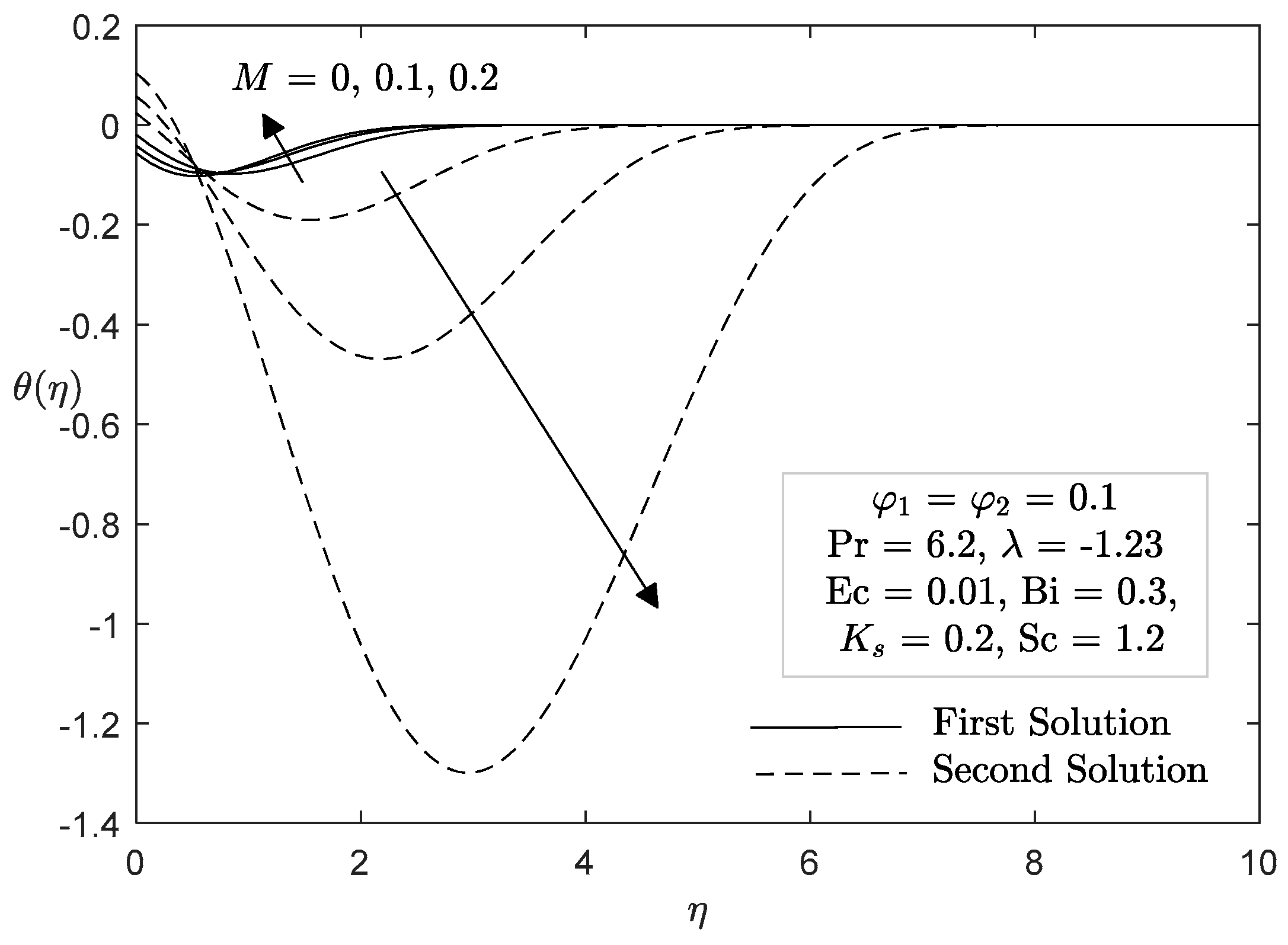
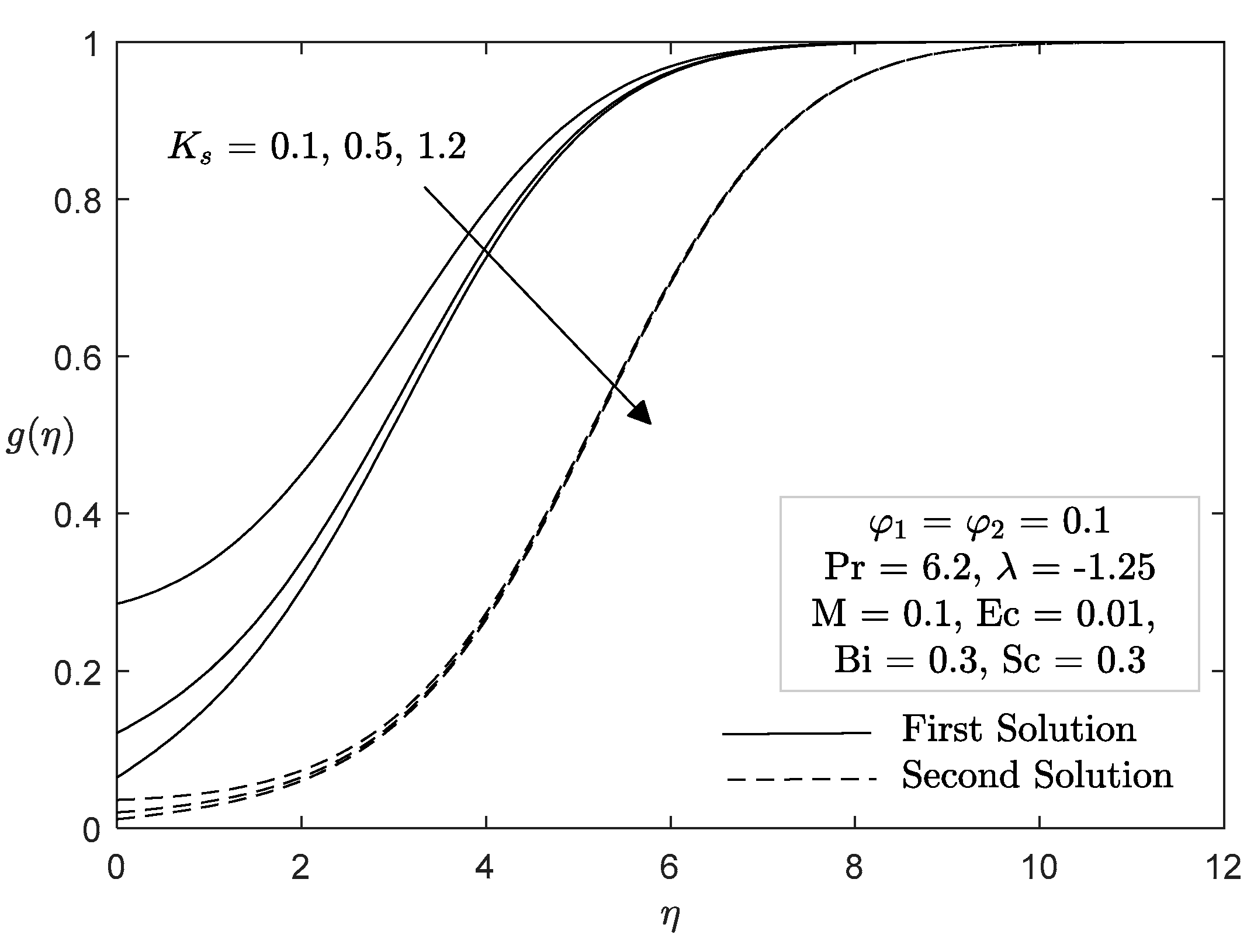
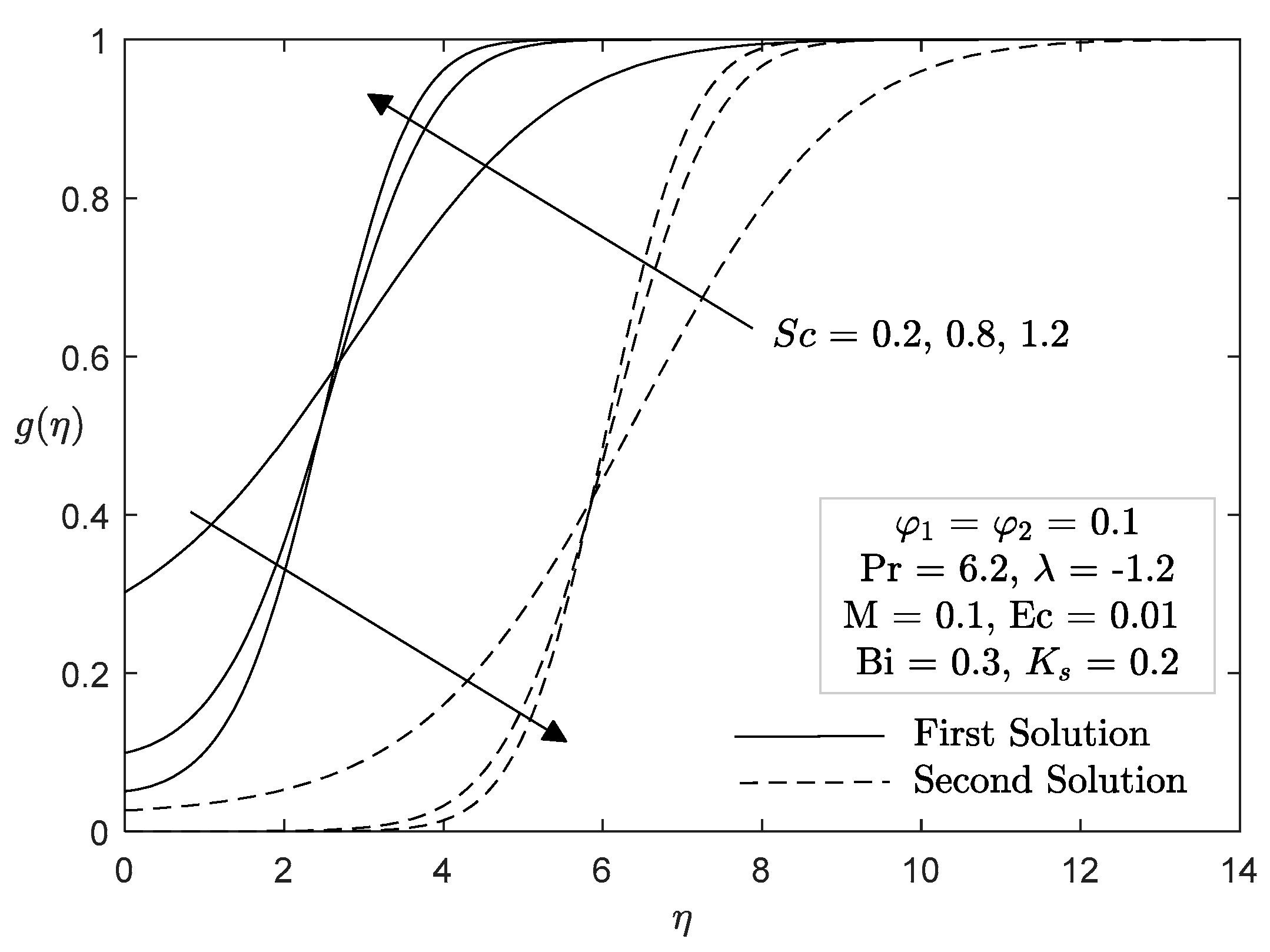
4. Analysis of Results

The set of transformed ODEs (11), (12) and (18) assigned with Conditions (15) and (19) were solved numerically, where the bvp4c function in computer software (MATLAB) was taken into practice. Following the work of Oztop and Abu-Nada [16], the value of $\mathrm{Pr}$ was fixed at 6.2 and the value of $\phi$ varied from 0 to 0.2. Comparisons with previously reported data from Bachok et al. [35] (viscous fluid) were made for several values of $\lambda$, as presented in

Table 2. Values of $f^{″}\left(0\right)$ at selected values of $\lambda$ when ${\phi }_1={\phi }_2=0,M=0$.

$\mathit{\lambda }$	Bachok et al. [35]		Present Result
	1st Solution	2nd Solution	1st Solution	2nd Solution
2	−1.887307		−1.887307
1	0		0
0.5	0.713295		0.713295
0	1.232588		1.232588
−1	1.328817	0	1.328817
−1.15	1.082231	0.116702	1.082231	0.116702
−1.2	0.932473	0.233650	0.932473	0.233650

, which show a favorable agreement, and thus give confidence that the numerical results obtained are accurate. The obtained results of reduced skin friction, $f^{″}\left(0\right)$, reduced heat transfer, $-{\theta }^{\prime }\left(0\right)$ and concentration, $g^{\prime }\left(0\right)$ are graphically illustrated for specific values of governing parameters, i.e., the Al₂O₃ nanoparticle ${\phi }_1$, Schmidt number $Sc$, Cu nanoparticle ${\phi }_2$, magnetic parameter $M$ and heterogeneous reaction parameter $K_s$. The variations of $f^{″}\left(0\right)$ and $-{\theta }^{\prime }\left(0\right)$ with the stretching/shrinking parameter $\lambda$ for different magnetic $M$ values are shown in Figure 1 and Figure 2, respectively. As the magnetic field occurs $\left(M>0\right)$, the separation of the boundary layer is bound to occur and hence the critical values of $\lambda$, which are given by ${\lambda }_c$, will become larger. This implies that the existence of a magnetic field will postpone the separation of the boundary layer. It is observed from these figures that non-unique solutions are visible in the range of ${\lambda }_c<\lambda <-1$ where ${\lambda }_c$ represents the critical value; a unique solution is visible as $\lambda \ge -1$ and no solution as $\lambda <{\lambda }_c$.

Figure 3 and Figure 4 demonstrate the effects of viscous flow, Al₂O₃-Cu/water hybrid nanofluid and Al₂O₃-water nanofluid on reduced skin friction $f^{″}\left(0\right)$ and heat transfer $-{\theta }^{\prime }\left(0\right)$. It is clearly seen that in the case of viscous flow $\left({\phi }_1={\phi }_2=0\right)$, the similarity solution only exists when $\lambda \ge {\lambda }_c=-1.3349$. However, when we considered Al₂O₃-water nanofluid $\left({\phi }_1=0.1,{\phi }_2=0\right)$, the range of solution became smaller $\left(\lambda \ge {\lambda }_c=-1.3048\right)$ and for Al₂O₃-Cu/water hybrid nanofluid $\left({\phi }_1={\phi }_2=0.1\right)$, the range of the similarity solution became even smaller $\left(\lambda \ge {\lambda }_c=-1.2953\right)$, respectively. This implies that Al₂O₃-Cu/water hybrid nanofluid quickens the separation of the boundary layer. The effects of the heterogeneous reaction parameter $K_s$ and Schmidt number $Sc$ on concentration $g^{\prime }\left(0\right)$ are graphically presented in Figure 5 and Figure 6. The concentration is clearly observed to be significantly enhanced with an increasing $K_s$ parameter. Additionally, higher values of $K_s$ cause the coefficient of diffusion to decrease, and thus fewer diffused particles intensify the concentration field. Further, it is noticed that the concentration increases for a large value of $Sc$ in the stretching sheet, and a contrary trend is seen for the shrinking sheet. It is worth mentioning that the Schmidt number is expressed as the ratio of momentum to mass diffusivity. As a result, the concentration profile is enhanced by the fact that the mass diffusivity is small for the increment values of the Schmidt number.

Figure 7 and Figure 8 show the variation of the skin friction coefficient ${\mathrm{Re}}_x^{1/2}{C}_f$ and Nusselt number ${\mathrm{Re}}_x^{-1/2}N{u}_x$ with the Al₂O₃ nanoparticle ${\phi }_1$ for different values of the Cu nanoparticle ${\phi }_2$ and magnetic parameter $M$. These figures show that the values of ${\mathrm{Re}}_x^{1/2}{C}_f$ and ${\mathrm{Re}}_x^{-1/2}N{u}_x$ increase almost linearly with the Al₂O₃ nanoparticle ${\phi }_1$. ${\mathrm{Re}}_x^{1/2}{C}_f$ increases with an increase of the Cu nanoparticle ${\phi }_2$ and magnetic parameter $M$, whereas ${\mathrm{Re}}_x^{-1/2}N{u}_x$ increases with an increase of the Cu nanoparticle ${\phi }_2$ and decreasing value of magnetic $M$ for the case of the stretching sheet $\lambda =0.5$. Figure 9, Figure 10, Figure 11 and Figure 12 present typical profiles for velocity $f^{\prime }\left(\eta \right)$, temperature $\theta \left(\eta \right)$ and concentration $g\left(\eta \right)$ for numerous parameters. It is clearly observed that all of these profiles satisfy Conditions (15) and (19) asymptotically with numerous shapes, hence supporting the findings of the present results. It should be noted that the existence of dual solutions in profiles of velocity, temperature and concentration supported the duality of the solutions mentioned in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6. Figure 9 and Figure 10 show that the momentum and thermal boundary layer thickness decrease as magnetic $M$ increases. The existence of a transverse magnetic field creates a Lorentz force that attracts more nanoparticles towards the surface, resulting in a retarding force on the flow velocity and higher temperature close to the wall. As expected, the boundary layer thickness of the first solution is always smaller than the second solution. However, different observations are seen from Figure 11 and Figure 12 in which increasing values of $K_s$ and $Sc$ cause the concentration thickness to increase.

Since non-unique solutions were visible in this study, it was important to conduct a stability analysis on the solutions. Therefore, by implementing the bvp4c package in Matlab software, the set of Equations (31)–(33) with the Boundary Condition (34) were solved, and the values of the smallest eigenvalues $\gamma$ in Equation (30) were obtained. When the values of $\gamma$ were negative, an initial rise in disturbances existed and the flow became unstable. Meanwhile, the initial decay occurred and the flow was said to be stable if the obtained value of $\gamma$ was positive.

Table 3. Smallest eigenvalues $\gamma$ at selected values of $M,{\phi }_2\mathrm{and}\lambda$ when ${\phi }_1=0.1,Ec=0.01,Bi=0.3,K_s=0.2$ and $Sc=1.2$.

$\mathit{M}$	${\mathit{\phi }}_2$	$\mathit{\lambda }$	1st Solution	2nd Solution
0.1	0	−1.3047	0.0269	−0.0268
		−1.304	0.0739	−0.0728
		−1.29	0.3224	−0.3033
	0.1	−1.2952	0.0346	−0.0344
		−1.295	0.0504	−0.0499
		−1.29	0.1923	−0.1853

illustrates the smallest eigenvalues $\gamma$ for some values of $\lambda$. The findings clearly show that the first and second solutions are represented by positive and negative $\gamma$, respectively. As mentioned earlier, the first solution is observed to be a stable flow whilst the second solution is an unstable flow. This is also consistent with the results obtained from previous researchers.

5. Conclusions

We investigated the problem of homogeneous–heterogeneous reactions in the MHD stagnation point flow of a hybrid nanofluid induced by a stretching/shrinking sheet with a convective boundary condition. The key findings were:

• Dual solutions were found to exist for the case of the shrinking sheet.
• The magnetic parameter $M$ widened the range of the solution to exist, whereas the hybrid nanofluid caused the range of similarity solutions to decrease.
• Hybrid nanofluid exhibited an outstanding performance in skin friction and heat transfer rates compared to other nanofluid.
• Increasing values of the magnetic parameter caused the skin friction increase and heat transfer rate to be decreased.
• The concentration increased as the heterogeneous reaction rate increased and the Schmidt number decreased.
• It was concluded that the first solution was stable and physically realizable, while the second solution was unstable.