On the Connection Problem for Painlevé Differential Equation in View of Geometric Function Theory

Abstract

Asymptotic analysis is a branch of mathematical analysis that describes the limiting behavior of the function. This behavior appears when we study the solution of differential equations analytically. The recent work deals with a special class of third type of Painlevé differential equation (PV). Our aim is to find asymptotic, symmetric univalent solution of this class in a symmetric domain with respect to the real axis. As a result that the most important problem in the asymptotic expansion is the connections bound (coefficients bound), we introduce a study of this problem.

1. Introduction

The advantage of the Painlevé differential equation (PV) is widely recognized in mathematics and mathematical physics, subsequently the outcomes indicate a part of the nonlinear explanation of special functions. Successively, various studies for the PVs have been offered from various points of vision, such as traditional outcomes, asymptotic, geometric or algebraic constructions. Asymptotic solution of PV-III is investigated extensively because of its requests in material sciences (see [1]). Shimomura [2] presented an asymptotic expansion formal by iteration, and showed the convergence utilizing a concept of majorant series. Kajiwara and Masuda [3] created the asymptotic expansion solution of PV-III by using an expression for the rational solutions whose entries are the Laguerre polynomials. Later, they extended the PV-III into the q-calculus and created the asymptotic expansion solutions by employing the symmetric affinity Weyl group [4]. Gu et al. studied the meromorphic results of PV-III by employing a technique of complex numbers [5]. Bothner et al. occupied the Bäcklund transformation of PV-III [6]. Fasondini et al. investigated the PV-III in a complex domain [7]. Bonelli et al. presented a generalization of PV-III by utilizing q-deformed calculus [8]. Amster and Rogers examined A Neumann-type boundary value problem for a hybrid PV-III. They established the existence properties of approximate outcomes [9]. Recently, Hong and Tu delivered meromorphic results for several types of q-difference PV-III [10]. Bilman et al. planned the fundamental rogue wave solutions of PV-III [11]. Newly, Zeng and Hu [12] suggested the connection problem of the second nonlinear differential equation involving a type of PV and they considered the asymptotic expansion solution.

In this work, we investigate a special class of generalized PV-III equations in a complex domain. We study the asymptotic expansion solution, univalent solution and approximate solution of this class in view of the geometric function theory. We formulate the PV-III as a boundary value problem in terms of the connection estimates. The consequences here are univalent solution with geometric illustration. The novelty of this work is to study a class of the PV equations analytically. The outcomes are based on the geometric function theory to describe the geometric behavior of these solutions. The upper bound of these solutions is indicated by using Janowski formula. Finally, we construct the symmetric solution by using a convex function in the open unit disk.

2. Methodology

The complex PV-III equation can be formulated by the following structure:

$${\displaystyle \zeta \chi (\zeta )\frac{d^2\chi (\zeta )}{d{\zeta }^2}=\zeta {\left(\frac{d\chi (\zeta )}{d\zeta }\right)}^2-\chi (\zeta )\frac{d\chi (\zeta )}{d\zeta }+\delta \zeta +\beta \chi (\zeta )+\alpha {\chi }^3(\zeta )+\gamma \zeta {\chi }^4(\zeta )},$$

(1)

where $\alpha ,\beta ,\gamma$ and $\delta$ are real constants. Kitaev [13] introduced the following special PV-III equation (see Equation (19), p. 83)

$$\zeta \frac{d^2\chi (\zeta )}{d{\zeta }^2}+\frac{d\chi (\zeta )}{d\zeta }=sin(\chi (\zeta )).$$

(2)

Asymptotically, Equation (2) becomes

$$\zeta \frac{d^2\chi (\zeta )}{d{\zeta }^2}+\frac{d\chi (\zeta )}{d\zeta }\approx \chi (\zeta ),$$

(3)

subjected to the boundary condition

$$\left(\chi (\zeta )=\zeta +{\chi }_2{\zeta }^2+O({\zeta }^3),|{\chi }_n|\le 1,n\ge 2,\zeta \in \cup =\{\zeta \in \mathbb{C}:|\zeta |<1\}\right),$$

(4)

where ${\chi }_n$ are indicated the coefficients of the expansion of $\chi (\zeta ).$ We are able to investigate the connection problem (coefficient bounds) of Equation (3) by studying the conforming connection problem of geometric classes in the open unit disk (∪). Our exploration method is selected from the GFT, specific the concept of subordination.

Let ∧ be the family of analytic functions $\chi \in \cup$ and normalized by the conditions $\chi (0)=0$ and ${\chi }^{\prime }(0)=1,$ formulating by

$$\chi (\zeta )=\zeta +\sum _{n=2}^{\infty }{\chi }_n{\zeta }^n,\zeta \in \cup .$$

(5)

A sub-class of ∧ is the class of univalent functions. Consequently, a function $\chi \in \wedge$ is starlike in ∪ if and only if $\Re (\zeta {\chi }^{\prime }(\zeta )/\chi (\zeta ))>0$. In addition, a function $\chi \in \wedge$ is convex in ∪ if and only if $1+\Re (\zeta {\chi }^{\prime }(\xi )/{\chi }^{\prime }(\zeta ))>0$.

It is clear that for functions $\chi \in \wedge ,$ we have $sin(\chi )\in \wedge .$ For example, the following asymptotic expansions for given functions in ∧ (see Figure 1)

$$sin\left(\frac{\zeta }{1-\zeta }\right)=\zeta +{\zeta }^2+(5{\zeta }^3)/6+{\zeta }^4/2+{\zeta }^5/120-(5{\zeta }^6)/8+O({\zeta }^7)$$

and

$$sin\left(\frac{\zeta }{{(1-\zeta )}^2}\right)=\zeta +2{\zeta }^2+(17{\zeta }^3)/6+3{\zeta }^4+(181{\zeta }^5)/120-(13{\zeta }^6)/4+O({\zeta }^7).$$

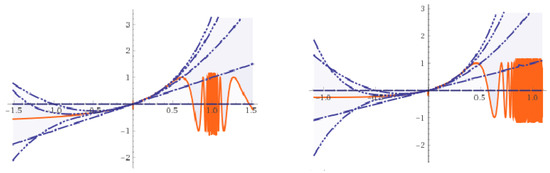
Figure 1. The asymptotic expansions of $sin\left(\frac{\zeta }{1-\zeta }\right)$ and $sin\left(\frac{\zeta }{{(1-\zeta )}^2}\right)$, respectively.

Definition 1.

For two functions χ and$\mathfrak{X}$in ∧ are subordinated$\chi \prec \mathfrak{X}$, if a Schwarz function ς with$\varsigma (0)=0$and$|\varsigma (\zeta )|<1$satisfying$\chi (\zeta )=\mathfrak{X}(\varsigma (\zeta )),\zeta \in \cup$(see [14]). Evidently,$\chi (\zeta )\prec \mathfrak{X}(\zeta )$equivalents to$\chi (0)=\mathfrak{X}(0)$and$\chi (\cup )\subset \mathfrak{X}(\cup ).$

Now, rearrange Equation (3), we have the formal

$$\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)=\rho (\zeta ),\zeta \in \cup ,$$

(6)

subjected to the boundary conditions (4), where $\rho (\zeta )=1+{\rho }_1\zeta +{\rho }_2{\zeta }^2+\dots .$

Definition 2.

For a function$\chi \in \wedge$, it is said to be in the class$\mathbf{V}(\rho )$if and only if

$$\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)\prec \rho (\zeta ),\zeta \in \cup ,$$

(7)

where$\rho (\zeta )=1+{\rho }_1\zeta +{\rho }_2{\zeta }^2+{\rho }_3{\zeta }^3+\dots$is convex in ∧ and positive real part with${\rho }^{\prime }(0)>0,\rho (0)=1$(we denote this class by$\mathcal{P}$).

For example, one can suggest the analytic function

$$\rho (\zeta )=\frac{1+\zeta }{1-\zeta }=1+2{\zeta }^2+2{\zeta }^3+\dots .$$

Remark 1.

Ma and Minda [15] formulated different sub-classes of starlike and convex functions for which either of the expressions$\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}$or$1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}$are subordinate to an additional common superordinate function. For this class, they presented an analytic function Θ with positive real part in ∪,$\mathsf{\Theta }(0)=1,{\mathsf{\Theta }}^{\prime }(0)>0,$and Θ maps ∪ onto an area starlike with respect to 1 and are symmetric with respect to the real axis. The class of Ma–Minda starlike functions contains function$\chi \in \wedge$satisfying the subordination$\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\prec \mathsf{\Theta }(\zeta )$. Likewise, the class of Ma–Minda convex functions involves the function$\chi \in \wedge$fluffing the subordination

$$1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\prec \mathsf{\Theta }(\zeta ).$$

Moreover, when$\mathsf{\Theta }(\zeta )=\frac{1+\zeta }{1-\zeta },$we obtain the main starlike and convex classes, respectively. Ali et al. [16] combined the two classes in the class

$$\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}+\frac{\zeta {\chi }^{″}(\xi )}{{\chi }^{\prime }(\zeta )}\prec \mathsf{\Theta }(\zeta ).$$

3. Connection Bounds

For functions in the class $\mathbf{V}(\rho )$, the following outcome is found.

Theorem 1.

If the function$\chi \in \mathbf{V}(\rho )$is formulated by (5), then

$$|{\chi }_2|\le \frac{{\rho }_1}{3},|{\chi }_3|\le \frac{{\rho }_2+{\rho }_1^2/3}{8},$$

(8)

where$\rho (\zeta )=1+{\rho }_1\zeta +{\rho }_2{\zeta }^2+{\rho }_3{\zeta }^3+\dots$is convex in ∧ and positive real coefficients.

Proof. 

Let $\chi \in \mathbf{V}(\rho )$ having the expansion

$$\chi (\zeta )=\zeta +{\chi }_2{\zeta }^2+{\chi }_3{\zeta }^3+\dots ,\zeta \in \cup .$$

Then by the definition of the subordination, there subsists a Schwarz function $\varsigma$ with $\varsigma (0)=0$ and $|\varsigma (\zeta )|<1$ satisfying

$$\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)=\rho (\varsigma (\zeta )),\zeta \in \cup .$$

Furthermore, we assume that $|\varsigma (\zeta )|=|\zeta |<1,$ then in view of Schwarz Lemma, there occurs a complex number $\tau$ with $|\tau |=1$ satisfying $\varsigma (\zeta )=\tau \zeta .$ Consequently, we obtain

$$\begin{array}{cc}\hfill \left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)& =\left(1+{\chi }_2\zeta +(2{\chi }_3-{\chi }_2^2){\zeta }^2+\dots \right)\hfill \\ \hfill & \times \left(1+2{\chi }_2\zeta +(6{\chi }_3-4{\chi }_2^2){\zeta }^2+\dots \right)\hfill \\ \hfill & =1+3{\chi }_2\zeta +(8{\chi }_3-3{\chi }_2^2){\zeta }^2+\dots \hfill \\ \hfill & =1+{\rho }_1\tau \zeta +{\rho }_2{\tau }^2{\zeta }^2+\dots .\hfill \end{array}$$

It follows that

$$|{\chi }_2|\le \frac{{\rho }_1|\tau |}{3}=\frac{{\rho }_1}{3}$$

and

$$|{\chi }_3|\le \frac{{\rho }_2+{\rho }_1^2/3}{8}.$$

 □

Example 1.

• Let$\rho (\zeta )=\frac{1+\zeta }{1-\zeta }=1+2{\zeta }^2+2{\zeta }^3+\dots$then$|{\chi }_2|\le \frac{2}{3},|{\chi }_3|\le \frac{{\rho }_2+{\rho }_1^2/3}{8}=0.416.$
• Let$\rho (\zeta )={\left(\frac{1+\zeta }{1-\zeta }\right)}^{0.5}=1+\zeta +{\zeta }^2/2+{\zeta }^3/2+(3{\zeta }^4)/8+(3{\zeta }^5)/8+O({\zeta }^6)\dots$then

  $$|{\chi }_2|\le \frac{1}{3},|{\chi }_3|\le \frac{0.5+1/3}{8}=0.104.$$

We have the following consequence.

Corollary 1.

If the function$\chi \in \mathbf{V}\left({\left(\frac{1+\zeta }{1-\zeta }\right)}^{\alpha }\right),\alpha \in (0,1]$then

$$|{\chi }_n|\le 1,n\ge 2.$$

(9)

4. Geometric Behaviors

In this section, we deal with some geometric behaviors of the boundary value problem (6).

Definition 3.

For a function$\chi \in \wedge$, it is said to be in the class$\mathbf{V}(\zeta +\sqrt{{\zeta }^2+1})$if and only if

$$\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)\prec \zeta +\sqrt{{\zeta }^2+1},\zeta \in \cup .$$

(10)

Note that (see Figure 2)

$$\zeta +\sqrt{{\zeta }^2+1}=1+\zeta +{\zeta }^2/2-{\zeta }^4/8+O({\zeta }^6)$$

and that the sub-classes of starlike and convex of the above definition are studied in [17].

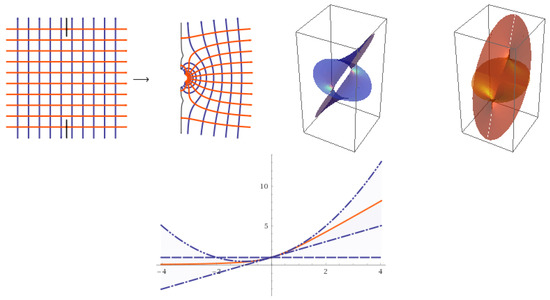
Figure 2. The complex plane, Riemann surface and the asymptotic expansions of $(\zeta +\sqrt{{\zeta }^2+1})$, respectively.

We request the following preliminary, which can be located in [17].

Lemma 1.

If P is analytic in ∪ and satisfies the subordination

$$P(\zeta )+\kappa \frac{\zeta P^{\prime }(\zeta )}{P(\zeta )}\prec (\zeta +\sqrt{{\zeta }^2+1}),\kappa >0,$$

then$P(\zeta )\prec (\zeta +\sqrt{{\zeta }^2+1}).$

Theorem 2.

If the function$\chi \in \wedge$is formulated by (5) fulfilling the subordination

$$\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)+\left(\frac{\zeta {\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)}^{\prime }}{\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)}+\frac{\zeta {\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)}^{\prime }}{\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)}\right)\prec (\zeta +\sqrt{{\zeta }^2+1})$$

(11)

then $\chi \in \mathbf{V}(\zeta +\sqrt{{\zeta }^2+1}).$ Moreover,

$$|{\chi }_2|\le \frac{1}{3},|{\chi }_3|\le \frac{24}{1152}.$$

Proof. 

Let $\chi \in \wedge$ having the expansion

$$\chi (\zeta )=\zeta +{\chi }_2{\zeta }^2+{\chi }_3{\zeta }^3+\dots ,\zeta \in \cup .$$

Furthermore, we let

$$P(\zeta ):=\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right).$$

Thus, in view of Lemma 1 with $\kappa =1$, we get

$$\begin{array}{cc}\hfill P(\zeta )+\frac{\zeta P^{\prime }(\zeta )}{P(\zeta )}& =\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)+\frac{\zeta {\left(\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)\right)}^{\prime }}{\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)}\hfill \\ \hfill & =\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)+\left(\frac{\zeta {\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)}^{\prime }}{\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)}+\frac{\zeta {\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)}^{\prime }}{\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)}\right)\hfill \\ \hfill & \prec (\zeta +\sqrt{{\zeta }^2+1})\hfill \end{array}$$

It follows that $P(\zeta )\prec (\zeta +\sqrt{{\zeta }^2+1}),$ which implies that $\chi \in \mathbf{V}(\zeta +\sqrt{{\zeta }^2+1}).$ Now, a computation implies that

$$\begin{array}{cc}\hfill \left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)& =1+3{\chi }_2\zeta +(8{\chi }_3-3{\chi }_2^2){\zeta }^2+\dots \hfill \\ \hfill & =1+\zeta +{\zeta }^2/2-{\zeta }^4/8+O({\zeta }^6).\hfill \end{array}$$

A comparison yields that

$$|{\chi }_2|\le \frac{1}{3},|{\chi }_3|\le \frac{24}{1152}.$$

 □

Next, result can be found in [18].

Lemma 2.

For analytic functions$\omega ,\varpi \in \cup ),$the subordination$\omega \prec \varpi$implies that

$${\int }_0^{2\pi }{|\omega (\zeta )|}^{q}d\theta \le {\int }_0^{2\pi }{|\varpi (\zeta )|}^{q}d\theta ,$$

where$\zeta =r{e}^{i\theta },0,r<1$and q is a positive number.

Theorem 3.

If the function$\chi \in \wedge$is formulated by (5) achieving the subordination inequality (11). Then

$$\begin{array}{cc}\hfill & {\int }_0^{2\pi }|\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right){|}^{q}d\theta \le 2\pi \hfill \end{array}$$

(12)

for all$q\ge 1$and$\zeta =r{e}^{i\theta }\in \cup$and $0<r<1.$

Proof. 

According to Theorem 2, we have

$$\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)\prec \zeta +\sqrt{{\zeta }^2+1}.$$

Then in view of Lemma 2, we conclude that

$$\begin{array}{cc}\hfill {\int }_0^{2\pi }|\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right){|}^{q}d\theta & \le {\int }_0^{2\pi }{|\zeta +\sqrt{{\zeta }^2+1}|}^{q}d\theta \hfill \\ & ={\int }_0^{2\pi }{|e^{i\theta }+\sqrt{{(e^{i\theta })}^2+1}|}^{q}d\theta ,r\to 1\hfill \\ & =2\pi .\hfill \end{array}$$

This completes the proof. □

Theorem 3 indicates the periodicity of solutions of the boundary value problem (6). We illustrate the following example (see Figure 3):

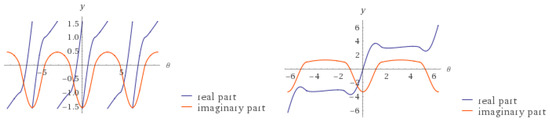
Figure 3. Periodic solution of Equation (6), when $q=1$ and $q=2$, respectively.

Example 2.

• Let$q=1$, we have

  $$\int |e^{i\theta }+\sqrt{{(e^{i\theta })}^2+1}|d\theta =-i(e^{i\theta }+\sqrt{1+e^{2i\theta }}-tan{h}^{-1}(\sqrt{1+e^{2i\theta })})+constant$$
• Let$q=2$then we get

  $$\int |e^{i\theta }+\sqrt{{(e^{i\theta })}^2+1}{|}^{2}d\theta =\theta -i{e}^{2i\theta }-i{e}^{i\theta }\sqrt{1+e^{2i\theta }}-i{sinh}^{-1}(e^{i\theta })+constant.$$

We proceed to study some geometric behaviors of Equation (6). We need the following concept.

Definition 4.

A majorization of two analytic functions having the asymptotic expansions respectively,$\chi (\zeta )={\sum }_{m=0}^{\infty }{\chi }_m{\zeta }^m$ and $\mathfrak{X}(\zeta )={\sum }_{m=0}^{\infty }{\mathfrak{X}}_m{\zeta }^m$is denoted by $\chi \ll \mathfrak{X}$and satisfies the connections bounds$|{\chi }_m|\le |{\mathfrak{X}}_m|,$for all$m.$

Definition 5.

For a function$\chi \in \wedge$, it is said to be in the class$\mathbf{V}(\frac{1+{\varrho }_1\zeta }{1+{\varrho }_2\zeta })$if and only if

$$\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)\prec \frac{1+{\varrho }_1\zeta }{1+{\varrho }_2\zeta },$$

(13)

where$\zeta \in \cup$and${\varrho }_1,{\varrho }_2\in \partial \cup .$

Theorem 4.

Let$\chi \in \mathbf{V}(\frac{1+{\varrho }_1\zeta }{1+{\varrho }_2\zeta }).$Then there is a probability measure ν on${(\partial \cup )}^2.$

Proof. 

Let $\chi \in \mathbf{V}(\frac{1+{\varrho }_1\zeta }{1+{\varrho }_2\zeta }).$ This yields that

$$\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)\prec \frac{1+{\varrho }_1\zeta }{1+{\varrho }_2\zeta }.$$

A calculation brings that $|{\chi }_n|\le 1$ for all $n\ge 1.$ Furthermore,

$$\begin{array}{cc}\hfill \frac{1+{\varrho }_1\zeta }{1+{\varrho }_2\zeta }& \ll \frac{1+\zeta }{1-\zeta }.\hfill \end{array}$$

(14)

According to Theorem 1.11 in [19], we obtain that the function $\frac{1+{\varrho }_1\zeta }{1+{\varrho }_2\zeta }$ indicates a probability measure $\nu$ in ${(\partial \cup )}^2$ achieving

$$\psi (\zeta )={\int }_{{(\partial \cup )}^2}\left(\frac{1+{\varrho }_1\zeta }{1+{\varrho }_2\zeta }\right)d\nu ({\varrho }_1,{\varrho }_2),\zeta \in \cup .$$

Then there is a diffusion constant A satisfying

$${\int }_{{(\partial \cup )}^2}\left(\frac{1+{\varrho }_1\zeta }{1+{\varrho }_2\zeta }\right)d\nu ({\varrho }_1,{\varrho }_2)=A{\int }_{{(\partial \cup )}^2}\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)d\nu ({\varrho }_1,{\varrho }_2)$$

$$\left(\zeta \in \cup ,A\in \mathbb{R},\chi \in \wedge \right).$$

 □

5. Symmetric Solution

In this section, we introduce a study regarding the symmetric solution of (6). For this purpose, we need to define a symmetric class as follows:

Definition 6.

For a function$\chi \in \wedge$, it is said to be in the symmetric class${\mathbf{V}}_{symmetric}(\mathsf{\Phi }),$where Φ takes the formula

$$\mathsf{\Phi }(\zeta )=\frac{1}{2}[\rho (\zeta )+\rho (-\zeta )],\zeta \in \cup ,\rho \in \mathcal{P},$$

where ρ is convex in ∪ if and only if

$$\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)\prec \mathsf{\Phi }(\zeta ),\zeta \in \cup .$$

(15)

In addition, a function$\chi \in \wedge$, is stated to be in the symmetric class${\mathbf{V}}_{symmetric}(\mathsf{\Psi }),$where Ψ is formulated by the symmetric construction

$$\mathsf{\Psi }(\zeta )=\frac{4\zeta \rho (\zeta )}{\rho (\zeta )-\rho (-\zeta )},\zeta \in \cup ,\rho \in \mathcal{P},$$

where ρ is convex in ∪ if and only if

$$\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)\prec \mathsf{\Psi }(\zeta ),\zeta \in \cup .$$

(16)

To establish the existence of symmetric solution of (6), we request the following result (see Theorem 3.2, p. 97 in [14]).

Lemma 3.

Let Φ be convex in ∪ such that$\mathsf{\Phi }(0)=1.$If ρ is the analytic solution of the equation

$$\rho (\zeta )+\frac{\zeta {\rho }^{\prime }(\zeta )}{\rho (\zeta )}=\mathsf{\Phi }(\zeta ),\rho (0)=1$$

and if$\Re (\rho )>0,$then ρ is univalent solution. If$P\in H[1,n]$(the class of analytic function) achieves the subordination

$$P(\zeta )+\frac{\zeta P^{\prime }(\zeta )}{P(\zeta )}\prec \mathsf{\Phi }(\zeta ),$$

then$P\prec \rho$and ρ is the best dominant.

Theorem 5.

Let$\chi \in {\mathbf{V}}_{symmetric}(\mathsf{\Phi }),$where$\rho \in \mathcal{P}$is convex and the functional

$$\mathsf{\Phi }(\zeta )=\frac{1}{2}[\rho (\zeta )+\rho (-\zeta )],\zeta \in \cup$$

satisfies the inequality

$$\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)+\left(\frac{\zeta {\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)}^{\prime }}{\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)}+\frac{\zeta {\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)}^{\prime }}{\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)}\right)\prec \mathsf{\Phi }(\zeta ).$$

(17)

Then$\chi \in \mathbf{V}(\rho ).$

Proof. 

Our aim is to achieve all the conditions of Lemma 3. Since $\rho$ is convex then $\mathsf{\Phi }$ is convex in ∪ such that $\mathsf{\Phi }(0)=1.$ Moreover, $\rho$ is the univalent solution of the equation

$$\frac{\zeta {\rho }^{\prime }(\zeta )}{\rho (\zeta )}=\frac{1}{2}[\rho (-\zeta )-\rho (\zeta )],\rho (0)=1$$

with $\Re (\rho )>0.$ Suppose that

$$P(\zeta ):=\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right).$$

Then, we obtain

$$\begin{array}{cc}\hfill P(\zeta )+\frac{\zeta P^{\prime }(\zeta )}{P(\zeta )}& =\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)+\frac{\zeta {\left(\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)\right)}^{\prime }}{\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)}\hfill \\ \hfill & =\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)+\left(\frac{\zeta {\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)}^{\prime }}{\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)}+\frac{\zeta {\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)}^{\prime }}{\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)}\right)\hfill \\ & \prec \mathsf{\Phi }(\zeta ).\hfill \end{array}$$

By Lemma 3, we have

$$\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)\prec \rho (\zeta ).$$

Hence, $\chi \in \mathbf{V}(\rho ).$ □

In the similar manner of Theorem 5, we have the following outcome

Theorem 6.

Let$\chi \in {\mathbf{V}}_{symmetric}(\mathsf{\Psi }),$where$\rho \in \mathcal{P}$is convex and the functional

$$\mathsf{\Psi }(\zeta )=\frac{4\zeta \rho (\zeta )}{\rho (\zeta )-\rho (-\zeta )},\zeta \in \cup$$

satisfies the inequality

$$\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)+\left(\frac{\zeta {\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)}^{\prime }}{\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)}+\frac{\zeta {\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)}^{\prime }}{\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)}\right)\prec \mathsf{\Psi }(\zeta ).$$

(18)

Then$\chi \in \mathbf{V}(\rho ).$

Example 3.

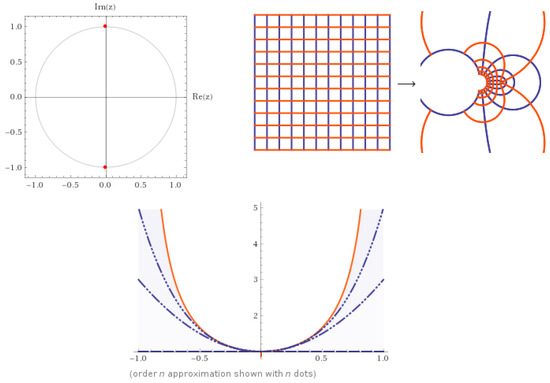
Consider the analytic function$\rho (\zeta )=\frac{1+\zeta }{1-\zeta },$where it maps ∪ onto the right half-plane convexly. Then$\mathsf{\Phi }(\zeta )=\frac{1+{\zeta }^2}{1-{\zeta }^2}=1+2{\zeta }^2+2{\zeta }^4+O({\zeta }^6),$where$\mathsf{\Phi }(0)=1$(see Figure 4). By assuming$\chi (\zeta )=\zeta ,$we have the subordination$P(\zeta )=\left(\frac{\zeta {\chi }^{\prime }(\zeta )}{\chi (\zeta )}\right)\left(1+\frac{\zeta {\chi }^{″}(\zeta )}{{\chi }^{\prime }(\zeta )}\right)\prec \mathsf{\Phi }(\zeta ).$Thus, the solution$\chi \in {\mathbf{V}}_{symmetric}(\frac{1+{\zeta }^2}{1-{\zeta }^2}).$

Figure 4. The behavior of $\mathsf{\Phi }(\zeta )=\frac{1+{\zeta }^2}{1-{\zeta }^2}$ with a symmetric domain for $|\zeta |,1$.

6. Conclusions

From above, we conclude that the asymptotic behaviors of a special class of Painlevé differential equations (see [13]) can be recognized by using a geometric representation of the equation. From this construction, we introduced the oscillatory, connection bound and other properties of the boundary value problem (6). In addition, Theorem 5 and Theorem 6 indicated that the set $\{\chi :\chi \in \mathbf{V}(\rho )\}$ has symmetric solutions for some symmetric region because ${\mathbf{V}}_{symmetric}(\mathsf{\Phi })\subset \mathbf{V}(\rho )$ and ${\mathbf{V}}_{symmetric}(\mathsf{\Psi })\subset \mathbf{V}(\rho ).$