On a Simplified Method of Defining Characteristic Function in Stochastic Games
Abstract
1. Introduction
2. Cooperative Stochastic Games
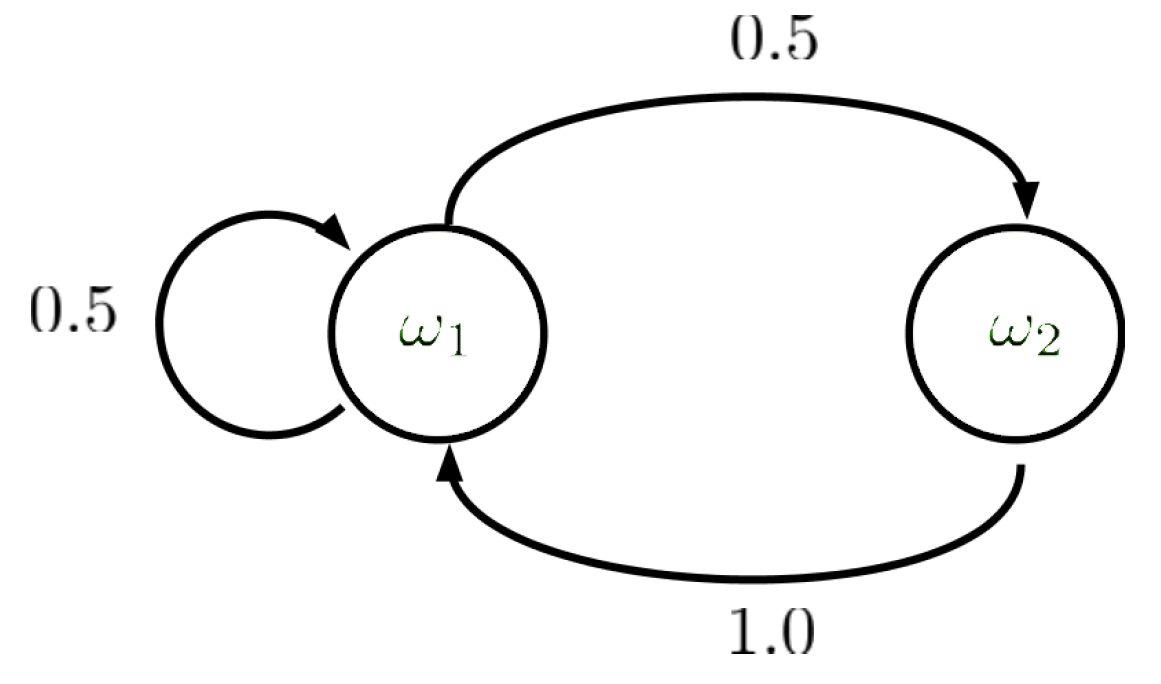
2.1. Model
- is the set of players.
- is the finite set of states.
- is the game in normal form associated with state . The set of players N is common for any state . Let be a finite set of actions of player in state , be an action of player in this state; be a payoff function of player i in state .
- is a transition function from state when action profile is realized, where is a probability distribution over set .
- is an initial state distribution.
- is a common discount factor.
2.2. Approximated Characteristic Function for State Games
- in state :
- in state :
- for state :
- for state :The first (second) element in any entry of the matrix is the probability of transition from the particular state and action profile to state (state ). One can easily notice that the probabilistic transitions are defined in state when players choose action profiles , and , and in state when players choose action profiles . All other transitions are deterministic.
2.3. New Approximated Characteristic Function for Stochastic Games
3. Strongly Subgame-Consistent Core in Stochastic Games
3.1. Imputation Distribution Procedure
- for any ;
- , where is the expected discounted sum of payments to player i in stochastic subgame starting from state ω, according to procedure β.
3.2. Strongly Subgame-Consistent Core
- Find the sum of over the set of players, we obtainor for any the equality is true.
- We prove that or in vector form , where . We have
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Von Neumann, J.; Morgenstern, O. Theory of Games and Economic Behavior; Princeton University Press: Princeton, NJ, USA, 1944. [Google Scholar]
- Aumann, R.J.; Peleg, B. Von Neumann-Morgenstern Solutions to Cooperative Games without Side Payments. Bull. Am. Math. 1960, 66, 173–179. [Google Scholar] [CrossRef]
- Chander, P.; Tulkens, H. The core of an economy with multilateral environmental externalities. Int. J. Game Theory 1997, 26, 379–401. [Google Scholar] [CrossRef]
- Chander, P. The gamma-core and coalition formation. Int. J. Game Theory 2007, 35, 539–556. [Google Scholar] [CrossRef]
- Petrosyan, L.; Zaccour, G. Time-consistent Shapley value allocation of pollution cost reduction. J. Econ. Dyn. Control. 2003, 27, 381–398. [Google Scholar] [CrossRef]
- Zaccour, G. Computation of Characteristic function values for linear-state differential games. J. Optim. Theory Appl. 2003, 117, 183–194. [Google Scholar] [CrossRef]
- Reddy, P.V.; Zaccour, G. A friendly computable characteristic function. Math. Soc. Sci. 2016, 82, 18–25. [Google Scholar] [CrossRef]
- Petrosyan, L.A.; Gromova, E.V. On an approach to constructing a characteristic function in cooperative differential games. Autom. Remote Control. 2017, 78, 1680–1692. [Google Scholar]
- Pankratova, Y.B.; Petrosyan, L.A. New Characteristic Function for Multistage Dynamic Games. 2018. Available online: https://cyberleninka.ru/article/n/new-characteristic-function-for-multistage-dynamic-games (accessed on 10 June 2020).
- Petrosjan, L.A. Consistency of Solutions of Differential Games with Many Players; Vestnik of Leningrad University, Series Mathematics, Mechanics; Astronomy: Saint Petersburg, Russia, 1977; pp. 46–52. [Google Scholar]
- Petrosjan, L.A.; Danilov, N.A. Time-Sonsitent Solutions of Non-Antagonistic Differential Games with Transferable Payoffs; Vestnik Leningrad University: Saint Petersburg, Russia, 1979; pp. 52–59. [Google Scholar]
- Petrosjan, L.A. Cooperative stochastic games. In Advances in Dynamic Games. Annals of the International Society of Dynamic Games; Haurie, A., Muto, S., Petrosjan, L.A., Raghavan, T.E.S., Eds.; Birkhauser: Boston, MA, USA, 2006; Volume 8, pp. 52–59. [Google Scholar]
- Avrachenkov, K.; Cottatellucci, L.; Maggi, L. Cooperative Markov decision processes: Time consistency, greedy players satisfaction, and cooperation maintenance. Int. J. Game Theory 2013, 42, 39–262. [Google Scholar] [CrossRef]
- Parilina, E.M. Stable cooperation in stochastic games. Autom. Remote. Control. 2015, 76, 1111–1122. [Google Scholar] [CrossRef]
- Parilina, E.; Zaccour, G. Node-Consistent Core for Games Played over Event Trees. Automatica 2015, 53, 304–311. [Google Scholar] [CrossRef]
- Petrosjan, L.A. Construction of Strongly Time Consistent Solutions in Cooperative Differential Games; Birkhäuser: Cham, Switzerland, 1992; pp. 33–38. [Google Scholar]
- Petrosyan, L. Strong Strategic Support of Cooperation in Multistage Games. Int. Game Theory Rev. 2019, 21, 1940004. [Google Scholar] [CrossRef]
- Parilina, E.M.; Petrosyan, L.A. Strongly Subgame-Consistent Core in Stochastic Games. Autom. Remote Control. 2018, 79, 1515–1527. [Google Scholar] [CrossRef]
- Petrosian, O.; Gromova, E.; Pogozhev, S. Strong Time-Consistent Subset of the Core in Cooperative Differential Games with Finite Time Horizon. Autom. Remote Control. 2018, 79, 1912–1928. [Google Scholar] [CrossRef]
- Sedakov, A.A. On the Strong Time Consistency of the Core. Autom. Remote Control. 2018, 79, 757–767. [Google Scholar] [CrossRef]
- Parilina, E.; Tampieri, A. Stability and Cooperative Solution in Stochastic Games. Theory Decis. 2018, 84, 601–625. [Google Scholar] [CrossRef]
- Shapley, L.S. Stochastic Games. Proc. Natl. Acad. Sci. USA 1953, 39, 1095–1100. Available online: https://www.pnas.org/content/39/10/1095.short (accessed on 28 May 2020). [CrossRef] [PubMed]
- Bondareva, O.N. Some applications of linear programming methods to the theory of cooperative games. Problemy Kybernetiki 1963, 10, 119–139. [Google Scholar]
- Shapley, L.S. On balanced sets and cores. Nav. Res. Logist. Q. 1967, 14, 453–460. [Google Scholar] [CrossRef]
- Peleg, B.; Sudhölter, P. Introduction to the Theory of Cooperative Games; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
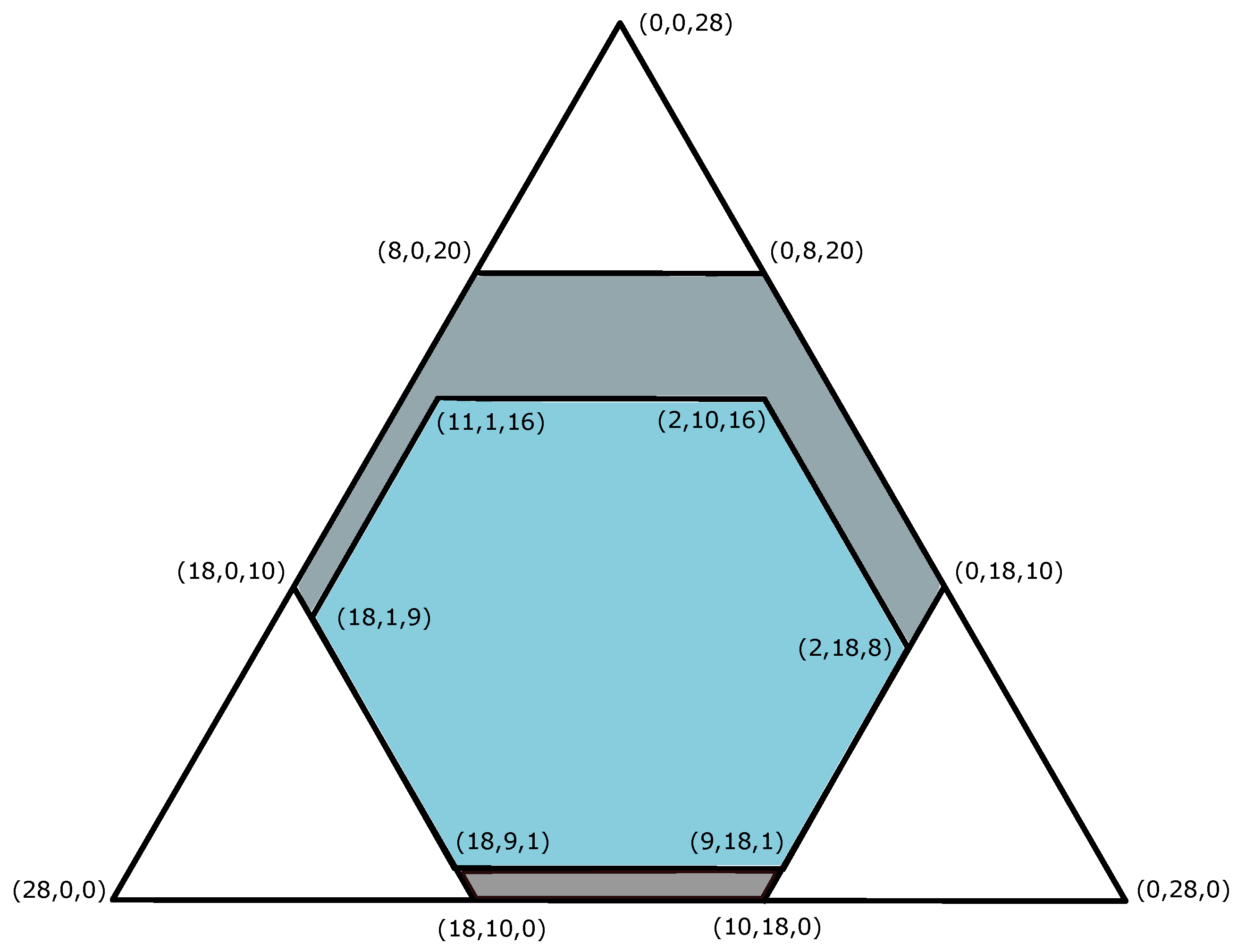

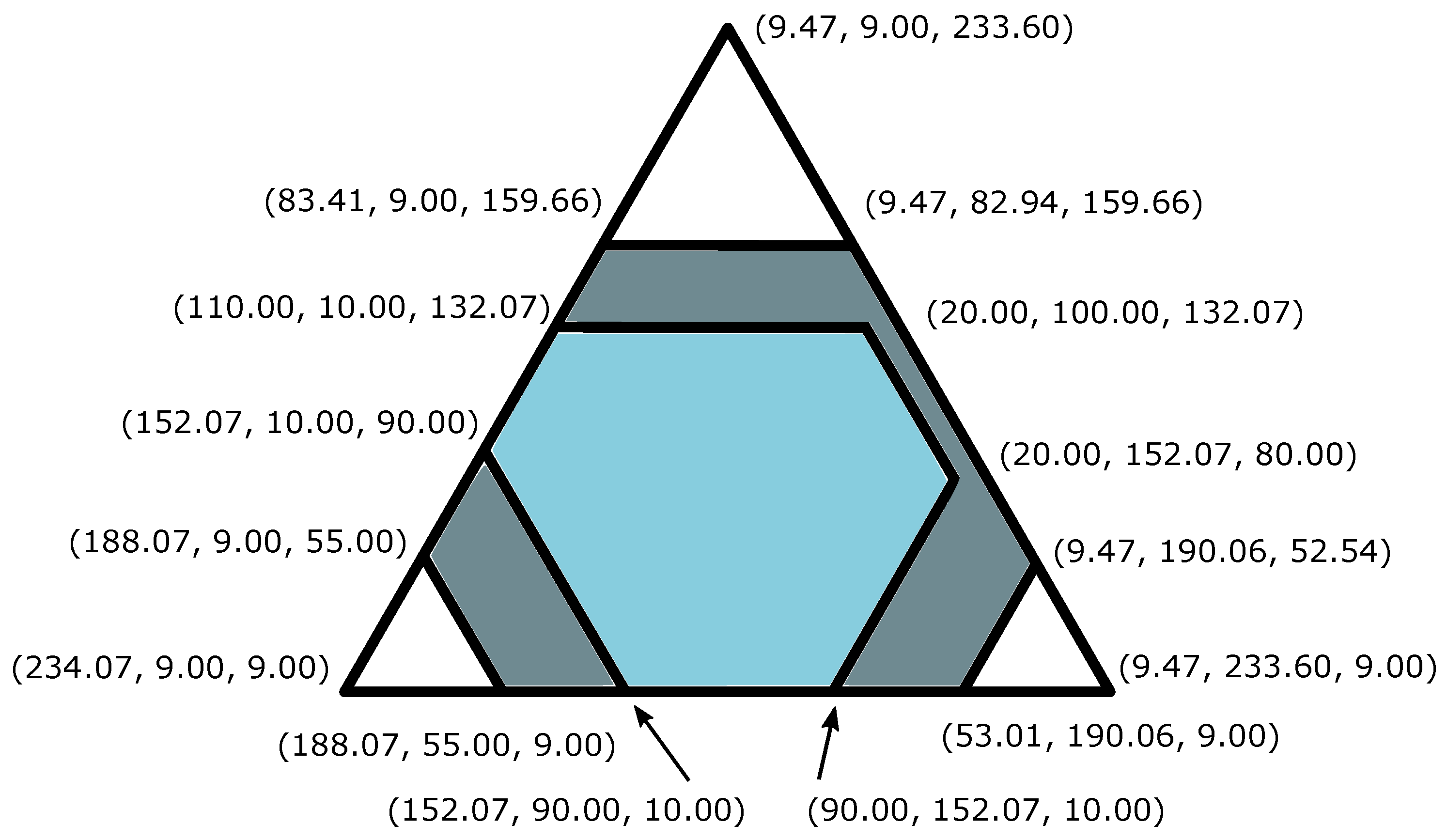
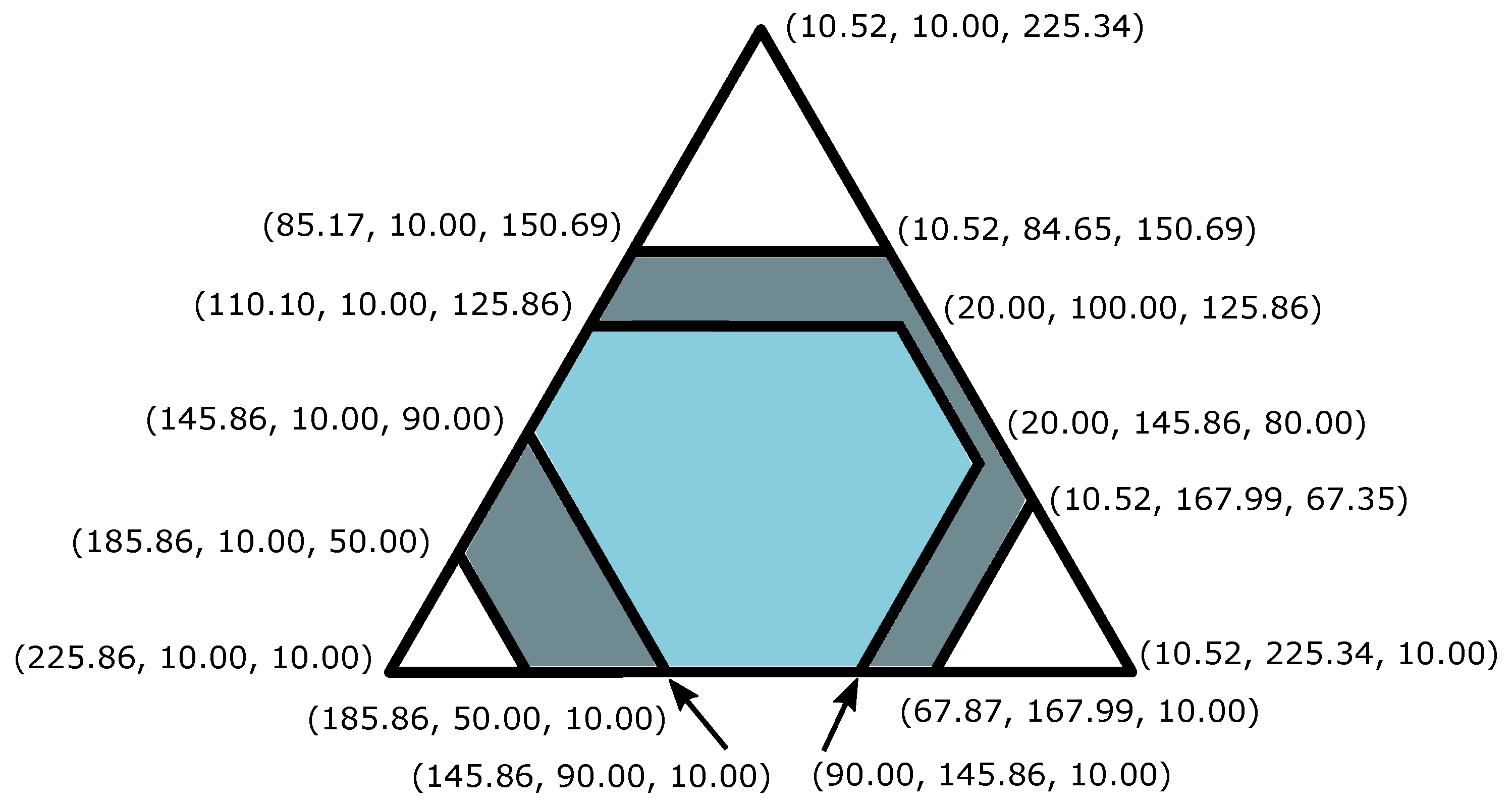
| S | |||||||
|---|---|---|---|---|---|---|---|
| 28 | 8 | 10 | 10 | 0 | 0 | 0 | |
| 19 | 12 | 6 | 8 | 2 | 1 | 1 | |
| 28 | 12 | 10 | 10 | 2 | 1 | 1 | |
| 19 | 12 | 10 | 10 | 2 | 1 | 1 |
| S | |||||||
|---|---|---|---|---|---|---|---|
| 252.07 | 92.41 | 62.01 | 64.00 | 9.47 | 9.00 | 9.00 | |
| 245.86 | 95.17 | 77.87 | 60.00 | 10.52 | 10.00 | 10.00 | |
| 252.07 | 120.00 | 100.00 | 100.00 | 20.00 | 10.00 | 10.00 | |
| 245.86 | 120.00 | 100.00 | 100.00 | 20.00 | 10.00 | 10.00 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parilina, E.; Petrosyan, L. On a Simplified Method of Defining Characteristic Function in Stochastic Games. Mathematics 2020, 8, 1135. https://doi.org/10.3390/math8071135
Parilina E, Petrosyan L. On a Simplified Method of Defining Characteristic Function in Stochastic Games. Mathematics. 2020; 8(7):1135. https://doi.org/10.3390/math8071135
Chicago/Turabian StyleParilina, Elena, and Leon Petrosyan. 2020. "On a Simplified Method of Defining Characteristic Function in Stochastic Games" Mathematics 8, no. 7: 1135. https://doi.org/10.3390/math8071135
APA StyleParilina, E., & Petrosyan, L. (2020). On a Simplified Method of Defining Characteristic Function in Stochastic Games. Mathematics, 8(7), 1135. https://doi.org/10.3390/math8071135





