Construction of Solitary Two-Wave Solutions for a New Two-Mode Version of the Zakharov-Kuznetsov Equation
Abstract
:1. Introduction
- and are the scaled space and time coordinates.
- is the height of the water’s free surface above the flat bottom.
- and are the phase velocities.
- and are the linearity parameters.
- and are the dispersion parameters.
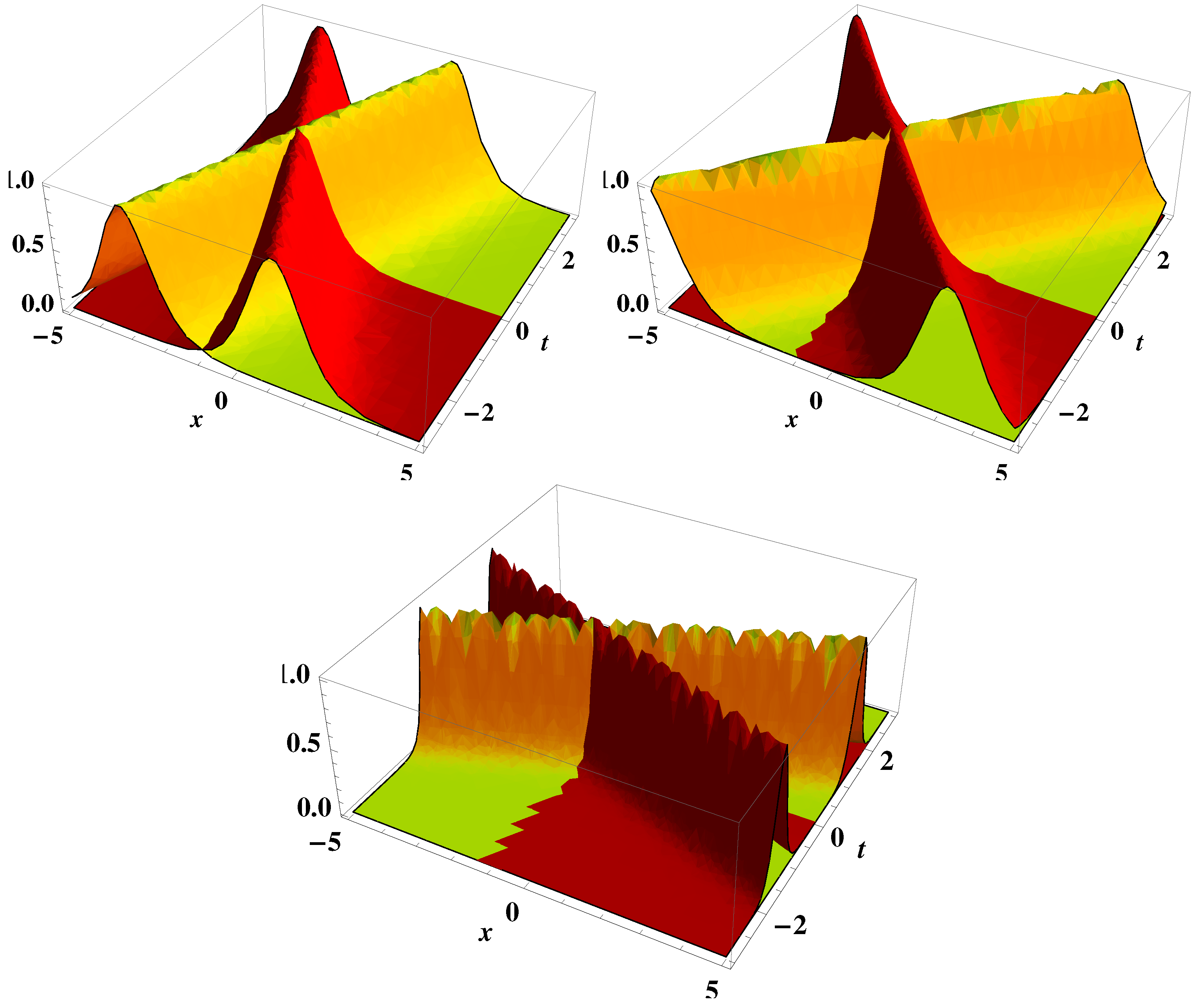
2. Bell-Shaped Soliton Solutions
3. Kudryashov Expansion Method
4. Simplified Bilinear Method
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Baskonus, H.M.; Koç, D.A.; Gülsu, M.; Bulut, H. New wave simulations to the (3+1)-dimensional modified KdV-Zakharov-Kuznetsov equation. AIP Conf. Proc. 2017, 1863, 560085. [Google Scholar]
- Yavuz, M.; Yokus, A. Analytical and numerical approaches to nerve impulse model of fractional-order. Numer. Methods Partial. Differ. Eq. 2020. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Bulut, H. On the complex structures of Kundu-Eckhaus equation via improved Bernoulli sub-equation function method. Waves Random Complex Media 2015, 25, 720–728. [Google Scholar] [CrossRef]
- Alquran, M.; Qawasmeh, A. Classifications of solutions to some generalized nonlinear evolution equations and systems by the sine-cosine method. Nonlinear Stud. 2013, 20, 263–272. [Google Scholar]
- Ali, M.; Alquran, M.; Jaradat, I.; Baleanu, D. Stationary wave solutions for new developed two-waves’ fifth-order Korteweg–de Vries equation. Adv. Diff. Eq. 2019, 2019, 263. [Google Scholar] [CrossRef] [Green Version]
- Ali, M.; Alquran, M.; Jaradat, I.; Afouna, N.A.; Baleanu, D. Dynamics of integer-fractional time-derivative for the new two-mode Kuramoto-Sivashinsky model. Rom. Rep. Phys. 2020, 72, 103. [Google Scholar]
- Alquran, M.; Jaradat, I.; Ali, M.; Baleanu, D. The dynamics of new dual-mode Kawahara equation: Interaction of dual-waves solutions and graphical analysis. Phys. Scr. 2020, 95, 045216. [Google Scholar] [CrossRef]
- Alquran, M.; Jaradat, I.; Ali, M.; Al-Ali, N.; Momani, S. Development of spreading symmetric two-waves motion for a family of two-mode nonlinear equations. Heliyon 2020, 6, e04057. [Google Scholar] [CrossRef] [PubMed]
- Zakharov, V.E.; Kuznetsov, E.A. On three-dimensional solitons. Sov. Phys. 1974, 39, 285–288. [Google Scholar]
- Monro, S.; Parkes, E.J. The derivation of a modified Zakharov-Kuznetsov equation and the stability of its solutions. J. Plasma Phys. 1999, 62, 305–317. [Google Scholar] [CrossRef]
- Monro, S.; Parkes, E.J. Stability of solitary-wave solutions to a modified Zakharov-Kuznetsov equation. J. Plasma Phys. 2000, 64, 411–426. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, X. The construction of solutions to Zakharov-Kuznetsov equation with fractional power nonlinear terms. Adv. Diff. Eq. 2019, 2019, 134. [Google Scholar] [CrossRef]
- Schamel, H. A modified Korteweg–de-Vries equation for ion acoustic waves due to resonant electrons. J. Plasma Phys. 1973, 9, 377–387. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Exact solutions with solitons and periodic structures for the Zakharov-Kuznetsov (ZK) equation and its modified form. Commun. Nonlinear Sci. Numer. Simul. 2005, 10, 597–606. [Google Scholar] [CrossRef]
- Li, B.; Chen, Y.; Zhang, H. Exact travelling wave solutions for a generalized Zakharov-Kuznetsov equation. Appl. Math. Comput. 2003, 146, 653–666. [Google Scholar] [CrossRef]
- Shivamoggi, B.K. The Painlevé analysis of the Zakharov-Kuznetsov equation. Phys. Scr. 1990, 42, 641–642. [Google Scholar] [CrossRef]
- Gear, J.A.; Grimshaw, R. Weak and strong interactions between internal solitary waves. Stud. Appl. Math. 1984, 70, 235–258. [Google Scholar] [CrossRef]
- Korsunsky, S.V. Soliton solutions for a second-order KdV equation. Phys. Lett. A 1994, 185, 174–176. [Google Scholar] [CrossRef]
- Zhao, P.F.; Qin, M.Z. Multisymplectic geometry and multisymplectic Preissmann scheme for the KdV equation. J. Phys. A 2000, 33, 3613–3626. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Two-mode Sharma-Tasso-Olver equation and two-mode fourth-order Burgers equation: Multiple kink solutions. Alexandria Eng. J. 2018, 57, 1971–1976. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A study on a two-wave mode Kadomtsev-Petviashvili equation: Conditions for multiple soliton solutions to exist. Math. Method Appl. Sci. 2017, 40, 4128–4133. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Two-mode fifth-order KdV equations: Necessary conditions for multiple-soliton solutions to exist. Nonlinear Dyn. 2017, 87, 1685–1691. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Two wave mode higher-order modified KdV equations: Essential conditions for multiple soliton solutions to exist. Int. J. Numer. Method Heat 2017, 27, 2223–2230. [Google Scholar] [CrossRef]
- Jaradat, H.M. Two-mode coupled Burgers equation: Multiple-kink solutions and other exact solutions. Alexandria Eng. J. 2018, 57, 2151–2155. [Google Scholar] [CrossRef]
- Syam, M.; Jaradat, H.M.; Alquran, M. A study on the two-mode coupled modified Korteweg–de Vries using the simplified bilinear and the trigonometric-function methods. Nonlinear Dyn. 2017, 90, 1363–1371. [Google Scholar] [CrossRef]
- Jaradat, H.M.; Syam, M.; Alquran, M. A two-mode coupled Korteweg–de Vries: Multiple-soliton solutions and other exact solutions. Nonlinear Dyn. 2017, 90, 371–377. [Google Scholar] [CrossRef]
- Alquran, M.; Jaradat, H.M.; Syam, M. A modified approach for a reliable study of new nonlinear equation: Two-mode Korteweg–de Vries-Burgers equation. Nonlinear Dyn. 2018, 91, 1619–1626. [Google Scholar] [CrossRef]
- Alquran, M.; Yassin, O. Dynamism of two-mode’s parameters on the field function for third-order dispersive Fisher: Application for fibre optics. Opt. Quant. Electron. 2018, 50, 354. [Google Scholar] [CrossRef]
- Jaradat, A.; Noorani, M.S.M.; Alquran, A.; Jaradat, H.M. Construction and solitary wave solutions of two-mode higher-order Boussinesq-Burger system. Adv. Diff. Eq. 2017, 2017, 376. [Google Scholar] [CrossRef] [Green Version]
- Jaradat, H.M.; Alquran, A.; Syam, I. A reliable study of new nonlinear equation: Two-mode Kuramoto-Sivashinsky. Int. J. Appl. Comput. Math. 2018, 4, 64. [Google Scholar] [CrossRef]
- Alquran, M.; Jarrah, A. Jacobi elliptic function solutions for a two-mode KdV equation. J. King Saud Univ. Sci. 2019, 31, 485–489. [Google Scholar] [CrossRef]
- Yassin, O.; Alquran, M. Constructing new solutions for some types of two-mode nonlinear equations. Appl. Math. Inform. Sci. 2018, 12, 361–367. [Google Scholar] [CrossRef]
- Jaradat, I.; Alquran, M.; Momani, S.; Biswas, A. Dark and singular optical solutions with dual-mode nonlinear Schrödinger’s equation and Kerr-law nonlinearity. Optik 2018, 172, 822–825. [Google Scholar] [CrossRef]
- Alquran, M.; Jaradat, I. Multiplicative of dual-waves generated upon increasing the phase velocity parameter embedded in dual-mode Schrödinger with nonlinearity Kerr laws. Nonlinear Dyn. 2019, 96, 115–121. [Google Scholar] [CrossRef]
- Abu Irwaq, I.; Alquran, M.; Jaradat, I.; Baleanu, D. New dual-mode Kadomtsev-Petviashvili model with strong-weak surface tension: Analysis and application. Adv. Diff. Eq. 2018, 2018, 433. [Google Scholar] [CrossRef]
- Jaradat, I.; Alquran, M.; Ali, M. A numerical study on weak-dissipative two-mode perturbed Burgers’ and Ostrovsky models: Right-left moving waves. Eur. Phys. J. Plus. 2018, 133, 164. [Google Scholar] [CrossRef]
- Alquran, M.; Jaradat, I.; Baleanu, D. Shapes and dynamics of dual-mode Hirota-Satsuma coupled KdV equations: Exact traveling wave solutions and analysis. Chin. J. Phys. 2019, 58, 49–56. [Google Scholar] [CrossRef]
- Alquran, M.; Ali, M.; Al-Khaled, K. Solitary wave solutions to shallow water waves arising in fluid dynamics. Nonlinear Stud. 2012, 19, 555–562. [Google Scholar]
- Kudryashov, N.A. One method for finding exact solutions of nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 2248–2253. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Shen, W.; Meng, Y.; Chen, X. Construction of new exact solutions to time-fractional two-component evolutionary system of order 2 via different methods. Opt. Quant. Electron. 2018, 50, 297. [Google Scholar] [CrossRef]
- Alquran, M.; Jaradat, H.M.; Al-Shara, S.; Awawdeh, F. A New Simplified Bilinear Method for the N-Soliton Solutions for a Generalized FmKdV Equation with Time-Dependent Variable Coefficients. Int. J. Nonlin. Sci. Num. 2015, 16, 259–269. [Google Scholar] [CrossRef]
- Jaradat, H.M.; Awawdeh, F.; Al-Shara, S.; Alquran, M.; Momani, S. Controllable dynamical behaviors and the analysis of fractal Burgers hierarchy with the full effects of inhomogeneities of media. Rom. J. Phy. 2015, 60, 324–343. [Google Scholar]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaradat, I.; Alquran, M. Construction of Solitary Two-Wave Solutions for a New Two-Mode Version of the Zakharov-Kuznetsov Equation. Mathematics 2020, 8, 1127. https://doi.org/10.3390/math8071127
Jaradat I, Alquran M. Construction of Solitary Two-Wave Solutions for a New Two-Mode Version of the Zakharov-Kuznetsov Equation. Mathematics. 2020; 8(7):1127. https://doi.org/10.3390/math8071127
Chicago/Turabian StyleJaradat, Imad, and Marwan Alquran. 2020. "Construction of Solitary Two-Wave Solutions for a New Two-Mode Version of the Zakharov-Kuznetsov Equation" Mathematics 8, no. 7: 1127. https://doi.org/10.3390/math8071127
APA StyleJaradat, I., & Alquran, M. (2020). Construction of Solitary Two-Wave Solutions for a New Two-Mode Version of the Zakharov-Kuznetsov Equation. Mathematics, 8(7), 1127. https://doi.org/10.3390/math8071127




