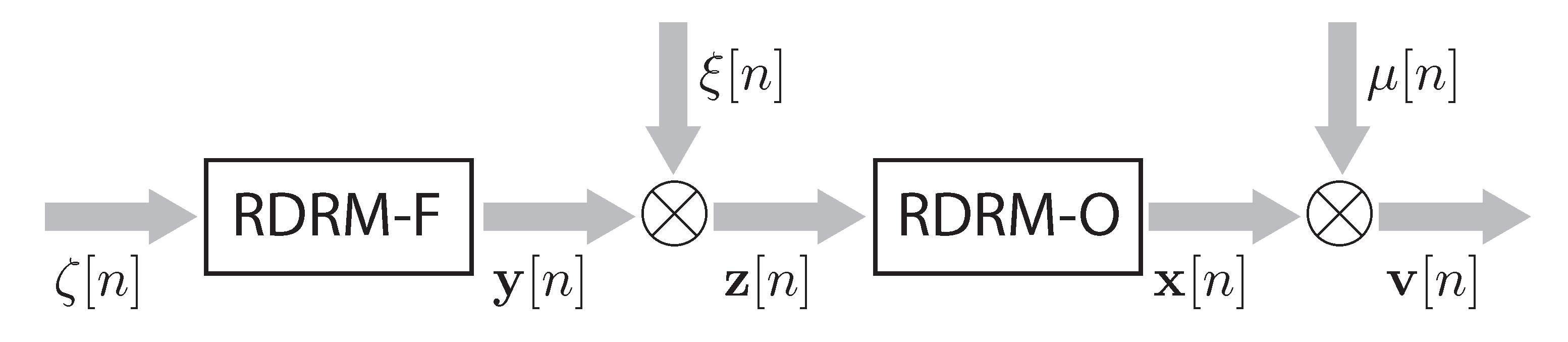1. Introduction
Due to the gradually increasing resources and computational power of computers, huge amounts of data can be accumulated and stored, both in natural and digitized formats. Then, the following question arises immediately: what should be done with these data, except for storage? Extracting new
knowledge from data seems to be a very interesting idea. The concepts of Data Mining (DM) [
1,
2], Big Data (BD) [
3] and Data Science (DS) [
4] were formulated and further developed by researchers accordingly.
A very tempting goal—extracting new knowledge from data—inevitably leads to the verbal or formal (mathematical) modeling of the “expected” knowledge. Therefore, any model has some predictive properties, which can be implemented only under known values of its quantitative characteristics (parameters). Data are a fundamental component of the three concepts above: data are adopted for estimating the characteristics of a model using machine learning (ML) procedures, which allows extracting new knowledge.
Unlike DM, BD, and DS, the concept of ML has a rich history of over 70 years as well as vast experience in solving numerous problems. The first publication in this field of research dates back to 1957; see [
5]. The notion of empirical risk, a key element of
ML procedures, was introduced in 1970 in the monograph [
6]. The method of potential functions for classification and recognition problems was also presented in 1970 in another monograph [
7]. The modern concept of
ML is based on the
deterministic parametrization of models and estimates using data sets with postulated properties. The quality of estimation is characterized by empirical risk functions, and their minimization gives optimal estimates [
8,
9].
As a rule, real problems that are solved by ML procedures are immersed in some uncertain environment. If the matter concerns data, they are acquired with inevitable errors, omissions or low reliability. The design and parametrization of models is a non-formalizable and subjective process that depends on the individual knowledge of a researcher. Therefore, in the mass application of ML procedures, the level of uncertainty is quite high.
All these circumstances indicate that it is necessary to somehow compensate uncertainty. Here a general trend is the application of its stochastic description to parametrized models and data. This means that the model parameters are assumed to be random (appropriately randomized), and the data are assumed to have random errors. Machine learning procedures with these properties belong to the class of
randomized machine learning (RML) procedures. Their difference from the conventional ML procedures is that optimal estimates are constructed not for the parameters but for the probability density functions (PDFs) of the random parameters and the PDFs of the worst-case random errors in the data. In the entropy-based RML procedures, the functional of generalized information entropy [
10] is used as an optimality criterion for estimates.
The core of an RML procedure is a parametrized predictive model designed for simulating the temporal (or spatiotemporal) evolution of a process under study. Therefore, such a model belongs to the class of dynamic models.
Parametric dynamic regression models (PDRMs) are most widespread representatives of this class, in which the current state of a model is determined by its past states on a certain time interval [
11,
12]. A formal image of PDRMs is difference equations, in the general case of the
pth order [
13]. Most applications are described by linear PDRMs. In particular, they naturally occur in many problems of macroeconomic modeling and forecasting, e.g., time series analysis of economic indices [
14], adequacy analysis of PDRMs [
15], and prediction of exchange rates [
16]. Linear PDRMs are effective enough for short-term forecasting, yet causing significant errors on large forecasting horizons. Therefore, attempts to improve forecasts by introducing various nonlinearities into
PDRMs are quite natural. The monograph [
17] was dedicated to a general approach to the formation and use of nonlinear
PDRMs. However, applications require a more “personalized” approach to choosing the most useful and effective nonlinearity. On this pathway, it seems fruitful, e.g., to forecast exchange rates using logistic and exponential nonlinearities [
18], or to predict the daily electrical load of a power system using periodic autoregressive models [
19] or multidimensional time series [
20].
Since forecasting is performed under uncertainty, the resulting errors caused by some unaccounted factors are often compensated, if possible, by assigning some probabilities to forecasts [
21,
22]. The most common approach is the use of Bayes’ theorem on posterior probability. Let a parametrized conditional probability density function of data and an a priori probability density function of parameters be specified; then their normalized product will determine the posterior probability density function of the parameters under fixed data. Fundamental problems in this field of investigations are connected with the structural choice of the conditional and prior PDFs. Typically, Gaussian PDFs or their mixture are selected, and the mixture weights are estimated using retrospective data [
23,
24,
25]. A similar approach was adopted in applications: population genetics [
26], where the method of numerical approximation of posterior PDFs was developed; the interaction between the financial sector of the economy and the labor market [
27], where the Metropolis–Hastings algorithm was used to estimate the parameters of the above PDFs; population dynamics [
28], where a hierarchy of Bayesian models was designed to predict fertility, mortality and migration rates. Probabilistic forecasts are constructed by other methods, taking into account the specifics of applications. In meteorology, retrospective weather forecasts are accumulated for estimating the PDFs; subsequently, these PDFs are used for short-term forecasting [
29,
30,
31,
32]. A rather interesting procedure is to form a probabilistic forecast as a mixture of forecasts obtained by different methods [
33].
In this paper, we propose a fundamentally different forecasting method—the so-called entropy-randomized forecasting (ERF). In accordance with this method, an ensemble of random forecasts is generated by a predictive dynamic regression model (PDRM) with random input and parameters. The corresponding probabilistic characteristics, namely the probability density functions, are determined using the entropy randomized machine learning procedure. The ensembles of forecasting trajectories are constructed by the sampling of the entropy-optimal PDFs.
The proposed method is adopted for randomized prediction of the daily electrical load of a regional power system. A hierarchical randomized dynamic regression model that describes the dependence of the load on the ambient temperature is constructed. The temporal evolution of the ambient temperature is represented by an oscillatory second-order dynamic regression model with a random parameter and a random input. The results of randomized learning of this model on the GEFCom2014 dataset [
34] are given. A randomized forecasting technology is suggested and its adequacy is investigated depending on the length of forecasting horizon.
2. Procedure of Entropy-Randomized Forecasting
Randomization as a means of imparting artificial and rationally organized random properties to naturally nonrandom events, indicators, or methods is a fairly common technique that yields a positive effect. There exist many examples in various fields of science, management, economics: randomized numerical optimization methods [
35,
36]; the mixed (random) strategies of trading on a stock exchange [
37]; the randomized forecasting of population dynamics [
38]; vibration control of industrial processes [
39]. As the result of randomization, nonrandom objects gain artificial stochastic properties with optimal probabilistic characteristics in a chosen sense. The question on appropriate quantitative characteristics of optimality has always been controversial and ambiguous. It requires arguments that would somehow reflect the important specifics of a randomized object. In particular, a fundamental feature of forecasting procedures is
uncertainty in the data, predictive models, methods for generating forecasts, etc.
In what follows,
information entropy [
40] will be used as a characteristic of uncertainty. In the works [
41,
42,
43], using the first law of thermodynamics it was demonstrated that entropy is a natural functional describing the processes of universal evolution. Moreover, in accordance with the second law of thermodynamics, entropy maximization determines the best state of an evolutionary process under the worst-case external disturbance (maximum uncertainty). Also, note another quality of information entropy associated with measurement errors and other types of errors, which are important attributes of data: with the factor of such errors being considered in terms of informational entropy, the probabilistic characteristics of noises exerting the worst-case impact on forecasting procedures can be estimated in explicit form.
The technology of entropy-randomized forecasting consists of the following stages. At the beginning (the first stage), a predictive randomized model (PRM) of a studied object is formed and its parameters are designed. A PRM transforms real data into a model output. In the general case, these transformations are assumed to be dynamic, i.e., the model output observed at a time instant n depends on the states observed on some past interval. The PRM parameters are assumed to be of the interval type and random, and their probabilistic properties are characterized by the corresponding PDFs.
The second stage of the technology under consideration—randomized machine learning (more specifically, its entropy version)—is intended to estimate the PDFs. At this stage, the estimates of the PDFs are calculated using learning data sets and also a learning algorithm in the form of a functional entropy-linear programming problem.
At the third stage, the optimized PRM (with the entropy-optimal PDFs) is tested using a test data set and accepted quantitative characteristics of the quality of learning. The optimized PRM actually generates an ensemble of random trajectories, vectors, or events with the entropy-optimal values of their parameters.
The learned and tested PRMs serve for forecasting. In this case, the ensembles of random forecasted trajectories generated by the entropy-optimal PRMs are used to calculate their numerical characteristics such as mean trajectories, variance curves, median trajectories, the PDF evolution of forecasted trajectories, etc.
3. Randomized Dynamic Regression Models with Random Input and Parameters
Randomized dynamic regression models (RDRMs) form a class of dynamic models with random parameters that describe a parametrized dependence of the object’s state at a given time instant on external factors and its states at some past time instants.
The structures of models are designed on the basis of existing knowledge and hypotheses about the properties of an object, which often turn out to be very inaccurate. Moreover, the external factors themselves can change over time and therefore should be predicted to model the object’s dynamics. Reliable information on realistically measured impacts leading to the temporal evolution of external factors is often unavailable. The aforementioned indicates the presence of
uncertainty, both in the development and further use of models. In [
10], a method for reducing the influence of uncertainty based on the randomization of models (including the class of RDRMs) was proposed. In the latter case, this method extends the idea of randomization to the modeling of external factors and their evolution.
The structure of the RDRM is shown in
Figure 1. It consists of a model of the main object (RDRM-O) with random parameters
and a model of external factors (RDRM-F) with random parameters
and a random input
The states of the object and its model belong to the vector space
, in which
are the state vectors of the object and
are the state vectors of RDRM-O. The external factors are characterized by the vector
while the changes in the state of RDRM-F over time by the vector
The variable
n denotes discrete time taking integer values on the interval
Consider
the linear version of RDRM-O. Its state
at a time instant
n is changing under the influence of
p retrospective states
and measurable external factors
. The corresponding equation has the form
with the following notations:
as the block column vector of parameters, where
is a random matrix of dimensions
with random elements of the interval type, i.e.,
as a matrix of dimensions
with random elements of the interval type, i.e.,
as the block row vector of
p retrospective states, where
denotes a block row vector.
The probabilistic properties of the block vector and the matrix are characterized by a joint PDF and a PDF respectively.
The state of RDRM-O is assumed to be measurable at each time instant
n and also to contain an additive noise
:
The random vectors
are of the interval type, i.e.,
with a PDF
. The random vectors measured at different time instants are assumed to be statistically independent.
Consider
the linear version of RDRM-F, which has a similar structure described by the equation
with the following notations:
as a block column vector formed by matrices
of dimensions
with random elements of the interval type, i.e.,
The probabilistic properties of the parameters are characterized by a continuously differentiable PDF
The random vector
is of the interval type, i.e.,
with a continuously differentiable PDF
The random vectors
measured at different time instants are statistically independent.
By analogy with RDRM-O, the state of RDRM-F is assumed to be measurable at each time instant
n and also to contain an additive noise
:
The random vectors
are of the interval type, i.e.,
with a continuously differentiable PDF
. The random vectors measured at different time instants are assumed to be statistically independent.
Thus, in the RDRM (RDRM-O and RDRM-F), the unknown characteristics are the PDFs , and of the model parameters and also the PDFs , and of the measurement noises, .
6. Entropy-Randomized Forecasting of Daily Electrical Load of Power System
The daily electrical load
L of a power system depends on many various factors. The analysis below is restricted to one of the most significant external factors—the ambient temperature
The daily temperature variations are fluctuating [
45,
46]. These fluctuations affect electrical load, but with some time delay due the inertia of a power network supplying electrical energy from the generator to consumers.
(1). Dynamic Regression Model.
In accordance with the general structure of the RDRM (see
Section 2), the electrical load model (the
model) describes the dynamic relationship between electrical load and ambient temperature while the ambient temperature model (the
model) describes the daily dynamics of ambient temperature. There exist quite a few versions of the
model, albeit all being static, i.e., describing the relationship between electrical load and ambient temperature at current time instants [
47]. The daily temperature dynamics are fluctuating, and such fluctuations are described, in particular, by the periodic autoregressive model [
48].
Please note that the effect of ambient temperature on electrical load is dynamic, i.e., the change in load due to temperature at a given time instant depends on its value at a previous time instant. A similar property applies to ambient temperature fluctuations.
Therefore, following the general randomized approach, the model is designed as a first-order dynamic regression model with random parameters, while the model is designed as a second-order dynamic regression with a random parameter and a random input Then the model is the composition of the two models above.
In the class of linear models, the randomized dynamic regression load–temperature model (
model) of the first order can be written in the form
where random independent parameters
a and
b take values within intervals
The probabilistic properties are characterized by PDFs
and
defined on the sets
and
respectively. The random noise
that simulates electrical load measurement errors is of the interval type as well. In the general case, for each time instant the intervals may have different limits, i.e.,
with PDFs
,
.
Consider the
model. The fluctuating character of the daily temperature variations is described by the randomized dynamic regression model of the second order
where
t is the mean daily temperature. These parameters are random and take values within given intervals
. The probabilistic properties of the parameters are characterized by PDFs
defined on corresponding intervals.
Equation (
36) contains random noises described by independent random variables
; in each measurement
their values may lie in different intervals, i.e.,
The probabilistic properties of the random variable
are characterized by a PDF
.
Thus, Equations (
33) and (
36) describing electrical load dynamics in a power system are characterized by the following PDFs:
the model, by the PDFs and of the model parameters and the PDF , of the measurement noises, ;
the model, by the PDFs of the model parameters and the PDFs of the measurement noises, .
(2). Learning Data Set.
For estimating the PDFs, the normalized real data from the GEFCom2014 dataset (see [
34]) on daily electrical load variations
, mean daily temperature variations
and temperature deviations
from the mean daily value can be used. (Here normalization means the reduction to the unit interval.)
The normalization procedure is performed in the following way:
where
,
,
,
.
In accordance with (
33) and (
36), the model variables and the corresponding real data on the learning interval
are described by the vectors
In terms of (
39), the
and
models on the learning interval
have the form
The random parameters take values within the intervals
The measurement noises take values within the intervals
(3). Entropy-Optimal Probability Density Functions of Parameters and Noises.
In accordance with the approach described in
Section 5, for the
model (
33)–(
35) the PDFs parametrized by the Lagrange multipliers
have the form
where
The Lagrange multipliers
are calculated by solving the system of balance equations
where
Consider the
model. The corresponding entropy-optimal PDFs parametrized by the Lagrange multipliers have the form
where
The Lagrange multipliers
are calculated by solving the system of balance equations
where
(4). Results of Model Learning.
Using the available data on daily variations of electrical load and ambient temperature (see
Figure 1) for the three days indicated above, the balance Equations (
44), (
45), (
47) and (
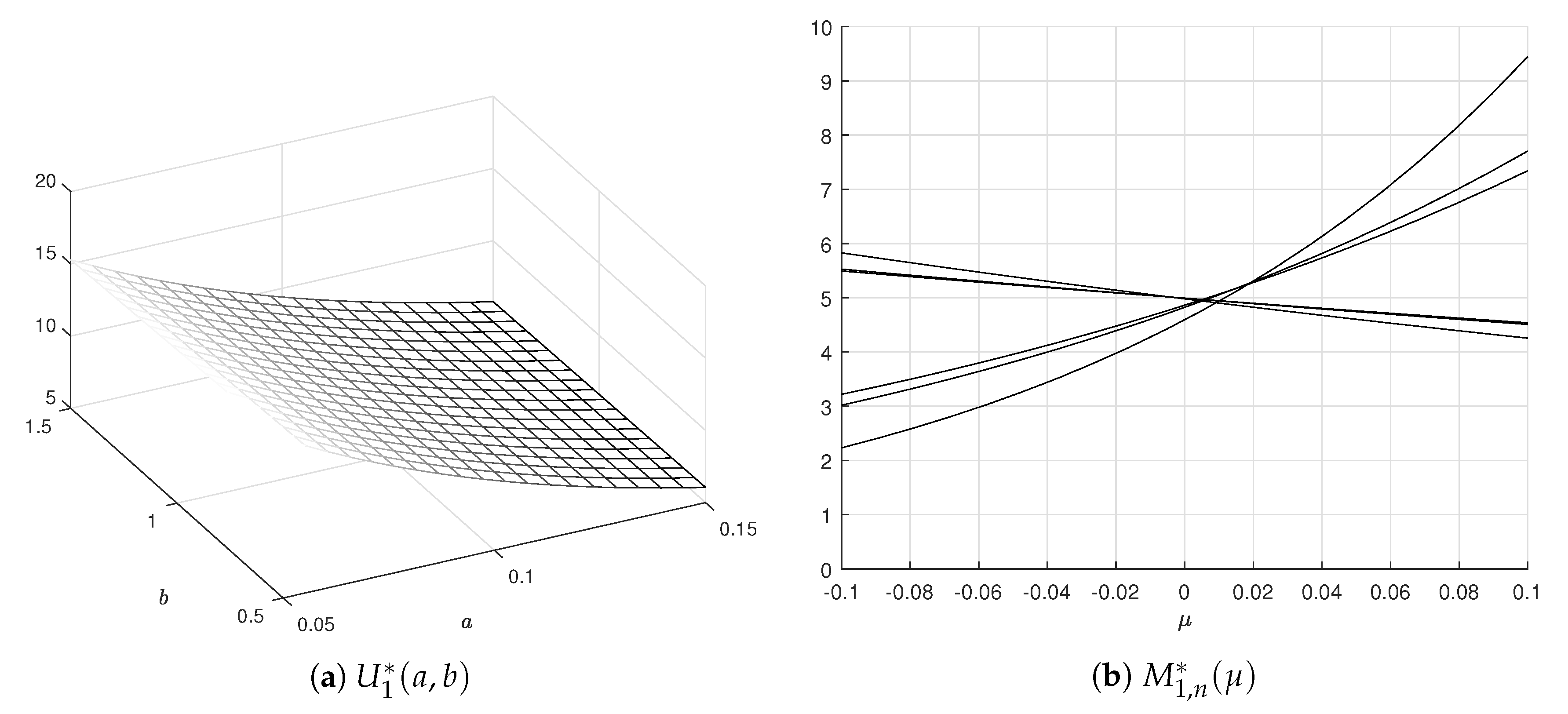
48) were formed. Their solution was determined by minimizing the quadratic residual between the left- and right-hand sides of the equations. Since the equations are significantly nonlinear, the resulting values of the Lagrange multipliers (see
Table 1) correspond to a local minimum of the residual. All calculations were implemented in MATLAB; optimization was performed using the
fsolve function.
Because the parameters of the
model are independent, the joint PDFs
of the parameters and noises have the form
Clearly, the PDFs are of exponential type. For
the graphs are shown in
Figure 2.
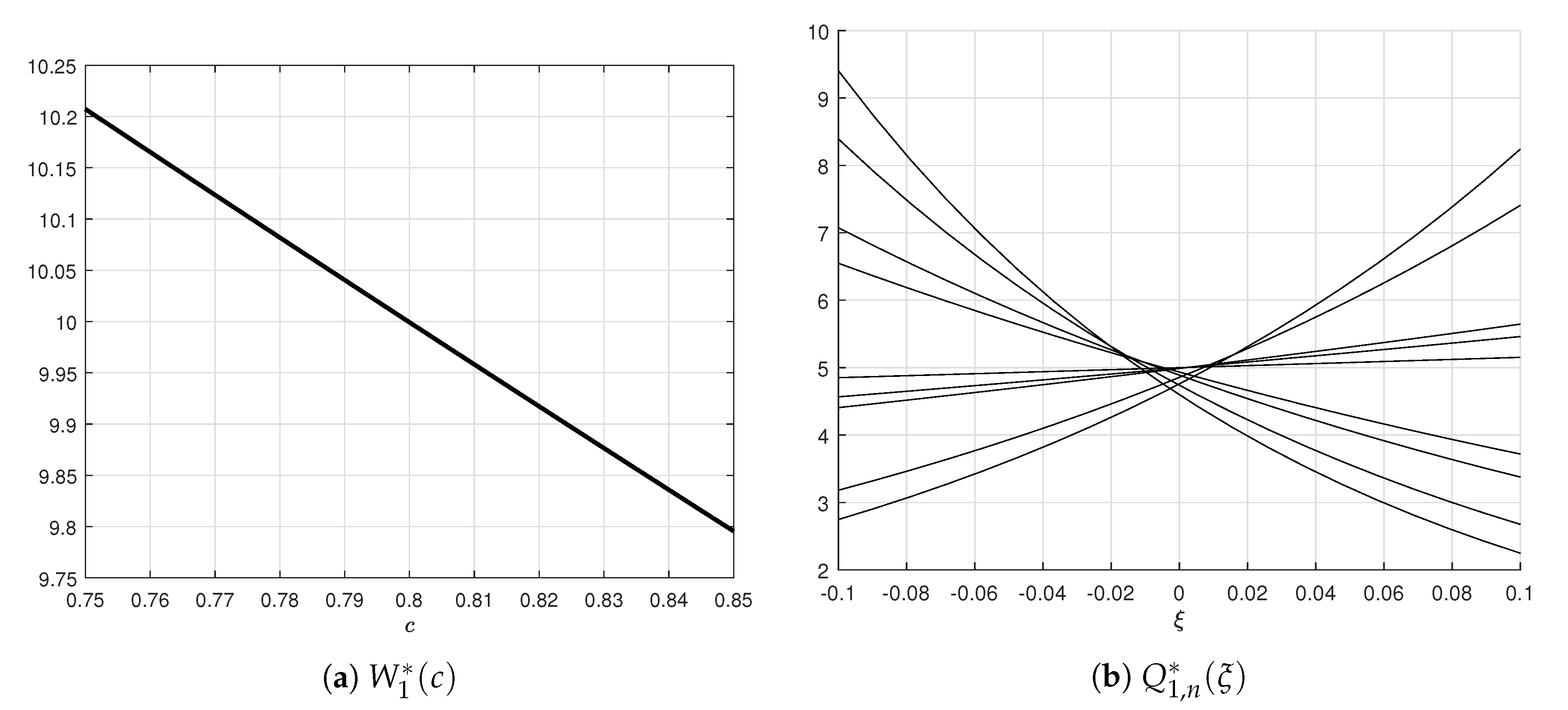
For the
model, the PDFs of the parameters and noises have the form
For
the graphs can be seen in
Figure 3.
Thus, the randomized
model generates random trajectories with the entropy-optimal PDFs of the model parameters and measurement noises:
The corresponding ensembles are generated by the sampling procedure of the resulting PDFs of the parameters and noises using the acceptance-rejection (AR) method (also known as rejection sampling (RS); see [
49]). During calculations, 100 samples for each parameter and 100 samples for each noise were used; in other words, the ensemble consisted of
trajectories.
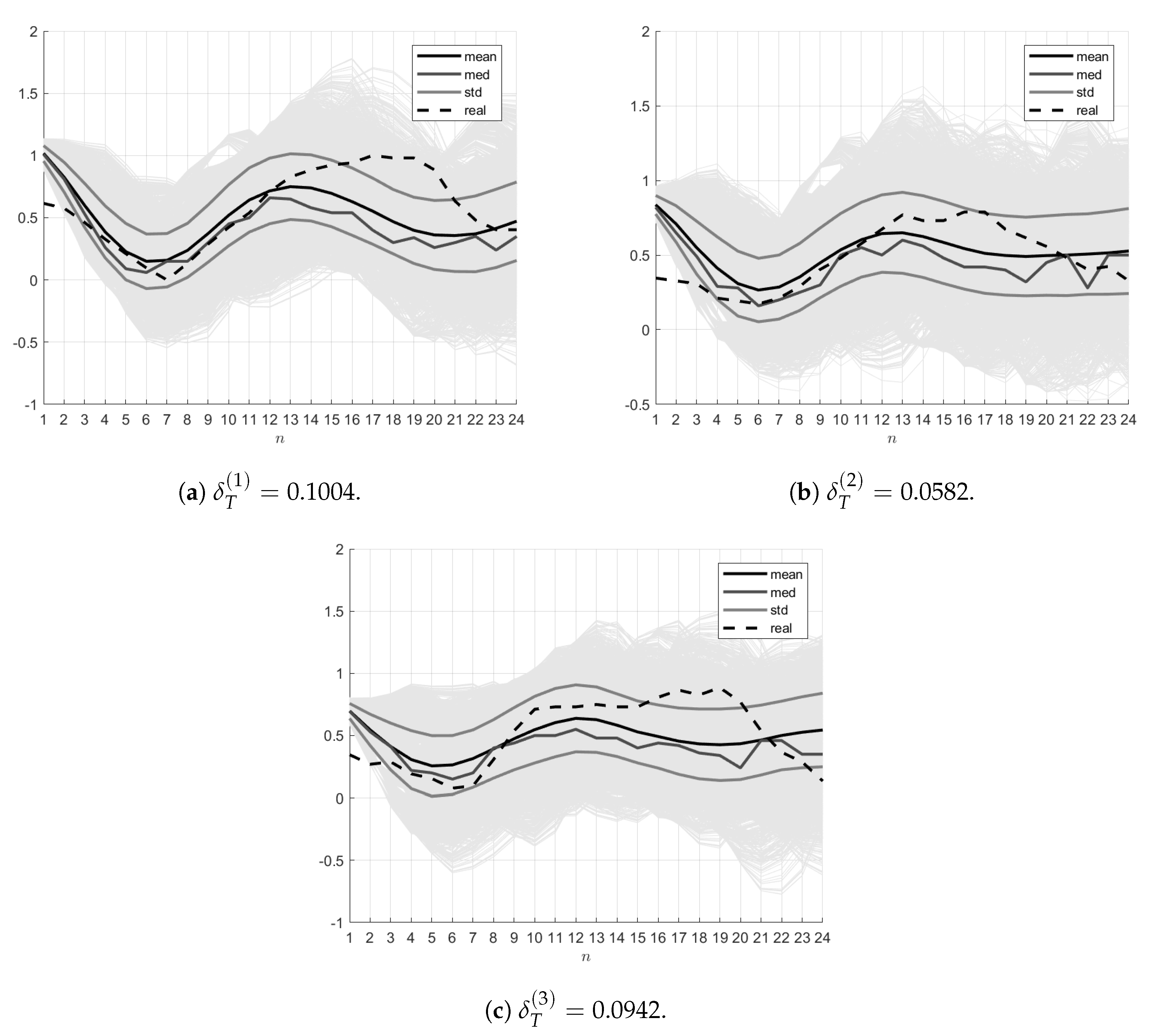
(5). Model Testing.
The adequacy of the model was analyzed by the self- and cross-testing of the
and
models on the real load–temperature data for 3–5 July 2016 (
). Self-testing means generating an ensemble of trajectories with the entropy-optimal parameters and noises for day
i, calculating the mean (
mean) and median (
med) trajectories and also the variance curve (
std±) of the ensemble, and comparing the mean trajectory with the real counterparts by electrical load and ambient temperature
for the same day i. The quality of approximation is characterized by relative errors,
in electrical load and
in ambient temperature.
Cross-testing represents a similar procedure in which the mean trajectories are compared with the real counterparts in terms of electrical load and ambient temperature for days
The quality of approximation is characterized by relative errors,
in electrical load and
in ambient temperature.
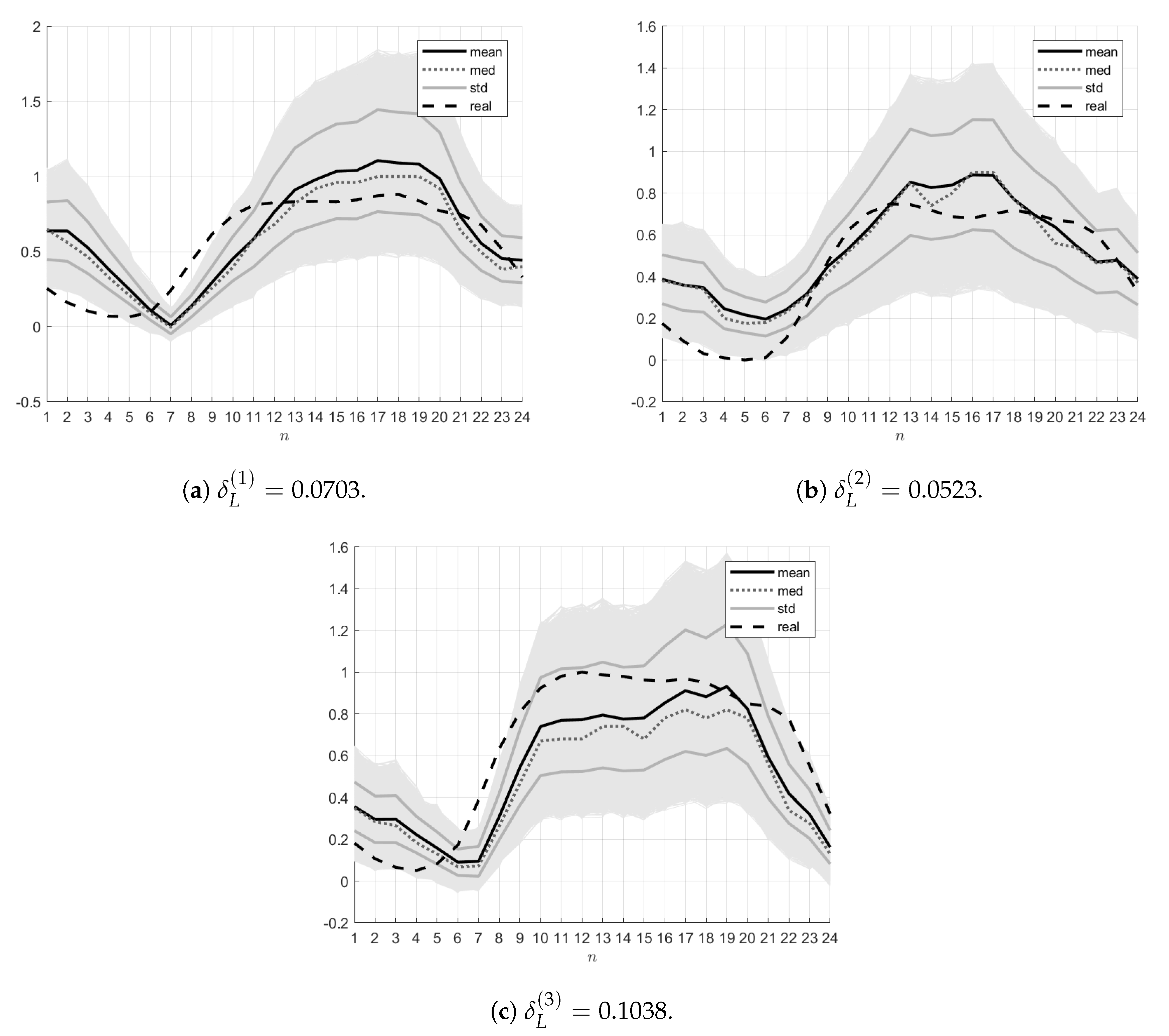
Self-testing. For the
model, the real ambient temperature data
as well as the entropy-optimal PDFs
and
of the parameters
and the PDFs
of the measurement noises
were used. The ensembles
were generated using the
sampling procedure of the above PDFs. The mean trajectory
, the median trajectory
and also the trajectories
corresponding to the limits of the variance graph were found. The errors
were calculated. The resulting ensembles and relative errors
for the three indicated days are demonstrated in
Figure 4.
The
model was tested by generating the ensemble
of random trajectories
,
with the entropy-optimal PDFs
and
through sampling. The mean trajectory
, the median trajectory
and the trajectory
corresponding to the limits of the variance curve are calculated. The resulting ensembles and relative errors
for the three days are shown in
Figure 5.
Cross-testing. For cross-testing, the
and
models learned on the data for day
i were used, and their mean trajectories were compared with the data for days
. The resulting errors are combined in
Table 2,
Table 3 and
Table 4.
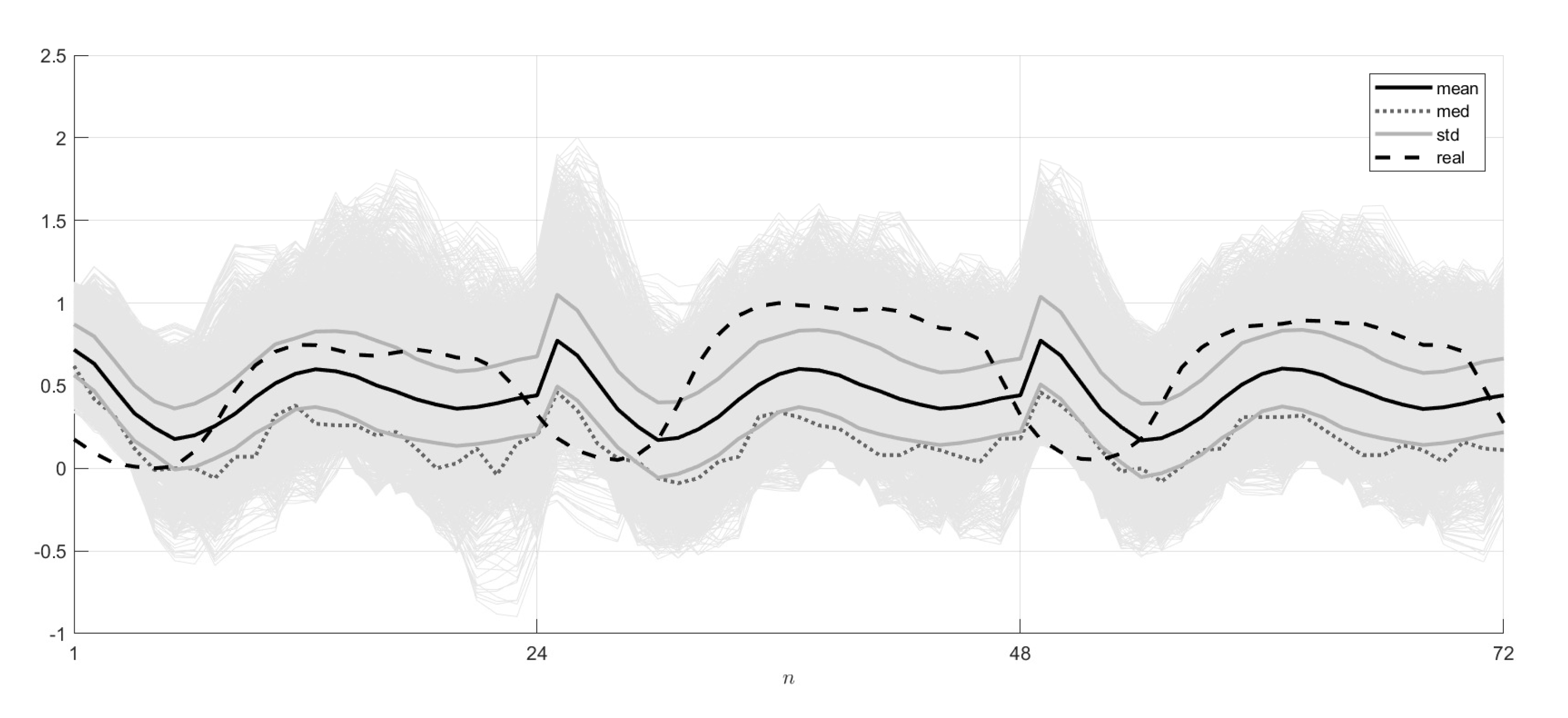
(6). Randomized Prediction of N-Daily Load.
In the randomized prediction of the N-daily load, the model learned on the interval was used. The quality of the forecast was characterized using the model with the entropy-optimal PDFs obtained on the real data for the first () day.
The 1-day (
), 2-day (
) and 3-day (
) ensembles were constructed by the sampling procedure of the above PDFs. For these ensembles, the mean trajectories
, the median trajectories
and also the limiting trajectories
of the variance curve were found. The forecast results were compared with the real data for 3–7 July 2006 (
). The forecasting quality was characterized by the relative errors calculated similar to (
53) and (
54).
The resulting 24-h, 48-h and 72-h randomized forecasts of electrical load and their probabilistic characteristics (the mean and median trajectories, the limit trajectories of the variance curves) are presented in
Figure 6. The errors, i.e., the deviations between the model forecasts and real data, can be seen in
Table 5.