Functional Location-Scale Model to Forecast Bivariate Pollution Episodes
Abstract
1. Introduction
2. Methodology
2.1. Mathematical Model
2.2. Estimation Algorithm
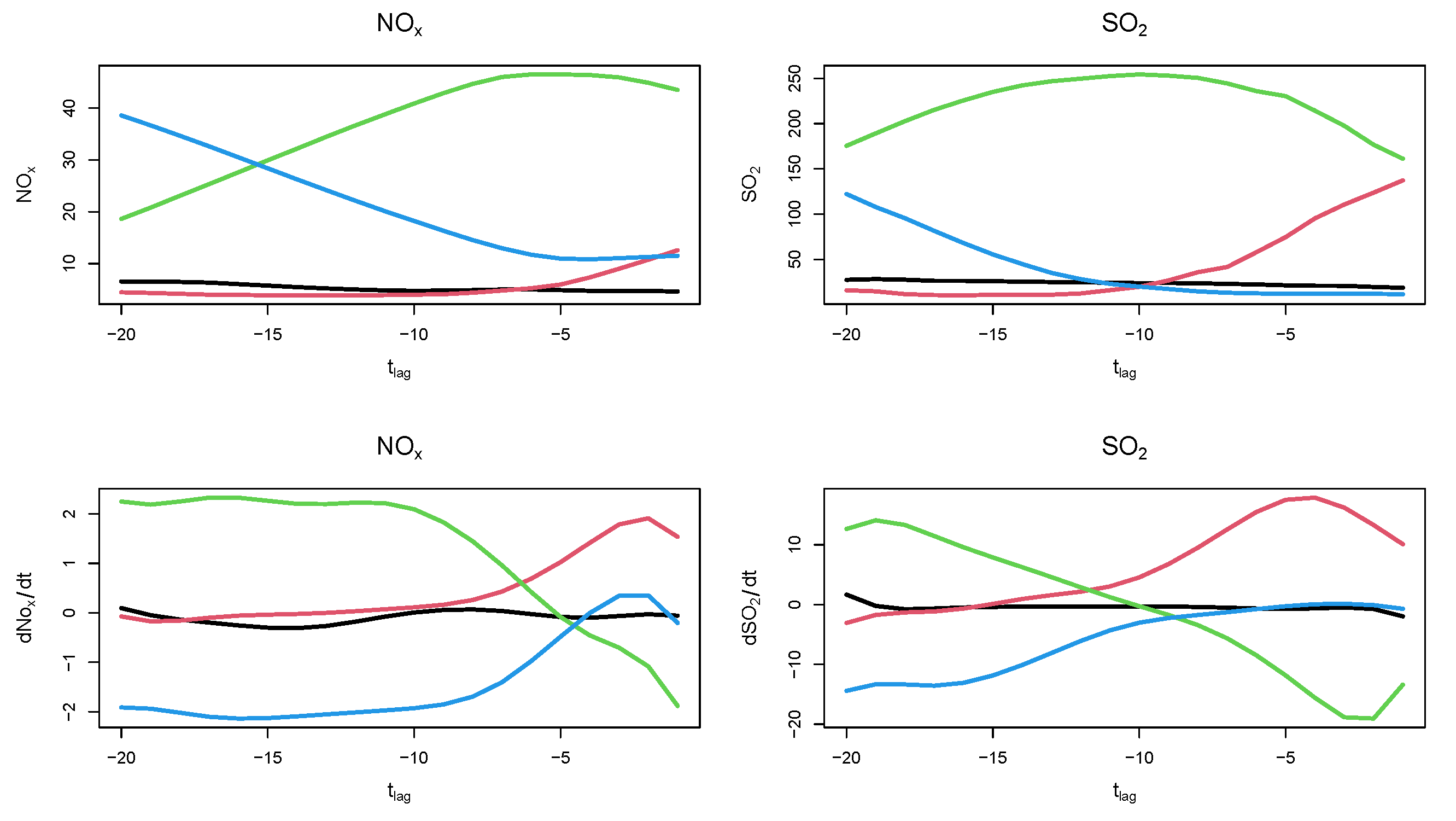
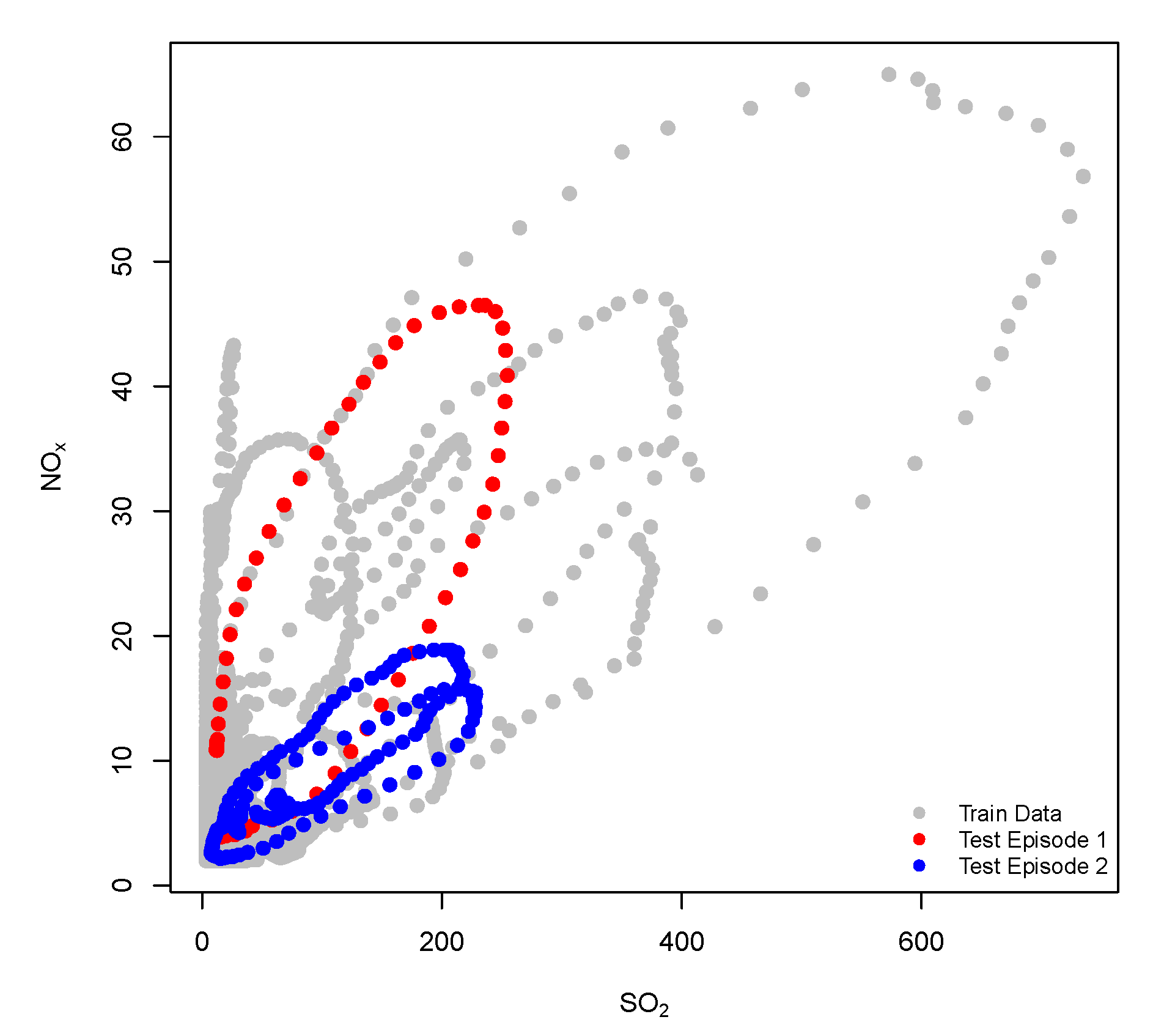
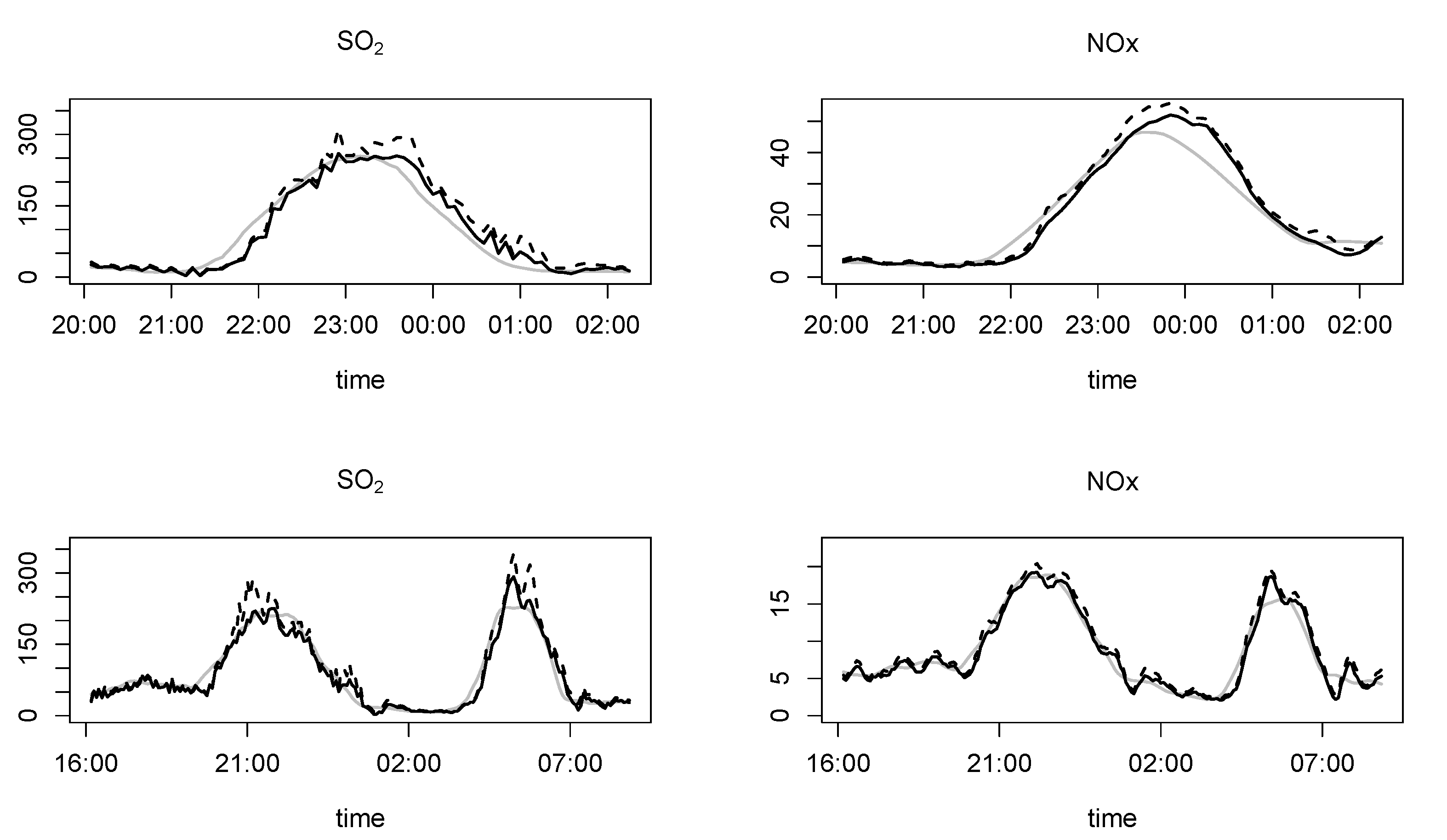
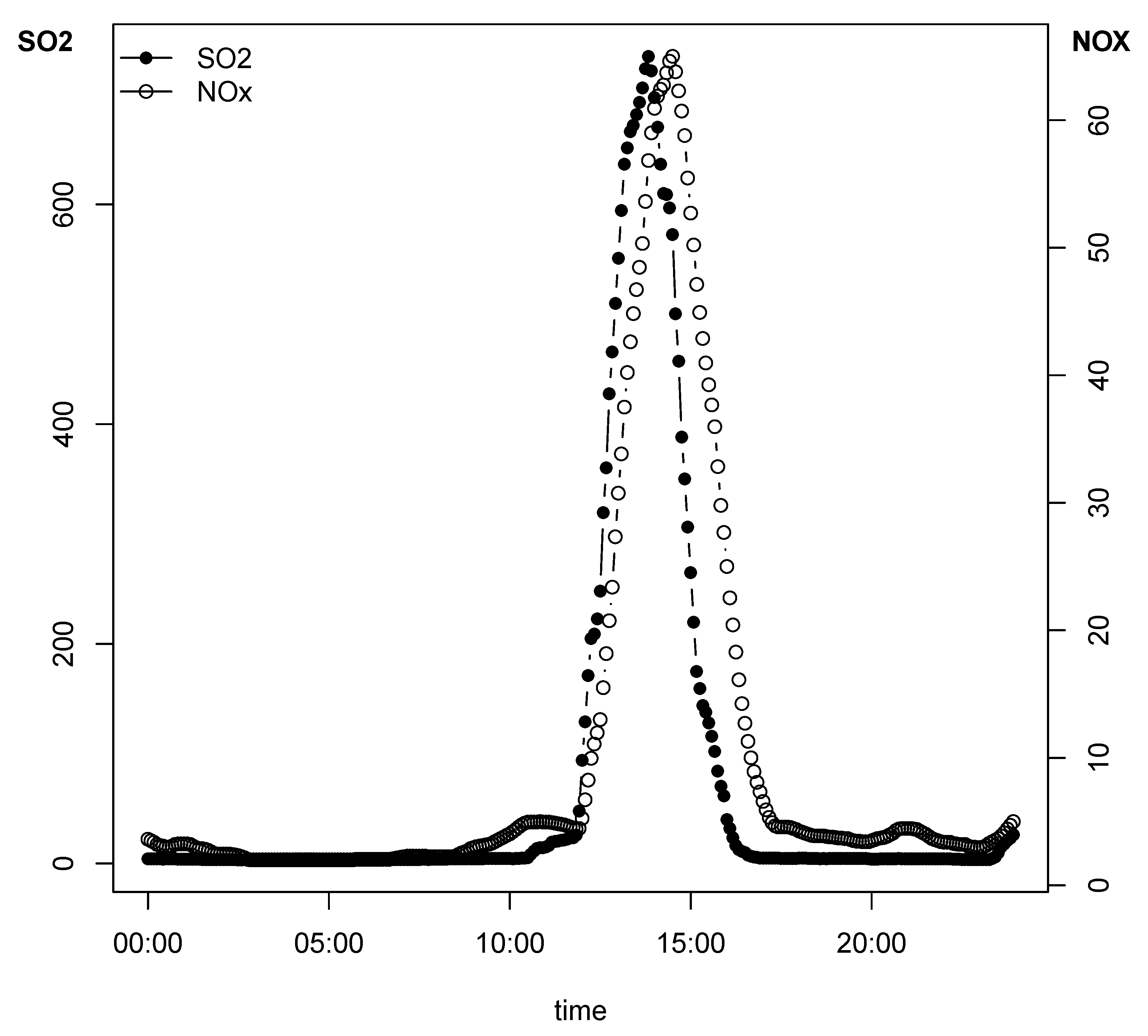
3. Case Study: Joint Forecasting of Pollution Episodes
4. Discussion
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Siew, L.Y.; Ching, L.Y.; Wee, P.M.J. ARIMA and integrated ARFIMA models for forecasting air pollution index in Shah Alam, Selangor. Malay. J. Anal. Sci. 2008, 12, 257–263. [Google Scholar]
- Ibrahim, M.Z.; Roziah, Z.; Marzuki, I.; Muhd, S.L. Forecasting and Time Series Analysis of Air Pollutants in Several Area of Malaysia. Am. J. Enverion. Sci. 2009, 5, 625–632. [Google Scholar] [CrossRef]
- Abhilash, M.S.K.; Thakur, A.; Gupta, D.; Sreevidya, B. Time Series Analysis of Air Pollution in Bengaluru Using ARIMA Model. In Ambient Communications and Computer Systems; Advances in Intelligent Systems and omputing; Perez, G., Tiwari, S., Trivedi, M., Mishra, K., Eds.; Springer: Singapore, 2018. [Google Scholar]
- Liu, P.W.G. Simulation of the daily average PM10 concentrations at Ta-Liao with Box-Jenkins time series models and multivariate analysis. Atmos. Environ. 2009, 43, 2104–2113. [Google Scholar] [CrossRef]
- Nazif, A.; Mohammed, N.I.; Malakahmad, A.; Abualqumboz, M.S. Regression and multivariate models for predicting particulate matter concentration level. Environ. Sci. Pollut. Res. Int. 2018, 25, 283–289. [Google Scholar] [CrossRef]
- Zhao, R.; Gu, X.; Xue, B.; Zhang, J.; Ren, W. Short period PM2.5 prediction based on multivariate linear regression model. PLoS ONE 2018, 13, e0201011. [Google Scholar] [CrossRef]
- Ng, K.Y.; Awang, N. Multiple linear regression and regression with time series error models in forecasting PM10 concentrations in Peninsular Malaysia. Environ. Monit. Assess. 2018, 190, 63. [Google Scholar] [CrossRef]
- Roca-Pardiñas, J.; Gonzàlez Manteiga, W.; Febrero-Bande, M.; Prada-Sànchez, J.M.; Cadarso-Suàrez, C. Predicting binary time series of SO2 using generalized additive models with unknown link function. Environmetrics 2004, 15, 729–742. [Google Scholar] [CrossRef]
- Martínez-Silva, I.; Roca-Pardiñas, J.; Ordóñez, C. Forecasting SO2 pollution incidents by means of quantile curves based on additive models. Environmetrics 2016, 27, 147–157. [Google Scholar] [CrossRef]
- Garcia, J.M.; Teodoro, F.; Cerdeira, R.; Coelho, L.M.R.; Prashant, K.; Carvalho, M.G. Developing a methodology to predict PM10 concentrations in urban areas using generalized linear models. Environ. Technol. 2016, 37, 2316–2325. [Google Scholar] [CrossRef]
- Roca-Pardiñas, J.; Ordóñez, C. Predicting pollution incidents through semiparametric quantile regression models. Stoch. Environ. Res. Risk Assess. 2019, 33, 673–685. [Google Scholar] [CrossRef]
- Azid, I.A.; Ripin, Z.M.; Aris, M.S.; Ahmad, A.L.; Seetharamu, K.N.; Yusoff, R.M. Predicting combined-cycle natural gas power plant emissions by using artificial neural networks. In Proceedings of the 2000 TENCON Proceedings, Intelligent Systems and Technologies for the New Millennium (Cat. No.00CH37119), Kuala Lumpur, Malaysia, 24–27 September 2000; Volume 3, pp. 512–517. [Google Scholar]
- Perez, P.; Trier, A.; Reyes, J. Prediction of PM2.5 Concentrations Several Hours in Advance Using Neural Networks in Santiago, Chile. Atmos. Environ. 2000, 34, 1189–1196. [Google Scholar] [CrossRef]
- Ferretti, G.; Piroddi, L. Estimation of NOx Emissions in Thermal Power Plants Using Neural Networks. J. Eng. Gas Turbines Power 2001, 132, 465–471. [Google Scholar] [CrossRef]
- Siwek, K.; Osowski, S. Improving the accuracy of prediction of PM10 pollution by the wavelet transformation and an ensemble of neural predictors. Eng. Appl. Artif. Intell. 2012, 25, 1246–1258. [Google Scholar] [CrossRef]
- Muñoz, E.; Martín, M.L.; Turias, I.J.; Jimenez-Come, M.J.; Trujillo, F.J. Prediction of PM10 and SO2 exceedances to control air pollution in the Bay of Algeciras, Spain. Stoch. Environ. Res. Risk Assess. 2014, 28, 1409–1420. [Google Scholar] [CrossRef]
- He, H.D.; Lu, W.Z.; Xue, Y. Prediction of particulate matters at urban intersection by using multilayer perceptron model based on principal components. Stoch Environ. Res. Risk. Assess. 2015, 29, 2107–2114. [Google Scholar] [CrossRef]
- Antanasijević, D.; Pocajt, V.; Perić-Grujić, A.; Ristić, M. Multiple-input–multiple-output general regression neural networks model for the simultaneous estimation of traffic-related air pollutants. Atmos. Pollut. Res. 2018, 9, 388–397. [Google Scholar] [CrossRef]
- Gilson, M.; Dahmen, D.; Moreno-Bote, R.; Insabato, A.; Helias, M. The covariance perceptron: A new paradigm for classification and processing of time series in recurrent neuronal networks. BioRxiv 2019. [Google Scholar] [CrossRef]
- Ramsay, J.O.; Silverman, B.W. Applied Functional Data Analysis: Methods and Case Studies; Springer: New York, NY, USA, 2002. [Google Scholar]
- Ferraty, F.; Vieu, P. Nonparametric Functional Data Analysis; Springer: New York, NY, USA, 2006. [Google Scholar]
- Febrero-Bande, M.; Galeano, P.; González-Manteiga, W. Outlier detection in functional data by depth measures with application to identify abnormal NOx levels. Environmetrics 2008, 19, 331–345. [Google Scholar] [CrossRef]
- Martinez, J.; Saavedra, Á.; García-Nieto, P.J.; Piñeiro, J.I.; Iglesias, C.; Taboada, J.; Sanchoa, J.; Pastor, J. Air quality parameters outliers detection using functional data analysis in the Langreo urban area (Northern Spain). Appl. Math. Comput. 2014, 241, 1–10. [Google Scholar] [CrossRef]
- Shaadan, N.; Jemain, A.A.; Latif, M.T. Anomaly detection and assessment of PM10, functional data at several locations in the Klang Valley, Malaysia. Atmos. Pollut. Res. 2015, 6, 365–375. [Google Scholar] [CrossRef]
- Ignaccolo, R.; Mateu, J.; Giraldo, R. Kriging with external drift for functional data for air quality monitoring. Stoch. Environ. Res. Risk Assess. 2014, 28, 1171–1186. [Google Scholar] [CrossRef]
- Wang, D.; Zhong, Z.; Kaixu, B.; Lingyun, H. Spatial and Temporal Variabilities of PM2.5 Concentrations in China Using Functional Data Analysis. Sustainability 2019, 11, 1620. [Google Scholar] [CrossRef]
- Aneiros-Pérez, G.; Cardot, H.; Estévez-Pérez, G.; Vieu, P.H. Maximum ozone concentration forecasting by functional non-parametric approaches. Environmetrics 2004, 15, 675–685. [Google Scholar] [CrossRef]
- Fernández de Castro, B.M.; González-Manteiga, W.; Guillas, S. Functional samples and bootstrap for predicting sulfur dioxide levels. Technometrics 2005, 47, 212–222. [Google Scholar] [CrossRef]
- Quintela-del-Río, A.; Francisco-Fernández, M. Nonparametric functional data estimation applied to ozone data: Prediction and extreme value analysis. Chemosphere 2001, 82, 800–808. [Google Scholar] [CrossRef]
- Besse, P.C.; Cardot, H.; Stephenson, D.B. Autoregressive forecasting of some functional climatic variations. Scand. J. Stat. 2000, 27, 673–687. [Google Scholar] [CrossRef]
- Damon, J.; Guillas, S. The inclusion of exogenous variables in functional autoregressive ozone forecasting. Environmetrics 2002, 13, 759–774. [Google Scholar] [CrossRef]
- Ruiz-Medina, M.D.; Espejo, R.M. Spatial autoregressive functional plug-in prediction of ocean surface temperature. Stoch. Environ. Res. Risk. Assess. 2012, 26, 335–344. [Google Scholar] [CrossRef]
- Ruiz-Medina, M.D.; Espejo, R.M.; Ugarte, M.D.; Militino, A.F. Functional time series analysis of spatio-temporal epidemiological data. Stoch. Environ. Res. Risk Assess. 2014, 28, 943–954. [Google Scholar] [CrossRef]
- Alvarez-Liebana, J.; Ruiz Medina, M.D. Prediction of air pollutants PM10 by ARBX(1) processes. Stoch. Environ. Res. Risk Assess. 2019, 33, 1721–1736. [Google Scholar] [CrossRef]
- Hsu, K.J. Time series analysis of the interdependence among air pollutants. Atm. Environ. Part B Urban Atmos. 1992, 26, 491–503. [Google Scholar] [CrossRef]
- Kadiyala, A.; Kumar, A. Vector time series models for prediction of air quality inside a public transportation bus using available software. Environ. Prog. Sustain. 2014, 33, 337–341. [Google Scholar] [CrossRef]
- García-Nieto, P.J.; Sánchez-Lasheras, F.; García-Gonzalo, E.; de Cos Juez, F.J. Estimation of PM10 concentration from air quality data in the vicinity of a major steelworks site in the metropolitan area of Avilés (Northern Spain) using machine learning techniques. Stoch Environ. Res. Risk Assess. 2018, 32, 3287–3298. [Google Scholar] [CrossRef]
- Hedeker, D.; Mermelstein, R.J.; Demirtas, H. An Application of a Mixed-Effects Location Scale Model for Analysis of Ecological Momentary Assessment (EMA) Data. Biometrics 2008, 64, 627–634. [Google Scholar] [CrossRef]
- Taylor, J.; Verbyla, A. Joint modelling of location and scale parameters of the t distribution. Stat. Model. 2004, 4, 91–112. [Google Scholar] [CrossRef]
- Pugach, O.; Hedeker, D.; Mermelstein, R. A Bivariate Mixed-Effects Location-Scale Model with application to Ecological Momentary Assessment (EMA) data. Health Serv. Outcomes Res. Methodol. 2014, 14, 194–212. [Google Scholar] [CrossRef]
- He, W.; Lawless, J.F. Bivariate location-scale models for regression analysis, with applications to lifetime data. J. R. Statist. Soc. B 2005, 67 Pt 1, 63–78. [Google Scholar] [CrossRef]
- Jäntschi, L.; Bálint, D.; Bolboaca, S.D. Multiple Linear Regressions by Maximizing the Likelihood under Assumption of Generalized Gauss-Laplace Distribution of the Error. Comput. Math. Methods Med. 2016, 2016, 8578156. [Google Scholar] [CrossRef]
- Rigby, R.A.; Stasinopoulos, D.M. Generalized additive models for location, scale and shape. J. R. Stat. Soc. Ser. C 2005, 54, 507–554. [Google Scholar] [CrossRef]
- Karhunen, K. Zur Spektraltheorie Stochastischer Prozesse. Annales Academiae Scientiarum Fennicae Series A1 Mathematica-Physica 1946, 54, 1–7. Available online: https://katalog.ub.uni-heidelberg.de/cgi-bin/titel.cgi?katkey=67295489 (accessed on 24 February 2020).
- Febrero-Bande, M.; Oviedo de la Fuente, M. Statistical Computing in Functional Data Analysis: The R Package fda.usc. J. Stat. Softw. 2012, 51, 12. [Google Scholar] [CrossRef]
- Dogruparmak, S.C.; Özbay, B. Investigating Correlations and Variations of Air Pollutant Concentrations under Conditions of Rapid Industrialization–Kocaeli (1987–2009). Clean-Soil Air Water 2011, 39, 597–604. [Google Scholar] [CrossRef]
| Model | ||||||||
| M | X | X | ||||||
| M | X | X | X | X | ||||
| M | X | X | X | X | ||||
| M | X | X | X | X | X | X | X | |
| K | M | M | M | M | |||
| 0.50 | 10 | 20 | 3 | 0.43 | 0.47 | 0.45 | 0.51 |
| 5 | 0.42 | 0.48 | 0.47 | 0.49 | |||
| 10 | 49 | 3 | 0.51 | 0.52 | 0.52 | 0.52 | |
| 5 | 0.51 | 0.50 | 0.50 | 0.50 | |||
| 20 | 20 | 3 | 0.45 | 0.49 | 0.44 | 0.49 | |
| 5 | 0.48 | 0.46 | 0.43 | 0.46 | |||
| 20 | 49 | 3 | 0.50 | 0.54 | 0.51 | 0.50 | |
| 5 | 0.49 | 0.49 | 0.49 | 0.48 | |||
| 0.75 | 10 | 20 | 3 | 0.70 | 0.73 | 0.72 | 0.75 |
| 5 | 0.69 | 0.74 | 0.73 | 0.74 | |||
| 10 | 49 | 3 | 0.76 | 0.78 | 0.78 | 0.78 | |
| 5 | 0.77 | 0.76 | 0.76 | 0.76 | |||
| 20 | 20 | 3 | 0.70 | 0.72 | 0.70 | 0.72 | |
| 5 | 0.70 | 0.71 | 0.69 | 0.69 | |||
| 20 | 49 | 3 | 0.77 | 0.78 | 0.75 | 0.73 | |
| 5 | 0.75 | 0.74 | 0.72 | 0.72 | |||
| 0.90 | 10 | 20 | 3 | 0.88 | 0.87 | 0.87 | 0.89 |
| 5 | 0.86 | 0.88 | 0.87 | 0.88 | |||
| 10 | 49 | 3 | 0.91 | 0.90 | 0.90 | 0.90 | |
| 5 | 0.90 | 0.90 | 0.90 | 0.90 | |||
| 20 | 20 | 3 | 0.87 | 0.87 | 0.85 | 0.86 | |
| 5 | 0.87 | 0.86 | 0.86 | 0.84 | |||
| 20 | 49 | 3 | 0.90 | 0.89 | 0.90 | 0.86 | |
| 5 | 0.87 | 0.87 | 0.88 | 0.85 | |||
| 0.95 | 10 | 20 | 3 | 0.93 | 0.93 | 0.93 | 0.93 |
| 5 | 0.93 | 0.93 | 0.93 | 0.93 | |||
| 10 | 49 | 3 | 0.96 | 0.93 | 0.93 | 0.93 | |
| 5 | 0.95 | 0.94 | 0.94 | 0.94 | |||
| 20 | 20 | 3 | 0.93 | 0.93 | 0.92 | 0.92 | |
| 5 | 0.92 | 0.92 | 0.93 | 0.90 | |||
| 20 | 49 | 3 | 0.95 | 0.94 | 0.95 | 0.92 | |
| 5 | 0.92 | 0.92 | 0.93 | 0.90 | |||
| Episode 1 | Episode 2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Repsonse | K | M | M | M | M | M | M | M | M | ||
| NO | 10 | 20 | 3 | 20.7 | 25.2 | 20.0 | 23.0 | 1.9 | 1.7 | 1.4 | 1.4 |
| 5 | 19.6 | 18.6 | 20.6 | 16.4 | 0.9 | 0.8 | 0.8 | 0.6 | |||
| 49 | 3 | 20.9 | 24.7 | 18.2 | 23.8 | 1.8 | 1.9 | 1.4 | 1.4 | ||
| 5 | 19.2 | 17.5 | 19.3 | 16.7 | 0.9 | 0.9 | 0.8 | 0.7 | |||
| 20 | 100 | 3 | 34.0 | 24.7 | 19.9 | 19.6 | 3.3 | 5.5 | 1.7 | 3.1 | |
| 5 | 40.9 | 23.3 | 46.5 | 29.2 | 1.5 | 2.5 | 1.0 | 1.8 | |||
| 49 | 3 | 30.2 | 18.2 | 18.7 | 20.4 | 3.4 | 5.3 | 1.7 | 2.8 | ||
| 5 | 36.2 | 27.6 | 39.8 | 35.6 | 1.5 | 2.5 | 1.0 | 1.8 | |||
| SO | 10 | 100 | 3 | 505.0 | 841.0 | 407.5 | 837.3 | 544.8 | 531.9 | 419.8 | 419.1 |
| 5 | 914.9 | 868.6 | 669.4 | 516.3 | 215.6 | 230.3 | 184.5 | 199.1 | |||
| 49 | 3 | 686.0 | 685.3 | 515.8 | 518.3 | 481.4 | 484.4 | 338.0 | 361.1 | ||
| 5 | 991.1 | 925.5 | 846.3 | 682.9 | 199.9 | 214.7 | 170.6 | 179.9 | |||
| 20 | 100 | 3 | 1463.4 | 2172.7 | 825.4 | 1199.9 | 1154.5 | 1133.1 | 709.5 | 659.0 | |
| 5 | 1470.6 | 2531.2 | 1002.9 | 1428.5 | 525.5 | 482.1 | 352.0 | 341.3 | |||
| 49 | 3 | 1.458.7 | 2485.4 | 768.4 | 698.4 | 1162.6 | 1125.8 | 644.8 | 628.7 | ||
| 5 | 1787.6 | 2811.0 | 1111.2 | 951.5 | 548.1 | 492.0 | 352.7 | 359.3 | |||
| Memory (MB) | Runtime (seconds) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| K | M | M | M | M | M | M | M | M | ||
| 10 | 20 | 3 | 652.70 | 1083.03 | 1319.57 | 2266.34 | 17.98 | 29.66 | 35.99 | 61.62 |
| 5 | 1090.78 | 1855.39 | 2299.14 | 4075.88 | 35.55 | 55.29 | 63.15 | 124.7 | ||
| 49 | 3 | 329.94 | 548.58 | 669.42 | 1153.38 | 10.53 | 17.42 | 21.38 | 37.01 | |
| 5 | 552.74 | 942.68 | 1171.67 | 2089.53 | 19.79 | 31.28 | 46.62 | 88.20 | ||
| 20 | 20 | 3 | 653.34 | 1084.15 | 1320.66 | 2268.16 | 18.11 | 29.63 | 35.97 | 61.21 |
| 5 | 1091.90 | 1857.26 | 2300.99 | 4078.95 | 32.14 | 49.51 | 72.45 | 124.81 | ||
| 49 | 3 | 330.10 | 548.84 | 669.69 | 1153.82 | 10.51 | 17.56 | 21.49 | 37.82 | |
| 5 | 553.01 | 943.13 | 1172.20 | 2090.36 | 17.80 | 36.44 | 39.03 | 76.11 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oviedo-de La Fuente, M.; Ordóñez, C.; Roca-Pardiñas, J. Functional Location-Scale Model to Forecast Bivariate Pollution Episodes. Mathematics 2020, 8, 941. https://doi.org/10.3390/math8060941
Oviedo-de La Fuente M, Ordóñez C, Roca-Pardiñas J. Functional Location-Scale Model to Forecast Bivariate Pollution Episodes. Mathematics. 2020; 8(6):941. https://doi.org/10.3390/math8060941
Chicago/Turabian StyleOviedo-de La Fuente, Manuel, Celestino Ordóñez, and Javier Roca-Pardiñas. 2020. "Functional Location-Scale Model to Forecast Bivariate Pollution Episodes" Mathematics 8, no. 6: 941. https://doi.org/10.3390/math8060941
APA StyleOviedo-de La Fuente, M., Ordóñez, C., & Roca-Pardiñas, J. (2020). Functional Location-Scale Model to Forecast Bivariate Pollution Episodes. Mathematics, 8(6), 941. https://doi.org/10.3390/math8060941






