Normal Partner Curves of a Pseudo Null Curve on Dual Space Forms

Abstract

In this work, a kind of normal partner curves of a pseudo null curve on dual space forms is defined and studied. The Frenet frames and curvatures of a pseudo null curve and its associate normal curve on de-Sitter space, its associate normal curve on hyperbolic space, are related by some particular function and the angles between their tangent vector fields, respectively. Meanwhile, the relationships between the normal partner curves of a pseudo null curve are revealed. Last but not least, some examples are given and their graphs are plotted by the aid of a software programme.

1. Introduction

In differential geometry, the space associate curves for which there exist some relations between their Frenet frames or curvatures compose a large class of fascinating subjects in the curve theory, such as Bertrand curve, Mannheim curve, central trace of osculating sphere, involute-evolute curves etc. [1,2,3]. Most of the researchers aimed to explore the relationships between the partner curves. For example, in Euclidean 3-space, the classical Bertrand curves are characterized by constant distance between the corresponding points of the partner curves and by constant angle between tangent vector fields of the partner curves. Naturally, the idea of partner curves research can be moved to other spaces, such as Lorentz-Minkowski space, Galilean space and so on.

The Lorentz-Minkowski metric divides the vectors into spacelike, timelike and lightlike (null) vectors [4]. Due to the causal character of vectors, some simple problems become a little complicated and strange, such as the arc-length of null curves can not be defined similar to the definition in Euclidean space; the angles between different type of vectors need to be classified according to different conditions [5,6]. In Minkowski space, the curves are divided into spacelike, timelike and lightlike (null) curves according to the causal character of their tangent vectors. Some particular curves such as the helix, the Bertrand curve, the Mannheim curve and the normal curve, the osculating curve and the rectifying curve have been surveyed by some researchers [5,7,8,9,10,11,12].

Based on pseudo null curves in Minkowski 3-space, in this work, we define a kind of normal partner curves of a pseudo null curve which lies on de-Sitter space and hyperbolic space, respectively. In Section 2, some fundamental facts about the pseudo null curves, the space forms and the angles between any two non-null vectors are recalled. In Section 3, the relationships between a pseudo null curve and its normal partner curves on dual space forms are explicitly expressed by some particular function and the angles between their tangent vector fields. Furthermore, the relationships between the normal partner curves of a pseudo null curve are presented through the pseudo null curve. Last but not least, some useful and interesting examples of pseudo null curves and their normal partner curves are shown vividly.

The curves in this paper are regular and smooth unless otherwise stated.

2. Preliminaries

The Minkowski 3-space ${\mathbb{E}}_1^3$ is provided with the standard indefinite flat metric given by

$$⟨·,·⟩=-d{x}_1^2+d{x}_2^2+d{x}_3^2$$

in terms of the natural coordinate system $(x_1,x_2,x_3)$. Recall that a vector v is said to be spacelike, timelike and lightlike (null), if $⟨v,v⟩>0$ or $v=0$, $⟨v,v⟩<0$ and $⟨v,v⟩=0$, $(v\ne 0)$, respectively. The norm (modulus) of v is defined by $\parallel v\parallel =\sqrt{|⟨v,v⟩|}$. For any two vectors $x=(x_1,x_2,x_3)$, $y=(y_1,y_2,y_3)\in {\mathbb{E}}_1^3$, the vector product is given by

$$x\times y=\left|\begin{array}{ccc}{e}_1& e_2& e_3\\ x_1& x_2& x_3\\ y_1& y_2& y_3\end{array}\right|=\left(-\left|\begin{array}{cc}{x}_2& x_3\\ y_2& y_3\end{array}\right|,\left|\begin{array}{cc}{x}_3& x_1\\ y_3& y_1\end{array}\right|,\left|\begin{array}{cc}{x}_1& x_2\\ y_1& y_2\end{array}\right|\right),$$

where $\{e_1,e_2,e_3\}$ is an orthogonal basis in ${\mathbb{E}}_1^3$.

An arbitrary curve $r(t):\mathbf{I}\to {\mathbb{E}}_1^3$ can locally be spacelike, timelike or lightlike (null) if all of its velocity vectors $r^{\prime }(t)$ are spacelike, timelike or lightlike, respectively. Furthermore, the spacelike curves can be classified into three kinds according to their principal normal vectors are spacelike, timelike or lightlike, which are called the first and the second kind of spacelike curve and the pseudo null curve, respectively [13]. Among of them, the pseudo null curve is defined as the following.

Definition 1.

([6]). A spacelike curve $r(t)$ framed by Frenet frame $\{T,N,B\}$ in ${\mathbb{E}}_1^3$ is called a pseudo null curve, if its principal normal vector N and binormal vector B are linearly independent lightlike (null) vectors.

Proposition 1.

([6]). Let $r(s):\mathbf{I}\to {\mathbb{E}}_1^3$ be a pseudo null curve parameterized by arc-length s, i.e., $\parallel r^{\prime }(s)\parallel =1$. Then there exists a unique Frenet frame $\{r^{\prime }(s)=T,N,B\}$ such that

$$\begin{array}{c}\left(\begin{array}{c}{T}^{\prime }(s)\\ N^{\prime }(s)\\ B^{\prime }(s)\end{array}\right)=\left(\begin{array}{ccc}0& 1& 0\\ 0& \kappa (s)& 0\\ -1& 0& -\kappa (s)\end{array}\right)\left(\begin{array}{c}T(s)\\ N(s)\\ B(s)\end{array}\right),\end{array}$$

where $⟨T,T⟩=⟨N,B⟩=1,$$⟨N,N⟩=⟨B,B⟩=⟨T,N⟩=⟨T,B⟩=0$ and $T\times N=N,$$N\times B=T,$$B\times T=B.$ In sequence, $T,N,B$ is called the tangent, principal normal and binormal vector fields of $r(s)$, respectively. The function $\kappa (s)$ is called the pseudo null curvature of $r(s)$.

Remark 1.

([8]). Every pseudo null curve $r(s)$ in ${\mathbb{E}}_1^3$ is planar no matter the value of the pseudo null curvature.

The authors of [14] characterized pseudo null curves with the structure function as the following.

Proposition 2

([14]). Let $r(s)$ be a pseudo null curve in ${\mathbb{E}}_1^3$. Then $r(s)$ and its pseudo null curvature $\kappa (s)$ can be written as

$$r(s)=\frac{1}{2}\int (c(g-1)+\frac{1}{c}(g+1),2g,c(g-1)-\frac{1}{c}(g+1))ds$$

and

$$\kappa (s)=\frac{g^{\prime \prime }(s)}{g^{\prime }(s)},$$

(1)

where $0\ne c\in \mathbb{R}$, $g=g(s)$ is non-constant function which is called the structure function of $r(s)$.

Definition 2

([15]). Let p be a fixed point in ${\mathbb{E}}_1^3$ and $r>0$ be a constant. Then the pseudo-Riemannian space forms, i.e., the de-Sitter space ${\mathbb{S}}_1^2(p,r)$, the hyperbolic space ${\mathbb{H}}_0^2(p,r)$ and the lightlike cone ${\mathbb{Q}}_1^2(p)$ are defined as

$${\mathbb{M}}^2(\delta )=\{x\in {\mathbb{E}}_1^3:⟨x-p,x-p⟩=\delta r^2\}=\left\{\begin{array}{c}{\mathbb{S}}_1^2(p,r)|\delta =1;\hfill \\ {\mathbb{H}}_0^2(p,r)|\delta =-1;\hfill \\ {\mathbb{Q}}_1^2(p)|\delta =0.\hfill \end{array}\right.$$

The point p is called the center of ${\mathbb{S}}_1^2(p,r)$, ${\mathbb{H}}_0^2(p,r)$ and ${\mathbb{Q}}_1^2(p)$. When p is the origin and $r=1$, we simply denote them by ${\mathbb{S}}_1^2$, ${\mathbb{H}}^2$ and ${\mathbb{Q}}_1^2$.

For a pseudo null curve $r(s)$ framed by $\{T,N,B\}$ in ${\mathbb{E}}_1^3$, the planes spanned by $\{T,N\}$, $\{T,B\}$ and $\{N,B\}$ are known as the osculating, the rectifying and the normal planes of $r(s)$, respectively. A curve $b(s)$ is called an associate osculating, an associate rectifying, or an associate normal curve of $r(s)$ when the position vector $b(s)$ always lies on the osculating, the rectifying, or the normal plane of $r(s)$, respectively. For an associate normal curve $b(s)$ of a pseudo null curve $r(s)$, we can write

$$b(s)=u(s)N(s)+v(s)B(s)$$

for some non-zero differentiable functions $u(s)$ and $v(s)$. In particular, if the associate normal curve $b(s)=u(s)N(s)+v(s)B(s)$ lies on ${\mathbb{S}}_1^2$ or ${\mathbb{H}}^2$, then $u(s)$ and $v(s)$ satisfy $u(s)v(s)=\frac{1}{2}$ or $u(s)v(s)=-\frac{1}{2}$. Without lose of generality, we have the following definition.

Definition 3.

Let $r(s)$ be a pseudo null curve framed by $\{T,N,B\}$ in ${\mathbb{E}}_1^3$. Then $b_1(s)=\frac{1}{\sqrt{2}}(\lambda N+\frac{1}{\lambda }B)$, $b_2(s)=\frac{1}{\sqrt{2}}(\lambda N-\frac{1}{\lambda }B)$ is called an associate normal curve of $r(s)$ on de-Sitter space, an associate normal curve of $r(s)$ on hyperbolic space for some non-zero differentiable function $\lambda =\lambda (s)$, respectively. In a word, $b_1(s)$ and $b_2(s)$ are called normal partner curves of $r(s)$ on dual space forms.

To serve the discussions, some fundamental facts of curves lying on space forms will be reviewed.

Proposition 3

([15]). Let $r=r(s):I\to {\mathbb{S}}_1^2$ be a curve parameterized by arc-length s. Then there exists a unique pseudo spherical Frenet frame $\{\alpha ,\beta ,\gamma =r\}$ such that

$$\begin{array}{c}\left(\begin{array}{c}{\alpha }^{\prime }(s)\\ {\beta }^{\prime }(s)\\ {\gamma }^{\prime }(s)\end{array}\right)=\left(\begin{array}{ccc}0& \kappa (s)& 0\\ \kappa (s)& 0& -{\delta }_0\\ 0& 1& 0\end{array}\right)\left(\begin{array}{c}\alpha (s)\\ \beta (s)\\ \gamma (s)\end{array}\right),\end{array}$$

(2)

where $⟨\gamma (s),\gamma (s)⟩=1$, $⟨\beta (s),\beta (s)⟩=-⟨\alpha (s),\alpha (s)⟩={\delta }_0=\pm 1.$ The function $\kappa (s)$ is called the pseudo spherical curvature of $r(s)$.

Proposition 4

([15]). Let $r=r(s):I\to {\mathbb{H}}^2$ be a curve parameterized by arc-length s. Then there exists a unique hyperbolic Frenet frame $\{\alpha ,\beta ,\gamma =r\}$ such that

$$\begin{array}{c}\left(\begin{array}{c}{\alpha }^{\prime }(s)\\ {\beta }^{\prime }(s)\\ {\gamma }^{\prime }(s)\end{array}\right)=\left(\begin{array}{ccc}0& \kappa (s)& 0\\ -\kappa (s)& 0& 1\\ 0& 1& 0\end{array}\right)\left(\begin{array}{c}\alpha (s)\\ \beta (s)\\ \gamma (s)\end{array}\right),\end{array}$$

(3)

where $⟨\gamma (s),\gamma (s)⟩=-1$, $⟨\beta (s),\beta (s)⟩=⟨\alpha (s),\alpha (s)⟩=1.$ The function $\kappa (s)$ is called the hyperbolic curvature of $r(s)$.

At last, let us recall the notion of angles between two arbitrary non-null vectors in ${\mathbb{E}}_1^3$.

Definition 4

([16]). Let u and v be spacelike vectors in ${\mathbb{E}}_1^3$.

• If u and v span a timelike vector subspace. Then we have $|⟨u,v⟩|>\parallel u\parallel \parallel v\parallel$ and hence, there is a unique positive real number θ such that

  $$|⟨u,v⟩|=\parallel u\parallel \parallel v\parallel cosh\theta .$$

  (4)
  The real number θ is called the Lorentz timelike angle between u and v.
• If u and v span a spacelike vector subspace. Then we have $|⟨u,v⟩|\le \parallel u\parallel \parallel v\parallel$ and hence, there is a unique real number $\theta \in [0,\frac{\pi }{2}]$ such that

  $$|⟨u,v⟩|=\parallel u\parallel \parallel v\parallel cos\theta .$$

  (5)
  The real number θ is called the Lorentz spacelike angle between u and v.

Definition 5

([16]). Let u be a spacelike vector and v a future pointing timelike vector in ${\mathbb{E}}_1^3$. Then there is a unique non-negative real number θ such that

$$|⟨u,v⟩|=\parallel u\parallel \parallel v\parallel sinh\theta .$$

(6)

The real number θ is called the Lorentz timelike angle between u and v.

Definition 6.

[16] Let u and v be future pointing (past pointing) timelike vectors in ${\mathbb{E}}_1^3$. Then there is a unique non-negative real number θ such that

$$|⟨u,v⟩|=\parallel u\parallel \parallel v\parallel cosh\theta .$$

(7)

The real number θ is called the Lorentz timelike angle between u and v.

Remark 2

([6]). Physically, this designation of the future pointing and past pointing timelike vectors corresponds to a choice of an arrow of time at the given point, therefore Equations (6) and (7) include all definitions of angles between non-null vectors and timelike vectors.

Remark 3.

The angles between a lightlike vector and an arbitrary spacelike vector, timelike vector or another lightlike vector which is independent to it have been defined in [6]. We do not recall the details here, because they are not involved in this paper.

3. Main Conclusions

In this section, the associate normal curves of a pseudo null curve on de-Sitter space and hyperbolic space, respectively will be discussed. At the same time, the relationships between the normal partner curves will be presented.

3.1. Associate Normal Curves of a Pseudo Null Curve on de-Sitter Space

Let $r(s)$ be a pseudo null curve framed by $\{T,N,B\}$, $b_1(s)=\frac{1}{\sqrt{2}}(\lambda N+\frac{1}{\lambda }B)$ its associate normal curve on de-Sitter space framed by $\{{\alpha }_1,{\beta }_1,{\gamma }_1=b_1\}$. From Proposition 3, we have

Case (1): ${\delta }_0=1$, i.e., ${\beta }_1$ is spacelike. In order to distinguish different cases, we rewrite Equation (2) as the following:

$$\begin{array}{c}\left(\begin{array}{c}{\alpha }_1^{{+}^{\prime }}(\overline{s})\\ {\beta }_1^{{+}^{\prime }}(\overline{s})\\ {\gamma }_1^{{+}^{\prime }}(\overline{s})\end{array}\right)=\left(\begin{array}{ccc}0& {\kappa }_1^{+}(\overline{s})& 0\\ {\kappa }_1^{+}(\overline{s})& 0& -1\\ 0& 1& 0\end{array}\right)\left(\begin{array}{c}{\alpha }_1^{+}(\overline{s})\\ {\beta }_1^{+}(\overline{s})\\ {\gamma }_1^{+}(\overline{s})\end{array}\right),\end{array}$$

where $\overline{s}$ is the arc-length of $b_1(s)$, and $⟨{\gamma }_1^{+}(\overline{s}),{\gamma }_1^{+}(\overline{s})⟩=1$, $⟨{\beta }_1^{+}(\overline{s}),{\beta }_1^{+}(\overline{s})⟩=-⟨{\alpha }_1^{+}(\overline{s}),{\alpha }_1^{+}(\overline{s})⟩=1.$

Taking derivative on both sides of ${\gamma }_1^{+}(\overline{s})=b_1(s)$ with respect to the arc-length s of $r(s)$, we get

$${\beta }_1^{+}\frac{d\overline{s}}{ds}=-\frac{1}{\sqrt{2}\lambda }T+\frac{f}{2\lambda }(\lambda N-\frac{1}{\lambda }B),$$

(8)

where $f=f(s)=\sqrt{2}({\lambda }^{\prime }+\lambda \kappa )$. Making inner product on both sides of Equation (8) with itself, we get ${(\frac{d\overline{s}}{ds})}^2=\frac{1}{2{\lambda }^2}(1-f^2),(f^2<1)$. Then, we have

$${ϵ}_0\frac{d\overline{s}}{ds}=\frac{1}{\sqrt{2}\lambda }\sqrt{1-f^2},({ϵ}_0=\pm 1),$$

(9)

substituting it into Equation (8), we get

$${ϵ}_0{\beta }_1^{+}=-\frac{1}{\sqrt{1-f^2}}T+\frac{f}{\sqrt{2(1-f^2)}}(\lambda N-\frac{1}{\lambda }B).$$

(10)

Due to $T,{\beta }_1^{+}$ are spacelike vectors and $T\times {\beta }_1^{+}=\frac{{ϵ}_{0}f}{\sqrt{2(1-f^2)}}(\lambda N+\frac{1}{\lambda }B)$ is spacelike, then T and ${\beta }_1^{+}$ span a timelike subspace. According to Equation (4), we have

$$|⟨T,{\beta }_1^{+}⟩|=\parallel T\parallel \parallel {\beta }_1^{+}\parallel cosh{\theta }_1^{+},$$

where ${\theta }_1^{+}$ is the Lorentz timelike angle between T and ${\beta }_1^{+}$. Together with $⟨T,{\beta }_1^{+}⟩=-\frac{{ϵ}_0}{\sqrt{1-f^2}}$, we get $cosh{\theta }_1^{+}=\frac{1}{\sqrt{1-f^2}}$, thus $sinh{\theta }_1^{+}=\frac{ϵf}{\sqrt{1-f^2}},(ϵ=\pm 1,f\ne 0)$. Explicitly, when $0<f<1$, $ϵ=1$; when $-1<f<0$, $ϵ=-1$. Then, Equation (10) can be rewritten as

$${ϵ}_0{\beta }_1^{+}=-cosh{\theta }_1^{+}T+\frac{ϵ}{\sqrt{2}}sinh{\theta }_1^{+}(\lambda N-\frac{1}{\lambda }B).$$

(11)

Differentiating Equation (11) with respect to s and by Equation (9), we have

$$\begin{array}{cc}\hfill {\kappa }_1^{+}{\alpha }_1^{+}-{\gamma }_1^{+}=& -\frac{(\sqrt{2}\lambda {\theta }_1^{{+}^{\prime }}-ϵ)sinh{\theta }_1^{+}}{\sqrt{1-f^2}}T+\frac{\lambda (ϵfsinh{\theta }_1^{+}+ϵ\sqrt{2}\lambda {\theta }_1^{{+}^{\prime }}cosh{\theta }_1^{+}-2cosh{\theta }_1^{+})}{\sqrt{2(1-f^2)}}N+\hfill \\ \hfill & \frac{ϵ(fsinh{\theta }_1^{+}-\sqrt{2}\lambda {\theta }_1^{{+}^{\prime }}cosh{\theta }_1^{+})}{\lambda \sqrt{2(1-f^2)}}B.\hfill \end{array}$$

(12)

Taking inner product on both sides of Equation (12) with itself, we get

$$1-{\kappa }_1^{{+}^2}=\frac{-2\lambda {\theta }_1^{{+}^{\prime }}(\lambda {\theta }_1^{{+}^{\prime }}-\sqrt{2}ϵ)+(1+f^2){sinh}^2{\theta }_1^{+}-ϵfsinh2{\theta }_1^{+}}{1-f^2},$$

(13)

considering $cosh{\theta }_1^{+}=\frac{1}{\sqrt{1-f^2}}$ and $sinh{\theta }_1^{+}=\frac{ϵf}{\sqrt{1-f^2}}$, by Equation (13) we have

$${ϵ}_1^{+}{\kappa }_1^{+}=ϵ\frac{f^2+\sqrt{2}\lambda f^{\prime }-1}{{(1-f^2)}^{\frac{3}{2}}}=(\sqrt{2}\lambda {\theta }_1^{{+}^{\prime }}-ϵ)cosh{\theta }_1^{+},({ϵ}_1^{+}=\pm 1).$$

(14)

Then, by substituting Equation (14) and ${\gamma }_1^{+}=\frac{1}{\sqrt{2}}(\lambda N+\frac{1}{\lambda }B)$ into Equation (12), we can obtain

$${ϵ}_1^{+}{\alpha }_1^{+}=-\frac{ϵf}{\sqrt{1-f^2}}T+\frac{ϵ}{\sqrt{2(1-f^2)}}(\lambda N-\frac{1}{\lambda }B)=-sinh{\theta }_1^{+}T+\frac{ϵ}{\sqrt{2}}cosh{\theta }_1^{+}(\lambda N-\frac{1}{\lambda }B).$$

Case (2): ${\delta }_0=-1$, i.e., ${\beta }_1$ is timelike. Similar to the process of Case 1, we can rewrite Equation (2) as the following:

$$\begin{array}{c}\left(\begin{array}{c}{\alpha }_1^{{-}^{\prime }}(\overline{s})\\ {\beta }_1^{{-}^{\prime }}(\overline{s})\\ {\gamma }_1^{{-}^{\prime }}(\overline{s})\end{array}\right)=\left(\begin{array}{ccc}0& {\kappa }_1^{-}(\overline{s})& 0\\ {\kappa }_1^{-}(\overline{s})& 0& 1\\ 0& 1& 0\end{array}\right)\left(\begin{array}{c}{\alpha }_1^{-}(\overline{s})\\ {\beta }_1^{-}(\overline{s})\\ {\gamma }_1^{-}(\overline{s})\end{array}\right),\end{array}$$

where $\overline{s}$ is the arc-length of $b_1(s)$, and $⟨{\gamma }_1^{-}(\overline{s}),{\gamma }_1^{-}(\overline{s})⟩=1$, $⟨{\beta }_1^{-}(\overline{s}),{\beta }_1^{-}(\overline{s})⟩=-⟨{\alpha }_1^{-}(\overline{s}),{\alpha }_1^{-}(\overline{s})⟩=-1.$

Taking derivative on both sides of ${\gamma }_1^{-}(\overline{s})=b_1(s)$ with respect to the arc-length s of $r(s)$, we get

$${\beta }_1^{-}\frac{d\overline{s}}{ds}=-\frac{1}{\sqrt{2}\lambda }T+\frac{f}{2\lambda }(\lambda N-\frac{1}{\lambda }B),$$

(15)

where $f=f(s)=\sqrt{2}({\lambda }^{\prime }+\lambda \kappa )$. Making inner product on both sides of Equation (15) with itself, we get ${(\frac{d\overline{s}}{ds})}^2=\frac{1}{2{\lambda }^2}(f^2-1),(f^2>1)$. Then, we have

$${ϵ}_0\frac{d\overline{s}}{ds}=\frac{1}{\sqrt{2}\lambda }\sqrt{f^2-1},({ϵ}_0=\pm 1),$$

(16)

substituting it into Equation (15), we get

$${ϵ}_0{\beta }_1^{-}=-\frac{1}{\sqrt{f^2-1}}T+\frac{f}{\sqrt{2(f^2-1)}}(\lambda N-\frac{1}{\lambda }B).$$

(17)

Due to T is spacelike, ${\beta }_1^{-}$ is timelike, according to Equation (6), we have

$$|⟨T,{\beta }_1^{-}⟩|=\parallel T\parallel \parallel {\beta }_1^{-}\parallel sinh{\theta }_1^{-},$$

where ${\theta }_1^{-}$ is the Lorentz timelike angle between T and ${\beta }_1^{-}.$ Together with $⟨T,{\beta }_1^{-}⟩=-\frac{{ϵ}_0}{\sqrt{f^2-1}}$, we get $sinh{\theta }_1^{-}=\frac{1}{\sqrt{f^2-1}},$ thus $cosh{\theta }_1^{-}=\frac{ϵf}{\sqrt{f^2-1}},$ ($ϵ=\pm 1$). Explicitly, when $f>1$, $ϵ=1$; when $f<-1$, $ϵ=-1$. Then, Equation (17) can be rewritten as

$${ϵ}_0{\beta }_1^{-}=-sinh{\theta }_1^{-}T+\frac{ϵ}{\sqrt{2}}cosh{\theta }_1^{-}(\lambda N-\frac{1}{\lambda }B).$$

(18)

Differentiating Equation (18) with respect to s and by Equation (16), we have

$$\begin{array}{cc}\hfill {\kappa }_1^{-}{\alpha }_1^{-}+{\gamma }_1^{-}=& -\frac{(\sqrt{2}\lambda {\theta }_1^{{-}^{\prime }}-ϵ)cosh{\theta }_1^{-}}{\sqrt{f^2-1}}T+\frac{\lambda (ϵfcosh{\theta }_1^{-}+ϵ\sqrt{2}\lambda {\theta }_1^{{-}^{\prime }}sinh{\theta }_1^{-}-2sinh{\theta }_1^{-})}{\sqrt{2(f^2-1)}}N+\hfill \\ \hfill & \frac{ϵ(fcosh{\theta }_1^{-}-\sqrt{2}\lambda {\theta }_1^{{-}^{\prime }}sinh{\theta }_1^{-})}{\lambda \sqrt{2(f^2-1)}}B.\hfill \end{array}$$

(19)

Taking inner product on both sides of Equation (19) with itself, we get

$$1+{\kappa }_1^{{-}^2}=\frac{2\lambda {\theta }_1^{{-}^{\prime }}(\lambda {\theta }_1^{{-}^{\prime }}-\sqrt{2}ϵ)+(1+f^2){cosh}^2{\theta }_1^{-}-ϵfsinh2{\theta }_1^{-}}{f^2-1},$$

(20)

considering $sinh{\theta }_1^{-}=\frac{1}{\sqrt{f^2-1}}$ and $cosh{\theta }_1^{-}=\frac{ϵf}{\sqrt{f^2-1}},$ by Equation (20) we have

$${ϵ}_1^{-}{\kappa }_1^{-}=ϵ\frac{f^2+\sqrt{2}\lambda f^{\prime }-1}{{(f^2-1)}^{\frac{3}{2}}}=(\sqrt{2}\lambda {\theta }_1^{{-}^{\prime }}-ϵ)sinh{\theta }_1^{-},({ϵ}_1^{-}=\pm 1).$$

(21)

Then, by substituting Equation (21) and ${\gamma }_1^{-}=\frac{1}{\sqrt{2}}(\lambda N+\frac{1}{\lambda }B)$ into Equation (19), we can obtain

$${ϵ}_1^{-}{\alpha }_1^{-}=-\frac{ϵf}{\sqrt{f^2-1}}T+\frac{ϵ}{\sqrt{2(f^2-1)}}(\lambda N-\frac{1}{\lambda }B)=-cosh{\theta }_1^{-}T+\frac{ϵ}{\sqrt{2}}sinh{\theta }_1^{-}(\lambda N-\frac{1}{\lambda }B).$$

Based on above discussions, we can get the following conclusions.

Theorem 1.

Let $r(s)$ be a pseudo null curve framed by $\{T,N,B\}$, $b_1(s)=\frac{1}{\sqrt{2}}(\lambda N+\frac{1}{\lambda }B)$ its associate normal curve on de-Sitter space framed by $\{{\alpha }_1,{\beta }_1,{\gamma }_1=b_1\}$.

• If ${\beta }_1={\beta }_1^{+}$ is spacelike, then the Frenet frame of $r(s)$ and the pseudo spherical Frenet frame of $b_1(s)$ can be related by $f=\sqrt{2}({\lambda }^{\prime }+\lambda \kappa )$ as

  $$\left\{\begin{array}{cc}\hfill & ϵ{ϵ}_1^{+}{\alpha }_1^{+}=-\frac{f}{\sqrt{1-f^2}}T+\frac{1}{\sqrt{2(1-f^2)}}(\lambda N-\frac{1}{\lambda }B),\hfill \\ \hfill & {ϵ}_0{\beta }_1^{+}=-\frac{1}{\sqrt{1-f^2}}T+\frac{f}{\sqrt{2(1-f^2)}}(\lambda N-\frac{1}{\lambda }B),\hfill \\ \hfill & {\gamma }_1^{+}=\frac{1}{\sqrt{2}}(\lambda N+\frac{1}{\lambda }B)\hfill \end{array}\right.$$
  or the Lorentz timelike angle ${\theta }_1^{+}$ between T and ${\beta }_1^{+}$ as

  $$\left\{\begin{array}{cc}\hfill & ϵ{ϵ}_1^{+}{\alpha }_1^{+}=-ϵsinh{\theta }_1^{+}T+\frac{1}{\sqrt{2}}cosh{\theta }_1^{+}(\lambda N-\frac{1}{\lambda }B),\hfill \\ \hfill & ϵ{ϵ}_0{\beta }_1^{+}=-ϵcosh{\theta }_1^{+}T+\frac{1}{\sqrt{2}}sinh{\theta }_1^{+}(\lambda N-\frac{1}{\lambda }B),\hfill \\ \hfill & {\gamma }_1^{+}=\frac{1}{\sqrt{2}}(\lambda N+\frac{1}{\lambda }B),\hfill \end{array}\right.$$
  where ${ϵ}_0=\pm 1$, ${ϵ}_1^{+}=\pm 1$, $f=ϵtanh{\theta }_1^{+}$ and when $0<f<1$, $ϵ=1$; when $-1<f<0$, $ϵ=-1$.
• If ${\beta }_1={\beta }_1^{-}$ is timelike, then the Frenet frame of $r(s)$ and the pseudo spherical Frenet frame of $b_1(s)$ can be related by $f=\sqrt{2}({\lambda }^{\prime }+\lambda \kappa )$ as

  $$\left\{\begin{array}{cc}\hfill & ϵ{ϵ}_1^{-}{\alpha }_1^{-}=-\frac{f}{\sqrt{f^2-1}}T+\frac{1}{\sqrt{2(f^2-1)}}(\lambda N-\frac{1}{\lambda }B),\hfill \\ \hfill & {ϵ}_0{\beta }_1^{-}=-\frac{1}{\sqrt{f^2-1}}T+\frac{f}{\sqrt{2(f^2-1)}}(\lambda N-\frac{1}{\lambda }B),\hfill \\ \hfill & {\gamma }_1^{-}=\frac{1}{\sqrt{2}}(\lambda N+\frac{1}{\lambda }B)\hfill \end{array}\right.$$
  or the Lorentz timelike angle ${\theta }_1^{-}$ between T and ${\beta }_1^{-}$ as

  $$\left\{\begin{array}{cc}\hfill & ϵ{ϵ}_1^{-}{\alpha }_1^{-}=-ϵcosh{\theta }_1^{-}T+\frac{1}{\sqrt{2}}sinh{\theta }_1^{-}(\lambda N-\frac{1}{\lambda }B),\hfill \\ \hfill & ϵ{ϵ}_0{\beta }_1^{-}=-ϵsinh{\theta }_1^{-}T+\frac{1}{\sqrt{2}}cosh{\theta }_1^{-}(\lambda N-\frac{1}{\lambda }B),\hfill \\ \hfill & {\gamma }_1^{-}=\frac{1}{\sqrt{2}}(\lambda N+\frac{1}{\lambda }B),\hfill \end{array}\right.$$
  where ${ϵ}_0=\pm 1$, ${ϵ}_1^{-}=\pm 1$, $f=ϵcoth{\theta }_1^{-}$ and when $f>1$, $ϵ=1$; when $f<-1$, $ϵ=-1$.

Theorem 2.

Let $r(s)$ be a pseudo null curve framed by $\{T,N,B\}$, $b_1(s)=\frac{1}{\sqrt{2}}(\lambda N+\frac{1}{\lambda }B)$ its associate normal curve on de-Sitter space framed by $\{{\alpha }_1,{\beta }_1,{\gamma }_1=b_1\}$.

• If ${\beta }_1={\beta }_1^{+}$ is spacelike, the pseudo spherical curvature ${\kappa }_1^{+}$ of $b_1(s)$ can be expressed by

  $${ϵ}_1^{+}{\kappa }_1^{+}=ϵ\frac{f^2+\sqrt{2}\lambda f^{\prime }-1}{{(1-f^2)}^{\frac{3}{2}}}=(\sqrt{2}\lambda {\theta }_1^{{+}^{\prime }}-ϵ)cosh{\theta }_1^{+}.$$
• If ${\beta }_1={\beta }_1^{-}$ is timelike, the pseudo spherical curvature ${\kappa }_1^{-}$ of $b_1(s)$ can be expressed by

  $${ϵ}_1^{-}{\kappa }_1^{-}=ϵ\frac{f^2+\sqrt{2}\lambda f^{\prime }-1}{{(f^2-1)}^{\frac{3}{2}}}=(\sqrt{2}\lambda {\theta }_1^{{-}^{\prime }}-ϵ)sinh{\theta }_1^{-},$$

where ϵ, ${ϵ}_1^{+},$${\theta }_1^{+}$, ${ϵ}_1^{-},$${\theta }_1^{-}$ and f as stated in Theorem 1.

It is obvious that the case $f=0$ is excluded in the first case of Theorems 1 and 2. In fact, when $f=0$, i.e., ${\lambda }^{\prime }+\lambda \kappa =0$, by solving the differential equation, we get

$$\lambda (s)=c{e}^{-\int \kappa (s)ds},(0\ne c\in \mathbb{R}).$$

Furthermore, from Equation (1), by substituting $\kappa (s)=\frac{g^{\prime \prime }(s)}{g^{\prime }(s)}$ into above equation, we have

$$\lambda (s)=\frac{c}{g^{\prime }(s)},(0\ne c\in \mathbb{R}).$$

Corollary 1.

Let $r(s)$ be a pseudo null curve framed by $\{T,N,B\}$ with pseudo null curvature $\kappa (s)$ and structure function $g(s)$, $b_1(s)=\frac{1}{\sqrt{2}}(\lambda N+\frac{1}{\lambda }B)$ its associate normal curve on de-Sitter space framed by $\{{\alpha }_1^{+},{\beta }_1^{+},{\gamma }_1^{+}=b_1\}$. If $\lambda (s)=c{e}^{-\int \kappa (s)ds}=\frac{c}{g^{\prime }(s)},(0\ne c\in \mathbb{R})$, then we have

• the arc-length $\overline{s}$ of $b_1(s)$ can be expressed by $\overline{s}=c_{0}g(s),(0\ne c_0\in \mathbb{R})$;
• the pseudo spherical curvature of $b_1(s)$ is ${\kappa }_1^{+}=\pm 1$;
• the Frenet frame of $r(s)$ and the pseudo spherical Frenet frame of $b_1(s)$ can be related by

  $$\begin{array}{c}\left(\begin{array}{c}{ϵ}_1^{+}{\alpha }_1^{+}\\ {ϵ}_0{\beta }_1^{+}\\ {\gamma }_1^{+}\end{array}\right)=\left(\begin{array}{ccc}0& -\frac{\lambda }{\sqrt{2}}& \frac{1}{\sqrt{2}\lambda }\\ -1& 0& 0\\ 0& \frac{\lambda }{\sqrt{2}}& \frac{1}{\sqrt{2}\lambda }\end{array}\right)\left(\begin{array}{c}T\\ N\\ B\end{array}\right),({ϵ}_0=\pm 1,{ϵ}_1^{+}=\pm 1).\end{array}$$

Proof of Corollary 1.

When $\lambda (s)=c{e}^{-\int \kappa (s)ds}=\frac{c}{g^{\prime }(s)},(0\ne c\in \mathbb{R})$, by taking derivative on both sides of ${\gamma }_1^{+}(\overline{s})=b_1(s)$ with respect to the arc-length s of $r(s)$, we get

$${\beta }_1^{+}\frac{d\overline{s}}{ds}=-\frac{1}{\sqrt{2}\lambda }T.$$

(22)

Making inner product on both sides of Equation (22) with itself, we get ${(\frac{d\overline{s}}{ds})}^2=\frac{1}{2{\lambda }^2}$. Then, we get

$${ϵ}_0\frac{d\overline{s}}{ds}=\frac{1}{\sqrt{2}\lambda }=\frac{c{g}^{\prime }(s)}{\sqrt{2}},({ϵ}_0=\pm 1,0\ne c\in \mathbb{R}).$$

(23)

Obviously, the arc-length $\overline{s}=c_{0}g(s),(0\ne c_0\in \mathbb{R})$ from Equation (23). Substituting Equation (23) into Equation (22), we get

$${ϵ}_0{\beta }_1^{+}=-T.$$

(24)

Taking derivative on both sides of Equation (24) with respect to s and by Equation (23), we have

$${\kappa }_1^{+}{\alpha }_1^{+}-{\gamma }_1^{+}=-\sqrt{2}\lambda N.$$

(25)

Making inner product on both sides of Equation (25) with itself, we have ${\kappa }_1^{+}=\pm 1$. Then from ${\gamma }_1^{+}=\frac{1}{\sqrt{2}}(\lambda N+\frac{1}{\lambda }B)$ and Equation (25), we can obtain

$${ϵ}_1^{+}{\alpha }_1^{+}=-\frac{1}{\sqrt{2}}(\lambda N-\frac{1}{\lambda }B),({ϵ}_1^{+}=\pm 1).$$

The proof is completed. □

Remark 4.

Obviously, the corresponding results in Theorems 1 and 2 still hold for $f=0$, i.e., $\lambda (s)=c{e}^{-\int \kappa (s)ds}=\frac{c}{g^{\prime }(s)},(0\ne c\in \mathbb{R})$.

3.2. Associate Normal Curves of a Pseudo Null Curve on Hyperbolic Space

Let $r(s)$ be a pseudo null curve framed by $\{T,N,B\}$, $b_2(s)=\frac{1}{\sqrt{2}}(\lambda N-\frac{1}{\lambda }B)$ its associate normal curve on hyperbolic space framed by $\{{\alpha }_2,{\beta }_2,{\gamma }_2=b_2\}$. From Proposition 4, we can rewrite Equation (3) as the following:

$$\begin{array}{c}\left(\begin{array}{c}{\alpha }_2^{\prime }(\overline{s})\\ {\beta }_2^{\prime }(\overline{s})\\ {\gamma }_2^{\prime }(\overline{s})\end{array}\right)=\left(\begin{array}{ccc}0& {\kappa }_2(\overline{s})& 0\\ -{\kappa }_2(\overline{s})& 0& 1\\ 0& 1& 0\end{array}\right)\left(\begin{array}{c}{\alpha }_2(\overline{s})\\ {\beta }_2(\overline{s})\\ {\gamma }_2(\overline{s})\end{array}\right),\end{array}$$

where $\overline{s}$ is the arc-length of $b_2(s)$, and $⟨{\gamma }_2(\overline{s}),{\gamma }_2(\overline{s})⟩=-1$, $⟨{\beta }_2(\overline{s}),{\beta }_2(\overline{s})⟩=⟨{\alpha }_2(\overline{s}),{\alpha }_2(\overline{s})⟩=1.$

Taking derivative on both sides of ${\gamma }_2(\overline{s})=b_2(s)$ with respect to the arc-length s of $r(s)$, we get

$${\beta }_2\frac{d\overline{s}}{ds}=\frac{1}{\sqrt{2}\lambda }T+\frac{f}{2\lambda }(\lambda N+\frac{1}{\lambda }B),$$

(26)

where $f=f(s)=\sqrt{2}({\lambda }^{\prime }+\lambda \kappa )$. Making inner product on both sides of Equation (26) with itself, we get ${(\frac{d\overline{s}}{ds})}^2=\frac{1}{2{\lambda }^2}(1+f^2)$. Then, we have

$${ϵ}_0\frac{d\overline{s}}{ds}=\frac{1}{\sqrt{2}\lambda }\sqrt{1+f^2},({ϵ}_0=\pm 1),$$

(27)

substituting it into Equation (26), we get

$${ϵ}_0{\beta }_2=\frac{1}{\sqrt{1+f^2}}T+\frac{f}{\sqrt{2(1+f^2)}}(\lambda N+\frac{1}{\lambda }B).$$

(28)

Due to $T,{\beta }_2$ are spacelike vectors and $T\times {\beta }_2=\frac{{ϵ}_{0}f}{\sqrt{2(1+f^2)}}(\lambda N-\frac{1}{\lambda }B),(f\ne 0)$ is timelike, then T and ${\beta }_2$ span a spacelike subspace. According to Equation (5), we have

$$|⟨T,{\beta }_2⟩|=\parallel T\parallel \parallel {\beta }_2\parallel cos{\theta }_2,$$

where ${\theta }_2$ is the Lorentz spacelike angle between T and ${\beta }_2$. Together with $⟨T,{\beta }_2⟩=\frac{{ϵ}_0}{\sqrt{1+f^2}}$, we can get $cos{\theta }_2=\frac{1}{\sqrt{1+f^2}}$, thus $sin{\theta }_2=\frac{ϵf}{\sqrt{1+f^2}},(ϵ=\pm 1).$ Explicitly, when $f>0,ϵ=1$; when $f<0,ϵ=-1$. Then, Equation (28) can be rewritten as

$${ϵ}_0{\beta }_2=cos{\theta }_{2}T+\frac{ϵ}{\sqrt{2}}sin{\theta }_2(\lambda N+\frac{1}{\lambda }B).$$

(29)

Differentiating Equation (29) with respect to s and by Equation (27), we have

$$\begin{array}{cc}\hfill -{\kappa }_2{\alpha }_2+{\gamma }_2=& -\frac{(\sqrt{2}\lambda {\theta }_2^{\prime }+ϵ)sin{\theta }_2}{\sqrt{f^2+1}}T+\frac{\lambda (ϵfsin{\theta }_2+ϵ\sqrt{2}\lambda {\theta }_2^{\prime }cos{\theta }_2+2cos{\theta }_2)}{\sqrt{2(f^2+1)}}N-\hfill \\ \hfill & \frac{ϵ(fsin{\theta }_2-\sqrt{2}\lambda {\theta }_2^{\prime }cos{\theta }_2)}{\lambda \sqrt{2(f^2+1)}}B.\hfill \end{array}$$

(30)

Taking inner product on both sides of Equation (30) with itself, we get

$${\kappa }_2^2-1=\frac{2\lambda {\theta }_2^{\prime }(\lambda {\theta }_2^{\prime }+\sqrt{2}ϵ)+(1-f^2){sin}^2{\theta }_2-ϵfsin2{\theta }_2}{f^2+1},$$

(31)

considering $cos{\theta }_2=\frac{1}{\sqrt{f^2+1}}$ and $sin{\theta }_2=\frac{ϵf}{\sqrt{f^2+1}}$, by Equation (31) we have

$${ϵ}_2{\kappa }_2=ϵ\frac{f^2+\sqrt{2}\lambda f^{\prime }+1}{{(1+f^2)}^{\frac{3}{2}}}=(\sqrt{2}\lambda {\theta }_2^{\prime }+ϵ)cos{\theta }_2,({ϵ}_2=\pm 1).$$

(32)

Then, by substituting Equation (32) and ${\gamma }_2=\frac{1}{\sqrt{2}}(\lambda N-\frac{1}{\lambda }B)$ into Equation (30), we can obtain

$${ϵ}_2{\alpha }_2=\frac{ϵf}{\sqrt{f^2+1}}T-\frac{ϵ}{\sqrt{2(f^2+1)}}(\lambda N+\frac{1}{\lambda }B)=sin{\theta }_{2}T-\frac{ϵ}{\sqrt{2}}cos{\theta }_2(\lambda N+\frac{1}{\lambda }B).$$

Summarize above discussions, we have the following conclusions.

Theorem 3.

Let $r(s)$ be a pseudo null curve framed by $\{T,N,B\}$, $b_2(s)=\frac{1}{\sqrt{2}}(\lambda N-\frac{1}{\lambda }B)$ its associate normal curve on hyperbolic space framed by $\{{\alpha }_2,{\beta }_2,{\gamma }_2=b_2\}$. Then the Frenet frame of $r(s)$ and the hyperbolic Frenet frame of $b_2(s)$ can be related by $f=\sqrt{2}({\lambda }^{\prime }+\lambda \kappa )$ as

$$\left\{\begin{array}{cc}\hfill & ϵ{ϵ}_2{\alpha }_2=\frac{f}{\sqrt{1+f^2}}T-\frac{1}{\sqrt{2(1+f^2)}}(\lambda N+\frac{1}{\lambda }B),\hfill \\ \hfill & {ϵ}_0{\beta }_2=\frac{1}{\sqrt{1+f^2}}T+\frac{f}{\sqrt{2(1+f^2)}}(\lambda N+\frac{1}{\lambda }B),\hfill \\ \hfill & {\gamma }_2=\frac{1}{\sqrt{2}}(\lambda N-\frac{1}{\lambda }B)\hfill \end{array}\right.$$

or the Lorentz spacelike angle ${\theta }_2$ between T and ${\beta }_2$ as

$$\left\{\begin{array}{cc}\hfill & ϵ{ϵ}_2{\alpha }_2=ϵsin{\theta }_{2}T-\frac{1}{\sqrt{2}}cos{\theta }_2(\lambda N+\frac{1}{\lambda }B),\hfill \\ \hfill & ϵ{ϵ}_0{\beta }_2=ϵcos{\theta }_{2}T+\frac{1}{\sqrt{2}}sin{\theta }_2(\lambda N+\frac{1}{\lambda }B),\hfill \\ \hfill & {\gamma }_2=\frac{1}{\sqrt{2}}(\lambda N-\frac{1}{\lambda }B),\hfill \end{array}\right.$$

where ${ϵ}_0=\pm 1$, ${ϵ}_2=\pm 1$, $f=ϵtan{\theta }_2$ and when $f>0,ϵ=1$; when $f<0,ϵ=-1$.

Theorem 4.

Let $r(s)$ be a pseudo null curve framed by $\{T,N,B\}$, $b_2(s)=\frac{1}{\sqrt{2}}(\lambda N-\frac{1}{\lambda }B)$ its associate normal curve on hyperbolic space framed by $\{{\alpha }_2,{\beta }_2,{\gamma }_2=b_2\}$. Then the hyperbolic curvature ${\kappa }_2$ of $b_2(s)$ can be expressed by

$${ϵ}_2{\kappa }_2=ϵ\frac{f^2+\sqrt{2}\lambda f^{\prime }+1}{{(1+f^2)}^{\frac{3}{2}}}=(\sqrt{2}\lambda {\theta }_2^{\prime }+ϵ)cos{\theta }_2,$$

where ϵ, ${ϵ}_2$, ${\theta }_2$ and f as stated in Theorem 3.

Similar to the procedure of the associate normal curve of a pseudo null curve on de-Sitter space $b_1(s)$, for the associate normal curve of a pseudo null curve on hyperbolic space $b_2(s)$, when $f=0$, i.e., $\lambda (s)=c{e}^{-\int \kappa (s)ds}=\frac{c}{g^{\prime }(s)},(0\ne c\in \mathbb{R})$, we have the following conclusions.

Corollary 2.

Let $r(s)$ be a pseudo null curve framed by $\{T,N,B\}$ with pseudo null curvature $\kappa (s)$ and structure function $g(s)$, $b_2(s)=\frac{1}{\sqrt{2}}(\lambda N-\frac{1}{\lambda }B)$ its associate normal curve on hyperbolic space framed by $\{{\alpha }_2,{\beta }_2,{\gamma }_2=b_2\}$. If $\lambda (s)=c{e}^{-\int \kappa (s)ds}=\frac{c}{g^{\prime }(s)},(0\ne c\in \mathbb{R})$, then we have

• the arc-length $\overline{s}$ of $b_2(s)$ can be expressed by $\overline{s}=c_{0}g(s),(0\ne c_0\in \mathbb{R})$;
• the hyperbolic curvature of $b_2(s)$ is ${\kappa }_2=\pm 1$;
• the Frenet frame of $r(s)$ and the hyperbolic Frenet frame of $b_2(s)$ can be related by

  $$\begin{array}{c}\left(\begin{array}{c}{ϵ}_2{\alpha }_2\\ {ϵ}_0{\beta }_2\\ {\gamma }_2\end{array}\right)=\left(\begin{array}{ccc}0& -\frac{\lambda }{\sqrt{2}}& -\frac{1}{\sqrt{2}\lambda }\\ 1& 0& 0\\ 0& \frac{\lambda }{\sqrt{2}}& -\frac{1}{\sqrt{2}\lambda }\end{array}\right)\left(\begin{array}{c}T\\ N\\ B\end{array}\right),({ϵ}_0=\pm 1,{ϵ}_2=\pm 1).\end{array}$$

Remark 5.

The proof of Corollary 2 is omitted here since it is very similar to Corollary 1. Obviously, the results in Theorems 3 and 4 still hold for $f=0$, i.e., $\lambda (s)=c{e}^{-\int \kappa (s)ds}=\frac{c}{g^{\prime }(s)},(0\ne c\in \mathbb{R})$.

3.3. The Relationships of the Normal Partner Curves

In this section, we state the relations of the normal partner curves on dual space forms using the knowledge of linear algebra and the results obtained in Section 3.1 and Section 3.2.

Theorem 5.

Let $r(s)$ be a pseudo null curve framed by $\{T,N,B\}$, $b_1(s)=\frac{1}{\sqrt{2}}(\lambda N+\frac{1}{\lambda }B)$ framed by $\{{\alpha }_1,{\beta }_1,{\gamma }_1=b_1\}$ and $b_2(s)=\frac{1}{\sqrt{2}}(\lambda N-\frac{1}{\lambda }B)$ framed by $\{{\alpha }_2,{\beta }_2,{\gamma }_2=b_2\}$ be normal partner curves of $r(s)$ on dual space forms.

• If ${\beta }_1={\beta }_1^{+}$ is spacelike, then the pseudo spherical Frenet frame of $b_1(s)$ and the hyperbolic Frenet frame of $b_2(s)$ can be related by $f=\sqrt{2}({\lambda }^{\prime }+\lambda \kappa )$ as

  $$\begin{array}{c}\left(\begin{array}{c}ϵ{ϵ}_1^{+}{\alpha }_1^{+}\\ {ϵ}_0{\beta }_1^{+}\\ {\gamma }_1^{+}\end{array}\right)=-\left(\begin{array}{ccc}\frac{f^2}{\sqrt{1-f^4}}& \frac{f}{\sqrt{1-f^4}}& -\frac{1}{\sqrt{1-f^2}}\\ \frac{f}{\sqrt{1-f^4}}& \frac{1}{\sqrt{1-f^4}}& -\frac{f}{\sqrt{1-f^2}}\\ \frac{1}{\sqrt{1+f^2}}& -\frac{f}{\sqrt{1+f^2}}& 0\end{array}\right)\left(\begin{array}{c}ϵ{ϵ}_2{\alpha }_2\\ {ϵ}_0{\beta }_2\\ {\gamma }_2\end{array}\right)\end{array}$$
  or the Lorentz timelike angle ${\theta }_1^{+}$ between T and ${\beta }_1^{+}$, the Lorentz spacelike angle ${\theta }_2$ between T and ${\beta }_2$ as

  $$\begin{array}{c}\left(\begin{array}{c}ϵ{ϵ}_1^{+}{\alpha }_1^{+}\\ ϵ{ϵ}_0{\beta }_1^{+}\\ {\gamma }_1^{+}\end{array}\right)=-\left(\begin{array}{ccc}sinh{\theta }_1^{+}sin{\theta }_2& sinh{\theta }_1^{+}cos{\theta }_2& -cosh{\theta }_1^{+}\\ cosh{\theta }_1^{+}sin{\theta }_2& cosh{\theta }_1^{+}cos{\theta }_2& -sinh{\theta }_1^{+}\\ cos{\theta }_2& -sin{\theta }_2& 0\end{array}\right)\left(\begin{array}{c}ϵ{ϵ}_2{\alpha }_2\\ ϵ{ϵ}_0{\beta }_2\\ {\gamma }_2\end{array}\right),\end{array}$$
  where ${ϵ}_0$, ${ϵ}_1^{+}$, ${\theta }_1^{+}$ and ${ϵ}_2$, ${\theta }_2$ as stated in Theorems 1 and 3, respectively. $f=ϵtanh{\theta }_1^{+}=ϵtan{\theta }_2$ and when $0<f<1$, $ϵ=1$; when $-1<f<0$, $ϵ=-1$.
• If ${\beta }_1={\beta }_1^{-}$ is timelike, then the pseudo spherical Frenet frame of $b_1(s)$ and the hyperbolic Frenet frame of $b_2(s)$ can be related by $f=\sqrt{2}({\lambda }^{\prime }+\lambda \kappa )$ as

  $$\begin{array}{c}\left(\begin{array}{c}ϵ{ϵ}_1^{-}{\alpha }_1^{-}\\ {ϵ}_0{\beta }_1^{-}\\ {\gamma }_1^{-}\end{array}\right)=-\left(\begin{array}{ccc}\frac{f^2}{\sqrt{f^4-1}}& \frac{f}{\sqrt{f^4-1}}& -\frac{1}{\sqrt{f^2-1}}\\ \frac{f}{\sqrt{f^4-1}}& \frac{1}{\sqrt{f^4-1}}& -\frac{f}{\sqrt{f^2-1}}\\ \frac{1}{\sqrt{1+f^2}}& -\frac{f}{\sqrt{1+f^2}}& 0\end{array}\right)\left(\begin{array}{c}ϵ{ϵ}_2{\alpha }_2\\ {ϵ}_0{\beta }_2\\ {\gamma }_2\end{array}\right)\end{array}$$
  or the Lorentz timelike angle ${\theta }_1^{-}$ between T and ${\beta }_1^{-}$, the Lorentz spacelike angle ${\theta }_2$ between T and ${\beta }_2$ as

  $$\begin{array}{c}\left(\begin{array}{c}ϵ{ϵ}_1^{-}{\alpha }_1^{-}\\ ϵ{ϵ}_0{\beta }_1^{-}\\ {\gamma }_1^{-}\end{array}\right)=-\left(\begin{array}{ccc}cosh{\theta }_1^{-}sin{\theta }_2& cosh{\theta }_1^{-}cos{\theta }_2& -sinh{\theta }_1^{-}\\ sinh{\theta }_1^{-}sin{\theta }_2& sinh{\theta }_1^{-}cos{\theta }_2& -cosh{\theta }_1^{-}\\ cos{\theta }_2& -sin{\theta }_2& 0\end{array}\right)\left(\begin{array}{c}ϵ{ϵ}_2{\alpha }_2\\ ϵ{ϵ}_0{\beta }_2\\ {\gamma }_2\end{array}\right),\end{array}$$

where ${ϵ}_0$, ${ϵ}_1^{-}$, ${\theta }_1^{-}$ and ${ϵ}_2$, ${\theta }_2$ as stated in Theorems 1 and 3, respectively. $f=ϵcoth{\theta }_1^{-}=ϵtan{\theta }_2,$ and when $f>1$, $ϵ=1$; when $f<-1$, $ϵ=-1$.

Proof of Theorem 5.

From Theorems 1 and 3, by some matrix calculations, it is easy to get the conclusions. □

At the same time, from Theorems 2 and 4, the following conclusions are straightforward.

Theorem 6.

Let $r(s)$ be a pseudo null curve framed by $\{T,N,B\}$, $b_1(s)=\frac{1}{\sqrt{2}}(\lambda N+\frac{1}{\lambda }B)$ framed by $\{{\alpha }_1,{\beta }_1,{\gamma }_1=b_1\}$ and $b_2(s)=\frac{1}{\sqrt{2}}(\lambda N-\frac{1}{\lambda }B)$ framed by $\{{\alpha }_2,{\beta }_2,{\gamma }_2=b_2\}$ be normal partner curves of $r(s)$ on dual space forms. Then the pseudo spherical curvature ${\kappa }_1$ of $b_1(s)$ and the hyperbolic curvature ${\kappa }_2$ of $b_2(s)$ satisfy

• if ${\beta }_1={\beta }_1^{+}$ is spacelike, ${\kappa }_1={\kappa }_1^{+}$, then we have

  $${\kappa }_1^{{+}^2}=\frac{{(f^2+\sqrt{2}\lambda f^{\prime }-1)}^2}{{(1-f^2)}^3}={(\sqrt{2}\lambda {\theta }_1^{{+}^{\prime }}-ϵ)}^2{cosh}^2{\theta }_1^{+},$$

  $${\kappa }_2^2=\frac{{(f^2+\sqrt{2}\lambda f^{\prime }+1)}^2}{{(1+f^2)}^3}={(\sqrt{2}\lambda {\theta }_2^{\prime }+ϵ)}^2{cos}^2{\theta }_2$$
  and they are related by $f=ϵtanh{\theta }_1^{+}=ϵtan{\theta }_2$, when $0<f<1$, $ϵ=1$; when $-1<f<0$, $ϵ=-1$. ${\theta }_1^{+}$ and ${\theta }_2$ as stated in Theorems 1 and 3, respectively;
• if ${\beta }_1={\beta }_1^{-}$ is timelike, ${\kappa }_1={\kappa }_1^{-}$, then we have

  $${\kappa }_1^{{-}^2}=\frac{{(f^2+\sqrt{2}\lambda f^{\prime }-1)}^2}{{(f^2-1)}^3}={(\sqrt{2}\lambda {\theta }_1^{{-}^{\prime }}-ϵ)}^2{sinh}^2{\theta }_1^{-},$$

  $${\kappa }_2^2=\frac{{(f^2+\sqrt{2}\lambda f^{\prime }+1)}^2}{{(f^2+1)}^3}={(\sqrt{2}\lambda {\theta }_2^{\prime }+ϵ)}^2{cos}^2{\theta }_2$$
  and they are related by $f=ϵcoth{\theta }_1^{-}=ϵtan{\theta }_2,$ when $f>1$, $ϵ=1$; when $f<-1$, $ϵ=-1$. ${\theta }_1^{-}$ and ${\theta }_2$ as stated in Theorems 1 and 3, respectively.

Considering Corollaries 1 and 2, when $f=0$, i.e., $\lambda (s)=c{e}^{-\int \kappa (s)ds}=\frac{c}{g^{\prime }(s)},(0\ne c\in \mathbb{R})$, we have the following conclusions.

Corollary 3.

Let $r(s)$ be a pseudo null curve framed by $\{T,N,B\}$ with pseudo null curvature $\kappa (s)$ and structure function $g(s)$, $b_1(s)=\frac{1}{\sqrt{2}}(\lambda N+\frac{1}{\lambda }B)$ framed by $\{{\alpha }_1,{\beta }_1,{\gamma }_1=b_1\}$ and $b_2(s)=\frac{1}{\sqrt{2}}(\lambda N-\frac{1}{\lambda }B)$ framed by $\{{\alpha }_2,{\beta }_2,{\gamma }_2=b_2\}$ be normal partner curves of $r(s)$ on dual space forms. If $\lambda (s)=c{e}^{-\int \kappa (s)ds}=\frac{c}{g^{\prime }(s)},(0\ne c\in \mathbb{R})$, then we have

• the arc-length of $b_1(s)$ and $b_2(s)$ all can be expressed by $\overline{s}=c_{0}g(s),(0\ne c_0\in \mathbb{R})$;
• the pseudo spherical curvature ${\kappa }_1^{+}$ of $b_1(s)$ and the hyperbolic curvature ${\kappa }_2$ of $b_2(s)$ satisfy

  $${\kappa }_1^{{+}^2}={\kappa }_2^2=1;$$
• the pseudo spherical Frenet frame of $b_1(s)$ and the hyperbolic Frenet frame of $b_2(s)$ can be related by

  $$\begin{array}{c}\left(\begin{array}{c}{ϵ}_2{\alpha }_2\\ {\beta }_2\\ {\gamma }_2\end{array}\right)=-\left(\begin{array}{ccc}0& 0& 1\\ 0& 1& 0\\ 1& 0& 0\end{array}\right)\left(\begin{array}{c}{ϵ}_1^{+}{\alpha }_1^{+}\\ {\beta }_1^{+}\\ {\gamma }_1^{+}\end{array}\right),({ϵ}_1^{+}=\pm 1,{ϵ}_2=\pm 1).\end{array}$$

Remark 6.

In Corollaries 1–3, for a given pseudo null curve $r(s)$, when the smooth function $\lambda (s)=c{e}^{-\int \kappa (s)ds}=\frac{c}{g^{\prime }(s)},(0\ne c\in \mathbb{R})$, the pseudo spherical curvature ${\kappa }_1^{+}=\pm 1$ of $b_1(s)$ and the hyperbolic curvature ${\kappa }_2=\pm 1$ of $b_2(s)$. How about the converse statement? i.e., when a pseudo spherical curve with spacelike normal vector field $b_1(s)$ has pseudo spherical curvature ${\kappa }_1^{+}=\pm 1$ or a hyperbolic curve $b_2(s)$ has hyperbolic curvature ${\kappa }_2=\pm 1$, how to find out the corresponding pseudo null curve $r(s)$ and what is the relationship between the smooth function $\lambda (s)$ and the null curvature function $\kappa (s)$ or the structure function $g(s)$ of $r(s)$ ? These problems are still in the air and can be considered in the future.

4. Examples

Example 1.

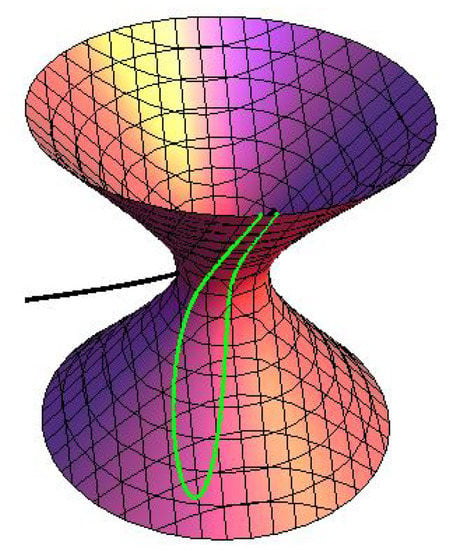
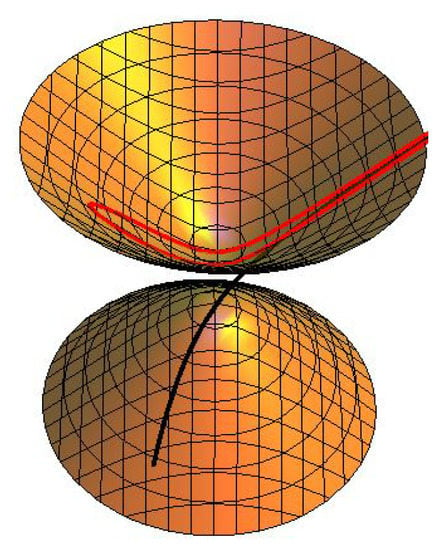
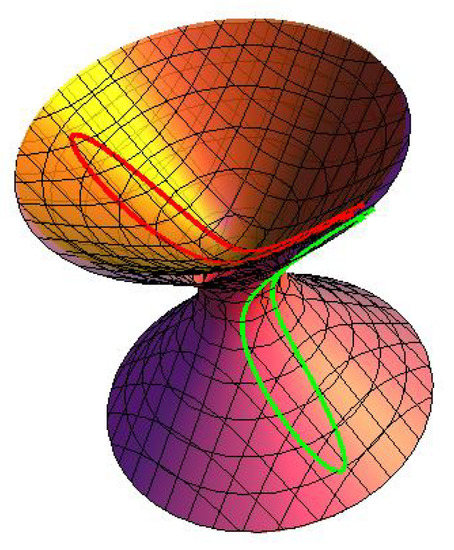
Consider a pseudo null curve $r(s)=(lns,-lns,s)$ framed by $\{T,N,B\}$ whose curvature is $\kappa (s)=-\frac{2}{s}$. From the Frenet formula of $r(s)$, then we know

$$N=\left(-\frac{1}{s^2},\frac{1}{s^2},0\right),B=\left(\frac{s^2+1}{2},\frac{s^2-1}{2},s\right).$$

Assuming $\lambda (s)=cosh\frac{s}{3}$, then the normal partner curves of $r(s)$ on dual space forms are written as (see Figure 1, Figure 2 and Figure 3)

$$b_1(s)=\frac{1}{\sqrt{2}}(-\frac{1}{s^2}cosh\frac{s}{3}+\frac{s^2+1}{2}\mathrm{sech}\frac{\mathrm{s}}{3},\frac{1}{{\mathrm{s}}^2}cosh\frac{\mathrm{s}}{3}+\frac{{\mathrm{s}}^2-1}{2}\mathrm{sech}\frac{\mathrm{s}}{3},\frac{1}{{\mathrm{s}}^{-1}}\mathrm{sech}\frac{\mathrm{s}}{3}),$$

$$b_2(s)=\frac{1}{\sqrt{2}}(-\frac{1}{s^2}cosh\frac{s}{3}-\frac{s^2+1}{2}\mathrm{sech}\frac{\mathrm{s}}{3},\frac{1}{{\mathrm{s}}^2}cosh\frac{\mathrm{s}}{3}-\frac{{\mathrm{s}}^2-1}{2}\mathrm{sech}\frac{\mathrm{s}}{3},-\frac{1}{{\mathrm{s}}^{-1}}\mathrm{sech}\frac{\mathrm{s}}{3}).$$

Figure 1. $r(s)$ (black) and $b_1(s)$ (green) in Example 1.

Figure 2. $r(s)$ (black) and $b_2(s)$ (red) in Example 1.

Figure 3. $b_1(s)$ (green) and $b_2(s)$ (red) in Example 1.

Example 2.

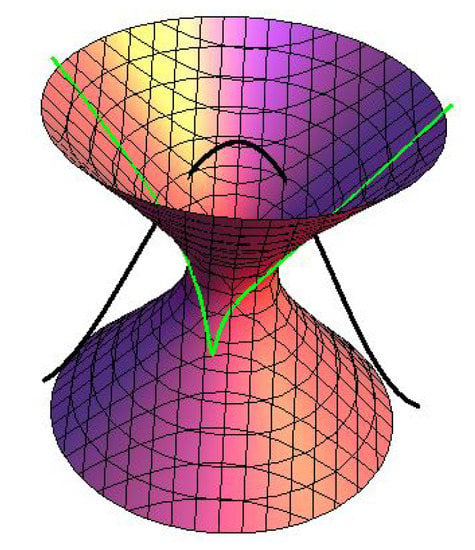
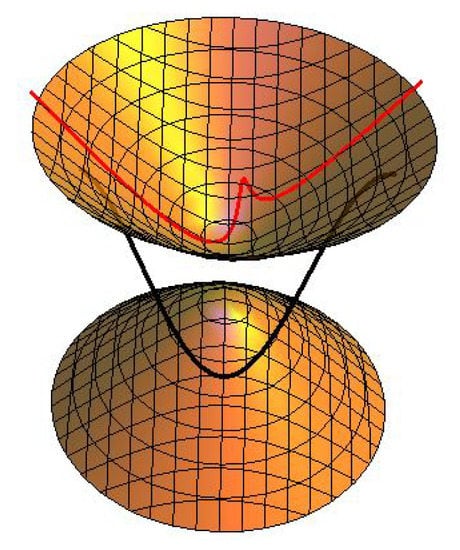
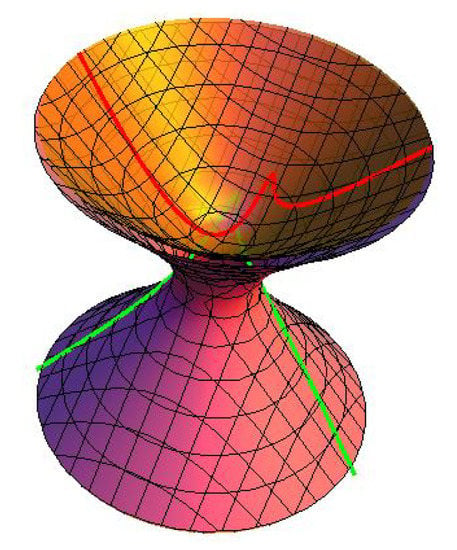
Consider a pseudo null curve $r(s)=-\left(2cos\frac{s}{\sqrt{2}},2cos\frac{s}{\sqrt{2}},s\right)$ framed by $\{T,N,B\}$ whose curvature is $\kappa (s)=-\frac{1}{\sqrt{2}}tan\frac{s}{\sqrt{2}}$. From the Frenet formula of $r(s)$, then we know

$$N=\left(cos\frac{s}{\sqrt{2}},cos\frac{s}{\sqrt{2}},0\right),B=\left(cos\frac{s}{\sqrt{2}}-\frac{3}{2}sec\frac{s}{\sqrt{2}},cos\frac{s}{\sqrt{2}}-\frac{1}{2}sec\frac{s}{\sqrt{2}},\sqrt{2}tan\frac{s}{\sqrt{2}}\right).$$

Assuming $\lambda (s)=e^s$, then the normal partner curves of $r(s)$ on dual space forms can be written as (see Figure 4, Figure 5 and Figure 6)

$$b_1(s)=\frac{1}{\sqrt{2}}((e^s+e^{-s})cos\frac{s}{\sqrt{2}}-\frac{3}{2}{e}^{-s}sec\frac{s}{\sqrt{2}},(e^s+e^{-s})cos\frac{s}{\sqrt{2}}-\frac{1}{2}{e}^{-s}sec\frac{s}{\sqrt{2}},\sqrt{2}{e}^{-s}tan\frac{s}{\sqrt{2}}),$$

$$b_2(s)=\frac{1}{\sqrt{2}}((e^s-e^{-s})cos\frac{s}{\sqrt{2}}+\frac{3}{2}{e}^{-s}sec\frac{s}{\sqrt{2}},(e^s-e^{-s})cos\frac{s}{\sqrt{2}}+\frac{1}{2}{e}^{-s}sec\frac{s}{\sqrt{2}},-\sqrt{2}{e}^{-s}tan\frac{s}{\sqrt{2}}).$$

Figure 4. $r(s)$ (black) and $b_1(s)$ (green) in Example 2.

Figure 5. $r(s)$ (black) and $b_2(s)$ (red) in Example 2.

Figure 6. $b_1(s)$ (green) and $b_2(s)$ (red) in Example 2.

Example 3.

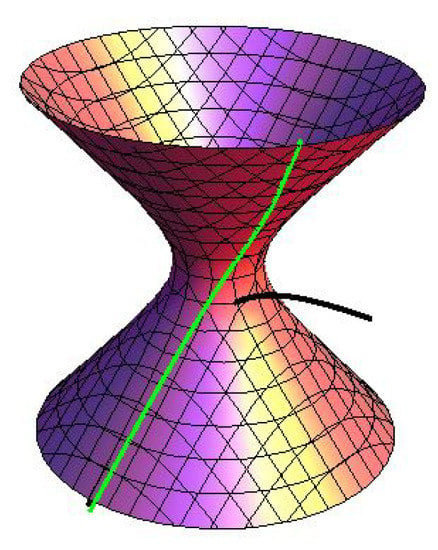
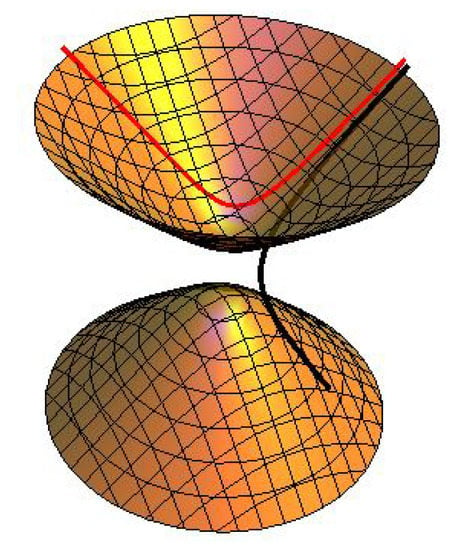
Consider a pseudo null curve $r(s)=\left(ln(1-e^{-s}),-ln(1-e^{-s}),s\right)$ framed by $\{T,N,B\}$ whose curvature is $\kappa (s)=\frac{1+e^s}{1-e^s}$. From the Frenet formula of $r(s)$, then we know

$$N=\left(-\frac{e^s}{{(1-e^s)}^2},\frac{e^s}{{(1-e^s)}^2},0\right),B=\left(\frac{{(1-e^s)}^2+1}{2e^s},\frac{{(1-e^s)}^2-1}{2e^s},\frac{e^s-1}{e^s}\right).$$

When $\lambda (s)=e^{-\int \kappa (s)ds}=\frac{e^{-s}}{{(1-e^s)}^2}$, then the normal partner curves of $r(s)$ on dual space forms can be written as (see Figure 7, Figure 8 and Figure 9)

$$b_1(s)=\frac{1}{\sqrt{2}}(-\frac{1}{{(1-e^s)}^4}+\frac{{(1-e^s)}^4+{(1-e^s)}^2}{2},\frac{1}{{(1-e^s)}^4}+\frac{{(1-e^s)}^4-{(1-e^s)}^2}{2},-{(1-e^s)}^3),$$

$$b_2(s)=\frac{1}{\sqrt{2}}(-\frac{1}{{(1-e^s)}^4}-\frac{{(1-e^s)}^4+{(1-e^s)}^2}{2},\frac{1}{{(1-e^s)}^4}-\frac{{(1-e^s)}^4-{(1-e^s)}^2}{2},{(1-e^s)}^3).$$

Figure 7. $r(s)$ (black) and $b_1(s)$ (green) in Example 3.

Figure 8. $r(s)$ (black) and $b_2(s)$ (red) in Example 3.

Figure 9. $b_1(s)$ (green) and $b_2(s)$ (red) in Example 3.