Implicit-Explicit Methods for a Convection-Diffusion-Reaction Model of the Propagation of Forest Fires
Abstract
1. Introduction
1.1. Scope
1.2. Related Work
1.3. Outline of the Paper
2. Mathematical Model
2.1. Model Development
2.2. Simplified Model in Final Form
2.3. Dimensionless Variables
2.4. Parameters Used for the Wildfire Model
3. Numerical Method
3.1. Notation and Semi-Discrete Formulation
3.2. Linearly Implicit IMEX-RK Scheme
| Algorithm 1 LI-IMEX Runge–Kutta scheme |
|
3.3. Linearly Implicit IMEX-RK Method with Strang-Type Splitting
4. Numerical Results
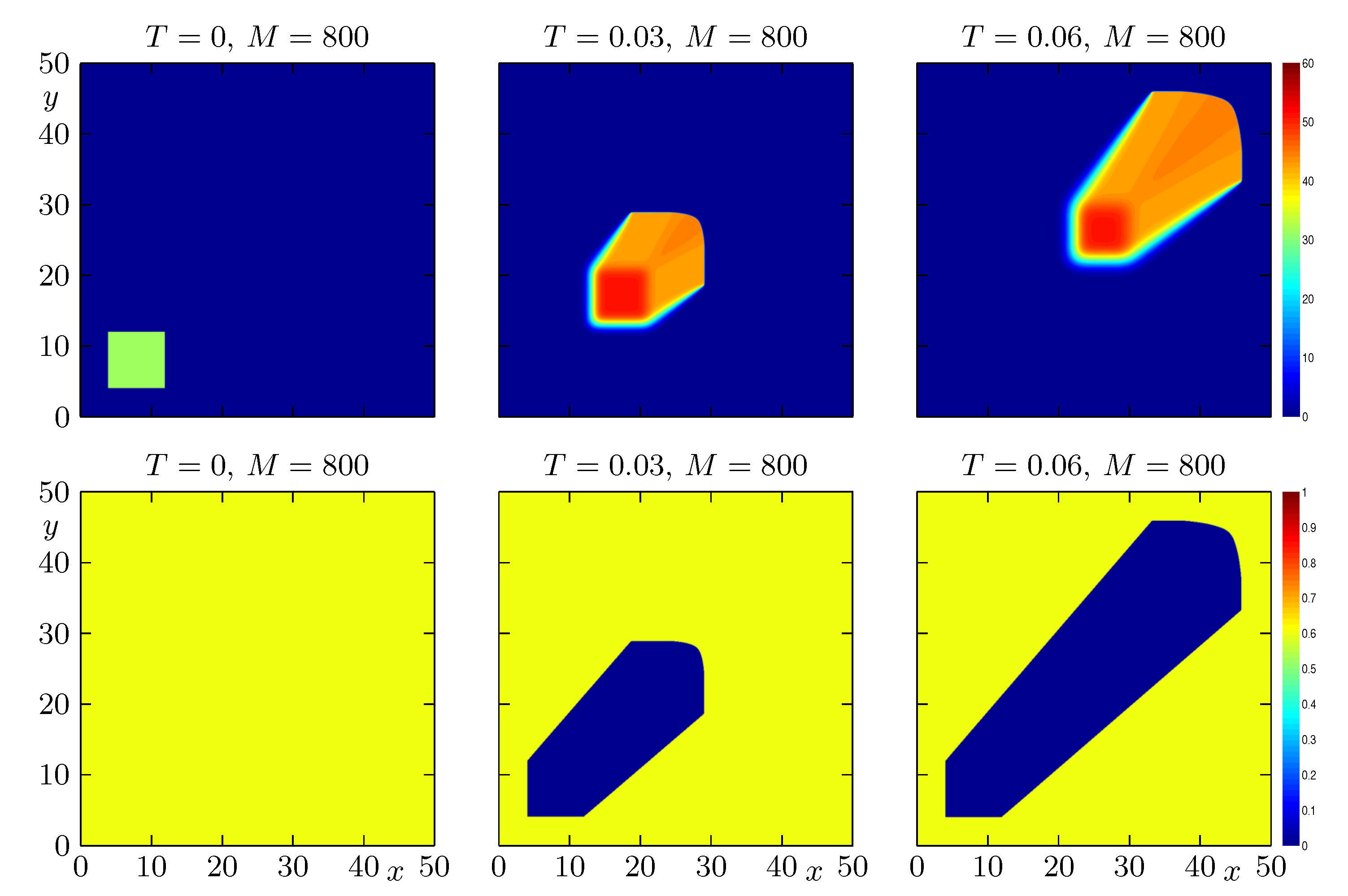
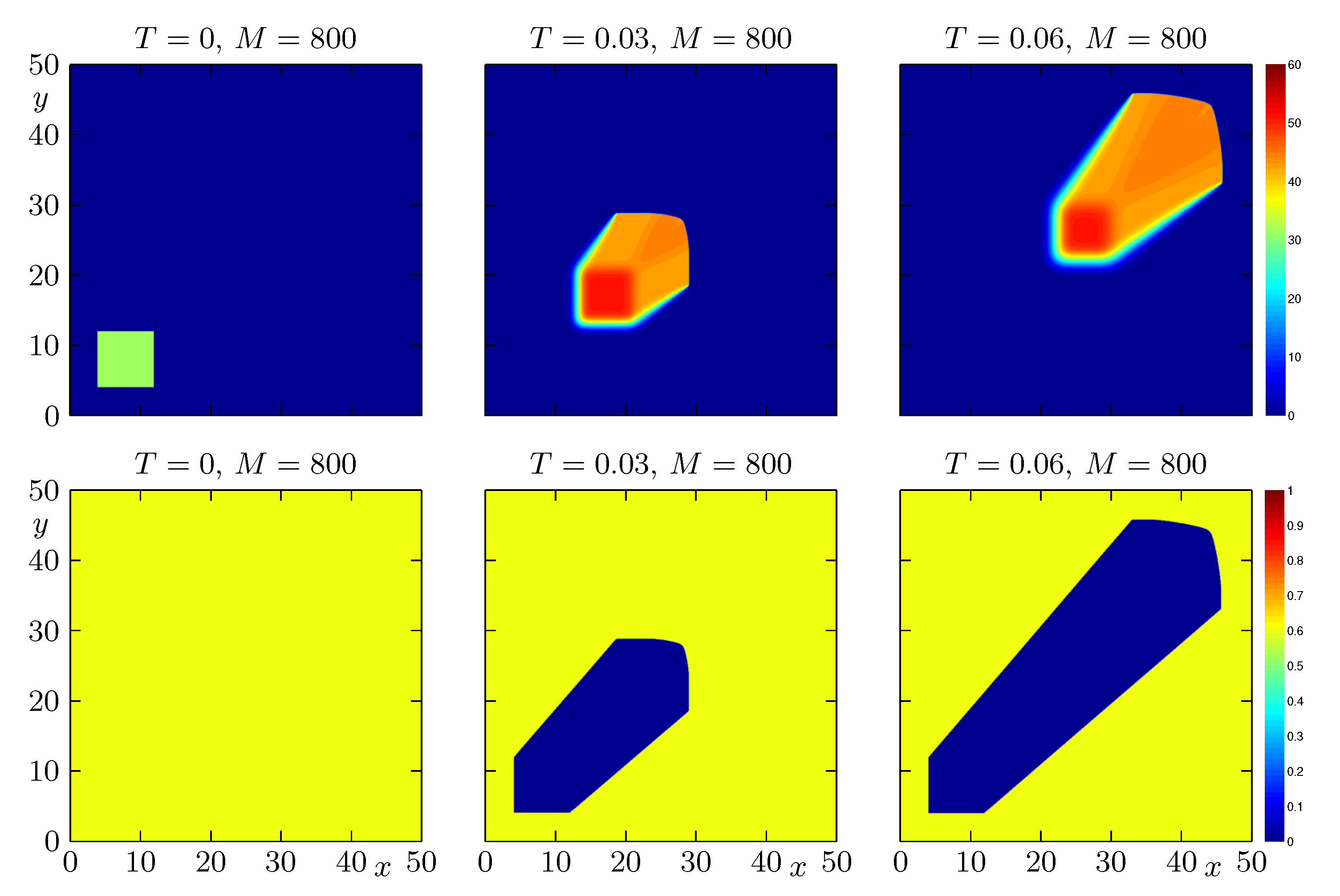
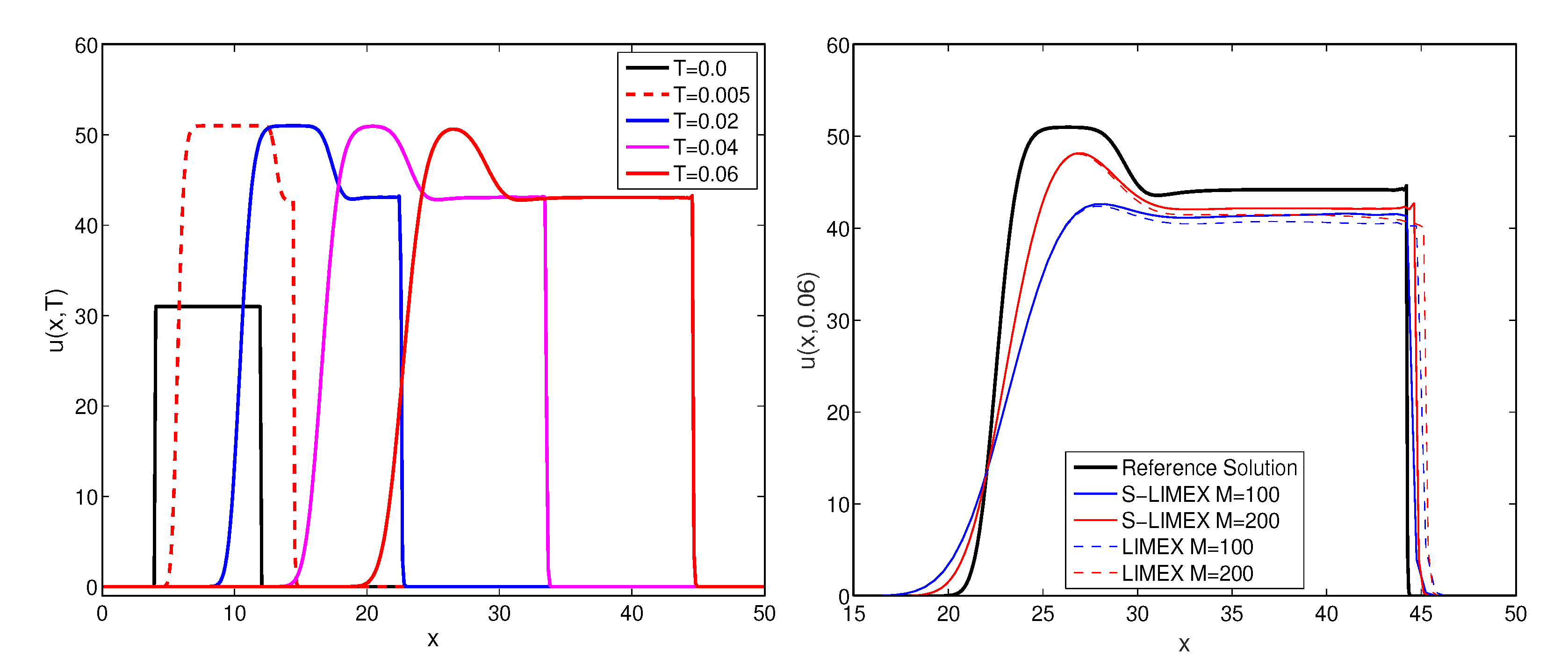
4.1. Example 1: Propagation of a Wildfire with Constant Initial Distribution of Fuel
4.2. Example 2: Propagation of a Wildfire with Distribution of Fuel Determined by Two Areas with Different Fuel Densities
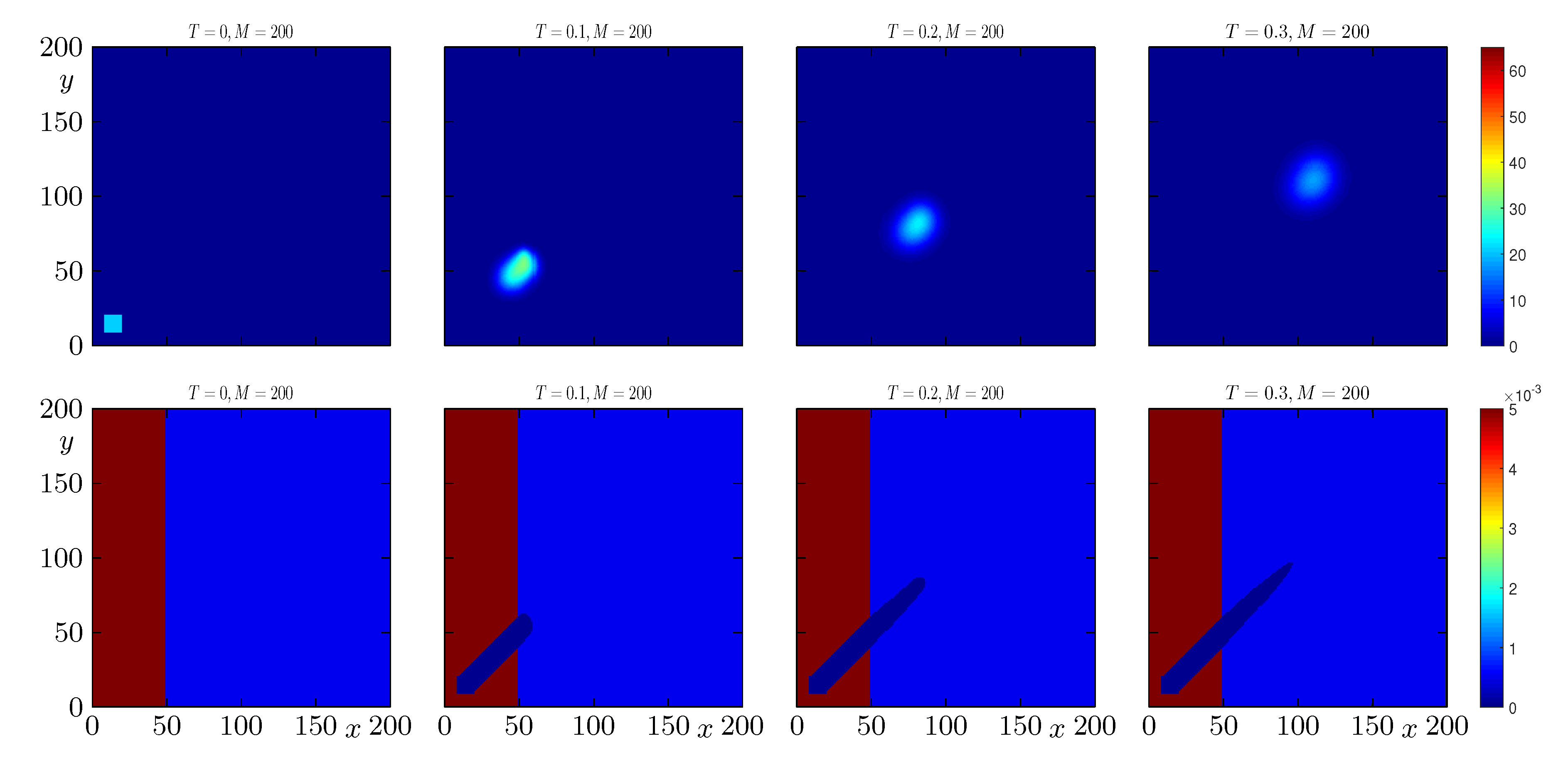
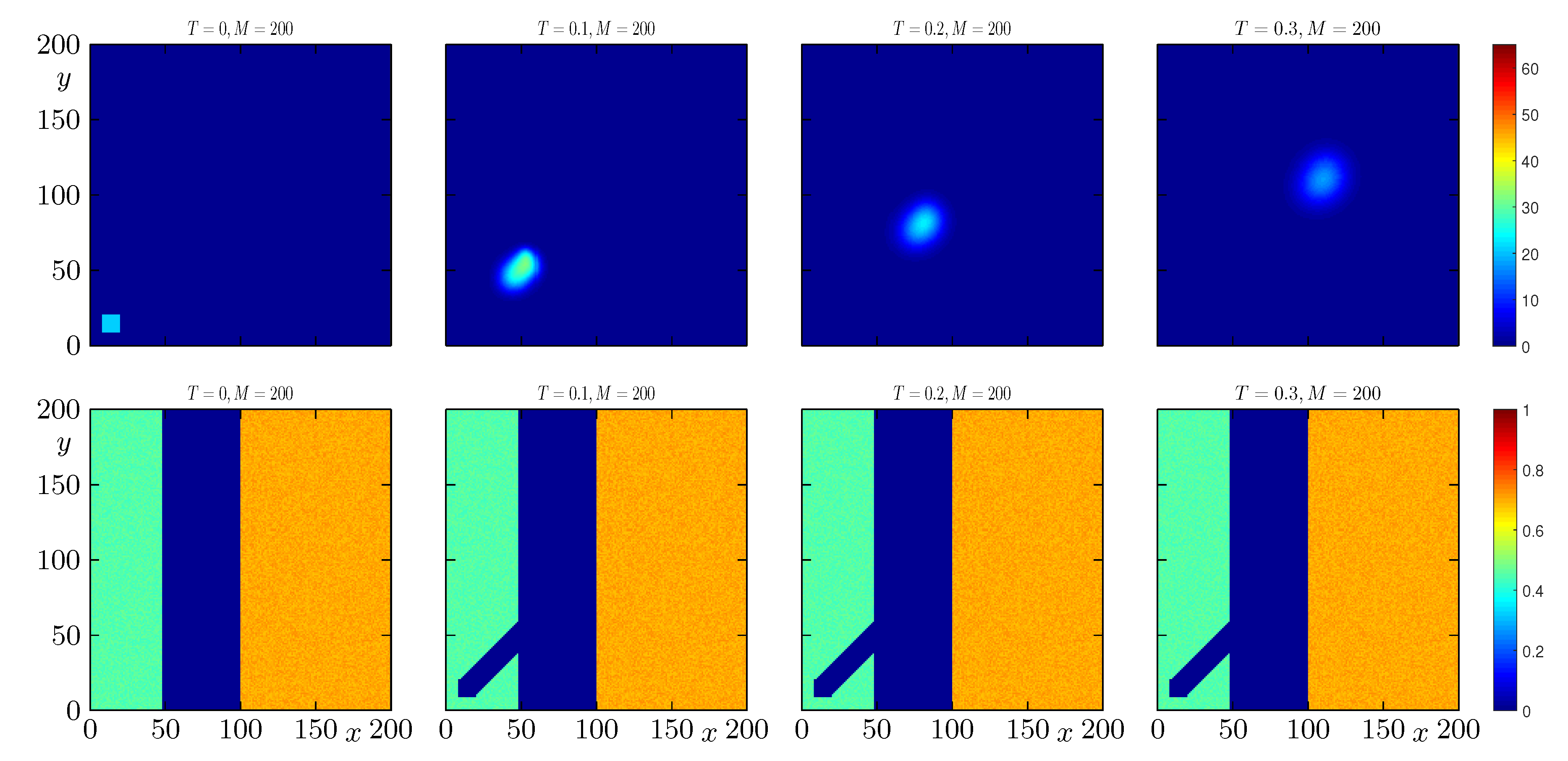
4.3. Example 3: Effect of a Firebreak in the Propagation of a Wildfire
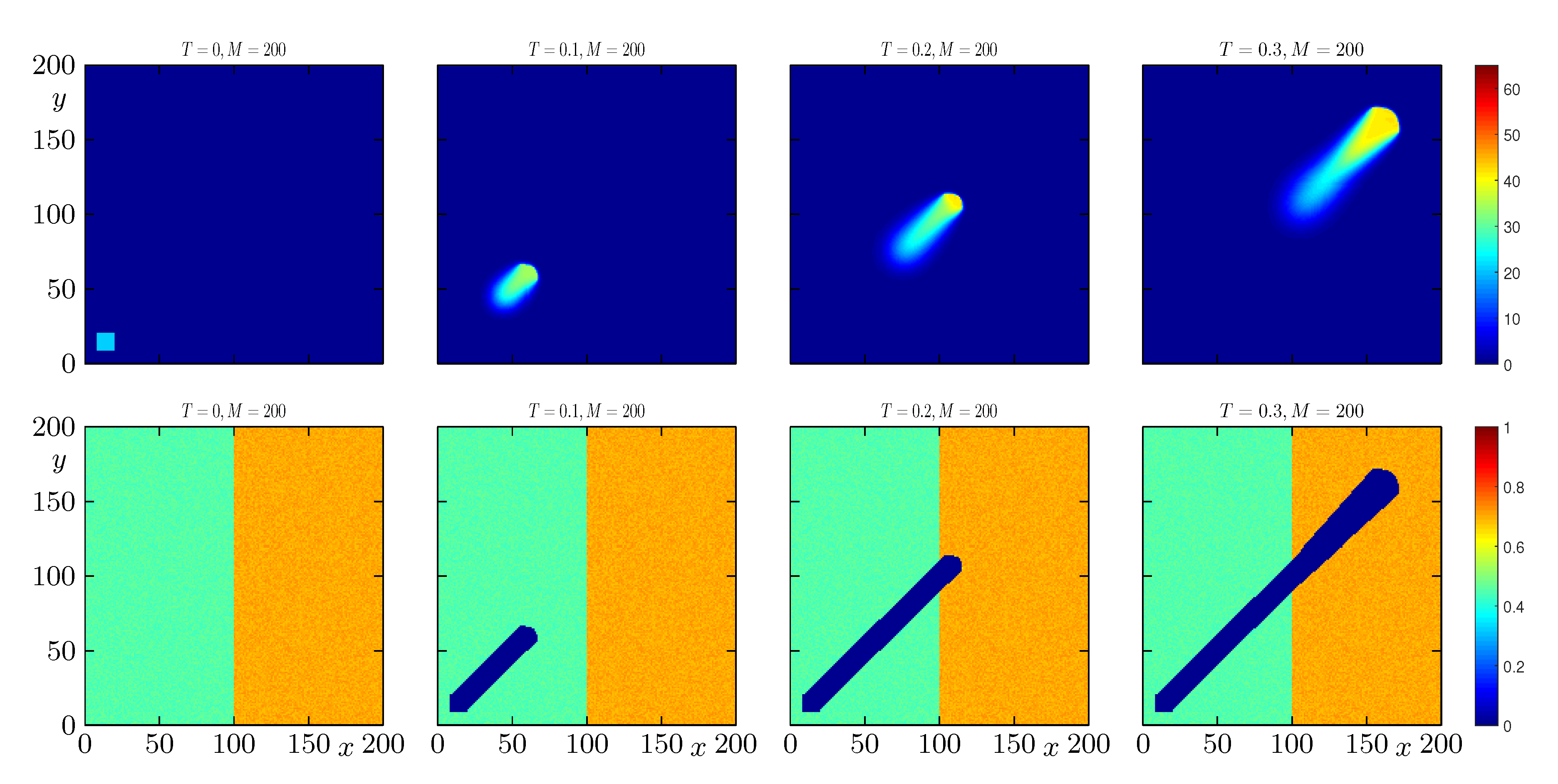
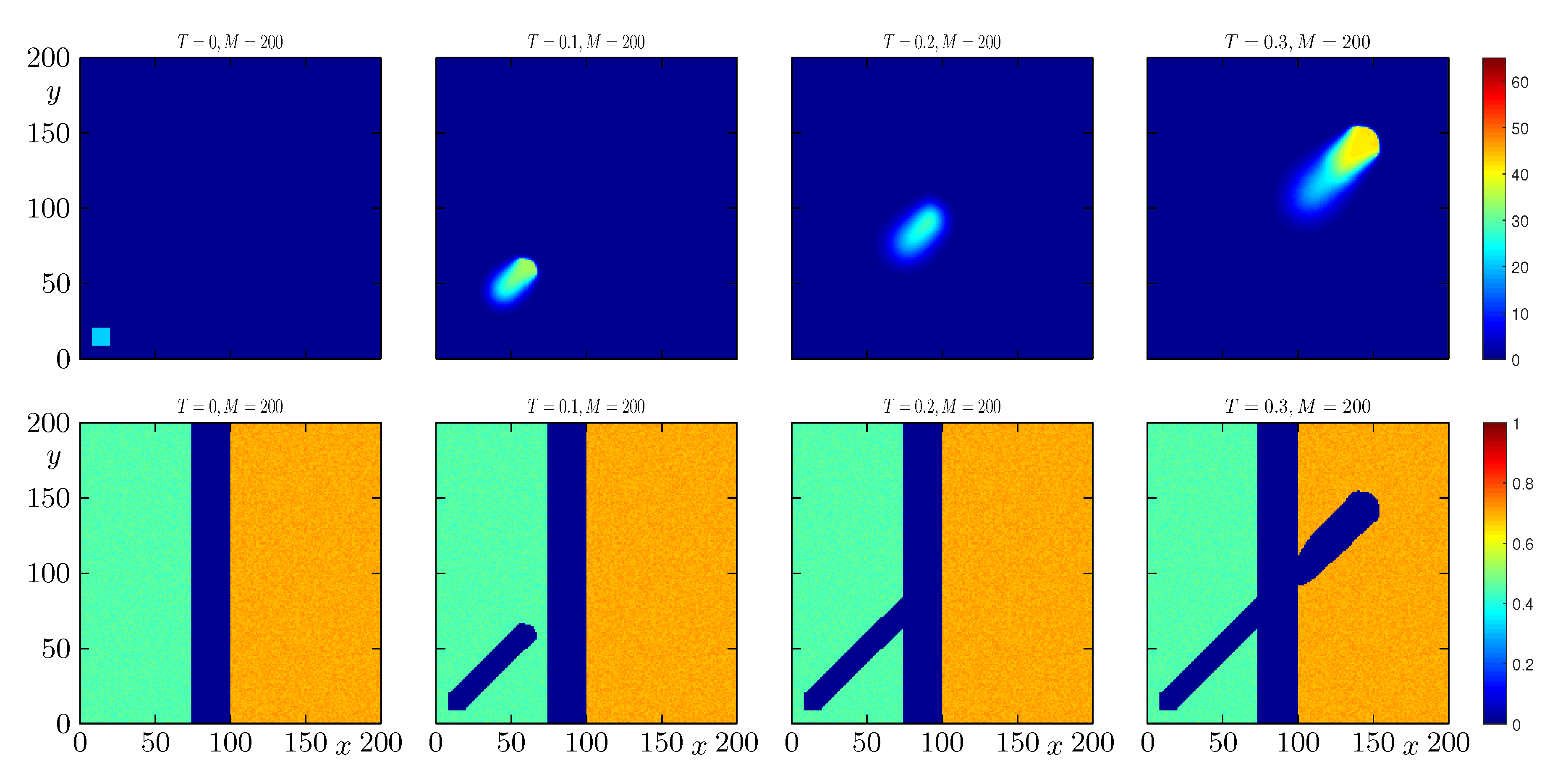
4.4. Example 4: Propagation of a Wildfire with Randomized Initial Distribution of Fuel and a Slight Change of Direction in the Wind
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CFL | Courant–Friedrichs–Lewy |
| CONAF | Corporación Nacional Forestal (Chilean forestry corporation) |
| CPU | central processing unit |
| DIRK | diagonally implicit Runge–Kutta |
| ERK | explicit Runge–Kutta |
| H-LDIRK3(2,2,2) | acronym of particular IMEX-RK scheme |
| IMEX | implicit-explicit |
| IMEX-RK | implicit-explicit Runge–Kutta |
| LI-IMEX | linearly implicit-explicit |
| LIMEX | linearly implicit-explicit Runge–Kutta scheme defined by Algorithm 1 |
| NI-IMEX | nonlinearly implicit-explicit |
| ODE | ordinary differential equation |
| PDE | partial differential equation |
| RK | Runge–Kutta |
| S-LIMEX | Strang-type splitting scheme |
| SSP | strong stability-preserving |
| WENO | weighted essentially non-oscillatory |
References
- Asensio, M.I.; Ferragut, L. On a wildland fire model with radiation. Int. J. Numer. Meth. Engrg. 2002, 54, 137–157. [Google Scholar] [CrossRef]
- LeVeque, R.J. Finite Volume Methods for Hyperbolic Problems; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Boscarino, S.; Bürger, R.; Mulet, P.; Russo, G.; Villada, L.M. Linearly implicit IMEX Runge-Kutta methods for a class of degenerate convection-diffusion problems. SIAM J. Sci. Comput. 2015, 37, B305–B331. [Google Scholar] [CrossRef]
- Boscarino, S.; Bürger, R.; Mulet, P.; Russo, G.; Villada, L.M. On linearly implicit IMEX Runge-Kutta Methods for degenerate convection-diffusion problems modelling polydisperse sedimentation. Bull. Braz. Math. Soc. (New Ser.) 2016, 47, 171–185. [Google Scholar] [CrossRef]
- Boscarino, S.; Filbet, F.; Russo, G. High order semi-implicit schemes for time dependent partial differential equations. J. Sci. Comput. 2016, 68, 975–1001. [Google Scholar] [CrossRef]
- Boscarino, S.; LeFloch, P.G.; Russo, G. High order asymptotic-preserving methods for fully nonlinear relaxation problems. SIAM J. Sci. Comput. 2014, 36, A377–A395. [Google Scholar] [CrossRef]
- Bürger, R.; Chowell, G.; Gavilán, E.; Mulet, P.; Villada, L.M. Numerical solution of a spatio-temporal gender-structured model for hantavirus infection in rodents. Math. Biosci. Eng. 2018, 15, 95–123. [Google Scholar] [CrossRef] [PubMed]
- Bürger, R.; Chowell, G.; Gavilán, E.; Mulet, P.; Villada, L.M. Numerical solution of a spatio-temporal predator-prey model with infected prey. Math. Biosci. Eng. 2019, 16, 438–473. [Google Scholar] [CrossRef] [PubMed]
- Bürger, R.; Inzunza, D.; Mulet, P.; Villada, L.M. Implicit-explicit schemes for nonlinear nonlocal equations with a gradient flow structure in one space dimension. Numer. Methods Partial Differ. Equ. 2019, 35, 1008–1034. [Google Scholar] [CrossRef]
- Bürger, R.; Inzunza, D.; Mulet, P.; Villada, L.M. Implicit-explicit methods for a class of nonlinear nonlocal gradient flow equations modelling collective behaviour. Appl. Numer. Math. 2019, 144, 234–252. [Google Scholar] [CrossRef]
- Bürger, R.; Mulet, P.; Villada, L.M. Regularized nonlinear solvers for IMEX methods applied to diffusively corrected multi-species kinematic flow models. SIAM J. Sci. Comput. 2013, 35, B751–B777. [Google Scholar] [CrossRef]
- Butcher, J.C. Numerical Methods for Ordinary Differential Equations, 2nd ed.; Wiley: Chichester, UK, 2008. [Google Scholar]
- Donat, R.; Guerrero, F.; Mulet, P. Implicit-explicit methods for models for vertical equilibrium multiphase flow. Comput. Math. Appl. 2014, 68, 363–383. [Google Scholar] [CrossRef]
- Generalitat Valenciana. Manual of Good Practices in Forest Fires Prevention. Available online: http://www.agroambient.gva.es/documents/162905929/162908886/Manual+de+Buenas+Pr%C3%A1cticas+en+Prevenci%C3%B3n+de+Incendios+Forestales+-+English+%28383%2C2k%29/65f00043-102a-4835-a129-0b4bd364df79 (accessed on 1 April 2020).
- Ortega, M. Manual Medidas Prediales de Protección Contra Incendios Forestales; Documento de trabajo 451; Corporación Nacional Forestal: Antofagasta, Chile, 2006. [Google Scholar]
- Pastor, E.; Zárate, L.; Planas, E.; Arnaldos, J. Mathematical models and calculation systems for the study of wildland fire behaviour. Progr. Energy Combust. Sci. 2003, 29, 139–153. [Google Scholar] [CrossRef]
- Eberle, S.; Freeden, W.; Matthes, U. Forest fire spreading. In Handbook of Geomathematics, 2nd ed.; Freeden, W., Nashed, M.Z., Sonar, T., Eds.; Springer-Verlag: Berlin, Germany, 2015; pp. 1349–1385. [Google Scholar]
- San Martín, D.; Torres, C.E. Ngen-Kütral: Toward an open source framework for Chilean wildfire spreading. In Proceedings of the 37th International Conference of the Chilean Computer Science Society (SCCC), Santiago, Chile, 5–9 November 2018; pp. 1–8. [Google Scholar]
- Ferragut, L.; Asensio, M.I.; Monedero, S. Modelling radiation and moisture content in fire spread. Commun. Numer. Meth. Engrg. 2007, 23, 819–833. [Google Scholar] [CrossRef]
- Ferragut, L.; Asensio, M.I.; Monedero, S. A numerical method for solving convection-reaction-diffusion multivalued equations in fire spread modelling. Adv. Engrg. Softw. 2007, 38, 366–371. [Google Scholar] [CrossRef]
- Prieto, D.; Asensio, M.I.; Ferragut, L.; Cascón, J.M.; Morillo, A. A GIS-based fire spread simulator integrating a simplified physical wildland fire model and a wind field model. Int. J. Geograph. Inf. Sci. 2017, 31, 2142–2163. [Google Scholar] [CrossRef]
- San Martín, D.; Torres, C.E. Exploring a spectral numerical algorithm for solving a wildfire mathematical model. In Proceedings of the 38th International Conference of the Chilean Computer Science Society (SCCC), Concepción, Chile, 4–9 November 2019; pp. 1–7. [Google Scholar]
- Barovik, D.; Taranchuk, V. Mathematical modelling of running crown forest fires. Math. Model. Anal. 2010, 15, 161–174. [Google Scholar] [CrossRef][Green Version]
- Taranchuk, V.; Barovik, D. Numerical modeling of surface forest fire spread in nonuniform woodland. In Computer Algebra Systems in Teaching and Research Vol. VIII; Prokopenya, A.N., Gil-Świderska, A., Siłuszyk, M., Eds.; Siedlce University of Natural Sciences and Humanities, Institute of Mathematics and Physics: Siedlce, Poland, 2019; pp. 159–168. [Google Scholar]
- Pareschi, L.; Russo, G. Implicit-Explicit Runge-Kutta schemes and applications to hyperbolic systems with relaxation. J. Sci. Comput. 2005, 25, 129–155. [Google Scholar]
- Glassman, I.; Yetter, R.A.; Glumac, N.G. Combustion, 5th ed.; Academic Press: Boston, MA, USA, 2015. [Google Scholar]
- Abgrall, R.; Shu, C.-W. Handbook of Numerical Analysis for Hyperbolic Problems. Basic and Fundamental Issues; North-Holland: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Hesthaven, J.S. Numerical Methods for Conservation Laws; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2018. [Google Scholar]
- Holden, H.; Karlsen, K.H.; Lie, K.-A.; Risebro, N.H. Splitting Methods for Partial Differential Equations with Rough Solutions; European Mathematical Society: Zurich, Switzerland, 2010. [Google Scholar]

| LIMEX | S-LIMEX | |||||
|---|---|---|---|---|---|---|
| cpu[s] | cpu[s] | |||||
| 50 | 2.32 | 2.1 | 0.7 | 1.74 | 1.5 | 0.3 |
| 100 | 1.22 | 1.8 | 6.3 | 1.11 | 9.6 | 3.5 |
| 200 | 0.96 | 1.1 | 19.1 | 0.83 | 8.1 | 18.8 |
| 400 | 0.59 | 6.3 | 133.6 | 0.59 | 6.6 | 162.0 |
| 800 | 0.27 | 3.3 | 1012.6 | 0.32 | 3.8 | 1405.0 |
| 50 | 4.01 | 7.5 | 3.2 | 2.99 | 3.8 | 1.2 |
| 100 | 3.12 | 4.2 | 13.3 | 2.54 | 3.3 | 7.7 |
| 200 | 2.38 | 3.6 | 38.6 | 2.05 | 2.8 | 36.9 |
| 400 | 1.51 | 2.1 | 266.6 | 1.51 | 2.2 | 324.7 |
| 800 | 0.72 | 1.1 | 2004.7 | 0.87 | 1.3 | 2737.4 |
| S-LIMEX | Fully Explicit | |||||
|---|---|---|---|---|---|---|
| cpu[s] | cpu[s] | |||||
| 20 | 2.13 | 1.9 | 0.1 | 2.51 | 2.1 | 2868.6 |
| 40 | 1.57 | 1.4 | 0.2 | 1.83 | 1.8 | 7145.7 |
| 80 | 1.08 | 9.3 | 0.5 | 1.17 | 1.3 | 11,086.3 |
| 160 | 0.89 | 7.4 | 3.6 | 0.99 | 8.5 | 42,906.2 |
| 20 | 2.32 | 2.5 | 0.1 | 2.81 | 2.7 | 5856.9 |
| 40 | 1.71 | 1.7 | 0.2 | 2.54 | 2.1 | 9854.2 |
| 80 | 1.19 | 1.3 | 0.6 | 1.32 | 1.6 | 16,823.7 |
| 160 | 0.94 | 9.7 | 5.1 | 1.03 | 1.1 | 65,305.5 |
| Time | |||
|---|---|---|---|
| 14,000.93 | 14,000.93 | 14,000.93 | |
| 13,826.65 | 14,000.93 | 14,000.93 | |
| 12,699.81 | 12,956.04 | 14,000.93 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bürger, R.; Gavilán, E.; Inzunza, D.; Mulet, P.; Villada, L.M. Implicit-Explicit Methods for a Convection-Diffusion-Reaction Model of the Propagation of Forest Fires. Mathematics 2020, 8, 1034. https://doi.org/10.3390/math8061034
Bürger R, Gavilán E, Inzunza D, Mulet P, Villada LM. Implicit-Explicit Methods for a Convection-Diffusion-Reaction Model of the Propagation of Forest Fires. Mathematics. 2020; 8(6):1034. https://doi.org/10.3390/math8061034
Chicago/Turabian StyleBürger, Raimund, Elvis Gavilán, Daniel Inzunza, Pep Mulet, and Luis Miguel Villada. 2020. "Implicit-Explicit Methods for a Convection-Diffusion-Reaction Model of the Propagation of Forest Fires" Mathematics 8, no. 6: 1034. https://doi.org/10.3390/math8061034
APA StyleBürger, R., Gavilán, E., Inzunza, D., Mulet, P., & Villada, L. M. (2020). Implicit-Explicit Methods for a Convection-Diffusion-Reaction Model of the Propagation of Forest Fires. Mathematics, 8(6), 1034. https://doi.org/10.3390/math8061034






