Lossless and Efficient Secret Image Sharing Based on Matrix Theory Modulo 256

Abstract

Most of today’s secret image sharing (SIS) schemes are based on Shamir’s polynomial-based secret sharing (SS), which cannot recover pixels larger than 250. Many exiting methods of lossless recovery are not perfect, because several problems arise, such as large computational costs, pixel expansion and uneven pixel distribution of shadow image. In order to solve these problems and achieve perfect lossless recovery and efficiency, we propose a scheme based on matrix theory modulo 256, which satisfies $(k,k)$ and $(k,k+1)$ thresholds. Firstly, a sharing matrix is generated by the filter operation, which is used to encrypt the secret image into n shadow images, and then the secret image can be obtained by matrix inverse and matrix multiplication with k or more shadows in the recovery phase. Both theoretical analyses and experiments are conducted to demonstrate the effectiveness of the proposed scheme.

1. Introduction

Shamir [1] and Blakley [2] proposed secret sharing (SS) in 1979, respectively. Due to the characteristics of the image, SS is applied to the image to achieve secret image sharing (SIS). A $(k,n)$ threshold SIS encrypts a secret image into n shadows (also called shares or shadow images) and distributes them among n participants, where any k or more shadows can reconstruct the secret while less than k shadows can obtain nothing of the secret. Unlike traditional encryption and information hiding, SIS has the feature of loss tolerance. SS has many application scenarios, such as access control, transmitting passwords, cloud computing security, block chain security, distributed storage system, etc. [3,4,5,6].

There are two primary branches in SIS, visual cryptography scheme (VCS) [7,8,9,10] and Shamir’s polynomial-based SIS scheme.

The original visual cryptography scheme was introduced by Naor and Shamir in 1995. The best advantage of VCS is that the secret image can be recovered by superposing shadows and human visual system (HVS) without cryptographic computation. It also has several drawbacks, such as lossy recovery and low visual quality of recovered images.

Original Shamir’s polynomial-based scheme is based on a $(k-1)$-degree polynomial, whose constant coefficients are used to cover secret pixels. In the recovery phase, the secret image can be obtained by k or more shadows modulo 251 based on Lagrange interpolation. The modular arithmetic is in a Galois Field of $GF\left(p\right)$. p is a prime number to ensure that each element in $GF\left(p\right)$ has a unique multiplicative inverse. Thien and Lin [11] applied original polynomial-based SS to an image for the first time, they employed all the coefficients of the polynomial for embedding secret, so the shadow size is reduced to $1/k$ times to the original image. However, because the adjacent pixels of the image are correlated, encryption must be performed before sharing to ensure that there is no information leakage in the shadow image, so this method permuted the pixels of the secret image before the sharing phase. Meanwhile, there is another disadvantage in their scheme that it cannot actually achieve lossless recovery, because the grayscale pixel value range is [0,255] and modulo 251 cannot cover it. Therefore, the pixel values of secret image between [251,255] are truncated as 250. Inspired by Thien and Lin’s research, some polynomial-based schemes [12,13] were proposed to obtain more features, such as meaningful shares [14], two-in-one recovery [15,16] and shares with different priorities [17]. The advantage of polynomial-based scheme is the secret can be recovered with high quality. Unfortunately, most polynomial-based SIS schemes suffer from lossy recovery.

To deal with lossy recovery and to obtain more features, the following polynomial-based schemes were therefore proposed [18,19,20]. In Thien-and-Lin’s scheme with lossless recovery [11], they divided a pixel larger than 250 into two parts and encrypted them separately, but it has the problem of random shape changes. When p is 257, it is possible that the shared value might be calculated as 256, but the maximum shadow pixel value is 255, so a part of the secret value is lost. Zhou et al. [21] mentioned a method to solve this problem with the help of a screening operation, which reperforms the sharing phase when the shared value is calculated as 256. However, the screening operation not only increases the calculation amount in the sharing phase but also results in uneven pixel distribution of shadow image. Some previous studies mentioned or used Galois Field $GF\left(2^8\right)$, but they did not give a specific implementation and analysis, Gong et al. [22] first theoretically analyze $GF\left(2^8\right)$ and its arithmetic operations, and then achieved SIS with lossless recovery. As a result that polynomial multiplication suffered from high computational complexity, they decided to use table lookup to do the multiplication, but this increased the space usage.

To sum up, the existing lossless recovery schemes have problems such as pixel expansion, uneven pixel distribution of shadow image and large computational costs. In order to solve the above problems and achieve perfect lossless recovery and high efficiency, we conduct this research.

In this paper, a lossless and efficient $(k,n)$ threshold SIS scheme based on matrix theory is presented. Denote the integer space of modulo 256 by $MS\left(256\right)$. We take the modulo as 256, ensuring that the elements in $MS\left(256\right)$ can one-to-one correspond to 256 pixel values, thus achieving lossless recovery. However, 256 is not a prime number, and there is no guarantee that all elements in $MS\left(256\right)$ have inverses, so Lagrange interpolation cannot be used in the recovery phase. Ding et al. [23] proved that Shamir’s sharing polynomial constructed by the Vandermonde matrix is only a special case of constructing a sharing polynomial satisfying $(k,n)$ threshold, therefore, we design our method from a broader perspective based on matrix theory. In the sharing phase, a sharing matrix is generated by a filter operation, which is used to encrypt the secret image into n shadows. The secret image can be reconstructed by matrix inverse and matrix multiplication with k or more shadows in the recovery phase. There is only one inversion operation in the whole process. Using matrix multiplication can also reduce the computational complexity of the recovery phase compared with Lagrange interpolation. Both theoretical analyses and experiments are conducted to demonstrate the effectiveness of the proposed scheme.

The rest of the paper is organized as follows. Section 2 introduces some preliminary techniques as the basis of the proposed scheme. The proposed SIS scheme is explicitly presented in Section 3. Furthermore, theoretical analyses are given in Section 4. Section 5 gives experimental results and analyses. Finally, the conclusions and our future work are drawn in Section 6.

2. Preliminaries

In this section, we introduce some previous studies as the basis for the proposed method. First, we introduce the implementation process of Shamir’s polynomial-based SS. Second we describe matrix method for polynomial-based SS. Then the common method solving inverse matrix is given.

The main notations used in this paper are as Table 1.

Table 1. Notations and descriptions.

Notations	Descriptions
$(k,n)$	threshold, $k⩽n$
$MS\left(256\right)$	the integer space of modulo 256
p	generally a prime number, we take 256 in this paper
K	a random matrix by a filter operation satisfying any k row vectors of the matrix K are linearly independent and the determinant of any $k\times k$ submatrix is coprime with 256
K	a $k\times k$ submatrix of K
a	a vector in which $a_0$ is the secret pixel value and others are generated randomly in [0,255]
f	a vector obtained by Ka = f, whose elements are $s{c}_i$
$s{c}_i$	a pixel in shadow image
$S{C}_i$	a shadow image corresponding to the i-th participant

2.1. Shamir’s Polynomial-Based SS

Shamir’s polynomial-based SS for $(k,n)$ threshold generates secret data s into n pieces based on a $(k-1)$-degree polynomial as Equation (1), in which $a_0=s$, $a_1,a_2,\cdots ,a_{k-1}$ are assigned randomly in $[0,p-1]$ and p is a prime number greater than $a_0$. All modulo operations are performed in a finite field of $GF\left(p\right)$.

$$f\left(x\right)=(a_0+a_{1}x+\cdots +a_{k-1}{x}^{k-1}) mod p$$

(1)

In the sharing phase, given n different random x, we can obtain n pieces by calculating $s{c}_1=f\left(x_1\right),s{c}_2=f\left(x_2\right),\cdots ,s{c}_n=f\left(x_n\right)$ and take $(x_i,s{c}_i)$ as a secret pair, where i serves as an identifying index or an order label corresponding to the i-th participants. These n pairs are distributed to n participants.

In the recovery phase, given any k pairs of the n shared pairs ${\left\{(x_i,s{c}_i)\right\}}_{i=1}^n$, we can obtain the coefficients of $f\left(x\right)$ by Lagrange interpolation as shown in Equation (2), and then $s=f\left(0\right)$.

$$f\left(x\right)=\sum _{j=1}^{k}f\left(i_j\right)\prod _{\genfrac{}{}{0pt}{}{l=1\hfill }{l\ne j\hfill }}^k\frac{(x-i_l)}{(i_j-i_l)}$$

(2)

Obviously, there are a large number of division operations in Lagrange interpolation, while all modular arithmetic is in a finite field in polynomial-based scheme and division operation must be converted to multiply the inverse. Therefore, p should be a prime to ensure that all elements in $GF\left(p\right)$ have multiplication inverses.

2.2. Matrix Method for Polynomial-Based SS

We mentioned Shamir’s polynomial-based SS in the previous subsection. In this subsection, we introduce the matrix method for polynomial-based SS. Without loss of generality, we can assume that the shared pairs are $(1,f(1\left)\right),(2,f(2\left)\right),$ $\cdots ,(n,f(n\left)\right)$. Therefore, we have n equations as follows:

$$\left\{\begin{array}{c}{a}_0+a_1\times 1+\cdots +a_{k-1}\times 1^{k-1}=f\left(1\right)\hfill \\ a_0+a_1\times 2+\cdots +a_{k-1}\times 2^{k-1}=f\left(2\right)\hfill \\ \cdots \hfill \\ a_0+a_1\times n+\cdots +a_{k-1}\times n^{k-1}=f\left(n\right)\hfill \end{array}\right.$$

(3)

Equation (3) can be converted to matrix multiplication as Equation (4)

$$\left[\begin{array}{ccccc}1& 1& 1& \cdots & 1\\ 1& 2& 2^2& \cdots & 2^{k-1}\\ 1& 3& 3^2& \cdots & 3^{k-1}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ 1& n& n^2& \cdots & n^{k-1}\end{array}\right]·\left[\begin{array}{c}{a}_0\\ a_1\\ a_2\\ ⋮\\ a_{k-1}\end{array}\right]=\left[\begin{array}{c}f\left(1\right)\\ f\left(2\right)\\ f\left(3\right)\\ ⋮\\ f\left(n\right)\end{array}\right]$$

(4)

The above equation can be simplified as:

$$\mathbf{K}\mathbf{a}=\mathbf{f}$$

(5)

It has been proved that linear equations in Equation (3) and vector equation in Equation (5) is equivalent and K is a Vandermonde matrix [23], which has a property that the rank of any $k\times k$ submatrix is k, that is, any k order submatrix of K is invertible. Therefore, we can use inverse matrix to obtain a. Randomly select k row vectors of K to form K, which is a full rank matrix, and compute a using Equation (6) with f(k corresponding $f\left(x\right)$). Then $a_0$ is easy to obtain.

$$\mathbf{a}=K^{-1}\mathbf{f}$$

(6)

2.3. The Method to Solve Inverse Matrix

The most common way to solve the inverse matrix is as follows [24]:

$$K^{-1}=\frac{K^{*}}{\left|K\right|}$$

(7)

$K^{*}$ is the adjoint matrix of K. The value of the $(i,j)$-th entry of $K^{*}$ is that ${(-1)}^{i+j}$ times the determinant of the matrix obtained by deleting the j-th row and i-th column of K. Note that the adjoint matrix can be computed without division, so there is only one division operation in the recovery phase through the matrix method. $\left|K\right|$ is the determinant of K. Since K is a full-rank matrix, the determinant value is not zero.

3. The Proposed Scheme

3.1. The Basic Idea

Most polynomial-based schemes specify 251 or 257 as the prime in the sharing polynomial, because which are the closest prime numbers to 256, while the pixel value range of grayscale image is [0,255], the elements in $GF\left(251\right)$ or $GF\left(257\right)$ cannot perfectly fit the grayscale pixels.

In our scheme, we take the modulo as 256, and share and recover based on matrix theory. We make K a random matrix by a filter operation in the sharing phase as Equation (8), which satisfies two conditions:

Condition 1:

Any k row vectors of the matrix K are linearly independent.

Condition 2:

The determinant of any $k\times k$ submatrix is coprime with 256.

$$\mathbf{K}=\left[\begin{array}{ccccc}{x}_{11}& x_{12}& x_{13}& \cdots & x_{1k}\\ x_{21}& x_{22}& x_{23}& \cdots & x_{2k}\\ x_{31}& x_{32}& x_{33}& \cdots & x_{3k}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ x_{n1}& x_{n2}& x_{n3}& \cdots & x_{nk}\end{array}\right]$$

(8)

In the recovery phase, the secret image can be recovered with the help of matrix inversion, but there is a division operation, that is, the determinant value is divided. Condition 1 guarantees the rank of any $k\times k$ submatrix is k and any k order submatrix of K is invertible.

It cannot guarantee that all elements in $MS\left(256\right)$ are coprime with 256, and only the elements that are coprime with 256 have multiplicative inverses, therefore, K should satisfy condition 2 such that the determinant of any $k\times k$ submatrix has a multiplicative inverse.

We can encrypt a secret image into n shadows with K and distribute them among n participants. Any k or more shadows can reconstruct the secret while less than k shadows can obtain nothing of the secret image.

3.2. The Sharing Phase

At first, to divide the secret pixel s into pieces $s{c}_i$, we generate a vector a$={(a_0,a_1,\cdots ,a_{k-1})}^T$ in which $a_0=s$ and $a_1,\cdots ,a_{k-1}$ are generated randomly in [0,255], and an $n\times k$ matrix K, which satisfies the two conditions mentioned in Section 3.1. Then we can obtain a shares vector f by Ka = f as follows:

$$\left[\begin{array}{ccccc}{x}_{11}& x_{12}& x_{13}& \cdots & x_{1k}\\ x_{21}& x_{22}& x_{23}& \cdots & x_{2k}\\ x_{31}& x_{32}& x_{33}& \cdots & x_{3k}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ x_{n1}& x_{n2}& x_{n3}& \cdots & x_{nk}\end{array}\right]·\left[\begin{array}{c}{a}_0\\ a_1\\ a_2\\ ⋮\\ a_{k-1}\end{array}\right]mod 256=\left[\begin{array}{c}s{c}_1\\ s{c}_2\\ s{c}_3\\ ⋮\\ s{c}_n\end{array}\right]$$

(9)

$s{c}_i$ is a pixel value of the i-th shadow image $S{C}_i$, which is corresponding to the i-th row vector $k_i$ of K and the i-th participant. Then put $s{c}_i$ into the corresponding position of $S{C}_i$. We take $(k_i,S{C}_i)$ as a shared pair and distribute them to n participants. The steps are described in Algorithm 1.

Algorithm 1 The sharing phase of the proposed scheme.

Input: The threshold parameters $(k,n)$, $n=k$ or $n=k+1$, and a grayscale secret image S with size of $M\times N$. Output: n shadows $S{C}_1,S{C}_2,\cdots ,S{C}_n$ and matrix K. Step 1: Generate an $n\times k$ matrix K randomly, and determine that the determinant of any $k\times k$ submatrix is not zero and is coprime with 256. If not, repeat Step 1. Step 2: For every secret pixel s in each position $S(i,j)$, $(i,j)\in \left\{(i,j)|1⩽i⩽M,1⩽j⩽N\right\}$, repeat Step 3–4. Step 3: Generate a vector a$={(a_0,a_1,\cdots ,a_{k-1})}^T$, set $a_0=s$, and generate $a_1,\cdots ,a_{k-1}$ randomly in [0,255]. Step 4: Compute f = Ka (mod 256), where $S{C}_1(i,j)=f\left(1\right),\cdots ,S{C}_n(i,j)=f\left(n\right)$. Step 5: Output n shadows $S{C}_1,S{C}_2,\cdots ,S{C}_n$ and matrix K.

In order to satisfy the conditions of K, we set a filter condition in Step 1 to obtain a suitable matrix. The condition that the determinant of any $k\times k$ submatrix is not zero is equivalent to any k row vectors of the matrix K being linearly independent.

For more applicable situations, some matrices that meet the conditions can be generated in advance, and the matrices can be directly used when encrypting, so as to save real-time computational overhead. The matrix itself does not need to be kept secret and can be made public.

To illustrate the sharing phase of our method more intuitively, we give Example 1 as follows.

Example 1.

Given the first pixel of secret image, whose value is 66, and threshold parameters $(3,4)$.

Firstly, we generate a $4\times 3$ matrix K satisfying the conditions mentioned in Section 3.1. We suppose that $\mathbf{K}=\left[\begin{array}{ccc}122& 251& 47\\ 130& 31& 24\\ 129& 127& 72\\ 147& 115& 117\end{array}\right]$. Secondly, we generate a vector a$={(a_0,a_1,a_2)}^T$ in which $a_0=66$, $a_1$ and $a_2$ are generated randomly in [0,255], so we suppose $a_1=129$ and $a_2=14$. Then f can be obtained by f = Ka = $\left[\begin{array}{ccc}122& 251& 47\\ 130& 31& 24\\ 129& 127& 72\\ 147& 115& 117\end{array}\right]·\left[\begin{array}{c}66\\ 129\\ 14\end{array}\right] mod 256=\left[\begin{array}{c}129\\ 115\\ 49\\ 63\end{array}\right]$. Then put the four elements $\{129,115,49,63\}$ of f into the first pixel position of four shadow images $S{C}_1,S{C}_2,S{C}_3$ and $S{C}_4$, respectively. Finally, distribute $\{S{C}_1,[122 251 47]\},\{S{C}_2,[130 31 24]\},\{S{C}_3,[129 127 72]\},\{S{C}_4,[147 115 117]\}$ to the corresponding four participants.

3.3. The Recovery Phase

In the recovery phase, randomly select k participants to get their shadows and row vectors $k_i$, we can combine their vectors into a $k\times k$ matrix K. Then compute the adjoint matrix $K^{*}$ and determinant $\left|K\right|$ of matrix K. Subsequently, concatenate k pixels in the same position in k shadows to generate f. Thus, we can finally obtain the vector a by $\mathbf{a}=K^{-1}\mathbf{f}$, $a_0$ is the pixel value of original secret image. The steps are described in Algorithm 2.

Algorithm 2 The recovery phase of the proposed scheme.

Input: The k shadows which are randomly selected from n shadows $S{C}_1,S{C}_2,\cdots ,S{C}_n$ and corresponding k vectors $k_i$. Output:The original secret image S. Step 1: Construct a matrix K by k vectors $k_i$. Step 2: Calculate the adjoint matrix $K^{*}$ and determinant $\left|K\right|$ of matrix K. Compute the inverse matrix $K^{-1}$ according to Equation (7). Step 3: For each position $S(i,j)$, $(i,j)\in \left\{(i,j)|1⩽i⩽M,1⩽j⩽N\right\}$, repeat Step 4–5. Step 4: Get a by $\mathbf{a}=\frac{K^{*}}{\left|K\right|}\mathbf{f}$. Step 5: Set the pixel $S(i,j)=a_0$. Step 6: Output the secret image S.

Obviously, if there are fewer than k participants getting together, the matrix K cannot be formed, and the secret image cannot be recovered.

Here, we give Example 2 to illustrate the recovery phase of the proposed scheme.

Example 2.

Given three shadow images $S{C}_1,S{C}_2,S{C}_3$ and three corresponding row vectors $[122 251 47]$,$[130 31 24]$,$[129 127 72]$.

Firstly, we combine three row vectors into a $3\times 3$ matrix $K=\left[\begin{array}{ccc}122& 251& 47\\ 130& 31& 24\\ 129& 127& 72\end{array}\right]$. Secondly, we compute the adjoint matrix $K^{*}=\left[\begin{array}{ccc}208& 185& 215\\ 136& 161& 110\\ 223& 245& 80\end{array}\right]$ and determinant value $\left|K\right|=105$. Then we calculate the inverse ${\left|K\right|}^{-1}=217$ of 105. Then the inverse matrix $K^{-1}$ can be obtained by $K^{-1}=\frac{K^{*}}{\left|K\right|}=K^{*}·{\left|K\right|}^{-1}=\left[\begin{array}{ccc}208& 185& 215\\ 136& 161& 110\\ 223& 245& 80\end{array}\right]·217 mod 256=\left[\begin{array}{ccc}80& 209& 63\\ 72& 121& 62\\ 7& 173& 208\end{array}\right]$. Next we take the pixel values from the first pixel position of the three shadow images $S{C}_1,S{C}_2,S{C}_3$ to form vector f = $\left[\begin{array}{c}129\\ 115\\ 49\end{array}\right]$. Finally, we can obtain vector a through $\mathbf{a}=K^{-1}\mathbf{f}$ = $\left[\begin{array}{ccc}80& 209& 63\\ 72& 121& 62\\ 7& 173& 208\end{array}\right]·\left[\begin{array}{c}129\\ 115\\ 49\end{array}\right] mod 256$ = $\left[\begin{array}{c}66\\ 129\\ 14\end{array}\right]$, the first element 66 is the secret pixel value.

4. Theoretical Analysis

4.1. Threshold Analysis

In this section, we analyze the threshold of our scheme to find out the relationship between k and n.

As mentioned in Section 3, we use the matrix K to encrypt the image, which satisfies the determinant of any $k\times k$ submatrix is not zero and is coprime with 256. All odd numbers in $MS\left(256\right)$ are coprime with 256, obviously the other even numbers including zero are not coprime with 256. The condition becomes that the determinant of any $k\times k$ submatrix is odd.

We first consider the case of $n=k$, that is, K is a square matrix. The formula for calculating the determinant is as follows:

$$\left|\begin{array}{ccccc}{x}_{11}& x_{12}& x_{13}& \cdots & x_{1k}\\ x_{21}& x_{22}& x_{23}& \cdots & x_{2k}\\ x_{31}& x_{32}& x_{33}& \cdots & x_{3k}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ x_{k1}& x_{k2}& x_{k3}& \cdots & x_{kk}\end{array}\right|=\sum _{j_1{j}_2\cdots j_k}{(-1)}^{\tau (j_1{j}_2\cdots j_k)}{x}_{1j_1}{x}_{2j_2}\cdots x_{k{j}_k}$$

(10)

Take a square matrix of $k=3$ as an example:

$$\begin{array}{cc}\hfill \left|\begin{array}{ccc}{x}_{11}& x_{12}& x_{13}\\ x_{21}& x_{22}& x_{23}\\ x_{31}& x_{32}& x_{33}\end{array}\right|=x_{11}{x}_{22}{x}_{33}& -x_{11}{x}_{23}{x}_{32}-x_{12}{x}_{21}{x}_{33}\hfill \\ \hfill +x_{12}{x}_{23}{x}_{31}& +x_{13}{x}_{21}{x}_{32}-x_{13}{x}_{22}{x}_{31}\hfill \end{array}$$

(11)

Theorem 1.

The determinant parity is only related to the parity of the square matrix elements, not to the size of the square matrix elements. We can use 1 for any odd number, and 0 for any even number, to compute the determinant in $GF\left(2\right)$ [25].

Proof of Theorem 1.

The value of the k-order integer determinant is the sum of $k!$ product terms, each of which has k integer factors.

• To make the determinant odd, we need to add an odd number of product terms with odd products. Corresponding to: to make the determinant to be 1, we need to add an odd number of product terms whose product is 1.
• To make the product term odd, all the factors need to be odd. Corresponding to: to make the product term to be 1, we need all 1 in the factor.
• There is one even number in the factor, then the product is even. Corresponding to: there is one 0 in the factor, then the product is 0.

□

The question becomes to find the non-singular matrix in $GF\left(2\right)$. Each such matrix corresponds to k linearly independent vectors, which are all non-zero vectors. There are $2^k-1$ possibilities for the first row vector. The second row vector must be outside the linear subspace generated by the first row vector, so there are $2^k-2^1$ possibilities. By analogy, the i-th row vector should be outside of the linear subspace generated by the first $i-1$ row vectors, and there are $2^k-2^{i-1}$ possibilities. When $n=k$ there exist matrixes that satisfy the conditions mentioned in Section 3. Hence, the probability that the k-order determinant is odd is:

$$\begin{array}{cc}\hfill P_{(k,k)}& =\frac{(2^k-2^0)(2^k-2^1)\dots (2^k-2^{k-1})}{2^{k^2}}\hfill \\ \hfill & =(1-\frac{1}{2^k})(1-\frac{1}{2^{k-1}})\dots (1-\frac{1}{2})\hfill \\ \hfill & =\prod _{i=1}^k(1-\frac{1}{2^i})\hfill \end{array}$$

(12)

$P_{(k,k)}$ is the probability that a randomly generated $k\times k$ matrix meets the two conditions.

When $n=k+1$, add another non-zero row vector below the square matrix, to satisfy that the $(k+1)$-th line is outside the linear subspace composed of any previous $k-1$ lines, there is only one possibility left. When $n=k+1$ there exist matrixes that satisfy the condition mentioned in Section 3. Hence, the probability that a $(k+1)\times k$ matrix is the matrix we need is:

$$P_{(k,k+1)}=\frac{1}{2^k}{P}_{(k,k)}=\frac{1}{2^k}\prod _{i=1}^k(1-\frac{1}{2^i})$$

(13)

When $n>k+1$, there is no matrix for our scheme. Therefore, the proposed scheme can achieve $(k,k)$ and $(k,k+1)$ thresholds.

Next we discuss how $P_{(k,k)}$ and $P_{(k,k+1)}$ change when k is very large. For the case of $n=k$, when k tends to infinity, $P_{(k,k)}={\displaystyle \prod _{i=1}^{\infty }}(1-\frac{1}{2^i})\approx 0.288788$. For the case of $n=k+1$, when k tends to infinity, $P_{(k,k+1)}=\frac{1}{2^{\infty }}{\displaystyle \prod _{i=1}^{\infty }}(1-\frac{1}{2^i})\approx 0$. This is because when discussing in $GF\left(2\right)$, the number of all $(k+1)\times k$ random matrices is $2^{(k+1)·k}$, but there is only one $(k+1)$-th row vector that makes the matrix K satisfy the conditions, and with the increase of k, the denominator of $P_{(k,k+1)}$ is growing rapidly. For large k, $P_{(k,k+1)}$ decreases rapidly to zero. Although $P_{(k,k+1)}$ tends to 0 when k tends to infinity, this does not mean that there is no matrix K that satisfies the conditions.

The size of the random matrix generated in the sharing phase is $n\times k$. Since each element of the matrix is randomly selected from [0,255], the total number of random matrices is ${256}^{n·k}$.

When $n=k$, the probability of the matrix satisfying the conditions is $P_{(k,k)}$, so the number of matrix K satisfying the conditins is $num\left(\mathbf{K}\right)={256}^{k^2}·P_{(k,k)}={128}^{k^2}·(2^k-2^0)(2^k-2^1)\dots (2^k-2^{k-1})$. It can be seen that as k increases, the number of K grows rapidly. For (3,3) threshold, $num\left(\mathbf{K}\right)=$ 1549526502191602335744, and for (7,7) threshold, $num\left(\mathbf{K}\right)\approx 2.935857\times {10}^{117}$.

When $n=k+1$, the probability of the matrix satisfying the conditions is $P_{(k,k+1)}$, so the number of matrix K satisfying the conditins is $num\left(\mathbf{K}\right)={256}^{(k+1)·k}·P_{(k,k+1)}={128}^{(k^2+k)}·(2^k-2^0)(2^k-2^1)\dots (2^k-2^{k-1})$. It can be seen that as k increases, the number of K grows rapidly. For (3,4) threshold, $num\left(\mathbf{K}\right)=$ 3249592603124123221610201088, and for (7,8) threshold, $num\left(\mathbf{K}\right)\approx 1.65274\times {10}^{132}$.

In practical applications, generally $k⩽6$, so the number of matrix K satisfying the conditions can fully meets the actual needs.

4.2. Security Analysis

In the previous subsection, we explained that the number of matrix K can fully meet the actual needs, and as the threshold increases, the number of K increases rapidly, so the probability of an attacker finding the corresponding sharing matrix is extremely small.

The proposed scheme provides two options, one is to generate a sharing matrix K to encrypt secret image during the sharing phase, and then distribute shadow images and corresponding row vectors. The other is to generate a large number of matrix K in advance, which is directly used to save real-time consumption during the sharing phase. In the second case, matrix K can be made public, because of the characteristics of the secret sharing scheme, even if the attacker knows the corresponding sharing matrix, the secret image cannot be recovered if k or more shadow images are not available. Therefore, the security of the second case is not on the sharing matrix, but mainly on whether a sufficient number of shadow images can be obtained.

In the proposed scheme, only one secret pixel value is encrypted per round, and the remaining elements of the vector a are randomly selected from [0,255], so there is no security problem caused by the correlation of adjacent pixels. Moreover, the elements in $MS\left(256\right)$ correspond to the grayscale pixel value range [0,255], so the shadow image pixel values are evenly distributed. All these guarantee that if the attacker gets less than k shadow images, he cannot recover the secret image. Even if the attacker gets $k-1$ shadow images, since grayscale pixel value range is [0,255], the secret image has a total of $256\times 256$ secret pixels, the attacker cannot guess the k-th shadow image, so the secret image will not be obtained.

4.3. Complexity Evaluation

There are a large number of pixels in an image, therefore every pixel of the secret image needs to be shared once, and every pixel of the shadow image needs to be decoded once, so time is spent on iterative operation.

For the $(k,n)$ threshold scheme, no matter whether the polynomial method or the matrix method is used, sharing a secret pixel value requires calculating n shared values. The scheme using polynomial method to calculate a shared value requires $k-1$ addition operations and $\frac{k(k-1)}{2}$ multiplication operations. For the proposed scheme using matrix multiplication, the process of calculating a shared value is the process of multiplying a k-dimensional row vector by a k-dimensional column vector, with a total of $k-1$ additions and k multiplications. When k is the same, polynomial method and matrix method need the same number of addition operations to calculate a shared value. When $k<3$, the polynomial method has fewer multiplication operations. When $k=3$, the two methods have the same multiplication operations. When $k>3$, the matrix method multiplies less times. Therefore, when $k<3$, the calculation amount in the sharing phase of the polynomial method is smaller.

The scheme for $p=257$ reperforms the sharing phase when the shared value is calculated as 256 and there are 257 elements in $GF\left(257\right)$, so the probability of each redo is $\frac{1}{257}$. For a $256\times 256$ grayscale image, approximately $\frac{256\times 256}{257}\approx 256$ times need to be redone during the sharing phase. Our scheme only needs to generate a matrix K by filtering before the sharing phase, which can be used in every subsequent sharing process. Take (3,3) threshold as an example, $P_{(3,3)}=\frac{21}{64}$, in other words, it takes about 3 cycles to get the matrix K. Now the (3,4) threshold, $P_{(3,4)}=\frac{21}{512}$, it takes about 24 cycles. All of these are far less than the number of redo of the scheme for $p=257$. When $k>3$, the time spent in the sharing phase of the proposed scheme is certainly less than that of the scheme for $p=257$. When $k<3$, we can not qualitatively analyze whether the influence of the filter operation is greater or that of the multiplication operation, so we will use experiments to quantitatively explain later.

The algorithm complexity for decryption of Shamir’s scheme is $O\left(k{log}^{2}k\right)$, which uses Lagrange interpolation in the recovery phase. Our scheme uses matrix multiplication during the recovery phase, a $k\times k$ matrix is multiplied with a $k\times 1$ matrix, so the algorithm complexity is $O(k\times k\times 1)=O\left(k^2\right)$. As a result that only $a_0$ is the secret pixel value, only the first element of f needs to be calculated, so the complexity can be reduced to $O\left(k\right)$, which is a little lower than that of Shamir.

4.4. Lossless Recovery Analysis

In the sharing phase, we use f = Ka (mod 256) to encrypt the secret image, in which the operation is matrix multiplication, which can be refined into integer multiplication and addition, without involving division, so there is no inverse operation. The remainder of modulo 256 is 0 to 255, which exactly corresponds to the pixel value of the grayscale image, so the shared value can be stored in the shadow images without loss.

In the recovery phase, we construct K and recover a through a = $K^{-1}$f. The initial filter operation guarantees the determinant of any $k\times k$ submatrix of K is not zero and is coprime with 256. K is a submatrix of K, so its determinant is not zero and is coprime with 256. $K^{-1}$ is calculated by $\frac{K^{*}}{\left|K\right|}$. $\left|K\right|$ is not zero, so it can be used as denominator. The calculation process of the adjoint matrix $K^{*}$ also does not involve division, so dividing by the determinant $\left|K\right|$ is the only division operation. $\left|K\right|$ is coprime with 256 so that it has an exact inverse of 256. Therefore, a can be correctly obtained by a = $K^{-1}$f and $a_0$ is the secret pixel value. Hence, the secret value is recovered losslessly and the proposed scheme is a lossless scheme.

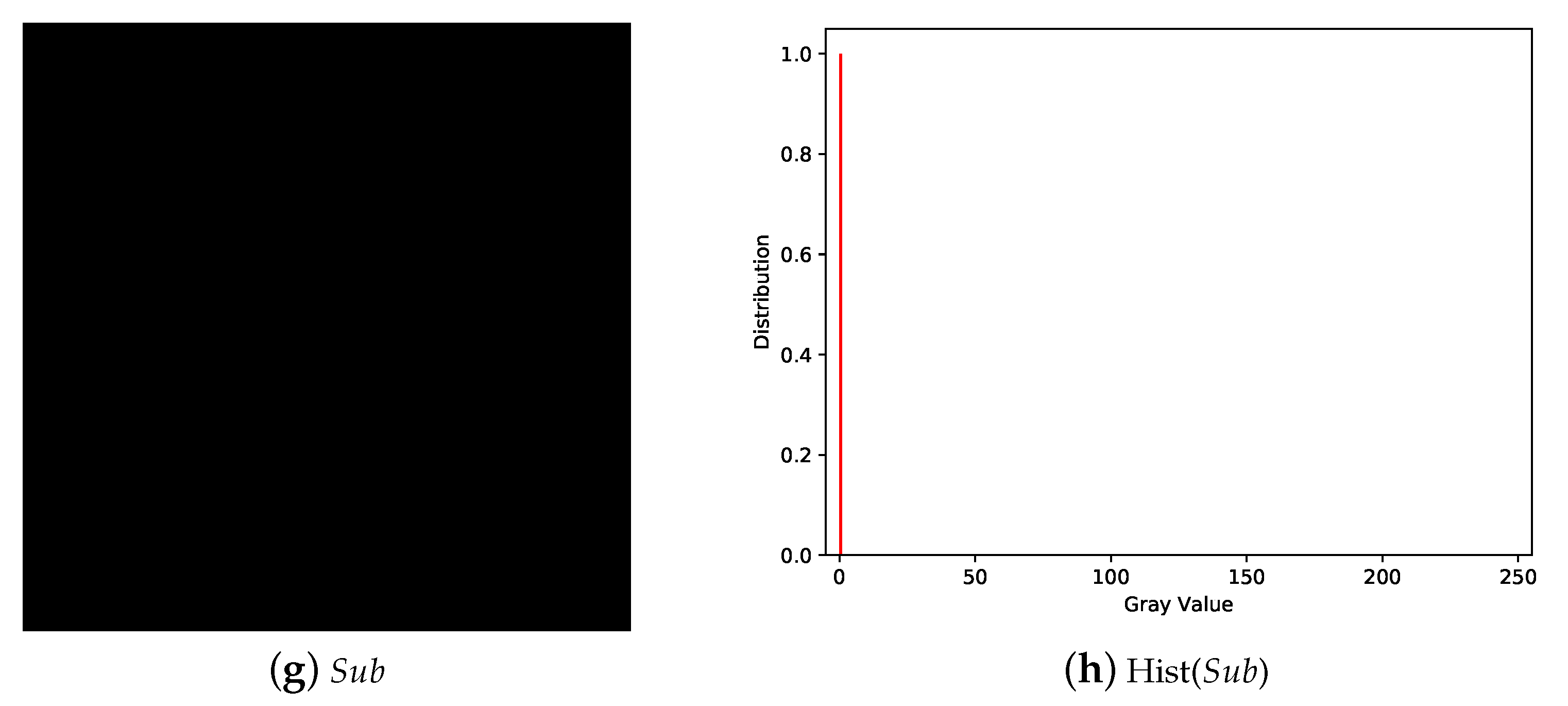
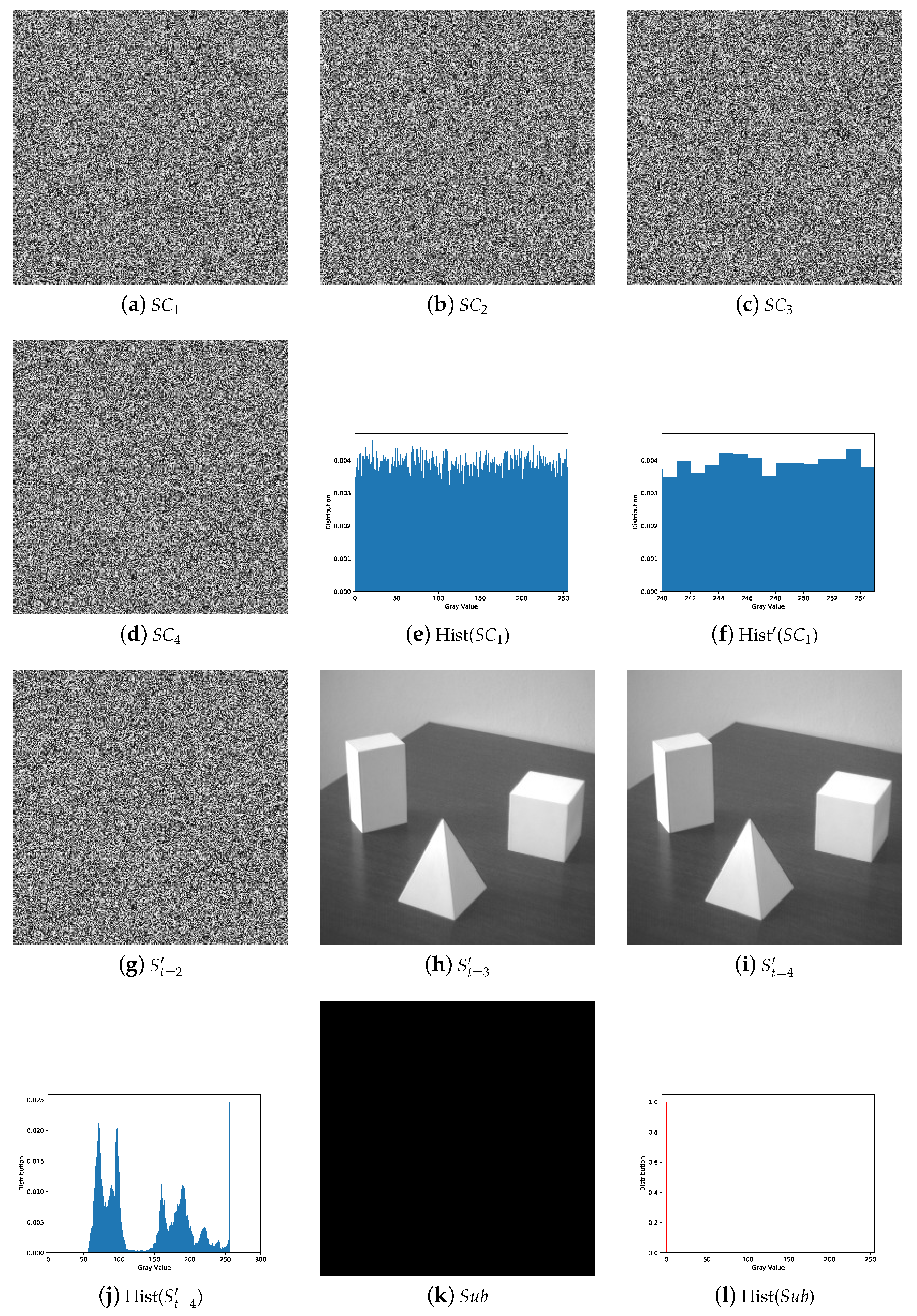
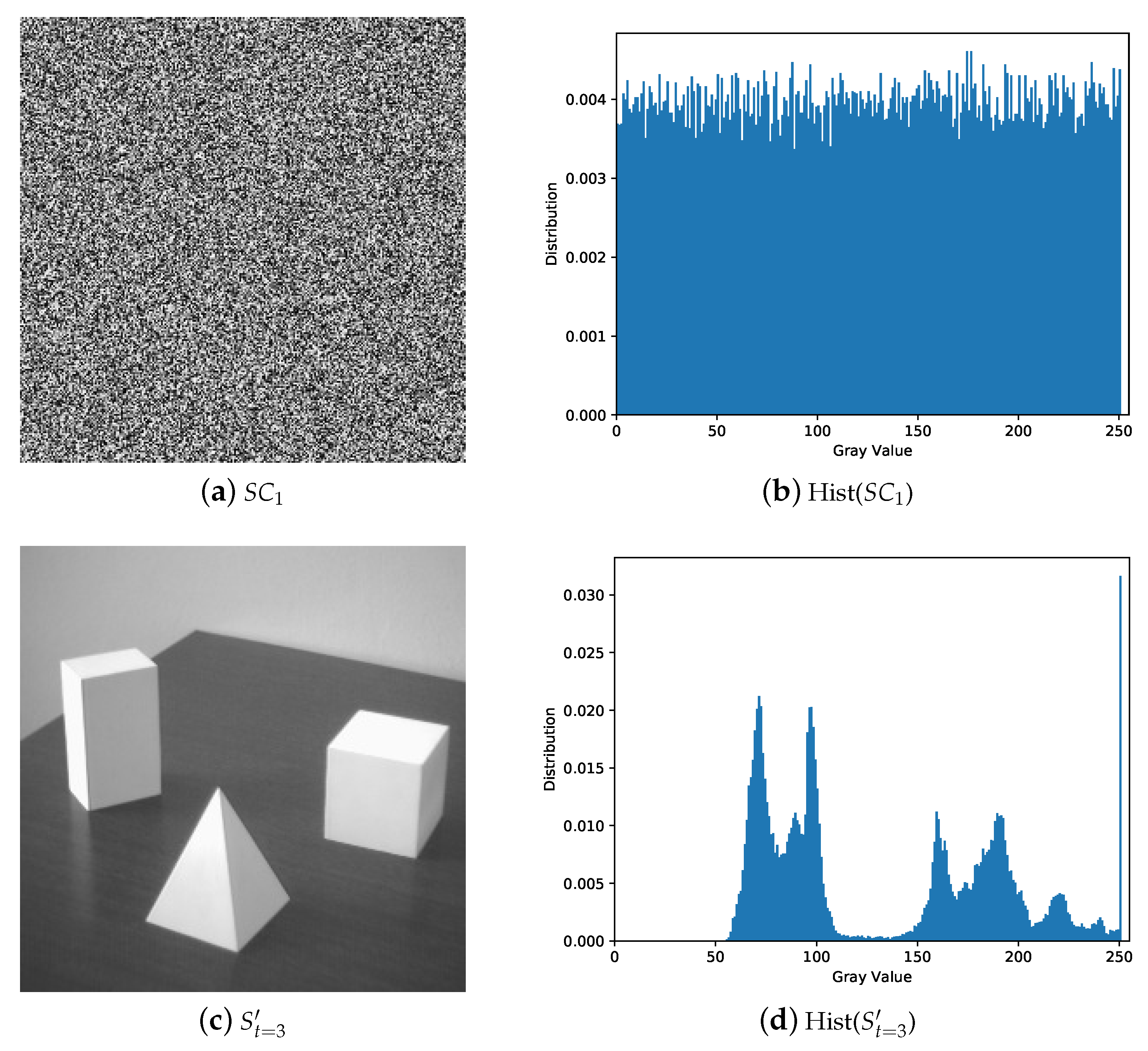
5. Experiments and Comparisons

In this section, experiments and analyses are conducted to evaluate the effectiveness of the proposed method.

5.1. Image Illustration

Figure 1 is the experimental results of our proposed scheme, where $k=3,n=3$. Figure 1a is the secret image. Figure 1b–d are three shadows, which are noisy-like. Figure 1e is the result of recovery by two shadows, from which we can know nothing of the secret. Therefore, obtaining any shadow alone or less than k shadows will not reveal secret information. Figure 1f is the result of recovery by three shadows. Figure 1g is the result of subtracting the pixel matrix of secret image and the recovered image. Figure 1h is the distribution histogram of pixel values of Figure 1g. It can be seen from Figure 1g,h that the difference between the pixel matrix of the recovered image and the pixel matrix of the secret image is a zero matrix, which means that lossless recovery is achieved.

Figure 1. Experimental results of our proposed scheme, where $k=3,n=3$. (a) Secret image; (b–d) three shadows $S{C}_1,S{C}_2$ and $S{C}_3$; (e) result of recovery by $S{C}_1,S{C}_2$; (f) result of recovery by $S{C}_1,S{C}_2$ and $S{C}_3$; (g) the difference between S and $S_{t=3}^{\prime }$; (h) the distribution histogram of pixel values of $Sub$.

Figure 2a is used as a comparison test image, whose distribution histogram of pixel values is Figure 2b. It can be seen from the histogram that the secret image has some pixels larger than 250. Figure 3, Figure 4 and Figure 5 are the results of (3,4) threshold sharing by our scheme and the other two schemes [1,21], respectively.

Figure 2. (a) The secret image S; (b) the distribution histogram of pixel values of the secret image S.

Figure 3. Experimental results of our proposed scheme, where $k=3,n=4$. (a–d) Four shadows $S{C}_1,S{C}_2,S{C}_3$ and $S{C}_4$; (e) the distribution histogram of pixel values of $S{C}_1$; (f) the latter part of (e); (g) result of recovery by $S{C}_1,S{C}_2$; (h) result of recovery by $S{C}_1,S{C}_2$ and $S{C}_3$; (i) result of recovery by $S{C}_1,S{C}_2,S{C}_3$ and $S{C}_4$; (j) the distribution histogram of pixel values of $S_{t=4}^{\prime }$; (k) the difference between S and $S_{t=4}^{\prime }$; (l) the distribution histogram of pixel values of $Sub$.

Figure 4. Experimental results of polynomial-based SIS modulo 251, where $k=3,n=4$. (a) A shadow $S{C}_1$; (b) the distribution histogram of pixel values of $S{C}_1$; (c) result of recovery by three shadows; (d) the distribution histogram of the recovered image.

Figure 5. Experimental results of polynomial-based SIS modulo 257 based on screening, where $k=3,n=4$. (a) A shadow $S{C}_1$; (b) result of recovery by three shadows; (c) the distribution histogram of pixel values of $S{C}_1$; (d) the latter part of (c).

As shown in Figure 3, Figure 3a–d are four shadows, which are noisy-like. The abscissa range of Figure 3e is [0,$p-1$], which is [0,255]. In order to observe the distribution of pixel values more carefully, we take the latter part of Figure 3e as Figure 3f. The pixel values of the shadows are evenly distributed. Figure 3g is the result of recovery by two shadows. Therefore, obtaining any shadow alone or less than k shadows will not reveal secret information. From Figure 3h–l we can know that the proposed scheme can achieve lossless recovery when k or more shadows are obtained.

5.2. Comparisons with Related Works

5.2.1. Illustration Comparison

Figure 4b,d have no pixel value larger than 250. The grayscale pixel value range is [0,255] and modular 251 cannot cover it, therefore the pixel values of secret image between [251,255] are truncated as 250.

Figure 5 shows a experimental result of polynomial-based SIS modulo 257 based on screening, of which p is 257. The abscissa range of Figure 5c is [0,$p-1$], which is [0,256]. From Figure 5c,d it can be seen that there are no pixel values in the shadow image at 256 points, indicating that the pixel values are unevenly distributed, so there will be security issues. If the attacker grasps the p-value and obtains such a shadow with uneven pixel distribution, he will doubt the encryption behavior.

5.2.2. Efficiency Comparison

We make statistics on the time consumption of the filter operation in the sharing phase as Table 2, the unit is second. It can be seen that the filter of $(k+1)\times k$ matrices takes more time than that of $k\times k$ matrices. For $(k,k)$, the time is similar. For $(k,k+1)$, the time is increasing with the increase of k, but this is within the acceptable range. For applicable situations, some matrices that meet the conditions can be generated in advance, so as to save real-time computational overhead.

Table 2. Time consumption of the filter operation.

$(\mathit{k},\mathit{k})$	Time	$(\mathit{k},\mathit{k}+1)$	Time
(2, 2)	0.000499	(2, 3)	0.000998
(3, 3)	0.000497	(3, 4)	0.001501
(4, 4)	0.000501	(4, 5)	0.004497
(5, 5)	0.000499	(5, 6)	0.009499
(6, 6)	0.000499	(6, 7)	0.031500

We conduct experiments on 20 different grayscale images, and the size of each image is $256\times 256$. The two schemes [21,22] are chosen for comparison, which can also recover losslessly. We compare the average sharing time as Table 3, average recovery time as Table 4 and average total time as Table 5. The unit is second.

Table 3. Average sharing time.

$(\mathit{k},\mathit{n})$	mod 257	mod $2^8$	mod 256 (Ours)
(2, 2)	1.040	1.116	0.906
(2, 3)	1.387	1.513	0.992
(3, 3)	1.522	1.752	1.131
(3, 4)	1.871	2.144	1.211

Table 4. Average recovery time.

$(\mathit{k},\mathit{n})$	mod 257	mod $2^8$	mod 256 (Ours)
(2, 2)	1.146	0.934	0.785
(2, 3)	1.139	0.923	0.789
(3, 3)	1.743	1.562	0.891
(3, 4)	1.746	1.561	0.878

Table 5. Average total time.

$(\mathit{k},\mathit{n})$	mod 257	mod $2^8$	mod 256 (Ours)
(2, 2)	2.187	2.050	1.691
(2, 3)	2.526	2.436	1.781
(3, 3)	3.266	3.314	2.022
(3, 4)	3.617	3.705	2.089

From the results, it can be observed that the higher the threshold, the more sharing time, and the more total time. The recovery time is only related to k. The larger the k, the longer the recovery time becomes, and the recovery time is close with the same k value in the same scheme. Compared with the other two lossless schemes, our scheme has obvious advantages in both sharing time and recovery time.

5.3. Brief Summary

Based on experimental results shown above, we can conclude that:

• The secret image can be reconstructed losslessly with k or more shadows and there is no leakage of secret information from the recovered image with less than k shadows.
• The shadows are noisy-like, thus every single shadow gives no clue about the secret. Pixel values of shadow are evenly distributed without security issues.
• The proposed scheme has obvious advantages in efficiency.

6. Conclusions

A lossless and efficient $(k,n)$ threshold SIS scheme based on matrix theory was presented in this paper. We also analyzed the threshold of the proposed scheme and proved that $(k,k)$ and $(k,k+1)$ thresholds can be achieved. Afterwards, the effectiveness and advantages of the proposed scheme compared with other schemes were demonstrated through experiments and analysis, that is, lossless recovery, efficiency and security.

We may further extend our work in the following ways.

• To further exploit the secret image sharing scheme, we can consider various recommendation mechanisms that provide content to the end users [26].
• We can use the personalized content retrieval mechanisms [27], in order to exploit the content, i.e., images, that the users consume to further improve our secret image sharing scheme.
• Big data that are available in complex systems [28] can be exploited to improve our analysis and model.