2. New Theoretical Model
In the classical theory, automata were considered as systems for transfering information of specific types. However, given complicated systems used nowadays, their benefits may not seem sufficient. In [
9,
13,
19,
20] we presented some real-life applications. In this section, we introduce an extension of ideas first included in [
21] regarding internal links in the cartesian composition of quasi-multiautomata. We discuss systems in which there is a whole set of internal links. For our theoretical purposes we will organize them in a matrix considered by, for example, Golestan et al. [
22]. In
Section 3, we show the application of our theoretical results in the context of autonomous cars and their navigation.
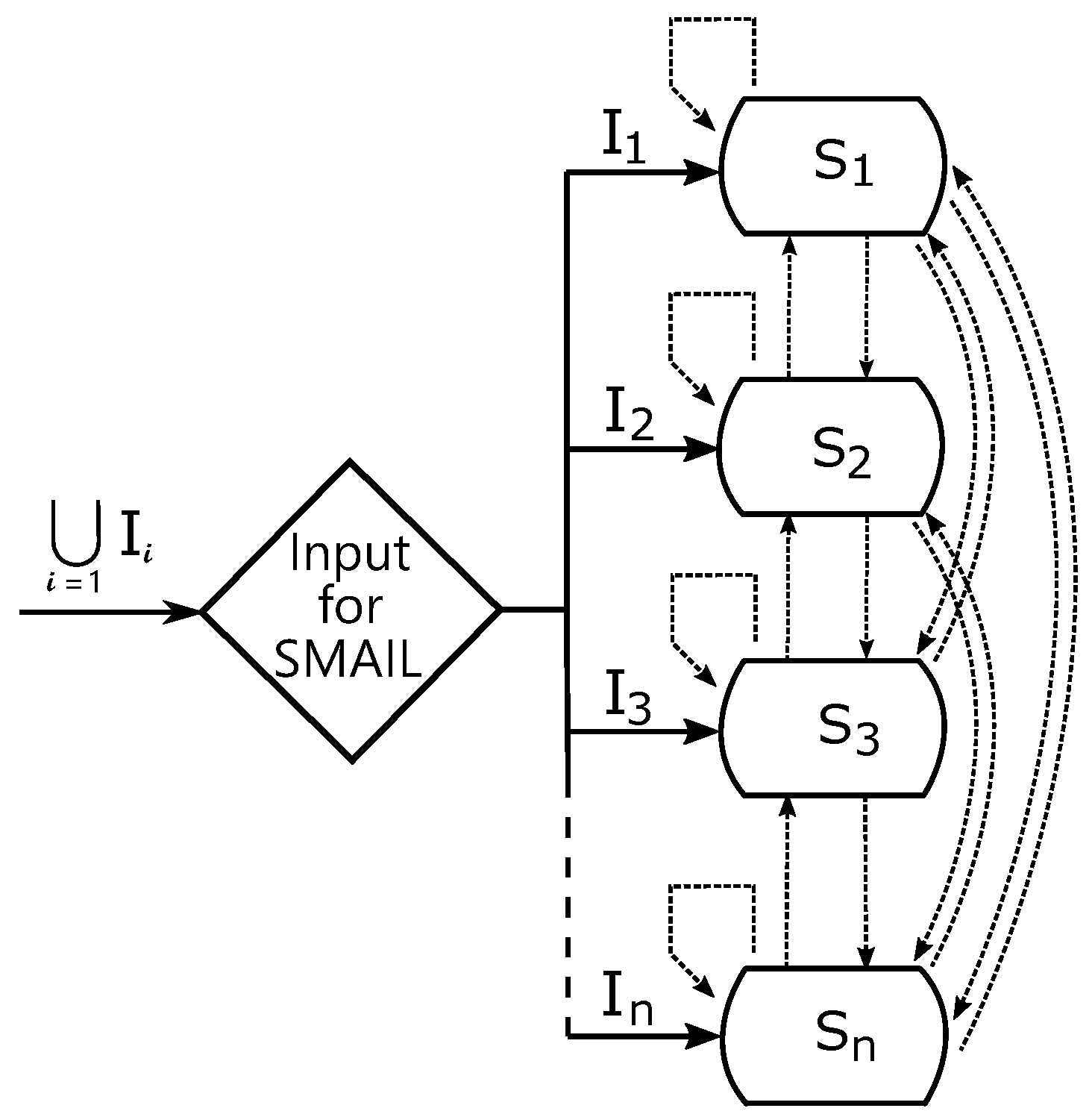
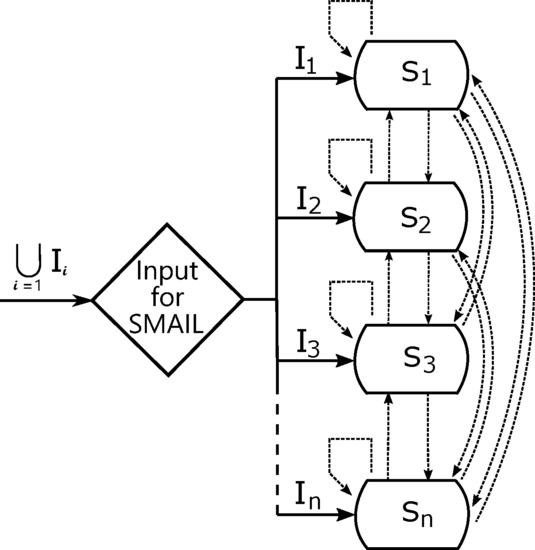
Notation 1. We are going to use the following notation: Definition 6. Let be e-quasi-multiautomata with input semihypergroups and satisfying condition By n-ary cartesian composition of the e-quasi-multiautomata we mean the following system of e-quasi-multiautomata with internal link ():where and matrix , called matrix of internal links, where for , i.e., is defined byand is for all defined bysatisfies the condition: One can easily explain what is meant by Definition 6 using
Figure 1. When an arbitrary input
is applied, the system, i.e., the cartesian composition, has to find out in which input set
x belongs. Therefore, we determine the correct line in Equation (
7), which through using we obtain a new state of the system. If, for example,
, the new state
will be computed. Then, it will be adjusted to
using
, i.e., by the self-mapping internal link. This new state
will be mapped to remaining input sets
as defined by the matrix of internal links. In other words, the matrix determines which other states can be influenced by the change of the primary state. We apply inputs on states using respective transition functions. If there is 0 instead of
in the matrix of internal links, then the link between the state set
and input set
does not exist. Notice that in Equation (
7) e.g.,
. Since we obviously have to regard directions (see the oriented arrows), the matrix of internal links is not symmetric.
In
Section 3 we apply the matrix of internal links in the context of modelling the navigation of autonomous vehicles. In this context, each vehicle obviously adjusts its behaviour based on the behaviour of other vehicles. Also obviously, not all vehicles need to be autonomous, which explains the use of zeros in the matrix (only autonomous vehicles communicate).
The above reasoning can be seen applied in the following example. Notice that we will use it also for the construction of the state set in Theorems 2 and 4 of
Section 3.
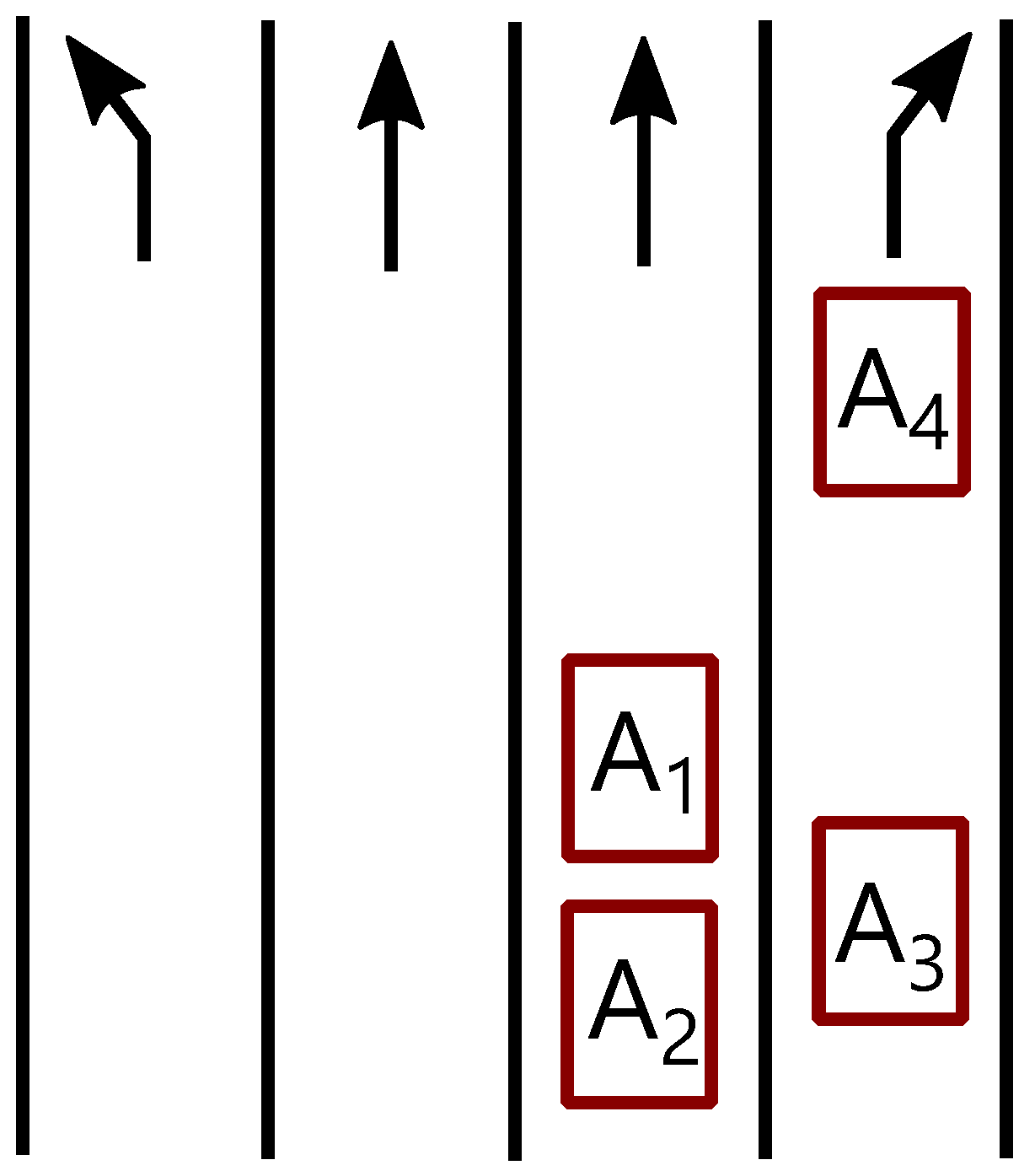
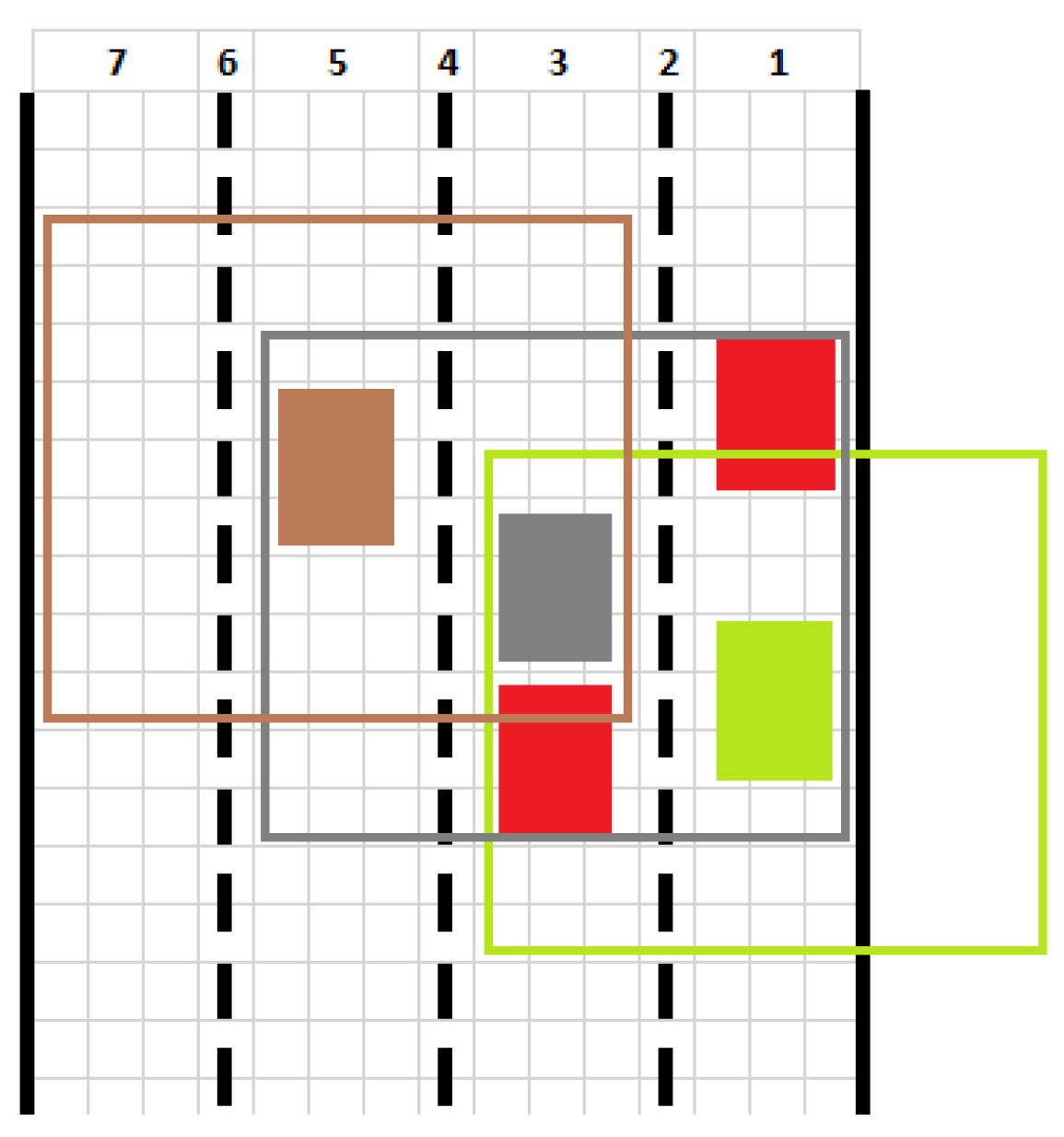
Example 1. Consider a section of a road in front of an autonomously controlled intersection in Figure 2. All vehicles are autonomous with compatible self-driving control parameters. Every car is in a certain state s, for example, car is in state , which means, for example, that car number 3 going at is in the position from the intersection in the 1st lane from the right. The first 0 means no change in speed while the second 0 means that the car is about to turn left. In our system it is obvious that vehicle does not need to communicate with vehicle because it is not an obstacle in its intended driving operation. Thus, introducing an internal link between and is not necessary. However, vehicles and are problematics for because it intends to turn left. Therefore, should increase its speed while should slow down.
Remark 1. Notice that some theoretical requests in the above example are not possible or even absurd, i.e., we have to keep in mind their feasibility. We already faced this problem in [12,23], where it was eliminated by using a suitable state set, input set, or operations on them. In this paper, we will choose special input and state sets as well. 3. —Application of the Theoretical Model for Autonomous Cooperation
We are going to construct our system, called , for the above context of Example 1. Naturally, Example 1 is an example of a possible usage of only.
First, we need to define suitable sets
and
, where
is the index. The elements of the state set are ordered pairs—the first component being an ordered sextuple of numbers while the second component is a matrix. The state set is
where
and
where
are a odd numbers. The state set describes the complete position of every vehicle in all lanes. Notice that this is the same approach as in [
24,
25]. Now, the elements of
defined by Equation (
10) correspond to states mentioned in Example 1, i.e.,
stands for the vehicle number,
for its speed,
for distance from the intersection,
for the respective lane (calculated from the right using odd numbers only, even number are reserved for positions between two lanes),
stands for changing velocity (i.e., an interval
is deceleration, an interval
is acceleration, 1 stands for constant speed),
stands for changing direction (i.e., an interval
means manoeuvring left, interval
means manoeuvring right, 0 means straight direction). Of course, more parameters can be used; for an example see [
26]. Matrices
used in Equation (
9) are taken from the set
defined by Equation (
11). Notice that we use these matrices in the form suggested in [
25,
27,
28] where, for the purpose of its control policy, the intersection is divided into a grid of reservation tiles. To be more precise,
where 0 are parts of the grid (or tiles) occupied by the given vehicle, 1 stands for tiles occupied by some other vehicles and
are free tiles. The above matrix
describes the situation depicted in
Figure 3 from the point of view of
.
Next, for construction of the
i-th quasi-multiautomaton and consequently
, we will need an input alphabet, i.e., input sets (since we will be working with quasi-multiautomata, these will be algebraic hyperstructures). As mentioned above, we will define
, where
is the index of the input set.
It is obvious that input sets
and
are disjunct for
, because the first component of every vector used in
is
p while the first component of every vector used in
is
q, i.e.,
Since vector components are real (or even natural) numbers, we can suppose that their sets are ordered; we write ≤ for this ordering. For all
we define hyperoperation
by:
In the following example we show what we mean by the hyperoperation. Notice that the hyperoperation will be later on used to construct a hypergroup in Theorem 1, which will fulfil the assumption regarding input alphabet stated in Definition 2.
Example 2. Consider two elements , where and . Then the hyperoperarionwhere is defined by Equation (
14),
i.e., . Theorem 1. For every index , the pairs are hypergroups.
Proof. First, we have to show that the associativity axiom holds, i.e., for all
there is
. Without losing generality, we can show that associativity axiom holds for both matrices and vectors. First, we consider vectors:
In the case of matrices, the proof is straightforward:
The reproductivity axiom holds automatically because the hyperoperation defined above is obviously extensive, i.e., for all there is . So for arbitrary we have . Thus, for all indices the structures are hypergroups. □
At this point, everything is ready for the construction of an e-quasi-multiautomaton with the state set and input set for p-th quasi-automaton, where .
Remark 2. We consider ordered pairs of vectors and matrices as elements of the input set and also of the state set. As a result, we will denote elements with index ı for input and with index s for the state, i.e., is an input word and is a state.
Theorem 2. For every index the triple is an e-quasi-multiautomtaton with input hypergroup , where transition function is defined by Proof. This proof is constructed as follows: first we calculate left hand side condition E-GMAC, second we show that left hand side is included in right hand side.
From the definition of hyperoproduct
in Equation (
14), we simply observe that the left hand side is not included in the right part of the right hand side union. Therefore, we have to proof, that the left hand side belongs to the left part of the right hand side union. Therefore we calculate:
There exist an input word
such that the vector is
and the matrix is
. Thus,
As a result, E-GMAC holds and the structure is an e-quasi-multiautomaton. □
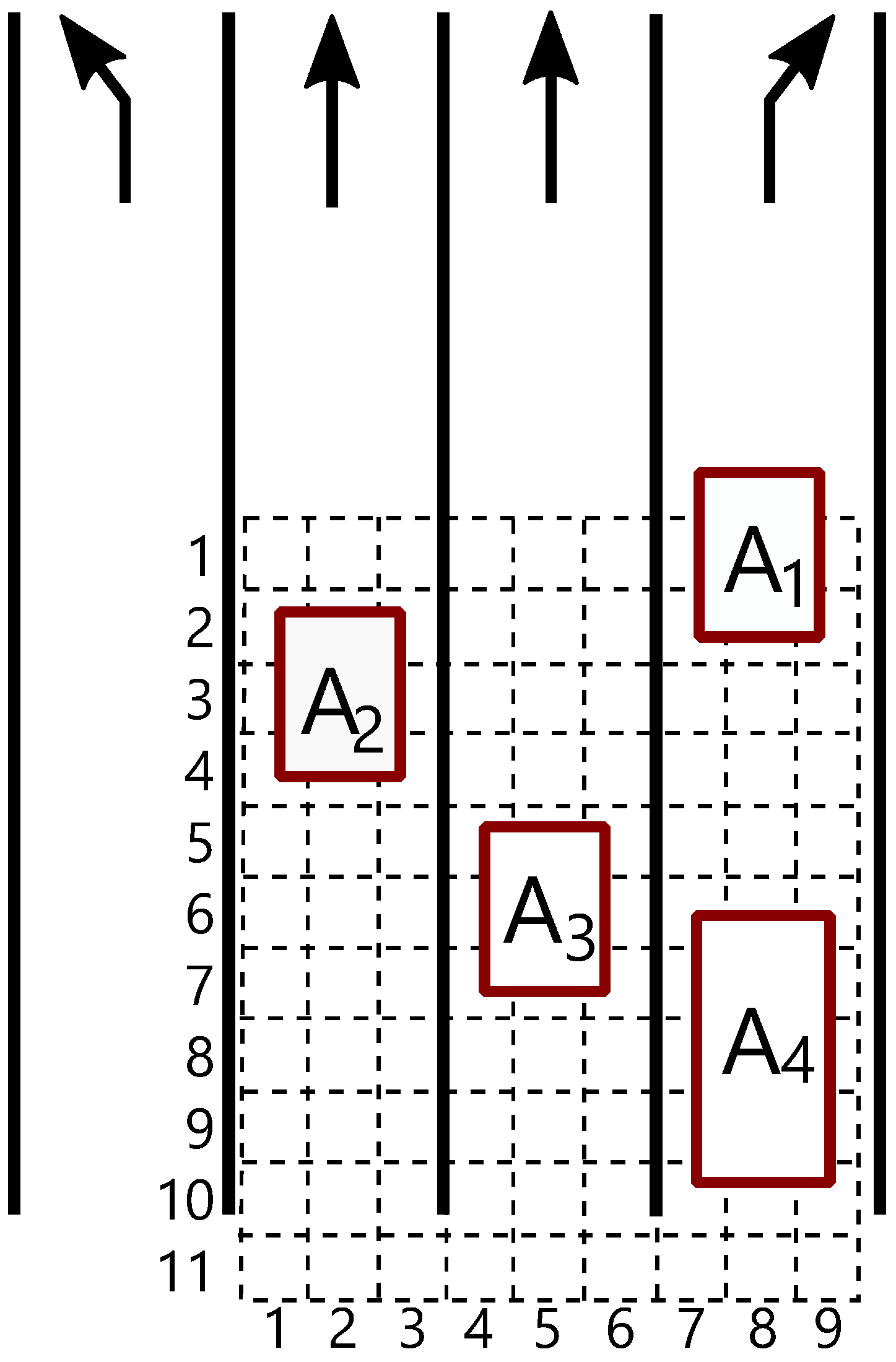
Once Theorem 2 is proved we will show a practical application af e-quasi-multiautomata in intelligent transport systems. In the following example, the e-quasi-multiautomaton represents an autonomous vehicle. Its state is described by parameters organized into a sextuple while the matrix is used to detect its environment. This example is also linked to Example 1.
Example 3. We consider matrix equivalent to matrix of Equation (
12),
which describes the situation in Figure 3. The vehicle —in Figure 4 depicted in green (while other, non-autonomous, vehicles are red)—detects its surroundings and saves the data to matrix . This model is suitable for a situation where only one vehicle, such as , is autonomous and it is not possible to establish communication with other vehicles (because they are not autonomous). We consider a state , where and values in matrix corresponding to values in the first picture of Figure 4. If we apply the input by the transition function , where and , then the first component of the input word is used to control the direction, i.e., it changes the state of the sextuple. The second component of the input word changes the matrix that detects the surroundings of a vehicle. This way we obtain a new state , where and the entries of the matrix are for and for other cases. We know from the new state that the vehicle does not change its velocity or its acceleration. We also know that the vehicle is positioned about 2 far from the intersection border and is between lane 2 and 3, and it turns to the left. We can see the position surroundings in Figure 4. Consequently, this is what we use in the next step as input for full inclusion in lane 3. We will use the e-quasi-multiautomata from Theorem 2 for the construction of a system called . Necessarily, a change on any component of the state of the system must trigger a change on another component of the state. However, there may be situations where the change of other components are not necessarily required. Therefore, we include the following theorem in which we assert that there are such inputs for which the state of the multiautomata do not change.
Theorem 3. For every e-quasi-mulltiautomaton there is an input for which holds Proof. Consider an arbitrary state
of the e-quasi-mulltiautomaton
. For input words
, where
, there holds Equation (
16). Indeed,
□
In Example 4 we consider different e-quasi-multiautomata as parts of a cooperative intelligent transport system. Some e-quasi-multiautomata represent autonomous vehicles while some are non-autonomous vehicles. Obviously, non-autonomous vehicles cannot detect their surroundings. In such cases we will use e-quasi-multiautomata, in which all entries of state matrices are 0. This explains the inclusion of the following lemma.
Lemma 1. Let then a structure is a sub-e-quasi-multiautomaton of e-quai-multiautomaton .
Proof. It is obvious that and . Next, we can see that E-GMAC holds because all entries in the state matrix are zero. Thus, the second component of the state can not change for any input. Therefore, the proof for the first component is the same as the proof of the Theorem 2. □
In what follows, we will note that every state is equal to and every input is equal to from e-quasi-multiautomaton , where is an index. In the other words, such as , the upper index s denotes state element, lower index 1 denotes position in the sextuple and the lower index p denotes the e-quasi-multiautomaton. The indices in matrices have the same meaning. As far as input words are regarded, we use upper index ı; other indices have the same meaning.
Now we need to define the matrix of internal links. First, we define
for all
by
where
and entries of the input matrix are dependent on the occupancy of the tiles.
Corollary 1. For mapping added to every e-quasi-multiautomaton from Theorem 2 there holds the condition E-GMAC.
Proof. The proof is obvious. On the left hand side we have up to four changes of the original state in the E-GMAC condition (two inputs and two applications of the internal link). However, we have a suitable input for the right hand side, similar to the proof of Theorem 2. □
Now we will define a mapping for two different e-quasi-multiautomata, i.e., from the state set of the
pth e-quasi-multiautomaton to the input set of the
qth e-quasi-multiautomaton. We define mapping
for all
, where
between two e-quai-multiautomata
and
by
where
Next we add a meaning of the parameters
and
At this point we can give the main theorem of this section in which we are going to use all results obtained above, i.e., e-quasi-multiautomata, hypergroups, and internal links. By Definition 6 we obtain the n-ary cartesian composition of e-quasi-multiautomata with internal links.
Theorem 4. Let be an e-quasi-multiautomata with disjoint input-sets , and . Then a quadrupleis a system of the cartesian composition of e-quasi-multiautomata with internal links. Proof. We have to demonstrate that the condition E-GMAC holds, i.e., that there is
We prove, while maintaining generality, that
i.e., Formula (
18) without the left part of the right hand side of E-GMAC. There are two cases. The first, both input words are in the same input set, and the second, input words are from different input sets.
- (a)
For the first case, we consider
. On the left hand of Equation (
19), we know that the input
works upon one component from
and the state can alter by the internal link
. This is performed again for input
, then we have an input
for which holds following (considering the proof of Theorem 2):
When the inputs or are applied on the state other states react to this change by mapping . It is obvious that mapping influences other states by the input from the respective input set. Then for every component of the state on the right side there exists an element from the corresponding input set, that state on the left hand side is included on the right hand side.
- (b)
For the second case, we consider different inputs now. On the left-hand side, we have an influence on two different components in the tuple it is evident that the same inputs are the same on the right-hand side if internal links , do not change. At the moment, , influence corresponding components of the state, we have suitable inputs on the right-hand side, as in proof of Theorem 2. For mapping the influence of and on other components, we have the same situation as case a). Thus, it is obvious that holds condition E-GMAC.
□
In the conclusion of this section, we will demonstrate the theory explained by using the example of to describe and model a situation with several autonomous vehicles in traffic lanes each intending to perform some action.
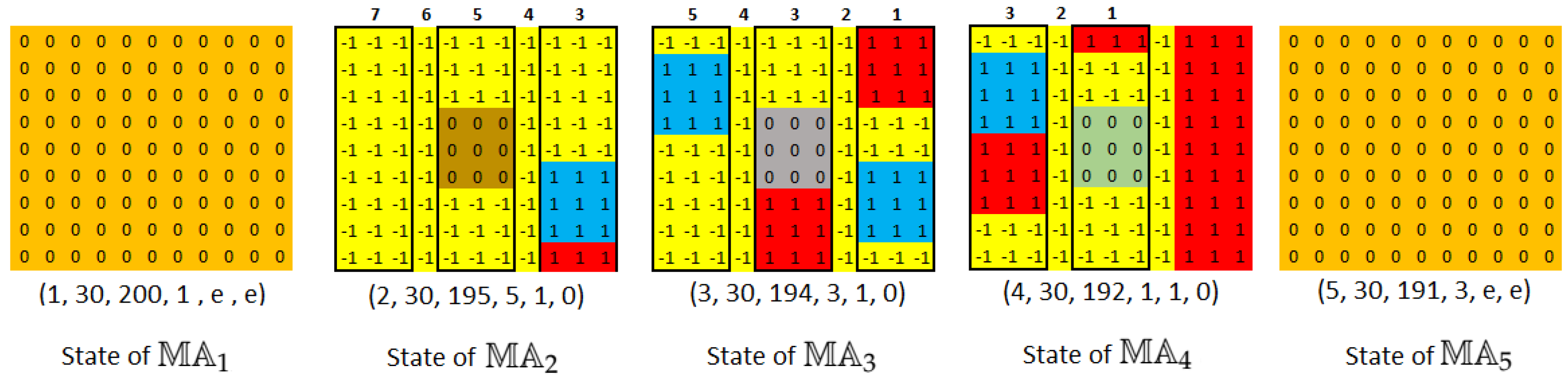
Example 4. We will consider five e-quasi-multiautomata , where every e-quasi-multiautomaton represents a vehicle. The e-quasi-multiautomata are autonomous vehicles and are ordinary vehicles. Figure 5 depicts the state of every vehicle, where the vehicles are denoted in red colour in the same as verge of the road and other colour are used for autonomous vehicles. The complete situation with detection field of each vehicle is presented in Figure 6. In fact, Figure 5 is state of , i.e., Next, we need a matrix of the internal linkwhere 0 means no internal link and φ mean internal link between vehicles given by the respective indices. We are going to describe how to proceed, i.e., what input symbols to use, if the grey car, represented by e-quasi-multiautomaton , wants to change lane and turn left to lane 5. We have two approaches to start changing the lane: we can correct of the state of the vehicle directly by the component on the 2nd, 3rd and 4th position in the input word, or to use the internal link and 6th component of the input. We will use an input , which will operate on the 6th component. Then, the resulting state—full correction—will be made by the internal link. The calculation will be done according to Equations (
7)
and (
15),
i.e., We obtain a state with new elements on the th positions where these components have an effect on other components by means of the internal link between the state and input of the e-quasi-multiautomaton . With this internal link, we obtain a new input: where , i.e., matrix to correct the state matrix detecting other vehicles or obstacles near vehicle .
When we apply a new input on the state , we obtain where matrix has the same size and entries as depicted for in Figure 7. Now consider internal link , i.e., state of the e-quasi-multiautomaton will be changed by the state
of the e-quasi-multiautomaton , which we obtained in Equation (
20).
We will proceed using the definition of the link between two different e-quasi-multiautomata given as Equation (
17).
where is a suitable matrix which enables us to obtain a state matrix with entries given in Figure 7 for the state of . After we apply the input obtained by the internal link in Equation (21) with the help of transition function , we get a new state depicted in Figure 7 for e-quasi-multiautomaton . Next state of the (vehicle) will not affect velocity by internal link , because the input obtained by from state has parameters and .
Thus, the input operates as neutral input on states of except for the distance given by . Thus, we will present a new situation on the lanes, i.e., a new state after the application of one input. See Figure 7.