Locating Arrays with Mixed Alphabet Sizes

Abstract

Locating arrays (LAs) can be used to detect and identify interaction faults among factors in a component-based system. The optimality and constructions of LAs with a single fault have been investigated extensively under the assumption that all the factors have the same values. However, in real life, different factors in a system have different numbers of possible values. Thus, it is necessary for LAs to satisfy such requirements. We herein establish a general lower bound on the size of mixed-level $(\overline{1},t)$-locating arrays. Some methods for constructing LAs including direct and recursive constructions are provided. In particular, constructions that produce optimal LAs satisfying the lower bound are described. Additionally, some series of optimal LAs satisfying the lower bound are presented.

1. Introduction

Testing is important in detecting failures triggered by interactions among factors. As reported in [1], owing to the complexity of information systems, interactions among components are complex and numerous. Ideally, one would test all possible interactions (exhaustive testing); however, this is often infeasible owing to the time and cost of tests, even for a moderately small system. Therefore, test suites that provide coverage of the most important interactions should be developed. Testing strategies that use such test suites are usually called combinatorial testing or combinatorial interaction testing (CIT). CIT has shown its effectiveness in detecting faults, particularly in component-based systems or configurable systems [2,3].

The primary combinatorial object used to generate a test suite for CIT is covering arrays (CAs). CAs are applied in the testing of networks, software, and hardware, as well as construction and related applications [4,5,6]. In a CA, the factors have the same number of values; however, in real life, different factors have different numbers of possible values. Thus, mixed-level CAs or mixed covering arrays (MCAs) are a natural extension of covering arrays, which improve their suitability for applications [1,7,8,9,10,11]. A CA or MCA as a test suite can be used to detect the presence of failure-triggered interactions; however, they do not guarantee that faulty interactions can be identified. Consequently, tests to reveal the location of interaction faults are of interest. To address this problem, Colbourn and McClary formalized the problem of non-adaptive location of interaction faults and proposed the notion of locating arrays (LAs) [12].

LAs are a variant of CAs with the ability to determine faulty interactions from the outcomes of the tests. An LA with parameters d and t is denoted by $(d,t)$-LA, where d and t represent the numbers of faulty interactions and of components or factors in a faulty interaction, respectively. t is often called strength. When the number of faulty interactions is at most, instead of exactly d, we use the notation $(\overline{d},t)$-LA to denote it. Generally, testing with a $(d,t)$-LA can not only detect the presence of faulty interactions, but can also identify d faulty interactions. Similarly, using a $(\overline{d},t)$-LA as a test suite allows one to identify all faulty interactions if the number is at most d.

LAs have been utilized in measurement and testing [13,14,15]; however, theoretical studies on LAs are still in an early stage. For example, when the number of factors is arbitrary, only the minimum number of tests in $(1,1)$-LA and $(\overline{1},1)$-LA is known precisely [16]. For other cases, the minimum number of rows in an LA is known only when the number of factors is small [17,18]. When $(d,t)=(1,2)$, three recursive constructions are provided in [19]. Apart from these few direct and recursive constructions, computational methods are applied to construct $(1,2)$-LAs. Some of these methods use a constraint satisfaction problem (CSP) solver and a satisfiability (SAT) solver [20,21,22]. Lanus et al. [23] described a randomized computational search algorithm called partitioned search with column resampling to construct $(1,t)$-LAs. Furthermore, column resampling can be applied to construct $(\overline{1},t)$-LA with $\delta \le 4$ [24]. The second and third authors extended the notion of LAs to expand the applicability to practical testing problems. Specifically, they proposed constrained locating arrays (CLAs) which can be used to detect and locate failure-triggering interactions in the presence of constraints. Computational constructions for this variant of LAs can be found in [25,26,27].

Although a few mathematical constructions exist for $(1,t)$-LAs and $(\overline{1},t)$-LAs, these methods do not treat cases where different factors have difference values. For real-world applications, it is desirable for LAs to satisfy such requirements. Herein, we focus on mixed-level $(\overline{1},t)$-LAs, which is equivalent to mixed-level $(1,t)$-LAs, as we show later.

The contribution of this paper can be summarized as follows:

• We provide a lower bound on the size of minimum (i.e., optimal) mixed-level $(\overline{1},t)$-LAs in a form of a mathematical expression.
• We developed several new mathematical constructions of mixed-level $(\overline{1},t)$-LAs.
• We prove some conditions that ensure the existence of mixed-level $(\overline{1},t)$-LAs that achieve the aforementioned lower bound. We also provide mathematical constructions for these optimal mixed-level LAs.

The remainder of the paper is organized as follows. Section 2 provides the definitions of basic concepts, such as MCAs and LAs. A general lower bound on the size of mixed-level $(\overline{1},t)$-LAs is established in Section 3, which will be regarded as benchmarks for the construction of optimal LAs with specific parameters. Some methods for constructing LAs including direct and recursive constructions are provided in Section 4. In particular, some constructions that produce optimal LAs satisfying the lower bound will be described in this section. Section 5 contains some concluding remarks.

2. Preliminaries

2.1. Definitions and Notations

The notation $I_n$ represents the set $\{1,2,\cdots ,n\}$, while the notations $N,k$ and t represent positive integers with $t<k$. We herein model CIT as follows. Suppose that k factors denoted by $F_1,F_2,\cdots ,F_k$ exist. The ith factor has a set of $v_i$ possible values (levels) from a set $V_i$, where $i\in I_k$. A test is a k-tuple $(a_1,a_2,\cdots ,a_k)$, where $a_i\in V_i$ for $1\le i\le k$. A test, when executed, has the following outcome: pass or fail. A test suite is a collection of tests, and the outcomes are the corresponding set of pass/fail results. A fault is evidenced by a failure outcome for a test.

Let $A=\left(a_{ij}\right)(i\in I_N,j\in I_k)$ be an $N\times k$ array with entries in the jth column from a set $V_j$ of $v_j$ symbols. A t-way interaction is a possible t-tuple of values for any t-set of columns, denoted by $T=\{(i,{\sigma }_i):{\sigma }_i\in V_i,i\in I\subseteq I_k,|I|=t\}$. We denote $\rho (A,T)=\{r:a_{ri}={\sigma }_i,\mathrm{for}\mathrm{all}(i,{\sigma }_i)\in T\}$ for the set of rows of A in which the interaction is included. For an arbitrary set $\mathcal{T}$ of t-way interactions, we define $\rho (A,\mathcal{T})={\cup }_{T\in \mathcal{T}}\rho (A,T)$. We use the notation ${\mathcal{I}}_t$ to denote the set of all t-way interactions of A.

The array A is termed MCAs, denoted by MCA_λ$(N;t,k,(v_1,v_2,\cdots ,v_k))$ if $\left|\rho \right(A,T\left)\right|\ge \lambda$ for all t-way interactions T of A. In other words, A is an MCA if each $N\times t$ sub-array includes all the t-tuples $\lambda$ times at the least. Here, the number of rows N is called the array size. The number $\lambda$ is termed as the array index. The number of columns k is called the number of factors (or variables), number of components or degree. The word “strength” is generally accepted for referring to the parameter t. When $\lambda =1$, the notation MCA$(N;t,k,(v_1,v_2,\cdots ,v_k))$ is used.

When $v_1=v_2=\cdots =v_k=v$, an MCA_λ $(N;t,k,(v_1,v_2,\cdots ,v_k))$ is merely a CA_λ$(N;t,k,v)$. When $\lambda =1$ in a CA, we omit the subscript. Without loss of generality, we often assume that the symbol set sizes are in a non-decreasing order, i.e., $v_1\le v_2\le \cdots \le v_k$. Hereinafter, these assumptions will continue to be used. When $v_i=1$, the presence of the ith factor does not affect the properties of the mixed covering arrays; thus, we often assume that $v_i\ge 2$ for $1\le i\le k$.

Following [12], if, for any ${\mathcal{T}}_1,{\mathcal{T}}_2\subseteq {\mathcal{I}}_t$ with $|{\mathcal{T}}_1|=|{\mathcal{T}}_2|=d$, we have

$$\rho (A,{\mathcal{T}}_1)=\rho (A,{\mathcal{T}}_2)\iff {\mathcal{T}}_1={\mathcal{T}}_2,$$

then the array A is regarded as a $(d,t)$-LA and denoted by $(d,t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$. Similarly, the definition is extended to permit sets of at most d interactions by writing $\overline{d}$ in place of d and permitting instead $|{\mathcal{T}}_1|\le d$ and $|{\mathcal{T}}_2|\le d$. In this case, we use the notation $(\overline{d},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$. Clearly, the condition $\rho (A,{\mathcal{T}}_1)=\rho (A,{\mathcal{T}}_2)\iff {\mathcal{T}}_1={\mathcal{T}}_2$ is satisfied if ${\mathcal{T}}_1\ne {\mathcal{T}}_2\Rightarrow \rho (A,{\mathcal{T}}_1)\ne \rho (A,{\mathcal{T}}_2).$ In the following, we fully apply this fact.

We herein focus on $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$ in this paper. One of the main problems regarding $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$ is the construction of such LAs having the minimum N when other parameters have been fixed; however, this is a difficult and challenging problem. The larger the strength t, the more difficult it is to construct a minimum LA. We use the notation $(\overline{1},t)$-LAN$(k,(v_1,v_2,\cdots ,v_k))$ to represent the minimum number N for which a $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$ exists. A $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$ is called optimal if $N=(\overline{1},t)$-LAN$(k,(v_1,v_2,\cdots ,v_k))$.

Lemma 1.

[21] Suppose that A is an $N\times k$ array. A is a $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$ if and only if it is a $(1,t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$ and an MCA.

Lemma 1 shows that A is a $(\overline{1},t)$-LA if A is an MCA and $\rho (A,T_1)\ne \rho (A,T_2)$ whenever $T_1$ and $T_2$ are distinct t-way interactions. We use this simple fact hereinafter.

2.2. Applications

As stated in Section 1, testing of information systems is the major application of mixed-level LAs. For example, suppose that we want to test a web browser-based software system. Also suppose that using test parameter analysis [2], we have successfully extracted factors and their values to be tested as shown in Table 1. In this example, a test is a tuple of size $k=3$ and there are a total of $2\times 2\times 3=12$ possible tests.

Table 1. Factors and values of a web browser-based software system.

Factor	Values
Web browser	Chrome (0), Edge (1)
Comm protocol	IPv4 (0), IPv6 (1)
OS version	Home (0), Pro (1), Enterprise (2)

Table 2 shows a set of tests that consists of nine of these possible tests. The test set is identical to a $(\overline{1},2)$-LA$(12;3,(2,2,3\left)\right)$, which is represented by the transpose of the following array.

0	0	0	0	0	1	1	1	1
0	0	1	1	1	0	0	1	1
1	2	0	1	2	0	2	0	1

Table 2. Test sets corresponding to locating arrays (LAs).

	${\mathit{F}}_1$: Web Browser	${\mathit{F}}_2$: Comm Protocol	${\mathit{F}}_3$: OS Version
1	Chrome	IPv4	Pro
2	Chrome	IPv4	Enterprise
3	Chrome	IPv6	Home
4	Chrome	IPv6	Pro
5	Chrome	IPv6	Enterprise
6	Edge	IPv4	Home
7	Edge	IPv4	Enterprise
8	Edge	IPv6	Home
9	Edge	IPv6	Pro

Due to the property that the $(\overline{1},2)$-LA has, up to one faulty interaction of strength two can always be located using the outcomes of executing these tests. For example, interaction (Chrome, Pro) is faulty if and only if the outcomes of tests 1 and 4 are fail and the others are pass. In mathematical notation, in this case, the interaction is represented as $T=\left\{\right(1,0),(3,1\left)\right\}$ and the set of all present faulty interactions is trivially $\mathcal{T}=\left\{T\right\}(\subseteq {\mathcal{I}}_2)$. The rows (tests) that contain the faulty interaction is $\rho (A,\mathcal{T})=\{1,4\}$, and by definition, $\rho (A,{\mathcal{T}}^{\prime })=\{1,4\}$ never holds for any other ${\mathcal{T}}^{\prime }\subseteq {\mathcal{I}}_2$ such that $|{\mathcal{T}}^{\prime }|=1$. The process of locating faulty interactions is schematically presented in Figure 1.

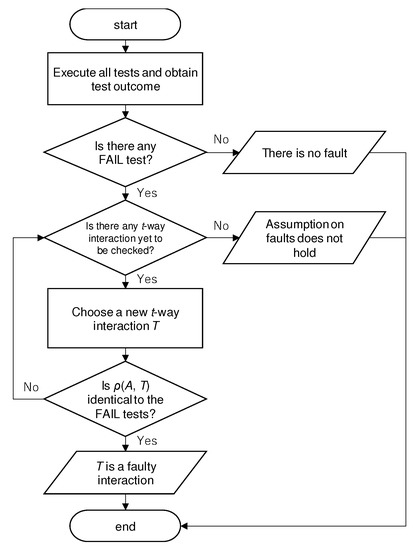
Figure 1. The process of locating a fault interaction using a $(\overline{1},t)$-LA A. $\rho (A,T)$ is the rows (tests) in which t-way interaction T is included. If no tests failed, then it is concluded that no faults exist. Otherwise, every t-way interaction T is examined: If $\rho (A,T)$ coincides with the set of FAIL tests, then T is determined to be faulty. If there is no such T, then it is concluded that the assumption on faults does not hold. In this case, for example, there can be multiple faults.

Another application example than information system testing is screening experiments, which aim to identify interactions that are most influential on a response of a complex system. Compared to exhaustive full-factorial designs, using locating arrays as experimental designs greatly decreases the number of design points, thus reducing the cost of experiments. In [13], mixed-level LAs were applied to the screening experiment for TCP throughput of a mobile wireless network.

3. A Lower Bound on the Size of $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$

A benchmark to measure the optimality for $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$ is described in this section. It follows from Lemma 1 that A is a $(\overline{1},t)$-LA only if A is an MCA, which implies that $\left|\rho \right(A,T\left)\right|\ge 1$ for any t-way interaction T of A. Consequently, $(\overline{1},t)$-LAN$(N;k,(v_1,v_2,\cdots ,v_k))\ge {\prod }_{i=k-t+1}^k{v}_i$, where $2\le v_1\le v_2\le \cdots \le v_k$. Suppose that A is a $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$ with $N={\prod }_{i=k-t+1}^k{v}_i$, where $2v_{k-t}>v_{k-t+1}$. Then, A is an MCA$(N;t,k,(v_1,v_2,\cdots ,v_k)$ by Lemma 1. Because $N={\prod }_{t=k-t+1}^k{v}_i$, we have $\left|\rho \right(A,T\left)\right|=1$ for any t-way interaction $T\in \mathcal{T}=\{\{(k-t+1,v_{k-t+1}),\cdots ,(k,v_k)\}:v_i\in V_i(k-t+1\le i\le k)\}$. As $N={\prod }_{i=k-t+1}^k{v}_i<2v_{k-t}{\prod }_{i=k-t+2}^k{v}_i$, there exists at least one t-way interaction $T^{\prime }\in {\mathcal{T}}^{\prime }=\{\{(k-t,v_{k-t}),(k-t+2,v_{k-t+2}),\cdots ,(k,v_k)\}:v_i\in V_i(k-t\le i\le k,i\ne v_{k-t+1})\}$ such that $\left|\rho \right(A,T^{\prime }\left)\right|=1$. Thus, $\rho (A,T^{\prime })=\rho (A,T)$ for a certain $T\in \mathcal{T}$. This contradicts the fact that A is a $(\overline{1},t)$-LA. This observation implies the following lemma.

Lemma 2.

Let $2\le v_1\le v_2\le \cdots \le v_{k-t},2v_{k-t}\le v_{k-t+1}\le \cdots \le v_k$. Then, $(\overline{1},t)$-LAN$(k,(v_1,v_2,\cdots ,v_k))\ge {\prod }_{i=k-t+1}^k{v}_i$.

It is remarkable that the lower bound on the size of $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$ in Lemma 2 can be achieved. We will present some infinite classes of optimal $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$ satisfying the lower bound in the next section. When $v_i=v_{i+1}=\cdots =v_{k-t}=v_{k-t+1}$, where $i\in \{1,2,\cdots ,k-t\}$, we can obtain a lower bound on the size of $(\overline{1},t)$-LA by a similar argument to the proof of Theorem 3.1 in [18]. We state it as follows.

Lemma 3.

Let $2\le v_1\le v_2\le \cdots \le v_k$. If $v_i=v_{i+1}=\cdots =v_{k-t}=v_{k-t+1}$, where $i\in \{1,2,\cdots ,k-t\}$, then $(\overline{1},t)$-LAN$(k,(v_1,v_2,\cdots ,v_k))\ge ⌈\frac{2{\sum }_{i\le j_1<\cdots <j_t\le k}{\prod }_{s=1}^t{v}_{j_s}}{1+\left(\genfrac{}{}{0pt}{}{k-i+1}{t}\right)}⌉$.

Proof. 

Let A be a $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$. We can obtain an $N\times (k-i+1)$ array $A^{\prime }$ by selecting the last $(k-i+1)$ columns of A (if $i=1$, then $A^{\prime }$ is merely A). In the array $A^{\prime }$, for any $i\le j_1<\cdots <j_t\le k$, we write $n_{j_1\cdots j_t}^{\ell }=\left|S_{j_1\cdots j_t}^{\ell }\right|$, where $S_{j_1\cdots j_t}^{\ell }=\left\{((j_1,x_1),\dots ,(j_t,x_t))|\left|\rho (A^{\prime },((j_1,x_1),\cdots ,(j_t,x_t)))\right|=\ell \right\},\ell =1,2,3,\cdots$.

As stated above, $\left|\rho \right(A,T\left)\right|\ge 1$ for any t-way interaction T of $A^{\prime }$. Consequently, ${\sum }_{\ell \ge 1}{n}_{j_1\cdots j_t}^{\ell }={\prod }_{s=1}^t{v}_{j_s}$ and ${\sum }_{\ell \ge 1}(\ell \times n_{j_1\cdots j_t}^{\ell })=N$ hold. It is deduced that $n_{j_1\cdots j_t}^1\ge 2{\prod }_{s=1}^t{v}_{j_s}-N$. It is clear that $A^{\prime }$ is a $(1,t)$-LA by Lemma 1. Thus, in any two of $\left(\genfrac{}{}{0pt}{}{k-i+1}{t}\right)$ sets, $\rho {(A^{\prime },S_{j_1\cdots j_t}^1)}^{\prime }$s with $i\le j_1<\cdots <j_t\le k$ share no common elements. Hence, ${\sum }_{i\le j_1<\cdots <j_t\le k}{n}_{j_1\cdots j_t}^1\le N$, which implies that ${\sum }_{i\le j_1<\cdots <j_t\le k}(2{\prod }_{s=1}^t{v}_{j_s}-N)\le {\sum }_{i\le j_1<\cdots <j_t\le k}{n}_{j_1\cdots j_t}^1\le N$, i.e., $N\ge ⌈\frac{2{\sum }_{i\le j_1<\cdots <j_t\le k}{\prod }_{s=1}^t{v}_{j_s}}{1+\left(\genfrac{}{}{0pt}{}{k-i+1}{t}\right)}⌉$. Hence, $(\overline{1},t)-\mathrm{LAN}(k,(v_1,v_2,\cdots ,v_k))\ge ⌈\frac{2{\sum }_{i\le j_1<\cdots <j_t\le k}{\prod }_{s=1}^t{v}_{j_s}}{1+\left(\genfrac{}{}{0pt}{}{k-i+1}{t}\right)}⌉$. □

Based on $i=1$ and $v_{k-t+1}=\cdots =v_k=v$ in Lemma 3, the following corollary can be easily obtained. It serves as a benchmark for a $(1,t)$-LA$(N;k,v)$, which was first presented in [18].

Corollary 1.

Let $v,t$ and k be integers with $t<k$. Then, $(1,t)$-LAN$(t,k,v)\ge ⌈\frac{2\left({}_t^k\right)v^t}{1+\left({}_t^k\right)}⌉$.

In a $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$, we often assume that $2\le v_1\le v_2\le \cdots \le v_{k-t}\le v_{k-t+1}\le \cdots \le v_k$. Lemma 2 and Lemma 3 consider the cases $v_{k-t}=v_{k-t+1}$ and $2v_{k-t}\le v_{k-t+1}$, respectively. The left case is $v_{k-t}<v_{k-t+1}<2v_{k-t}$, which is considered in the following lemma.

Lemma 4.

Let $2\le v_1\le v_2\le \cdots \le v_k$. If $v_{k-t}<v_{k-t+1}<2v_{k-t}$, then $(\overline{1},t)$-LAN$(k,(v_1,v_2,\cdots ,v_k))\ge m$, where

$$m=\left\{\begin{array}{cc}max\{⌈\frac{2{\sum }_{k-t\le j_1<\cdots <j_t\le k}{\prod }_{s=1}^t{v}_{j_s}}{t+2}⌉,\prod _{i=k-t+1}^k{v}_i+\prod _{i=k-t+2}^k{v}_i\},\hfill & ift\ge 2;\hfill \\ ⌈\frac{2v_{k-1}+2v_k}{3}⌉,\hfill & ift=1.\hfill \end{array}\right.$$

Proof. 

From the above argument, it is known that $(\overline{1},t)$-LAN$(k,(v_1,v_2,\cdots ,v_k))\ge M={\prod }_{i=k-t+1}^k{v}_i$. Suppose that A is a $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$, where $N=M+L$ and $L\ge 0$. Select the last $(t+1)$ columns of A to form an $N\times (t+1)$ array $A^{\prime }$. Clearly, $A^{\prime }$ is a $(\overline{1},t)$-LA$(N;t+1,(v_t,v_{t+1},\cdots ,v_k))$. Similar to the proof of Lemma 3, we can prove that $N\ge ⌈\frac{2{\sum }_{k-t\le j_1<\cdots <j_t\le k}{\prod }_{s=1}^t{v}_{j_s}}{t+2}⌉$. When $t=1$, we can obtain $m=⌈\frac{2v_{k-1}+2v_k}{3}⌉$. For $t\ge 2$, we prove that $N\ge M+{\prod }_{i=k-t+2}^k{v}_i$, i.e., $L\ge {\prod }_{i=k-t+2}^k{v}_i$. Without loss of generality, suppose that $A^{\prime }$ contains two parts: the first part is an $M\times (t+1)$ array B containing an $M\times t$ sub-array comprising all t-tuples over $V_{k-t+1}\times V_{k-t+2}\times \cdots \times V_k$; the left part is an $L\times (t+1)$ array C; (if $L=0$, then $B=A^{\prime }$).

If $L<{\prod }_{i=k-t+2}^k{v}_i$, then at least one $(t-1)$-way interaction $T=\{(i,a_i):i\in I_k\setminus I_{k-t+1},a_i\in V_i\}$ exists such that it is not included by any row of C (If $B=A^{\prime }$, then all the $(t-1)$-way interactions satisfy the condition. We can choose an arbitrary one). Hence, we have $\left|\rho \right(A^{\prime },T_1\left)\right|=1$ for any t-way interaction $T_1\in {\mathcal{T}}_1=\{T\cup (k-t+1,i):i\in V_{k-t+1}\}$. Since A is a $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$, $\left|\rho \right(A^{\prime },T_2\left)\right|\ge 1$ for any t-way interaction $T_2\in {\mathcal{T}}_2=\{T\cup (k-t,i):i\in V_{k-t}\}$. It is clear that $\rho (A^{\prime },{\mathcal{T}}_1)=\rho (B,T)=\rho (A^{\prime },T)=\rho (A^{\prime },{\mathcal{T}}_2)$ with $|\rho (A^{\prime },{\mathcal{T}}_1)|=v_{k-t+1}$.

Because $|{\mathcal{T}}_2|=v_{k-t}<|{\mathcal{T}}_1|=v_{k-t+1}<2\left|{\mathcal{T}}_2\right|$, at least one t-way interaction $T^{\prime }\in {\mathcal{T}}_2$ exists such that $\left|\rho \right(A^{\prime },T^{\prime }\left)\right|=1$. Otherwise, $\left|\rho \right(A^{\prime },T^{\prime }\left)\right|\ge 2$ for any t-way interaction $T^{\prime }\in {\mathcal{T}}_2$, which implies that $|\rho (A^{\prime },{\mathcal{T}}_2)|\ge 2|{\mathcal{T}}_2|=2v_{k-t}$, but $|\rho (A^{\prime },{\mathcal{T}}_2)|=|\rho (A^{\prime },{\mathcal{T}}_1)|=v_{k-t+1}<2v_{k-t}$. It follows that $\rho (A^{\prime },T^{\prime })=\rho (A^{\prime },T_1^{\prime })$, where $T_1^{\prime }$ is a certain t-way interaction of ${\mathcal{T}}_1$. It is obvious that $T^{\prime }\ne T_1^{\prime }$. Consequently, $A^{\prime }$ is not a $(1,t)$-LA. Thus, $L\ge {\prod }_{i=k-t+2}^k{v}_i$. Consequently, $m=\max \{⌈\frac{2{\sum }_{k-t\le j_1<\cdots <j_t\le k}{\prod }_{s=1}^t{v}_{j_s}}{t+2}⌉,{\prod }_{i=k-t+1}^k{v}_i+{\prod }_{i=k-t+2}^k{v}_i\}$ if $t\ge 2$. □

Combining Lemmas 2–4, a lower bound on the size of $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$ can be obtained, which serves as a benchmark to measure the optimality.

Theorem 1.

Let $2\le v_1\le v_2\le \cdots \le v_k$. Then, $(\overline{1},t)$-LAN$(k,(v_1,v_2,\cdots ,v_k))\ge$

1.

${\prod }_{i=k-t+1}^k{v}_i$, if $2v_{k-t}\le v_{k-t+1}$;

2.

$⌈\frac{2{\sum }_{i\le j_1<\cdots <j_t\le k}{\prod }_{s=1}^t{v}_{j_s}}{1+\left(\genfrac{}{}{0pt}{}{k-i+1}{t}\right)}⌉$, if $v_i=v_{i+1}=\cdots =v_{k-t}=v_{k-t+1}$, where $i\in \{1,2,\cdots ,k-t\}$;

3.

$max\{⌈\frac{2{\sum }_{k-t\le j_1<\cdots <j_t\le k}{\prod }_{s=1}^t{v}_{j_s}}{t+2}⌉,{\prod }_{i=k-t+1}^k{v}_i+{\prod }_{i=k-t+2}^k{v}_i\}$, if $v_{k-t}<v_{k-t+1}<2v_{k-t}$ and $t\ge 2$;

4.

$⌈\frac{2v_{k-1}+2v_k}{3}⌉$, if $v_{k-t}<v_{k-t+1}<2v_{k-t}$ and $t=1$.

Table 3 presents a lower bound on the size of certain mixed-level $(\overline{1},2)$-LAs. The first column lists the types, while the second column displays the lower bound on the size of mixed-level $(\overline{1},2)$-LAs with the type. The last column presents the size obtained by simulated annealing [28].

Table 3. Lower bounds on the size of $(\overline{1},2)$-LA.

Type	Minimum Size	Simulated Annealing
(2,3,4)	16	16
(3,3,4)	17	17
(2,4,4)	16	16
(2,2,3,4)	16	16
(2,2,5,5)	25	25
(2,3,3,4)	17	17

A $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$ is called optimal if its size is $(\overline{1},t)$-LAN$(k,(v_1,v_2,\cdots ,v_k))$. In what follows, we focus on some constructions for mixed level LAs from combinatorial design theory. Some constructions that produce optimal LAs satisfying the lower bound in Lemma 2 will also be provided.

4. Constructions of $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$

Some constructions and existence results for $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$ are presented in this section.

4.1. Methods for Constructing $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$

In this subsection, we modify some constructions for MCAs to the case of $(\overline{1},t)$-LAs. The next two lemmas provide the “truncation” and “derivation” constructions, which were first used to construct mixed CAs.

Lemma 5.

(Truncation) Let $2\le v_1\le v_2\le \cdots \le v_{i-1}\le v_i\le v_{i+1}\le \cdots \le v_k$. Then, $(\overline{1},t)$-LAN$(k-1,(v_1,v_2,\cdots ,v_{i-1},v_{i+1},\cdots ,v_k))\le$$(\overline{1},t)$-LAN$(k,(v_1,v_2,\cdots ,v_{i-1},v_i,v_{i+1},\cdots ,v_k))$.

Proof. 

Let A be a $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_{i-1},v_i,v_{i+1},\cdots ,v_k))$ with $N=(\overline{1},t)$-LAN$(k,(v_1,v_2,\cdots ,v_{i-1},v_i,v_{i+1},\cdots ,v_k))$. Delete the ith column from A to obtain a $(\overline{1},t)$-LA$(N;k-1,(v_1,v_2,\cdots ,v_{i-1},v_{i+1},\cdots ,v_k))$. Thus, $(\overline{1},t)$-LAN$(k-1,(v_1,v_2,\cdots ,v_{i-1},v_{i+1},\cdots ,v_k))\le N=(\overline{1},t)$-LAN$(k,(v_1,v_2,\cdots ,v_{i-1},v_i,v_{i+1},\cdots ,v_k))$. □

Lemma 6.

(Derivation) Let $2\le v_1\le v_2\le \cdots \le v_{i-1}\le v_i\le v_{i+1}\le \cdots \le v_k$. Then $v_i·(\overline{1},t-1)$-LAN$(k-1,(v_1,v_2,\cdots ,v_{i-1},v_{i+1},\cdots ,v_k))\le$$(\overline{1},t)$-LAN$(k,(v_1,v_2,\cdots ,v_{i-1},v_i,v_{i+1},\cdots ,v_k))$, where $t\ge 2$.

Proof. 

Let A be a $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$ with $N=(\overline{1},t)$-LAN$(k,(v_1,v_2,\cdots ,v_k))$. By Lemma 1, A is an MCA and a $(1,t)$-LA. For each $x\in \{0,1,\cdots ,v_i-1\}$, taking the rows in A that involve the symbol x in the ith columns and omitting the column yields an MCA$(N_x;t-1,k-1,(v_1,v_2,\cdots ,v_{i-1},v_{i+1},\cdots ,v_k))$. We use $A\left(x\right)$ to denote the derived array. Next, we prove that $A\left(x\right)$ is a $(1,t-1)$-LA$(N_x;k-1,(v_1,v_2,\cdots ,v_{i-1},v_{i+1},\cdots ,v_k))$. In fact, for any $(t-1)$-way interactions $T_1$ and $T_2$ with $T_1\ne T_2$, if $\rho (A\left(x\right),T_1)=\rho (A\left(x\right),T_2)$, we can form two t-way interactions $T_1^{\prime }$ and $T_2^{\prime }$ by inserting $(i,x)$ into $T_1$ and $T_2$, respectively. Hence, $\rho (A,T_1^{\prime })=\rho (A,T_2^{\prime })$, where $|\rho (A,T_1^{\prime })|=|\rho (A\left(x\right),T_1)|$ but $T_1^{\prime }\ne T_2^{\prime }$. Consequently, A is not a $(1,t)$-LA. It is clear that $N_i\ge (\overline{1},t-1)$-LAN$(k-1,(v_1,v_2,\cdots ,v_{i-1},v_{i+1},\cdots ,v_k))$ for $0\le i\le v_i-1$. Thus, $N=N_0+N_1+\cdots +N_{v_i-1}\ge v_i·(\overline{1},t-1)$-LAN$(k-1,(v_1,v_2,\cdots ,v_{i-1},v_{i+1},\cdots ,v_k))$. □

The following product construction can be used to produce a new LA from old LAs, which is a typical construction in combinatorial design.

Construction 1.

(Product Construction) If both a $(\overline{1},t)$-LA$(N_1;k,(v_1,v_2,\cdots ,v_k))$ and an MCA$(N_2;t,k,(s_1,s_2,\cdots ,s_k))$ exist, then a $(\overline{1},t)$-LA$(N_1{N}_2;k,(v_1{s}_1,v_2{s}_2,\cdots ,v_k{s}_k))$ exists, where $t<k$. In particular, if both a $(\overline{1},t)$-LA$(N_1;k,(v_1,v_2,\cdots ,v_k))$ and a $(\overline{1},t)$-LA$(N_2;k,(s_1,s_2,\cdots ,s_k))$ exist, then a $(\overline{1},t)$-LA$(N_1{N}_2;k,(v_1{s}_1,v_2{s}_2,\cdots ,v_k{s}_k))$ also exists, where $t<k$.

Proof. 

Let $A=\left(a_{ij}\right)(i\in I_{N_1},j\in I_k)$ and $B=\left(b_{ij}\right)(i\in I_{N_2},j\in I_k)$ be the given $(\overline{1},t)$-LA$(N_1;k,(v_1,v_2,\cdots ,v_k))$ and MCA$(N_2;t,k,(s_1,s_2,\cdots ,s_k))$, respectively. We form an $N_1{N}_2\times k$ array as follows. For each row $(a_{i1},a_{i2},\cdots ,a_{ik})$ of A and each row $(b_{h1},b_{h2},\cdots ,b_{hk})$ of B, include the row $((a_{i1},b_{h1}),(a_{i2},b_{h2}),\cdots ,(a_{ik},b_{hk}))$ as a row of $\overline{A}$, where $1\le i\le N_1,1\le h\le N_2$.

From the typical method in design theory, the resultant array $\overline{A}$ is an MCA$(N_1{N}_2;t,k,(v_1{s}_1,v_2{s}_2,\cdots ,v_k{s}_k))$, as both A and B are MCAs. By Lemma 1, we only need to prove that $\overline{A}$ is a $(1,t)$-LA. Suppose that $\rho (\overline{A},T_1)=\rho (\overline{A},T_2)$, where $T_1=\{(i,(a_{hi},b_{ci})):i\in I,\left|I\right|=t,I\subset \{1,2,\cdots ,k\},h\in I_{N_1},c\in I_{N_2}\}$ and $T_2=\{(j,(a_{h^{\prime }j},b_{c^{\prime }j})):j\in I^{\prime },|I^{\prime }|=t,I^{\prime }\subset \{1,2,\cdots ,k\},h^{\prime }\in I_{N_1},c^{\prime }\in I_{N_2}\}$ with $T_1\ne T_2$. It is noteworthy that the projection on the first component of $T_1$ and $T_2$ is the corresponding t-way interaction of A, while the projection on the second component is the corresponding t-way interaction of B. Therefore, A is not a $(1,t)$-LA. The first assertion is then proved because a $(\overline{1},t)$-LA$(N_2;k,(s_1,s_2,\cdots ,s_k))$ is an MCA$(N_2;t,k,(s_1,s_2,\cdots ,s_k))$. The second assertion can be proven by the first assertion. □

The following construction can be used to increase the number of levels for a certain factor.

Construction 2.

If a $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$ exists, then a $(\overline{1},t)$-LA$(2N;k,(v_1,v_2,\cdots ,v_{i-1},a,v_{i+1},\cdots ,v_k))$ exists, where $i\in \{1,2,3,\cdots ,k\}$ and $v_i<a\le 2v_i$.

Proof. 

Let $A=\left(a_{ij}\right),(i\in I_N,j\in I_k)$ be the given $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$ with entries in the ith column from a set $V_i$ of size $v_i$. For a certain $i\in I_k$, we replace the symbols $0,1,\cdots ,a-v_i-1$ in the ith column of A by $v_i,v_i+1,\cdots ,a-1$, respectively. We denote the resultant array by $A^{\prime }$. Clearly, permuting the symbols in a certain column does not affect the property of $(\overline{1},t)$-LAs. Thus, $A^{\prime }$ is also a $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$, where entries in the ith column of $A^{\prime }$ from the set $\{a-v_i,a-v_i+1,\cdots ,v_i-1,v_i,v_i+1,\cdots ,a-1\}$. Subsequently, write $M={\left(A^T\right|{\left(A^{\prime }\right)}^T)}^T$. It is easy to prove that M is a $(1,t)$-LA$(2N;k,(v_1,v_2,\cdots ,v_{i-1},a,v_{i+1},\cdots ,v_k))$ and an MCA$(2N;t,k,(v_1,v_2,\cdots ,v_{i-1},a,v_{i+1},\cdots ,v_k))$. By Lemma 1, M is the desired array. □

The following example illustrates the idea in Construction 2.

Example 1.

The transpose of the following array is a $(\overline{1},2)$-LA$(12;5,(2,2,2,2,3\left)\right)$

0	0	0	0	0	0	0	1	1	1	1	1
0	0	0	0	1	1	1	0	0	1	1	1
0	0	0	1	0	1	1	1	1	0	0	1
0	0	1	0	1	0	1	1	1	0	1	0
0	2	1	0	1	1	2	0	1	0	2	2

Replace the symbols $0,1$ by $2,3$ in the 3th column, respectively. Juxtapose two such arrays from top to bottom to obtain the following array M; we list it as its transpose to conserve space.

0	0	0	0	0	0	0	1	1	1	1	1	0	0	0	0	0	0	0	1	1	1	1	1
0	0	0	0	1	1	1	0	0	1	1	1	0	0	0	0	1	1	1	0	0	1	1	1
0	0	0	1	0	1	1	1	1	0	0	1	2	2	2	3	2	3	3	3	3	2	2	3
0	0	1	0	1	0	1	1	1	0	1	0	0	0	1	0	1	0	1	1	1	0	1	0
0	2	1	0	1	1	2	0	1	0	2	2	0	2	1	0	1	1	2	0	1	0	2	2

It is easy to verify that M is a $(\overline{1},2)$-LA$(24;5,(2,2,4,2,3\left)\right)$.

Replace the symbol 0 by 2 in the 3th column. Juxtapose two such arrays from top to bottom to obtain the following array $M^{\prime }$; we list it as its transpose to conserve space.

0	0	0	0	0	0	0	1	1	1	1	1	0	0	0	0	0	0	0	1	1	1	1	1
0	0	0	0	1	1	1	0	0	1	1	1	0	0	0	0	1	1	1	0	0	1	1	1
0	0	0	1	0	1	1	1	1	0	0	1	2	2	2	1	2	1	1	1	1	2	2	1
0	0	1	0	1	0	1	1	1	0	1	0	0	0	1	0	1	0	1	1	1	0	1	0
0	2	1	0	1	1	2	0	1	0	2	2	0	2	1	0	1	1	2	0	1	0	2	2

It is easy to verify that $M^{\prime }$ is a $(\overline{1},2)$-LA$(24;5,(2,2,3,2,3\left)\right)$. □

Remark 1.

Construction 2 may produce an optimal $(\overline{1},t)$-LA. For example, a $(\overline{1},2)$-LA$(16;(2,2,3,4\left)\right)$ is shown in Table 1. By Construction 2, we can obtain a $(\overline{1},2)$-LA$(32;(2,2,3,8\left)\right)$, which is optimal by Lemma 4.

Fusion is an effective construction for MCAs from CAs, for example, see [29]. As with CAs, fusion for $(\overline{1},t)$-LAs guarantees the extension of uniform constructions to mixed cases; however, fusion for a $(\overline{1},t)$-LA$(N;k,v)$ may not produce mixed-level $(\overline{1},t)$-LAs. This problem can be circumvented by introducing the notion of detecting arrays (DAs). Suppose that all the factors have the same levels. If, for any $\mathcal{T}\subseteq {\mathcal{I}}_t$ with $\left|\mathcal{T}\right|=d$ and any $T\in {\mathcal{I}}_t$, we have $\rho (A,T)\subseteq \rho (A,\mathcal{T})\iff T\in \mathcal{T},$ then the array A is called a $(d,t)$-DA or a $(d,t)$-DA$(N;k,v)$.

Construction 3.

(Fusion) Suppose that A is a $(1,t)$-DA$(N;k,v)$ with $t\ge 2$. If A is also a $(\lceil \frac{v}{v_i}\rceil ,t)$-LA$(N;k,v)$, then a $(\overline{1},t)$-LA$(N;k,(v,\cdots ,v,v_i,v,\cdots ,v))$ exists, where $2\le v_i<v$.

Proof. 

Let A be a $(1,t)$-DA$(N;k,v)$ over the symbol set V of size v. Suppose that $a_i(i=1,2,\cdots ,v_i)$ are positive integers with $a_1+a_2+\cdots +a_{v_i}=v$. It is clear that there exists a certain $a_i$ such that $a_i=\lceil \frac{v}{v_i}\rceil$ and $a_i\ge a_j$, where $1\le i\ne j\le v_i$. We select $a_1,a_2,\cdots ,a_{v_i}$ elements from V in the ith column of A to form the element sets $A_i(1\le i\le v_i)$, respectively. The elements in $A_i(1\le i\le v_i)$ are identical with $1,2,\cdots ,v_i$, respectively. Then, we obtain an $N\times k$ array $A^{\prime }$. Clearly, $A^{\prime }$ is an MCA. We only need to prove that $A^{\prime }$ is a $(1,t)$-LA by Lemma 1, i.e., for any two distinct t-way interactions $T_1=\{(a_1,u_{a_1}),\cdots ,(a_t,u_{a_t})\}$ and $T_2=\{(b_1,s_{b_1}),\cdots ,(b_t,s_{b_t})\}$, we have $\rho (A^{\prime },T_1)\ne \rho (A^{\prime },T_2)$. It is clear that $\rho (A,T_1)=\rho (A^{\prime },T_1)$ and $\rho (A^{\prime },T_2)=\rho (A,T_2)$ when $i\notin \{a_1,\cdots ,a_t\}$ and $i\notin \{b_1,\cdots ,b_t\}$. Hence, $\rho (A^{\prime },T_1)\ne \rho (A^{\prime },T_2)$.

When $i\in \{a_1,\cdots ,a_t\}$ and $i\notin \{b_1,\cdots ,b_t\}$, we can obtain a t-way interaction $T_1^{\prime }=\{(a_1,u_{a_1}),\cdots ,(i,a),\cdots ,(a_t,u_{a_t})\}$ of A, where $a\in A_{u_i}$. If $\rho (A^{\prime },T_1)=\rho (A^{\prime },T_2)$, then $\rho (A,T_1^{\prime })\subset \rho (A^{\prime },T_1)=\rho (A^{\prime },T_2)=\rho (A,T_2)$; however, $T_1^{\prime }\ne T_2$; as such, it is a contradiction that A is a $(1,t)$-DA$(N;k,v)$. If $i\notin \{a_1,\cdots ,a_t\}$ and $i\in \{b_1,\cdots ,b_t\}$, then the similar argument can prove the conclusion.

When $i\in \{a_1,\cdots ,a_t\}$ and $i\in \{b_1,\cdots ,b_t\}$, it is clear that $\rho (A^{\prime },T_1)\ne \rho (A^{\prime },T_2)$ if $u_i\ne s_i$. The case $u_i=s_i$ remains to be considered. Without loss of generality, suppose that $a_j$ elements are identical with $u_i$. It is clear that $T_1$ and $T_2$ can be obtained from ${\mathcal{T}}_1$ and ${\mathcal{T}}_2$ by fusion, respectively, where ${\mathcal{T}}_1$ and ${\mathcal{T}}_2$ are sets of t-way interactions with $|{\mathcal{T}}_1|=|{\mathcal{T}}_2|=a_j$. If $\rho (A^{\prime },T_1)=\rho (A^{\prime },T_2)$, then $\rho (A^{\prime },T_1)=\rho (A,{\mathcal{T}}_1)=\rho (A^{\prime },T_2)=\rho (A,{\mathcal{T}}_2)$. It is a contradiction that A is a $(\lceil \frac{v}{v_i}\rceil ,t)$-LA$(N;k,v)$ because the existence of $(\lceil \frac{v}{v_i}\rceil ,t)$-LA$(N;k,v)$ implies the existence of $(a_j,t)$-LA$(N;k,v)$ [12]. □

Constructions 2 and 3 provide an effective and efficient method to construct a mixed-level $(\overline{1},t)$-LA from a $(1,t)$-LA$(N;k,v)$. The existence of $(d,t)$-DA$(N;k,v)$ with $d\ge 1$ implies the existence of $(d,t)$-LA$(N;k,v)$ [12]. Hence, the array A in Construction 3 can be obtained by a $(d,t)$-DA$(N;k,v)$, which is characterized in terms of super-simple OAs. The existence of super-simple OAs can be found in [17,30,31,32,33,34]. It is noteworthy that the derived array is not optimal. In the remainder of this section, we present two “Roux-type” recursive constructions [35].

Construction 4.

If both a $(\overline{1},t)$-LA$(N_1;k,(v_1,v_2,\cdots ,v_k))$ and a $(\overline{1},t-1)$-LA$(N_2;k-1,(v_1,v_2,\cdots ,v_{i-1},v_{i+1},\cdots ,v_k))$ exist, then a $(\overline{1},t)$-LA$(N_1+e{N}_2;k,(v_1,v_2,\cdots ,v_{i-1},v_i+e,v_{i+1},v_{i+2}\cdots ,v_k))$ exists, where $e\ge 0$.

Proof. 

Let A and B be the given $(\overline{1},t)$-LA$(N_1;k,(v_1,v_2,\cdots ,v_k))$ and $(\overline{1},t-1)$-LA$(N_2;k-1,(v_1,v_2,\cdots ,v_{i-1},v_{i+1},\cdots ,v_k))$, respectively. Clearly, if $e=0$, then A is the required array. Now, suppose that $e\ge 1$. Insert a column vector $(j,j,\cdots ,j)$ of length $N_2$ to the front of the ith column of B to form an $N_2\times k$ array $B_j$, where $j\in \{v_i,v_i+1,v_i+2,\cdots ,v_i+e-1\}$. Let $M=(A^T|B_{v_i}^T|B_{v_i+1}^T|\cdots |B_{v_i+e-1}^T{)}^T$. Clearly, M is an MCA$(N_1+e{N}_2;t,k,(v_1,v_2,\cdots ,v_{i-1},v_i+e,v_{i+1},v_{i+2}\cdots ,v_k))$ [9]. By Lemma 1, we only need to prove that M is a $(1,t)$-LA, i.e., $\rho (M,T_1)\ne \rho (M,T_2)$ for any two distinct t-way interactions $T_1$ and $T_2$, where $T_1=\{(a_1,u_{a_1}),\cdots ,(a_t,u_{a_t})\}$ and $T_2=\{(b_1,s_{b_1}),\cdots ,(b_t,s_{b_t})\}$. Next, we distinguish the following cases.

Case 1. $i\notin \{a_1,\cdots ,a_t\}$ and $i\notin \{b_1,\cdots ,b_t\}$

In this case, because A is a $(\overline{1},t)$-LA, $\rho (A,T_1)\ne \rho (A,T_2)$, $\rho (M,T_1)\ne \rho (M,T_2)$ as A is part of M.

Case 2. $i\notin \{a_1,\cdots ,a_t\}$ and $i\in \{b_1,\cdots ,b_t\}$ or $i\in \{a_1,\cdots ,a_t\}$ and $i\notin \{b_1,\cdots ,b_t\}$

When $i\notin \{a_1,\cdots ,a_t\}$ and $i\in \{b_1,\cdots ,b_t\}$, if $s_i\notin \{v_i,v_i+1,\cdots ,v_i+e-1\}$, then $\rho (A,T_1)\ne \rho (A,T_2)$. Thus, $\rho (M,T_1)\ne \rho (M,T_2)$. If $s_i\in \{v_i,v_i+1,\cdots ,v_i+e-1\}$, then $T_2$ must be included by rows of $B_i$, where $i\in \{v_i,v_i+1,\cdots ,v_i+e-1\}$; however, it must not be included by any row of A. Clearly, $T_1$ must be included by some rows of A. Consequently, $\rho (M,T_1)\ne \rho (M,T_2)$. When $i\in \{a_1,\cdots ,a_t\}$ and $i\notin \{b_1,\cdots ,b_t\}$, the same argument can prove the conclusion.

Case 3. $i\in \{a_1,\cdots ,a_t\}$ and $i\in \{b_1,\cdots ,b_t\}$

Clearly, $\rho (M,T_1)\ne \rho (M,T_2)$ holds whenever $u_i\ne s_i$. If $u_i=s_i\notin \{v_i,v_i+1,\cdots ,v_i+e-1\}$, then $\rho (A,T_1)\ne \rho (A,T_2)$, which implies that $\rho (M,T_1)\ne \rho (M,T_2)$. If $u_i=s_i\in \{v_i,v_i+1,\cdots ,v_i+e-1\}$, then $T_1$ and $T_2$ must be included by some rows for a certain $B_i$, where $i\in \{v_i,v_i+1,\cdots ,v_i+e-1\}$. Because B is a $(\overline{1},t-1)$-LA, $\rho (B_i,T_1)\ne \rho (B_i,T_2)$, which implies $\rho (M,T_1)\ne \rho (M,T_2)$. □

More generally, we have the following construction.

Construction 5.

Let $p\ge 0,q\ge 0$ and $1\le i<j\le k$. If a $(\overline{1},t)$-LA$(N_1;k,(v_1,v_2,\cdots ,v_{i-1},v_i,v_{i+1},\cdots ,v_{j-1},v_j,v_{j+1},\cdots ,v_k))$, $(\overline{1},t-1)$-LA$(N_2;k-1,(v_1,v_2,\cdots ,v_{i-1},v_{i+1},\cdots ,v_k))$, a $(\overline{1},t-1)$-LA$(N_3;k-1,(v_1,v_2,\cdots ,v_{j-1},v_{j+1},\cdots ,v_k))$ and $(\overline{1},t-2)$-LA$(N_4;k-2,(v_1,v_2,\cdots ,v_{i-1},v_{i+1},\cdots ,v_{j-1},v_{j+1},\cdots ,v_k))$ exist, then a $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_{i-1},v_i+p,v_{i+1},\cdots ,v_{j-1},v_j+q,v_{j+1},\cdots ,v_k))$ exists, where $N=N_1+p{N}_2+q{N}_3+pq{N}_4$.

Proof. 

We begin with a $(\overline{1},t)$-LA$(N_1;k,(v_1,v_2,\cdots ,v_{i-1},v_i,v_{i+1},\cdots ,v_{j-1},v_j,v_{j+1},\cdots ,v_k))$, an $N_1\times k$ array A that is on $V_1\times \cdots \times V_{i-1}\times V_i^{\prime }\times V_{i+1}\times \cdots \times V_{j-1}\times V_j^{\prime }\times V_{j+1}\times \cdots \times V_k$. Let $H_1$ and $H_2$ be two sets with $|H_1|=p$ and $|H_2|=q$ such that $H_1\bigcap V_i^{\prime }=\varnothing$ and $H_2\bigcap V_j^{\prime }=\varnothing$, respectively. Suppose that $B^{\prime }$, an $N_2\times (k-1)$ array, is a $(\overline{1},t-1)$-LA$(N_2;k-1,(v_1,v_2,\cdots ,v_{i-1},v_{i+1},\cdots ,v_k))$, which is on $V_1\times \cdots \times V_{i-1}\times V_{i+1}\times \cdots \times V_k$. For each row $(a_1$, $a_2,\cdots ,a_{i-1},a_{i+1},\cdots ,a_k)$ of $B^{\prime }$, add $x\in H_1$ to obtain a k-tuple $(a_1$, $a_2,\cdots ,a_{i-1},x,a_{i+1},\cdots ,a_k)$. Then, we obtain a $p{N}_2\times k$ array from $B^{\prime }$, denoted by B. Similarly, from a $(\overline{1},t-1)$-LA$(N_3;k-1,(v_1,v_2,\cdots ,v_{j-1},v_{j+1},\cdots ,v_k))$, we obtain a $q{N}_3\times k$ array, denoted by C. For each pair $(x,y)\in H_1\times H_2$, we construct k-tuple $(a_1,a_2,\cdots ,a_{i-1},x,a_{i+1},\cdots ,a_{j-1},y,a_{j+1},\cdots ,a_k)$ for each row of the given $(\overline{1},t-2)$-LA$(N_4;k-2,(v_1,v_2,\cdots ,v_{i-1},v_{i+1},\cdots ,v_{j-1},v_{j+1},\cdots ,v_k))$. These tuples result in a $pq{N}_4\times k$ array, denoted by D.

Denote $V_i^{\prime }\cup H_1=V_i$, $V_j^{\prime }\cup H_2=V_j$ and $F=\left(\begin{array}{c}A\hfill \\ B\hfill \\ C\hfill \\ D\hfill \end{array}\right)$. We claim that F, an $(N_1+p{N}_2+q{N}_3+pq{N}_4)\times k$ array, is a $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_{i-1},v_i+p,v_{i+1},\cdots ,v_{j-1},v_j+q,v_{j+1},\cdots ,v_k)$ which is on $V_1\times \cdots \times V_{i-1}\times V_i\times V_{i+1}\times \cdots \times V_{j-1}\times V_j\times V_{j+1}\times \cdots \times V_k$.

Clearly, F is an MCA $(N;t,k,(v_1,v_2,\cdots ,v_{i-1},v_i+p,v_{i+1},\cdots ,v_{j-1},v_j+q,v_{j+1},\cdots ,v_k)$. To prove this assertion, we only need to demonstrate that $\rho (F,T_a)\ne \rho (F,T_b)$ for any two distinct t-way interactions $T_a=\{(a_1,u_{a_1}),\cdots ,(a_t,u_{a_t})\}$ and $T_b=\{(b_1,v_{b_1}),\cdots ,(b_t,v_{b_t})\}$. By similar argument as the proof of Construction 4, we can prove the conclusion except for the case where $i,j\in \{a_1,a_2,\cdots ,a_t\}$ and $i,j\in \{b_1,b_2,\cdots ,b_t\}$, $u_i=v_i\in H_1$, and $u_j=v_j\in H_2$. In this case, $T_a$ and $T_b$ are only included by some rows of D. If $\rho (F,T_a)=\rho (F,T_b)$, then $\rho (D,T_a)=\rho (D,T_b)=\rho (F,T_a)=\rho (F,T_b)$. Consequently, $\rho (D,T_a\setminus \{(i,u_i),(j,u_j)\})=\rho (D,T_b\setminus \{(i,u_i),(j,u_j)\})$, which implies that $\rho (D^{\prime },T_a\setminus \{(i,u_i),(j,u_j)\})=\rho (D^{\prime },T_b\setminus \{(i,u_i),(j,u_j)\})$ by the construction of D. It is a contradiction with $D^{\prime }$ being a $(\overline{1},t-2)$-LA$(N_4;k-2,(v_1,v_2,\cdots ,v_{i-1},v_{i+1},\cdots ,v_{j-1},v_{j+1},\cdots ,v_k))$. The proof is completed. □

4.2. Constructions and Existence of Optimal $(\overline{1},t)$-LA$({\prod }_{i=k-t+1}^k{v}_i;k,(v_1,v_2,\cdots ,v_k))$

Let $2\le v_1\le v_2\le \cdots \le v_k$. An $N\times k$ array A is called ${\mathrm{MCA}}_2^{\ast }({\prod }_{i=k-t+1}^k{v}_i;t,k,(v_1,v_2,\cdots ,v_k))$ if $\left|\rho \right(A,T\left)\right|=1$ for any t-way interaction $T\in \mathcal{T}=\{\{(k-t+1,v_{k-t+1}),\cdots ,(k,v_k)\}:v_i\in V_i(k-t+1\le i\le k)\}$ and $\left|\rho \right(A,T^{\prime }\left)\right|\ge 2$ for any t-way interaction $T^{\prime }\notin \mathcal{T}$. If an optimal $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$ with $N={\prod }_{i=k-t+1}^k{v}_i$ exists, then the following condition must be satisfied.

Lemma 7.

Let $2\le v_1\le v_2\le \cdots \le v_{k-t},2v_{k-t}\le v_{k-t+1}\le v_{k-t+2}\le \cdots \le v_k$. If A is an optimal $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$ with $N={\prod }_{i=k-t+1}^k{v}_i$. Then, A is an ${\mathit{MCA}}_2^{\ast }(N;t,k,(v_1,v_2,\cdots ,v_k))$.

Proof. 

Let A be the given optimal $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$ with $N={\prod }_{t=k-t+1}^k{v}_i$. Then, A is an MCA$(N;t,k,(v_1,v_2,\cdots ,v_k)$ by Lemma 1. Because $N={\prod }_{t=k-t+1}^k{v}_i$, we have $\left|\rho \right(A,T\left)\right|=1$ for any t-way interaction $T\in \mathcal{T}$. It follows that $\left|\rho \right(A,T^{\prime }\left)\right|\ge 2$ for any t-way interaction $T^{\prime }$ of A from the definition of $(\overline{1},t)$-LA, where $T^{\prime }\notin \mathcal{T}$. Hence, A is an ${\mathrm{MCA}}_2^{\ast }({\prod }_{i=k-t+1}^k{v}_i;t,k,(v_1,v_2,\cdots ,v_k))$, as desired. □

Clearly, an ${\mathrm{MCA}}_2^{\ast }(N;t,k,(v_1,v_2,\cdots ,v_k))$ is not always a $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$. Next, we present a special case of ${\mathrm{MCA}}_2^{\ast }$, which produces optimal $(\overline{1},t)$-LAs. First, we introduce the notion of mixed orthogonal arrays (MOAs).

An MOA, or MOA$(N;t,k,(v_1,v_2,\cdots ,v_k))$ is an $N\times k$ array with entries in the ith column from a set $V_i$ of size $v_i$ such that each $N\times t$ sub-array contains each t-tuple occurring an equal number of times as a row. When $v_1=v_2=\cdots =v_k=v$, an MOA is merely an orthogonal array, denoted by OA$(N;t,k,v)$.

The notion of mixed or asymmetric orthogonal arrays, introduced by Rao [36], have received significant attention in recent years. These arrays are important in experimental designs as universally optimal fractions of asymmetric factorials. Without loss of generality, we assume that $v_1\le v_2\le \cdots \le v_k$. By definition of MOA, all t-tuples occur in the same number of rows for any $N\times t$ sub-array of an MOA. This number of rows is called index. It is obvious that $\left(\genfrac{}{}{0pt}{}{k}{t}\right)$ indices exist. We denote it by ${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_{\left(\genfrac{}{}{0pt}{}{k}{t}\right)}$. If ${\lambda }_i\ne {\lambda }_j$ for any $i\ne j$, then an MOA is termed as a pairwise distinct index mixed orthogonal array, denoted by PDIMOA$(N;t,k,(v_1,v_2,\cdots ,v_k))$. Moreover, if ${\lambda }_i=1$ for a certain $i\in \{1,2,\cdots ,\left(\genfrac{}{}{0pt}{}{k}{t}\right)\}$ holds, then it is termed as ${\mathrm{PDIMOA}}^{\ast }(N;t,k,(v_1,v_2,\cdots ,v_k))$. It is clear that $N={\prod }_{i=k-t+1}^k{v}_i$ in the definition of ${\mathrm{PDIMOA}}^{\ast }$.

Example 2.

The transpose of the following array is a ${\mathit{PDIMOA}}^{\ast }(24;2,3,(2,4,6))$.

$$\left(\begin{array}{cccccccccccccccccccccccc}1& 0& 0& 0& 1& 1& 1& 0& 1& 0& 0& 1& 0& 1& 1& 1& 0& 0& 0& 1& 0& 1& 1& 0\\ 2& 2& 2& 2& 2& 2& 1& 1& 1& 1& 1& 1& 3& 3& 3& 3& 3& 3& 0& 0& 0& 0& 0& 0\\ 1& 2& 3& 4& 5& 0& 1& 2& 3& 4& 5& 0& 1& 2& 3& 4& 5& 0& 1& 2& 3& 4& 5& 0\end{array}\right)$$

□

The following lemma can be easily obtained by the definition of ${\mathrm{PDIMOA}}^{\ast }$; therefore, we omit the proof herein.

Lemma 8.

Suppose that $v_1\le v_2\le \cdots \le v_k$. If A is a ${\mathit{PDIMOA}}^{\ast }({\prod }_{i=k-t+1}^k{v}_i;t,k,(v_1,v_2,\cdots ,v_k))$, then $v_1<v_2<\cdots <v_k$ and $v_i|v_j$, where $1\le i\le k-t$ and $k-t+1\le j\le k$.

Lemma 9.

Let $2<v_1<v_2<\cdots <v_k$. If a PDIMOA$(N;t,k,(v_1,v_2,\cdots ,v_k))$ exists, then a $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$ exists. Moreover, if $N={\prod }_{i=k-t+1}^k{v}_i$, then the derived $(\overline{1},t)$-LA is optimal.

Proof. 

Let A be a PDIMOA$(N;t,k,(v_1,v_2,\cdots ,v_k))$. Clearly, A is an MCA. By Lemma 1, we only need to prove that $T_1\ne T_2$ implies $\rho (A,T_1)\ne \rho (A,T_2)$, where $T_1$ and $T_2$ are two t-way interactions. In fact, if $\rho (A,T_1)=\rho (A,T_2)$, then $|\rho (A,T_1)|=|\rho (A,T_2)|$, which contradicts the definition of a PDIMOA. The optimality can be obtained by Theorem 1. □

We construct an optimal $(\overline{1},t)$-LA$(N;k,(v_1,v_2,\cdots ,v_k))$ with $N={\prod }_{i=k-t+1}^k{v}_i$ in terms of ${\mathrm{PDIMOA}}^{\ast }$. First, we have the following simple and useful construction for ${\mathrm{PDIMOA}}^{\ast }$. A similar construction for MOAs was first stated in [37].

Construction 6.

Let $b=r_1{r}_2\cdots r_m<v_2<\cdots <v_k$ and $r_1<r_2<\cdots <r_m$. If a ${\mathit{PDIMOA}}^{\ast }({\prod }_{i=k-t+1}^k{v}_i;t,k,(r_1{r}_2\cdots r_m,v_2,v_3,\cdots v_k))$ exists, then a ${\mathit{PDIMOA}}^{\ast }({\prod }_{i=k-t+1}^k{v}_i;t,k+m-1,(r_1,r_2,\cdots ,r_m,v_2,v_3,\cdots ,v_k))$ also exists.

Proof. 

Let A be ${\mathrm{PDIMOA}}^{\ast }(N;t,k,(b,v_2,v_3,\cdots v_k))$ with $b=r_1{r}_2,\cdots r_m$. We can form an $N\times (k+m-1)$ array $A^{\prime }$ by replacing the symbols in $V_b$ by those of $V_{r_1}\times V_{r_2}\times \cdots \times V_{r_m}$. It is easily verified that $A^{\prime }$ is the required ${\mathrm{PDIMOA}}^{\ast }$. □

The following construction can be obtained easily; thus, we omit its proof.

Construction 7.

Let $a_1<a_2<\cdots <a_k$ and $b_1<b_2<\cdots <b_k$. If both a ${\mathit{PDIMOA}}^{\ast }({\prod }_{i=k-t+1}^k{a}_i;t,k,(a_1,a_2,\cdots ,a_k))$ and a ${\mathit{PDIMOA}}^{\ast }({\prod }_{i=k-t+1}^k{b}_i;t,k,(b_1,b_2,\cdots ,b_k))$ exist, then a ${\mathit{PDIMOA}}^{\ast }({\prod }_{i=k-t+1}^k{a}_i{b}_i;t,k,(a_1{b}_1,a_2{b}_2,\cdots ,a_k{b}_k))$ exists. In particular, if both a ${\mathit{PDIMOA}}^{\ast }({\prod }_{i=k-t+1}^k{a}_i;t,k,(a_1,a_2,\cdots ,a_k))$ and an OA$(t,k,v)$ exist, then a ${\mathit{PDIMOA}}^{\ast }({\prod }_{i=k-t+1}^k{a}_i{v}^t;t,k,(a_{1}v,a_{2}v,\cdots ,a_{k}v))$ exists.

Next, some series of optimal mixed-level $(\overline{1},t)$-LAs are presented. First, we list some known results for later use.

Lemma 10.

[38] An OA$(v^t;t,t+1,v)$ exists for any integer $v\ge 2,t\ge 2$.

The existence of ${\mathrm{PDIMOA}}^{\ast }{(t,t+1,(v_1,v_2,\cdots ,v_t,v_{t+1}))}^{\prime }$s is determined completely by the following theorem.

Theorem 2.

Let $v_1<v_2<\cdots <v_{t+1}$. A ${\mathit{PDIMOA}}^{\ast }({\prod }_{i=2}^{t+1}{v}_i;t,t+1,(v_1,v_2,\cdots ,v_t,v_{t+1}))$ exists if and only if $v_1|v_i$ for $2\le i\le t+1$.

Proof. 

The necessity can be easily obtained by Lemma 8. For sufficiency, we write $v_i=v_1{r}_i$ for $i=2,3,\cdots ,t+1$. Clearly, $r_i\ge 2$ and $r_i\ne r_j$ for $2\le i\ne j\le t+1$. We list all t-tuples from $Z_{r_2}\times Z_{r_3}\times \cdots \times Z_{r_{t+1}}$ to form an MOA$({\prod }_{i=2}^{t+1}{r}_i;t,t,(r_2,r_3,\cdots ,r_t,r_{t+1}))$, which is also a ${\mathrm{PDIMOA}}^{\ast }({\prod }_{i=2}^{t+1}{r}_i;t,t+1,(1,r_2,r_3,\cdots ,r_t,r_{t+1})$. Apply Construction 7 with an OA$(v_1^t;t,t+1,v_1)$ given by Lemma 10 to obtain the required ${\mathrm{PDIMOA}}^{\ast }$. □

More generally, we have the following results.

Theorem 3.

Let $v_1<v_2<\cdots <v_k$ and $v_i=k_i{v}_1{v}_2\cdots v_{k-t}$, where $k_i\ge 2$, $i=k-t+1,k-t+2,\cdots ,k$. Then, a ${\mathit{PDIMOA}}^{\ast }({\prod }_{i=k-t+1}^k{v}_i;t,k,(v_1,v_2,\cdots ,v_k))$ exists.

Proof. 

Let $M=v_1{v}_2\cdots v_{k-t}$. Then, $v_i=M{k}_i$, where $i=k-t+1,\cdots ,k$. By Theorem 2, a ${\mathrm{PDIMOA}}^{\ast }(N;t,t+1,(M,v_{k-t+1},\cdots ,v_k))$ with $N={\prod }_{i=k-t+1}^k{v}_i$ exists. Apply Construction 6 to obtain a ${\mathrm{PDIMOA}}^{\ast }({\prod }_{i=k-t+1}^k{v}_i,t,k,(v_1,v_2,\cdots ,v_k))$ as desired. □

Theorem 4.

Let $v_1\le v_2\le v_3$ with $v_2\ge 2v_1$. Then, an optimal $(\overline{1},2)$-LA$(v_2{v}_3;3,(v_1,v_2,v_3))$ exists.

Proof. 

First, we construct a $v_2{v}_3\times 3$ array $A=\left(a_{ij}\right)$ : $a_{i+r{v}_3,1}=(i-1+r)mod{v}_1$, where $i=1,2,\cdots ,v_3$ and $r=0,1,\cdots ,v_2-1$; $a_{i,2}=⌊\frac{i-1}{v_3}⌋$ and $a_{i,3}=(i-1)mod{v}_3$ for $i=1,2,\cdots ,v_2{v}_3$.

We prove that A is an optimal $(\overline{1},2)$-LA. Optimality is guaranteed by Theorem 1. It is clear that A is ${\mathrm{MCA}}_2^{\ast }(v_2{v}_3,(v_1,v_2,v_3))$. Consequently, $\left|\rho \right(A,\left\{\right(1,a),(2,b\left)\right\}\left)\right|\ge 2,\left|\rho \right(A,\left\{\right(1,c),(3,d\left)\right\}\left)\right|\ge 2$ and $\left|\rho \right(A,\left\{\right(2,e),(3,f\left)\right\}\left)\right|=1$, where $a,c\in V_1,b,e\in V_2,d,f\in V_3$. It is clear that $\rho (A,\{(1,a),(2,b)\left\}\right)\ne \rho (A,\{(2,e),(3,f)\left\}\right)$ and $\rho (A,\{(1,c),(3,d)\left\}\right)\ne \rho (A,\{(2,e),(3,f)\left\}\right)$. We only need to prove $\rho (A,\{(1,a),(2,b)\left\}\right)\ne \rho (A,\{(1,c),(3,d)\left\}\right)$. In fact, by construction, $\rho (A,\{(1,a),(2,b)\})\subset \{r{v}_3+1,r{v}_3+2,\cdots ,(r+1)v_3\}$ for a certain $r\in \{0,1,2,\cdots ,v_2-1\}$ but $\{i,i+v_1{v}_3\}\subset \rho (A,\{(1,c),(3,d)\})$, where $i\in \{1,2,\cdots ,v_1{v}_3\}$, which implies $\rho (A,\{(1,a),(2,b)\left\}\right)\ne \rho (A,\{(1,c),(3,d)\left\}\right)$. Thus, A is a $(\overline{1},t)$-LA by Lemma 1. □

The following example illustrates the idea in Theorem 4.

Example 3.

The transpose of the following array is an optimal $(\overline{1},2)$-LA$(42;3,(3,6,7\left)\right)$

0	1	2	0	1	2	0	1	2	0	1	2	0	1	2	0	1	2	0	1	2	0	1	2	0	1	2	0	1	2	0	1	2	0	1	2	0	1	2	0	1	2
0	0	0	0	0	0	0	1	1	1	1	1	1	1	2	2	2	2	2	2	2	3	3	3	3	3	3	3	4	4	4	4	4	4	4	5	5	5	5	5	5	5
0	1	2	3	4	5	6	0	1	2	3	4	5	6	0	1	2	3	4	5	6	0	1	2	3	4	5	6	0	1	2	3	4	5	6	0	1	2	3	4	5	6

Theorem 5.

Let $2<w<v$ with $v\ge 2w$. Then, an optimal $(\overline{1},1)$-LA$(v;w+1,(w,w,\cdots ,w,v\left)\right)$ exists.

Proof. 

First, we construct a $2w\times (w+1)$ array $A=\left(a_{ij}\right)$ as follows:

$$A=\left[\begin{array}{ccccc}0& 0& \cdots & 0& 0\\ 1& 1& \cdots & 1& 1\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ w-1& w-1& \cdots & w-1& w-1\\ 0& 1& \cdots & w-1& w\\ 1& 2& \cdots & 0& w+1\\ ⋮& ⋮& ⋮& ⋮& \\ w-1& 0& \cdots & w-2& 2w-1\end{array}\right]$$

When $v>2w$, let $C=\left(c_{ij}\right)$ be a $(v-2w)\times (w+1)$ array with $c_{i,(w+1)}=i-1$ for $i=2w+1,2w+2,\cdots ,v$ and $c_{i,j}$ be an arbitrary element for $\{0,1,\cdots ,w-1\}$ with $i=2w+1,2w+2,\cdots ,v,j=1,2,\cdots ,w$. Let $M=A$ and $N={\left(A^T\right|C^T)}^T$. It is easy to prove that M and N are the required arrays if $v=2w$ and $v>2w$, respectively. □

The following results need the notion of a Latin square. A Latin square of order n is an $n\times n$ array of n symbols in which each symbol occurs exactly once in each row and in each column. The diagonal of such a square is a set of entries that contains exactly one representative of each row and column, respectively. A transversal is a diagonal in which none of the symbols are repeated. For $n\ne 2,6$, there exists a Latin square of order n with n distinct transversals [39].

Theorem 6.

Let $2<w\ne 6$ and $v\ge 3w$. Then, an optimal $(\overline{1},1)$-LA$(v;2w^{⌊\frac{v-2w}{w}⌋}+1,(w,w,\cdots ,w,v))$ exists.

Proof. 

Let $L_0={\left(a_{ij}\right)}_{w\times w}$ with $a_{ij}=i-1$, where $i=1,2,\cdots ,w,j=1,2,3,\cdots ,w$. For $2<w\ne 6$, a latin square of order w with w disjoint transversals, denoted by $L_1$, exists. We take each of the w disjoint transversals from $L_1$ as a column to form a $w\times w$ array $L_2$, which, clearly, is also a Latin square. Let $\pi =(1,2,3,\cdots ,w)$. The permutation $\pi$ is applied to the columns of L to obtain a new array denoted by $L^{\left(\pi \right)}$. If L is a Latin square of w, then $L^{\left(\pi \right)},L^{\left({\pi }^2\right)},\cdots ,L^{\left({\pi }^{w-1}\right)}$ are also Latin squares of order w. The corresponding $1,2,\cdots ,w$ columns of $L^{\left({\pi }^i\right)}$ and $L^{\left({\pi }^j\right)}$ for $0\le i\ne j\le w-1$ have no common symbols.

Let $A=\left(\begin{array}{c}{L}_0\\ L_1\\ L_1\end{array}\right|\left.\begin{array}{c}{L}_0\\ L_2\\ L_2^{\left(\pi \right)}\end{array}\right)$ be a $3w\times 2w$ array. It is easy to verify that A is a $(\overline{1},1)$-LA$(3w;2w,w)$. For each part $\left(\begin{array}{c}{L}_x\\ L_y\\ L_z\end{array}\right)$ of A, we can construct a $4w\times w^2$ array of the form $\left(\begin{array}{c}{L}_x\\ L_y\\ L_z\\ L_z\end{array}\right|\left.\begin{array}{c}{L}_x\\ L_y\\ L_z\\ L_z^{\left(\pi \right)}\end{array}\right|\left.\begin{array}{c}\cdots \\ \cdots \\ \cdots \\ \cdots \end{array}\right|\left.\begin{array}{c}{L}_x\\ L_y\\ L_z\\ L_z^{\left({\pi }^{w-1}\right)}\end{array}\right)$. Next, juxtapose these resultant arrays to obtain a $4w\times 2w^2$ array $A^{\prime }$, which is easily verified to be a $(\overline{1},1)$-LA$(4w;2w^2,w)$. Continue this process until the $(⌊\frac{v-2w}{w}⌋+2)w\times 2w^{⌊\frac{v-2w}{w}⌋}$ array B can be obtained. Clearly, B is a $(\overline{1},1)$-LA$((⌊\frac{v-2w}{w}⌋+2)w;2w^{⌊\frac{v-2w}{w}⌋},w)$.

Let $V={(0,1,2,\cdots ,v-1)}^T$. Suppose C is a $(v-(⌊\frac{v-2w}{w}⌋+2)w)\times 2w^{⌊\frac{v-2w}{w}⌋}$ array with entries from $\{0,1,\cdots ,w-1\}$, where $v\ne kw$. Write $B^{\prime }=B$; if $v=kw$, $B^{\prime }={\left(B^T\right|C^T)}^T$ if $v\ne kw$. It is easy to verify that $M=\left(B^{\prime }\right|V)$ is the required array. □

The following theorem considers the case $w=2$.

Theorem 7.

Let $v\ge 4$ be a positive integer. Then an optimal $(\overline{1},1)$-LA$(v;2^v-2v-1,(2,2,\cdots ,2,v))$ exists.

Proof. 

Let $V={(0,1,2,\cdots ,v-1)}^T$. We only need to construct a $(\overline{1},1)$-LA$(v;2^v-2v-2,2)$, A, because $\left(A\right|V)$ is the required array. As $v\ge 4$, the number of occurrences of 0, 1 should be at least 2. It is easy to prove that all the different column vectors of length v with entries from $\{0,1\}$ form the $(\overline{1},1)$-LA$(v;k,2)$ as desired. Thus, all that remains is to calculate the number of all the different column vectors. Write x and y as the number of 0s and 1s in a column vector of length v, respectively. Clearly, $x+y=v$ and $x\ge 2,y\ge 2$. Because there exist x positions with 0s, the number of different column vectors is $\left(\genfrac{}{}{0pt}{}{v}{x}\right)$. Consequently, the number of all the different column vectors is $\left(\genfrac{}{}{0pt}{}{v}{2}\right)+\cdots +\left(\genfrac{}{}{0pt}{}{v}{v-2}\right)=2^v-2v-2$. □

5. Concluding Remarks

LAs can be used to generate test suites for combinatorial testing and identify interaction faults in component-based systems. In this study, a lower bound on the size of $(\overline{1},t)$-LAs with mixed levels was determined. In addition, some constructions of $(\overline{1},t)$-LAs were proposed. Some of these constructions produce optimal locating arrays. Based on the constructions, some infinite series of optimal locating arrays satisfying the lower bound in Lemma 2 were presented. Obtaining new constructions for mixed-level $(\overline{1},t)$-LAs and providing more existence results are potential future research directions.