Abstract
The decision-making trial and evaluation laboratory (DEMATEL) method is one of the most significant multi-criteria techniques for defining the relationships among criteria and for defining the weight coefficients of criteria. Since multi-criteria models are very often used in management and decision-making under conditions of uncertainty, the fuzzy DEMATEL model has been extended in this paper by D numbers (fuzzy DEMATEL-D). The aim of this research was to develop a multi-criteria methodology that enables the objective processing of fuzzy linguistic information in the pairwise comparison of criteria. This aim was achieved through the development of the fuzzy DEMATEL-D method. Combining D numbers with trapezoidal fuzzy linguistic variables (LVs) allows for the additional processing of uncertainties and ambiguities that exist in experts’ preferences when comparing criteria with each other. In addition, the fuzzy DEMATEL-D methodology has a unique reasoning algorithm that allows for the rational processing of uncertainties when using fuzzy linguistic expressions for pairwise comparisons of criteria. The fuzzy DEMATEL-D methodology provides an original uncertainty management framework that is rational and concise. In order to illustrate the effectiveness of the proposed methodology, a case study with the application of the proposed multi-criteria methodology is presented.
1. Introduction
A dynamic environment in which almost all scientific and professional fields operate requires the timely and precise management of processes, which involves decision-making at its each stage. The decisions are made on the basis of a number of inputs that are an integration of qualitative and quantitative criteria. If a certain number of experts with their different preferences in group decision-making are added, the problem is complicated in multiple ways. Therefore, it is necessary to take into account all possible uncertainties that arise in group decision-making in order to gain better and more accurate output. Certainly, an extremely important stage in a decision-making process is determining the significance of the criteria by which the most acceptable solution or ranking of solutions is defined in a further process of solving multi-criteria problems. Therefore, the aim of this paper was to develop a new methodology for determining the significance of criteria that takes aspects of uncertainty and diversity in decision-makers’ preferences into account. Accordingly, an extension of the fuzzy decision-making trial and evaluation laboratory (DEMATEL) model is performed by D numbers (fuzzy DEMATEL-D), which is explained in detail in the following section. The DEMATEL method was developed by Gabus and Fontel [1], and it has thus far been widely applied in its basic or extended form, as confirmed in the study [2]. The authors carried out a comprehensive review of the literature published in a period of a decade in terms of developing various extensions of this method and its applications in different decision-making areas. Taking into account the evident wide application of this method and the need to adequately handle uncertain situations and determine the precise weights of criteria, fuzzy set theory is integrated with D numbers. In that way, an overall synergistic effect is achieved in decision-making processes.
Dempster–Shafer evidence theory [3,4] is an area of artificial intelligence because it processes and analyzes uncertainties and inaccuracies in information. It is also a convenient algorithm for reasoning in a dynamic and uncertain environment, which is recommended for use in expert systems. Since Dempster–Shafer evidence theory (DST) allows for the processing of nonspecific, ambiguous, and juxtaposed information, numerous researchers favor DST over traditional approaches, such as Bayesian probability theory [5,6]. In addition to the benefits that DST possesses for solving various real-world problems, such as network problems [7], decision-making problems [8,9,10], and risk theory [11], there are also limitations to DST that represent a kind of barrier to its wider application for solving real-world problems. One of the most well-known limitations that restricts the wider practical application of DST is the exclusivity of elements when parsing elements of a subset [12,13]. This limitation is shown through the following example. Giving a diagnosis in medicine is a typical area that includes different types of uncertainties [12]. Say there is patient with the symptoms of fever, polypnea, and cough; taking into account the mentioned cases, they are likely caused by the flu (F), bacterial (B) infection, or an upper respiratory infection (U). There are two independent diagnostic reports that were submitted by two doctors. The first doctor made a diagnosis that the patient got F with a possibility of 0.7 and B or U with a possibility of 0.2. The reminder 0.1 possibility is for an unknown diagnosis: . The second doctor made a diagnosis which showed: . The questions is: What disease does the patient have? The DST in this scenario would show following results: m (B) = 0.1304; m (B, U) = 0.058, and m (F, B, U) = 0.0290. It can be seen that there is an invisible hypothesis that the possibility of the unknown is equal to that of {F, B, U}. Based on the presented results, it can be concluded that the set of all diseases, which are manifested through the considered symptoms, can be presented as a set {F, B, U}. However, the set {F, B, U} contains only three types of diseases that are considered in this example. Obviously, this unseen hypothesis is not reasonable. Such a problem cannot be addressed by applying DST (Figure 1a) because DST implies the exclusivity of the elements, in our case being diagnosed diseases. This problem can be successfully eliminated by D numbers [12,13]. After the application of D numbers, D (F) = 0.6147 and D (B) = 0.1054 are obtained. The result shows that the patient having the flu is the highest probability. In comparison to DST, in the D numbers theory, the unknown is inherited during the reasoning.
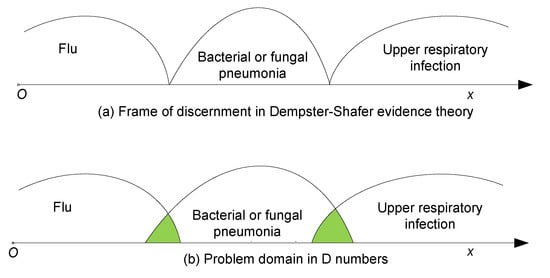
Figure 1.
The frame of discernment in Dempster–Shafer evidence theory (DST) and in D numbers.
D numbers, as a reliable and effective expression of uncertain information (and according to Xiao [14]), are good at handling these types of uncertainties. Deng and Jiang [15] developed a decision-making model to solve the adversarial problem under uncertainty with D numbers. Their model integrated fuzzy set theory, game theory, and D number theory (DNT). The same authors in [16] showed the advantages of using D numbers in green supply chain management in a fuzzy environment.
Overcoming the problem was recognized by Zhou et al. [17], who performed an integration of crisp DEMATEL and D numbers to identify the critical success factors (CSFs) in emergency management. The same method was applied in [18] for the risk identification and analysis of an energy power system. The advantages of the D-DEMATEL method are reflected when simultaneously considering ambiguities and subjectivity, which is impossible with classical approaches, as stated by Zhou et al. [17]. By developing an extension of the DEMATEL method with trapezoidal fuzzy numbers (TrFN) and D numbers in this paper, uncertainties are considered at a higher level with input parameters manifested through output functions.
In addition to the needs and aims presented in the introduction, the paper is has several other sections. Section 2 presents the preliminaries that outline the basics of D numbers and fuzzy theory. Section 3 is an extension of TrFN DEMATEL with D numbers, while Section 4 shows the application of the developed methodology with a specific example. Section 5 summarizes the contributions of the paper, with an overview of further research related to this paper.
2. Background
2.1. D Numbers
D numbers represent an extension of DST with the aim to present more effectively uncertainties in the information being processed. As shown in Figure 1b, D numbers do not require the exclusivity of the elements of a set, which significantly broadens the domain of the practical application of D numbers.
Definition 1
([12]). Let be a finite nonempty set, and a D number is a mapping that , with:
where ∅ is an empty set and A is any subset of . As stated in the previous section of the paper, the theory of D numbers does not require the elements of a set to be mutually exclusive. The information presented by D numbers is called complete information if the condition of is filled. If , the information is incomplete.
If is a discrete set of elements , where and (when ), then we can express D numbers by:
in addition to expressing D numbers using Equation (2), there is another simplified way to express D numbers: … , … . This presentation also satisfies the condition that and .
Definition 2
([12]). Let two D numbers and , … be given. Then, we can define the rule for the combination of D numbers as follows:
Rule (3) is a generalization of Dempster’s rule [8]. If D1 and D2 are defined in the frame of discernment and if and , then the rule of combining D numbers (Rule (3)) is transformed into Dempster’s rule. Rule (3) of numbers is an algorithm for the combination and fusion of uncertain information presented in D numbers.
For a discrete D number … , … , we can define the integration operator as follows:
where i .
2.2. Fuzzy Set Theory
Fuzzy set theory is widely used to model uncertainties [19,20,21,22,23]. In some decision-making models, qualitative assessments are given in natural language. These linguistic variables (LVs) can be presented by linguistic expressions [24,25,26].
Definition 3.
Let X crisp be a universe of generic elements containing a fuzzy set as a subset. For each element, let be a number ; then, we can call the number the grade of membership of x in [27].
Definition 4.
A fuzzy set of the universe of discourse X is convex if and only if for every element, , thus implying that:
where .
Definition 5.
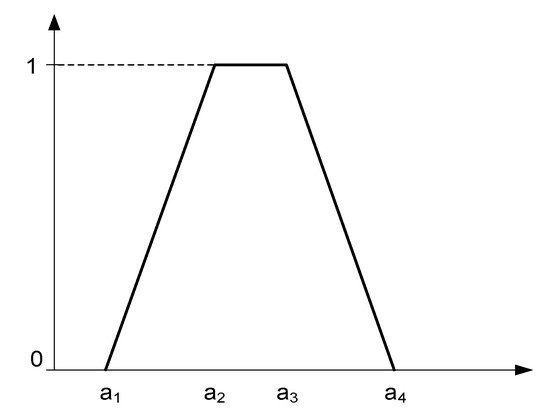
The trapezoidal fuzzy number can be defined as , as shown in Figure 2.

Figure 2.
Trapezoidal number membership function.
The concept of an LV is very appropriate in activities where the processing of complex or poorly defined information that cannot be well described by traditional quantitative formulations is needed. The LVs are expressed by words, sentences, or artificial languages. Each linguistic value can be presented by a fuzzy set [28]. Linguistic modelling permits experts to express themselves by labels belonging to a specific linguistic label set [29]. In this paper, experts’ preferences, according to different criteria, were considered as linguistic variables. LVs can be expressed by positive TrFN, shown in Table 1, as was the case in our study.

Table 1.
Linguistic variables.
Basic arithmetic operations with TrFN and are presented in the next section [30,31]:
- (1)
- Addition:
- (2)
- Multiplication:
- (3)
- Subtraction:
- (4)
- Division:
- (5)
- Reciprocal values:
3. TrFN DEMATEL-D Methodology
Due to the imprecision and subjectivity evident in group decision-making, an extension of the fuzzy DEMATEL methodology was made using D numbers. The use of D numbers makes it possible to: (1) take the uncertainties that exist in experts’ comparisons of criteria into account and (2) define the intervals of fuzzy linguistic expressions on the basis of uncertainties and inaccuracies that exist in experts’ judgment. Numerous multi-criteria models imply the introduction of fuzzy numbers to express the uncertainties that exist in group decision-making [32,33,34,35,36,37]. The introduction of D numbers makes it possible to take additional uncertainties that arise when selecting fuzzy linguistic variables from a predefined set into account. In addition to fuzzy linguistic variables, D numbers introduce the probability of choosing a fuzzy linguistic variable, thus increasing the objectivity and quality of existing data in group decision-making. Since it is a new extension of the fuzzy DEMATEL methodology by D numbers, the following section details the algorithm which includes six steps:
Step 1: Experts’ analysis of factors: Suppose that there are m experts divided into two homogeneous expert groups EG1 and EG2, and there are n criteria considered in a comparison matrix. Let the fuzzy linguistic variables used to compare the criteria be expressed by trapezoidal fuzzy numbers , where t represents the total number of fuzzy linguistic variables.
Each expert group defines the degree of influence of the criterion i on the criterion j. The comparative analysis of the pair of ith and jth criterion by the expert group is denoted by the D number
where and represent the D numbers used to express the preferences of EG1 and EG2, respectively, and t represents the number of fuzzy linguistic variables used to compare the criteria. As a result of the comparison, two nonnegative matrices of rank n×n are obtained, and each element of the matrix and represents a D number. The diagonal elements of the matrices and have a value of zero because the same factors have no effect. Thus, we can get one matrix and for each expert group.
Step 2: Forming a single fuzzy direct-relation matrix : The transformation of D matrices into a single matrix of fuzzy linguistic values is carried out through three phases.
Phase 1: In the first phase, the uncertainties presented in the initial experts’ preferences are fused. Accordingly, applying the rules for the combination of D numbers , (Equation (3)), the analysis and synthesis of the data provided by D numbers in expert matrices and are performed.
Phase 2: After implementing the rules for the combination of D numbers, the uncertainties presented at the intersection of fuzzy linguistic variables (FLVs) (Figure 3) are transformed into unique fuzzy linguistic variables.
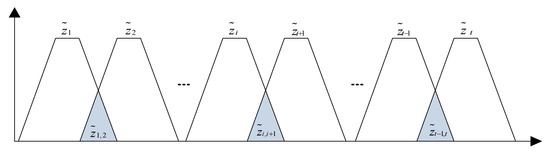
Figure 3.
Fuzzy linguistic variables.
We can define FLVs as the term-set , where is an FLV presented in and . Each term is presented as trapezoidal fuzzy number , i.e., , where and represent the middle points of the trapezoidal fuzzy number (TrFN), and and are the lower and upper limits, respectively, of the fuzzy interval.
FLV transformation is performed on the basis of the ratio of the surfaces located at the intersection and the corresponding area of the FLVs.
where represents the intersection between the linguistic variable and the linguistic variable , while and represent the area of the linguistic variable and , respectively.
After the FLV transformation, we can obtain a single D matrix .
Phase 3: The elements of the D matrix are transformed into a single fuzzy direct-relation matrix , where represents the elements of the matrix expressed by trapezoidal fuzzy numbers. The elements of the matrix are obtained by applying the operator of integration of D numbers (Equation (4)), i.e., , where e represents the number of FLVs contained in the D number.
Step 3: Computing the elements of a normalized fuzzy direct-relation matrix: After forming a single fuzzy direct-relation matrix by applying Equations (16) and (17), we can obtain the elements of the normalized fuzzy direct-relation matrix (Equation (15)).
where represents the normalized values of the matrix , which are obtained by applying Equations (16) and (17):
Step 4: Determining the fuzzy number-based total relation matrices: By applying Equations (18)–(20), we can obtain a total influence matrix , where is an identity matrix. Since the matrix is presented by trapezoidal fuzzy numbers, we can form four submatrices , where , , , and . In addition, , , , and , where represents the zero matrix.
The total relation fuzzy matrix T is obtained by computing each of the sub-elements:
where , , , and . Submatrices , , , and form the single fuzzy total relation matrix , which is presented as follows:
where is the total assessment of experts’ effect for each criterion i and criterion j, thus expressing their mutual influence and dependence.
Step 5: Computing the sum of rows and columns of the total relation matrix: Presented by vectors R and C of rank n × 1, Equations (21) and (22) are:
The value Ri represents the sum of the ith raw of the matrix T. The determined value presents the total direct and indirect effects that the criterion i provides for the other criteria. Meanwhile, the value of Ci represents the sum of the jth column of the matrix T and shows the effects that the criterion j receives from the other criteria [37].
Step 6. Determining the weight coefficients of the criterion (): This is achieved via Equation (23):
where the values and are obtained using Equations (24) and (25):
The normalization of the weight coefficients is carried out by Equation (26):
where n is the number of criteria and is the fuzzy values of the criteria weight. The values of the criteria weight are in the interval , where the condition is fulfilled for each evaluation criterion. However, the requirement that the sum of the weight coefficients of the criteria be generally equal to one must be fulfilled. Since these are fuzzy coefficients of criteria, using Equation (26) allows for the obtainment of the weight coefficients for which and . This fulfills the condition that the criteria weight are in the interval .
4. Application of TrFN D-DEMATEL Method
This section describes the application of the TrFN D-DEMATEL method for determining the quality of logistics services in order to obtain an adequate insight into the management processes of the service provider. The research by Prentkovskis et al. [38] was used to test the methodology presented. The dimensions that affect the measurement of logistics service quality were taken from the study [38], and they were evaluated using the TrFN D-DEMATEL methodology. There were five defined dimensions: reliability (C1), assurance (C2), tangibles (C3), empathy (C4), and responsiveness (C5). The study involved six experts who evaluated the dimensions. A detailed description of applying the TrFN D-DEMATEL methodology is presented in the following section.
Step 1: Experts’ analysis of factors.
Six experts participated in the study, and they were divided into two homogenous expert groups: EG1 and EG2. Expert groups expressed their preferences when comparing dimensions using a nine-degree fuzzy linguistic scale; see Table 1. Each expert group defined the mutual degree of influence of the criteria by D numbers; see Table 2.

Table 2.
Experts’ analysis of dimensions.
Table 2 shows the experts’ comparisons of dimensions using D numbers, where the D number D1 represents the experts’ preferences of the EG1 expert group and D2 represents the experts’ preferences of the EG2 expert group.
Step 2: Forming a single fuzzy direct-relation matrix.
Phase I: In order to obtain aggregated experts’ preferences, a fusion of the uncertainties expressed in the group experts’ preferences D1 and D2 is performed. For the uncertainty fusion, the rule for the combination of D numbers (Equation (3)) is used. Thus, an aggregated D matrix of experts’ preferences is obtained; see Table 3.

Table 3.
Aggregated D matrix of experts’ preferences.
In order to clarify the application of the rules for combining D numbers, the following section shows the application of the rules for the combination of D numbers for position C2−C1 in the experts’ analysis of dimensions (Table 2).
Based on the data in Table 2, for position C2–C1, we can distinguish two D numbers that represent the experts’ preferences of homogeneous expert groups: D1 = {(VH,0.2), (VH;EH,0.35), (EH,0.4)} (where VH is ‘very high’ and EH is ‘extremely high’) and D2 = {(VH,0.25), (VH;EH,0.45), (EH,0.1)}. Table 4 provides an analysis of the data on D numbers whose combination was considered, .

Table 4.
Intersection table to combine and .
By applying Equation (4), we can calculate the relationships defined by the rule for the combination of D numbers.
Thus, we can obtain:
Phase II: After applying the rule for the combination of D numbers, we can obtain a D number located between the fuzzy linguistic variables VH and EH, and so it is necessary to transform the uncertainty found between the fuzzy variables VH and EH into unique FLVs. The transformation of uncertainty is performed by applying Equations (13) and (14). The following section presents the procedure for the transformation of uncertainty between the fuzzy variables VH and EH. A graphical display of the fuzzy linguistic variables VH and EH is given in Figure 4.
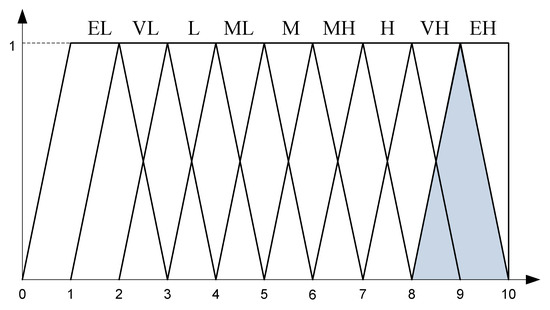
Figure 4.
Fuzzy linguistic variables VH (very high) and EH (extremely high).
The transformation of FLVs is performed on the basis of the ratio of the surfaces located at the intersection and the area that covers the fuzzy variables VH and EH, i.e., and . Using Equations (13) and (14), we can obtain finite values of D numbers for the fuzzy variables VH and EH:
Thus, we can obtain D number DC2−C1 = {(VH,0.350), (EH,0.410)} which is in the first position C2−C1. The remaining values of the aggregated D matrix of experts’ preferences are obtained in a similar way (Table 3).
Phase III: Using Equation (4), the values of the aggregated D matrix of experts’ preferences are integrated into the corresponding fuzzy values; see Table 5. By this procedure, the uncertainties expressed by D numbers are transformed into unique trapezoidal fuzzy numbers.

Table 5.
Single fuzzy direct-relation matrix.
Using Equations (4), (7), and (8), the element C2−C1 of the single fuzzy direct-relation matrix (Table 5) is obtained as follows:
Similarly, we can obtain the remaining elements of the single fuzzy direct-relation matrix (Table 5).
Steps 3 and 4: Computing the elements of the normalized fuzzy direct-relation matrix and total fuzzy influence matrix.
By applying Equations (16) and (17), we can obtain the elements of the normalized fuzzy direct-relation matrix; see Table 6.

Table 6.
Normalized fuzzy direct-relation matrix.
In the next step, by using Equations (18)–(20), we can obtain the total influence matrix ; see Table 7.

Table 7.
Total fuzzy influence matrix.
Steps 5 and 6: Computing the sum of rows and columns of the fuzzy total relation matrix and determining the optimal values of the weight coefficients of dimensions.
The optimal values of the weight coefficients of dimensions are defined on the basis of the total direct/indirect effects that the criterion i provides for other criteria (Ri) and the total direct/indirect effects that the criterion j receives from other criteria (Ci). The values of Ri and Ci are obtained by using Equations (21) and (22). After calculating the values of Ri and Ci (Table 8), we can obtain the optimal values of the dimensions by using Equations (23)–(26).

Table 8.
Ranking the weight coefficients of the dimensions.
The final values of the weight coefficients of the dimensions are: reliability (w1 = 0.226), assurance (w2 = 0.211), tangibles (w3 = 0.213), empathy (w4 = 0.160), and responsiveness (w5 = 0.190). Based on presented results, we can define the final ranking as C1 > C3 > C2 > C5 > C4.
Compared to crisp DEMATEL, the proposed method has two main advantages. The first advantage of proposed model is the elimination of disadvantage in the DST where the elements in the frame of discernment are required to be independent. While both evidence DEMATEL [39] and DEMATEL-D can decrease the subjectivity of expert preferences, the DST is not very applicable for the presentation of linguistic estimates in conditions where it is required that the elements within the distinction must be mutually exclusive. As shown In Figure 1a, the variables must have boundaries in DST. However, it was found that this demand is difficult to be satisfied for LVs such as “F”, “B”, and “U”. As shown in Figure 1b, the D numbers theory overcomes this poorness and permit overlap between LVs, which makes it more applicable for linguistic assessments. Furthermore, in DST, the sum of basic probability assignment must present the complete information, i.e., the sum of probability must be 1. However, in the D numbers theory, the information can be incomplete, which is more practical and realistic.
The second advantage of proposed DEMATEL-D model is related to reducing experts subjectivity. Even though both fuzzy DEMATEL [40] and the TrFN DEMATEL consider fuzziness, the developed method is more objective than fuzzy DEMATEL because it can reduce the impact of expert subjectivity by fusing group opinions.
The precedence of the D numbers theory is the ability to integrate group information. Therefore, in order to perform the verification and validity of the developed method, this study computed the result in each expert group and compared the opinions of these two expert groups with the final result, as shown in Table 8. In these three cases (the first group, the second group, and the aggregated values), C1 was the most significant element but the ranking of the other elements was quite various, thus showing that the final rank was sensitive to the knowledge of experts. Consequently, the need for the integration of expert information in various fields using the D numbers theory has been shown.
The D numbers theory is used to fuse the expert preferences in decision-making processes. Therefore, it is reasonable to expect the aggregate values to be close to the values represented by the expert preferences. The final values of the criteria obtained using the DEMATEL-D model in this study were between the results that have been proposed through expert evaluations. This shows us that the proposed model respects the uncertainties that exist in group decision-making and that the model gives results that are valid and reasonable.
5. Conclusions
In this paper, the fuzzy DEMATEL methodology was expanded by D numbers to overcome uncertainties and subjectivities that are inevitable in group decision-making processes, especially with numerous decision-makers. The integration of fuzzy DEMATEL with D numbers allows for the consideration of uncertainties that exist in experts’ comparisons of criteria, and that the intervals of fuzzy linguistic expressions are defined based on the uncertainties and imprecision that exist in experts’ judgment. The introduction of D numbers makes it possible to take the additional uncertainties that arise when selecting fuzzy linguistic variables from a predefined set into account. D numbers, in addition to fuzzy linguistic variables, introduce the probability of choosing a fuzzy linguistic variable, thus increasing the objectivity and quality of existing data in group decision-making. This can be proven, for example, by determining the quality of logistics services in order to obtain an adequate insight into the management processes. Considering that this is a new extension of the fuzzy DEMATEL method by D numbers, which was demonstrated on a real study, it can be concluded that there is a justification for the development of the presented methodology. Future research may be based on the greater application of MCDM methods and D numbers. In addition, it is possible to integrate rough numbers with D numbers, which could provide a more comprehensive concept for managing decision-making processes.
Author Contributions
Conceptualization, I.P. and Ž.S.; methodology, I.P.; D.P., and Ž.S.; validation, S.D. and D.K.D.; writing—original draft preparation, D.P and O.M.; writing—review and editing, D.K.D. and S.D.; supervision, Ž.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gabus, A.; Fontela, E. World Problems, an Invitation to Further Thought within the Framework of DEMATEL; Battelle Geneva Research Centre: Geneva, Switzerland, 1972. [Google Scholar]
- Si, S.L.; You, X.Y.; Liu, H.C.; Zhang, P. DEMATEL technique: A systematic review of the state-of-the-art literature on methodologies and applications. Math. Probl. Eng. 2018, 1, 1–33. [Google Scholar] [CrossRef]
- Dempster, A.P. Upper and lower probabilities induced by a multivalued mapping. Ann. Math. Stat. 1967, 38, 325–339. [Google Scholar] [CrossRef]
- Shafer, G. A mathematical theory of evidence. Technometrics 1978, 20, 242. [Google Scholar]
- Yang, J.; Huang, H.-Z.; He, L.-P.; Zhu, S.-P.; Wen, D. Risk evaluation in failure mode and effects analysis of aircraft turbine rotor blades using Dempster-Shafer evidence theory under uncertainty. Eng. Fail. Anal. 2011, 18, 2084–2092. [Google Scholar] [CrossRef]
- Xiao, F. A novel multi-criteria decision making method for assessing health-care waste treatment technologies based on D numbers. Eng. Appl. Artif. Intell. 2018, 71, 216–225. [Google Scholar] [CrossRef]
- Kang, B.; Deng, Y.; Sadiq, R.; Mahadevan, S. Evidential cognitive maps. Knowl. Based Syst. 2012, 35, 77–86. [Google Scholar] [CrossRef]
- Ju, Y.; Wang, A. Emergency alternative evaluation under group decision makers: A method of incorporating DS/AHP with extended TOPSIS. Expert Syst. Appl. 2012, 39, 1315–1323. [Google Scholar] [CrossRef]
- Ma, W.; Xiong, W.; Luo, X. A model for decision making with missing, imprecise, and uncertain evaluations of multiple criteria. Int. J. Intell. Syst. 2013, 28, 152–184. [Google Scholar] [CrossRef]
- Fei, L.; Deng, Y.; Hu, Y. DS-VIKOR: A new multi-criteria decision-making method for supplier selection. Int. J. Fuzzy Syst. 2019, 21, 157–175. [Google Scholar] [CrossRef]
- Sadiq, R.; Kleiner, Y.; Rajani, B. Estimating risk of contaminant intrusion in water distribution networks using Dempster–Shafer theory of evidence. Civ. Eng. Environ. Syst. 2006, 23, 129–141. [Google Scholar] [CrossRef]
- Deng, X.; Hu, Y.; Deng, Y.; Mahadevan, S. Environmental impact assessment based on D numbers. Expert Syst. Appl. 2014, 41, 635–643. [Google Scholar] [CrossRef]
- Deng, X.; Hu, Y.; Deng, Y. Bridge condition assessment using D numbers. Sci. World J. 2014, 2014, 358057. [Google Scholar] [CrossRef] [PubMed]
- Xiao, F. A multiple-criteria decision-making method based on D numbers and belief entropy. Int. J. Fuzzy Syst. 2019, 21, 1144–1153. [Google Scholar] [CrossRef]
- Deng, X.; Jiang, W. D number theory based game-theoretic framework in adversarial decision making under a fuzzy environment. Int. J. Approx. Reason. 2019, 106, 194–213. [Google Scholar] [CrossRef]
- Deng, X.; Jiang, W. Evaluating green supply chain management practices under fuzzy environment: A novel method based on D number theory. Int. J. Fuzzy Syst. 2019, 21, 1389–1402. [Google Scholar] [CrossRef]
- Zhou, X.; Shi, Y.; Deng, X.; Deng, Y. D-DEMATEL: A new method to identify critical success factors in emergency management. Saf. Sci. 2017, 91, 93–104. [Google Scholar] [CrossRef]
- Lin, S.; Li, C.; Xu, F.; Liu, D.; Liu, J. Risk identification and analysis for new energy power system in China based on D numbers and decision-making trial and evaluation laboratory (DEMATEL). J. Clean. Prod. 2018, 180, 81–96. [Google Scholar] [CrossRef]
- Karabašević, D.; Popović, G.; Stanujkić, D.; Maksimović, M.; Sava, C. An approach for hotel type selection based on the single-valued intuitionistic fuzzy numbers. Int. Rev. 2019, 1–2, 7–14. [Google Scholar] [CrossRef]
- Stojić, G.; Sremac, S.; Vasiljković, I. A fuzzy model for determining the justifiability of investing in a road freight vehicle fleet. Oper. Res. Eng. Sci. Theory Appl. 2018, 1, 62–75. [Google Scholar] [CrossRef]
- Stankovic, M.; Stevic, Z.; Das, D.K.; Subotic, M.; Pamucar, D. A New Fuzzy MARCOS Method for Road Traffic Risk Analysis. Mathematics 2020, 8, 457. [Google Scholar] [CrossRef]
- Petrović, G.; Mihajlović, J.; Ćojbašić, Ž.; Madić, M.; Marinković, D. Comparison of three fuzzy MCDM methods for solving the supplier selection problem. Facta Univ. Ser. Mech. Eng. 2019, 17, 455–469. [Google Scholar] [CrossRef]
- Vesković, S.; Milinković, S.; Abramović, B.; Ljubaj, I. Determining criteria significance in selecting reach stackers by applying the fuzzy PIPRECIA method. Oper. Res. Eng. Sci. Theory Appl. 2020, 3, 72–88. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning II. Inf. Sci. 1975, 8, 301–357. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning-III. Inf. Sci. 1975, 9, 43–80. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Zimmermann, H. Fuzzy Set Theory and Its Applications; Kluwer: Boston, MA, USA, 1991. [Google Scholar]
- Morente-Molinera, J.A.; Wu, X.; Morfeq, A.; Al-Hmouz, R.; Herrera-Viedma, E. A novel multi-criteria group decision-making method for heterogeneous and dynamic contexts using multi-granular fuzzy linguistic modelling and consensus measures. Inf. Fusion 2020, 53, 240–250. [Google Scholar] [CrossRef]
- Wel, S.H.; Chen, S.M. A new approach for fuzzy risk analysis based on similarity. Expert Syst. Appl. 2009, 36, 589–598. [Google Scholar]
- Rao, P.P.B.; Ravi Shankar, N. Ranking Generalized Fuzzy Numbers using Area, Mode, Spreads and Weights. Int. J. Appl. Sci. Eng. 2012, 10, 41–57. [Google Scholar]
- Pamucar, D.; Mihajlović, M.; Obradović, R.; Atanasković, P. Novel approach to group multi-criteria decision making based on interval rough numbers: Hybrid DEMATEL-ANP-MAIRCA model. Expert Syst. Appl. 2017, 88, 58–80. [Google Scholar] [CrossRef]
- Chatterjee, K.; Pamucar, D.; Zavadskas, E.K. Evaluating the performance of suppliers based on using the R’AMATEL-MAIRCA method for green supply chain implementation in electronics industry. J. Clean. Prod. 2018, 184, 101–129. [Google Scholar] [CrossRef]
- Roy, J.; Adhikary, K.; Kar, S.; Pamucar, D. A rough strength relational DEMATEL model for analysing the key success factors of hospital service quality. Decis. Mak. Appl. Manag. Eng. 2018, 1, 121–142. [Google Scholar] [CrossRef]
- Liu, F.; Aiwu, G.; Lukovac, V.; Vukic, M. A multicriteria model for the selection of the transport service provider: A single valued neutrosophic DEMATEL multicriteria model. Decis. Mak. Appl. Manag. Eng. 2018, 1, 121–130. [Google Scholar] [CrossRef]
- Chatterjee, P.; Stević, Ž. A two-phase fuzzy AHP-fuzzy TOPSIS model for supplier evaluation in manufacturing environment. Oper. Res. Eng. Sci. Theory Appl. 2019, 2, 72–90. [Google Scholar] [CrossRef]
- Pamučar, D.; Božanić, D.; Lukovac, V.; Komazec, N. Normalized weighted geometric Bonferroni mean operator of interval rough numbers—Application in interval rough DEMATEL-COPRAS. Facta Univ. Ser. Mech. Eng. 2018, 16, 171–191. [Google Scholar] [CrossRef]
- Prentkovskis, O.; Erceg, Ž.; Stević, Ž.; Tanackov, I.; Vasiljević, M.; Gavranović, M. A New Methodology for Improving Service Quality Measurement: Delphi-FUCOM-SERVQUAL Model. Symmetry 2018, 10, 757. [Google Scholar] [CrossRef]
- Li, Y.; Hu, Y.; Zhang, X.; Deng, Y.; Mahadevan, S. An evidential DEMATEL method to identify critical success factors in emergency management. Appl. Soft Comput. 2014, 22, 504–510. [Google Scholar] [CrossRef]
- Pamučar, D.; Ćirović, G. The selection of transport and handling resources in logistics centres using Multi-Attributive Border Approximation area Comparison (MABAC). Expert Syst. Appl. 2015, 42, 3016–3028. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).