Exact Traveling and Nano-Solitons Wave Solitons of the Ionic Waves Propagating along Microtubules in Living Cells
Abstract
1. Introduction
2. Application
2.1. Explicit Analytical Wave Solutions
2.2. Semi-Analytical Wave Solutions
3. Results and Discussion
- The modified Riccati expansion method and Adomian decomposition method were applied to the weakly nonlinear shallow water wave equation for constructing the exact traveling and semi-analytical wave solutions. These methods are considered as recent schemes in this field and they were not applied to this model previously.
- Figure 1 shows the breath wave solution Equation (16) in the three-dimensional plot (a) to illustrate the perspective view of the solution, the two-dimensional plot (b) to present the wave propagation pattern of the wave along x-axis, and the contour plot (c) to explain the overhead view of the solution when .
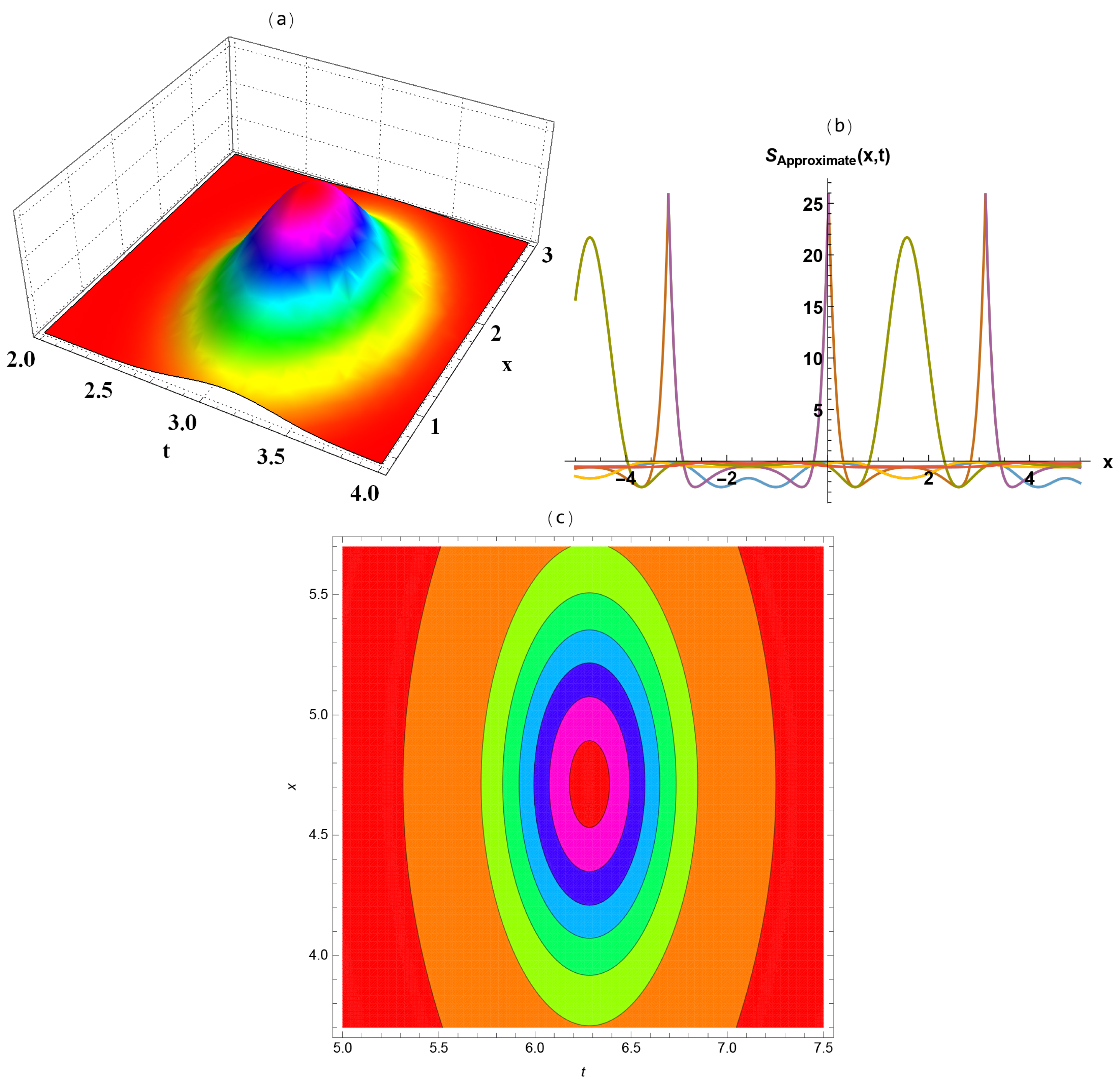
- Figure 2 shows the kink wave solution Equation (20) in the three-dimensional plot (a) to clarify the perspective view of the solution, the two-dimensional plot (b) to illustrate the wave propagation pattern of the wave along x-axis, and the contour plot (c) to exhibit the overhead view of the solution when .
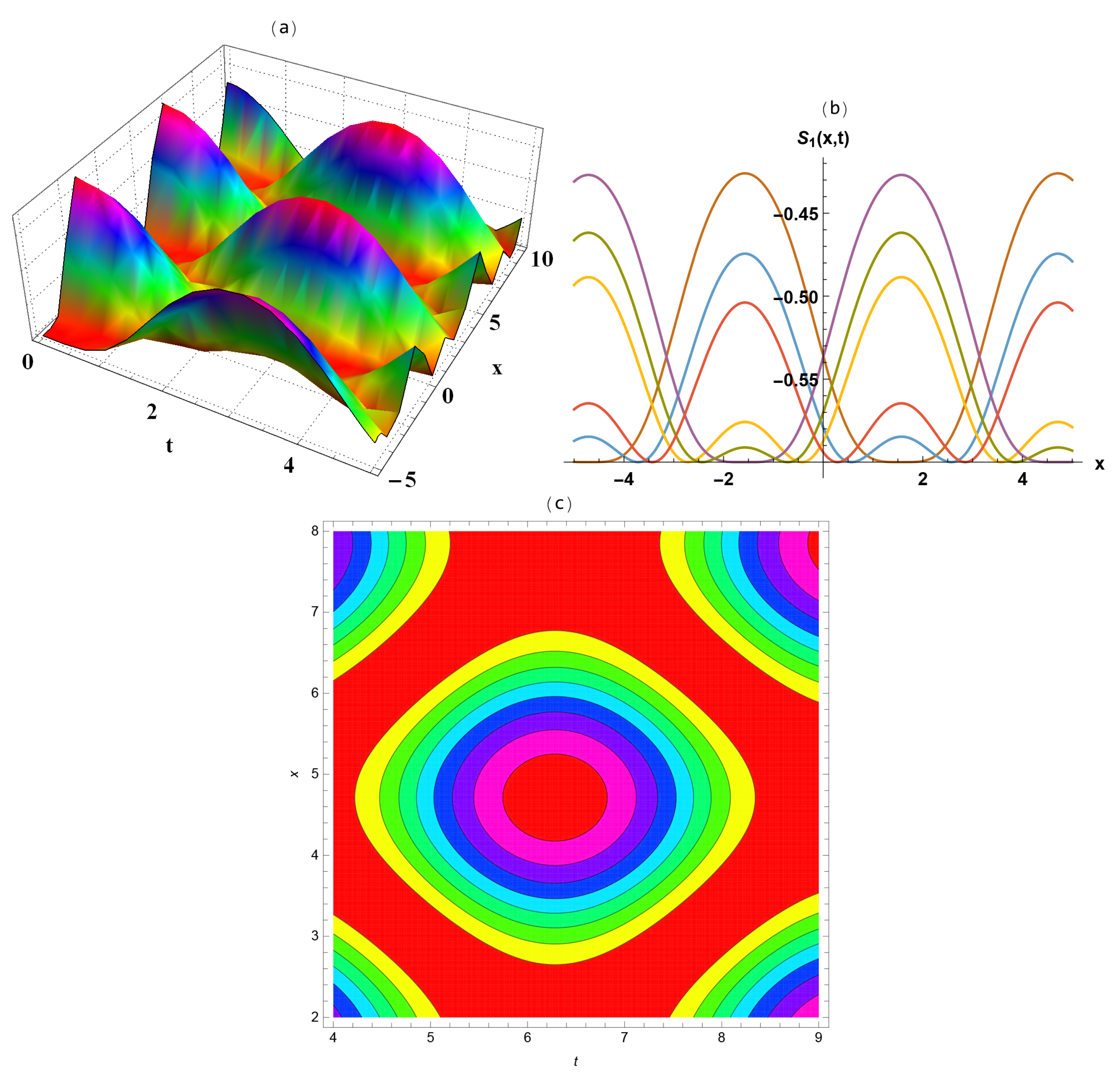
- Figure 3 shows the periodic-wave solution Equation (24) in the three-dimensional plot (a) to exalt the perspective view of the solution, the two-dimensional plot (b) to exhibit the wave propagation pattern of the wave along x-axis, and the contour plot (c) to explain the overhead view of the solution when .
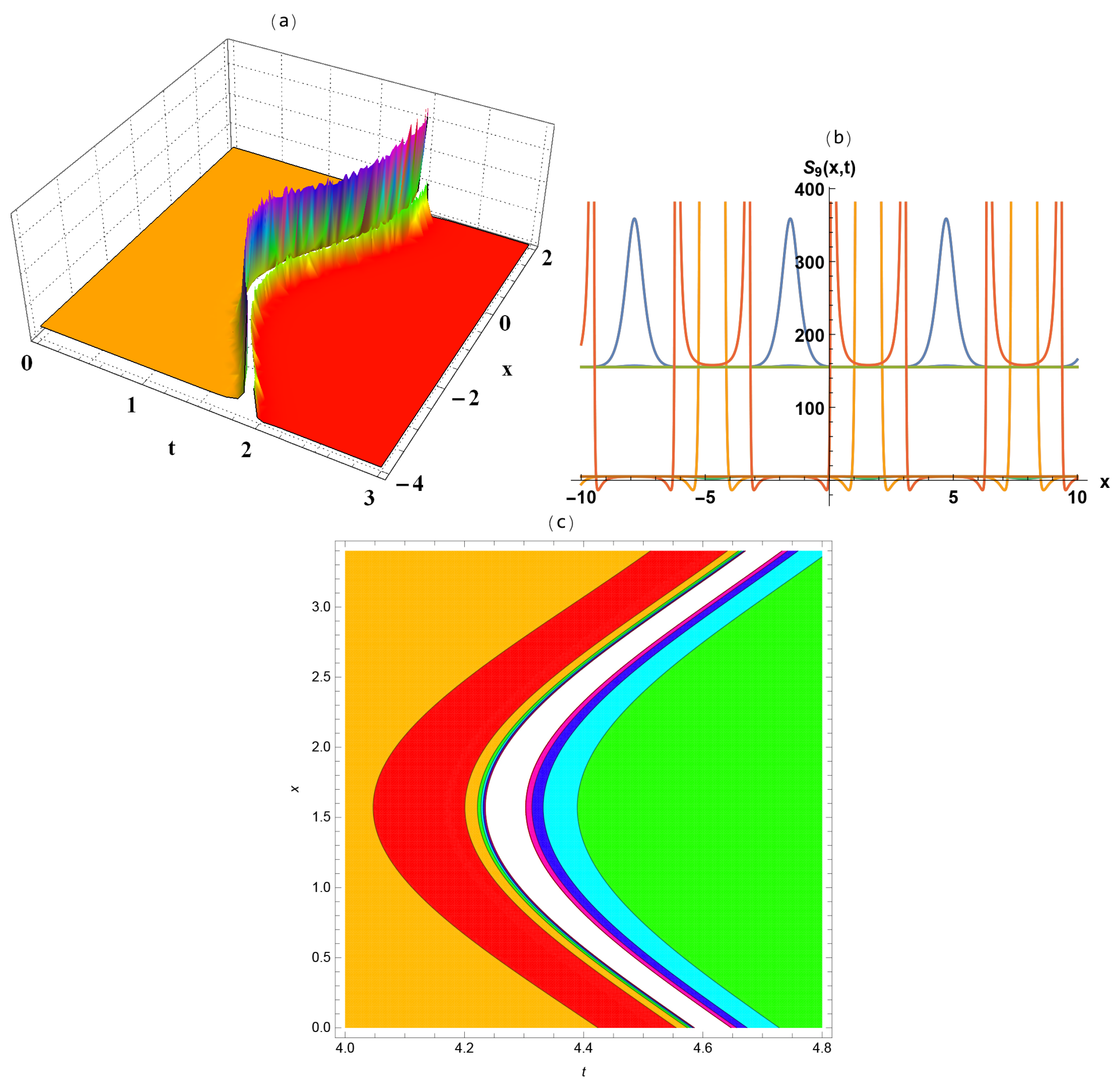
- Figure 4 shows the cone-wave solution Equation (30) in the three-dimensional plot (a) to illustrate the perspective view of the solution, the two-dimensional plot (b) to explain the wave propagation pattern of the wave along x-axis, and the contour plot (c) to clarify the overhead view of the solution when .
- Table 1 shows the accuracy of the obtained analytical where the absolute value of error between analytical and semi-analytical solutions are imperceptible.
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Brinks, R.; Hoyer, A. Illness-death model: Statistical perspective and differential equations. Lifetime Data Anal. 2018, 24, 743–754. [Google Scholar] [CrossRef] [PubMed]
- Mellit, A.; Eleuch, H.; Benghanem, M.; Elaoun, C.; Pavan, A.M. An adaptive model for predicting of global, direct and diffuse hourly solar irradiance. Energy Convers. Manag. 2010, 51, 771–782. [Google Scholar] [CrossRef]
- Barfield, M.; Martcheva, M.; Tuncer, N.; Holt, R.D. Backward bifurcation and oscillations in a nested immuno-eco-epidemiological model. J. Biol. Dyn. 2018, 12, 51–88. [Google Scholar] [CrossRef]
- Xu, Z.; Chow, K. Breathers and rogue waves for a third order nonlocal partial differential equation by a bilinear transformation. Appl. Math. Lett. 2016, 56, 72–77. [Google Scholar] [CrossRef]
- Lin, Y.; Gao, J. Research on Diffusion Effect of Ecological Population Model Based on Delay Differential Equation. Caribb. J. Sci. 2019, 52, 333–335. [Google Scholar]
- He, Z.; Han, Z.; Yuan, J.; Sinyukov, A.M.; Eleuch, H.; Niu, C.; Zhang, Z.; Lou, J.; Hu, J.; Voronine, D.V.; et al. Quantum plasmonic control of trions in a picocavity with monolayer WS2. Sci. Adv. 2019, 5, eaau8763. [Google Scholar] [CrossRef]
- Cheemaa, N.; Seadawy, A.R.; Chen, S. Some new families of solitary wave solutions of the generalized Schamel equation and their applications in plasma physics. Eur. Phys. J. Plus 2019, 134, 117. [Google Scholar] [CrossRef]
- Granados, S.; Salazar, M.; Toral, R.; Tavera, R.; Velázquez, A.; Hernández, L.; Cid, R.; López, G.; González, R. Pressure wave equation far from thermodynamics equilibrium. J. Phys. Conf. Ser. 2019, 1221, 012055. [Google Scholar] [CrossRef]
- Odashima, M.M.; Prado, B.G.; Vernek, E. Pedagogical introduction to equilibrium Green’s functions: Condensed-matter examples with numerical implementations. Revista Brasileira de Ensino de Física 2017, 39. [Google Scholar] [CrossRef]
- Newell, A. Nonlinear Optics; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Baudouin, L.; Rondepierre, A.; Neild, S. Robust control of a cable from a hyperbolic partial differential equation model. IEEE Trans. Control Syst. Technol. 2018, 27, 1343–1351. [Google Scholar] [CrossRef]
- Laskin, N. Nonlocal quantum mechanics: Fractional calculus approach. Appl. Phys. 2019, 207–236. [Google Scholar] [CrossRef]
- Vallejos, P.; Johnson, T.; Hellsten, T. Modeling RF waves in spatially dispersive inhomogeneus plasma using an iterative wavelet spectral method. In EPJ Web of Conferences; EDP Sciences: Les Ulis, France, 2017; Volume 157, p. 03059. [Google Scholar]
- Shao, L.; Guo, X.; Liu, S.; Zheng, G. Effective Stress and Equilibrium Equation for Soil Mechanics; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Rezazadeh, H.; Kumar, D.; Neirameh, A.; Eslami, M.; Mirzazadeh, M. Applications of three methods for obtaining optical soliton solutions for the Lakshmanan–Porsezian–Daniel model with Kerr law nonlinearity. Pramana 2020, 94, 39. [Google Scholar] [CrossRef]
- Mirhosseini-Alizamini, S.M.; Rezazadeh, H.; Eslami, M.; Mirzazadeh, M.; Korkmaz, A. New extended direct algebraic method for the Tzitzica type evolution equations arising in nonlinear optics. Comput. Methods Differ. Equ. 2020, 8, 28–53. [Google Scholar]
- Souleymanou, A.; Korkmaz, A.; Rezazadeh, H.; Mukam, S.P.T.; Bekir, A. Soliton solutions in different classes for the Kaup–Newell model equation. Mod. Phys. Lett. B 2020, 34, 2050038. [Google Scholar] [CrossRef]
- Attia, R.A.; Lu, D.; Ak, T.; Khater, M.M. Optical wave solutions of the higher-order nonlinear Schrödinger equation with the non-Kerr nonlinear term via modified Khater method. Mod. Phys. Lett. B 2020, 34, 2050044. [Google Scholar] [CrossRef]
- Khater, M.M.; Park, C.; Abdel-Aty, A.H.; Attia, R.A.; Lu, D. On new computational and numerical solutions of the modified Zakharov–Kuznetsov equation arising in electrical engineering. Alex. Eng. J. 2020. [Google Scholar] [CrossRef]
- Khater, M.M.; Attia, R.A.; Abdel-Aty, A.H.; Abdou, M.; Eleuch, H.; Lu, D. Analytical and semi-analytical ample solutions of the higher-order nonlinear Schrödinger equation with the non-Kerr nonlinear term. Results Phys. 2020, 16, 103000. [Google Scholar] [CrossRef]
- Park, C.; Khater, M.M.; Attia, R.A.; Alharbi, W.; Alodhaibi, S.S. An explicit plethora of solution for the fractional nonlinear model of the low-pass electrical transmission lines via Atangana–Baleanu derivative operator. Alex. Eng. J. 2020. [Google Scholar] [CrossRef]
- Khater, M.M.; Attia, R.A.; Baleanu, D. Abundant new solutions of the transmission of nerve impulses of an excitable system. Eur. Phys. J. Plus 2020, 135, 1–12. [Google Scholar] [CrossRef]
- Yue, C.; Khater, M.M.; Attia, R.A.; Lu, D. The plethora of explicit solutions of the fractional KS equation through liquid–gas bubbles mix under the thermodynamic conditions via Atangana–Baleanu derivative operator. Adv. Differ. Equ. 2020, 2020, 1–12. [Google Scholar] [CrossRef]
- Khater, M.M.; Park, C.; Lu, D.; Attia, R.A. Analytical, semi-analytical, and numerical solutions for the Cahn–Allen equation. Adv. Differ. Equ. 2020, 2020, 1–12. [Google Scholar] [CrossRef]
- Qin, H.; Khater, M.; Attia, R.A.; Lu, D. Approximate Simulations for the Non-linear Long-Short Wave Interaction System. Front. Phys. 2020, 7, 230. [Google Scholar] [CrossRef]
- Khater, M.; Attia, R.A.; Lu, D. Computational and numerical simulations for the nonlinear fractional Kolmogorov–Petrovskii–Piskunov (FKPP) equation. Phys. Scr. 2020, 95, 055213. [Google Scholar] [CrossRef]
- Qin, H.; Attia, R.A.; Khater, M.; Lu, D. Ample soliton waves for the crystal lattice formation of the conformable time-fractional (N + 1) Sinh-Gordon equation by the modified Khater method and the Painlevé property. J. Intell. Fuzzy Syst. 2020, 38, 2745–2752. [Google Scholar] [CrossRef]
- Khater, M.M.; Lu, D.; Attia, R.A. Dispersive long wave of nonlinear fractional Wu-Zhang system via a modified auxiliary equation method. AIP Adv. 2019, 9, 025003. [Google Scholar] [CrossRef]
- Attia, R.A.; Lu, D.; MA Khater, M. Chaos and relativistic energy-momentum of the nonlinear time fractional Duffing equation. Math. Comput. Appl. 2019, 24, 10. [Google Scholar] [CrossRef]
- Liang, J.F.; Wang, X. Investigation of Interaction Solutions for Modified Korteweg-de Vries Equation by Consistent Riccati Expansion Method. Math. Probl. Eng. 2019, 2019. [Google Scholar] [CrossRef]
- Liang, J.; Wang, X. Consistent Riccati expansion for finding interaction solutions of (2 + 1)-dimensional modified dispersive water-wave system. Math. Methods Appl. Sci. 2019, 42, 6131–6138. [Google Scholar] [CrossRef]
- Zhao, Z. Bäcklund transformations, rational solutions and soliton-cnoidal wave solutions of the modified Kadomtsev–Petviashvili equation. Appl. Math. Lett. 2019, 89, 103–110. [Google Scholar] [CrossRef]
- Thiam, L.; Liu, X.Z. Residual Symmetry Reduction and Consistent Riccati Expansion to a Nonlinear Evolution Equation. Complexity 2019, 2019. [Google Scholar] [CrossRef]
- Chen, J.; Ma, Z. Consistent Riccati expansion solvability and soliton-cnoidal wave interaction solution of a (2 + 1)-dimensional Korteweg–de Vries equation. Appl. Math. Lett. 2017, 64, 87–93. [Google Scholar] [CrossRef]
- Bakodah, H.; Al Qarni, A.; Banaja, M.; Zhou, Q.; Moshokoa, S.P.; Biswas, A. Bright and dark Thirring optical solitons with improved Adomian decomposition method. Optik 2017, 130, 1115–1123. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Parametrized Adomian decomposition method with optimum convergence. ACM Trans. Model. Comput. Simul. (TOMACS) 2017, 27, 1–22. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Determination of the correct range of physical parameters in the approximate analytical solutions of nonlinear equations using the Adomian decomposition method. Mediterr. J. Math. 2016, 13, 4019–4037. [Google Scholar] [CrossRef]
- Nouri, K. Study on efficiency of the Adomian decomposition method for stochastic differential equations. Int. J. Nonlinear Anal. Appl. 2017, 8, 61–68. [Google Scholar]
- Keskin, A.Ü. Adomian decomposition method (ADM). In Boundary Value Problems for Engineers; Springer: Berlin/Heidelberg, Germany, 2019; pp. 311–359. [Google Scholar]
- Satarić, M.V.; Dragić, M.S.; Sekulić, D.L. From giant ocean solitons to cellular ionic nano-solitons. Rom. Rep. Phys. 2011, 63, 624–640. [Google Scholar]
- Gui, G.; Liu, Y.; Sun, J. A nonlocal shallow-water model arising from the full water waves with the Coriolis effect. J. Math. Fluid Mech. 2019, 21, 27. [Google Scholar] [CrossRef]
- Slunyaev, A.; Ezersky, A.; Mouaze, D.; Chokchai, W. Standing Gravity Wave Regimes in a Shallow-Water Resonator. In Nonlinear Waves and Pattern Dynamics; Springer: New York, NY, USA, 2018; pp. 63–75. [Google Scholar]
- Quirchmayr, R. A new highly nonlinear shallow water wave equation. J. Evol. Equ. 2016, 16, 539–567. [Google Scholar] [CrossRef]
- Zahran, E.H. Exact traveling wave solutions for Nano-solitons of Ionic waves propagation along Microtubules in living cells and Nano-Ionic currents of MTs. World J. Nano Sci. Eng. 2015, 5, 78–87. [Google Scholar] [CrossRef][Green Version]
- Khater, M.M.A.; Seadawy, A.R.; Lu, D. New and more general exact and approximate solutions for the model of weakly nonlinear shallow water wave regime. Results Phys. 2019. submitted. [Google Scholar]

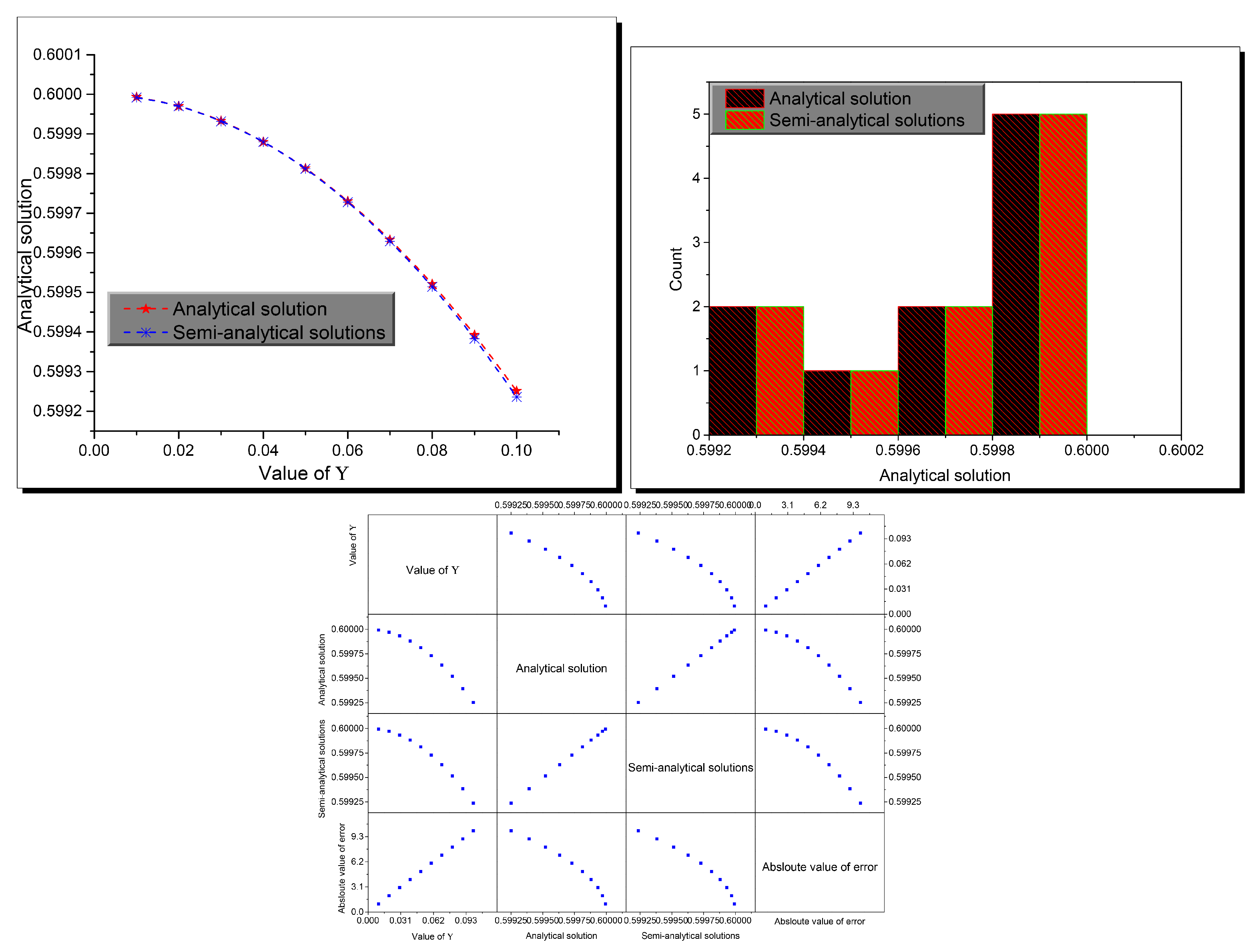
| Value of Y | Analytical Solution | Semi-Analytical Solutions | Absloute Value of Error |
|---|---|---|---|
| 0.01 | 0.599993 | 0.599992 | 1.49999 × |
| 0.02 | 0.59997 | 0.59997 | 2.3999 × |
| 0.03 | 0.599933 | 0.599932 | 1.21489 × |
| 0.04 | 0.59988 | 0.59988 | 3.83938 × |
| 0.05 | 0.599813 | 0.599812 | 9.37265 × |
| 0.06 | 0.59973 | 0.599728 | 1.9433 × |
| 0.07 | 0.599633 | 0.599629 | 3.59973 × |
| 0.08 | 0.599521 | 0.599514 | 6.14005 × |
| 0.09 | 0.599393 | 0.599383 | 9.83348 × |
| 0.1 | 0.599251 | 0.599236 | 1.49849 × |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdel-Aty, A.-H.; Khater, M.M.A.; Attia, R.A.M.; Eleuch, H. Exact Traveling and Nano-Solitons Wave Solitons of the Ionic Waves Propagating along Microtubules in Living Cells. Mathematics 2020, 8, 697. https://doi.org/10.3390/math8050697
Abdel-Aty A-H, Khater MMA, Attia RAM, Eleuch H. Exact Traveling and Nano-Solitons Wave Solitons of the Ionic Waves Propagating along Microtubules in Living Cells. Mathematics. 2020; 8(5):697. https://doi.org/10.3390/math8050697
Chicago/Turabian StyleAbdel-Aty, Abdel-Haleem, Mostafa M. A. Khater, Raghda A. M. Attia, and Hichem Eleuch. 2020. "Exact Traveling and Nano-Solitons Wave Solitons of the Ionic Waves Propagating along Microtubules in Living Cells" Mathematics 8, no. 5: 697. https://doi.org/10.3390/math8050697
APA StyleAbdel-Aty, A.-H., Khater, M. M. A., Attia, R. A. M., & Eleuch, H. (2020). Exact Traveling and Nano-Solitons Wave Solitons of the Ionic Waves Propagating along Microtubules in Living Cells. Mathematics, 8(5), 697. https://doi.org/10.3390/math8050697







