A Versatile Stochastic Duel Game
Abstract
1. Introduction
2. Antagonistic Stochastic Duel Game
3. Special Case: Deterministic Iteration Times
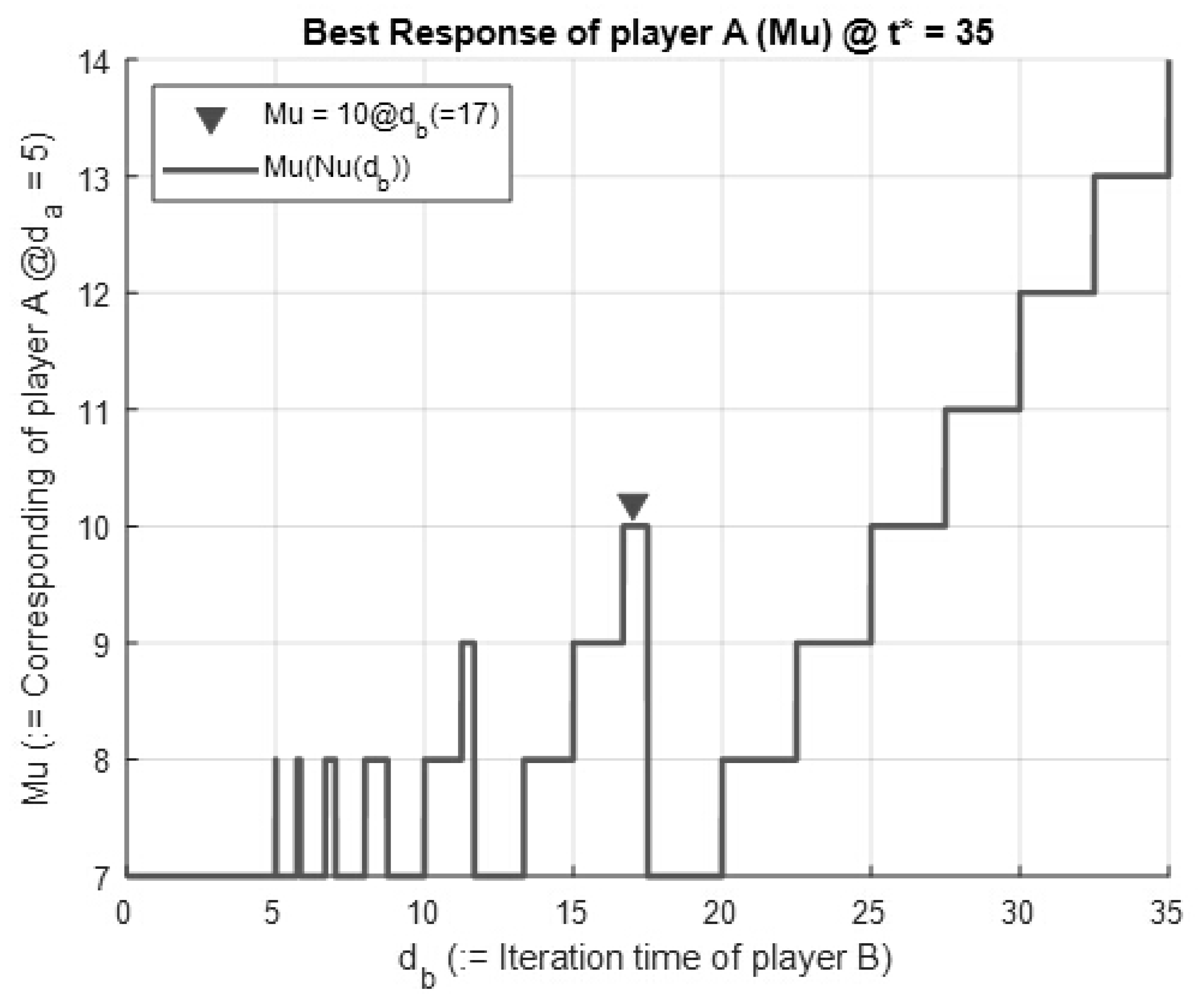
3.1. Best Strategies for Player A
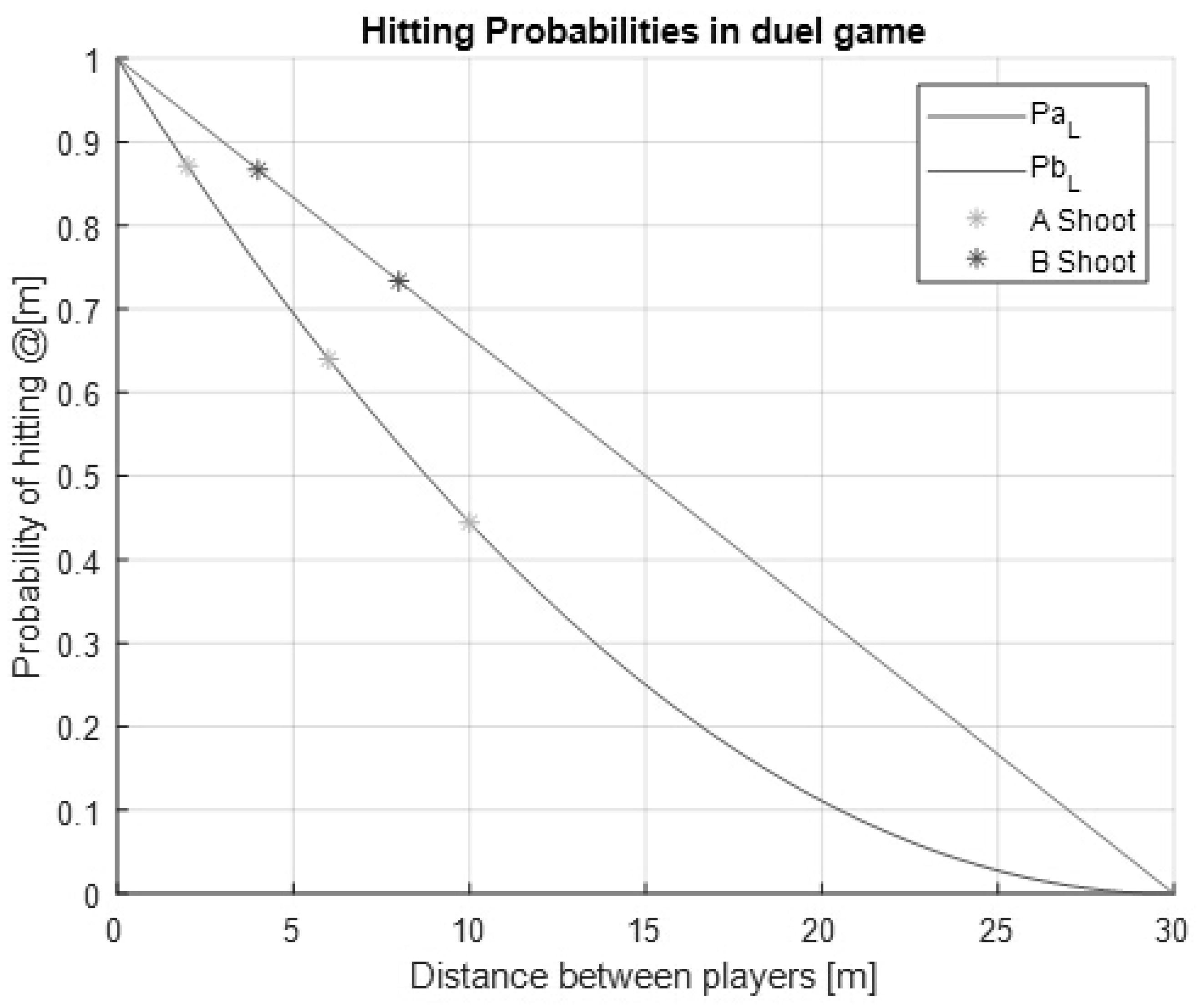
3.2. Reconstructing a Conventional Duel Game
- Each player (Players A, B) has a gun with a single bullet, and Player A starts the game;
- they are facing each other with a distance of L;
- let be the probability of Player A hitting Player B if Player A shoots at distance l;
- let be Player B’s probability of hitting Player A if Player B shoots at distance l;
- the probability of hitting for each player is give as follows:
- players alternatively have the chance to make the decision;
- either “shoot” or “one step forward”;
- every turn makes closer to each other if both players are moving forward instead of shooting;
- the hitting probabilities of both players are known (i.e., perfect information).
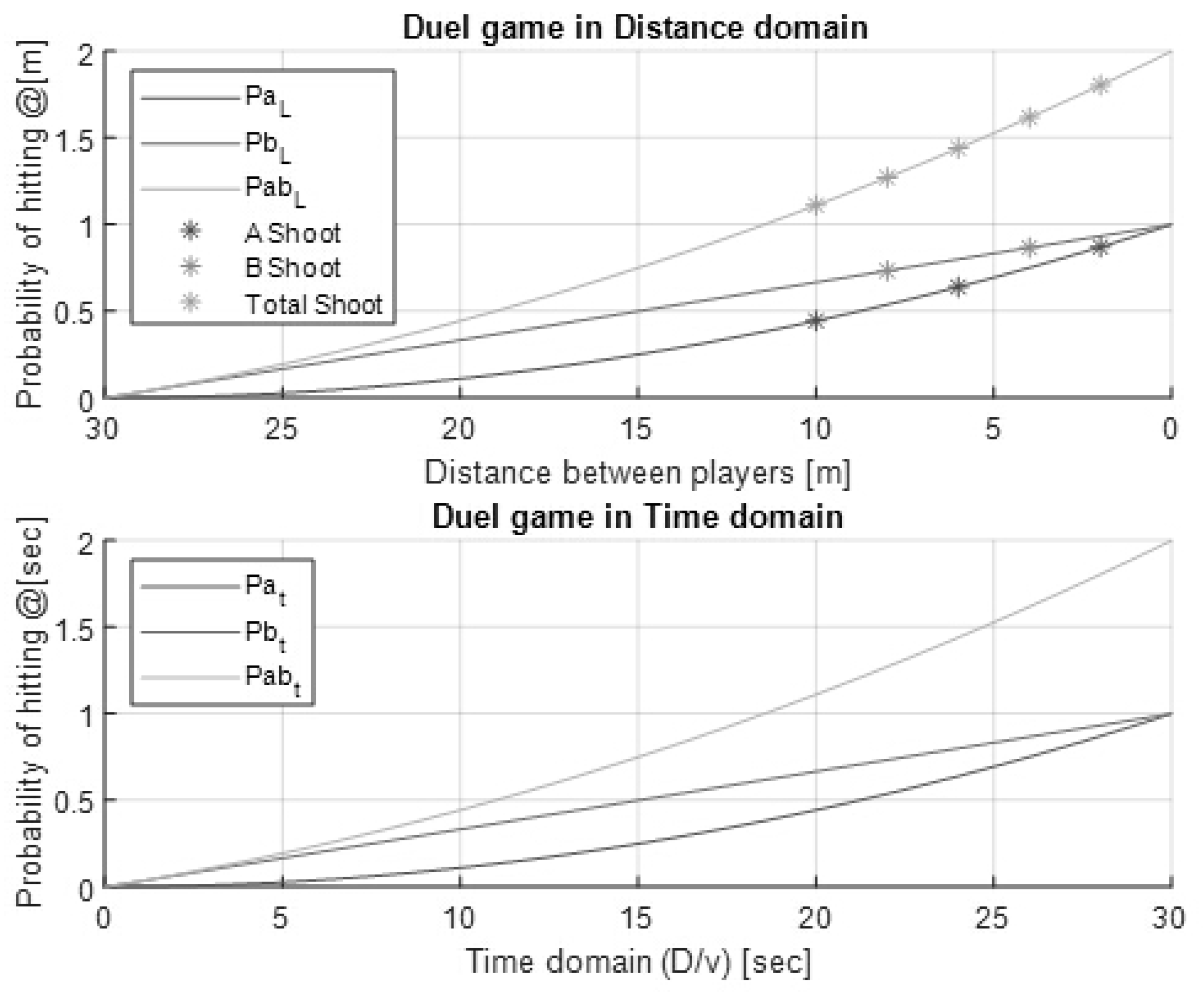
4. Case: New Product Launching Strategy
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Kim, S.-K.; Yeun, C.Y.; Damiani, E.; Al-Hammadi, Y.; Lo, N.-W. New Blockchain Adoptation For Automotive Security by Using Systematic Innovation. In Proceedings of the 2019 IEEE Transportation Electrification Conference and Expo Asia-Pacific, Jeju, Korea, 8–10 May 2019; pp. 1–4. [Google Scholar]
- Kim, S.-K. Blockchain Governance Game. Comp. Indust. Eng. 2019, 136, 373–380. [Google Scholar] [CrossRef]
- Moschini, G. Nash equilibrium in strictly competitive games: Live play in soccer. Econ. Lett. 2004, 85, 365–371. [Google Scholar] [CrossRef]
- Polak, B. Discussion of Duel. Open Yale Courses. 2008. Available online: http://oyc.yale.edu/economics/econ-159/lecture-16 (accessed on 1 May 2019).
- Dshalalow, J.H.; Iwezulu, K. Discrete versus continuous operational calculus in antagonistic stochastic games. Sao Paulo J. Math. Sci. 2017, 11, 471–489. [Google Scholar] [CrossRef]
- Dshalalow, J.H. Random Walk Analysis in Antagonistic Stochastic Games. Stoch. Anal. Appl. 2008, 26, 738–783. [Google Scholar] [CrossRef]
- Dshalalow, J.H.; Iwezulu, K.; White, R.T. Discrete Operational Calculus in Delayed Stochastic Games. 2019. Available online: https://arxiv.org/abs/1901.07178 (accessed on 1 May 2019).
- Kingston, C.G.; Wright, R.E. The deadliest of games: The institution of dueling. South. Econ. J. 2010, 76, 1094–1106. [Google Scholar] [CrossRef]
- Konstantinov, R.V.; Polovinkin, E.S. Mathematical simulation of a dynamic game in the enterprise competition problem. Cybern. Syst. Anal. 2004, 40, 720–725. [Google Scholar] [CrossRef]
- Dshalalow, J.H.; Huang, W.; Ke, H.-J.; Treerattrakoon, A. On Antagonistic Game With a Constant Initial Condition. Marginal Functionals and Probability Distributions. Nonlinear Dyn. Syst. Theory 2016, 16, 268–275. [Google Scholar]
- Azzone, G.; Pozza, I.D. An integrated strategy for launching a new product in the biotech industry. Manag. Decis. 2003, 41, 832–843. [Google Scholar] [CrossRef]
- Kam, S.; Wong, S.; Tong, C. The influence of market orientation on new product success. Eur. J. Innov. Manag. 2012, 15, 99–121. [Google Scholar]
- Kalish, S.; Mahajan, V.; Muller, E. Waterfall and sprinkler new-product strategies in competitive global markets. Int. J. Res. Mark. 1995, 12, 105–119. [Google Scholar] [CrossRef]
- Krider, R.E.; Weinberg, C.B. Competitive Dynamics and the Introduction of New Products: The Motion Picture Timing Game. J. Mark. Res. 1998, 35, 1–15. [Google Scholar] [CrossRef]
- Radas, S.; Shugan, S.M. Seasonal Marketing and Timing New Product Introductions. J. Mark. Res. 1998, 35, 296–315. [Google Scholar] [CrossRef]
- Tholke, J.M.; Hultinka, E.J.; Robbenb, H.S.J. Launching new product features: A multiple case examination. J. Prod. Innov. Manag. 2001, 18, 3–14. [Google Scholar] [CrossRef]
- Wind, Y.; Robertson, T.S. Marketing Strategy: New Directions for Theory and Research. J. Mark. 1983, 42, 12–25. [Google Scholar] [CrossRef]
- Lang, J.P.; Kimeldorf, G. Duels with continuous firing. Manag. Sci. 1975, 22, 470–476. [Google Scholar] [CrossRef]
- Lang, J.P.; Kimeldorf, G. Silent Duels with Nondiscrete Firing. SIAM J. Appl. Math. 1976, 31, 99–110. [Google Scholar] [CrossRef]
- Radzik, T. Games of Timing Related to Distribution of Resources. J. Optmization Theory Appl. 1988, 58, 443–471. [Google Scholar] [CrossRef]
- Radizik, T. Silent Mixed Duels. Optimization 1989, 20, 553–556. [Google Scholar] [CrossRef]
- Schwalbe, U.; Walker, P. Zermelo and the Early History of Game Theory. Games Econ. Behav. 2001, 34, 123–137. [Google Scholar] [CrossRef]
- Dshalalow, J.H. First excess level process. In Advances in Queueing; CRC Press: Boca Raton, FL, USA, 1995; pp. 244–261. [Google Scholar]
- Dshalalow, J.H.; Ke, H.-J. Layers of noncooperative games. Nonlinear Anal. 2009, 71, 283–291. [Google Scholar] [CrossRef]
- Kim, S.-K.; Dshalalow, J.H. Stochastic disaster rcovery systems with external resources. Math. Comput. Model. 2002, 36, 1235–1257. [Google Scholar] [CrossRef]

| Distance Domain | Deterministic Time Domain |
|---|---|
| l | |
| Parameter | Value | Description |
|---|---|---|
| 0 | Initial development cycle of Samsung | |
| 6 | Development cycle of Samsung | |
| 5 | Initial development cycle of Apple (after Samsung) | |
| 4 | Development cycle of Apple |
| Parameter | Value | Description |
|---|---|---|
| Best moment that whichever player wins the game | ||
| 3 | Number of development cycles that is best for Samsung | |
| 18 | Best time to launch the product for Samsung | |
| 4 | Number of development cycles that is best for Apple | |
| 21 | Best time to launch the product for Apple |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.-K. A Versatile Stochastic Duel Game. Mathematics 2020, 8, 678. https://doi.org/10.3390/math8050678
Kim S-K. A Versatile Stochastic Duel Game. Mathematics. 2020; 8(5):678. https://doi.org/10.3390/math8050678
Chicago/Turabian StyleKim, Song-Kyoo (Amang). 2020. "A Versatile Stochastic Duel Game" Mathematics 8, no. 5: 678. https://doi.org/10.3390/math8050678
APA StyleKim, S.-K. (2020). A Versatile Stochastic Duel Game. Mathematics, 8(5), 678. https://doi.org/10.3390/math8050678