Abstract
We study the dynamics of a modified Leslie–Gower one prey–two predators model with competition between predator populations. The model describes complex dynamics in the permanence, global stability and bifurcation. It is shown that there are eight possible equilibrium states. Two equilibrium states, i.e., the extinction of all of the species state and the extinction of both predators state are always unstable, while the other equilibrium states are conditionally locally and globally asymptotically stable. We also analyzed numerically the effect of competition between predators. Our numerical simulations showed that the competition rate of the second-predator may induce the transcritical bifurcation, the saddle-node bifurcation as well as the bi-stability phenomenon. Such numerical results are consistent with the analytical results.
1. Introduction
The model of population interaction has attracted great interest of many scholars. One of the important mathematical models is the model of the predator–prey interaction [1]. A well-known model that describes the predator–prey interaction is the Leslie–Gower model [2]. In this model, the predator is assumed to grow logistically, where its carrying capacity is proportional to the density of prey. In the case of prey scarcity, predators can consume other populations but their growth will be bounded by the fact that their main prey is not abundantly available. To account for such a situation, Aziz-Alaoui and Okiye [3] proposed a modified Leslie–Gower model by introducing a constant that measures the environment protection for the predator. Since then, many researchers have studied the modified Leslie–Gower models with various types of functional responses [4,5], harvesting [6,7,8,9], Allee effect [10,11,12,13], etc.
The model of predator–prey interaction is one of the food chain building block models that involves two species. Although predator–prey interaction models have been widely studied or developed, many ecological and modeling problems remain open. One of the developments that has been made includes adding another prey or another predator. For example, some scholars have proposed mathematical models that describe the interaction between two preys and one predator and have studied dynamics such as the stability of equilibrium states to determine conditions of coexistence in ecosystems, species extinction, existence of stable periodic solutions or transitions between prey and predator [14,15,16,17,18]. There are also many mathematical models describing the interaction of one prey with two predators. Sarwandi et al. [19] studied the effects of a prey refuge on the two competing predators. Sayekti et al. [20] considered the effects of prey harvesting on the interaction of one prey and two predators. They found that coexistence can be obtained if the prey harvesting rate is less than the prey intrinsic growth rate. We notice that all above mentioned models are derived based on the Lotka–Volterra predator–prey model. Recently, Alebraheem and Abu-Hasan [21,22,23] introduced mathematical models of one prey–two predators interactions, which are based on the Leslie–Gower model. Hence, they considered that the two predators grow following a logistic model, where the carrying capacity is only dependent on the prey density.
Recently, we [24] revisited the model of Alebraheem and Abu-Hasan [23]. We assumed in [24] that without competition, the interaction of prey with the two predators follows the Leslie–Gower model with a Holling type I functional response. If competition is also considered, then the model is
where represent the population density of the prey, the predator-1 and the predator-2 at time t, respectively and and are, respectively, the intrinsic growth rate of and . The carrying capacity of prey is . Parameters and are the maximum value of the per capita reduction rate of due to and , respectively. Parameters and denote the competition rate of predator-1 and predator-2, respectively. All parameters in the model are positive. As opposed to the model in [23], the intrinsic growth rates of both predators in system (1) are constant. In [23], the intrinsic growth rates of both predators are proportional to the density of prey. The dynamical behavior of system (1) was studied by Savitri et al. [24]. They only focused on local stability analysis and show some phase portraits by numerical simulations; transcritical bifurcation and saddle-node bifurcation have not been observed.
As explained by Aziz-Alaoui and Okiye [3], the Leslie–Gower term in the system (1) describes the reduced predator population due to scarcity of its favorite foods. In this article it is assumed that if there is a severe scarcity of prey, predators can consume other populations, but their growth will be bounded by the fact that their favorite food () is not available in large quantities. To take into account such a situation, following Aziz-Alaoui and Okiye [3], we add a constant in the denominator to obtain a modified Leslie–Gower one prey–two predators model with competition between predators.
where and are measures of environmental protection for predator-1 and predator-2, respectively.
In this article we investigate the dynamics of system (2), which includes the permanence, the existence of equilibrium states and local and global stability of equilibrium states. We also discuss the bifurcation numerically using MatCont. This article is organized in the following manner. In Section 2, we give some preliminary theorems and show that all solutions of the model are always non-negative, permanent and bounded. We analyze the existence of the equilibrium states, and the local and global stability in Section 3. In Section 4 we show numerical simulations to illustrate the analytical results and explore transcritical bifurcation, saddle-node bifurcation and bistability. Finally, we end with a brief conclusion in Section 5.
2. Non-Negativity, Boundedness and Permanence
2.1. Non-Negativity
Notice that model (2) describes the interaction of three populations, and therefore, for biological relevance, we require that the solutions of this model must be non-negative. The non-negativity of solutions are assured by the following theorem:
Theorem 1.
All solutions of system (2) with initial values ,and zare always non-negative.
Proof.
From system (2) we show that
Because exponential function for any real number u, and the initial values are positive, i.e., , and z, system (3) shows that , and . □
2.2. Boundedness
In nature, resources for every population are always limited such that the population should also be bounded. The boundedness of population prey and predators as solution of system (2) is demonstrated by utilizing the following comparison lemma:
Lemma 1.
Suppose that ,and. Then for, we have
and for, we have
[25].
Theorem 2.
All solutions of system (2) with initial values ,and zare always bounded above.
Proof.
From the first equation of system (2), we have
Since and , Lemma 1 gives
Then, for any sufficiently small , there is a such that
Based on this result and the second equation of system (2) we have
From Lemma 1 we obtain
Taking , we get
Finally, the third equation of system (2) leads to
Again, Lemma 1 gives
If we let , then
□
2.3. Permanence
In this part, we show the permanence of system (2). System (2) is said to be permanent if there exist positive constants l and L such that
Theorem 3.
System (2)with initial values ,and zis permanent if and .
Proof.
From Theorem 2, we have that for any sufficiently small , there are a such that
Let . Using Theorem 2 and the first equation in system (2), we can show that for any ,
By applying Lemma 1 and taking we obtain
where .
Similarly, using the second equation in system (2), we get for any ,
By using Lemma 1 and letting we obtain
where
As in the previous case, the third equation in system (2) gives
and therefore (by Lemma 1 and taking ) we get
where
Observe that if and then . Hence, by choosing and , we can easily see that system (2) is permanent. This completes the proof. □
3. Equilibrium States and Their Stability
3.1. Equilibrium State
By solving the following system of equations, we can show that system (2) has eight feasible positive equilibrium states:
All equilibrium states and their existence conditions are shown in Table 1. We remark that in the equilibrium state is the positive solution of the cubic equation
where

Table 1.
Equilibrium states and their existence conditions.
- .
- .
- .
- .
The existence of positive root of a cubic equation can be easily derived by Cardano’s criteria. The detail of Cardano’s criteria can be seen, for example, in [10] and is not discussed here. Furthermore, the values of and are respectively given by
and
We also require that and be positive.
3.2. Local Stability of Equilibrium States
The local behavior of system (2) is investigated by considering its linear approximation around each equilibrium state. The variational matrix of the linearized system around a point is given by
The stability of an equilibrium state is determined by the eigenvalues of the variational matrix evaluated at the corresponding equilibrium state, i.e., .
Theorem 4.
- (i)
- Equilibrium statesandare unstable.
- (ii)
- Ifandthen equilibrium stateis locally asymptotically stable.
- (iii)
- Ifandthen equilibrium stateis locally asymptotically stable.
Proof.
- (i)
- All eigenvalues of the variational matrix are . Hence, is unstable. The variational matrix at has the following eigenvalues: , and . Since there are positive eigenvalues, is also unstable (saddle-point).
- (ii)
- The eigenvalues of variational matrix at are < 0, ,. If and then we have and . This completes the proof.
- (iii)
- The variational matrix at point has eigenvalues and . Clearly, if and then is locally asymptotically stable. □
Theorem 5.
Let and . The equilibrium state is locally asymptotically stable if .
Proof.
See Appendix A. □
Theorem 6.
Let and . The equilibrium state is locally asymptotically stable if .
Proof.
See Appendix B. □
Theorem 7.
Let and . The equilibrium state is locally asymptotically stable if and .
Proof.
See Appendix C. □
Theorem 8.
The coexistence equilibrium stateis locally asymptotically stable ifand , where
Proof.
See Appendix D. □
Remark 1.
- (i)
- We notice that model (1) has only four equilibrium states (see [24]). This is a consequence of the use of the Leslie–Gower model, which does not allow the extinction of prey, and therefore equilibrium states , ,anddo not exist in the model (1). In the model (2) we introduced environmental protection for both predators, which are denoted byand, respectively. Both constants cause model (2) to have an additional four equilibrium states where each density of prey equilibrium states is zero, i.e., ,, and .
- (ii)
- From Theorems 4–8, we can classify the stability of each equilibrium state, as seen in Table 2. The extinction of all of the species state and the extinction of the both predators state are always unstable, while other equilibrium states are conditionally stable. This can be interpreted as meaning that the two predators cannot become extinct at the same time, even though there are no prey in the environment. This phenomenon can be understood from model (2) that predator-1 and predator-2 have environmental protection. We can see in Table 2 that the environmental protection is very important in determining the stability of the equilibrium points.
 Table 2. The type stability and stability condition of all of the equilibrium states
Table 2. The type stability and stability condition of all of the equilibrium states
3.3. Global Stability of Equilibrium States
In the following we present the global stability analysis of some equilibrium states. The global stability is performed by choosing an appropriate Lyapunov function for each equilibrium state.
Theorem 9.
Theequilibrium stateof the system (2) is globally asymptotically stable ifand .
Proof.
We assume that and construct a Lyapunov function where . The time derivative of this Lyapunov function is
It is clear that if then . We observe that if and only if and . Hence, according to La Salle’s invariant principle, the equilibrium state is globally asymptotically stable if and . □
Theorem 10.
Theequilibriumof the system (2) is globally asymptotically stable ifand .
Proof.
The theorem can be proven using a similar procedure as in the Proof of Theorem 9, i.e., by choosing a Lyapunov function . The detail of the Proof can be seen in Appendix E. □
Theorem 11.
The coexistence equilibriumof system (2) is globally asymptotically stable ifand where
Proof.
The theorem can be proven by defining a Lyapunov function , where , and Detail of the Proof can be seen in Appendix F. □
4. Numerical Simulations
In this section we solve model (2) using the 4th-order Runge–Kutta method with parameter values given in Table 3. The numerical simulations are performed to study the dynamics of model (2), particularly to investigate the change of dynamical behavior due to the change of the competition rate of predator-2 (). To give a view on the dynamical behavior, we consider four different cases (, , , ) as the consequence of the previous stability analysis. Such dynamical behavior is depicted in Figure 1, which shows some phase portraits of model (2) for four different values of .

Table 3.
Values of parameters.
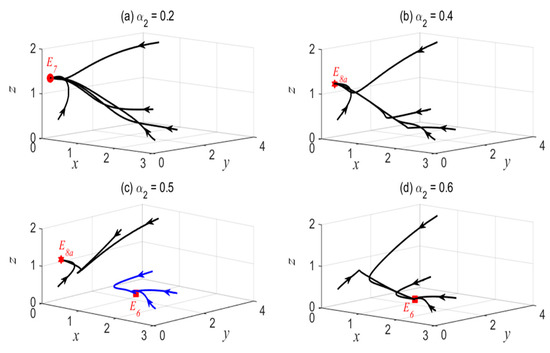
Figure 1.
Phase portraits of model (2) for different value of competition rate of predator-2 (). (a) , (b) , (c) , (d) .
Case (1). When , it is found that and therefore according to Theorem 7, is asymptotically stable. In this case, no other equilibrium state is stable (see Figure 1a).
Case (2). If we increase the competition rate of predator-2 such that , then we have a unique coexistence equilibrium state, namely is asymptotically stable since the Routh–Hurwitz criterion in Theorem 8 is satisfied. Our numerical simulation shown in Figure 1b confirms this stability property.
Case (3). If we take then From Theorem 6 we know that is asymptotically stable. Further inspection shows that there are coexistence equilibrium states, namely and . Using Theorem 8, we can show that is asymptotically stable, while is unstable. Hence, for the case of , model (2) exhibits a bi-stability phenomenon as there are two stable equilibrium states. The bi-stability phenomenon can be observed clearly in our numerical simulation depicted in Figure 1c.
Case (4). Finally, we take and show the result of our numerical simulation in Figure 1d. From Figure 1d, it is observed that only is stable. This can be understood from the fact that only the stability condition in Theorem 7 is satisfied (), while the stability conditions for other equilibrium states are not fulfilled.
From previous numerical simulations, we observe that the dynamical property of model (2) changes as we vary the value of . To understand the dynamics of model (2) with parameters values in Table 3, we check the existence of equilibrium states and their local stability properties using the previous theoretical results. From the existence conditions, it is found that our model has the following equilibrium states: and . The extinction of the predator-1 equilibrium state does not exist, while the prey extinction equilibrium state exists if . Based on Theorems 4–7, we can check that and are unstable. is stable if and the stability of is achieved whenever .
The density of the prey population in the coexistence equilibrium state is determined by the cubic Equation (7). We applied the well-known Cardano formula in MAPLE Software to verify all possible real roots of Equation (7) as well as to check the existence of the coexistence equilibrium state. For biological reasons, the coexistence equilibrium state exists if the densities of prey , predator-1 and predator-2 are positive. Based on the cubic Equation (7), there are three possible roots. We denote those possible roots as and and the respective coexistence equilibrium states as and . We found that one of roots of Equation (7), say , is a real number if . Under this condition, and are positive, but is positive only if . Hence, exists if . The second root is a positive real number if . However, and can be achieved only if , so that exists if . Finally, it is found that the third root is also a real number whenever . However, and therefore is not biologically feasible. The stability of the coexistence equilibrium point can be checked by applying the Routh–Hurwitz criteria (see Theorem 8). Due to the explicit forms of the coexistence equilibrium points and being very complicated, we investigated the stability of coexistence equilibrium points numerically using a numerical continuation package MatCont. The numerical continuation was performed not only to study the stability of the coexistence equilibrium points, but also to examine all possible equilibrium states and their stability properties. In Figure 2 we plot the equilibrium state density of predator-1 (y) as the value of is changed. It is noticed that the equilibrium state density of prey (x) and that of predator-2 (z) are similar to this graph. It appears that our theoretical results are confirmed by the results of numerical continuation. The detail of the dynamics shown in Figure 2 could be explained as follows.
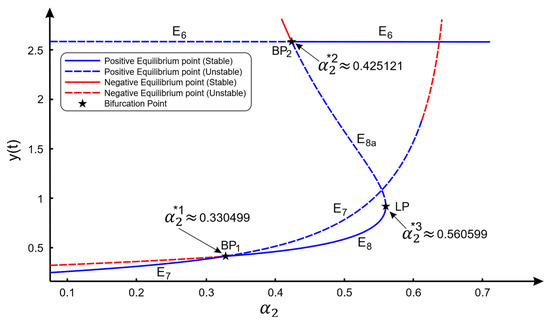
Figure 2.
Equilibrium state density of predator-1 as function of competition rate of predator-2 ().
4.1. Transcritical Bifurcation
From Figure 1a,b we observe the exchange of stability between the prey extinction equilibrium state and the coexistence equilibrium state , indicating there occurs a transcritical bifurcation caused by . The transcritical bifurcation is more clearly seen in Figure 2. For a relatively small , only the equilibrium state is stable. As increases, there appears a branch point (BP1) at . This BP1 indicates the appearance of transcritical bifurcation, i.e., there is a change of stability between the extinction of the prey equilibrium state and the coexistence equilibrium state When , is asymptotically stable while is unstable. On the other hand, if , then is unstable while becomes asymptotically stable. This shows that when the competition rate of predator-2 is relatively low, the predator-2 can grow well, while if the competition rate of predator-2 is large enough, then the growth of predators is reduced and therefore predation is decreased. As a result, prey can survive, which is shown by the stability of the coexistence equilibrium state ().
Another transcritical bifurcation may also occur between and , where the bifurcation point is at BP2 (or ). We remark that those phenomena of transcritical bifurcations are only possible mathematically. Indeed, does not biologically exist for , since in this case the value of is negative. Similarly, does not exist for biological reasons for . Thus, the transcritical bifurcations in our case are not biologically feasible.
4.2. Saddle-Node Bifurcation
As seen in Figure 2, if then there exists a unique coexistence equilibrium state (), which is asymptotically stable (see also Figure 1b). A further observation shows that for there are two coexistence equilibrium states. One of them is asymptotically stable while the other one is unstable. The stability of one of these coexistence equilibrium states can also be seen in Figure 1c. Then, these two coexistence equilibrium states collide at the limit point (LP), i.e., at . If , then the two coexistence equilibrium states disappear and only the extinction of predator-2 equilibrium state is stable. Hence there occurs a saddle-node bifurcation driven by .
4.3. Bi-Stability
Another interesting dynamics that can be observed in Figure 2 is the appearance of two different stable equilibrium states. This interesting occurrence is known as the bi-stability phenomenon. The bi-stability phenomenon occurs when . In this case, both extinction of the predator-2 equilibrium state and the coexistence equilibrium are asymptotically stable. Here the dynamics of model (2) are very sensitive to the initial values. For some relatively large initial values of predator-2, we have a situation where the solutions converge to the coexistence equilibrium state , as shown by the black-trajectories in Figure 1c. Hence, all three species (prey, predator-1 and predator-2) can coexist. On the other hand, whenever the initial predator-2 is relatively small, then the solutions converge to the extinction of the predator-2 equilibrium state (see blue-trajectories in Figure 1c).
5. Conclusions
We have discussed a model that describes the interaction of one prey–two predators with competition between the two predators. The model is derived from the modified Leslie–Gower predator–prey model. The model is proven to be permanent and all solutions of the model are always non-negative and bounded. We found that the proposed model has eight equilibrium states. There are two equilibrium states that are always unstable, namely the extinction of all of the species and the extinction of the two predators. Other equilibrium states are conditionally stable. We have also shown the global stability of some equilibrium states by defining suitable Lyapunov functions. The results of dynamical analysis were confirmed by our numerical simulations. Moreover, our numerical simulations have shown that the proposed model exhibits rich dynamics as we observed the occurrence of transcritical bifurcation, saddle-node bifurcation and bi-stability phenomenon, which are driven by the competition rate of predator-2 species.
Author Contributions
Conceptualization, A.S.; Data curation, D.S.; Formal analysis, D.S. and A.S.; Funding acquisition, A.S.; Investigation, D.S. and A.S.; Methodology, A.S.; Project administration, A.S.; Software, D.S. and A.S.; Supervision, A.S., W.M.K. and A.; Validation, W.M.K.; Visualization, D.S. and A.; Writing—original draft, D.S.; Writin—review & editing, A.S., W.M.K. and A. All authors have read and approved the final manuscript.
Funding
This research received no external funding.
Acknowledgments
This research and APC were funded by the Directorate of Research and Community Service, the Directorate General of Strengthening Research and Development, and the Ministry of Research, Technology and Higher Education (Brawijaya University), Indonesia, via Doctoral Dissertation Research, in accordance with the Research Contract No. 055/SP2H/LT/DRPM/2019, dated 11 March 2019. The authors thank Hasan S. Panigoro (University of Brawijaya and State University of Gorontalo) for discussion about the continuation method).
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.
Appendix A. Proof of Theorem 5
If we evaluate the variational matrix at , then we get
One of the eigenvalues of is , while the others (say ) are determined by , where and . Since and , we have . Thus, is locally asymptotically stable if or when .
Appendix B. Proof of Theorem 6
The variational matrix at is
The eigenvalues of are and the roots of , where and . Clearly the last two eigenvalues are negative and is negative if . This completes the proof.
Appendix C. Proof of Theorem 7
The variational matrix evaluated at is
The first eigenvalue of is and other eigenvalues are determined by quadratic equation , where and . , is stable if and , that is, when and . Hence, we have the theorem.
Appendix D. Proof of Theorem 8
By evaluating the variational matrix at , we obtain
The characteristic equation of is given by where and are given as above. By applying the Routh–Hurwitz criteria, the real parts of all characteristic roots are negative if and . It is clear that . Hence, is locally asymptotically stable if and .
Appendix E. Proof of Theorem 10
Assume that and consider the following Lyapunov function where . If we take the time derivative of , then we get
It is found that if then . Moreover, if and only if and . By applying La Salle’s invariant principle, we find that the equilibrium state is globally asymptotically stable if and .
Appendix F. Proof of Theorem 11
Consider the following Lyapunov function , where and The time derivative of and along the solutions of system (2) are, respectively, as follows.
Hence, the derivative of with respect to is given by
We note that if then
while if then . Similarly, if we have then
while if then . Thus, if we take
and
then we obtain
It is obvious that if and then . We can also check that if and only if and . From La Salle’s invariant principle, it is concluded that the equilibrium state is globally asymptotically stable.
References
- Berryman, A.A. The origins and evolution of predator-prey theory. Ecology 1992, 73, 1530–1535. [Google Scholar] [CrossRef]
- Leslie, P.H.; Gower, J.C. The properties of a stochastic model for the predator-prey type of interaction between two species. Biometrica 1960, 47, 219–234. [Google Scholar] [CrossRef]
- Aziz-Alaoui, M.A.; Okiye, M.D. Boundedness and global stability for a predator-prey model with modified Leslie-Gower and Holling-type II schemes. Appl. Math. Lett. 2003, 16, 1069–1075. [Google Scholar] [CrossRef]
- Yu, S. Global asymptotic stability for a predator-prey model with modified Leslie-Gower and Holling-type II schemes. Discrete Dyn. Nat. Soc. 2012, 2012, 208167. [Google Scholar] [CrossRef]
- Yu, S. Global asymptotic stability a modified Leslie-Gower with Beddington-DeAngelis functional response. Adv. Differ. Equ. 2014, 84, 1–14. [Google Scholar] [CrossRef]
- Zhang, N.; Chen, F.; Su, Q.; Wu, T. Dynamics behaviors of a harvesting Leslie-Gower predator-prey model. Discrete Dyn. Nat. Soc. 2011, 2011, 473949. [Google Scholar] [CrossRef]
- Gupta, R.P.; Chandra, P. Bifurcation analysis of modified Leslie-Gower predator prey model with Michaelis-Menten type prey harvesting. J. Math. Anal. Appl. 2013, 398, 278–295. [Google Scholar] [CrossRef]
- Darti, I.; Suryanto, A. Stability preserving non-standard finite difference scheme for a harvesting Leslie–Gower predator–prey model. J. Differ. Equ. Appl. 2015, 21, 528–534. [Google Scholar] [CrossRef]
- Darti, I.; Suryanto, A. Dynamics preserving nonstandard Finite difference method for the modified Leslie-Gower predator-prey model with Holling type II functional responses. Far East. J. Math. Sci. 2016, 998, 719–733. [Google Scholar] [CrossRef]
- Cai, Y.; Zhao, C.; Wang, W.; Wang, J. Dynamics of Leslie-Gower predator-prey model with additive Allee effect. Appl. Math. Model. 2015, 39, 2092–2106. [Google Scholar] [CrossRef]
- Crow, Y.; Jang, S. Asymptotic dynamics of the Leslie-Gower competition system with Allee effects and stocking. Adv. Differ. Equ. 2015, 2, 1–19. [Google Scholar] [CrossRef]
- Pal, P.J.; Mandal, P.K. Bifurcation analysis of a modified Leslie–Gower predator–prey model with Beddington–DeAngelis functional response and strong Allee effect. Math. Comput. Simulat. 2014, 97, 123–146. [Google Scholar] [CrossRef]
- Indrajaya, D.; Suryanto, A.; Alghofari, A.R. Dynamics of modified Leslie-Gower predator-prey model with Beddington-DeAngelis functional response and additive Allee effect. Int. J. Ecol. Dev. 2003, 31, 60–71. [Google Scholar]
- Kar, T.K.; Batabyal, A. Persistence and stability of a two prey one predator system. Int. J. Eng. Sci. Technol. 2010, 2, 174–190. [Google Scholar] [CrossRef]
- Tripathi, J.P.; Abbas, S.; Thakur, M. Local and global stability analysis of a two prey one predator model with help. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 3284–3297. [Google Scholar] [CrossRef]
- Deka, B.D.; Patra, A.; Tushar, J.; Dubey, B. Stability and Hopf-bifurcation in a general Gauss type two-prey and one-predator system. Appl. Math. Model. 2016, 40, 5793–5818. [Google Scholar] [CrossRef]
- Reddy, K.S.; Srinivas, M.N.; Kumar, C.V.P. Dynamics of a two prey and one predator system with time interruption and random fluctuations. Pac. Sci. Rev. A Natur. Sci. Eng. 2016, 18, 150–156. [Google Scholar] [CrossRef][Green Version]
- Raymond, C.; Hugo, A.; Kung’aro, M. Modeling dynamics of prey-predator fishery model with harvesting: A bioeconomic model. J. Appl. Math. 2019, 2019, 2601648. [Google Scholar] [CrossRef]
- Sarwandi, S.; Mandal, P.K.; Ray, S. Dynamical behaviour of a two-predator model with prey refuge. J. Biol. Phys. 2013, 39, 701–722. [Google Scholar] [CrossRef]
- Sayekti, I.M.; Malik, M.; Aldila, D. One-Prey Two-Predator Model with Prey Harvesting in a Food Chain Interaction. AIP Conf. Proc. 2017, 1862, 030124. [Google Scholar] [CrossRef]
- Alebraheem, J.; Abu-Hasan, Y. Persistence of predator in a two predator-one prey model with non-periodic solution. Appl. Math. Sci. 2012, 6, 943–956. [Google Scholar]
- Alebraheem, J.; Abu-Hasan, Y. Dynamics of a two predator–one prey system. Comput. Appl. Math. 2014, 33, 767–780. [Google Scholar] [CrossRef]
- Alebraheem, J.; Abu-Hasan, Y. The effects of capture efficiency on the coexistence of a predator in a two predators—One prey model. J. Appl. Sci. 2011, 11, 3717–3724. [Google Scholar] [CrossRef]
- Savitri, D.; Suryanto, A.; Kusumawinahyu, W.M.; Abadi. A dynamics behaviour of two predators and one prey interaction with competition between predators. IOP Conf. Ser. Mater. Sci. Eng. 2019, 546, 052069. [Google Scholar] [CrossRef]
- Chen, F.D. On a nonlinear non-autonomous predator-prey model with diffusion and distributed delay. J. Comput. Appl. Math. 2005, 180, 33–49. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).