Abstract
In this paper, we discuss an explicit model function that can estimate the total number of deaths in the population, and particularly, estimate the cumulative number of deaths in the United States due to the current Covid-19 virus. We compare the modeling results to two related existing models based on a new criteria and several existing criteria for model selection. The results show the proposed model fits significantly better than the other two related models based on the U.S. Covid-19 death data. We observe that the errors of the fitted data and the predicted data points on the total number of deaths in the U.S. on the last available data point and the next coming day are less than 0.5% and 2.0%, respectively. The results show very encouraging predictability for the model. The new model predicts that the maximum total number of deaths will be approximately 62,100 across the United States due to the Covid-19 virus, and with a 95% confidence that the expected total death toll will be between 60,951 and 63,249 deaths based on the data until 22 April, 2020. If there is a significant change in the coming days due to various testing strategies, social-distancing policies, the reopening of community strategies, or a stay-home policy, the predicted death tolls will definitely change. Future work can be explored further to apply the proposed model to global Covid-19 death data and to other applications, including human population mortality, the spread of disease, and different topics such as movie reviews in recommender systems.
1. Introduction
Coronaviruses consist of viruses that cause illness ranging from mild common cold, to more severe diseases, to severe illness and death. Recent Covid-19, known as Coronavirus disease 2019, has spread through people, first identified in Wuhan City, China, since December 2019.Covid-19 is a new disease, and even experts in the field are still learning how it spreads. It has rapidly spread to many countries around the world, including the United States [1].
The virus is spreading through people who are in close contact with one another by touching an infected surface or object and then touching their mouth or nose. Symptoms of infected persons with Covid-19 may include mild fever, cough, runny nose, sore throat, headache, shortness of breath, severe illness, or death [2].
According to the U.S. Centers for Disease Control and Prevention [3], people can prevent the spread of viruses by staying home when they are sick, not touching their nose and mouth and covering their sneeze, and washing their hands more often with soap before eating or after touching objects from outside.
The outbreak of Covid-19 has rapidly spread to countries around the world, including the United States. As of 23 April 2020, more than 46,000 people in the United States have died of coronavirus and there are at least 183,000 worldwide reported deaths, according to a tally by Johns Hopkins University [4].
On 17 April, the University of Washington’s Institute for Health Metrics Evaluation (IHME) projected that there would be 60,308 Covid-19 deaths with an estimated range between 34,063 and 140,381 deaths by 4 August, which is down from 68,841 as predicted earlier on 13 April [5]. Recently, Chin et al. [6] studied the stability and detection of severe respiratory syndrome coronavirus in various environmental conditions including variables such as different temperatures and surfaces.
In this study, we are interested in developing a model that can estimate the cumulative number of deaths due to the ongoing Covid-19 virus pandemic occurring during the writing of this paper. Our preliminary analysis based on the Covid-19 global and United States death data appears to be that the cumulative number of deaths seem to follow an S-shaped curve. There are a number of existing S-shaped logistic models in the literature [7,8,9,10,11,12,13,14,15,16,17,18] and related logistic regression models [19]. Pham [13] recently developed a logistic model to estimate the number of failures.
In this paper, we modify the model in reference [13] by considering different unknown parameters that would allow flexibility to reflect the uncertainty of Covid-19 virus, such as different groups, age, and different environments and areas in the population. We compare the modeling results of the proposed model to two other slightly modified models as shown in Table 1. We also discuss a new model selection criterion, called PC (Pham’s criterion) and how to select the best model based on new criteria and several existing criteria, including SSE (sum of squared error), MSE (mean squared error), AIC (Akaike’s information criterion), BIC (Bayesian information criterion), PIC (Pham’s information criterion), PRR (the predictive ratio risk), and PP (the predictive power). With the new model, we illustrate the proposed model in estimating the cumulative number of deaths in the United States.

Table 1.
Models.
Section 2 discusses a closed-form new model function to estimate the total number of deaths in the population and also briefly discusses a new criterion for model selection and some existing criteria. Section 3 discusses the modeling results based on the Covid-19 death data in the United States. Section 4 briefly discusses the findings and makes some concluding remarks.
2. Model Development on Estimating the Number of Deaths
In this study, we develop a model that can estimate the cumulative number of deaths in the population. We use the proposed model to estimate the cumulative number of deaths due to Covid-19, the current deadly virus. In this section, we first present the model assumptions and the results of the proposed model.
2.1. Model Considerations
In this study, we assume that
- There are a few people in the population who have already been infected with Covid-19, and are spreading the virus into the community but do not know that they are infected with the virus. The virus is spreading through people who are in close contact with one another. An infected person may, for example, cough or sneeze, spreading the virus through the bacteria eventually coming in contact with the mouths or noses of other people who are nearby or possibly directly inhaled into their lungs. A person can get Covid-19 by touching an infected surface or object and then touching their own mouth, nose, or possibly their eyes [2].
- The virus is spreading throughout the areas based on a time-dependent infection rate per person in which it will spread at a very slow rate from the beginning due to a small number of infected people and will spread at a growth rate much faster due to a higher number of people who have already been infected with the virus and who are in close contact with non-infected individuals as time progresses. The growth rate will then continue to grow slowly until it reaches the maximum total number of Covid-19 deaths.
- The rate of change of the death is the derivative of the number of deaths p’(t) is directly proportional to both the number of deaths p(t) who have infected the virus and the number of people in the susceptible population who have not yet been infected, based on the time-dependent rate infections per person per unit time.
- Deaths are proportional to infections, but with a lag. There can be a significant time lag between when someone is infected and when they die. We assume that death data is more reliable than the reported number of cases and hospitalizations due to the uncertainty of testing mechanisms and the recognized symptoms and treatments. Additionally, it is easier to determine cause of death than cause of hospitalizations and test cases. In fact, we need to know how tests are being conducted; otherwise, there will be a lot of uncertainty about the number of Covid-19 cases, so they will not be very useful indicators.
2.2. Model Development
Let p(t) denote the cumulative number of deaths at time t, b(t) denote the time-dependent death rate per person per unit time, and a denote the maximum total number of deaths. Numerous researchers in the past several decades have studied the areas of population growth and disease spread, and several well-known population growth models, including logistic model in the literature [7,8,9,10,13,14,19]. Given a vast literature in this area [13,14], we can write the differential equation (with the initial condition m(0) ≠ 0 in this case) governing death rate growth as follows:
Based on the model considerations above and the generalized death rate change differential function as given in Equation (1), in this paper we propose the following model to estimate the cumulative number of deaths at time t as follows:
where a, b, c, d, and β are the unknown constant parameters.
As from assumption 1, there are a few people in the population who have already been infected with Covid-19 at the beginning at time t = 0. From Equation (2), it is easy to realize that the initial value of the function p(t) at time 0 is as follows:
At t →∞, p(∞) = a. This indicates that the maximum total number of deaths in the population is a, where a can be estimated based on given data.
We estimate these unknown parameters a, b, c, d, and β by using the least squares estimate method and compare their results based on various model criteria. In general, adding more parameters in the model improves the goodness of the fit. Some existing model selection criteria have taken into account the penalty imposed by adding more parameters to the model. The two common criteria are AIC [11] and BIC [12]. For example, BIC has taken into account the sample size that shows how strongly it impacts the penalty by adding the number of parameters in the model, while AIC does not depend on the sample size.
In the next section, we present a new criterion for model selection that takes into account the uncertainty in the model and the number of parameters in the model by slowly increasing the penalty when adding parameters in the model each time where the sample is too small compared to the sample size.
3. Modeling Analysis and Prediction Results
In this section, we use the model given in Equation (2) to calculate the total number of deaths based on the death data in the U.S. consisting of 54 days obtained from Worldometer [20] for a period beginning from 29 February 2020 to 22 April 2020.
We compare the modeling results of the new model to two slightly related models as shown in Table 1 and select a best model based on a proposed new criteria PC and several existing criteria such as SSE, MSE, AIC, BIC, PIC, PRR, and PP. Table 2 provides a brief definition of those criteria to be used in selecting the best model from among the models in Table 1. For all these criteria, the smaller the value, the better the model fits.

Table 2.
Some criteria model selection.
The cumulative number of deaths data in the United States is shown in Table 3. We use the least square estimate (LSE) method to estimate the model parameters using R software. We also compare the results of the models listed in Table 1. We then discuss the best model among the models in Table 1 based on various model selection criteria. Table 4 summarizes the results of the parameter estimates of all three models from Table 1 using LSE. Table 5 shows the calculation results and the rank of each model based on the modeling criteria as given in Table 2.

Table 3.
US deaths data [20] during 2/29/20—4/22/20.

Table 4.
Parameter estimates using least squares method.

Table 5.
Modeling results and rankings based on various criteria.
As we can observe from Table 5, the new model has the smallest values and their corresponding rankings are first according to criteria such as SSE, MSE, AIC, PIC, and PC (new criteria) but not BIC, PP, and PRR criteria. We observe that the results of proposed PC agree with MSE and AIC criteria but not BIC. It is worth noting that the new PC takes into account the uncertainty in the model and the dynamic penalty depending on both the same size and the number of parameters in the model where the penalty term in BIC for the number of parameters in the model heavily depend on the same size. The plots in Figure 1, Figure 2, Figure 3 and Figure 4 show the estimated cumulative number of deaths versus the actual death data in the United States during the period of 29 February 2020 to 22 April 2020. The results indicate the proposed model is the best fit to estimate the cumulative number of deaths for the United States Covid-19 data.
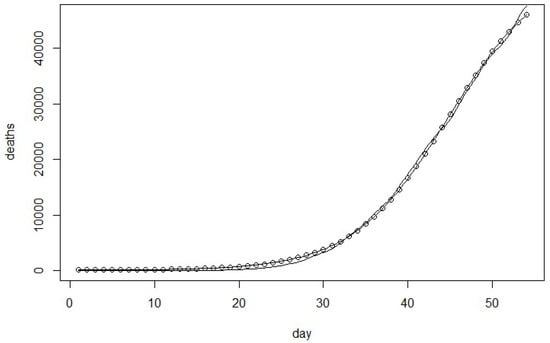
Figure 1.
The estimated cumulative number of deaths vs. actual death data from Model 1.
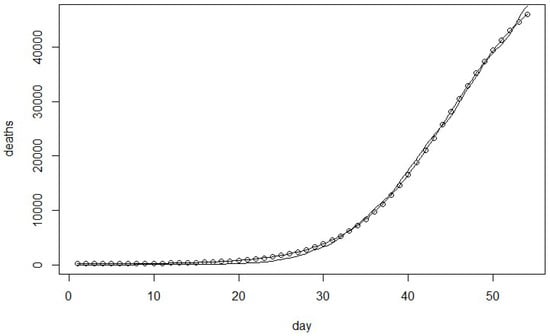
Figure 2.
The estimated cumulative number of deaths vs. actual death data from Model 2.
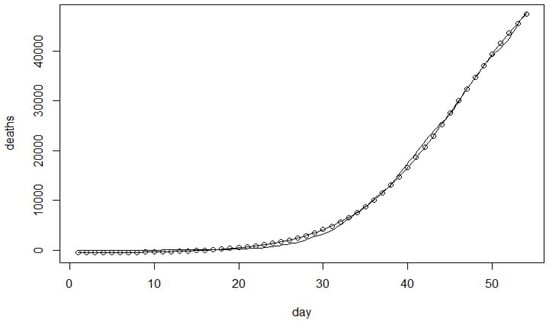
Figure 3.
The estimated cumulative number of deaths vs. actual death data from Model 3.
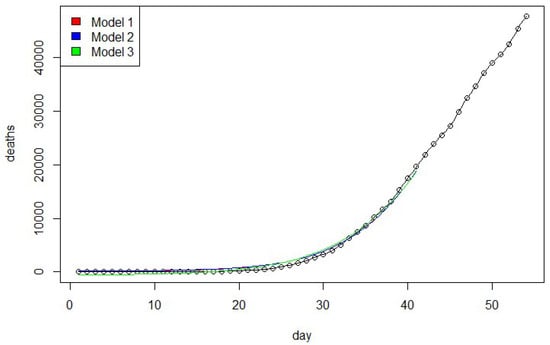
Figure 4.
The estimated cumulative number of deaths vs. actual death data from all three models.
The new model as shown in Figure 3 and Table 5 indicates that it provides the best fit based on SSE, MSE, AIC, PIC, and PC. The proposed model fits significantly better than the other related models as shown in Table 6 for the U.S. Covid-19 death data.

Table 6.
Prediction results.
We observe that the errors of the fitted and predicted data points on the death toll in the U.S. on the last available data point and the next coming day are less than 0.5% and 2.0%, respectively. Our model fits significantly well based on the U.S. death data. The results show very encouraging predictability for the model. The new model predicts that the maximum total number of deaths will be approximately 62,100 across the U.S. due to the Covid-19 virus, with a 95% confidence that the expected total death toll will be between 60,951 and 63,249 deaths based on the data until 22 April 2020. If there is a significant change in the coming days due to various testing strategies, social-distancing policies, reopening the community, or stay-home policy, the predicted death tolls will definitely change. Obviously, further analysis in broader validation of this conclusion is needed by updating the real current Covid-19 data into the model.
4. Conclusions
In this paper, an explicit model function to predict the total number of deaths in the population is presented. We also discuss a new criterion that can choose the best model in the set of candidates. The results of the model parameter estimates of the proposed model and two related proposed models using the least squares method for the Covid-19 death data in the U.S. are presented. The proposed model fits significantly better than two other related models based on the Covid-19 death data in the United States. The results show very encouraging predictability for the model.
Further work can be done to apply the proposed model to Covid-19 global death data as well as any other countries such as Italy and Spain where they also have a large cumulative number of deaths due to Covid-19. In the future, we intend to use the model in applications of population mortality, the spread of disease, and different topics such as movie reviews in recommender systems.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
| SSE | sum of squared error |
| MSE | mean squared error |
| AIC | Akaike’s information criterion |
| BIC | Bayesian information criterion |
| LSE | least square estimate |
| PC | Pham’s criterion |
| PP | the predictive power |
| PIC | Pham’s information criterion |
| PRR | the predictive ratio risk |
References
- Available online: https://patch.com/new-jersey/oceancity/nj-coronavirus-update-gov-murphy-considers-curfew-31-new-cases (accessed on 16 March 2020).
- Available online: https://www.osha.gov/SLTC/covid-19/medicalinformation.html (accessed on 17 March 2020).
- Centers for Disease Control and Prevention. Available online: https://www.cdc.gov/coronavirus/2019-ncov/prevent-getting-sick/social-distancing.html (accessed on 8 April 2020).
- Available online: https://www.cnn.com/world/live-news/coronavirus-pandemic-04-23-20-intl/index.html (accessed on 23 April 2020).
- Available online: http://www.healthdata.org/news-release/ihme-hold-media-briefing-4-pm-eastern-today-details-below (accessed on 17 April 2020).
- Chin, A.W.H.; Chu, J.T.S.; Perera, M.R.A.; Hui, K.P.Y.; Yen, H.-L.; Chan, M.C.W.; Paris, M.; Poon, L.L.M. Stability of SARS-CoV-2 in different environmental conditions. Lancet Mircobe 2020, 20. [Google Scholar] [CrossRef]
- Verhulst, P. Recherches mathematiques sur la loi d’accroissement de la population. Nouv. Mem. de l’Academie Royale des Sci. et Belles-Lettres de Bruxelles 1845, 18, 1–41. [Google Scholar]
- Pham, H.; Pham, D.H.; Pham, H., Jr. A New Mathematical Logistic Model and Its Applications. Int. J. Inf. Manag. Sci. 2014, 25, 79–99. [Google Scholar]
- Pham, H.; Modeling, U.S. Mortality and Risk-Cost Optimization on Life Expectancy. IEEE Trans. Reliab. 2011, 60, 125–133. [Google Scholar] [CrossRef]
- Pham, H. A New Criteria for Model Selection. Mathematics 2019, 7, 1215. [Google Scholar] [CrossRef]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Proceedings of the Second International Symposium on Information Theory; Petrov, B.N., Caski, F., Eds.; AkademiaiKiado: Budapest, Hungary, 1973; pp. 267–281. [Google Scholar]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Pham, H. A Logistic Fault-Dependent Detection Software Reliability Model. J. Univers. Comput. Sci. 2018, 24, 1717–1730. [Google Scholar]
- Pham, H. System Software Reliability; Springer: London, UK, 2006. [Google Scholar]
- Pham, T.; Pham, H.A. Generalized Software Reliability Model with Stochastic Fault-detection Rate. Ann. Oper. Res. 2019, 277, 83–93. [Google Scholar] [CrossRef]
- Zhu, M.; Pham, H. A Software Reliability Model Incorporating Martingale Process with Gamma-Distributed Environmental Factors. Ann. Oper. Res. 2018. [Google Scholar] [CrossRef]
- Li, Q.; Pham, H. NHPP Software Reliability Model Considering the Uncertainty of Operating Environments With Imperfect Debugging and Testing Coverage. Appl. Math. Model. 2017, 51, 68–85. [Google Scholar] [CrossRef]
- Sharma, M.; Singh, V.B.; Pham, H. Entropy Based Software Reliability Analysis of Multi-Version Open Source Software. IEEE Trans. Softw. Eng. 2018, 44, 1207–1223. [Google Scholar]
- Pham, H.; Pham, D.H. A Novel Generalized Logistic Dependent Model to Predict the Presence of Breast Cancer Based on Biomarkers. Concurr. Comput. Pract. Exp. 2020, 32, e5467. [Google Scholar] [CrossRef]
- Available online: https://www.worldometers.info/coronavirus/?utm_campaign=homeAdvegas1?#countries (accessed on 22 April 2020).
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).