A Revisit of the Boundary Value Problem for Föppl–Hencky Membranes: Improvement of Geometric Equations

Abstract

In this paper, the well-known Föppl–Hencky membrane problem—that is, the problem of axisymmetric deformation of a transversely uniformly loaded and peripherally fixed circular membrane—was resolved, and a more refined closed-form solution of the problem was presented, where the so-called small rotation angle assumption of the membrane was given up. In particular, a more effective geometric equation was, for the first time, established to replace the classic one, and finally the resulting new boundary value problem due to the improvement of geometric equation was successfully solved by the power series method. The conducted numerical example indicates that the closed-form solution presented in this study has higher computational accuracy in comparison with the existing solutions of the well-known Föppl–Hencky membrane problem. In addition, some important issues were discussed, such as the difference between membrane problems and thin plate problems, reasonable approximation or assumption during establishing geometric equations, and the contribution of reducing approximations or relaxing assumptions to the improvement of the computational accuracy and applicability of a solution. Finally, some opinions on the follow-up work for the well-known Föppl–Hencky membrane were presented.

1. Introduction

The mathematical modeling of the mechanical behavior of engineering structures or structural components [1,2] and the solving techniques for the resulting boundary value problems [3,4] are often found to be necessary. Membrane structures or structural components have received considerable attention in many applications [5,6,7]. However, the large deflection phenomena exhibited by elastic membrane structures or structural components are usually difficult to deal with analytically, due to the somewhat intractable nonlinear equations [8,9,10,11,12,13]. The famous German scientist Hencky, originally dealt with the problem of axisymmetric deformation of a transversely uniformly loaded and peripherally fixed circular membrane, and presented its closed-form solution in the form of a power series in 1915 [14]. Chien [15] and Alekseev [16] corrected the computational error in [14]. This well-known problem is usually called the Föppl–Hencky membrane problem, or simply the well-known Hencky problem, while its solution is called the well-known Hencky solution, which is often cited in studies of related issues [17,18,19,20,21,22,23].

As is known, almost all analytical solutions of mechanical problems have been obtained based on some necessary approximations or assumptions; likewise, the well-known Hencky solution was obtained in the same way. Therefore, further research on the well-known Hencky problem should focus on reducing approximations or relaxing assumptions. Our interest in the well-known Hencky problem lies mainly in its axisymmetric character, which is convenient for analytical solving. In recent years, we have devoted ourselves to further studies on the well-known Hencky problem. At first, a detailed solving process was presented for the well-known Hencky problem [24], where the membrane equations were directly established by analyzing the deflected membrane, rather than Hencky’s originally method [14]. Hencky started from a thin plate bending problem in regards to the origins of the membrane problem, and because the “membrane” is usually thin enough, the bending term in the well-known von Karman large deflection equations for thin plates is ignored. In another paper, the assumption of zero for the initial membrane stress that the well-known Hencky solution must follow was given up and an extended Hencky solution was presented [25], where the initial membrane stress is allowed to be nonzero and the extended solution can regress to the well-known Hencky solution if the initial membrane stress is zero. Furthermore, we replaced the so-called small rotation angle assumption for membranes, which the well-known Hencky solution must also follow, with a new closed-form solution without small rotation angle assumption [26]. In this new solution, the rotation angle of the membrane, θ, is allowed to be arbitrary, since the basic trigonometric function relation $\sin \theta =\sqrt{1+1/{\tan }^2\theta }$ was used during the derivation of this new solution, while during the derivation of the well-known Hencky solution, sin θ was replaced by tan θ based on the small rotation angle assumption of the membrane (i.e., due to $\sin \theta \cong \tan \theta \cong \theta$ when θ is small enough). Of course, the applicability of the well-known Hencky solution is limited by the size of the rotation angle of the membrane due to the adoption of the small rotation angle assumption. Following this, in order to achieve synchronous characterization for the surface and interface of thin film–substrate systems with residual stress, the closed-form solution without the small rotation angle assumption was further extended into the more general situation, where the initial membrane stress is allowed to be nonzero [27]. Recently, by giving up the small rotation angle assumption, we presented a closed-form solution for the contact problem between transversely uniformly loaded circular membranes and frictionless rigid plates [28]. In fact, it is usually difficult to clarify the qualitative or quantitative influence of new approximations or assumptions on the computational accuracy and applicability of a solution; however, when it is turned over it is different, meaning it is usually not necessary to conduct a qualitative or quantitative analysis to clarify the influence of reducing approximations or relaxing assumptions (on the basis of existing theories) on the computational accuracy and applicability of the solution. Therefore, in this sense, on the basis of existing theories, any effort to reduce approximations or relax assumptions will have a significant positive impact on the improvement of the computational accuracy and applicability of the solution, which may be seen from the results and discussions below.

In this study, the effort to relax the assumption or increase the degree of approximation is further considered, and a more refined closed-form solution of the well-known Hencky problem is presented. The conducted numerical example indicates that the presented closed-form solution has higher computational accuracy in comparison with the existing solutions. The detailed derivation of the more refined closed-form solution is arranged in the next section. In Section 3, some important issues are discussed, such as the difference between membrane problems and thin plate problems, reasonable approximations or assumptions during establishing geometric equations, and the contribution of reducing approximations or relaxing assumptions to the improvement of the computational accuracy and applicability of a solution. In Section 4, some opinions on the follow-up research for the well-known Hencky problem are presented.

2. Membrane Equation and Its Solution

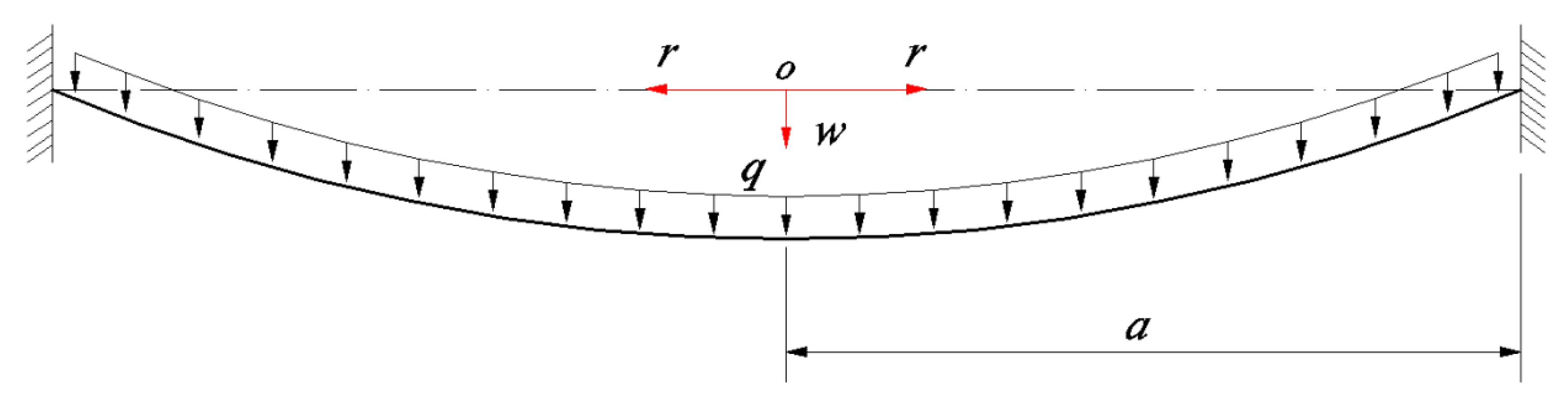
The uniformly distributed transverse loads q is quasi-statically applied onto the surface of a peripherally fixed and initially flat circular membrane with Poisson’s ratio v, Young’s modulus of elasticity E, radius a, and thickness h, as shown in Figure 1, where r is the radial coordinate, the dash dotted line represents the geometric middle plane of the initially flat circular membrane (in which the polar coordinate plane is located), and 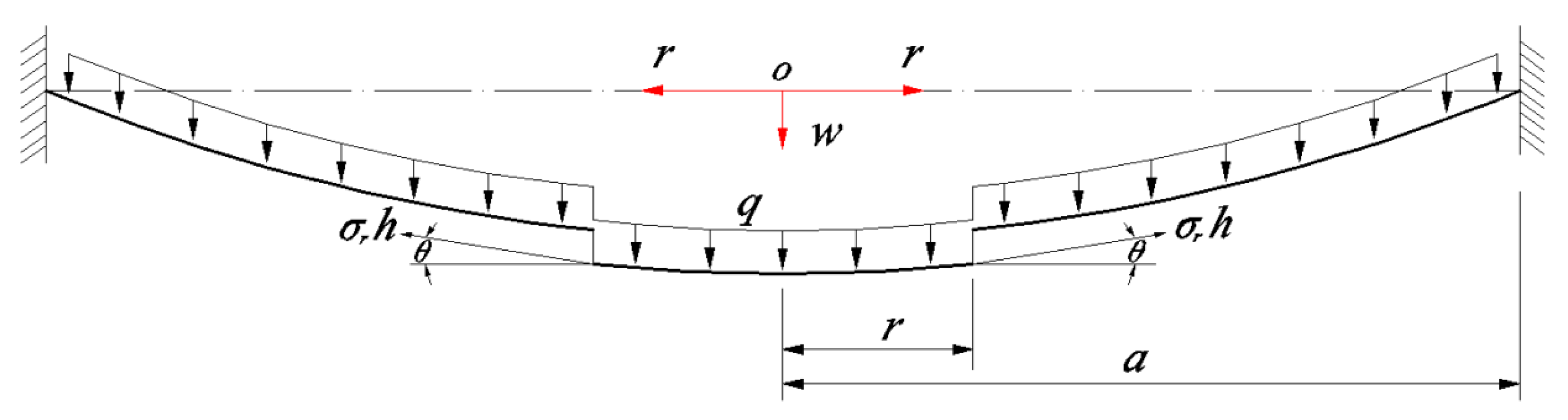w is the transversal coordinate as well as the transversal displacement of the deformed circular membrane. Let us take a piece of the circular membrane with radius 0 ≤ r ≤ a in the central portion of the deformed circular membrane, with a view of studying the static equilibrium problem of this deformed circular membrane under the transverse loads q and the membrane force ${\sigma }_{r}h$ acted on the boundary of radius r, as shown in Figure 2, where ${\sigma }_r$ denotes the radial stress (the mean stress over the cross-section of the deformed circular membrane), and θ is the rotation angle of the deflected membrane, that is, the usually so-called meridional rotation angle.

Throughout the derivation, we assume that the thickness of the membrane is always constant during its deformation, that is, the change in thickness is ignored. Along the vertical direction perpendicular to the initially flat circular membrane (see Figure 2), there are two vertical forces. These are the total external force πr²q and the total vertical force $2\pi r{\sigma }_{r}h\sin \theta$ which is produced by the membrane force ${\sigma }_{r}h$. Thus, the usually so-called out-of-plane equation of equilibrium is

$$2\pi r{\sigma }_{r}h\sin \theta =\pi r^{2}q,$$

(1)

where

$$\sin \theta =1/\sqrt{1+1/{\tan }^2\theta }=1/\sqrt{1+1/{(-dw/dr)}^2}.$$

(2)

Equation (2) follows the basic relationship between trigonometric functions, and its use is intended to give up the so-called small rotation angle assumption of the membrane, that is, sin θ can be replaced by tan θ because $\sin \theta \cong \tan \theta \cong \theta$ when θ is small enough, which is adopted in the well-known Hencky solution. Substituting Equation (2) into Equation (1), one has

$$\frac{1}{2}rq\sqrt{1+1/{(dw/dr)}^2}={\sigma }_{r}h.$$

(3)

In the horizontal plane, there are the joint actions of the circumferential membrane force ${\sigma }_{t}h$ and the horizontal force produced by the membrane force ${\sigma }_{r}h$, where ${\sigma }_t$ is the circumferential stress. So, the so-called in-plane equation of equilibrium can be written as

$$\frac{d}{dr}(r{\sigma }_{r}h)-{\sigma }_{t}h=0.$$

(4)

The detailed derivation of Equation (4) can be found in any general theory for plates and shells [29], so there is no need to discuss it here. As for the so-called geometric equations, that is, the relationships of the strain and displacement, the classic geometric equations [14,24,25,26,27] was modified and replaced by

$$e_r={[{(1+\frac{du}{dr})}^2+{(\frac{dw}{dr})}^2]}^{1/2}-1$$

(5)

and

$$e_t=\frac{u}{r},$$

(6)

where $e_r$ denotes the radial strain, $e_t$ denotes the circumferential strain, and u denotes the radial displacement. Equation (5) was obtained by relaxing some assumptions, and thus it has a higher accuracy in comparison with the classic geometric equations (however for brevity, its detailed derivation and the discussion on its accuracy were arranged in the next section). Moreover, the relationships of the stress and strain, that is, the so-called physical equations, are still assumed to satisfy linear elasticity, and after ignoring the change in membrane thickness it can be written as [29]

$${\sigma }_r=\frac{E}{1-{\nu }^2}(e_r+\nu e_t)$$

(7)

and

$${\sigma }_t=\frac{E}{1-{\nu }^2}(e_t+\nu e_r).$$

(8)

Substituting Equations (5) and (6) into Equations (7) and (8) yields

$${\sigma }_r=\frac{E}{1-{\nu }^2}\{{[{(1+\frac{du}{dr})}^2+{(\frac{dw}{dr})}^2]}^{1/2}-1+\nu \frac{u}{r}\}$$

(9)

and

$${\sigma }_t=\frac{E}{1-{\nu }^2}\{\frac{u}{r}+\nu {[{(1+\frac{du}{dr})}^2+{(\frac{dw}{dr})}^2]}^{1/2}-v\}.$$

(10)

By means of Equations (4), (9) and (10), it is found that

$$\frac{u}{r}=\frac{1}{Eh}({\sigma }_{t}h-\nu {\sigma }_{r}h)=\frac{1}{Eh}[\frac{d}{dr}(r{\sigma }_{r}h)-\nu {\sigma }_{r}h].$$

(11)

After substituting the u of Equation (11) into Equation (9), the so-called consistency equation can then be written as

$$\begin{array}{l}{\{\frac{d}{dr}[r\frac{d}{dr}(r{\sigma }_{r}h)]\}}^2+2Eh\frac{d}{dr}[r\frac{d}{dr}(r{\sigma }_{r}h)]-2v\frac{d}{dr}(r{\sigma }_{r}h)\times \frac{d}{dr}[r\frac{d}{dr}(r{\sigma }_{r}h)]\\ +2v{\sigma }_{r}h\frac{d}{dr}(r{\sigma }_{r}h)-2Eh({\sigma }_{r}h)-{({\sigma }_{r}h)}^2+E^2{h}^2{(\frac{dw}{dr})}^2=0\end{array}$$

(12)

The boundary conditions are

$$\frac{u}{r}=\frac{1}{Eh}[\frac{d}{dr}(r{\sigma }_{r}h)-\nu {\sigma }_{r}h]=0\mathrm{at}r=a,$$

(13)

$$w=0\mathrm{at}r=a$$

(14)

and

$$\frac{dw}{dr}=0\mathrm{at}r=0.$$

(15)

Let us introduce the following dimensionless variables

$$Q=\frac{aq}{hE},W=\frac{w}{a},S_r=\frac{{\sigma }_r}{E},S_t=\frac{{\sigma }_t}{E},x=\frac{r}{a}.$$

(16)

Transform Equations (3), (4), (11), (12), (13), (14) and (15) into

$$\begin{array}{l}{\{\frac{d}{dx}[x\frac{d}{dx}(x{S}_r)]\}}^2+2\frac{d}{dx}[x\frac{d}{dx}(x{S}_r)]-2v\frac{d}{dx}(x{S}_r)\times \frac{d}{dx}[x\frac{d}{dx}(x{S}_r)]\\ +2v{S}_r\frac{d}{dx}(x{S}_r)-2S_r-S_r^2+{(\frac{dW}{dx})}^2=0\end{array}$$

(17)

$${(\frac{dW}{dx})}^2=\frac{x^2{Q}^2}{4S_r^2-x^2{Q}^2},$$

(18)

$$S_t=S_r+x\frac{d{S}_r}{dx},$$

(19)

$$\frac{u}{r}=\frac{1}{Eh}[\frac{d}{dr}(rh{\sigma }_r)-\nu h{\sigma }_r]=x\frac{d{S}_r}{dx}+(1-\nu )S_r,$$

(20)

$$\frac{u}{r}=x\frac{d{S}_r}{dx}+(1-\nu )S_r=0\mathrm{at}x=1,$$

(21)

$$W=0\mathrm{at}x=1$$

(22)

and

$$\frac{dW}{dx}=0\mathrm{at}x=0.$$

(23)

Eliminating the $dW/dx$ from Equations (17) and (18), a second-order nonlinear ordinary differential equation containing only S_r can be obtained

$$\begin{array}{l}{\{\frac{d}{dx}[x\frac{d}{dx}(x{S}_r)]\}}^2+2\frac{d}{dx}[x\frac{d}{dx}(x{S}_r)]-2v\frac{d}{dx}(x{S}_r)\times \frac{d}{dx}[x\frac{d}{dx}(x{S}_r)]\\ +2v{S}_r\frac{d}{dx}(x{S}_r)-2S_r-S_r^2+\frac{x^2{Q}^2}{4S_r^2-x^2{Q}^2}=0\end{array}$$

(24)

Expand S_r into the power series of the x, that is, let

$$S_r(x)={\displaystyle \sum _{i=0}^{\infty }{b}_i{x}^i}.$$

(25)

After substituting Equation (25) into Equation (24) it is found that, b_i ≡ 0 (i = 1, 3, 5, …), and b_i (i = 2, 4, 6, …) can be expressed into the polynomial of the undetermined constant b₀ (see Appendix A). The undetermined constant b₀ can be determined by using the boundary condition at x = 1. From Equations (25), the condition of Equation (21) gives

$${\displaystyle \sum _{i=1}^{\infty }i{b}_i}+(1-\nu ){\displaystyle \sum _{i=0}^{\infty }{b}_i}=0.$$

(26)

After substituting all expressions of b_i (i = 2, 4, 6, …) into Equation (26), we can obtain an equation containing only b₀. Thus, the undetermined constant b₀ can be determined by solving its single variable equation, and the expression of S_r can thus be determined. As for S_t, it can easily be obtained by using Equation (19) with the known expressions of S_r, so it is not necessary to derive it here. On the other hand, W can also be expanded into the power series of the x

$$W(x)={\displaystyle \sum _{i=0}^{\infty }{c}_i{x}^i}.$$

(27)

Please note that at this time, the coefficients b_i in the expression of S_r were known. Hence, after substituting Equations (25) and (27) into Equation (18) it is found that, $c_i\equiv 0$ (i = 1, 3, 5, …), and $c_i$ (i = 2, 4, 6, …) can be expressed into the polynomial of the known b_i and another undetermined constant $c_0$ (see Appendix B). Furthermore, from Equation (27), Equation (22) gives

$$c_0=-{\displaystyle \sum _{i=1}^{\infty }{c}_i}.$$

(28)

After substituting all expressions of $c_i$ into Equation (28), we can also obtain an equation containing only $c_0$, and the undetermined constant $c_0$ can thus be determined. With the known $c_0$, the expression of W can be determined. Thus, the closed-form solution of the problem dealt with here can be obtained.

Finally, let us see whether the closed-form solution obtained above meets the boundary condition Equation (15) or Equation (23), that is, $dw/dr=0$ at $r=0$ or $dW/dx=0$ at $x=0$, which has not been used yet during the derivation above. The first derivative on both sides of Equation (27) is

$$\frac{dW}{dx}={\displaystyle \sum _{i=1}^{\infty }i{c}_i{x}^{i-1}}.$$

(29)

Thus, it is not difficult to obtain $dW/dx=c_1$ at $x=0$. However, from the derivation above we know $c_i\equiv 0$ when i = 1, 3, 5, …, this means $c_1\equiv 0$. Thus we can obtain $dW/dx=0$ at $x=0$ or $dw/dr=0$ at $r=0$. This indicates that the closed-form solution presented here can meet the physical phenomenon of axisymmetric deformation of the circular membrane.

3. Results and Discussion

From the derivation above, it can be seen that the well-known Hencky problem was regarded as a membrane problem, where the equilibrium equations, that is, Equations 1 and 4, were directly established by analyzing the forces on the deformed membrane. However, Hencky originally started from a thin plate bending problem to reach this problem, and because the “membrane” is usually sufficiently thin, the bending term in the well-known von Karman large deflection equations for thin plates was ignored [14]. But in terms of some questions from the peer review of our previous works, our above solving means do not seem to be widely accepted, and some scholars may be inclined to utilizing Hencky’s originally method.

Perhaps, the so-called “membrane” should have a unified definition in mechanics. Thin plates ought to become thin films if sufficiently thin, and they all have three-dimensional shapes, but the “membrane” does not emphasize the three-dimensional shape in mechanics, or more specifically, does not emphasize its thickness. The “membrane”, regardless of its thickness, should refer to a completely stretched thin plate (or thin film) fixed at its edge, because there is only tensile stress and no compressive stress on its cross-section after deformation. The so-called “neutral layer”, which is never stretched and compressed during deflection, is not in existence, and thus there is no “resultant couple moment” of the “neutral layer”, that is, the usually so-called bending moment. By way of examples, a peripherally fixed circular plate under transverse loads, no matter how thick or thin it is, is always called “membrane” in mechanics, because its upper and lower surfaces are always stretched during deflection. Thus, there is always only tensile stress and no compressive stress on its cross-section after deformation. This means that only the tensile stress resists to external loads, so only the tensile strength of materials is involved. On the contrary, a freely supported circular plate under transverse loads, no matter how thin it is (even a very thin film), can only rely on its bending moment to resist external loads if the friction at its support is ignored. Therefore, for freely supported circular plates, the tensile and compressive strength of materials are both our concern, and it is often necessary to analyze the distribution of the tensile and compressive stresses on the cross-section of a deformed plate (even a very thin deformed film). Thus, the so-called “membrane problem” should refer to a completely stretching problem of a thin plate (or thin film) under transverse loads, while the so-called “plate problem” often refers to a bending problem of a freely supported thin plate (or thin film) under transverse loads, regardless of its thickness. To say the least, the so-called “membrane” may be a thin plate or a thin film, but it must, regardless of its thickness, be fixed at its edge in order to limit the displacement at its edge. In mechanics, as the term “membrane” is always a concept associated with the action of external loads, in this sense, without “action” the “membrane” will lose its significance.

Of course, the well-known Hencky problem should be understood as a membrane problem, because the edge displacement of the membrane is completely limited by “fixed”. However, Hencky dealt with this problem from the point of view of the bending problem of a thin plate, by using the well-known von Karman large deflection equations for thin plates and ignoring the terms related to bending. This maybe seems somewhat farfetched, but Hencky does offer an effective solution. This is because the membrane force and bending moment were simultaneously taken into account during the establishment of the well-known von Karman large deflection equations. Therefore, after ignoring the bending-related terms, only the membrane force is left in the well-known von Karman equations. This could be where the well-known von Karman equations played its potentiality, however, for the membrane problem dealt with here, it can do nothing, because it contains some approximations or assumptions that are not allowed here. Thus, in this sense, dealing with a membrane problem does not need to follow the classic theories for thin plate bending problems, but needs to start from the physical phenomena. Moreover, the precondition that the rotation angle at the edge of the thin plate is equal to zero is usually used for thin plate bending problems. However, from the boundary conditions Equations (13)–(15), it can be seen that such a condition is not used, and in fact, from Equation (27), it can also be found that $dw/dr\ne 0$ at r = a. This could be where membrane problems are different from thin plate bending problems.

Compared with the existing studies on the well-known Hencky problem, the innovation in this study lies mainly in the modification to the classic geometric equation, resulting in the modified geometric equation as shown in Equation (5), and the more refined closed-form solution. Then, where does the modified geometric equation come from, and what will be the effect of the more refined closed-form solution presented here? Now let us address these two issues. The detailed derivation of Equation (5) is shown as follows. As for Equation (6), it can be derived out easily, so it is not necessary to discuss it here.

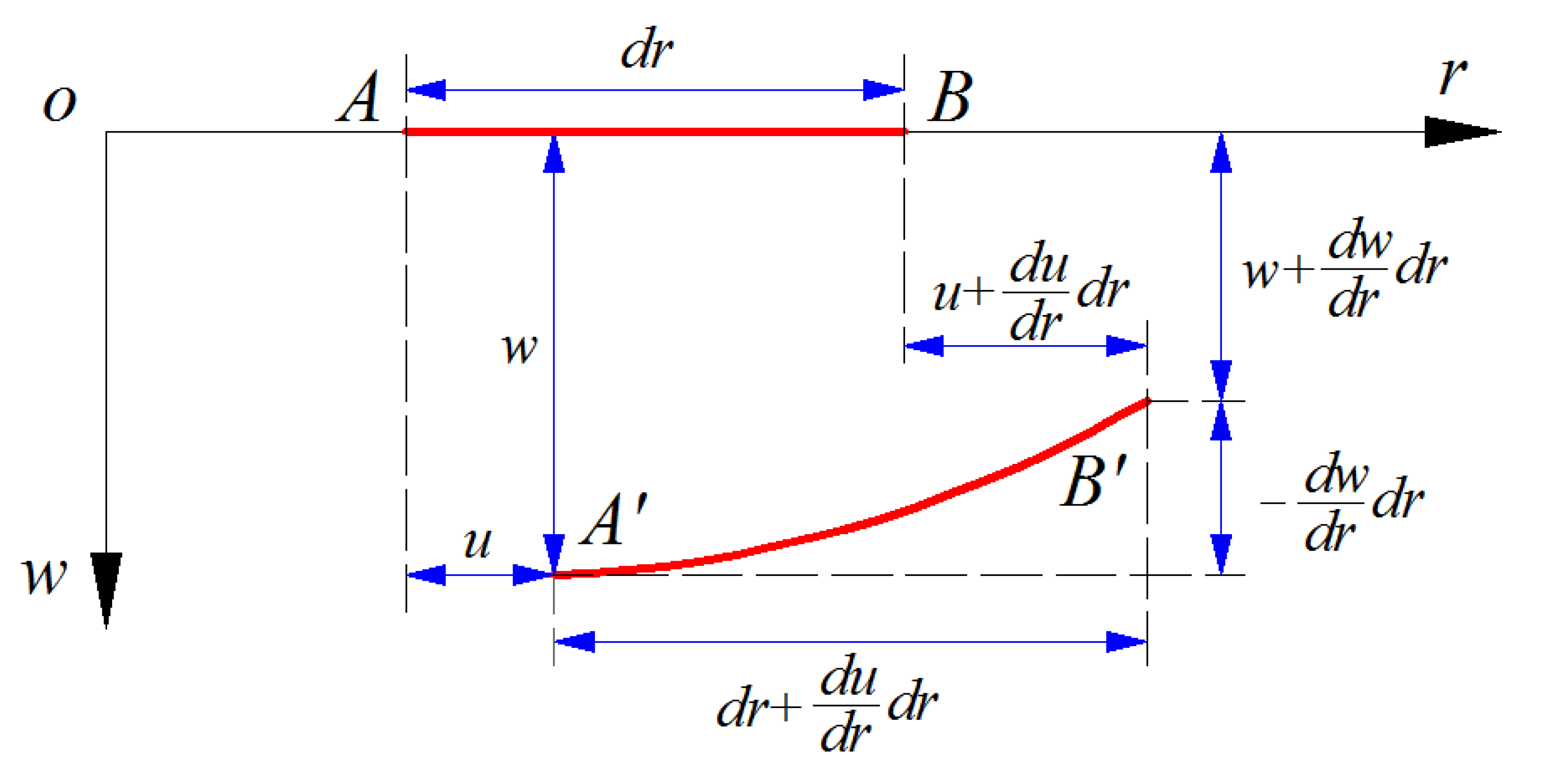
Suppose that, a straight line micro element $\overline{AB}$ with the length dr, which originally lies in the geometric middle plane of the initially flat circular membrane, is taken along the r axis of the polar coordinate system, and under the action of the uniformly-distributed transverse loads q, it will become the curve $\stackrel{⌢}{A^{\prime }{B}^{\prime }}$ along with the deformation of the circular membrane, as shown in Figure 3. Therefore, the elongation degree of this line micro element, that is, the radial strain, should be

$$e_r=\frac{\stackrel{⌢}{A^{\prime }{B}^{\prime }}-\overline{AB}}{\overline{AB}}.$$

(30)

If the radial displacement and deflection at point $A^{\prime }$ is denoted as u and w, respectively, then after expanded into Taylor series, the radial displacement and deflection at point $B^{\prime }$ can be written as

$$u+\frac{du}{dr}dr+\frac{1}{2!}\frac{d^{2}u}{d{r}^2}{(dr)}^2+\frac{1}{3!}\frac{d^{3}u}{d{r}^3}{(dr)}^3+\cdots$$

(31)

and

$$w+\frac{dw}{dr}dr+\frac{1}{2!}\frac{d^{2}w}{d{r}^2}{(dr)}^2+\frac{1}{3!}\frac{d^{3}w}{d{r}^3}{(dr)}^3+\cdots ,$$

(32)

respectively.

Here there are two kinds of reasonable methods for approximation or assumption in accordance with different deflection situations of the membrane, they are: ① assume that before and after the deflection of the membrane, the length of the line microelement is approximately equal, that is, $\stackrel{⌢}{A^{\prime }{B}^{\prime }}\cong \overline{AB}$; ② assume that after the deflection of the membrane the length of the curve $\stackrel{⌢}{A^{\prime }{B}^{\prime }}$ is approximately equal to the length of the straight line $\overline{A^{\prime }{B}^{\prime }}$, that is, $\stackrel{⌢}{A^{\prime }{B}^{\prime }}\cong \overline{A^{\prime }{B}^{\prime }}$. The assumption ① is suitable for the classic large deflection problems in the existing studies, where the deflection of the membrane is not too large, while the assumption ② is clearly relaxed in comparison with the assumption ①, because the degree of approximation of $\stackrel{⌢}{A^{\prime }{B}^{\prime }}\cong \overline{A^{\prime }{B}^{\prime }}$ is higher than that of $\stackrel{⌢}{A^{\prime }{B}^{\prime }}\cong \overline{AB}$. Therefore, the assumption ② is suitable for a larger deflection in comparison with assumption ①. In fact, the assumption ① belongs to the case of the so-called microdeformation from the point of view of the modern theory of elasticity, and in this sense, the assumption ② should be a relaxation towards the so-called finite deformation. It is clear that, if assumption ① holds, then the assumption ② also hold, that is, $\stackrel{⌢}{A^{\prime }{B}^{\prime }}\cong \overline{A^{\prime }{B}^{\prime }}$ so long as $\stackrel{⌢}{A^{\prime }{B}^{\prime }}\cong \overline{AB}$. In addition to the above two assumptions, it is usually also necessary to further make the following approximation: all the high order differential terms in Equations (31) and (32) must be ignored, with only the first order differential term remaining to reflect the dynamics of the displacement and deflection (the nonlinearity), as done in the existing studies. To this end, the radial displacement and deflection at point $B^{\prime }$ were approximately written as u + (du/dr)dr and w + (dw/dr)dr, respectively, as shown in Figure 3. Thus, under the condition of assumption ①, Equation (30) can be further written as, with the help of assumption ②,

$$e_r=\frac{\stackrel{⌢}{A^{\prime }{B}^{\prime }}-\overline{AB}}{\overline{AB}}=\frac{(\stackrel{⌢}{A^{\prime }{B}^{\prime }}+\overline{AB})(\stackrel{⌢}{A^{\prime }{B}^{\prime }}-\overline{AB})}{(\stackrel{⌢}{A^{\prime }{B}^{\prime }}+\overline{AB})\overline{AB}}\cong \frac{{(\overline{A^{\prime }{B}^{\prime }})}^2-{(\overline{AB})}^2}{2{(\overline{AB})}^2}\cong \frac{du}{dr}+\frac{1}{2}{(\frac{dw}{dr})}^2.$$

(33)

Equation (33) is the classic geometric equation used in existing studies. While only under the condition of assumption ②, Equation (30) can be further written as

$$\begin{array}{l}{e}_r=\frac{\stackrel{⌢}{A^{\prime }{B}^{\prime }}-\overline{AB}}{\overline{AB}}\cong \frac{\overline{A^{\prime }{B}^{\prime }}-\overline{AB}}{\overline{AB}}\\ {{}_{}^{}}_{}^{}{}_{}^{}\cong \frac{\sqrt{{(dr+\frac{du}{dr}dr)}^2+{(-\frac{dw}{dr}dr)}^2}-dr}{dr}=\sqrt{{(1+\frac{du}{dr})}^2+{(\frac{dw}{dr})}^2}-1\end{array}$$

(34)

Equation (34) is the so-called modified geometric equation in this study, which is shown in Equation (5). This is the reason why the degree of approximation of the modified geometric equation (Equation (34) or Equation (5)) is higher than that of the classic geometric equation (Equation (33)).

It should be pointed out that, probably due to the difficulties during the analytical solving, one might think of the further simplification of Equation (34), for example, with the help of expansion of $\sqrt{{(1+du/dr)}^2+{(dw/dr)}^2}$ [30], Equation (34) may be further approximated as

$$e_r=\sqrt{{(1+\frac{du}{dr})}^2+{(\frac{dw}{dr})}^2}-1\cong \frac{du}{dr}+\frac{1}{2}{(\frac{dw}{dr})}^2[1-\frac{1}{4}{(\frac{dw}{dr})}^2].$$

(35)

As mentioned above, however, it is difficult to conduct a qualitative or quantitative analysis to make clear how much influence of such an approximation has on the computational accuracy of the solution. Therefore, it would be best not to make such a further approximation unless you have to.

Now let us consider a numerical example to discuss the contribution of reducing approximations or relaxing assumptions to the improvement of the computational accuracy and applicability of the solution. Suppose that a peripherally fixed circular rubber thin-film with $a=20 \mathrm{mm}$, $h=0.06 \mathrm{mm}$, $E=7.84\mathrm{MPa}$ and $\nu =0.47$ is subjected to the uniformly transverse loads $q=$ 0.001 MPa and 0.03 MPa, respectively. Three closed-form solutions are used here: the well-known Hencky solution [24] which contains the small rotation angle assumption and uses the classical geometric equation (i.e., Equation (33)), our earlier closed-form solution [26] which does not contain the small rotation angle assumption but uses Equation (33), and the more refined closed-form solution presented in this study which does not contain the small rotation angle assumption and uses the modified geometric equation (i.e., Equation (5) or (34)).

Figure 4 shows the two sets of numerical results for the deflection profiles, that is, the variations of the deflection $w$ with the radius $r$ when the loads q takes 0.001 and 0.03 MPa, respectively, in which the solid lines represent the results obtained by using the solution presented in this study, the dashed lines by our earlier solution [26], and the dash dotted lines by the well-known Hencky solution [24]. From Figure 4, it can be seen that when q = 0.001 MPa the three deflection curves are very close to each other, which indicates that for this deflection situation, the efforts made to reduce approximations or relax assumptions result in a very little effect on the improvement of the computational accuracy of the solution, while when q = 0.03 MPa there are obvious differences between the three deflection curves, which indicates that the approximations or assumptions in the classic geometric equation as well as the small rotation angle assumption will give rise to a greater influence on the computational accuracy of the solution. These two sets of results also show that the applicability of the solution presented in this study has been improved after reducing approximations or relaxing assumptions.

Usually, under the uniformly distributed transverse loads q, the rotation angle θ of the deformed membrane in the central portion of the circular membrane is smaller than that in the region far away from the center of the circular membrane. Therefore, the contribution of giving up the small rotation angle assumption to the improvement of the computational accuracy of the solution in the central portion should be smaller than that in the region far away from the center. Hence, the difference between the upper dash dotted line and the second dashed line in the central portion (about 0 ≤ r ≤ 5 mm) is smaller than that in the region far away from the center, as shown in the deflection profile for q = 0.03 MPa in Figure 4. It is clear that this difference is caused only by the so-called small rotation angle assumption of the membrane, because compared with the well-known Hencky solution (corresponding to the upper dash dotted line), our earlier solution (corresponding to the second dashed line) only gives up the small rotation angle assumption. Of course, such a difference also indicates that our earlier work in which only the small rotation angle assumption was given up [26] is also of positive significance to the improvement of the computational accuracy of the solution.

On the other hand, the rotation angle in the central portion is smaller than that in the region far away from the center, which also means that the deflected membrane in the central portion is flatter than that in the region far away from the center. Consequently, the assumption ② used to the modify geometric equation, that is, the condition $\stackrel{⌢}{A^{\prime }{B}^{\prime }}\cong \overline{A^{\prime }{B}^{\prime }}$, should be satisfied more easily in the central portion than in the region far away from the center. In other words, the contribution of the somewhat relaxed assumption $\stackrel{⌢}{A^{\prime }{B}^{\prime }}\cong \overline{A^{\prime }{B}^{\prime }}$ to the improvement of the computational accuracy of the solution in the central portion should be somewhat bigger than that in the region far away from the center. This also means that, however, there are still computational errors in the region far away from the center, and the farther away from the center the greater the computational error. This is the role the modified geometric equation plays in the more refined closed-form solution of the well-known Hencky problem. Therefore, the deflection outline (the third solid line for q = 0.03 MPa presented in Figure 4) is maybe not as reliable in 5 mm < r < 20 mm as that in 0 < r < 5 mm, and in a real situation, it could slightly swell to the left and right. The qualitative interpretation is that, in 5 mm < r < 20 mm, the straight line $\overline{A^{\prime }{B}^{\prime }}$ is clearly shorter than the curve $\stackrel{⌢}{A^{\prime }{B}^{\prime }}$. This means that a smaller value is involved in the computational operation for the reason of replacing $\stackrel{⌢}{A^{\prime }{B}^{\prime }}$ with $\overline{A^{\prime }{B}^{\prime }}$, so the calculation results of deflection value should be inclined to being small. This is also something to be aware of when using the modified geometric equation—Equation (5) or Equation (34).

4. Concluding Remarks

In this paper, the well-known Föppl–Hencky membrane problem was resolved, where the so-called small rotation angle assumption of the membrane was given up when establishing the out-of-plane equation of equilibrium, and a new and more effective geometric equation was, for the first time, established to replace the classic one. The new boundary value problem of the resulting nonlinear differential equation was successfully solved by using the power series method, and a more refined closed-form solution of the problem was presented. The numerical example conducted indicates that the solution presented here has a higher computational accuracy in comparison with the existing solutions.

The study on the well-known Hencky problem has come a long way in the last one hundred years, but it has even further to go. By way of examples, the approximate treatment of ignoring all the high order differential terms in Equations (31) and (32) still continues; the assumption of constant thickness of the deformed membrane is also still present. In fact, these approximations or assumptions are still where they were. Therefore, the follow-up research of the well-known Hencky problem should focus on the following two aspects.

Due to the approximate treatment of ignoring all the high order differential terms in Equations (31) and (32) (especially Equation (32)), the modified geometric equation (i.e., Equation (5)) is still not very satisfactory, especially for overlarge deflection situations. Therefore, it seems to be more important to find a more efficient way to establish a more effective geometric equation, as it cannot be directly established by taking into account a few of the high order differential items in Equations (31) or (32). The other aspect is that the thickness of the deformed membrane could be considered as a function with respect to the radial coordinate variable, but the resulting change in physical equations also needs to be considered. These issues will be addressed in our further studies.