Theoretical Aspects on Measures of Directed Information with Simulations
Abstract
1. Introduction
2. Measures of Directed Entropy
2.1. Discrete Case
- 1.
- .
- 2.
- If , then where is the Shannon entropy.
- 3.
- If for some then irrespectively of the values of the weights .
- 4.
- If and where , , then .
- 5.
- , for any .
- 6.
- For every non-negative, real number λ we have . The weight of the union of two incompatible events E and F is given by:If the events are complementary the reduces to .
- 7.
- If the equation holds then for and , then:
2.2. Continuous Case
3. Measures of Directed Divergence
3.1. Discrete Case
- It is a continuous function of , and .
- It is permutationally symmetric function of , and , i.e., it does not change when the triplets (, , ), (, , ), ⋯, (, , ) are permuted among themselves.
- It is always greater than or equal to zero for all possible choices of weights and vanishes when for each .
- It is a convex function of which has its minimum value zero when for each .
- It reduces to an ordinary measure of directed divergence upon ignoring weights .
3.2. Continuous Case
3.3. Asymptotic Distribution of CWKL Divergence Estimator
4. Simulations
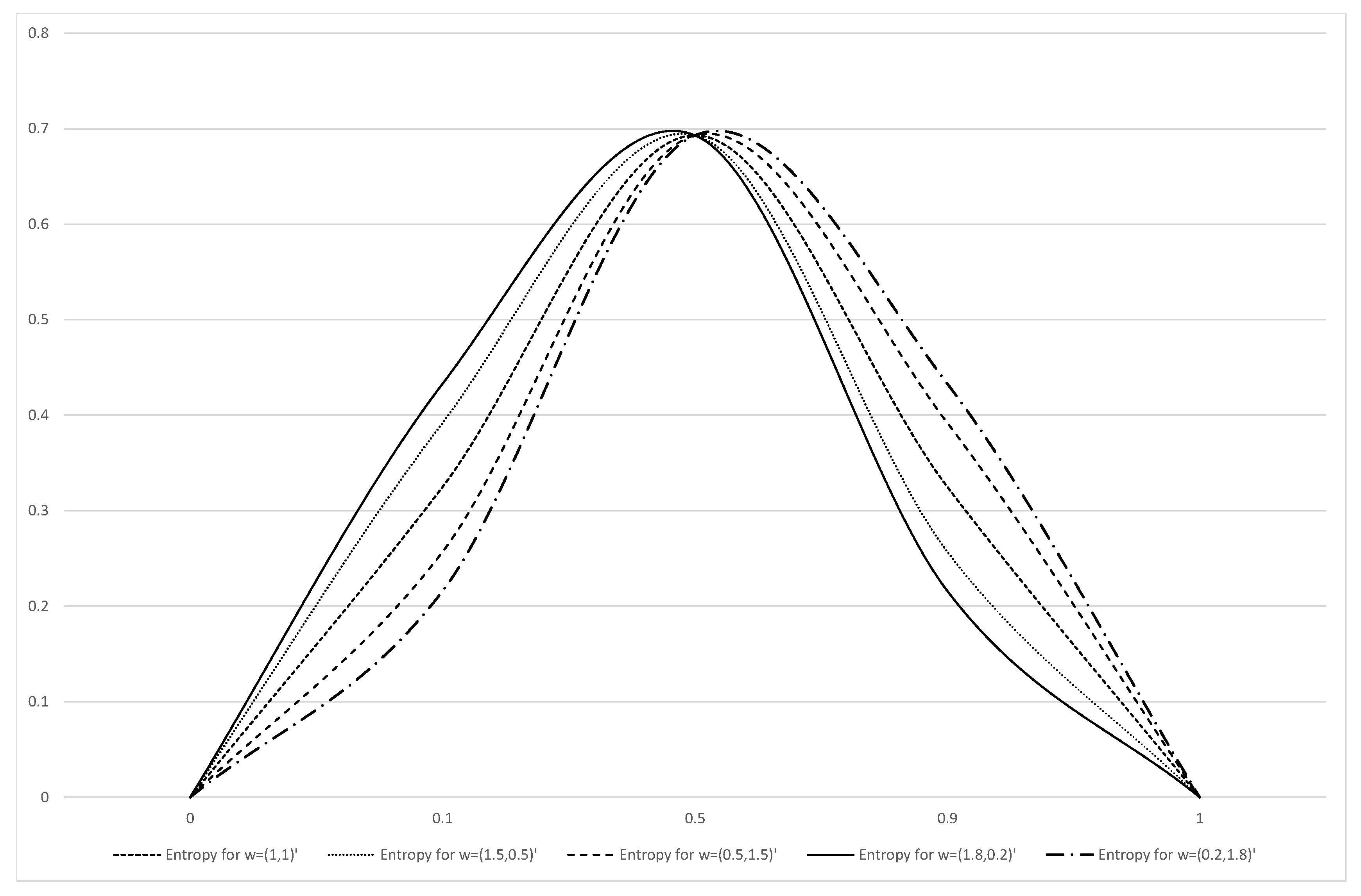
4.1. Weighted Shannon Entropy
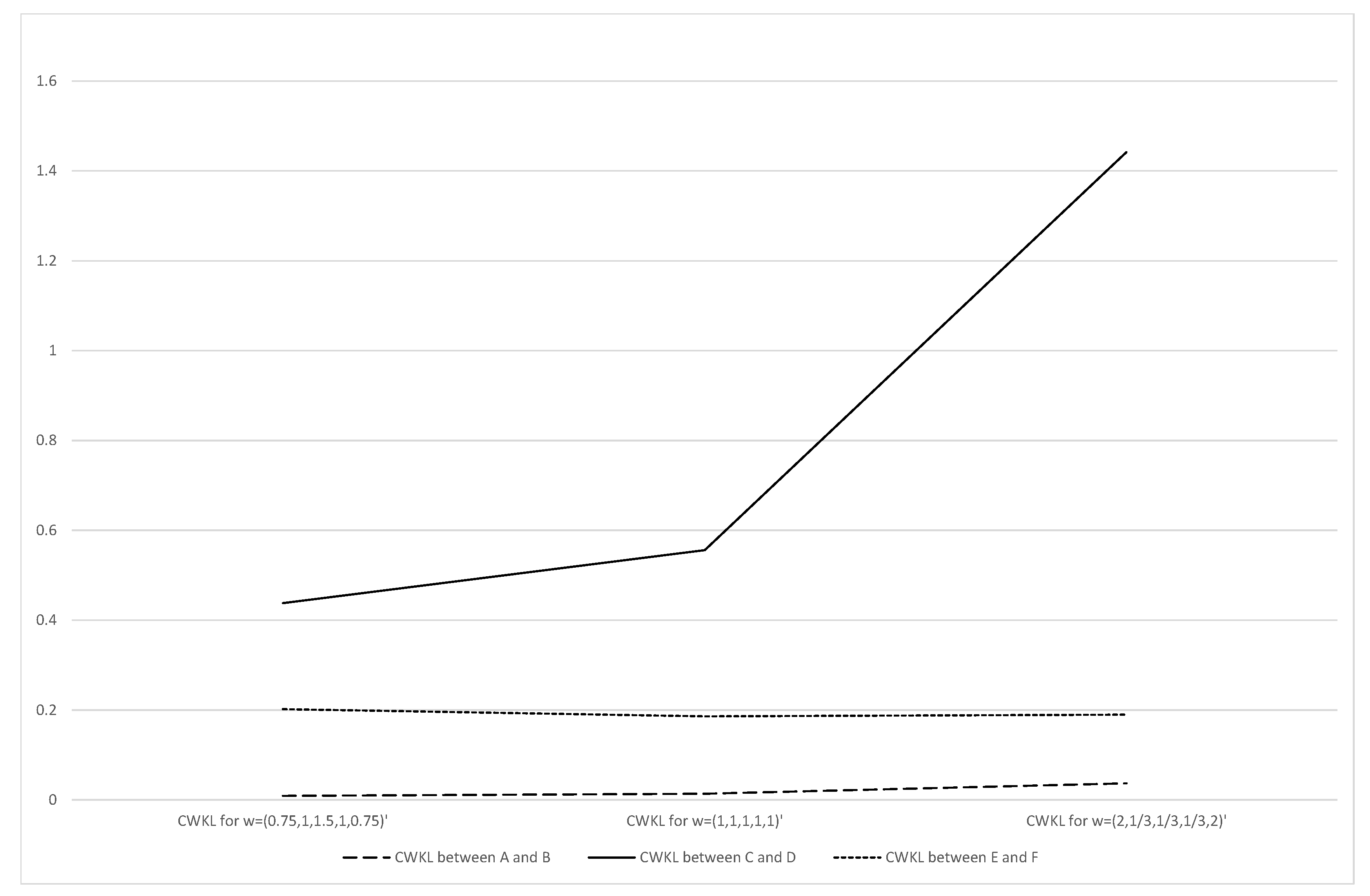
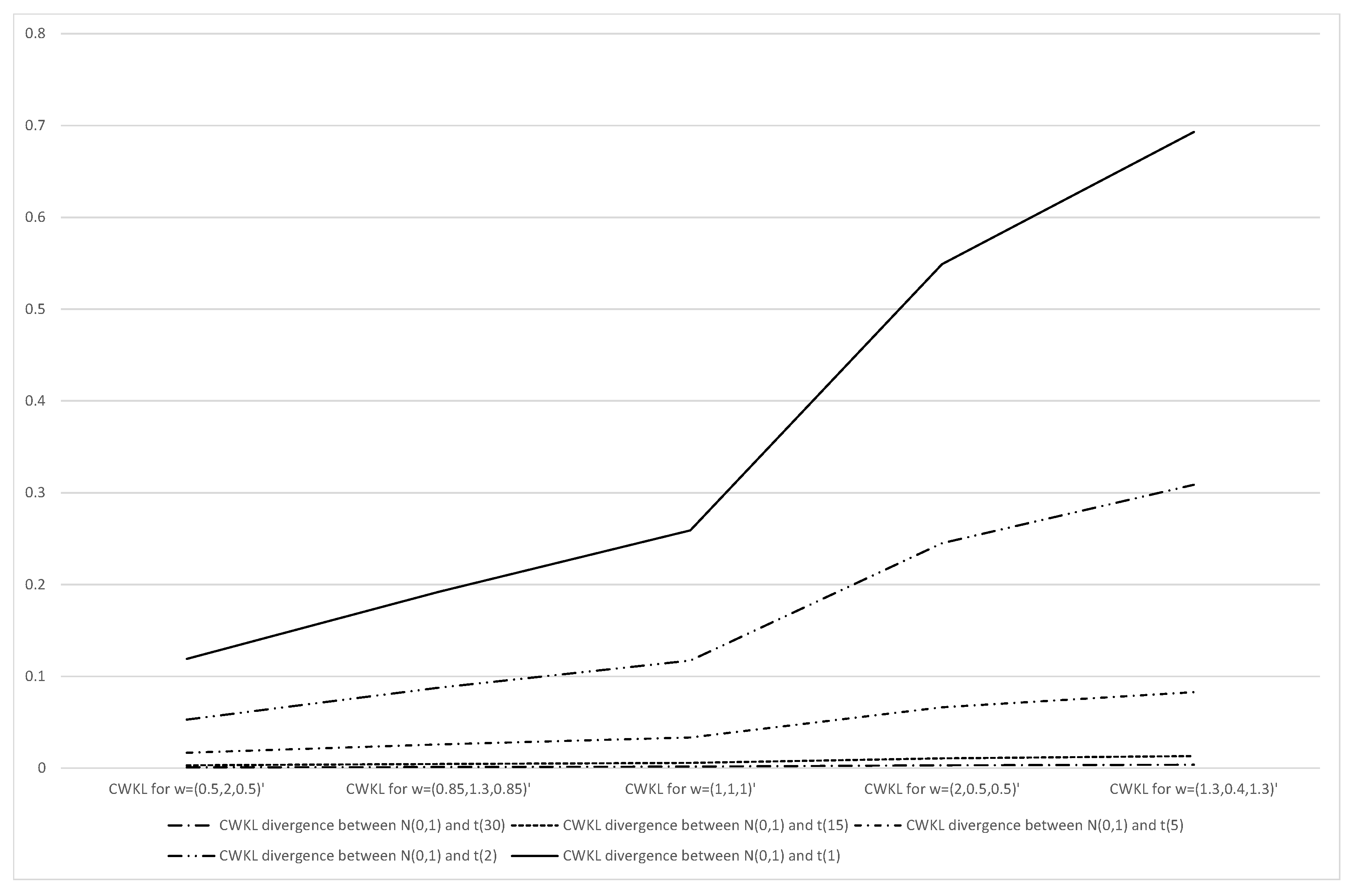
4.2. CWKL Divergence
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nawrocki, D.N.; Harding, W.H. State-value weighted entropy as a measure of investment risk. Appl. Econ. 1986, 18, 411–419. [Google Scholar] [CrossRef]
- Basseville, M. Distance measures for signal processing and pattern recognition. Signal Process. 1989, 18, 349–369. [Google Scholar] [CrossRef]
- Jimenez-Gamero, M.D.; Batsidis, A. Minimum distance estimators for count data based on the probability generating function with applications. Metrika 2017, 80, 503–545. [Google Scholar] [CrossRef]
- Pardo, L. Statistical Inference Based on Divergence Measures; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Cressie, N.; Read, T.R. Multinomial goodness-of-fit tests. J. R. Stat. Soc. Ser. B Methodol. 1984, 46, 440–464. [Google Scholar] [CrossRef]
- Lee, S.; Vonta, I.; Karagrigoriou, A. A maximum entropy type test of fit. Comput. Stat. Data Anal. 2011, 55, 2635–2643. [Google Scholar] [CrossRef]
- Cavanaugh, J.E. Criteria for linear model selection based on Kullback’s symmetric divergence. Aust. N. Z. J. Stat. 2004, 46, 257–274. [Google Scholar] [CrossRef]
- Shang, J.; Cavanaugh, J.E. Bootstrap variants of the Akaike information criterion for mixed model selection. Comput. Stat. Data Anal. 2008, 52, 2004–2021. [Google Scholar] [CrossRef]
- Toma, A. Model selection criteria using divergences. Entropy 2014, 16, 2686. [Google Scholar] [CrossRef]
- Guiaşu, S. Weighted Entropy. Rep. Math. Phys. 1971, 2, 165–179. [Google Scholar] [CrossRef]
- Frank, O.; Men é ndez, M.L.; Pardo, L. Asymptotic distributions of weighted divergence between discrete distributions. Commun. Stat. Theory Methods 1998, 27, 867–885. [Google Scholar] [CrossRef]
- Barbu, V.S.; Karagrigoriou, A.; Preda, V. Entropy and divergence rates for markov chains: II. The weighted case. Proc. Rom. Acad. Ser. A 2018, 1, 3–10. [Google Scholar]
- Avlogiaris, G.; Micheas, A.; Zografos, K. On local divergences between two probability measures. Metrika 2016, 79, 303–333. [Google Scholar] [CrossRef]
- Belis, M.; Guiaşu, S. A quantitative-qualitative measure of information in cubernetic systems. IEEE Trans. Inf. Theory 1968, 14, 593–594. [Google Scholar] [CrossRef]
- Guiaşu, S. Grouping data by using the weighted entropy. J. Stat. Plan. Inference 1990, 15, 63–69. [Google Scholar] [CrossRef]
- Di Crescenzo, A.; Longobardi, M. On weighted residual and past entropies. arXiv 2007, arXiv:math/0703489. [Google Scholar]
- Suhov, Y.; Zohren, S. Quantum weighted entropy and its properties. arXiv 2014, arXiv:11411.0892. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Moddemeijer, R. On estimation of entropy and mutual information of continuous distributions. Signal Process. 1989, 16, 233–248. [Google Scholar] [CrossRef]
- Marsh, C. Introduction to Continuous Entropy; Department of Computer Science, Princeton University: Princeton, NJ, USA, 2013. [Google Scholar]
- Kullback, S.; Leibler, R. On information and sufficiency. Ann. Math. Stat. 1951, 22, 571–575. [Google Scholar] [CrossRef]
- Kapur, J.N. Measures of Information and Their Applications; Publishing House: New York, NY, USA, 1994. [Google Scholar]
- Csiszar, I. On infinite products of random elements and infinite convolutions of probability distributions on locally compact groups. Z. Wahrscheinlichkeitstheorie verw Gebiete 1966, 5, 279–295. [Google Scholar] [CrossRef]
- Zografos, K.; Ferentinos, K.; Papaioannou, T. Divergence statistics: Sampling properties and multinomial goodness of fit and divergence tests. Commun. Stat. Theory Methods 1990, 19, 1785–1802. [Google Scholar] [CrossRef]
- Morales, D.; Pardo, L.; Vajda, I. Asymptotic divergence of estimates of discrete distributions. J. Stat. Plan. Inference 1995, 48, 347–369. [Google Scholar] [CrossRef]
- Johnson, R.A.; Wichern, D.W. Applied Multivariate Statistical Analysis, 3rd ed.; Publishing House, Prentice Hall International Editions: Englewood Cliffs, NJ, USA, 1992. [Google Scholar]
- Barndorff-Nielsen, O.E.; Shephard, N. Non-Gaussian Ornstein-Uhlenbeck-based models and some of their uses in financial economics. J. R. Stat. Soc. Ser. B 2001, 63, 167–241. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E.; Shephard, N. Modelling by Lévy processes for financial econometrics. In Lévy Processes; Birkhäuser: Boston, MA, USA, 2001; pp. 283–318. [Google Scholar]
- Barndorff-Nielsen, O.E. Superposition of Ornstein-Uhlenbeck type processes. Theory Probab. Appl. 2001, 45, 175–194. [Google Scholar] [CrossRef]
| 0.325 | 0.693 | 0.325 | |
| 0.392 | 0.693 | 0.257 | |
| 0.257 | 0.693 | 0.392 | |
| 0.433 | 0.693 | 0.216 | |
| 0.216 | 0.693 | 0.433 |
| State i | Return | A() | B() | C() | D() | E() | F() |
|---|---|---|---|---|---|---|---|
| 1 | |||||||
| 2 | |||||||
| 3 | |||||||
| 4 | |||||||
| 5 |
| Population | Sample Size | Estimates |
|---|---|---|
| 31 | ||
| 28 | ||
| 26 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gkelsinis, T.; Karagrigoriou, A. Theoretical Aspects on Measures of Directed Information with Simulations. Mathematics 2020, 8, 587. https://doi.org/10.3390/math8040587
Gkelsinis T, Karagrigoriou A. Theoretical Aspects on Measures of Directed Information with Simulations. Mathematics. 2020; 8(4):587. https://doi.org/10.3390/math8040587
Chicago/Turabian StyleGkelsinis, Thomas, and Alex Karagrigoriou. 2020. "Theoretical Aspects on Measures of Directed Information with Simulations" Mathematics 8, no. 4: 587. https://doi.org/10.3390/math8040587
APA StyleGkelsinis, T., & Karagrigoriou, A. (2020). Theoretical Aspects on Measures of Directed Information with Simulations. Mathematics, 8(4), 587. https://doi.org/10.3390/math8040587






