One Dimensional Discrete Scan Statistics for Dependent Models and Some Related Problems

Abstract

The one dimensional discrete scan statistic is considered over sequences of random variables generated by block factor dependence models. Viewed as a maximum of an 1-dependent stationary sequence, the scan statistics distribution is approximated with accuracy and sharp bounds are provided. The longest increasing run statistics is related to the scan statistics and its distribution is studied. The moving average process is a particular case of block factor and the distribution of the associated scan statistics is approximated. Numerical results are presented.

1. Introduction

There are many situations when an investigator observes an accumulation of events of interest and wants to decide if such a realisation is due to hazard or not. These types of problems belong to the class of cluster detection problems, where the basic idea is to identify regions that are unexpected or anomalous with respect to the distribution of events. Depending on the application domain, these anomalous agglomeration of events can correspond to a diversity of phenomena—for example one may want to find clusters of stars, deposits of precious metals, outbreaks of disease, minefield detections, defectuous batches of pieces and many other possibilities. If such an observed accumulation of events exceeds a preassigned threshold, usually determined from a specified significance level corresponding to a normal situation (the null hypothesis), then it is legitimate to say that we have an unexpected cluster and proper measures has to be taken accordingly.

Searching for unusual clusters of events is of great importance in many scientific and technological fields, including DNA sequence analysis ([1,2]), brain imaging ([3]), target detection in sensors networks ([4,5]), astronomy ([6,7]), reliability theory and quality control ([8]) among many other domains. One of the tools used by practitioners to decide on the unusualness of such agglomeration of events is the scan statistics. Basically, the tests based on scan statistics are looking for events that are clustered amongst a background of those that are sporadic.

Let $2\le m\le T$ be two positive integers and $X_1,\dots ,X_T$ be a sequence of independent and identically distributed random variables with the common distribution $F_0$. The one dimensional discrete scan statistics is defined as

$${\displaystyle S_m\left(T\right)=\underset{1\le i\le T-m+1}{max}{W}_i,}$$

(1)

where the random variables $W_i$ are the moving sums of length m given by

$${\displaystyle W_i=\sum _{j=i}^{i+m-1}{X}_j.}$$

(2)

Usually, the statistical tests based on the one dimensional discrete scan statistics are employed when one wants to detect a local change in the signal within a sequence of T observations via testing the null hypothesis of uniformity, $H_0$, against a cluster alternative, $H_1$ (see References [9,10]). Under $H_0$, the random observations $X_1,\dots ,X_T$ are i.i.d. distributed as $F_0$, while under the alternative hypothesis, there exists a location $1\le i_0\le T-m+1$ where $X_i$, $i\in \{i_0,\dots ,i_0+m-1\}$, are distributed according to $F_1\ne F_0$ and outside this region $X_i$ are distributed as $F_0$.

We observe that whenever $S_m\left(T\right)$ exceeds the threshold $\tau$, where the value of $\tau$ is computed based on the relation ${\mathbb{P}}_{H_0}\left(S_m\left(T\right)\ge \tau \right)=\alpha$ and $\alpha$ is a preassigned significance level of the testing procedure, the generalized likelihood ratio test rejects the null hypothesis in the favor of the clustering alternative (see Reference [9]). It is interesting to note that most of the research has been done for $F_0$ being binomial, Poisson or normal distribution (see References [9,10,11,12,13]). More recently, Reference [14] proposed a testing procedure based on one-dimensional scan statistic for geometric and negative binomial distributions.

There are three main approaches used for investigating the exact distribution of the one dimensional discrete scan statistics—the combinatorial methods ([12,15]), the Markov chain imbedding technique ([16,17]) and the conditional probability generating function method ([18,19]). Due to the high complexity and the limited range of application of the exact formulas, a considerable number of approximations and bounds have been developed for the estimation of the distribution of the one dimensional discrete scan statistics, for example, References [9,12,13,20]. A full treatment of these results is presented in References [10,11].

Even if in general the $X_i$’s are supposed to be i.i.d distributed, there are applications, such as detecting similarities between DNA sequences, where the $X_i$’s are not independent ([21]). In order to evaluate the effect of dependence, the alternative model is in many cases a Markov chain the whole dependence structure of which depends only on the joint distribution of two consecutive random variables.

In this work we introduce dependence models based on block-factors obtained from i.i.d. sequences in the context of the one dimensional discrete scan statistics. We derive approximations and their corresponding errors with application to the longest increasing run distribution and the moving average process.

The paper is structured as follows. In Section 2 we introduce the block factor model and present the approximation technique for the distribution of the scan statistics under this model. As a particular block factor model, the distribution of the length of the longest increasing run in a trial of i.i.d real random variables and the moving average processes are related to the scan statistics distribution in Section 3. Numerical results based on simulations illustrate the accuracy of the approximation. Concluding remarks end the paper.

2. One Dimensional Scan Statistics for Block-Factor Dependence Model

Most of the research devoted to the one dimensional discrete scan statistic considers the independent and identically distributed model for the random variables that generate the sequence which is to be scanned. In this section, we define a dependence structure for the underlying random sequence based on a block-factor type model.

2.1. The Block-Factor Dependence Model

Let us recall (see also Reference [22]) that the sequence ${\left\{X_i\right\}}_{i\ge 1}$ of random variables with state space $S_W$ is said to be k block-factor of the sequence ${\left\{Y_i\right\}}_{i\ge 1}$ with state space $S_Y$ if there is a measurable function $f:S_Y^k\to S_W$ such that

$$X_i=f\left(Y_i,Y_{i+1},\dots ,Y_{i+k-1}\right),\forall i\ge 1.$$

(3)

The Figure 1 presents the sequence ${\left\{X_i\right\}}_{i=1,\dots ,T}$ of length T obtained as a k block-factor from a sequence ${\left\{Y_i\right\}}_{i=1,\dots ,\tilde{T}}$ of length $\tilde{T}=T+k-1$ throughout some function f.

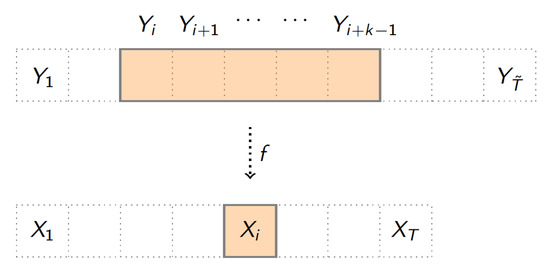
Figure 1. The block factor model.

As an example of block-factor model, in Reference [23], the authors consider an i.i.d. sequence ${\left\{Y_n\right\}}_{n\ge 1}$ of standard normal distributed random variables and the 2 block-factor defined by

$$X_i=a{Y}_i+b{Y}_{i+1},i\ge 1,\mathrm{for}f(x,y)=ax+by,a,b\in \mathbb{R}.$$

Therefore, due to the overlapping structure of $X_i$ and $X_{i+1}$, they obtain a Gaussian stationary process ${\left\{X_i\right\}}_{i\ge 1}$ with some correlation structure for which the scan statistics distribution is studied.

More generally, let observe that if a sequence ${\left\{X_i\right\}}_{i\ge 1}$ of random variables is a k block-factor, then the sequence is $(k-1)$-dependent. Recall that a sequence ${\left\{X_i\right\}}_{i\ge 1}$ is m-dependent with $m\ge 1$ (see Reference [22]), if for any $h\ge 1$ the $\sigma$-fields generated by $\{X_1,\dots ,X_h\}$ and $\{X_{h+m+1},\dots \}$ are independent.

2.2. Scan Statistics Viewed as Maximum of 1-Dependent Sequence

Let $\{X_1,\dots ,X_T\}$ be a k-block factor of the i.i.d. sequence $\{Y_1,\dots ,Y_{\tilde{T}}\}$, where ${\tilde{T}}_1\ge k$ and $T=\tilde{T}-k+1$, and $S_m\left(T\right)$ be the scan statistics associated to the sequence ${\left\{X_i\right\}}_{i=1,\dots ,T}$ as defined in (1) for some scanning window of length m, $1\le m\le T$.

Put $T=(L-1)(m+k-2)+m-1$ for some integer $L\ge 1$ and define, for each $j\in \{1,\dots ,L-1\}$, the random variables

$${\displaystyle Z_j=\underset{(j-1)(m+k-2)+1\le i\le j(m+k-2)}{max}{W}_i,}$$

(4)

where $W_i={\sum }_{s=i}^{i+m-1}{X}_s$. That is, for each $j\in \{1,\dots ,L-1\}$, $Z_j$ is the scan statistic associated to the sequence of length $2m+k-3$, $\{X_{(j-1)(m+k-2)+1},\dots ,X_{j(m+k-2)+m-1}\}$. An illustration of the construction of variables $Z_j$ is presented in Figure 2 for $L=5$ and $k=1$.

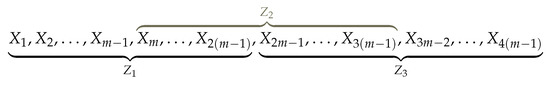
Figure 2. Construction of $Z_j$.

Then, ${\left\{Z_j\right\}}_{j=1,\dots ,L-1}$ is 1-dependent and stationary and we have that

$${\displaystyle S(m,T)=\underset{1\le j\le L-1}{max}{Z}_j.}$$

(5)

Thus, for any block factor model obtained from an i.i.d sequence, the distribution of the associated scan statistics is the distribution of the maximum of some 1-dependent stationary sequence.

2.3. Approximation

In References [24,25] the authors extended the approximation results obtained in Reference [26] for the distribution of the maximum of a 1-dependent stationary sequence. The main results is stated in the following theorem.

Let ${\left\{Z_j\right\}}_{j\ge 1}$ be a strictly stationary 1-dependent sequence of random variables and for $x<sup\left\{u\right|\mathbb{P}(Z_1\le u)<1\}$, let

$$1q_n=q_n\left(x\right)=\mathbb{P}(max(Z_1,\dots ,Z_n)\le x).$$

(6)

Theorem 1.

For all x such that $q_1\left(x\right)\ge 1-\alpha \ge 0.9$, the following approximation formula holds:

$$\left|q_n-\frac{2q_1-q_2}{{\left[1+q_1-q_2+2{(q_1-q_2)}^2\right]}^n}\right|\le nF(\alpha ,n){(1-q_1)}^2$$

(7)

with

$$F(\alpha ,n)=1+\frac{3}{n}+\left[\frac{\Gamma \left(\alpha \right)}{n}+K\left(\alpha \right)\right](1-q_1)$$

(8)

where $\Gamma \left(\alpha \right)=L\left(\alpha \right)+E\left(\alpha \right)$,

$$\begin{array}{cc}\hfill K\left(\alpha \right)& =\frac{\frac{11-3\alpha }{{(1-\alpha )}^2}+2l(1+3\alpha )\frac{2+3l\alpha -\alpha (2-l\alpha ){(1+l\alpha )}^2}{{\left[1-\alpha {(1+l\alpha )}^2\right]}^3}}{1-\frac{2\alpha (1+l\alpha )}{{\left[1-\alpha {(1+l\alpha )}^2\right]}^2}}\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill L\left(\alpha \right)& =3K\left(\alpha \right)(1+\alpha +3{\alpha }^2)[1+\alpha +3{\alpha }^2+K\left(\alpha \right){\alpha }^3]+{\alpha }^6{K}^3\left(\alpha \right)\hfill \\ & +9\alpha (4+3\alpha +3{\alpha }^2)+55.1\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill E\left(\alpha \right)& =\frac{{\eta }^5{\left[1+(1-2\alpha )\eta \right]}^4\left[1+\alpha (\eta -2)\right]\left[1+\eta +(1-3\alpha ){\eta }^2\right]}{2{(1-\alpha {\eta }^2)}^4\left[{(1-\alpha {\eta }^2)}^2-\alpha {\eta }^2{(1+\eta -2\alpha \eta )}^2\right]}\hfill \end{array}$$

(11)

and where $\eta =1+l\alpha$ with $l=l\left(\alpha \right)=t_2^3\left(\alpha \right)+\epsilon$, for arbitrarily small $\epsilon >0$, and $t_2\left(\alpha \right)$ the second root in magnitude of the equation $\alpha t^3-t+1=0$.

The evaluation of the functions K and $\Gamma$ for some selected values of $\alpha$ is presented in Table 1. These values allow to compute directly the error bound approximation in (7).

Table 1. Selected values for l, K and $\Gamma$ functions in Theorem 1 for $\epsilon ={10}^{-6}$.

$\mathit{\alpha }$	$\mathit{l}(\mathit{\alpha })$	$\mathit{K}(\mathit{\alpha })$	$\mathbf{\Gamma }\left(\mathit{\alpha }\right)$
$0.1$	$1.5347$	$38.63$	$480.69$
$0.05$	$1.1893$	$21.28$	$180.53$
$0.025$	$1.0835$	$17.56$	$145.20$
$0.01$	$1.0313$	$15.92$	$131.43$

Applying Theorem 1 to the sequence ${\left\{Z_j\right\}}_{j=1,\dots ,L-1}$ defined in (4), from (5) we obtain an approximation and the associated error bound for $\mathbb{P}\left(S\right(m,T)\le x)$ in the following way. Put for $s\in \{2,3\}$,

$${\displaystyle Q_s=Q_s\left(x\right)=\mathbb{P}\left(\bigcap _{j=1}^{s-1}\{Z_j\le x\}\right)}$$

(12)

and observe that using the notation of (6) we have $Q_s=q_{s-1}$. For x such that $Q_2\left(x\right)\ge 1-\alpha \ge 0.9$ we apply the result from Theorem 1 to obtain the approximation

$$\mathbb{P}\left(S(m,T)\le x\right)\approx \frac{2Q_2-Q_3}{{\left[1+Q_2-Q_3+2{(Q_2-Q_3)}^2\right]}^{(L-1)}},$$

(13)

with an error bound of about $(L-1)F({\alpha }_1,L-1){(1-Q_2)}^2$. Observe that $Q_2$ and $Q_3$ represent the distributions of the scan statistics over sequences of variable $Z_j$ of lengths $2m+k-3$ and respectively $3m+2k-5$. $Q_2$ and $Q_3$ are generally estimated by Monte Carlo simulation.

Thus, if ${\widehat{Q}}_s$ is an estimate of $Q_s$, $s\in \{2,3\}$, with $\left|{\widehat{Q}}_s-Q_s\right|\le {\beta }_s$ and x is such that $1-{\widehat{Q}}_2\left(x\right)\le 0.1$ then

$$\left|\mathbb{P}\left(S(m,T)\le x\right)-\left(2{\widehat{Q}}_2-{\widehat{Q}}_3\right){\left[1+{\widehat{Q}}_2-{\widehat{Q}}_3+2{({\widehat{Q}}_2-{\widehat{Q}}_3)}^2\right]}^{1-L}\right|\le E_{total},$$

(14)

where $E_{total}$ is the total error of the approximation given by

$$E_{total}=(L-1)\left[{\beta }_2+{\beta }_3+F\left({\widehat{Q}}_2,L-1\right){\left(1-{\widehat{Q}}_2+{\beta }_2\right)}^2\right].$$

(15)

One of the main advantage of this approximation method with respect to the product-type approximation proposed in Reference [12], who uses the same quantities $Q_2$ and $Q_3$, is that it provides sharp error bounds for the approximation.

3. Some Related Problems to the Scan Statistics under Block-Factor Dependence Model

In order to illustrate the efficiency of the approximation (14) and the obtained error bounds, in this section we present two examples of statistics related to discrete scan statistics.

3.1. Length of the Longest Increasing Run in a i.i.d Sequence

Let $Y_1$, $Y_2$, …, $Y_{\tilde{T}}$ be a sequence of length $\tilde{T}$, $\tilde{T}\ge 1$, of independent and identically distributed random variables with the common distribution F. We say that the subsequence $\left(Y_k,\dots ,Y_{k+l-1}\right)$ forms an increasing run (or ascending run) of length $l\ge 1$, starting at position $k\ge 1$, if it verifies the following relation

$$Y_{k-1}>Y_k<Y_{k+1}<\cdots <Y_{k+l-1}>Y_{k+l}.$$

(16)

We denote the length of the longest increasing run among the first $\tilde{T}$ random variables by $M_{\tilde{T}}$. This run statistics plays an important role in many applications in fields such computer science, reliability theory or quality control. The asymptotic behaviour of $M_{\tilde{T}}$ has been investigated by several authors depending on the common distribution, F. In the case of a continuous distribution [27] (see also Reference [28]) has shown that this behaviour does not depend on the common law. For the particular setting of uniform $U\left(\right[0,1\left]\right)$ random variables, this problem was addressed by References [29,30,31]. Under the assumption that the distribution F is discrete, the limit behaviour of $M_{\tilde{T}}$ depends strongly on the common law F, as in Reference [32] (see also References [33,34]) proved for the case of geometric and Poisson distribution. In Reference [35], the case of discrete uniform distribution is investigated, while in Reference [36], the authors study the asymptotic distribution of $M_{\tilde{T}}$ when the variables are uniformly distributed but not independent.

In this section, we evaluate the distribution of the length of the longest increasing run using the methodology developed in Section 2. The idea is to express the distribution of the random variable $M_{\tilde{T}}$ in terms of the distribution of the scan statistics random variable.

Let $T=\tilde{T}-1$ and define the block-factor transformation $f:{\mathbb{R}}^2\to \mathbb{R}$ by

$$f(x,y)=\left\{\begin{array}{c}1,\mathrm{if} x<y\hfill \\ 0,\mathrm{otherwise}.\hfill \end{array}\right.$$

(17)

Then, our block-factor model becomes

$$X_i=f(Y_i,Y_{i+1})={\mathbf{1}}_{Y_i<Y_{i+1}}.$$

(18)

and $X_1$, …, $X_T$ form a 1-dependent and stationary sequence of random variables.

Notice that the distribution of $M_{\tilde{T}}$ and the distribution of the length of the longest run of ones, $L_T$, among the first T binary random variables $X_i$, are related and satisfy the following identity

$$\mathbb{P}\left(M_{\tilde{T}}\le m\right)=\mathbb{P}\left(L_T<m\right),\mathrm{for} m\ge 1.$$

(19)

The statistics $L_T$ is also known as the length of the longest success run or head run and was extensively studied in the literature. One can consult the monographs of References [16,17] for applications and further results concerning this statistic. Moreover, the random variable $L_T$ can be interpreted as a particular case of the scan statistics random variable and between the two we have the relation

$$\mathbb{P}\left(L_T\ge m\right)=\mathbb{P}\left(S(m,T)=m\right).$$

(20)

Hence, combining (19) and (20), we can express the distribution of the length of the longest increasing run as

$$\mathbb{P}\left(M_{\tilde{T}}\le m\right)=\mathbb{P}\left(S(m,T)<m\right).$$

(21)

Thus, we can estimate the distribution of $M_{\tilde{T}}$ using the foregoing identity and the approximations developed in Section 2 for the discrete scan statistics random variable.

We should also note that in Reference [30] the authors studied the asymptotic behaviour of $L_T$ over a sequence of m-dependent binary random variables. They showed that, given a stationary m-dependent sequence of random variables with values 0 and 1, ${\left\{V_k\right\}}_{k\ge 1}$, if there exist positive constants t, C such that

$$\mathbb{P}\left(V_{k+1}=1|V_1=\cdots =V_k=1\right)\ge \frac{1}{C{k}^t},\mathrm{for} \mathrm{all} k\ge C,$$

(22)

then, as $N\to \infty$

$${\displaystyle \underset{1\le k\le N}{max}\left|\mathbb{P}\left(L_N<k\right)-e^{-Nr\left(k\right)}\right|=\mathcal{O}\left(\frac{{(lnN)}^h}{N}\right),}$$

(23)

where $r\left(k\right)=\mathbb{P}\left(V_1=\cdots =V_k=1\right)-\mathbb{P}\left(V_1=\cdots =V_{k+1}=1\right)$ and $h=sup\{mt,1\}$.

In order to illustrate the accuracy of the approximation of $M_{\tilde{T}}$ based on scan statistics, using the methodology developed in Section 2, we consider that the random variables $Y_i$’s have a common uniform $U\left([0,1]\right)$ distribution. Simple calculations show that $\mathbb{P}\left(X_1=\cdots =X_k=1\right)=\frac{1}{(k+1)!}$ and

$$\mathbb{P}\left(X_{k+1}=1|X_1=\cdots =X_k=1\right)=\frac{1}{k+2}\ge \frac{1}{2k},$$

(24)

thus $C=2$, $t=1$ and $h=1$. In the context of our particular situation, the result of Reference [30] in Equation (23) becomes:

$${\displaystyle \underset{1\le m\le T}{max}\left|\mathbb{P}\left(L_T<m\right)-e^{-Tr\left(m\right)}\right|=\mathcal{O}\left(\frac{lnT}{T}\right),}$$

(25)

where $r\left(m\right)=\mathbb{P}\left(X_1=\cdots =X_m=1\right)-\mathbb{P}\left(X_1=\cdots =X_{m+1}=1\right)=\frac{m+1}{(m+2)!}$.

In Table 2, we consider a numerical comparison study between the simulated value (column $Sim$) obtained by Monte Carlo simulation with $ITE{R}_{sim}={10}^4$ trials, the approximation based on scan statistics (column $App$) computed from the Equation (14) where ${\widehat{Q}}_2$ and ${\widehat{Q}}_3$ are computed with $ITE{R}_{app}={10}^5$ trials and the limit distribution (column $LimApp$) of the distribution of the length of the longest increasing run, $\mathbb{P}\left(M_{\tilde{T}}\le m\right)$, in a sequence of $\tilde{T}=10001$ random variables distributed uniformly over $[0,1]$. The results show that both our method and the asymptotic approximation in (25) are very accurate. It is worth mentioning that for our simulations we used an adapted version of the Importance Sampling procedure introduced in Reference [3], an efficient method that proved to perform very well for small p values (where naive Monte Carlo methods tend to break down) [37].

Table 2. The distribution of the length of the longest increasing run: $\tilde{T}=10001$, $ITE{R}_{sim}={10}^4$, $ITE{R}_{app}={10}^5$.

m	Sim	App	${\mathit{E}}_{\mathbf{total}}$	LimApp
		Equation (14)	Equation (15)	Equation (25)
5	0.00000700	0.00000733	0.14860299	0.00000676
6	0.17567262	0.17937645	0.01089628	0.17620431
7	0.80257424	0.80362353	0.00110990	0.80215088
8	0.97548510	0.97566460	0.00011579	0.97550345
9	0.99749821	0.99751049	0.00001114	0.99749792
10	0.99977074	0.99977183	0.00000098	0.99977038
11	0.99998075	0.99998083	0.00000008	0.99998073
12	0.99999851	0.99999851	0.00000001	0.99999851
13	0.99999989	0.99999989	0.00000000	0.99999989
14	0.99999999	0.99999999	0.00000000	0.99999999
15	1.00000000	1.00000000	0.00000000	1.00000000

3.2. The Moving Average - Like Process of Order q Model

We consider the particular situation of the one dimensional discrete scan statistics defined over a sequence of random variables obtained as a linear block factor of a discrete Gaussian white noise. Because of the similarity with the definition of a classical moving average process, we call that block factor model a moving average - like process. It is worth mentioning that the distribution of the scan statistics in the context of a moving average process for normal data was studied in Reference [38] where the authors compared the product-type approximation developed in Reference [13] with the approximation of Reference [23]. In the block-factor model introduced in (3), let $q\ge 1$ be a positive integer and $Y_1$, $Y_2$, …, $Y_{\tilde{T}}$ be a sequence of independent and identically Gaussian distributed random variables with known mean $\mu$ and variance ${\sigma }^2$.

Let $\mathbf{a}=(a_1,\dots ,a_{q+1})\in {\mathbb{R}}^{q+1}$ be a fixed non null vector and take $f:{\mathbb{R}}^{q+1}\to \mathbb{R}$, the (measurable) transformation that defines the block-factor model, to be equal with

$$f(y_1,\dots ,y_{q+1})=a_1{y}_1+a_2{y}_2+\cdots +a_{q+1}{y}_{q+1}.$$

(26)

For $i\in \{1,\dots ,T\}$, with $T=\tilde{T}-q$, our dependent model is defined by the relation

$$X_i=a_1{Y}_i+a_2{Y}_{i+1}+\cdots +a_{q+1}{Y}_{i+q}.$$

(27)

The moving sums of size m, $W_i$, $1\le i\le T-m+1$ can be expressed as

$${\displaystyle W_i=\sum _{j=i}^{i+m-1}{X}_j=b_1{Y}_i+b_2{Y}_{i+1}+\cdots +b_{m+q}{Y}_{i+m-1+q},}$$

(28)

where the coefficients $b_1$, …, $b_{m+q}$ are evaluated by

(a)

For $m\ge q$,

$$b_k=\left\{\begin{array}{cc}{\displaystyle \sum _{j=1}^k{a}_j}\hfill & ,k\in \{1,\dots ,q\}\hfill \\ {\displaystyle \sum _{j=1}^{q+1}{a}_j}\hfill & ,k\in \{q+1,\dots ,m\}\hfill \\ {\displaystyle \sum _{j=k-m+1}^{q+1}{a}_j}\hfill & ,k\in \{m+1,\dots ,m+q\}\hfill \end{array}\right.$$

(29)

(b)

For $m<q$,

$$b_k=\left\{\begin{array}{cc}{\displaystyle \sum _{j=1}^k{a}_j}\hfill & ,k\in \{1,\dots ,m\}\hfill \\ {\displaystyle \sum _{j=k-m+1}^k{a}_j}\hfill & ,k\in \{m+1,\dots ,q\}\hfill \\ {\displaystyle \sum _{j=k-m+1}^{q+1}{a}_j}\hfill & ,k\in \{q+1,\dots ,m+q\}.\hfill \end{array}\right.$$

(30)

Therefore, for each $i\in \{1,\dots ,T-m+1\}$, the random variable $W_i$ follows a normal distribution with mean $\mathbb{E}\left[W_i\right]=(b_1+\cdots +b_{m+q})\mu$ and variance $Var\left[W_i\right]=\left(b_1^2+\cdots +b_{m+q}^2\right){\sigma }^2$. Moreover, a simple calculation shows that the covariance matrix $\Sigma =\left\{Cov\left[W_t,W_s\right]\right\}$ has the entries

$$Cov\left[W_t,W_s\right]=\left\{\begin{array}{cc}{\displaystyle \left(\sum _{j=1}^{m+q-|t-s|}{b}_j{b}_{|t-s|+j}\right){\sigma }^2}\hfill & ,|t-s|\le m+q-1\hfill \\ 0\hfill & ,\mathrm{otherwise}.\hfill \end{array}\right.$$

(31)

Given the mean and the covariance matrix of the vector $(W_1,\dots ,W_{T-m+1})$, one can use the importance sampling algorithm developed in Reference [3] (see also Reference [37]) or the one presented in Reference [39] to estimate the distribution of the one dimensional discrete scan statistics $S(m,T)$. Another way is to use the quasi-Monte Carlo algorithm developed in Reference [40] to approximate the multivariate normal distribution.

In our application example we adopt the importance sampling procedure developed in Reference [3]. In order to evaluate the accuracy of the approximation developed in (14), we consider $q=2$, $T=1000$, $m=20$, $Y_i\sim \mathcal{N}(0,1)$ and the coefficients of the moving average model to be $(a_1,a_2,a_3)=(0.3,0.1,0.5)$. We compare our approximation (column $App$) given in (14) with the one (column AppPT) given in Reference [41] using product-type approximations. In Table 3, we present numerical results for the setting described above. In our algorithms we used $ITE{R}_{app}={10}^6$ trials for the computation of ${\widehat{Q}}_2$(x) and ${\widehat{Q}}_3\left(x\right)$ and $ITE{R}_{sim}={10}^5$ trials for the Monte-Carlo simulation of the $\mathbb{P}\left(S\right(m,T)\le x)$.

Table 3. MA-like(q = 2) model: $m=20$, $T=1000$, $X_i=0.3Y_i+0.1Y_{i+1}+0.5Y_{i+2}$, $ITE{R}_{app}={10}^6$, $ITE{R}_{sim}={10}^5$.

x	Sim	AppPT	App	${\mathit{E}}_{\mathbf{total}}$
			Equation (14)	Equation (15)
11	0.582252	0.589479	0.584355	0.015156
12	0.770971	0.773700	0.771446	0.004010
13	0.889986	0.890009	0.889431	0.001167
14	0.951529	0.954536	0.951723	0.000370
15	0.980653	0.982433	0.980675	0.000124
16	0.992827	0.993690	0.992791	0.000042
17	0.997486	0.995471	0.997499	0.000014
18	0.999186	0.999411	0.999188	0.000004
19	0.999754	0.999717	0.999754	0.000001
20	0.999930	1	0.999930	0.000000

4. Conclusions

Block factor models defined from i.i.d. sequence generate random sequences with a particular type of dependence structure. For this type of dependence, the scan statistics can be viewed as the maximum of a 1-dependent stationary sequence, for which the distribution can be approximated with high accuracy. The approximation error can be controlled by using efficient algorithms of simulation as for example the importance sampling approach proposed in Reference [3] (see also Reference [25]). We approximated the distribution of longest increasing run statistics over an i.i.d sequence as a particular case of scan statistics distribution over a block factor model.