An Evolve-Then-Correct Reduced Order Model for Hidden Fluid Dynamics
Abstract
:1. Introduction
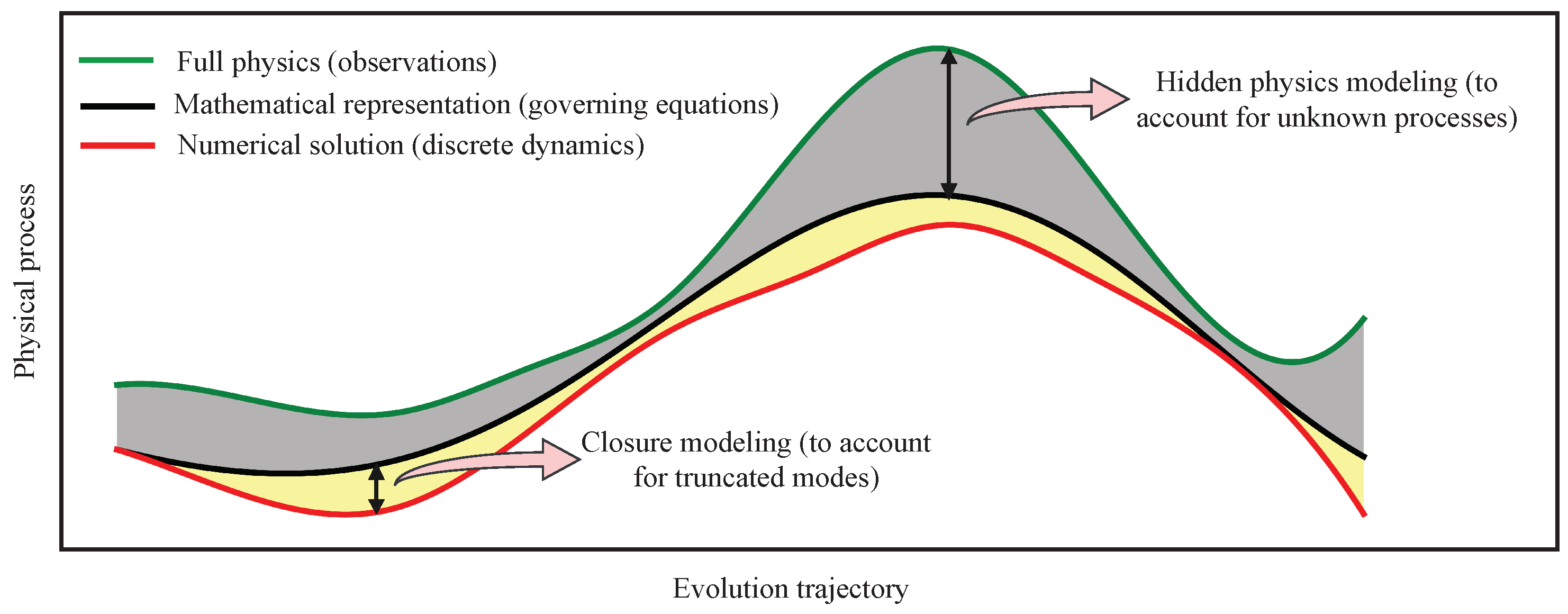
2. Motivating Examples
3. Evolve-Then-Correct Approach
3.1. ETC-LS: Least-Squares Correction
3.2. ETC-LSTM: Long Short-Term Memory Correction
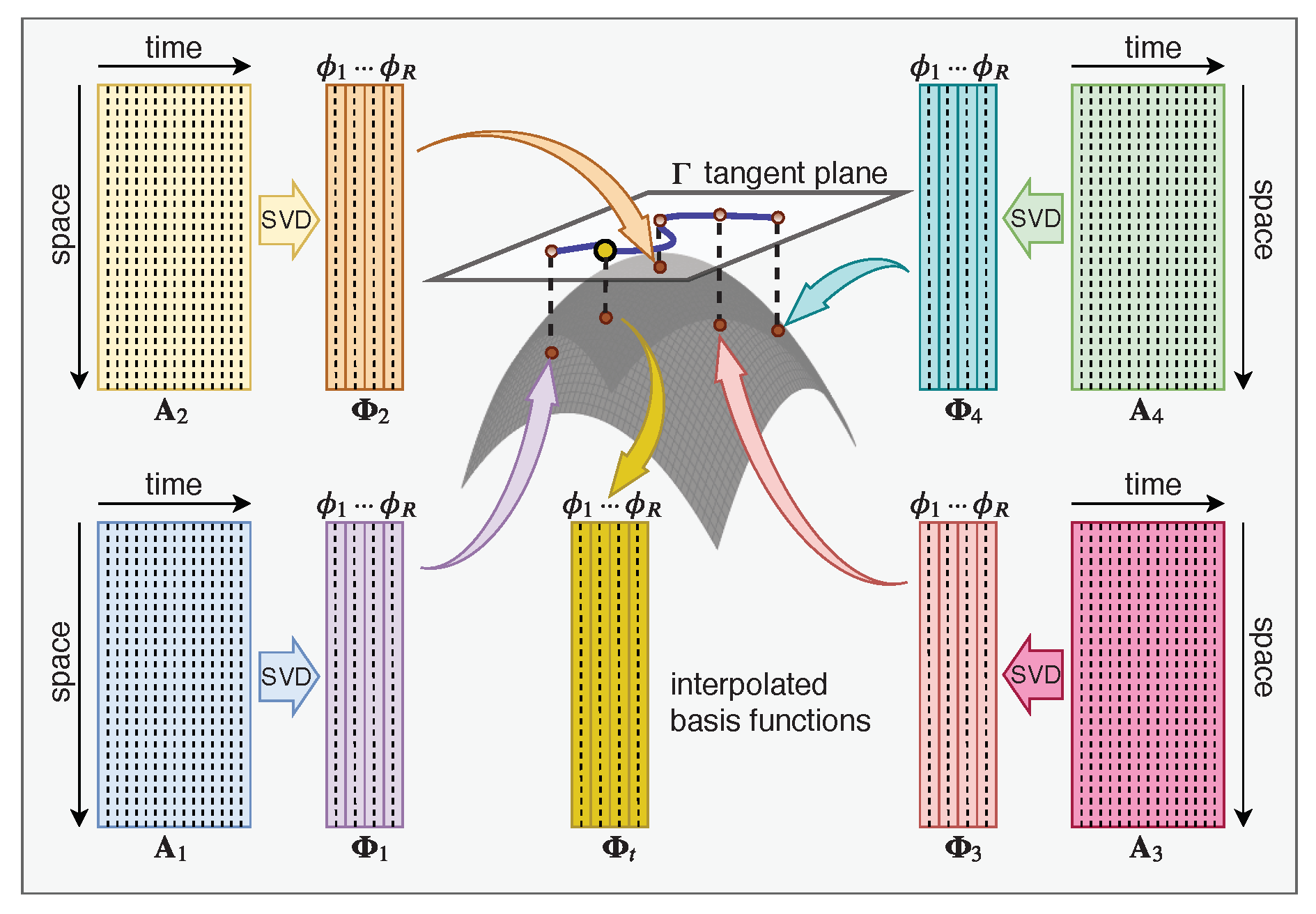
3.3. Grassmann Manifold Interpolation
| Algorithm 1 Grassmann manifold interpolation. | |
| 1: | Given a set of basis functions corresponding to the offline simulations (i.e., with mapping ) parameterized by . |
| 2: | Select a point corresponding to the basis function set as the reference point. |
| 3: | Map each point to a matrix , which represents the tangent space using logarithm map :
|
| 4: | Construct matrix corresponding to the test parameter using the Lagrange interpolation of matrices , corresponding to :
|
| 5: | Compute the POD basis functions corresponding to the test parameter using the exponential map.
|
| where the trigonometric operators apply only to the diagonal elements. | |
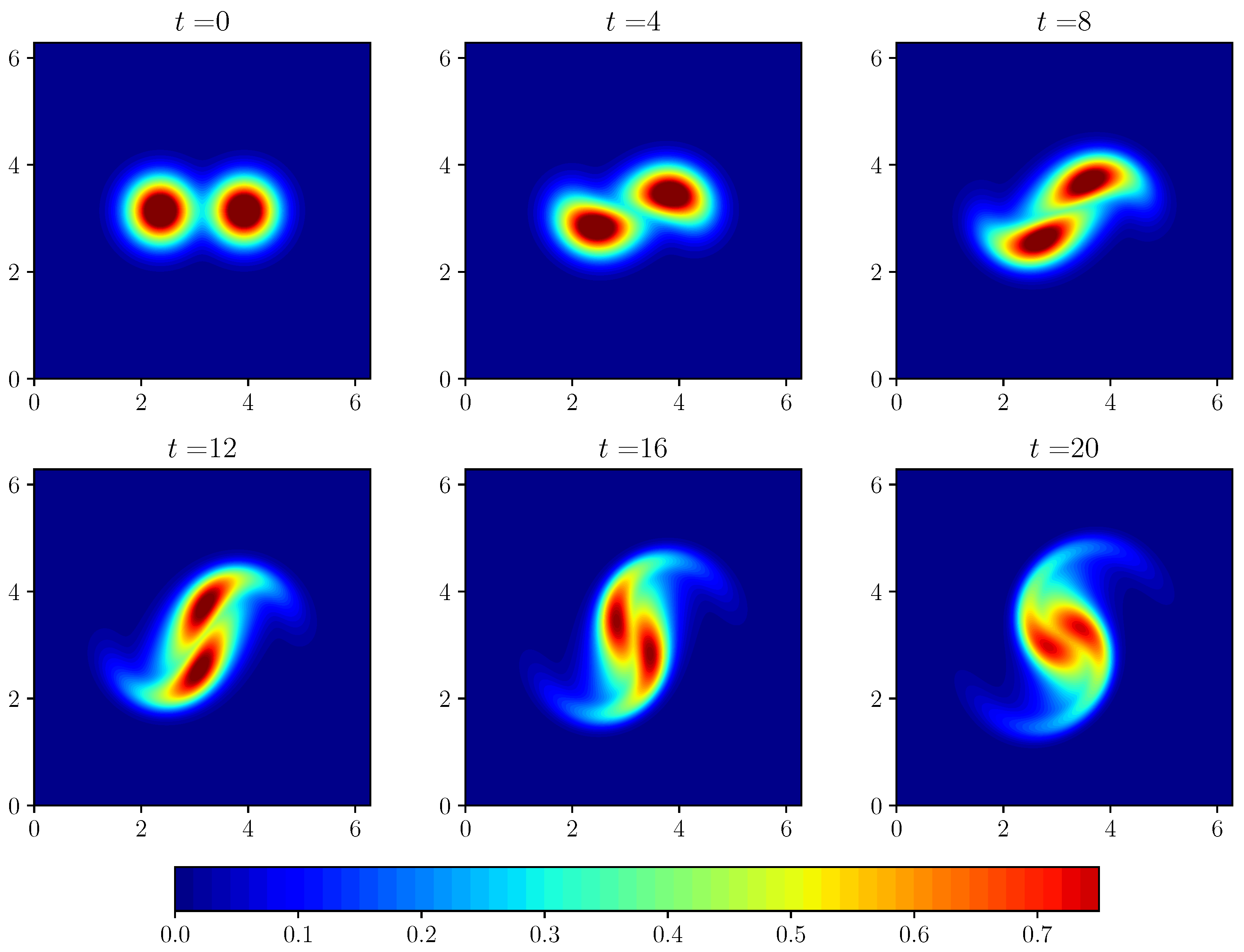
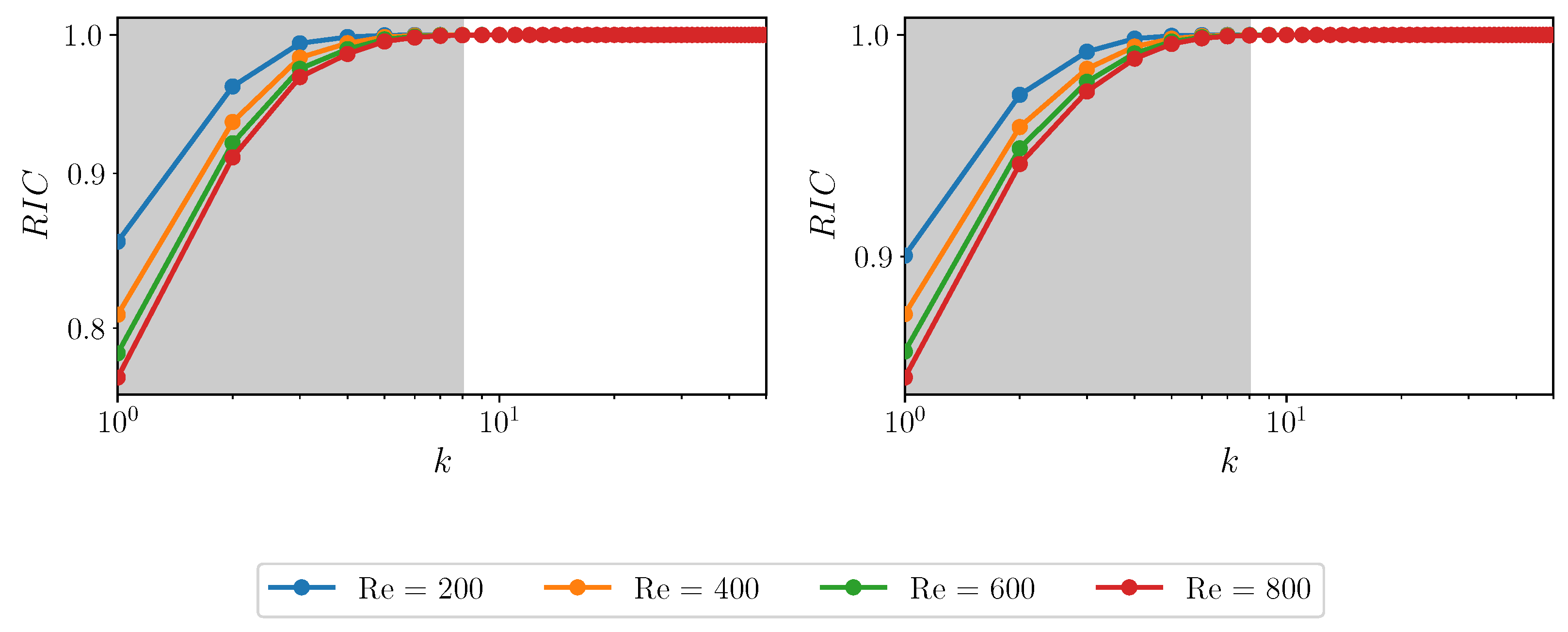
4. Numerical Results
5. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Noack, B.R.; Afanasiev, K.; Morzyński, M.; Tadmor, G.; Thiele, F. A hierarchy of low-dimensional models for the transient and post-transient cylinder wake. J. Fluid Mech. 2003, 497, 335–363. [Google Scholar] [CrossRef] [Green Version]
- Lucia, D.J.; Beran, P.S.; Silva, W.A. Reduced-order modeling: New approaches for computational physics. Prog. Aerosp. Sci. 2004, 40, 51–117. [Google Scholar] [CrossRef] [Green Version]
- Quarteroni, A.; Rozza, G. Reduced Order Methods for Modeling and Computational Reduction; Springer: Cham, Switzerland, 2014; Volume 9. [Google Scholar]
- Noack, B.R.; Morzynski, M.; Tadmor, G. Reduced-Order Modelling for Flow Control; Springer: Vienna, Austria, 2011; Volume 528. [Google Scholar]
- Taira, K.; Brunton, S.L.; Dawson, S.T.; Rowley, C.W.; Colonius, T.; McKeon, B.J.; Schmidt, O.T.; Gordeyev, S.; Theofilis, V.; Ukeiley, L.S. Modal analysis of fluid flows: An overview. AIAA J. 2017, 55, 4013–4041. [Google Scholar] [CrossRef] [Green Version]
- Benner, P.; Gugercin, S.; Willcox, K. A survey of projection-based model reduction methods for parametric dynamical systems. SIAM Rev. 2015, 57, 483–531. [Google Scholar] [CrossRef]
- Taira, K.; Hemati, M.S.; Brunton, S.L.; Sun, Y.; Duraisamy, K.; Bagheri, S.; Dawson, S.T.; Yeh, C.A. Modal analysis of fluid flows: Applications and outlook. AIAA J. 2019, 58, 998–1022. [Google Scholar] [CrossRef]
- Puzyrev, V.; Ghommem, M.; Meka, S. pyROM: A computational framework for reduced order modeling. J. Comput. Sci. 2019, 30, 157–173. [Google Scholar] [CrossRef]
- Berkooz, G.; Holmes, P.; Lumley, J.L. The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 1993, 25, 539–575. [Google Scholar] [CrossRef]
- Ito, K.; Ravindran, S. A reduced-order method for simulation and control of fluid flows. J. Comput. Phys. 1998, 143, 403–425. [Google Scholar] [CrossRef] [Green Version]
- Rowley, C.W.; Colonius, T.; Murray, R.M. Model reduction for compressible flows using POD and Galerkin projection. Phys. D Nonlinear Phenom. 2004, 189, 115–129. [Google Scholar] [CrossRef]
- Stankiewicz, W.; Morzyński, M.; Noack, B.R.; Tadmor, G. Reduced order Galerkin models of flow around NACA-0012 airfoil. Math. Model. Anal. 2008, 13, 113–122. [Google Scholar] [CrossRef]
- Akhtar, I.; Nayfeh, A.H.; Ribbens, C.J. On the stability and extension of reduced-order Galerkin models in incompressible flows. Theor. Comput. Fluid Dyn. 2009, 23, 213–237. [Google Scholar] [CrossRef]
- Krasnopolsky, V.M.; Fox-Rabinovitz, M.S.; Chalikov, D.V. New approach to calculation of atmospheric model physics: Accurate and fast neural network emulation of longwave radiation in a climate model. Mon. Weather Rev. 2005, 133, 1370–1383. [Google Scholar] [CrossRef] [Green Version]
- Krasnopolsky, V.M.; Fox-Rabinovitz, M.S. Complex hybrid models combining deterministic and machine learning components for numerical climate modeling and weather prediction. Neural Netw. 2006, 19, 122–134. [Google Scholar] [CrossRef] [PubMed]
- Brenowitz, N.D.; Bretherton, C.S. Prognostic validation of a neural network unified physics parameterization. Geophys. Res. Lett. 2018, 45, 6289–6298. [Google Scholar] [CrossRef]
- Peherstorfer, B.; Willcox, K. Data-driven operator inference for nonintrusive projection-based model reduction. Comput. Methods Appl. Mech. Eng. 2016, 306, 196–215. [Google Scholar] [CrossRef] [Green Version]
- Kutz, J.N. Deep learning in fluid dynamics. J. Fluid Mech. 2017, 814, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Brunton, S.L.; Noack, B.R.; Koumoutsakos, P. Machine learning for fluid mechanics. Annu. Rev. Fluid Mech. 2019, 52, 477–508. [Google Scholar] [CrossRef] [Green Version]
- Brenner, M.; Eldredge, J.; Freund, J. Perspective on machine learning for advancing fluid mechanics. Phys. Rev. Fluids 2019, 4, 100501. [Google Scholar] [CrossRef]
- Duraisamy, K.; Iaccarino, G.; Xiao, H. Turbulence modeling in the age of data. Annu. Rev. Fluid Mech. 2019, 51, 357–377. [Google Scholar] [CrossRef] [Green Version]
- Xie, X.; Zhang, G.; Webster, C.G. Non-intrusive inference reduced order model for fluids using deep multistep neural network. Mathematics 2019, 7, 757. [Google Scholar] [CrossRef] [Green Version]
- Iten, R.; Metger, T.; Wilming, H.; Del Rio, L.; Renner, R. Discovering physical concepts with neural networks. Phys. Rev. Lett. 2020, 124, 010508. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, J.; Hesthaven, J.S. Flowfield Reconstruction Method Using Artificial Neural Network. AIAA J. 2019, 57, 482–498. [Google Scholar] [CrossRef]
- Lee, K.; Carlberg, K.T. Model reduction of dynamical systems on nonlinear manifolds using deep convolutional autoencoders. J. Comput. Phys. 2020, 404, 108973. [Google Scholar] [CrossRef] [Green Version]
- Faghmous, J.H.; Banerjee, A.; Shekhar, S.; Steinbach, M.; Kumar, V.; Ganguly, A.R.; Samatova, N. Theory-guided data science for climate change. Computer 2014, 47, 74–78. [Google Scholar] [CrossRef]
- Wagner, N.; Rondinelli, J.M. Theory-guided machine learning in materials science. Front. Mater. 2016, 3, 28. [Google Scholar] [CrossRef] [Green Version]
- Karpatne, A.; Atluri, G.; Faghmous, J.H.; Steinbach, M.; Banerjee, A.; Ganguly, A.; Shekhar, S.; Samatova, N.; Kumar, V. Theory-guided data science: A new paradigm for scientific discovery from data. IEEE Trans. Knowl. Data Eng. 2017, 29, 2318–2331. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Rahman, S.; San, O.; Rasheed, A. A hybrid approach for model order reduction of barotropic quasi-geostrophic turbulence. Fluids 2018, 3, 86. [Google Scholar] [CrossRef] [Green Version]
- San, O.; Maulik, R. Neural network closures for nonlinear model order reduction. Adv. Comput. Math. 2018, 44, 1717–1750. [Google Scholar] [CrossRef] [Green Version]
- Wan, Z.Y.; Vlachas, P.; Koumoutsakos, P.; Sapsis, T. Data-assisted reduced-order modeling of extreme events in complex dynamical systems. PLoS ONE 2018, 13, e0197704. [Google Scholar] [CrossRef]
- Xie, X.; Mohebujjaman, M.; Rebholz, L.G.; Iliescu, T. Data-driven filtered reduced order modeling of fluid flows. SIAM J. Sci. Comput. 2018, 40, B834–B857. [Google Scholar] [CrossRef] [Green Version]
- Mohebujjaman, M.; Rebholz, L.G.; Iliescu, T. Physically constrained data-driven correction for reduced-order modeling of fluid flows. Int. J. Numer. Methods Fluids 2019, 89, 103–122. [Google Scholar] [CrossRef] [Green Version]
- Maulik, R.; Sharma, H.; Patel, S.; Lusch, B.; Jennings, E. Accelerating RANS turbulence modeling using potential flow and machine learning. arXiv 2019, arXiv:1910.10878. [Google Scholar]
- Discacciati, N.; Hesthaven, J.S.; Ray, D. Controlling oscillations in high-order Discontinuous Galerkin schemes using artificial viscosity tuned by neural networks. J. Comput. Phys. 2020, 409, 109304. [Google Scholar] [CrossRef] [Green Version]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Pan, S.; Duraisamy, K. Physics-informed probabilistic learning of linear embeddings of non-linear dynamics with guaranteed stability. arXiv 2019, arXiv:1906.03663. [Google Scholar]
- Zhu, Y.; Zabaras, N.; Koutsourelakis, P.S.; Perdikaris, P. Physics-constrained deep learning for high-dimensional surrogate modeling and uncertainty quantification without labeled data. J. Comput. Phys. 2019, 394, 56–81. [Google Scholar] [CrossRef] [Green Version]
- Márquez-Neila, P.; Salzmann, M.; Fua, P. Imposing hard constraints on deep networks: Promises and limitations. arXiv 2017, arXiv:1706.02025. [Google Scholar]
- Pawar, S.; Ahmed, S.E.; San, O.; Rasheed, A. Data-driven recovery of hidden physics in reduced order modeling of fluid flows. arXiv 2019, arXiv:1910.13909. [Google Scholar] [CrossRef] [Green Version]
- Wells, D.; Wang, Z.; Xie, X.; Iliescu, T. An evolve-then-filter regularized reduced order model for convection-dominated flows. Int. J. Numer. Methods Fluids 2017, 84, 598–615. [Google Scholar] [CrossRef]
- Gunzburger, M.; Iliescu, T.; Mohebujjaman, M.; Schneier, M. An evolve-filter-relax stabilized reduced order stochastic collocation method for the time-dependent Navier–Stokes equations. SIAM/ASA J. Uncertain. Quantif. 2019, 7, 1162–1184. [Google Scholar] [CrossRef]
- Freund, J.; Colonius, T. Turbulence and sound-field POD analysis of a turbulent jet. Int. J. Aeroacoustics 2009, 8, 337–354. [Google Scholar] [CrossRef]
- Barbagallo, A.; Sipp, D.; Schmid, P.J. Closed-loop control of an open cavity flow using reduced-order models. J. Fluid Mech. 2009, 641, 1–50. [Google Scholar] [CrossRef] [Green Version]
- LeGresley, P.; Alonso, J. Airfoil design optimization using reduced order models based on proper orthogonal decomposition. In Proceedings of the Fluids 2000 Conference and Exhibit, Denver, CO, USA, 19–22 June 2000; p. 2545. [Google Scholar]
- Ribeiro, J.H.M.; Wolf, W.R. Identification of coherent structures in the flow past a NACA0012 airfoil via proper orthogonal decomposition. Phys. Fluids 2017, 29, 085104. [Google Scholar] [CrossRef]
- Xiao, D.; Du, J.; Fang, F.; Pain, C.; Li, J. Parameterised non-intrusive reduced order methods for ensemble Kalman filter data assimilation. Comput. Fluids 2018, 177, 69–77. [Google Scholar] [CrossRef]
- Arcucci, R.; Mottet, L.; Pain, C.; Guo, Y.K. Optimal reduced space for variational data assimilation. J. Comput. Phys. 2019, 379, 51–69. [Google Scholar] [CrossRef]
- San, O.; Borggaard, J. Principal interval decomposition framework for POD reduced-order modeling of convective Boussinesq flows. Int. J. Numer. Methods Fluids 2015, 78, 37–62. [Google Scholar] [CrossRef]
- Ballarin, F.; Manzoni, A.; Quarteroni, A.; Rozza, G. Supremizer stabilization of POD–Galerkin approximation of parametrized steady incompressible Navier–Stokes equations. Int. J. Numer. Methods Eng. 2015, 102, 1136–1161. [Google Scholar] [CrossRef]
- Benosman, M.; Borggaard, J.; San, O.; Kramer, B. Learning-based robust stabilization for reduced-order models of 2D and 3D Boussinesq equations. Appl. Math. Model. 2017, 49, 162–181. [Google Scholar] [CrossRef] [Green Version]
- Schlegel, M.; Noack, B.R. On long-term boundedness of Galerkin models. J. Fluid Mech. 2015, 765, 325–352. [Google Scholar] [CrossRef] [Green Version]
- Cordier, L.; Noack, B.R.; Tissot, G.; Lehnasch, G.; Delville, J.; Balajewicz, M.; Daviller, G.; Niven, R.K. Identification strategies for model-based control. Exp. Fluids 2013, 54, 1580. [Google Scholar] [CrossRef]
- Takane, Y. Nonlinear multivariate analysis by neural network models. In Data Science, Classification, and Related Methods; Springer: Tokyo, Japan, 1998; pp. 527–538. [Google Scholar]
- Milano, M.; Koumoutsakos, P. Neural network modeling for near wall turbulent flow. J. Comput. Phys. 2002, 182, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Masci, J.; Meier, U.; Cireşan, D.; Schmidhuber, J. Stacked convolutional auto-encoders for hierarchical feature extraction. In International Conference on Artificial Neural Networks; Springer: Berlin/Heidelberg, Germany, 2011; pp. 52–59. [Google Scholar]
- Xu, J.; Duraisamy, K. Multi-level Convolutional Autoencoder Networks for Parametric Prediction of Spatio-temporal Dynamics. arXiv 2019, arXiv:1912.11114. [Google Scholar]
- Mohan, A.; Daniel, D.; Chertkov, M.; Livescu, D. Compressed convolutional LSTM: An efficient deep learning framework to model high fidelity 3D turbulence. arXiv 2019, arXiv:1903.00033. [Google Scholar]
- Borggaard, J.; Iliescu, T.; Wang, Z. Artificial viscosity proper orthogonal decomposition. Math. Comput. Model. 2011, 53, 269–279. [Google Scholar] [CrossRef]
- Balajewicz, M.; Dowell, E.H. Stabilization of projection-based reduced order models of the Navier–Stokes. Nonlinear Dyn. 2012, 70, 1619–1632. [Google Scholar] [CrossRef]
- Wang, Z.; Akhtar, I.; Borggaard, J.; Iliescu, T. Proper orthogonal decomposition closure models for turbulent flows: A numerical comparison. Comput. Methods Appl. Mech. Eng. 2012, 237, 10–26. [Google Scholar] [CrossRef] [Green Version]
- Lassila, T.; Manzoni, A.; Quarteroni, A.; Rozza, G. Model order reduction in fluid dynamics: Challenges and perspectives. In Reduced Order Methods for Modeling and Computational Reduction; Springer: Cham, Switzerland, 2014; pp. 235–273. [Google Scholar]
- Vlachas, P.R.; Byeon, W.; Wan, Z.Y.; Sapsis, T.P.; Koumoutsakos, P. Data-driven forecasting of high-dimensional chaotic systems with long short-term memory networks. Proc. R. Soc. A: Math. Phys. Eng. Sci. 2018, 474, 20170844. [Google Scholar] [CrossRef] [Green Version]
- Pathak, J.; Wikner, A.; Fussell, R.; Chandra, S.; Hunt, B.R.; Girvan, M.; Ott, E. Hybrid forecasting of chaotic processes: Using machine learning in conjunction with a knowledge-based model. Chaos: Interdiscip. J. Nonlinear Sci. 2018, 28, 041101. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Xiu, D. On generalized residue network for deep learning of unknown dynamical systems. arXiv 2020, arXiv:2002.02528. [Google Scholar]
- Rahman, S.; Pawar, S.; San, O.; Rasheed, A.; Iliescu, T. A nonintrusive reduced order modeling framework for quasi-geostrophic turbulence. Phys. Rev. E 2019, 100, 053306. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ahmed, S.E.; Rahman, S.M.; San, O.; Rasheed, A.; Navon, I.M. Memory embedded non-intrusive reduced order modeling of non-ergodic flows. Phys. Fluids 2019, 31, 126602. [Google Scholar] [CrossRef] [Green Version]
- Lui, H.F.; Wolf, W.R. Construction of reduced-order models for fluid flows using deep feedforward neural networks. J. Fluid Mech. 2019, 872, 963–994. [Google Scholar] [CrossRef] [Green Version]
- Zucatti, V.; Lui, H.F.S.; Pitz, D.B.; Wolf, W.R. Assessment of reduced-order modeling strategies for convective heat transfer. Numer. Heat Transf. Part A Appl. 2020, 77, 709–729. [Google Scholar] [CrossRef]
- Wang, Z.; Xiao, D.; Fang, F.; Govindan, R.; Pain, C.C.; Guo, Y. Model identification of reduced order fluid dynamics systems using deep learning. Int. J. Numer. Methods Fluids 2018, 86, 255–268. [Google Scholar] [CrossRef] [Green Version]
- Wu, P.; Sun, J.; Chang, X.; Zhang, W.; Arcucci, R.; Guo, Y.; Pain, C.C. Data-driven reduced order model with temporal convolutional neural network. Comput. Methods Appl. Mech. Eng. 2020, 360, 112766. [Google Scholar] [CrossRef]
- Kou, J.; Zhang, W. Multi-kernel neural networks for nonlinear unsteady aerodynamic reduced-order modeling. Aerosp. Sci. Technol. 2017, 67, 309–326. [Google Scholar] [CrossRef]
- Kou, J.; Zhang, W. A hybrid reduced-order framework for complex aeroelastic simulations. Aerosp. Sci. Technol. 2019, 84, 880–894. [Google Scholar] [CrossRef]
- Baiges, J.; Codina, R.; Castañar, I.; Castillo, E. A finite element reduced-order model based on adaptive mesh refinement and artificial neural networks. Int. J. Numer. Methods Eng. 2020, 121, 588–601. [Google Scholar] [CrossRef]
- Xiao, D.; Fang, F.; Pain, C.; Navon, I. A parameterized non-intrusive reduced order model and error analysis for general time-dependent nonlinear partial differential equations and its applications. Comput. Methods Appl. Mech. Eng. 2017, 317, 868–889. [Google Scholar] [CrossRef] [Green Version]
- Xiao, D.; Heaney, C.; Mottet, L.; Fang, F.; Lin, W.; Navon, I.; Guo, Y.; Matar, O.; Robins, A.; Pain, C. A reduced order model for turbulent flows in the urban environment using machine learning. Build. Environ. 2019, 148, 323–337. [Google Scholar] [CrossRef] [Green Version]
- Xiao, D.; Fang, F.; Heaney, C.E.; Navon, I.; Pain, C. A domain decomposition method for the non-intrusive reduced order modelling of fluid flow. Comput. Methods Appl. Mech. Eng. 2019, 354, 307–330. [Google Scholar] [CrossRef]
- Gonzalez, F.J.; Balajewicz, M. Deep convolutional recurrent autoencoders for learning low-dimensional feature dynamics of fluid systems. arXiv 2018, arXiv:1808.01346. [Google Scholar]
- Maulik, R.; Lusch, B.; Balaprakash, P. Reduced-order modeling of advection-dominated systems with recurrent neural networks and convolutional autoencoders. arXiv 2020, arXiv:2002.00470. [Google Scholar]
- Luchtenburg, D.M.; Günther, B.; Noack, B.R.; King, R.; Tadmor, G. A generalized mean-field model of the natural and high-frequency actuated flow around a high-lift configuration. J. Fluid Mech. 2009, 623, 283–316. [Google Scholar] [CrossRef]
- Loiseau, J.C.; Noack, B.R.; Brunton, S.L. Sparse reduced-order modelling: Sensor-based dynamics to full-state estimation. J. Fluid Mech. 2018, 844, 459–490. [Google Scholar] [CrossRef] [Green Version]
- Mou, C.; Liu, H.; Wells, D.R.; Iliescu, T. Data-driven correction reduced order models for the quasi-geostrophic equations: A numerical investigation. Int. J. Comput. Fluid Dyn. 2020, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Ripamonti, N.; Hesthaven, J.S. Recurrent neural network closure of parametric POD-Galerkin reduced-order models based on the Mori-Zwanzig formalism. J. Comput. Phys. 2020, 410, 109420. [Google Scholar] [CrossRef]
- Holmes, P.; Lumley, J.L.; Berkooz, G.; Rowley, C.W. Turbulence, Coherent Structures, Dynamical Systems and Symmetry; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Rowley, C.W.; Dawson, S.T. Model reduction for flow analysis and control. Annu. Rev. Fluid Mech. 2017, 49, 387–417. [Google Scholar] [CrossRef] [Green Version]
- Algazi, V.; Sakrison, D. On the optimality of the Karhunen-Loève expansion (Corresp.). IEEE Trans. Inf. Theory 1969, 15, 319–321. [Google Scholar] [CrossRef]
- Hand, D.J. Principles of data mining. Drug Saf. 2007, 30, 621–622. [Google Scholar] [CrossRef] [PubMed]
- Ramakrishnan, N.; Bailey-Kellogg, C.; Tadepalli, S.; Pandey, V.N. Gaussian processes for active data mining of spatial aggregates. In Proceedings of the 2005 SIAM International Conference on Data Mining, Newport Beach, CA, USA, 21–23 April 2005; pp. 427–438. [Google Scholar]
- Wu, X.; Zhu, X.; Wu, G.Q.; Ding, W. Data mining with big data. IEEE Trans. Knowl. Data Eng. 2013, 26, 97–107. [Google Scholar]
- Vaddireddy, H.; Rasheed, A.; Staples, A.E.; San, O. Feature engineering and symbolic regression methods for detecting hidden physics from sparse sensor observation data. Phys. Fluids 2020, 32, 015113. [Google Scholar] [CrossRef] [Green Version]
- Quade, M.; Abel, M.; Shafi, K.; Niven, R.K.; Noack, B.R. Prediction of dynamical systems by symbolic regression. Phys. Rev. E 2016, 94, 012214. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luo, C.; Zhang, S.L. Parse-matrix evolution for symbolic regression. Eng. Appl. Artif. Intell. 2012, 25, 1182–1193. [Google Scholar] [CrossRef] [Green Version]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2016, 113, 3932–3937. [Google Scholar] [CrossRef] [Green Version]
- Rudy, S.H.; Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Data-driven discovery of partial differential equations. Sci. Adv. 2017, 3, e1602614. [Google Scholar] [CrossRef] [Green Version]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Mohan, A.T.; Gaitonde, D.V. A deep learning based approach to reduced order modeling for turbulent flow control using LSTM neural networks. arXiv 2018, arXiv:1804.09269. [Google Scholar]
- Amsallem, D.; Farhat, C. Interpolation method for adapting reduced-order models and application to aeroelasticity. AIAA J. 2008, 46, 1803–1813. [Google Scholar] [CrossRef] [Green Version]
- Zimmermann, R.; Peherstorfer, B.; Willcox, K. Geometric subspace updates with applications to online adaptive nonlinear model reduction. SIAM J. Matrix Anal. Appl. 2018, 39, 234–261. [Google Scholar] [CrossRef]
- Ştefănescu, R.; Sandu, A.; Navon, I.M. Comparison of POD reduced order strategies for the nonlinear 2D shallow water equations. Int. J. Numer. Methods Fluids 2014, 76, 497–521. [Google Scholar] [CrossRef] [Green Version]
- Dimitriu, G.; Ştefănescu, R.; Navon, I.M. Comparative numerical analysis using reduced-order modeling strategies for nonlinear large-scale systems. J. Comput. Appl. Math. 2017, 310, 32–43. [Google Scholar] [CrossRef]
- Barrault, M.; Maday, Y.; Nguyen, N.C.; Patera, A.T. An Empirical Interpolation Method: Application to Efficient Reduced-Basis Discretization of Partial Differential Equations. C. R. Math. 2004, 339, 667–672. [Google Scholar] [CrossRef]
- Chaturantabut, S.; Sorensen, D.C. Discrete empirical interpolation for nonlinear model reduction. In Proceedings of the 48th IEEE Conference on Decision and Control, Shanghai, China, 15–18 December 2009; pp. 4316–4321. [Google Scholar]
- Chaturantabut, S.; Sorensen, D.C. Nonlinear model reduction via discrete empirical interpolation. SIAM J. Sci. Comput. 2010, 32, 2737–2764. [Google Scholar] [CrossRef]
- Everson, R.; Sirovich, L. Karhunen–Loeve procedure for gappy data. JOSA A 1995, 12, 1657–1664. [Google Scholar] [CrossRef] [Green Version]
- Carlberg, K.; Farhat, C.; Cortial, J.; Amsallem, D. The GNAT method for nonlinear model reduction: Effective implementation and application to computational fluid dynamics and turbulent flows. J. Comput. Phys. 2013, 242, 623–647. [Google Scholar] [CrossRef] [Green Version]
- Astrid, P.; Weiland, S.; Willcox, K.; Backx, T. Missing point estimation in models described by proper orthogonal decomposition. IEEE Trans. Autom. Control 2008, 53, 2237–2251. [Google Scholar] [CrossRef] [Green Version]
- Zimmermann, R.; Willcox, K. An accelerated greedy missing point estimation procedure. SIAM J. Sci. Comput. 2016, 38, A2827–A2850. [Google Scholar] [CrossRef] [Green Version]
- Reinaud, J.N.; Dritschel, D.G. The critical merger distance between two co-rotating quasi-geostrophic vortices. J. Fluid Mech. 2005, 522, 357–381. [Google Scholar] [CrossRef] [Green Version]
- San, O.; Iliescu, T. A stabilized proper orthogonal decomposition reduced-order model for large scale quasi-geostrophic ocean circulation. Adv. Comput. Math. 2015, 41, 1289–1319. [Google Scholar] [CrossRef] [Green Version]
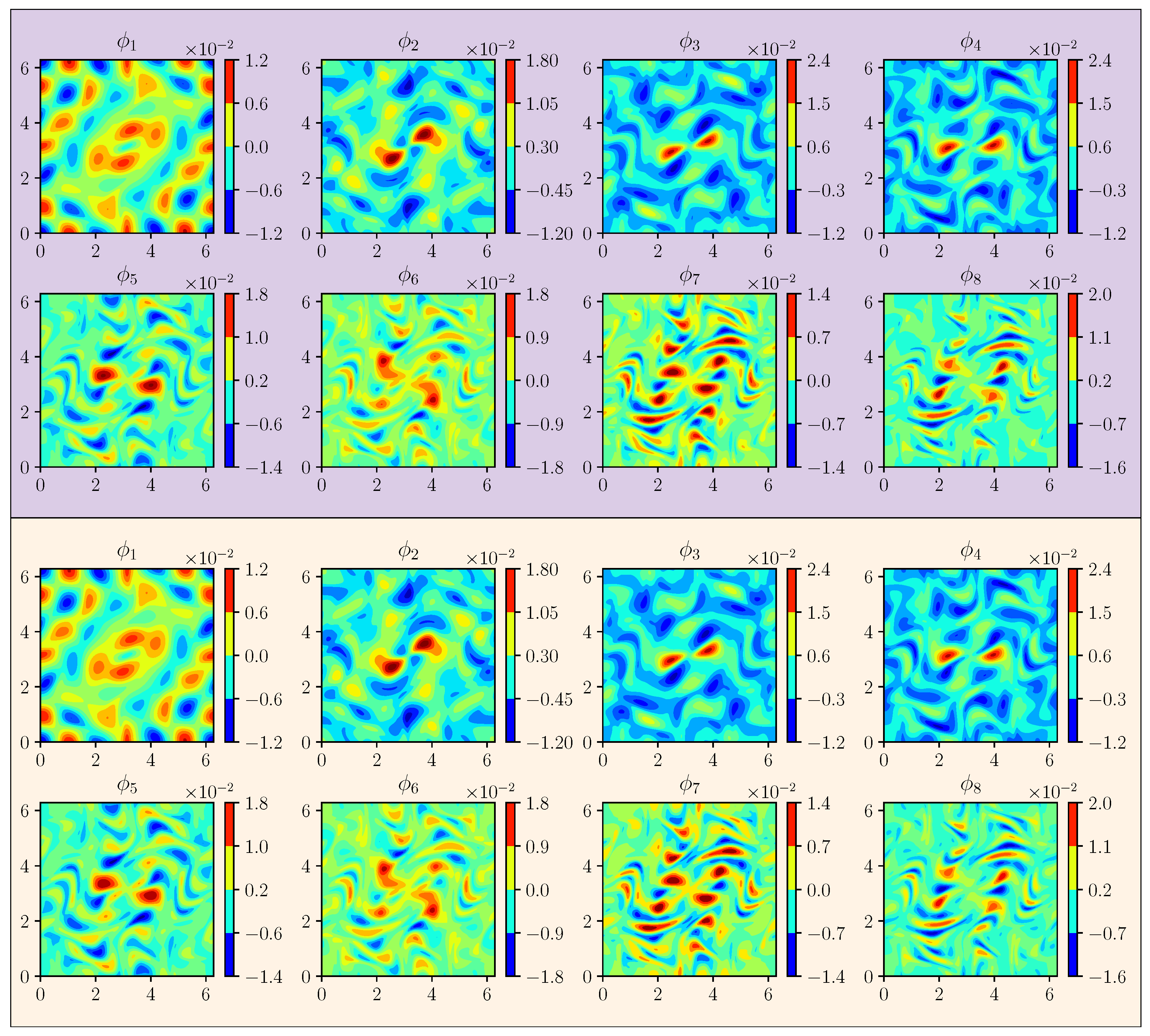
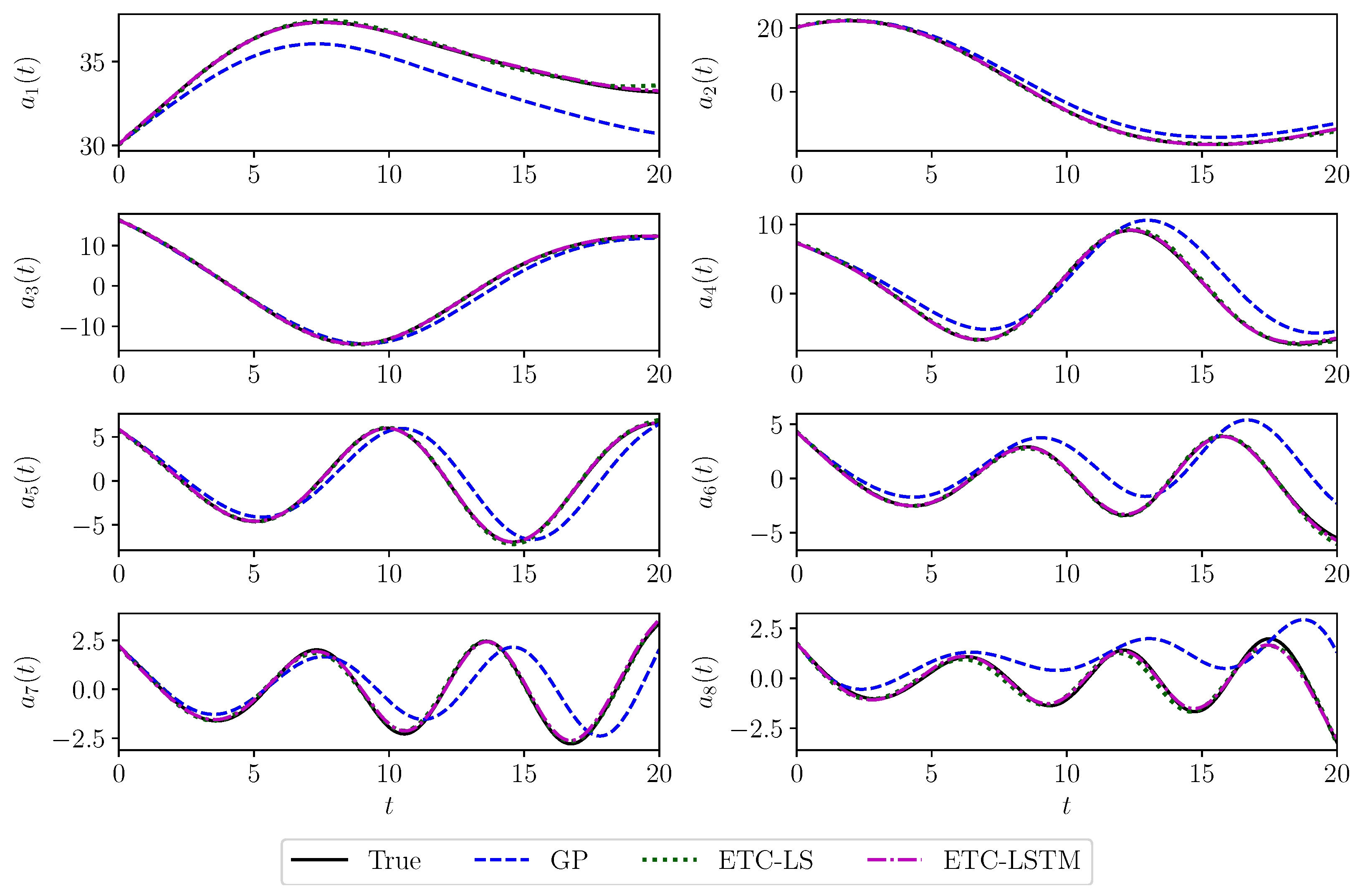
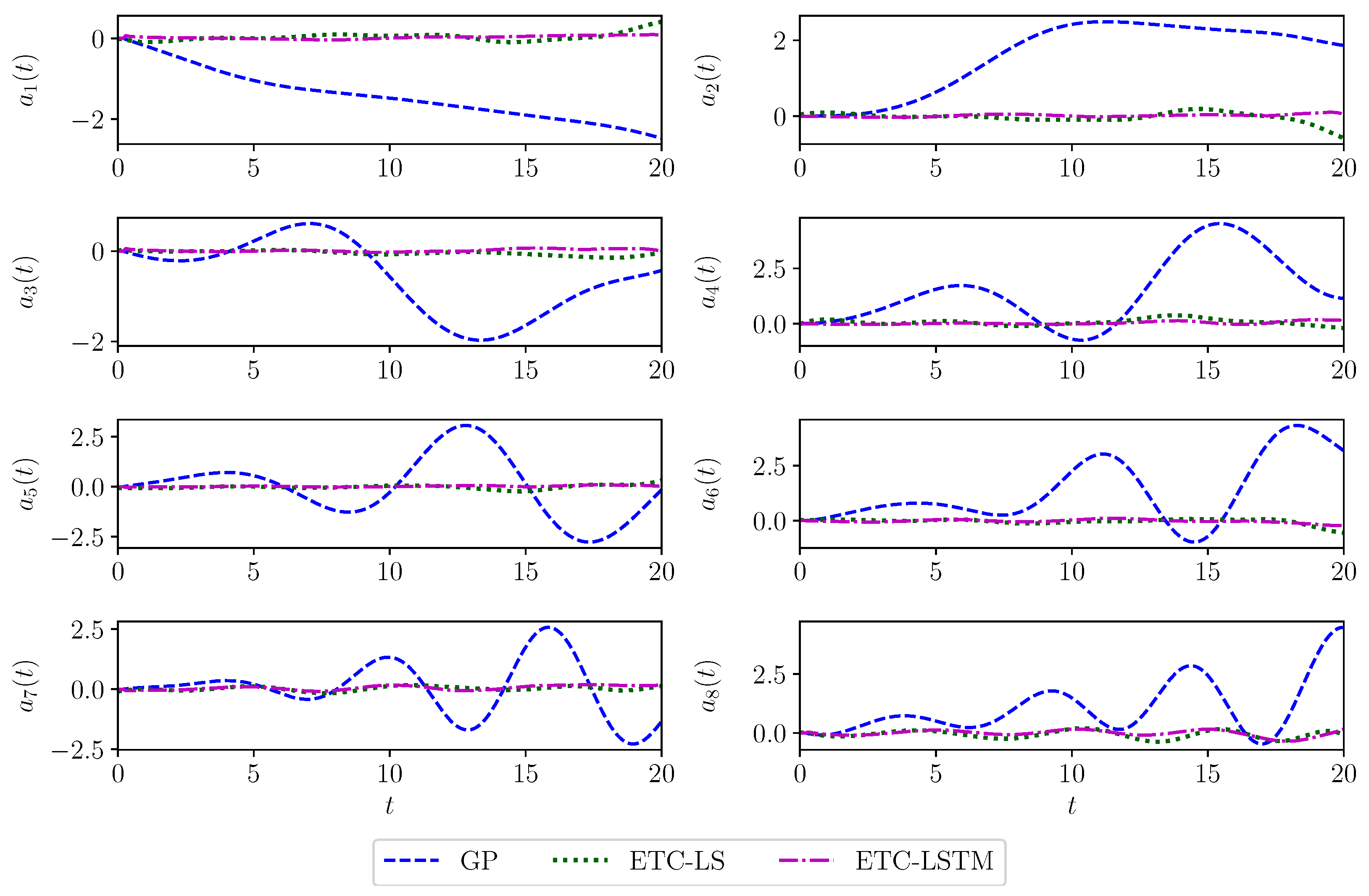
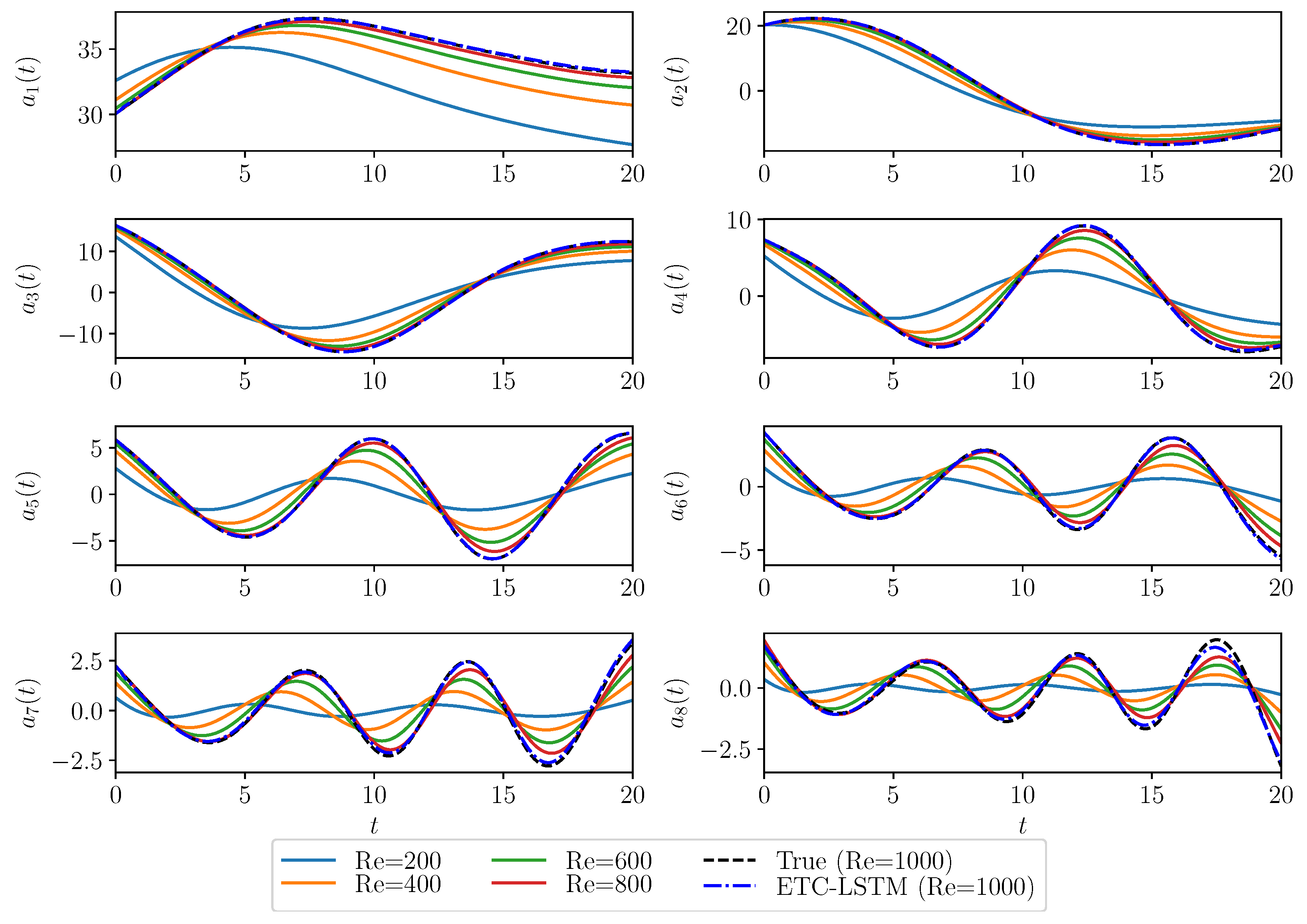

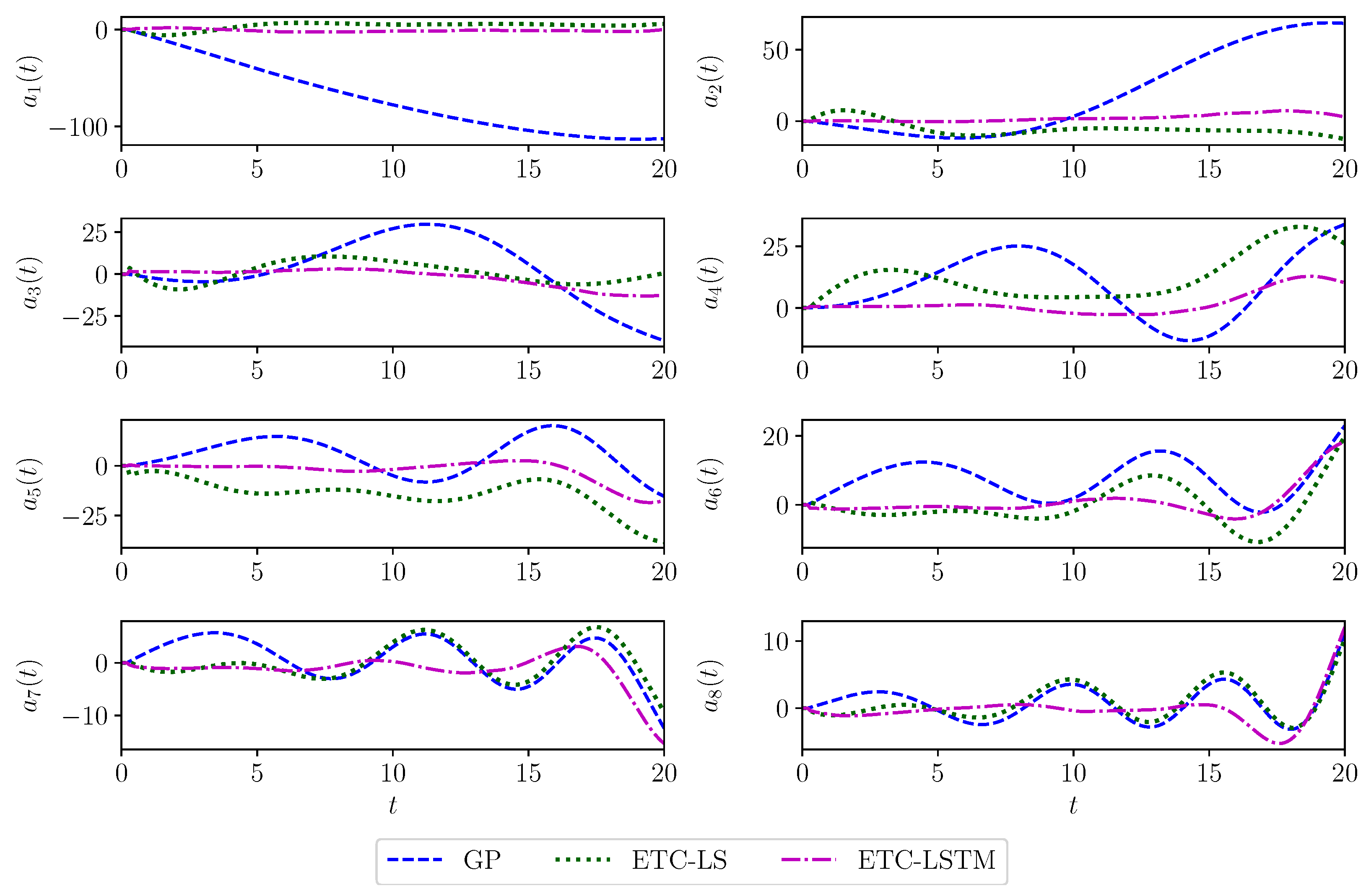
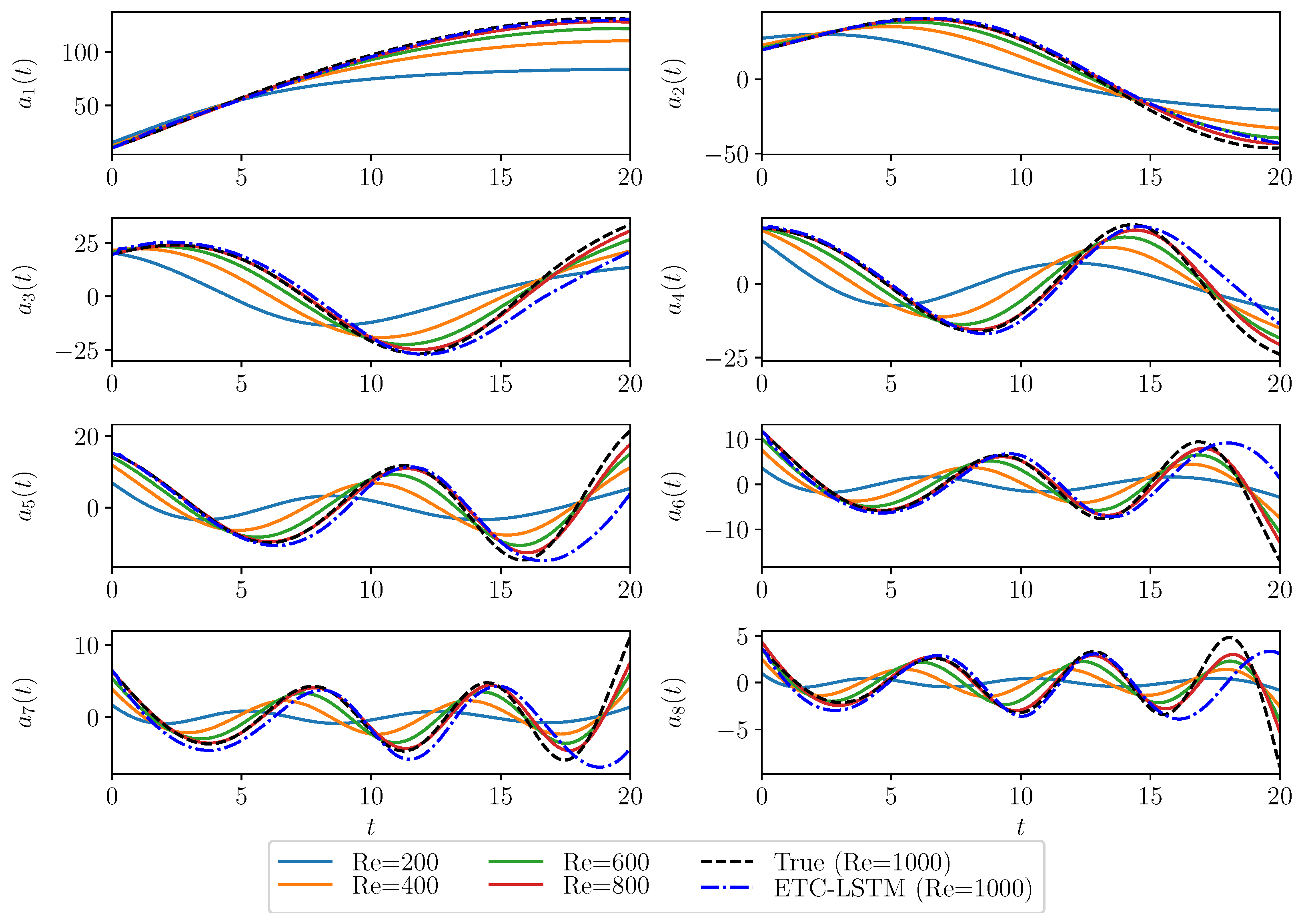

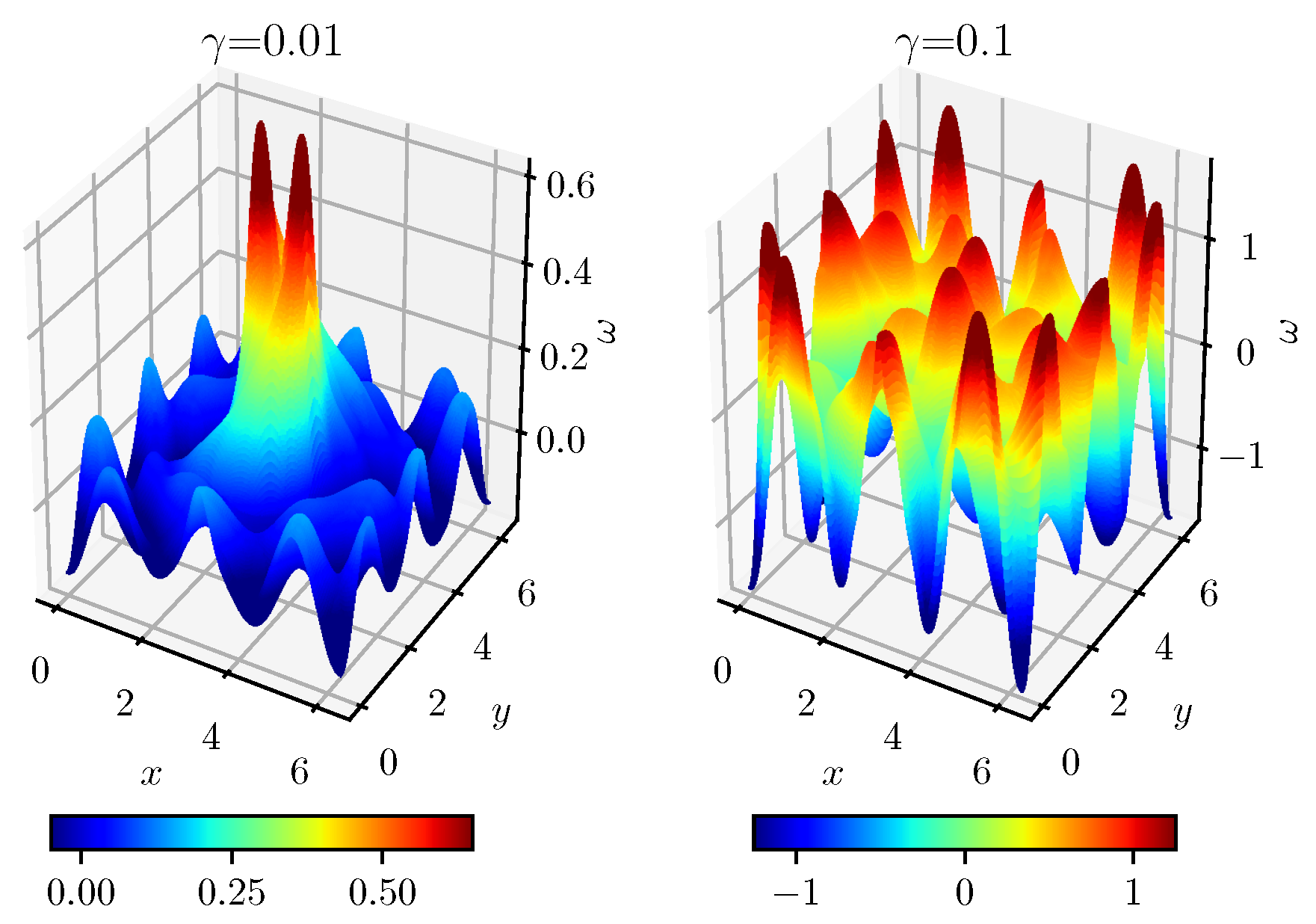
| True | GP | GP (C) | ETC-LS | ETC-LSTM | |
| GP | GP (C) | ETC-LS | ETC-LSTM | |
| 0.5127 | 0.4977 | 0.5968 | 0.8823 | |
| 0.5041 | 0.5410 | 0.5718 | 0.7818 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pawar, S.; Ahmed, S.E.; San, O.; Rasheed, A. An Evolve-Then-Correct Reduced Order Model for Hidden Fluid Dynamics. Mathematics 2020, 8, 570. https://doi.org/10.3390/math8040570
Pawar S, Ahmed SE, San O, Rasheed A. An Evolve-Then-Correct Reduced Order Model for Hidden Fluid Dynamics. Mathematics. 2020; 8(4):570. https://doi.org/10.3390/math8040570
Chicago/Turabian StylePawar, Suraj, Shady E. Ahmed, Omer San, and Adil Rasheed. 2020. "An Evolve-Then-Correct Reduced Order Model for Hidden Fluid Dynamics" Mathematics 8, no. 4: 570. https://doi.org/10.3390/math8040570
APA StylePawar, S., Ahmed, S. E., San, O., & Rasheed, A. (2020). An Evolve-Then-Correct Reduced Order Model for Hidden Fluid Dynamics. Mathematics, 8(4), 570. https://doi.org/10.3390/math8040570






