Abstract
The evaluation of the cutoff wavenumbers of metallic waveguides can be related to the numerical resolution of a suitable nonlinear eigenproblem defined on the domain C described by the contour of its transverse cross section. In this work, we show that the symmetries of C can be exploited to obtain a block diagonal matrix representation of the nonlinear eigenproblem, which enables a remarkable reduction in the computational effort involved in its resolution.
1. Introduction
The computation of the cutoff wavenumbers of metallic waveguides is a classic problem in electromagnetic engineering [1]. It is well known that the knowledge of these parameters plays a paramount role in the design of a significant number of microwave and millimetre waves devices as power combiners, transducers, T-junctions, and mode transformers [2]. In recent decades, renewed interest in the subject, mainly focused on the treatment of guiding structures with an arbitrarily shaped transverse cross section, has been shown by researchers, and several numerical procedures have been proposed for the evaluation, for example, [3,4,5] and the references within. In [6], it was demonstrated that these parameters coincide with the eigenvalues of a suitable nonlinear eigenproblem of the form [7]
where the operator is defined as a boundary integral equation having as its domain the contour C described by the transverse cross section of the guiding structure. The main feature of this approach, as discussed in [8], is the absence of spurious (or ghost) solutions. In [9], it was shown that these nonlinear eigenvalues can be reliably computed by means of the Singular Value Decomposition (SVD) applied to the homogeneous matrix system arising by the discretization of the operatorial Equation (1). Although effective, the SVD approach is time consuming due to its asymptotic computational cost on the order of [10]. In [11], one of the present authors proposed a quick numerical procedure for computing the nonlinear eigenvalues based on the use of both the QR decomposition and an adaptive technique for their localization. In this paper, an enhancement of the approach described in [11] obtained by means of group theory is presented with the aim of computing, in a fast and effective manner, the cutoff wavenumbers of metallic waveguides characterized by a symmetric transverse cross section. Group theory has been applied with success in the context of electromagnetic theory and applications, e.g., eddy current analysis [12], electromagnetic scattering [13], antenna theory [14], microwave engineering [15], microwave imaging [16], plasmonics [17], and metamaterials [18]. Inspired by [13,19], the approach we propose exploits the symmetries of C to obtain a block diagonal matrix representation of the operator , thereby reducing the computational effort involved in the use of the procedure [11]. The paper is organized as follows. In Section 2, we provide a brief account of the main concepts concerning the formulation of the cutoff wavenumbers of a metallic waveguide as nonlinear eigenvalues of a suitable nonlinear eigenproblem [6] and of the numerical technique described in [11] for its resolution. In Section 3, we present elements of group theory and group representation theory that are essential to understanding the rationale of the proposed approach. In Section 4, we demonstrate how the theoretical results given in Section 3 can be used to enhance the computational performance of the technique [11] to compute the cutoff wavenumbers of metallic waveguides with symmetry. For this purpose, guiding structures characterized by a symmetric transverse cross section that is invariant (i) to reflection operations about the orthogonal planes intersecting the propagation axis, and (ii) to the rotation operation of radians around this axis, have been considered. In Section 5, numerical results are discussed. Conclusions are provided in Section 6.
2. Cutoff Wavenumbers as Nonlinear Eigenvalues
2.1. Nonlinear Eigenproblem Formulation
Following [6], we consider a metallic waveguide with PEC walls filled by a medium with dielectric permittivity and magnetic permeability , characterized by an transverse cross section along the -axis. The problem of the computation of the cutoff wavenumbers of this structure can be stated as follows: the electric field inside the metallic waveguide can be expressed as
where the vector potential and the scalar potential are given by [8]
where C is the contour of the waveguide cross section, is the Hankel function of second kind and zero order, is the wavenumber, j is the imaginary unit and and are the source and position vectors, respectively. The boundary conditions on the waveguide walls are
where is the unit vector orthogonal to the surface of the PEC walls. Equation (5) can be written in operatorial form as [6]
2.2. Nonlinear Eigenvalues Computation
The operatorial Equation (6) defines a nonlinear eigenproblem of the form (1), where the cutoff wavenumbers are the nonlinear eigenvalues [6,10]. By applying the method of moments [1] to (6), it is reduced to a homogeneous matrix equation of the form
In principle, the computation of the nonlinear eigenvalues of Equation (7) requires a search for the values of the parameter for which the matrix becomes singular, i.e., the values for which
holds [6,9,11]. From a numerical perspective, a more stable and accurate way to ascertain the singularity of is the Singular Value Decomposition (SVD) for [9,10]. Exploiting the fact that the smallest singular value of corresponds to the Euclidean distance between the matrix and the set of all the matrices with rank [10], the cutoff wavenumbers can be evaluated by searching for the zeros of the function over the domain for . However, as discussed in [11], due to discretization errors, this search has to be accomplished on the minima of the function . To save computational time, an algorithm for rapid evaluation of nonlinear eigenvalues is presented in [11]. The algorithm is based on the definition of an auxiliary function that is able to locate all the minima of while being computationally less expensive to evaluate than . This result is obtained by (i) exploiting the QR decomposition (instead of the SVD) of the matrix (where is a unitary matrix and is a upper triangular matrix), (ii) choosing a suitable algorithm to estimate the smallest singular value of a triangular matrix (considering the fact that )) [11], and (iii) exploiting a suitable adaptive technique to evaluate . The adaptive method requires two levels of resolution and to be fixed and a tolerance for evaluating the function . The computation stops when all the minima of remain unchanged between two computational steps of the evaluation procedure. The overall asymptotic computational cost of the algorithm is , where n is the order of the matrix and () is the number of sample points used to compute the function in the domain for (see [11] for a detailed discussion of these points).
3. Basic Concepts and Definitions of Group Theory and Group Representation Theory
A symmetry operation can be defined as a transformation applied to an object that leaves its geometric structure indistinguishable from its initial configuration [20,21]. For an object that exhibits some degree of symmetry, several symmetry operations can be defined. The set of all these operations yields an abstract algebraic structure called the symmetry group, whose properties are described by group theory [20,21]. In the following, we provide a brief review of the elements of group theory and group representation theory that are essential to understanding the rationale of the approach adopted in this study to reduce the computational effort related to the computation of the cutoff wavenumbers of metallic waveguides with symmetries.
3.1. Basics of Group Theory
An abstract group (or simply a group) [20] is an algebraic structure composed of a non-empty set of abstract elements , rigged with a binary operation ⊙, that fulfils the following four axioms:
- , (closure property)
- , (associative property)
- , (existence of the identity element)
- (existence of the inverse element)
Group is called an abelian group if its binary operation ⊙ is commutative. The number of elements of (its cardinality, ) gives the order of group . In the following, only groups with finite order are considered. An abstract element is the conjugate of the abstract element if with . The set of all the elements that are conjugated to each other forms a conjugacy class , and denotes its cardinality. The number P of conjugacy classes belonging to a given group is . Finally, the sets are disjoint to each other [20,21].
3.2. Basics of Group Representation Theory
Roughly speaking, group representation theory enables the description of the operations on the elements belonging to the abstract group in terms of matrices and linear transformations [20,21]. From a formal perspective, if can be placed in correspondence with the group of linear operators on Hilbert space , then is called the carrier space for [20]. By selecting a set of n linearly independent functions , each can be represented as a square matrix of order n. The set of all these matrices (which is a group itself) defines a representation of dimension n for [20,21]. As matrices belonging to the same conjugacy class are related to each other by a similarity transformation (see the definition of conjugate elements given in Section 3.1), they are characterized by the same trace [20,21]. This number determines the character of class , and it is denoted by the symbol [20,21]. A given representation can be reducible or irreducible: if all the elements can be transformed into a block diagonal form by a linear transformation
is called a reducible representation; otherwise, it is called an irreducible representation. Every abstract group is characterized by a finite number of irreducible representations that coincides with the number of its classes [20]. From this latter result, we have that all the matrices belonging to a reducible representation can always be expressed as a direct sum of the matrices as follows:
where the symbol ⊕ stands for the operation of the direct sum and the coefficients indicate the number of times the matrices recur in [20]. They are given by
where and are the cardinality and the character of the i-th class belonging to , respectively, and is the complex conjugate of the character of the k-th class belonging to . A reducible representation in which all the elements are in the form given by the Equation (5) is called fully reduced. One way to directly obtain an n-dimensional fully reduced representation for the abstract group is to exploit a suitable set of basis functions called the symmetry-adapted basis functions [21]. This set can be built by applying the following projection operators to each element of the set of linear independent functions initially exploited to obtain the reducible representation [13,20]
where is the dimension of the irreducible representation and is the conjugate of the character for class containing the element . Finally, if an operator commutes with all the linear operators belonging to the group , its matrix representation , obtained by using the symmetry-adapted basis functions , has to commute with all the elements . Accordingly, must have the same block diagonal structure as that of these elements [20]..
4. Computation of Cutoff Wavenumbers of Metallic Waveguides with Symmetries
In the following, we apply the theoretical results discussed in Section 3 to reduce the computational effort involved in the computation of the cutoff wavenumbers of metallic waveguides by using the nonlinear eigenproblem formulation (7) via the algorithm described in Section 2.2 [11]. Specifically, we consider metallic guiding structures characterized by a transverse cross section with two symmetry axes orthogonal to the direction of propagation (see Figure 1). Denoting the operations of reflection about the planes -, - with the symbols and , respectively, the operation of rotation of radians around the -axis with the symbol , and the identity operation with the symbol e, we have that the set yields a group known as the point symmetry group [20,21]. As is an abelian group, the number of classes P coincides with the group cardinality . Each class contains a distinct element of , so . Furthermore, has four irreducible representations , which are all one-dimensional [20,21]. Table 1 shows the characters of the four classes belonging to the four irreducible representations . A reducible representation can be obtained by considering the action of each element of on the set of the subsectional basis functions (The following convention is adopted for numbering these functions: the index i specifies the quadrant of the plane (-) on which the basis function is defined, and the index j specifies the order of the subsectional basis function [13].) (with ) used to discretize the relation (5) via the method of moments [13,19]. The representation is abelian, with and . Table 2 shows the characters of the four classes belonging to . The representation can be reduced on the basis of the considerations given in Section 3.2. By inserting the values of , , and given above and the values of the characters reported in Table 1 and Table 2 into relations (11) and (12), we obtain that all the elements of the fully reduced representation can be written as block diagonal matrices of order as
where . The diagonal sub-matrices of order p have the form
i.e., they are given by the direct sum of the irreducible matrices taken times [20]. Using the arguments stated in [13,22,23], the operator-valued function of (6) commutes with all the elements of the group . This property, as clearly stated in Section 3, indicates that (6) can be reduced to a homogeneous matrix system of the form (7) with coefficient matrix reduced into block diagonal form by means of the Galerkin method [24], with the set of symmetry-adapted basis functions generated by applying the projection operators
given by (13) to the set of the sub-sectional basis functions used to obtain a reducible representation for the group . Due to the commutability constraint, the coefficient matrix must have the same block form as that of the elements , i.e.,
whose submatrix elements have the form
where the terms , ,,, , , , and are, respectively, the potentials related to the symmetry-adapted basis functions , and the symbol denotes the inner product [6] (a full account of the numerical treatment of the matrix elements (20)–() for the TE and TM modes can be found in [8] and will be not repeated here). Accordingly, the eigenproblem (19) is composed of four nonlinear eigenproblems of order . As can be easily verified, the overall asymptotic computational complexity involved in the numerical resolution by means of the algorithm described in [11] is , where . If we compare this result with , where , that is, the required overall computational complexity for solving the eigenproblem (8), it is evident that (for large p) a theoretical speed-up by a factor of 16 is achieved.
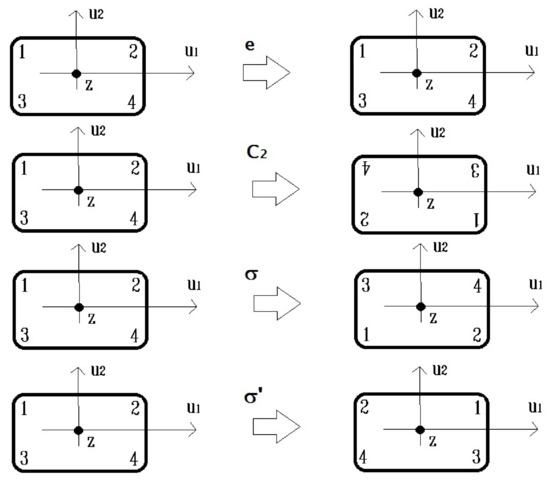
Figure 1.
Geometric effect of the symmetry operations.

Table 1.
Character table for the irreducible representations of .

Table 2.
Character table for the reducible representation of .
5. Numerical Results
The procedure described in Section 4 is implemented in computer code using MATLAB. As a case study, we consider the computation of the cutoff wavenumbers for the following metallic waveguides (see Figure 2 for details), (i) coaxial, (ii) rectangular with rounded corners, and (iii) double ridged, which are characterized by a transverse cross section with a symmetry degree described by the symmetry group . All the numerical computations are performed on an Intel Xeon DP E5405 Quad Core 2.0 workstation with 20 GB of main memory. Numerical results for the cutoff wavenumbers for the TE and TM modes are obtained and compared with those published in the literature [5,25,26]. The values of the parameters , , and employed in the numerical computations are 6, 11, and , respectively. We exploited a number of symmetry adapted basis functions equal to in the case of coaxial waveguide, in the case of rectangular waveguide with rounded corner, and in the case of double ridged waveguide. Table 3, Table 4 and Table 5 show that a good agreement is achieved for all the considered guiding structures. The differences are very small and always less than . The computational time involved to obtain these numerical results was of 0.92 s, 0.85 s, and 1.1 s for each frequency point for the case, while was of 1.96 s, 1.71 s, and 2.4 s for each frequency point for the case. The computational speed-up (when compared with the numerical simulations conducted by [11] without the use of the group theoretical approach) ranges between factors of 9 and 11. From a practical perspective, these speed-up values can be considered to be close to the expected theoretical speed-up predicted by the considerations given in Section 4, thus demonstrating the usefulness of exploiting symmetry to reduce the computational effort involved in the calculation of the cutoff wavenumbers.
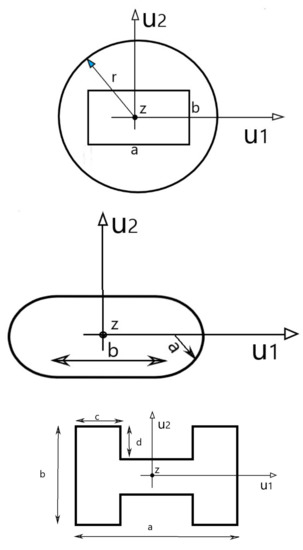
Figure 2.
Symmetric waveguides considered in the present work: (Top) coaxial waveguide (r = 1 cm, a = 0.5 cm, b = 0.25 cm, [5]), (Middle) rectangular waveguide with rounded corners (a = 0.1 cm, b = 0.2 cm, [25]), (Bottom); double-ridged waveguide (a = 1.27 cm, b = 1.016 cm, c = 0.508 cm, d = 0.3683 cm, [26]).

Table 3.
Cutoff wavenumbers [rad·cm] for the coaxial waveguide.

Table 4.
Cutoff wavenumbers for the rectangular waveguide with rounded corners.

Table 5.
Cutoff wavenumbers for the double-ridged waveguide.
6. Conclusions
In this paper, a group theoretical approach to reducing the computational effort related to the evaluation of the cutoff wavenumbers of symmetric metallic guiding structures using a nonlinear eigenvalue problem formulation has been presented. To illustrate, in a simple way, that the group theoretical machinery works, we have tested our approach on metallic waveguides with a transverse cross section described by the symmetric point group . The numerical results demonstrate that a significant improvement in the computational performance related to the use of the algorithm described in [11] can be obtained in this way. To conclude, we note that the proposed approach can be used without any substantial changing to the method of addressing waveguides characterized by a transverse cross section with any kinds of symmetries.
Author Contributions
Conceptualization, G.A. and M.V.; methodology, G.A.; software, G.A., M.V. and S.C.; validation, G.A., M.V. and S.C.; formal analysis, G.A.; writing—original draft preparation, S.C.; writing—review and editing, G.A., M.V. and S.C.; supervision, G.A.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SVD | Singular Value Decomposition |
| PEC | Perfect electric conductor |
| GB | Gigabyte |
References
- Rothwell, E.; Cloud, M.J. Electromagnetics, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Pozar, D.M. Microwave Engineering, 4th ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Lin, S.L.; Li, L.W.; Yeo, T.S.; Leong, M.S. Analysis of metallic waveguides of a large class of cross sections using polynomial approximation and superquadric functions. IEEE Trans. Microw. Theory Tech. 2001, 49, 1136–1139. [Google Scholar] [CrossRef]
- Lin, S.L.; Li, L.W.; Yeo, T.S.; Leong, M.S. Cutoff wavenumbers in truncated waveguides. IEEE Microw. Wirel. Compon. Lett. 2001, 11, 214–216. [Google Scholar] [CrossRef]
- Rodriguez, B.S.; Sensale, B.; Leitao, V. Determination of the TE and TM modes in arbitrarily shaped waveguides using a hypersingular boundary element formulation. AEU Int. J. Electron. Commun. 2008, 62, 576–581. [Google Scholar] [CrossRef]
- Spielman, B.E.; Harrington, R.F. Waveguides of arbitrary cross section by solution of a nonlinear integral eigenvalue equation. IEEE Trans. Microw. Theory Tech. 1971, 20, 578–585. [Google Scholar] [CrossRef]
- Hanson, G.; Yakovlev, A. Operator Theory for Electromagnetics; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Swaminarthan, M.; Arvas, E.; Sarkar, T.K.; Djordjevic, A.E. Computation of cutoff wavenumbers of TE and TM modes in waveguides of arbitrary cross sections using a surface integral formulation. IEEE Trans. Microw. Theory Tech. 1990, 38, 154–159. [Google Scholar] [CrossRef]
- Labay, V.A.; Bornemann, J. Matrix singular value decomposition for pole-free solutions of homogeneous matrix equations as applied to numerical modeling methods. IEEE Microw. Guided Wave Lett. 1992, 2, 49–51. [Google Scholar] [CrossRef]
- Higham, N.J. Accuracy and Stability of Numerical Algorithms; SIAM: Philadelphia, PA, USA, 2002. [Google Scholar]
- Angiulli, G. On the computation of nonlinear eigenvalues in electromagnetic problems. J. Electromagn. Waves Appl. 2007, 21, 527–532. [Google Scholar] [CrossRef]
- Lobry, J. Use of group theory in symmetrical 3-D eddy current problems. IEE Proc. Sci. Meas. Technol. 1996, 143, 369–376. [Google Scholar] [CrossRef]
- Tripp, A.L.; Hohmann, G.W. Block diagonalization of the electromagnetic impedance matrix of a symmetric buried body using group theory. IEEE Trans. Geosci. Remote Sens. 1984, 22, 62–69. [Google Scholar] [CrossRef]
- Baum, C.E.; Kritikos, H.N. Electromagnetic Symmetry; Taylor & Francis: Abingdon, UK, 1995. [Google Scholar]
- Angiulli, G.; Versaci, M.; Morabito, F.C. Computation of nonlinear eigenvalues related to parameters of microwave structures by using group theory. In Proceedings of the 2017 International Applied Computational Electromagnetics Society Symposium - Italy (ACES), Florence, Italy, 26–30 March 2017. [Google Scholar]
- Patel, H.N.; Ghodgaonkan, D.K. Application of group theory for computation reduction in microwave imaging of human breast model at 500 MHz. Progr. Electromagn. Res. M 2016, 51, 165–173. [Google Scholar] [CrossRef]
- Zheng, X.; Verellen, N.; Vercruysse, D.; Volskiy, V.; Van Dorpe, P.; Vandenbosch, G.A.; Moshchalkov, V. On the use of group theory in understanding the optical response of a nanoantenna. IEEE Trans. Antennas Propag. 2015, 63, 1589–1602. [Google Scholar] [CrossRef]
- Wongkasem, N.; Akyurtlu, A.; Marx, K.A. Group theory based design of isotropic negative refractive index metamaterials. Progr. Electromagn. Res. 2006, 63, 295–310. [Google Scholar] [CrossRef][Green Version]
- Ballisti, R.; Hafner, C.; Leuchtmann, P. Application of the representation theory of finite groups to field computation problems with symmetrical boundaries. IEEE Trans. Magn. 1982, 18, 584–587. [Google Scholar] [CrossRef]
- Inui, T.; Tanabe, Y.; Onodera, Y. Group Theory and Its Applications in Physics; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Ladd, M. Symmetry and Group Theory in Chemistry; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Cohoon, D.K. Reduction of the cost of solving an integral equation arising in electromagnetic scattering through the use of group theory. IEEE Trans. Antennas Propag. 1980, 28, 104–107. [Google Scholar] [CrossRef]
- Knorr, J.B. Consequences of symmetry in the computation of characteristic modes for conducting bodies. IEEE Trans. Antennas Propag. 1973, 21, 899–902. [Google Scholar] [CrossRef]
- Angiulli, G.; Cacciola, M.; Calcagno, S.; De Carlo, D.; Morabito, C.F.; Sgró, A.; Versaci, M. A numerical study on the performances of the flexible BiCGStab to solve the discretized E-field integral equation. Int. J. Appl. Electromag. Mech. 2014, 46, 547–553. [Google Scholar] [CrossRef]
- Ooi, B.L.; Zhai, G. Element-free method for the analysis of arbitrarily shaped hollow conducting waveguides. IEE Proc. Microw. Antennas Propag. 2004, 152, 369–376. [Google Scholar] [CrossRef]
- Guan, J.M.; Su, C.C. Analysis of metallic waveguides with rectangular boundaries by using the finite-difference method and the simultaneous iteration with Chebyshev acceleration. IEEE Trans. Microw. Theory Tech. 1995, 43, 374–382. [Google Scholar] [CrossRef]
- Shen, Z.; Lu, X. Modal analysis of a rectangular waveguide with rounded sides. Microw. Opt. Technol. Lett. 2002, 33, 154–159. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).