Stability Analysis of an Age-Structured SEIRS Model with Time Delay
Abstract
1. Introduction
2. An Age-Structured SEIRS Model with Time Delay
3. Traveling Wave Solution
4. Stability Analysis of System
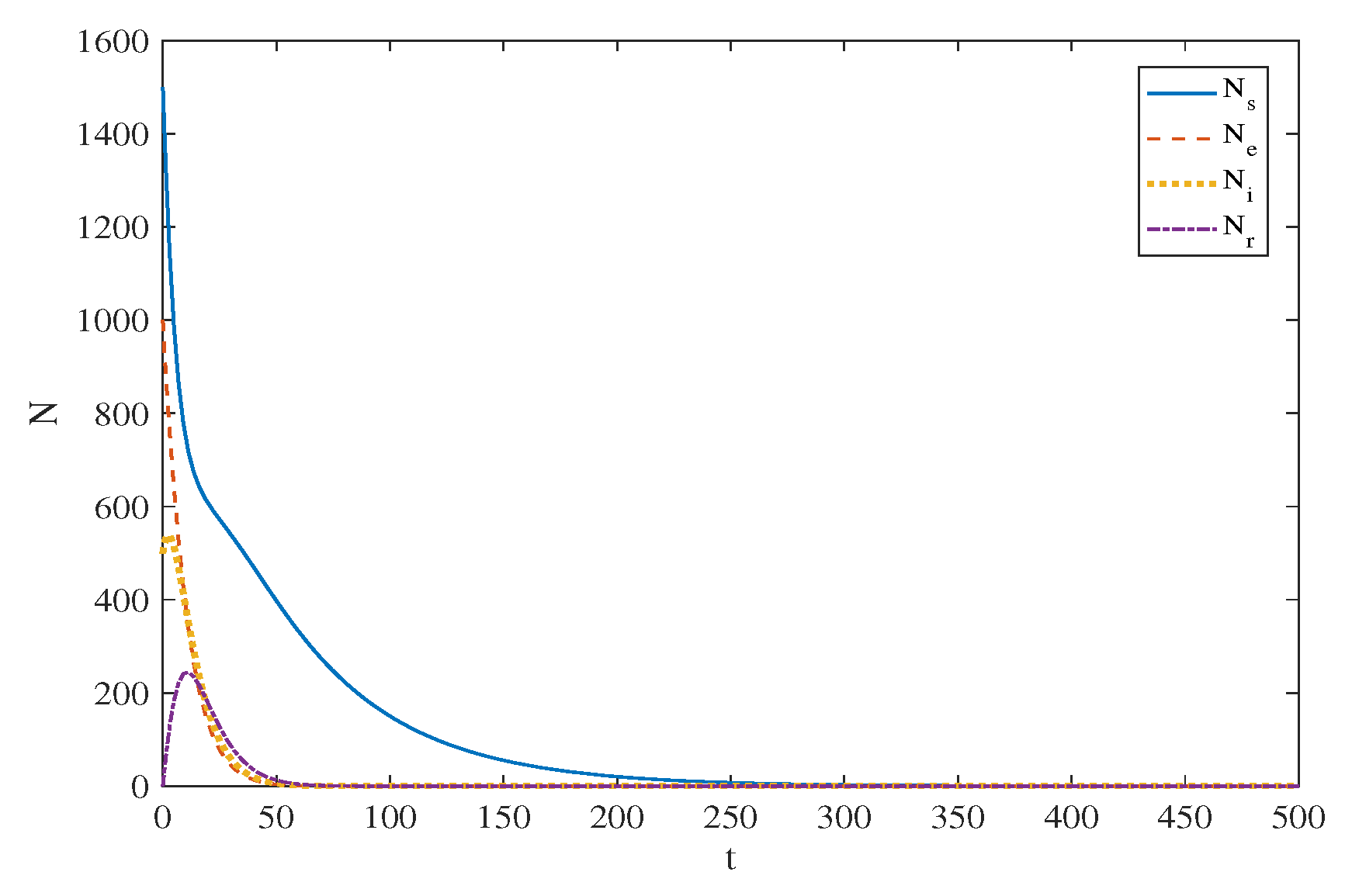
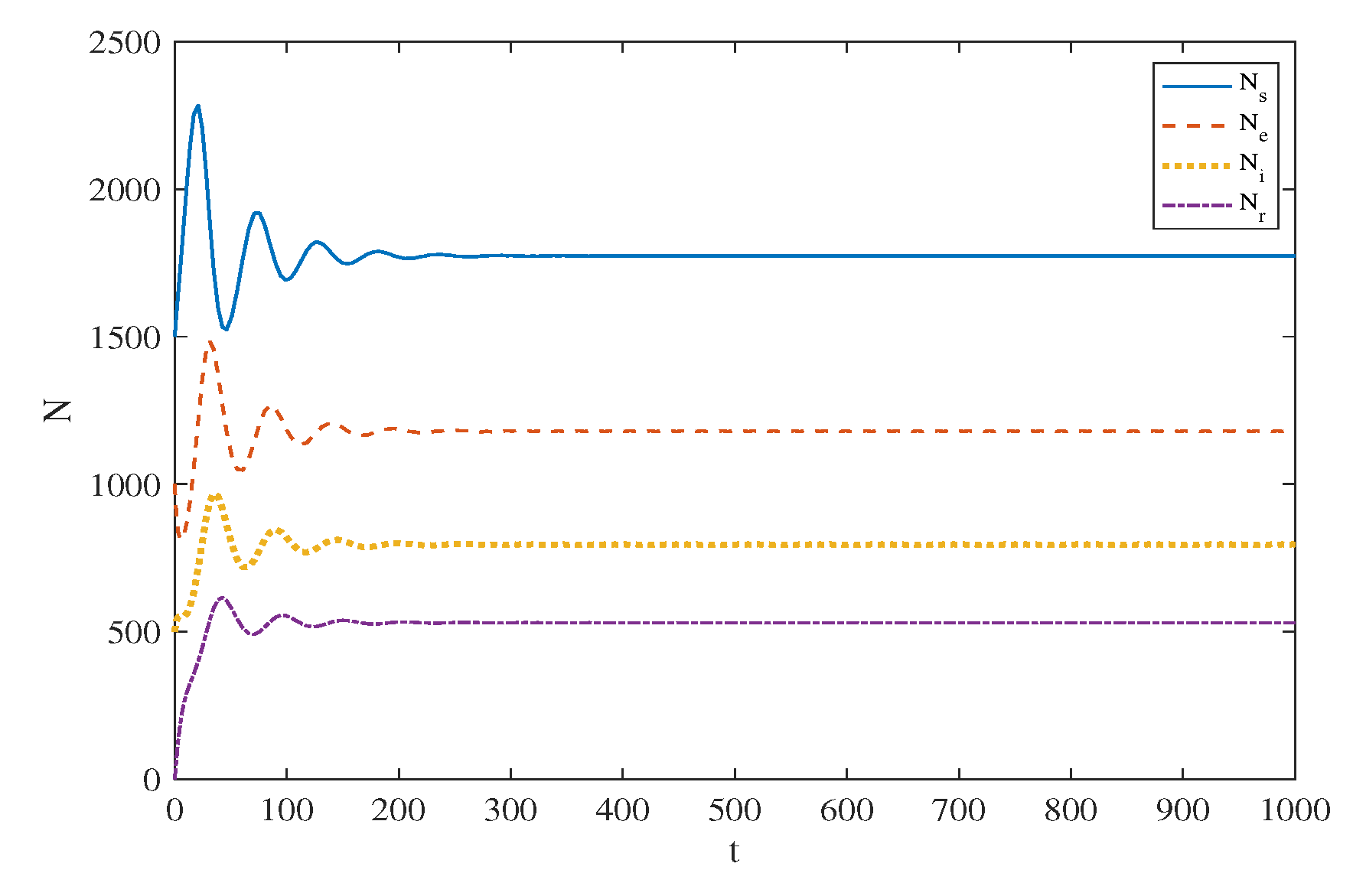
5. Simulation
6. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. A 1927, 115, 700–721. [Google Scholar] [CrossRef]
- Brauer, F.; Castillo-Chavez, C. Mathematical Models in Population Biology and Epidemiology; Springer: New York, NY, USA, 2012. [Google Scholar]
- Zhou, X.; Cui, J.A. Analysis stability and bifurcation for an SEIR epidemic model with saturated recovery rate. Commun. Nonliear Sci. Numer. Simul. 2011, 16, 4438–4450. [Google Scholar] [CrossRef]
- Chauhan, S.; Misra, O.P.; Dhar, J. Stability Analysis of SIR Model with Vaccination. J. Comput. Appl. Math. 2014, 4, 17–23. [Google Scholar]
- Vargas-De-Len, C. On the global stability of SIS, SIR and SIRS epidemic model with standard incidence. Chaos Solitons Fractals 2011, 44, 1106–1110. [Google Scholar] [CrossRef]
- Shaikhet, L. Stability of SIR Epidemic Model Equilibrium Points; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Chen, L.J.; Sun, J.T. Global stability and optimal control of an SIRS epidemic model on heterogeneous networks. Physica A 2014, 15, 196–204. [Google Scholar] [CrossRef]
- Lakshmanan, M.; Senthilkumar, D.V. Dynamics of Nonlinear Time-Delay Systems; Springer: Berlin/Heidelberg, Germany, 2010; p. 313. [Google Scholar]
- Smith, H. An Introduction to Delay Differential Equations with Application to the Life Sciences; Springer: Berlin/Heidelberg, Germany, 2011; p. 172. [Google Scholar]
- Sharma, S.; Mondal, A.; Pal, A.K.; Samanta, G.P. Stability analysis and optimal control of avian influenza virus A with time delays. Int. J. Dyn. Control 2018, 6, 1351–1366. [Google Scholar] [CrossRef]
- Xu, R.; Ma, Z.E.; Wang, Z.P. Global stability of a delayed SIRS epidemic model with saturation incidence and temporary immunity. J. Comput. Appl. Math. 2010, 59, 3211–3221. [Google Scholar] [CrossRef][Green Version]
- Shu, H.Y.; Fan, D.J.; Wei, J.J. Global stability of multi-group SEIR epidemic models with distributed delays and nonlinear transmission. Nonlinear Anal. RWA 2012, 13, 1581–1592. [Google Scholar] [CrossRef]
- De la Sena, M.; Alonso-Quesadaa, S.; Ibeasb, A. On the stability of an SEIR epidemic model with distributed time-delay and a general class of feedback vaccination rules. Appl. Math. Comput. 2015, 270, 953–976. [Google Scholar] [CrossRef]
- Cooke, K.L.; Driessche, P. Analysis of an SEIRS epidemic model with two delays. J. Math. Biol. 1996, 35, 240–260. [Google Scholar] [CrossRef]
- Gao, S.J.; Chen, L.S.; Teng, Z.d. Impulsive Vaccination of an SEIRS Model with Time Delay and Varying Total Population Size. Bull. Math. Biol. 2007, 69, 731–745. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.D. Global behavior of an SEIRS epidemic model with time delays. Appl. Math. Lett. 2002, 15, 423–428. [Google Scholar] [CrossRef]
- Schenzle, D. An age-structured model of pre-and post-vaccination measles transmission. IMA J. Appl. Math. 1984, 1, 169–191. [Google Scholar] [CrossRef] [PubMed]
- Metz, J.A.J.; Diekmann, O. The Dynamics of Physiologically Structured Populations. In Lecture Notes in Biomathematics; Springer: Berlin, Germany, 1986; p. 68. [Google Scholar]
- Iannelli, M. Mathematical Theory of Age-Structured Population Dynamics; Giardini Editorie Stampatori: Pisa, Italy, 1995. [Google Scholar]
- Hethcote, H.W. The mathematics of infectious diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Mccluskey, C. Global stability for an SEI epidemiological model with continuous age-structure in the exposed and infectious classes. Math. Biosci. Eng. 2012, 9, 819–841. [Google Scholar]
- Zou, L.; Ruan, S.; Zhang, W. An age-structured model for the transmission dynamics of hepatitis B. SIAM J. Math. Appl. 2010, 70, 3121–3139. [Google Scholar] [CrossRef]
- Gandolfi, A.; Iannelli, M.; Marinoschi, G. An age-structured model of epidermis growth. J. Math. Biol. 2011, 62, 111–141. [Google Scholar] [CrossRef]
- Alexanderian, A.; Gobbert, M.K.; Fister, K.R.; Gaff, H.; Lenhart, S.; Schaefer, E. An age-structured model for the spread of epidemic cholera. Nonlinear Anal. RWA 2011, 12, 3483–3498. [Google Scholar] [CrossRef]
- Akimenko, V.V. Asymptotically stable states of non-linear age-structured monocyclic cell population model I. Travelling wave solution. Math. Comput. Simul. 2017, 133, 2–23. [Google Scholar] [CrossRef]
- Akimenko, V.V. Asymptotically stable states of non-linear age-structured monocyclic cell population model II. Numerical simulation. Math. Comput. Simul. 2017, 133, 24–38. [Google Scholar] [CrossRef]
- Akimenko, V.V. Nonlinear age-structured models of polycyclic population dynamics with death rates as a power functions with exponent n. Math. Comput. Simul. 2017, 133, 175–205. [Google Scholar] [CrossRef]
- Akimenko, V.V. An age-structured SIR epidemic model with fixed incubation period of infection. Math. Comput. Appl. 2017, 73, 1485–1504. [Google Scholar] [CrossRef]
- Guo, Z.K.; Huo, H.F.; Xiang, H. Global dynamics of an age-structured malaria model with prevention. Math. Biosci. Eng. 2019, 16, 1625–1653. [Google Scholar] [CrossRef] [PubMed]
- Huo, H.F.; Yang, P.; Xiang, H. Dynamics for an SIRS epidemic model with infection age and relapse on a scale-free network. J. Frankl. Inst. 2019, 356, 7411–7443. [Google Scholar]
- Diekmann, O.; Heesterbeek, J.A.P.; Metz, J.A.J. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990, 28, 365. [Google Scholar] [CrossRef] [PubMed]
- Hassard, B.; Kazarinoff, N.; Wan, Y.H. Theory and Applications of Hopf Bifurcation; Cambridge University Press: London, UK, 1981. [Google Scholar]
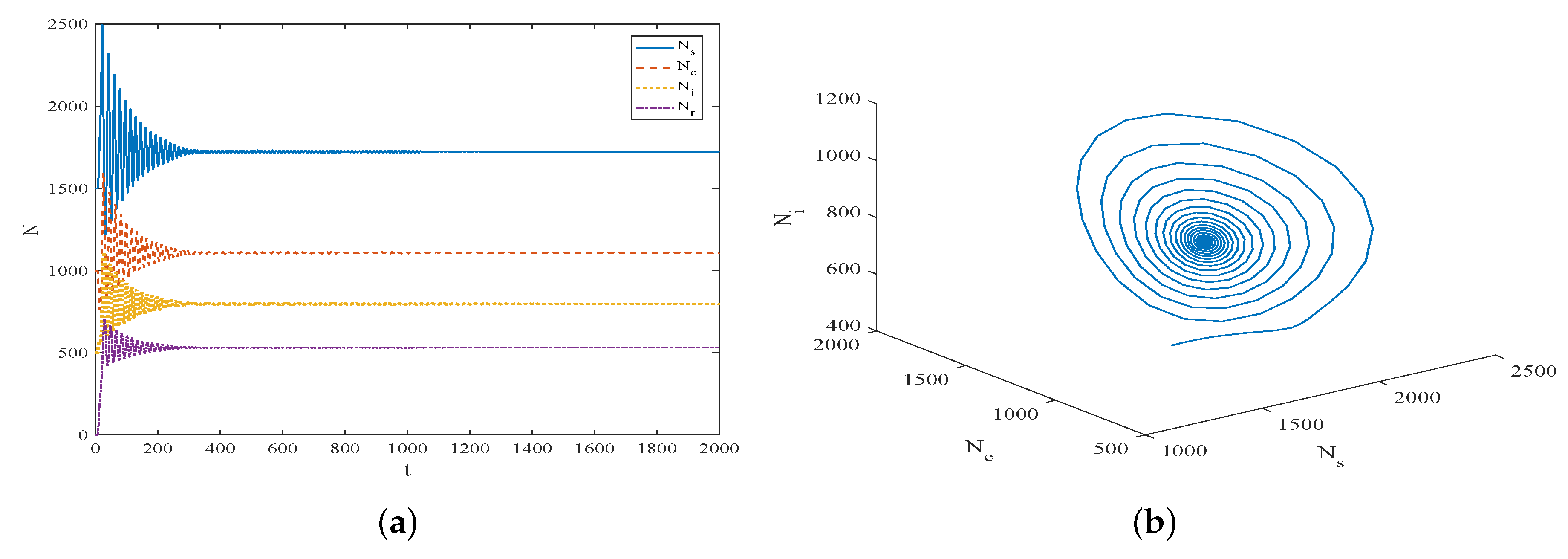
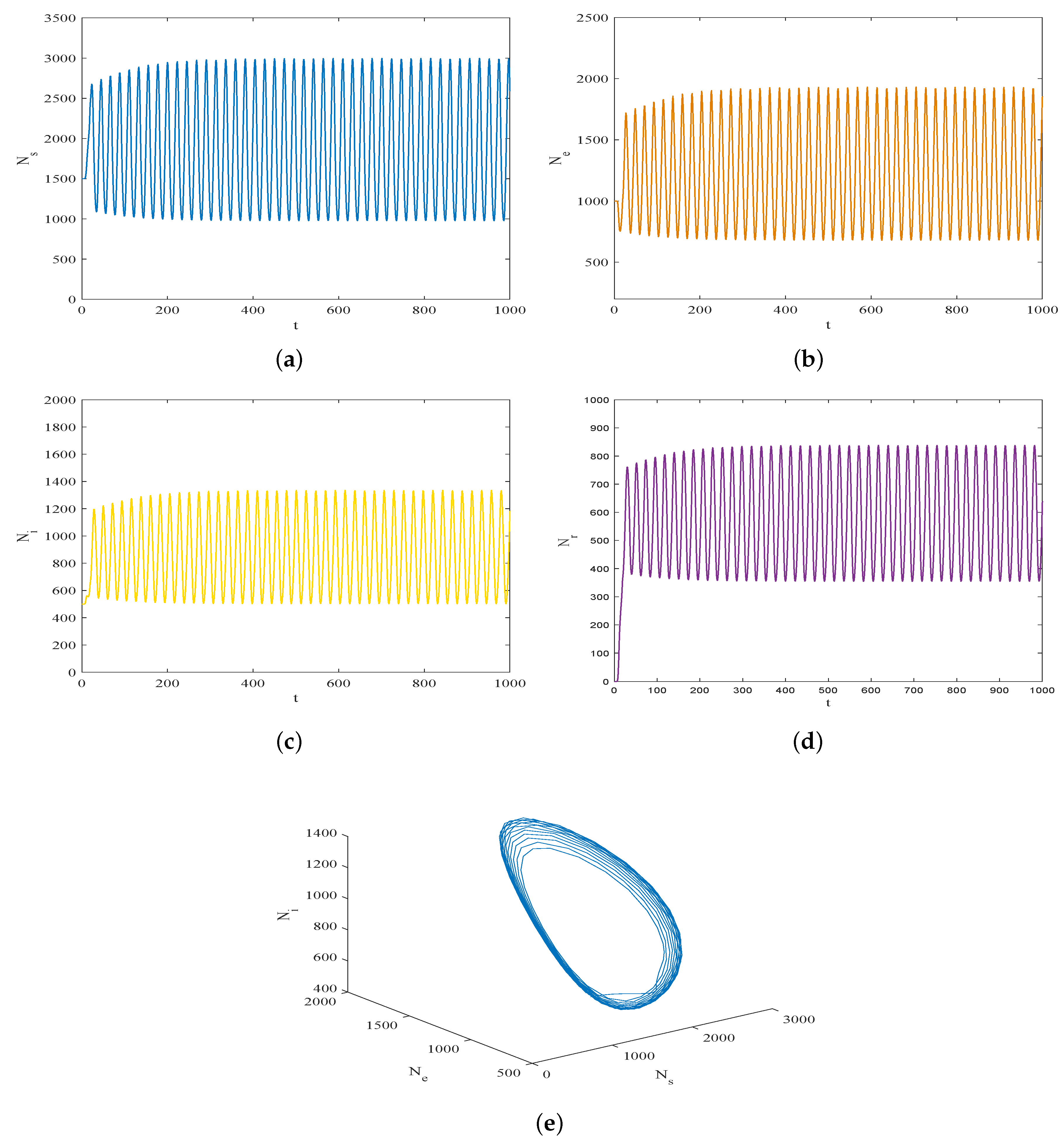
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Z.; Yu, Y.; Lu, Z. Stability Analysis of an Age-Structured SEIRS Model with Time Delay. Mathematics 2020, 8, 455. https://doi.org/10.3390/math8030455
Yin Z, Yu Y, Lu Z. Stability Analysis of an Age-Structured SEIRS Model with Time Delay. Mathematics. 2020; 8(3):455. https://doi.org/10.3390/math8030455
Chicago/Turabian StyleYin, Zhe, Yongguang Yu, and Zhenzhen Lu. 2020. "Stability Analysis of an Age-Structured SEIRS Model with Time Delay" Mathematics 8, no. 3: 455. https://doi.org/10.3390/math8030455
APA StyleYin, Z., Yu, Y., & Lu, Z. (2020). Stability Analysis of an Age-Structured SEIRS Model with Time Delay. Mathematics, 8(3), 455. https://doi.org/10.3390/math8030455





