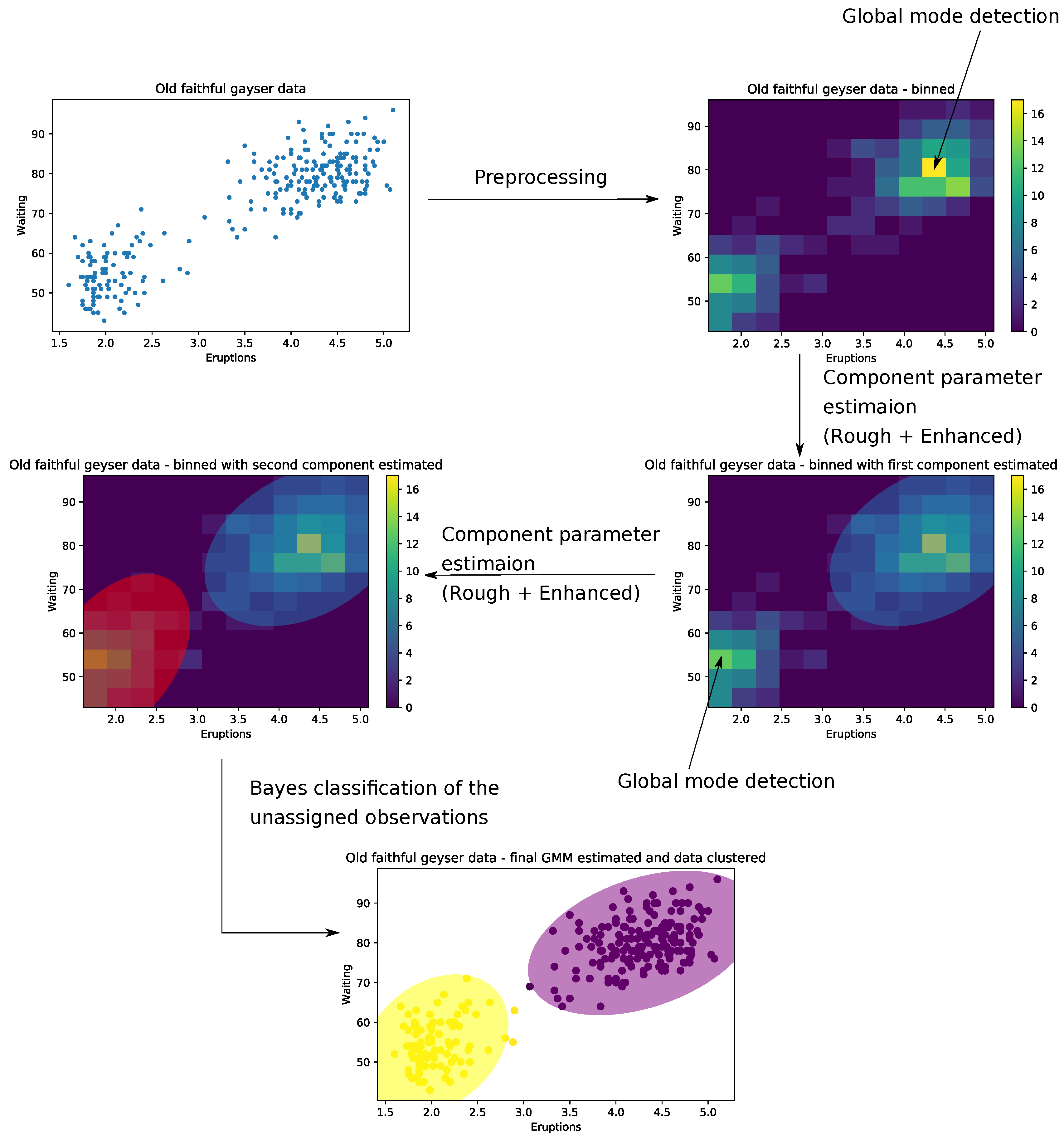
5.1. Results on Artificially Generated Datasets
First, let us introduce the parameters used for the proposed strategies. The Exhaustive REBMIX&EM and Best REBMIX&EM strategies require an ordered set of the numbers of bins
K, and the Single REBMIX&EM strategy requires a single number of bins
v as the input. The ordered set of the numbers of bins
K had 3–100 bins. For the Single REBMIX&EM strategy, the number of bins
v was estimated using the Knuth rule [
40]. The maximum number of components
and the minimum numbers of components
is kept the same for every strategy, along with the Kmeans&EM and the Random&EM. The threshold value for the average log-likelihood value (for the convergence assumption) was
and the maximum number of EM iterations allowed was 1000. The choice of convergence of the EM with the average log-likelihood value was made because it removes the impact of larger and smaller datasets (in terms of the number of observations). The average log-likelihood was calculated simply by dividing the log-likelihood value
by the number of observations
n in the dataset.
Secondly, let us describe the methodology used to compare the strategies here. As explained in
Section 3.1.1, the purpose of the model-selection procedure is to choose the appropriate GMM parameters based on the defined measure, which was in our case BIC. Therefore, the quality of the estimated GMM parameters can be expressed by the corresponding value of the BIC. If the strategy estimated the GMM parameters that gave the best value of the BIC, i.e., the lowest value compared to other strategies used, then we assume that the strategy also estimated the best GMM parameters. This is a reasonable and commonly used method for comparing the quality of the estimated GMM parameters [
14,
32]. In addition, the use of the MixSim R package to sample the artificial datasets (
Section 4.1) allows the true density estimation and the clustering for each artificial dataset to be determined based on the fact that the GMM from which the data set was sampled is known. This was used to additionally compare the clustering (
Section 5.1.1) and density-estimation (
Section 5.1.2) performance of the estimated GMM parameters.
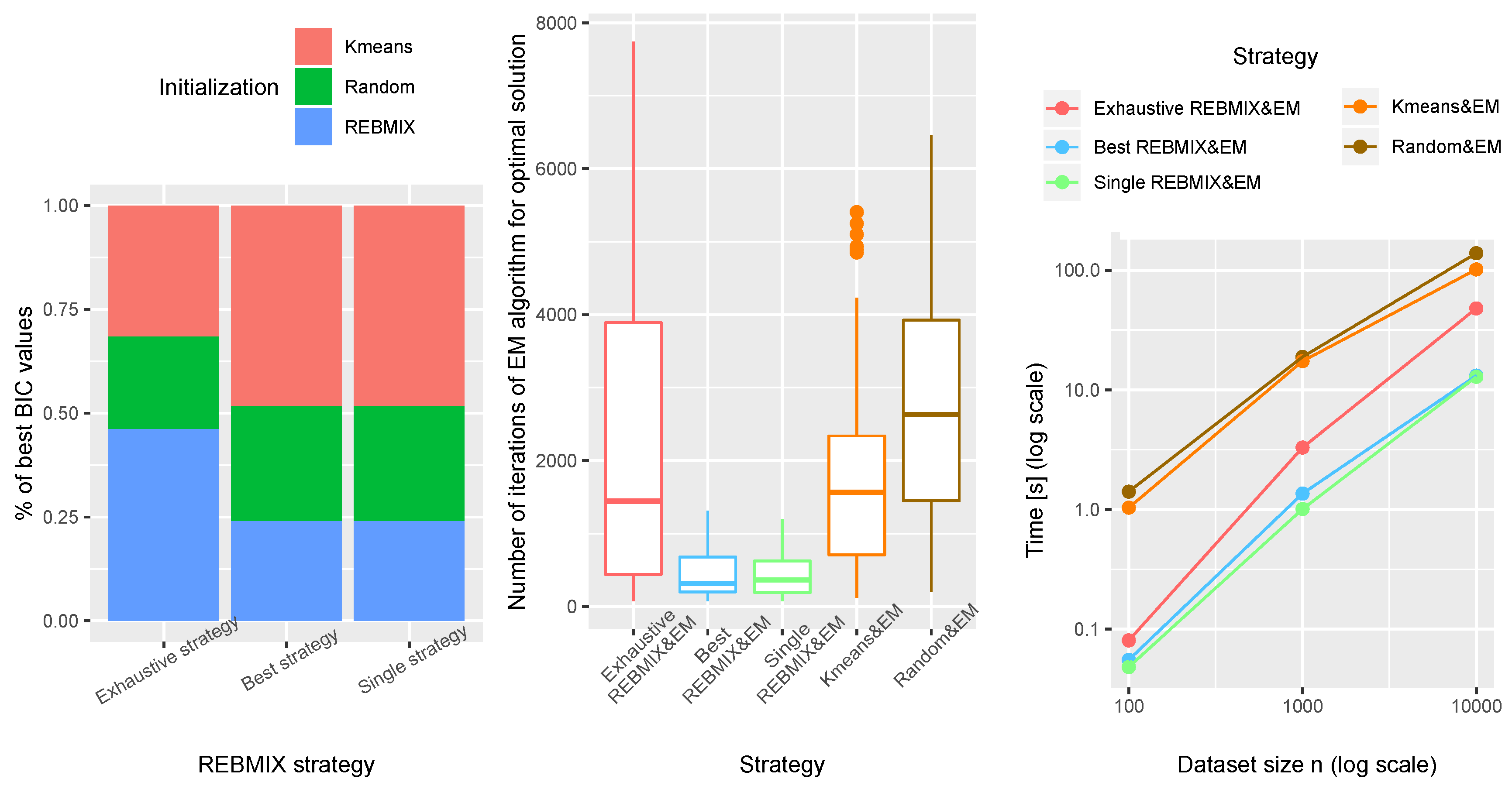
The general results are presented in
Figure 4 which are acquired on all artificial datasets. The first plot represents the percentage of selected GMM with the best BIC value for each REBMIX&EM strategy versus the Kmeans&EM and Random&EM strategy. Exhaustive REBMIX&EM selected better GMM on more datasets than Kmeans&EM and Random&EM strategy, judging by the BIC value. On other hand, strategies Best and Single REBMIX&EM had a smaller number of datasets on which they yielded best GMM in terms of BIC value than Kmeans&EM and equal to the Random&EM strategy. The second plot represents the box-plots of the EM iterations used by each strategy. The Random&EM strategy needed the largest number of EM iterations. Following this is the Exhaustive REBMIX&EM strategy, then the Kmeans&EM strategy, and the smallest number of iterations was needed by the Best and Single REBMIX&EM strategies. This is inferred based on the median value of the box-plots (horizontal line inside the box). In addition, the Best and Single REBMIX&EM strategies had a much smaller number of iterations of the EM algorithm, due to the fact that they had only one set of initial parameters for each number of components
, as opposed to, e.g., the Random&EM, which had five sets of initial parameters for each number of components. However, interestingly, the Exhaustive REBMIX&EM strategy had at least 90 different sets of initial parameters for each number of components and still had a smaller number of iterations than the Random&EM and had the same median value as the distribution of the number of iterations for the Kmeans&EM. That does seem to be beneficial to the REBMIX algorithm, which seems to provide very close to the initial parameters of the GMM to the final estimated parameters. Finally, the third plot shows the amount of time spent on estimating the GMM parameters with different strategies. The Best and Single REBMIX&EM strategies had similar computing times and therefore their effectiveness seems to be equivalent. Most of the differences in the performance of these two strategies stem from the fact that the Best REBMIX&EM strategy had a multiple number of bins
v (3–100) for the REBMIX algorithm, as opposed to the Single REBMIX&EM strategy, for which we used the Knuth rule to obtain the single number of bins
v. Moving forward, the Exhaustive REBMIX&EM strategy gradually increased the required computation time with the increase in the number of observations. This is to be expected, since this strategy required the most EM iterations (second plot) compared to the other two REBMIX&EM strategies. The Random&EM and Kmeans&EM strategy had the worst performance in terms of the computing time. Although the Random&EM strategy needed less time when the number of observations was lower, the Kmeans&EM strategy outperformed it as the number of observations increased. Judging by the actual values, however, the difference between these two strategies was not great.
5.1.1. Application to Clustering
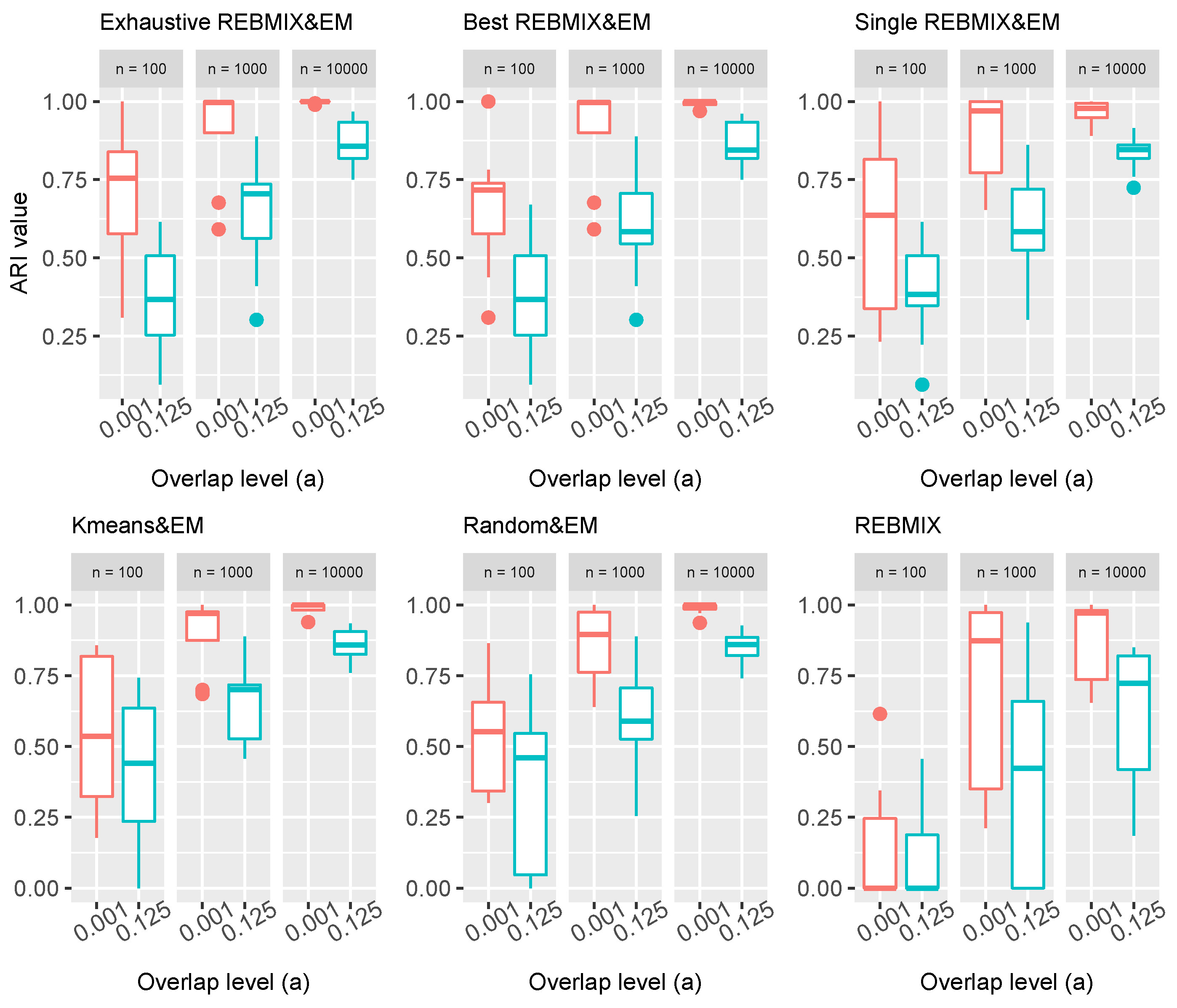
The ARI is used to study the clustering performance. The results are given as box-plots in
Figure 5. The grouping in
Figure 5 was selected because it reflects the difficulty of the dataset, i.e., a small number of observations in the dataset along with a high degree of overlap between the components can be seen as a difficult clustering problem, while the large number of observations with a small degree of overlap can be seen as a simpler clustering problem.
The performance of the Exhaustive REBMIX&EM strategy and the Best REBMIX&EM strategy on smaller datasets () with a lower degree of overlap was better than the multiple repeated Kmeans&EM and multiple repeated Random&EM strategy. The Kmeans&EM strategy improved the results for the datasets with a larger number of observations with smaller overlap although the Exhaustive REBMIX&EM strategy and the Best REBMIX&EM strategy performed equivalently or better. The Random&EM only had equivalent results on the largest datasets n = 10,000. The Single REBMIX&EM performed slightly worse than the Exhaustive REBMIX&EM strategy and the Best REBMIX&EM strategy, although equivalently to the Kmeans&EM strategy and mostly better than the Random&EM strategy. On the other hand, the datasets with larger overlap reduced the clustering performance of all the strategies, especially for datasets with and . In this context, the Kmeans&EM performed better than all the REBMIX&EM strategies for datasets with a small number of observations . On datasets with a larger number of observations only the Exhaustive REBMIX&EM strategy performed as well as the Kmeans&EM strategy, while only the Random&EM strategy performed poorly. On the datasets with the largest number of observations n = 10,000, the strategies Exhaustive and Best REBMIX&EM slightly outperformed the other strategies. We have also included the results we obtained just by running the REBMIX algorithm. For the K, we chose the 3–100 range—in other words, the same as for the Exhaustive and Best REBMIX&EM strategy. The results for the were mainly worse than the results from all the other strategies. As this number increased, i.e., and n = 10,000, the performance improved, although the other strategies still performed better.
5.1.2. Application to the Density Estimation
To study the performance of the estimated GMM with different strategies in terms of density estimation, we used the mean square error (MSE) measure [
33]. The MSE is defined as:
where
are estimated GMM parameters with different strategies and
are the true GMM parameters from simulation. The choice of MSE instead of MISE was made here because the distributions used for sampling the datasets had higher dimensions, i.e., 3, 5, and 10, and the creation of the good integration grid requires a lot of computing power in terms of memory. The results are therefore presented as box-plots of MSE values in the upper plot in
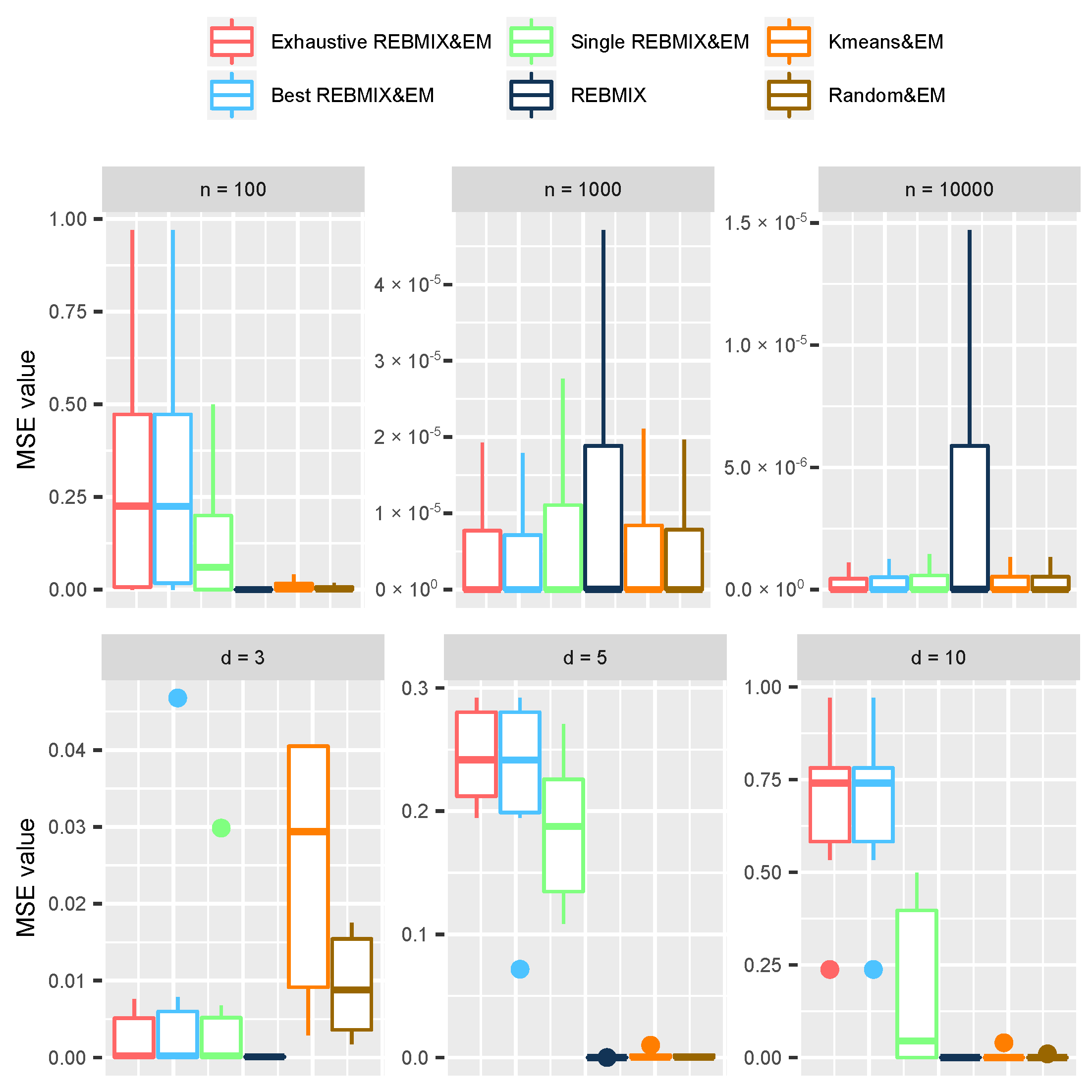
Figure 6. These box-plots are grouped by the number of observations in the dataset. Again, for the estimation, we have used all the strategies and the stand-alone REBMIX algorithm.
Judging by the values presented, all the strategies and the stand-alone REBMIX gave good results for the datasets with
and
. In contrast, for
, the Kmeans&EM, Random&EM, and REBMIX had much better results than the REBMIX&EM strategies. To study more carefully why this happened, the box-plots for the datasets with
observations only are given in the lower plot (
Figure 6), grouped by the number of dimensions
d in the dataset. It is clear that, as the dimensionality of the dataset increased, the results became worse. Although the stand-alone REBMIX algorithm had good results, it is clear that the results of the REBMIX&EM strategies deteriorated. To understand why this happened, we must recall that the log-likelihood function, defined in Equation (
3), for the GMM is unbounded. Namely, a singularity in one of the component covariance matrices
can arise when
[
33]. When this problem appears, the EM can be jeopardized and the obtained solution can degenerate. A high-dimensional setting, such as
or
, emphasizes this problem even more [
14]. Because we did not include any of the safeguards for the EM algorithm, in terms of bounding the log-likelihood function, the resulting log-likelihood increased and the model-selection procedure was misled into choosing the degenerated solution.
5.2. Density-Estimation Tasks
For the density estimates, the same parameters were used for the three REBMIX&EM strategies as in the case of the Artificial datasets and also the same for the Random&EM and Kmeans&EM strategies. For the ADEBA algorithm, we used the parameters for the ADEBA −
implementation (see [
11],
Section 3), i.e., the parameter
is chosen with Bayesian averaging and
for which we will use the generic term ADEBA.
The acquired values of MISE for each pair of strategy/method and distribution are shown on different plots in
Figure 7. In general, the GMM estimates using different strategies yielded better results with an increase in the dataset size
n. For the small dataset sizes, e.g.,
and
, ADEBA usually had the best results, although the REBMIX&EM strategies proved to be good competitors, which can be seen from the results on the distributions
Bend 2-d,
Bend 3-d,
Trips-2d,
Blob 2-d,
Tetra 3-d and
Wave 2-d. For the datasets sampled from the distributions
Trips-2d and
Trips-3d with an increasing size of the dataset, all the strategies used outperformed the ADEBA. This is expected because the
Trips-2d and
Trips-3d distributions are actually GMM distributions with
non-overlapping components. Interestingly, the ADEBA outperformed all the strategies used for all the dataset sizes
n on the
Blob 2-d distribution, which is also a GMM distribution with
overlapping components. However, as the dimension of the distribution increased (i.e., the distribution
Blob 3-d is only the same distribution as
Blob 2-d in three-dimensional space), the results from the ADEBA deteriorated. On the distributions
Bend 2-d and
Bend 3-d, all the estimators had their performance deteriorated. Kmeans&EM and Random&EM performed worse than the REBMIX&EM strategies and the ADEBA. On the
Spiral 3-d distribution for the
REBMIX&EM strategies, the Kmeans&EM and Random&EM strategy performed worse than the ADEBA, although their performance improved as the
n increased (for the REBMIX&EM strategies again from
and and for the Kmeans&EM and Random&EM strategies from the
and
, respectively). For the distributions
Tetra 3-d and
Wave 2-d, the results are similar to the ones for the
Blob 2-d distribution. Between the different REBMIX&EM strategies, the results did not differ greatly. The slight difference can be seen on the smaller dataset sizes
n. However, as
n increased, the results were almost identical. We have also evaluated REBMIX, as a stand-alone algorithm, for this experiment. Again,
K was 3–100. REBMIX was better when the number of observations in the dataset was small, usually only for
. On other hand, just the increase from the
to
improved the results from the REBMIX&EM strategies on many distributions, most notably on the GMM distributions such as
Trips 3d.
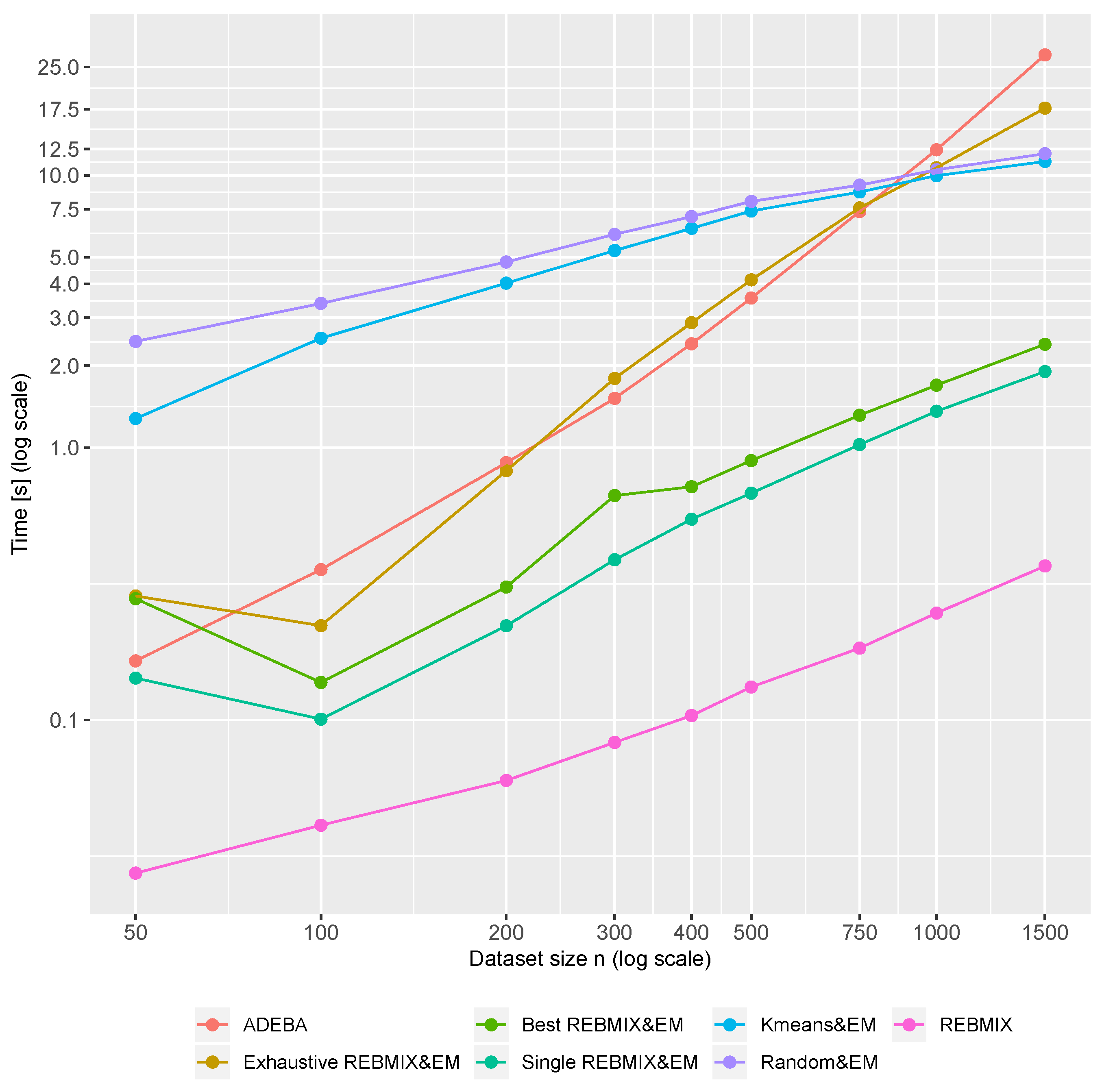
To study the performance of different EM strategies and the ADEBA, the computation times for each method/strategy were measured for different distributions and different dataset sizes
n. The values are grouped by the dataset size n and the method/strategy, and the mean values are shown in
Figure 8. The Single and Best REBMIX&EM strategy far outperformed all the other strategies used and the ADEBA algorithm for all the dataset sizes, with the exception of size
, where the ADEBA and REBMIX&EM strategies achieved equivalent results. The Exhaustive REBMIX&EM strategy performed as well as the ADEBA. The Kmeans&EM and Random&EM performed worse on all the dataset sizes, with the exception of the dataset size
, where they performed slightly better than the ADEBA and Exhaustive REBMIX&EM. The REBMIX stand-alone outperformed all the used strategies and the ADEBA algorithm in terms of computation efficacy.
5.3. Image-Segmentation Tasks
The image segmentations were carried out using the following strategies: the Single REBMIX&EM strategy, where the number of bins v was estimated using the Knuth rule; the Single REBMIX&EM strategy, where the number of bins v was taken to be ; the Best REBMIX&EM strategy, with the range of the number of bins being 3–100; and the Kmeans&EM strategy and the Random&EM strategy. The number of bins was taken as the color-channel value. The intensities of the RGB images only have integer values and, therefore, the frequency of each color channel is estimated. Furthermore, using , the marginal distributions of the color-channel value’s intensity are represented. The maximum number of components for each strategy is kept the same, i.e., . The threshold value for the EM algorithm was and the maximum allowed number of EM iterations was 1000.
The numerical results in terms of the number of components
c and the ARI value are given in
Table 3. From the numerical results, one of the REBMIX&EM strategies always had the best ARI values. Additionally, the Single REBMIX&EM with
yielded very good results in terms of ARI value on the flower image (
353013), herd image (
38092), and woman image (
216053); therefore, the intuitive guess of
was shown to be beneficial. Finally, the selected GMMs with all strategies had a large number of components
c, which can be related to the BIC model selection criteria.
To establish some qualitative comparison, the segmentations of the flower and herd images are given in
Figure 9. First, the issue of the black or white colored background. Namely, the black or white colored background caused a high density on the edges of the feature space, creating a heavy-tailed distribution, for which GMMs are not suitable. The GMMs estimated with each strategy needed at least two components to address the heavy tails of distribution; therefore, a background like on the flower image (label
353013) was mostly over-segmented and caused a lower ARI value. Next, the strategies mostly had problems with the objects that occupied a large part of the image scene and had little variation in color (for example, the flower object on the flower image or soil on the herd image). Namely, the object that occupied larger parts of the scene caused a high-density peak in the distribution. This high-density peak caused a certain asymmetry in the distribution and the strategies tried to fit multiple components of the GMM for that part. This caused a lot of noise in the segmentation, which can be seen in
Figure 9. This problem was slightly reduced by the Single REBMIX&EM strategy with
, which mostly did tie the peaks with one component of the GMM (flower object in the flower image or the soil-ground part of the herd image in
Figure 9). This also led to a much higher ARI value for those segmentations. The sky gradients mostly caused over-segmentations, which were not properly addressed by any strategy.
Additionally, we also included results from purely clustering algorithms, such as the MeanShift (MS) algorithm or the newer Cutting edge spatial clustering (CutESC) [
41], which exhibited good results in their study. We have used scikit-learn Python MS implementation [
42] with default values. The segmentation was made on the original pixel-color values. For the CutESC algorithm, we followed their recommendation. First, we calculated superpixels of the images with scikit-image SLIC implementation [
43] with defaults values and then constructed a shrunken dataset, containing the spatial and color values.
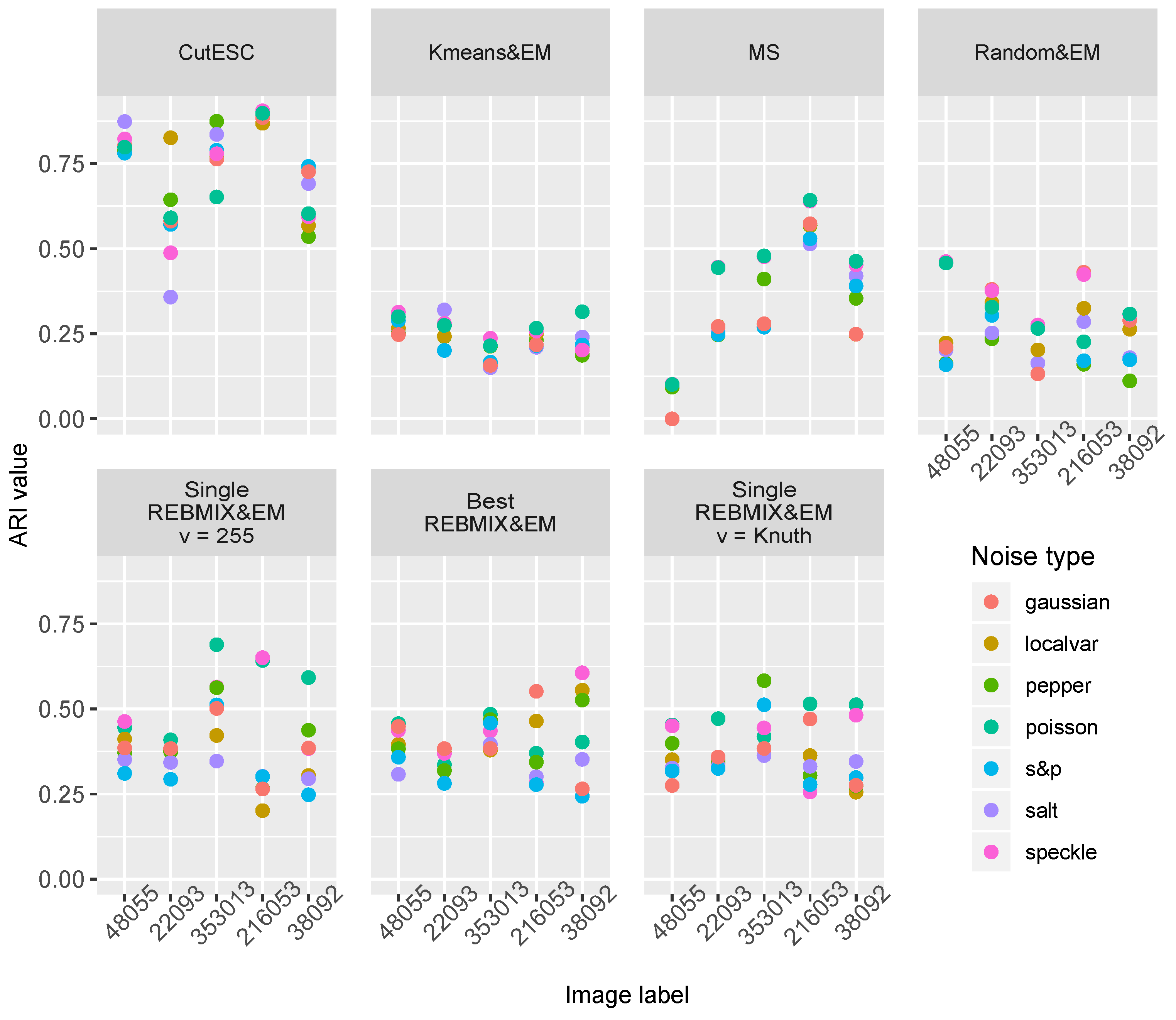
Table 4 summarizes the ARI values obtained using their algorithms. In addition, to obtain consistently good segmentations for the CutESC algorithm, parameters
and
were set to 0.5. As expected, CutESC outperformed all the other strategies/algorithm. The GMM estimated with the REBMIX&EM strategies outperformed the MS clustering algorithm on images
353013,
38092 and
48055, and MS yielded slightly better results on images
216053 and
22093.
To investigate the robustness of the different strategies in a clustering scenario of the image-segmentation tasks, we added different types of noise to the images used. Seven types of noise,
salt,
pepper,
salt&pepper or shortly (s&p),
Gaussian,
Poisson,
speckle,
localvar implemented in the Scikit-image python module, and their effects can be seen in the herd image in
Figure 10. The results of the ARI value are shown on the plots in
Figure 11 for each strategy/method and the corresponding image and noise type.
As expected, the different types of noise contributed differently to the quality of the segmentation; however, surprisingly, not all the types of noise deteriorated the results in terms of reducing the ARI value. The
Poisson had an improving effect on almost every image and every method/strategy used. Noises such as
salt,
pepper and
salt&pepper generally had a deteriorating effect on the results of the segmentation. With certain methods/strategies, this type of noise deteriorated the quality of the segmentation by up to 20%. In order to better evaluate the results, we provided additional box-plots (
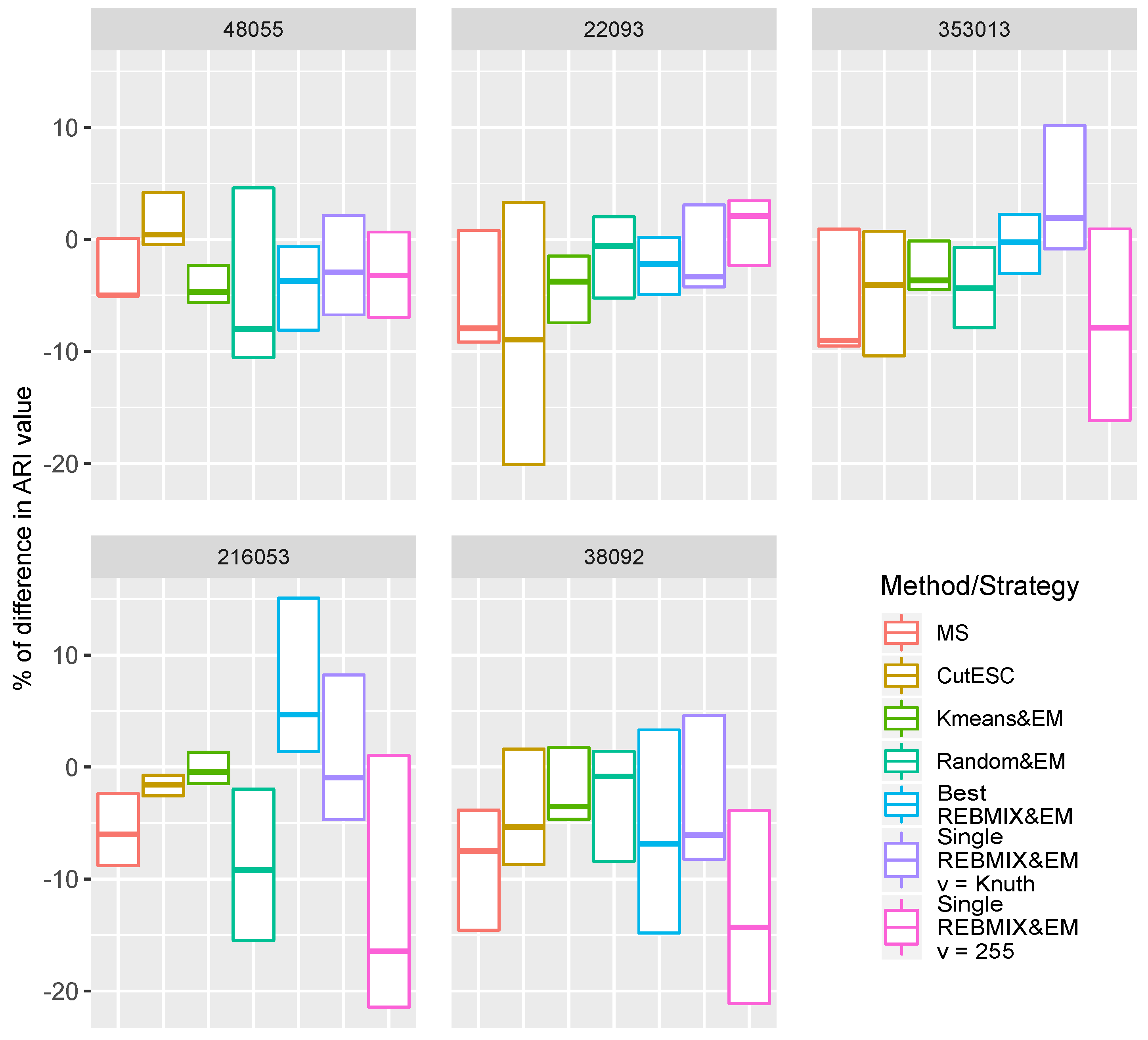
Figure 12) of the different methods/strategies that show the percentage of difference between the results of the non-noisy images and the results of the noisy images. The box-plots are constructed as follows. The upper limit of the box is the maximum value of the difference (positive value means improvement), and the lower limit is the minimum value (negative value means deterioration) and the horizontal line within the box median value. Since the ARI measure is bounded between −1 and 1, the difference of 10% can be interpreted as 0.05 of the difference of the ARI value.
The following general remarks can be derived from the box plots in
Figure 12. The results of the segmentation from the MS algorithm have usually deteriorated. However, this deterioration was only minor and ranged from 5% up to 10%. On the other hand, the CutESC algorithm on the image
48055 mostly had improvements, while on the image
216053 it produced only a slight deterioration of the segmentation results. On the image
22093, there were slight improvements in the segmentation results for certain noise types, while there were large deteriorations for the others. On the images
353013 and
38092, the noise usually deteriorated the segmentation results from the CutESC algorithm. Forwardly, the noise had the following effects on the results of the segmentation using the Kmeans&EM and Random&EM strategies. Different noise types had little effect (either improving or deteriorating) on the segmentation results with the Kmeans&EM strategy, while the noise deteriorated the segmentation results with the Random&EM strategy in most cases, although the specific noise types improved the segmentation results for the images
48055 and
22093.
The REBMIX&EM strategies used were influenced by the noise and the different types of noise in different ways. We will start with the Single REBMIX&EM strategy with the number of bins
. This strategy had the greatest deterioration for the images
353013,
216053, and
38092. Although it is still not as significant, since 20% represents the decrease of the ARI value of 0.1, it indicates that this method should be used with caution in the presence of noise. On the other hand, the Best REBMIX&EM and Single REBMIX&EM strategy with the number of bins
v estimated with the Knuth rule had minor to mild (image
38092 with Best REBMIX&EM strategy) deterioration of the segmentation results, and, interestingly, the greatest improvements of the segmentation results in the presence of different types of noise. In fact, the Best REBMIX&EM only had improvements of the segmentation results for the image 216053 without any deterioration (the resulting rectangle in
Figure 12 is above zero). The Single REBMIX&EM strategy with the number of bins
v estimated with the Knuth rule had similar results for the
353013 image. This can be interpreted as follows. By adding noise to particular images, the density shape of the image pixel values became more similar to those that the GMM can generate, so the REBMIX&EM strategies were able to successfully estimate them.
The results of the different strategies/algorithms regarding image segmentation with noise applied to the images revealed some interesting facts, such as the fact that adding some types of noise could improve the results of the GMM-based image segmentation. The in-depth investigation of when and why this happened goes beyond the scope of this article and also goes beyond the topic, so we conclude with a final remark. In many cases, the noise will deteriorate the results of the segmentation; however, this is to be expected. For most of the strategies/algorithms used, the amount of deterioration was low. If the present amount of noise is large, the Random&EM strategy or the Single REBMIX&EM with the number of bins is not recommended, while the others are safe to use. It should also be considered as to whether the addition of some artificial noise can improve the result of the segmentation.
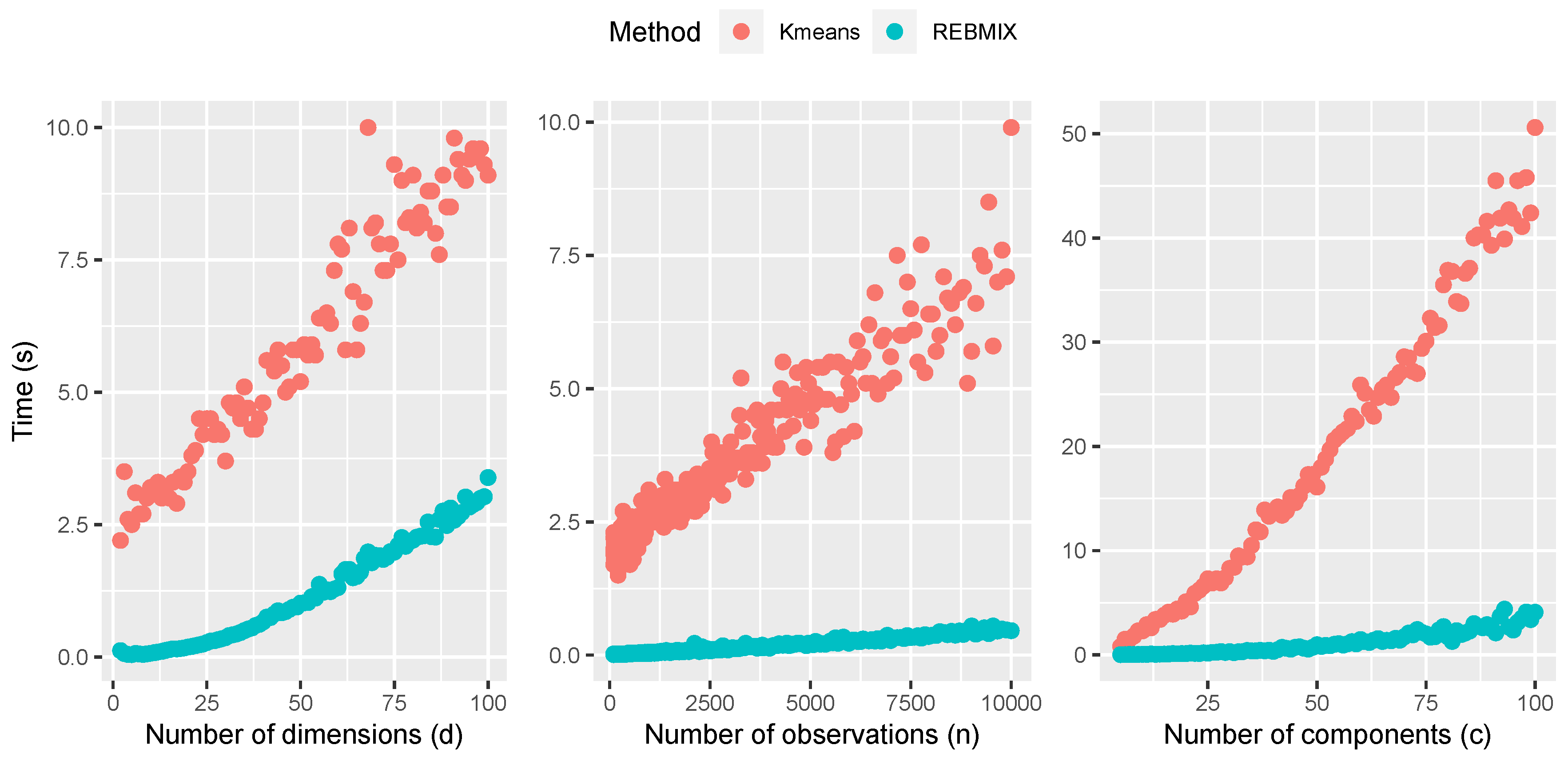
5.4. Comparison of the Time Complexity of REBMIX and k-Means Algorithm
As the
k-means algorithm is more or less the fastest used algorithm to initialize the parameters for the EM estimation of the GMM, we compared the time complexity of the
k-means algorithm and the REBMIX algorithm. It is hard to estimate theoretically the time complexity for both algorithms. Judging by [
31], the theoretical time complexity of the
k-means is
, where t is the number of iterations needed,
c is the number of components,
n is the number of observations, and
d is the dimension of the dataset. It is hard to know how many iterations
t will the
k-means algorithm need. On the other hand, the time complexity of the REBMIX algorithm depends on multiple factors. First, the most important is definitely the number of non-empty bins
in the histogram preprocessing. Forward, it depends on the chosen maximum value of the components
and the dimension of the problem
d. Finally, it depends on the different number of bins
v for the histogram preprocessing, e.g., the 3–100 range has 97 values. Therefore, we have chosen to give an empirical comparison of both algorithms in terms of the number of observations
n, the number of dimensions
d, and the maximum number of components
. The results are presented in
Figure 13. For the REBMIX algorithm, we used the
REBMIX function provided by the
rebmix R package. For the
k-means algorithm, we used the default R
kmeans implementation provided in the
base R package. Although the
k-means algorithm needs a different number of iterations, here we considered 100 iterations of the
k-means algorithm. This seems reasonable due to the fact that repetitions of the
k-means are often preferable [
31]. In addition, due to the fact that, for the GMM initialization, the
k-means algorithm needs to be repeated
times, we have taken this into consideration by repeating the
k-means algorithm for each
. For the REBMIX algorithm, we have used the setting in which the number of bins
v is not known and the range used was 3–100. In addition, when the time complexity with respect to the one parameter is evaluated, the other two were kept constant. In other words, when comparing the time complexity with respect to the number of dimensions
d, the number of observations
and the maximum number of components
was kept constant. For the comparison with respect to the number of observations
n, the number of dimensions was
and the maximum number of components
. Finally, for the comparison with respect to the maximum number of components
, the number of dimensions was
and the number of observations was
.
First, we will start with a comparison with respect to the number of dimensions
d, which is given in the first plot of
Figure 13. We can see that the time complexity of
k-means is linear with respect to this parameter. Therefore, it agrees with the theoretical assumption. On other hand, the REBMIX seems to have a nonlinear complexity with respect to the parameter
d. The nonlinearity with respect to this parameter comes from the definition of the multivariate Gaussian distribution in Equation (
2). To calculate the PDF of the GMM, the inverse of the covariance matrix
for each component is required. The matrix inversion is a nonlinear operation; therefore, nonlinear dependence in time is justified. The second parameter for which the comparison was made was the number of observations
n in the dataset. The results are shown on second plot of
Figure 13. Both the REBMIX and
k-means algorithms exhibited a linear dependency in respect to the number of observations
n, and, finally,
k-means had a linear dependency with respect to the
parameter, while the REBMIX has nonlinear. The nonlinear complexity in terms of the parameter
comes from its empirical stopping criteria, which does not guarantee that each iteration adds exactly one more component to the GMM (details of the stopping criteria of the REBMIX algorithm are explained in the last two paragraphs of
Section 3.2). The nonlinear dependencies of the REBMIX algorithm with respect to the parameters
d and
are troublesome, given that
k-means has a linear dependence. This gives the
k-means algorithm an advantage over the REBMIX algorithm. However, if the time complexity with respect to the number of observations
n is observed, they have proven to be equal competitors. In the end, with the obtained values of time spent for the REBMIX algorithm and the
k-means algorithm, the REBMIX algorithm was generally faster.
5.5. Note on Selection of Hyperparameters for the REBMIX&EM Strategies and Their Impact on Performance
In this section, we will discuss the hyperparameters of the REBMIX&EM strategies used for the presented experiments. There were five different hyperparameters used for all the experiments, in particular the number of bins v, the minimum number of components in the GMM, the maximum number of components in the GMM, the maximum number of iterations of the EM algorithm, and the threshold for convergence of the EM algorithm.
First, we will discuss the choice of the number of bins
v for the histogram preprocessing. There is no general rule for estimating the number of bins
v in the histogram [
44]. Some common estimators are Sturges’ rule
originating in [
45] and the RootN rule
from [
46]. In [
16], it was suggested to create the lower and upper bounds for the bin range
K based on these rules. Strurges’ rule always yields a smaller number of bins
v and is suitable for the lower bound, while the RootN rule gives a larger number of bins
v and thus can be used for the upper bound. The ranges
K based on those two rules are narrow for datasets with a smaller number of observations
n, e.g., for
, the range is 7–10 bins. For the dataset with a large number of observations, e.g.,
n = 10,000 leads to the range of 14–100, which is very wide. The choice of the bin range 3–100 as a constant for each experiment was chosen to test whether these additional ranges can be used to better estimate the GMM parameters using the REBMIX algorithm and thus allow a better initialization of the EM algorithm, or only cause an unnecessary computational effort. For the estimation of the number of bins
v for the Single REBMIX&EM strategy, we have used the Knuth rule. The Knuth rule uses a Bayesian approach to estimate the number of bins
v in a histogram, thus making this estimation dependent on the observations from the dataset. Ref. [
40] gives a straightforward extension to multivariate histograms. Although, in the original paper, the multivariate histograms can have a different number of bins for each dimension, i.e.,
, it is worth noting that we only used the same number of bins
v in each dimension. The number of bins
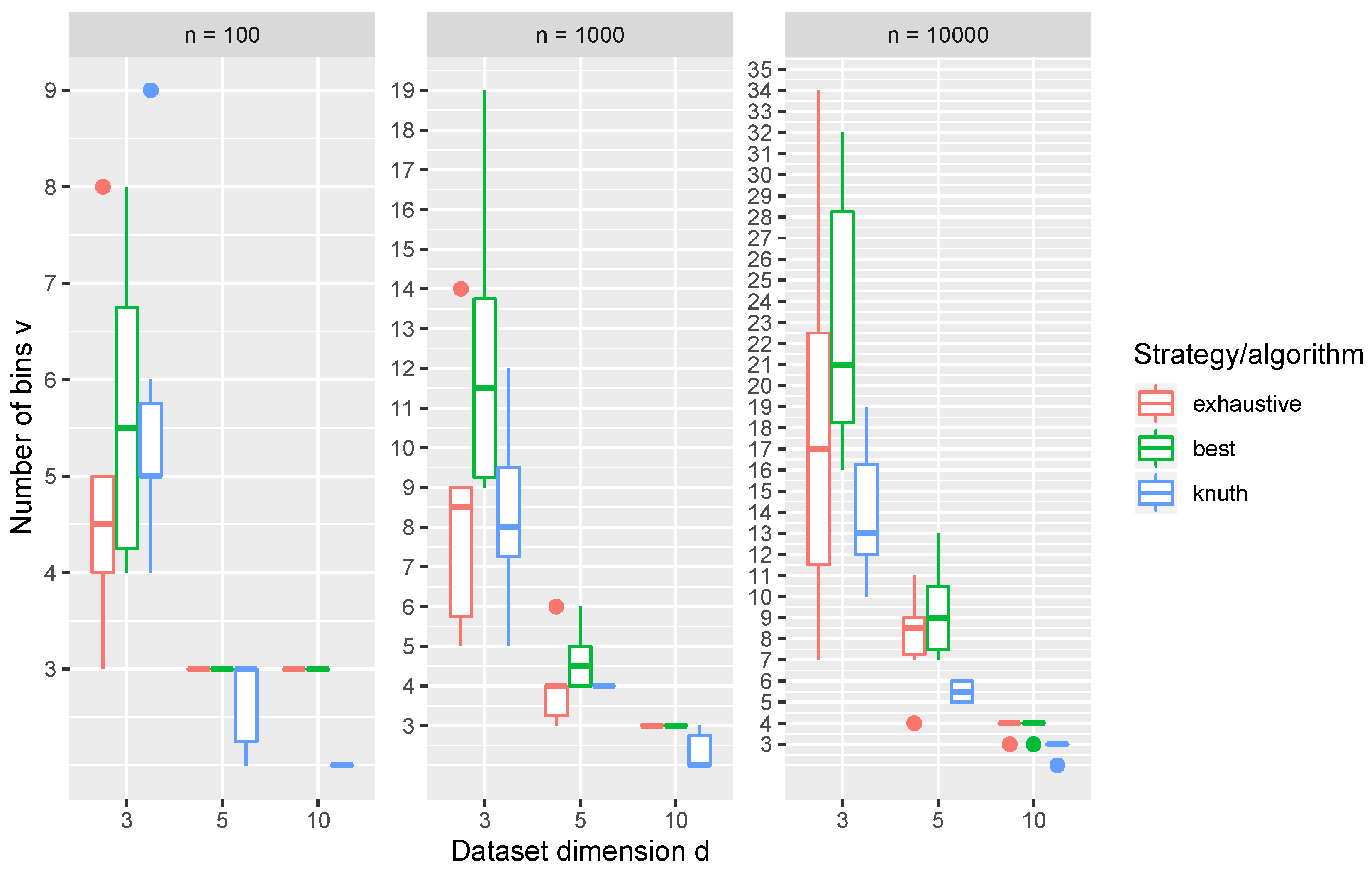
v estimated with the Knuth rule for datasets from
Section 4.1 is shown in
Figure 14. It is clear from
Figure 14 that the Knuth rule depends on both the dimension
d of the dataset and the number of observations
n, unlike the above-mentioned estimators. In addition, it had a different number of bins
v for the datasets with the same dimension
d and number of observations
n (boxes span over multiple values of
v), which indicates that
n and
d are not the only influences. In addition, it is clear that the number of bins
v is greatly reduced as the dimensions of the dataset increased. This can be tied to what is called the curse of dimensionality [
44]. There are many bins in a high-dimensional histogram grid. Just for the
and
settings, there are 9,765,625 bins. Such an extremely large number of bins leads to many empty bins, i.e., for which the frequency was
, which were heavily penalized by the Knuth rule (it can be seen that, for
, the estimated number of bins was mostly
or
).
Additionally, in
Figure 14, the number of bins
v that yielded the optimal GMM parameters using the Exhaustive and Best REBMIX&EM strategies given for the datasets. Although we have given a large range, judging by the values in
Figure 14, it can be seen that both the Exhaustive and the Best REBMIX&EM strategies estimated the GMM parameters for a different number of bins
v than what is proposed by the Knuth estimator, which leads in some experiments to benefits, while in another leads to some numerical instabilities. For example, the number of optimal GMM parameters estimated with the Exhaustive REBMIX&EM strategy was the greatest if we recall
Figure 4. On the other hand, regarding what was found by comparing the density-estimation performance in
Section 5.1.2 for a small number of observations
, this caused some of the degeneracies in the estimated GMM parameters. The Best REBMIX&EM strategy favored a larger number of bins
v in the histogram preprocessing in all the presented cases. This is also a useful insight because in the image-segmentation experiment (
Table 3) the results were better than what was acquired with a Single REBMIX&EM strategy with the number of bins
v estimated with the Knuth rule. For the density-estimation tasks in
Section 5.2, the results seem to have not been very impacted by the chosen REBMIX&EM strategy, at least in terms of the MISE value (
Figure 7). Let us recall that we also used the intuitive
for the image-segmentation tasks. As we already said, this intuition was made based on the fact that digital images have 255 different intensity values for each color channel. This assumption was shown to be good, judging by the results we obtained with it; however, it was probably most sensitive to the noise along with the Random&EM strategy.
To conclude, the Single REBMIX&EM strategy with the Knuth rule can be safely used when a short computation time is preferred, and the dimension of the dataset is small. The datasets in the density-estimation tasks in
Section 5.2 had
or
. For the Exhaustive and Best REBMIX&EM strategies, we recommend the RootN rule for the upper bound and the Knuth rule for the lower bound. The RootN rule will mostly overestimate the number of bins for larger
n, judging by the obtained values in
Figure 14. However, due to the fact that a smaller number of EM iterations was needed with the REBMIX, as an initialization technique, this remains acceptable. If the time efficacy is a major concern, to obtain the best-possible results for the datasets with a larger number of observations
n, the Best REBMIX&EM strategy could be used to obtain the upper bound for the histogram preprocessing number of bins
v range. Then, the Exhaustive REBMIX&EM strategy could be used with this value as the upper bound, while keeping the Knuth rule for the lower bound, for the histogram preprocessing number of bins
v range.
We would like to mention some points about the selection of the
and
values for the GMM or any other MM parameter estimation. The number of MM parameters increases with the increasing dimension, especially the GMM parameters. It is, therefore, always advisable to check to see whether the number of observations
n in the dataset is larger than the number of parameters
M, i.e.,
. For a dataset with a smaller number of observations
n, this can be used as a rule-of-thumb selector of
. Choosing a smaller value for
when the number of observations
n is also small can additionally reduce the probability of estimating the degenerated solution. Otherwise, the maximum number of components
can be as large as required, depending on the application of the GMM. For example, in the image-segmentation tasks, the number of observations was large. As can be seen in
Table 3, the estimated number of components
c was always high. The images used had a resolution of 480 × 320 or 320 × 480, which resulted in a number of observations equal to
n =153,600. Based on our above rule of thumb, the value of
can go as high as
= 15,000. However, this would be numerically unstable due to the floating arithmetic. For this kind of example, where the number of observations
n is high and we can expect a large number of components in the GMM, this hyperparameter can also be fine-tuned. Some lower value can be used as the starting point to obtain some information about how the IC (in our case the BIC) is changing with respect to an increase in the number of components
c in the GMM. If there are some large fluctuations in the value of BIC, or the slope of the BIC-
c curve seems too steep, we can try to increase the value of
until the curve stabilizes and the values of BIC slowly start to increase. If some other IC is used instead of the BIC, then the same analogy applies. As for the
, it is advisable to use
for the minimum value to check whether the dataset fits well into the non-mixture distribution.
For the values of the maximum number of iterations of the EM algorithm and the threshold of the EM algorithm, we have chosen 1000 and 0.0001, respectively. These two values are chosen in this paper based on some empirical evidence from other software that implemented the EM algorithm (for example, Sklearn’s EM implementation for the GMM estimation has a default value of 100 maximum iterations and 0.001 for the average log-likelihood threshold). Choosing these values should always be based on pragmatic grounds, i.e.,
we expect that this threshold can be reached in this amount of iterations. For example, the authors of [
25] argue that even perhaps the most efficient way of managing the convergence of the EM algorithm, for the GMM parameter estimation, is to use only the specified number of iterations as stopping criteria because setting small threshold values can be hazardous in terms of the computation times due to the unboundedness of the log-likelihood function. However, in our experiments, we have observed that the REBMIX algorithm tends to estimate the initial parameters close to the final ones and we usually did not even use half of the expected iterations (see the second plot in
Figure 4). To conclude, we can safely recommend these values as starting points; however, if necessary, fine-tuning can also be applied.